Open Access Article
Open Access ArticleHigh-quality K0.47Na0.53NbO3 single crystal toward high performance transducer
Chengpeng Hua,
Hao Tian *a,
Xiangda Menga,
Guang Shia,
Wenwu Caob and
Zhongxiang Zhou*a
*a,
Xiangda Menga,
Guang Shia,
Wenwu Caob and
Zhongxiang Zhou*a
aDepartment of Physics, Harbin Institute of Technology, Harbin 150001, P. R. China. E-mail: tianhao@hit.edu.cn; zhouzx@hit.edu.cn
bMaterials Research Institute, The Pennsylvania State University, University Park, Pennsylvania 16802, USA
First published on 20th January 2017
Abstract
A large-sized, high-quality single crystal of K0.47Na0.53NbO3 was grown by the top-seeded solution growth method. A complete set of elastic, dielectric, and piezoelectric constants for a [001]C-poled K0.47Na0.53NbO3 single crystal was determined via combined resonance and ultrasonic methods. The [001]C-poled K0.47Na0.53NbO3 (KNN47) single crystal exhibits a large piezoelectric coefficient (d33 = 220 pC N−1), high coupling coefficients (k33 = 0.759 and kt = 0.702), high dielectric constants (εT11 = 2194 and εS11 = 2162), and relatively high elastic compliance constants (SE11 = 14.3 × 10−12 N m−2 and SE33 = 17.6 × 10−12 N m−2). Furthermore, a large electrical field induced strain of 0.16% was measured from the slope in the unipolar strain versus electric field dependence. The piezoelectric coefficient, 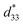 , was determined to be as high as 401 pm V−1, likely resulting due to the morphotropic phase boundary around x = 0.5. These excellent properties make KNN47 a good candidate for application as a high-performance transducer material.
, was determined to be as high as 401 pm V−1, likely resulting due to the morphotropic phase boundary around x = 0.5. These excellent properties make KNN47 a good candidate for application as a high-performance transducer material.
Introduction
Despite the favorable properties of lead-based piezoelectric materials, research on alternative lead-free piezoelectric materials has attracted a lot of attention over the last decade in order to mitigate concerns over the environmental and health effects of lead-based products in the atmosphere.1–4 Among these lead-free piezoelectric materials, potassium sodium niobate (KxNa1−xNbO3, referred to as KNNx%) based materials are one of the most promising classes for real-world applications due to their relatively good piezoelectric response and high Curie temperature (TC = 415 °C of KNN50)5 compared with other lead-free materials, such as barium titanate.6–8 However, studying the nature of KNN materials in ceramics is more challenging than similar studies on single crystals because of the presence of grain boundaries in ceramics.9Among the pure KNN materials, the composition of potassium sodium niobate with x = 0.5 is the most interesting due to the presence of a turning point in the structural parameters,10–12 a phase transition from rhombohedral to orthorhombic and orthorhombic to tetragonal,12,13 and its density,11 remanent polarization, coercive field,14 and piezoelectric coefficient, d33.15 Nearly all studies have typically focused on the monoclinic–orthorhombic morphotropic phase boundary in KNN with x = 0.5, which differs from the orthorhombic–tetragonal polymorphic phase transition in Li and Ta doped-KNN materials. The piezoelectric constant, d33, of pure KNN crystal has been reported to be as high as 160 pC N−1,16,17 with a high thickness electromechanical coupling coefficient, kt, of 0.7 in large-sized [001]C-poled Lix(Na0.5K0.5)1−xNbO3 (x ≈ 0.02) single crystals.18 For both device design and fundamental studies, it is necessary to know the complete set of piezoelectric, dielectric and elastic properties of KNN single crystals. In order to obtain a large-sized single crystal with improved piezoelectric properties, recent years have seen significant efforts to develop more effective growth methods for larger KNN single crystals.18,19 Comparing with the flux, Bridgman and solid-state single crystal growth methods, it is more difficult to manipulate the crystal growth through controlling the temperature and growth rate. It is more dependent on experience, but ignoring the thermal stress and nucleation problems during the crystal growth. In a previous work, we have reported a complete set of matrix properties for domain engineered KNN80 single crystals.20 However, it has been found that high-quality, large single crystals of KNN50 are still challenging to grow due to difficulties in controlling the compositional uniformity, amongst other factors. There have been no reports of the piezoelectric, dielectric and elastic tensor properties in pure KNN crystal around the x = 0.5 boundary. The availability of a complete set of material constants for KNN80 single crystals motivates further studies to obtain a similarly complete set of data for KNN single crystals around x = 0.5.
In this study, a sufficiently large and high-quality single crystal of KNN47, with no cracks, was grown via the top-seeded solution growth (TSSG) method of large crucible with a mount of solution to grown relatively small crystal, as shown in Fig. 1. The dimensions of the KNN47 single crystal were 9 × 9 × 35 mm3. For the first time, we report a full property matrix set for the [001]C-poled KNN47 single crystal from measured data around the x = 0.5 boundary.
Experimental procedure
Powders of K2CO3, Na2CO3, and Nb2O5 with purities of 99.99% were used as the raw materials and were mass-weighted to obtain the composition of KNN47; excess amounts of 10% (by mole) solutions of Na2CO3 and K2CO3 were added as a self-flux. The materials were mixed in a ball mill with ethanol for 24 h, and then placed into a Pt crucible and calcined at 850 °C for 6 h. The KNN47 single crystal was then grown at 1110 °C in a medium-frequency induction furnace under an air atmosphere. The velocities of rotation and pulling of the crystal were approximately 30 rpm and 4.0 mm per day, respectively. After about 5–6 days, the crystals were cooled down to room temperature at a rate of 0.5 °C min−1. The crystal structures were confirmed by X-ray diffraction (XRD) (XRD-6000, Shimadzu, Kyoto, Japan), and the strain vs. electric field (S–E) loop of the crystals was recorded using a ferroelectric test system (Precision Premier II, Radiant Technology, Inc., Albuquerque, NM, USA).For the effective macroscopic symmetry with the tetragonal point group 4 mm, there are a total of 11 independent material constants: six elastic constants, three piezoelectric constants, and two dielectric constants. All samples were oriented by a Laue X-ray machine with an accuracy of ±0.5° and cut from the same slice with uniform composition and aspect ratios. Silver electrodes were painted on the two desired surfaces of each sample, and the samples were poled under an electric field of 100–200 V mm−1 at 180 °C. Combined resonance/anti-resonance and ultrasonic methods were used to retrieve the 11 independent constants, allowing the determination of these coefficients with a high degree of self-consistency. In the resonance and anti-resonance frequency method, the electromechanical coupling factors, k15, k31, k33, kt, piezoelectric strain constants, d31, d33, and elastic compliance constants, sE11, sD11, sE33, sD33, were calculated with an Agilent, E4294A impedance-phase analyzer. The free and clamped dielectric constants, εT11, εT33, εS11, εS33, were determined from low- and high-frequency capacitance measurements. In ultrasonic measurements, a cube of sample (1.2 mm edge length) with orientation [001]C × [010]C × [100]C was used by a 15 MHz longitudinal wave transducer and a 20 MHz shear wave transducer (Panametrics Com.). Five elastic stiffness constants, cE11, cE44 (=cE55), cE66, cD33, cD44 (=cD55), and cD66, can be deduced from the phase velocities of the longitudinal and shear waves measured along [001]C, [010]C, [100]C, respectively. The density of the samples was determined by applying Archimedes' principle.
Results and discussion
Fig. 2a shows the temperature dependence of the dielectric constants of [001]C-oriented KNN47 single crystals for heating and cooling processes. It can be seen that the dielectric constants exhibit two anomalies in both the heating and cooling process. The anomalies occurred at approximately 205 °C and 428 °C for the warming process and 186 °C and 425 °C for the cooling process. These values correspond to the orthorhombic–tetragonal phase transition temperature, TO–T, and the tetragonal–cubic phase transition temperature, TC, respectively. The differences between TO–T and TC for the heating and cooling processes are approximately 19 °C and 3 °C, respectively. The orthorhombic phase structure is demonstrated from the power XRD pattern of a KNN47 single crystal, exhibiting the typical perovskite structure of an orthorhombic phase, as shown in Fig. 2b. These data show that the KNN47 single crystals exhibit an orthorhombic phase structure at room temperature and, as TO–T is far from room temperature, the properties can be determined reliably.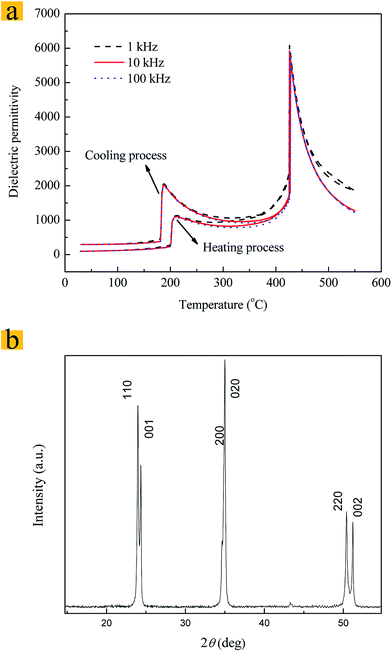 | ||
| Fig. 2 (a) Temperature dependence of dielectric constants for heating and cooling processes. (b) X-ray powder diffraction patterns of the KNN47 single crystal. | ||
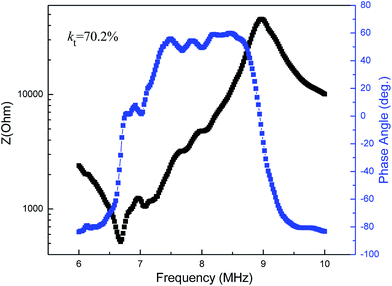
The complete set of elastic, piezoelectric, and dielectric constants for the [001]C-poled KNN47 single crystal are listed in Table 1, where they are compared to those of KNN80 and KNNT single crystals.20,22 The density was determined to be 4.412 × 103 kg m−3. The d33, d31, d15 values, which were measured using the resonance method, are 220 pC N−1, −40 pC N−1, and 60 pC N−1 along [001]C, respectively. The measured kt, k33, k31, k15 were 0.702, 0.759, 0.151, 0.120, respectively. It is of particular interest that the elastic stiffness constants of the KNN47 single crystal are much smaller than those of the KNN80 single crystal, except for CE12 and CD12. By contrast, the elastic compliance constants are much larger than those of a KNN80 single crystal, except for SE12, SE13, SD12 and SD13. Among them, SE11 and SE33 in KNN47 single crystals are over 2 times greater than those in KNN80 single crystals, which strongly indicates a greater transverse mechanical adaptability along the [100]C and [001]C direction. The KNN47 single crystal also exhibits high transverse dielectric constants, with εT11 = 2194 and εS11 = 2162. These are much higher than the longitudinal dielectric constant, εT33 = 540, and the transverse dielectric constants seen in other materials.20–23 In comparison to the electromechanical coupling coefficient in KNN80 single crystal, kt and k33 in KNN47 are significantly greater, while k31 and k15 are reduced. The impedance spectrum of electromechanical coupling coefficient, kt, which is calculated from the formula: 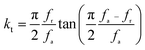 , where fr and fa represent the resonant and anti-resonant frequencies, is shown in Fig. 3.
, where fr and fa represent the resonant and anti-resonant frequencies, is shown in Fig. 3.
| Elastic stiffness constants: CEij and CDij (1010 N m−2) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Material | CE11 | CE12 | CE13 | CE33 | CE44 | CE66 | CD11 | CD12 | CD13 | CD33 | CD44 | CD66 |
| a ρ = 4.412 × 103 kg m−3. | ||||||||||||
| KNN47 | 22.2 | 18.3 | 4.6 | 6.7 | 7.7 | 7.16 | 24.1 | 20.2 | 1.1 | 13.3 | 7.8 | 7.16 |
| KNN80 | 27.4 | 15.0 | 6.2 | 14.6 | 7.9 | 8.5 | 28.3 | 15.9 | 3.0 | 26.4 | 9.1 | 8.5 |
| KNNT | 17.2 | 11.0 | 10.2 | 13.8 | 8.3 | 9.3 | 22.9 | 16.8 | 2.8 | 23.2 | 8.9 | 9.3 |
| Elastic compliance constants: sEij and sDij (10−12 N m−2) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Material | SE11 | SE12 | SE13 | SE33 | SE44 | SE66 | SD11 | SD12 | SD13 | SD33 | SD44 | SD66 |
| KNN47 | 14.3 | −11.4 | −2.0 | 17.6 | 13.0 | 14.0 | 14.0 | −11.7 | −0.2 | 7.5 | 12.8 | 14.0 |
| KNN80 | 5.4 | −2.7 | −1.2 | 7.9 | 12.7 | 12.0 | 5.2 | −2.9 | −0.3 | 3.9 | 11.0 | 12.0 |
| KNNT | 11.9 | −4.3 | −5.6 | 15.5 | 12.0 | 10.7 | 9.4 | −6.8 | −0.3 | 4.4 | 11.2 | 10.7 |
| Piezoelectric coefficients: eiλ (C m−2), diλ (10−12 C N−1), giλ (10−3 Vm N−1), and hiλ (108 V m−1) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Material | e15 | e31 | e33 | d15 | d31 | d33 | g15 | g31 | g33 | h15 | h31 | h33 |
| KNN47 | 4.6 | −5.9 | 11.1 | 60 | −40 | 220 | 3.1 | −8.3 | 46 | 2.4 | −31.5 | 59.3 |
| KNN80 | 7.4 | −3.4 | 12.3 | 93.7 | −23.2 | 104.2 | 27.1 | −8.4 | 37.6 | 13.4 | −26.6 | 97.1 |
| KNNT | 3.7 | −5.2 | 6.7 | 45 | −77 | 162 | 17.4 | −32.6 | 68.5 | 15.5 | −110.0 | 140.0 |
| Relative dielectric constants: ε (ε0), β (10−4 ε0−1) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Material | εT11 | εT33 | εS11 | εS33 | βT11 | βT33 | βS11 | βS33 |
| KNN47 | 2194 | 540 | 2162 | 211.4 | 4.56 | 18.5 | 4.63 | 47.3 |
| KNN80 | 390 | 313 | 320 | 141 | 25.6 | 31.9 | 31.2 | 70.9 |
| KNNT | 291 | 267 | 272 | 54 | 34.4 | 37.5 | 36.8 | 186 |
| Electromechanical coupling coefficient: k | ||||
|---|---|---|---|---|
| Material | k15 | k31 | k33 | kt |
| KNN47 | 0.120 | 0.151 | 0.759 | 0.702 |
| KNN80 | 0.45 | 0.19 | 0.706 | 0.67 |
| KNNT | 0.234 | 0.46 | 0.827 | 0.646 |
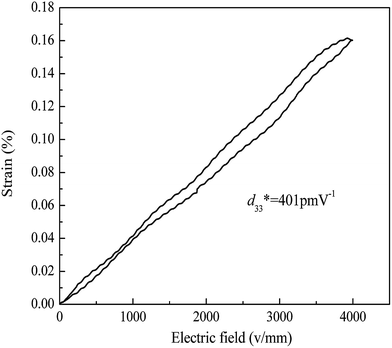
Fig. 4 shows the dependence of the unipolar strain on the applied electric field of KNN47 single crystals, under a maximum electric field of 4 kV mm−1. The curve exhibits a small hysteresis with the measurement frequency of 1 Hz. The maximum strain of 0.16%, and corresponding piezoelectric coefficient, 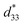 , of 401 pm V−1, derived from the slope of the strain–field curve, were obtained when the electrical field reached 4 kV mm−1. The large value of
, of 401 pm V−1, derived from the slope of the strain–field curve, were obtained when the electrical field reached 4 kV mm−1. The large value of 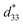 , which is much higher than that measured via the resonance method (220 pC N−1) and Berlincourt method (250 pC N−1), is likely due to the morphotropic phase boundary around x = 0.5. A brief comparison of the properties of KNN based materials is made in Table 2. The value of
, which is much higher than that measured via the resonance method (220 pC N−1) and Berlincourt method (250 pC N−1), is likely due to the morphotropic phase boundary around x = 0.5. A brief comparison of the properties of KNN based materials is made in Table 2. The value of 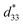 is much higher than those reported in ref. 24 and 25. At this time, the electromechanical coupling coefficient, kt = 0.702, is the highest of any reported in the literature for KNN-based materials.
is much higher than those reported in ref. 24 and 25. At this time, the electromechanical coupling coefficient, kt = 0.702, is the highest of any reported in the literature for KNN-based materials.
| Materials | d33 (pC N−1) | kt (%) | k33 (%) | εT33 (ε0) (1 kHz) | TC (°C) | Ref. |
|---|---|---|---|---|---|---|
| a Determined by resonance method.b Measured by d33 meter.c Calculated from the slope of high field strain curve. | ||||||
| KNN47 | 220a, 250b, 401c | 70.2 | 75.9 | 540 | 428 | This work |
| KNN80 | 104.2a, 110b | 67 | 70.6 | 313 | 455 | 20 |
| KNNT | 162a, 200b | 64.6 | 82.7 | 267 | 291 | 21 |
| Mn-doped KNN | 161b | — | 64 | 424 (10 kHz) | 407 | 26 |
| KNN | 160b | 45 | — | 240 | 393 | 16 |
| 0.95KNN–0.05LiNbO3 | 405b | 61 | — | 185 | 426 | 18 |
| KNN47 | 110c | — | — | 600 | 390 | 24 |
| LF4T | 416a, 750c | 61 (kp) | — | 1570 | 253 | 5 |
| PZT4 | 410b, 700c | 60 (kp) | 2300 | 250 | 5 | |
Conclusion
In summary, we have grown a large-sized, high-quality KNN47 single crystal using the top seeded solution growth method. In order to better understand the properties of KNN47 single crystal, a complete set of elastic, dielectric, and piezoelectric constants for a [001]C-poled KNN47 single crystal has been determined via combined resonance and ultrasonic methods. The [001]C-poled KNN47 single crystal exhibits a large piezoelectric coefficient (d33 = 220 pC N−1, which is the highest in pure KNN materials), high electromechanical coupling coefficients (k33 = 0.759 and kt = 0.702, which are at the highest range), high dielectric constants (εT11 = 2194 and εS11 = 2162), and relatively high elastic compliance constants (SE11 = 14.3 × 10−12 N m−2 and SE33 = 17.6 × 10−12 N m−2). Furthermore, a large electrical field induced strain of 0.16% was measured. The piezoelectric coefficient,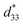 , was measured to be as high as 401 pm V−1, likely arising due to the morphotropic phase boundary around x = 0.5. These excellent properties make this KNN47 single crystal an ideal candidate for application as a high-performance transducer material.
, was measured to be as high as 401 pm V−1, likely arising due to the morphotropic phase boundary around x = 0.5. These excellent properties make this KNN47 single crystal an ideal candidate for application as a high-performance transducer material.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 50902034, 11074059, and 61205011), the Science Fund for Distinguished Young Scholars of Heilongjiang Province (Grant No. JC200710), and the Program for Innovation Research of Science at the Harbin Institute of Technology (No. B201504). The authors wish to thank the Laboratory of Micro-Optics and Photonic Technology of Heilongjiang Province for help with the experiments.References
- Q. M. Zhang, H. Wang, N. Kim and L. E. Cross, J. Appl. Phys., 1994, 75, 454–459 CrossRef CAS.
- C. He, X. Z. Li, Z. J. Wang, Y. Liu, D. Q. Shen, T. Li, X. F. Long and Z. G. Ye, CrystEngComm, 2012, 14, 4513–4519 RSC.
- Y. Liu, X. Z. Li, Z. J. Wang, C. He, T. Li, L. D. Ai, T. Chu, D. F. Pang and X. F. Long, CrystEngComm, 2013, 15, 1643–1650 RSC.
- R. M. Fernando, D. C. Adolfo, L. J. Rigoberto, J. R. Juan and F. F. José, J. Mater. Chem., 2012, 22, 9714 RSC.
- Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84–87 CrossRef CAS PubMed.
- E. Hollenstein, M. Davis, D. Damjanovic and N. Setter, Appl. Phys. Lett., 2005, 87, 182905 CrossRef.
- J. Rodel, W. Jo, K. T. P. Seifert, E.-M. Anton, T. Granzow and D. Damjanovic, J. Am. Ceram. Soc., 2009, 92, 1153 CrossRef.
- K. Wang, F.-Z. Yao, W. Jo, D. Gobeljic, V. V. Shvartsman, D. C. Lupascu, J.-F. Li and J. Rodel, Adv. Funct. Mater., 2013, 23, 4079 CrossRef CAS.
- H. Deng, X. Y. Zhao, H. W. Zhang, C. Chen, X. B. Li, D. Lin, B. Ren, J. Jiao and H. S. Luo, CrystEngComm, 2014, 16, 2760 RSC.
- V. J. Tennery and K. W. Hang, J. Appl. Phys., 1968, 39, 4749–4753 CrossRef CAS.
- B. P. Zhang, J. F. Li, K. Wang and H. Zhang, J. Am. Ceram. Soc., 2006, 89, 1605–1609 CrossRef CAS.
- M. Ahtee and A. M. Glazer, Acta Crystallogr., 1976, 32, 434–446 CrossRef.
- L. Egerton and D. M. Dillon, J. Am. Ceram. Soc., 1959, 42, 438–442 CrossRef CAS.
- G. H. Haertling, J. Am. Ceram. Soc., 1967, 50, 329–330 CrossRef CAS.
- L. Wu, J. L. Zhang, C. L. Wang and J. C. Li, J. Appl. Phys., 2008, 103, 084116 CrossRef.
- D. Lin, Z. Li, S. Zhang, Z. Xu and X. Yao, Solid State Commun., 2009, 149, 1646–1649 CrossRef CAS.
- H. Tian, C. Hu, X. Meng, P. Tan, Z. Zhou, J. Li and B. Yang, Cryst. Growth Des., 2015, 15, 1180 CAS.
- K. Chen, G. S. Xu, D. F. Yang, X. F. Wang and J. B. Li, J. Appl. Phys., 2007, 101, 044103 CrossRef.
- H. Ursic, A. Benĉan, M. Skarabot, M. Godec and M. Kosec, J. Appl. Phys., 2010, 107, 033705 CrossRef.
- H. Tian, C. Hu, X. Meng, Z. Zhou and G. Shi, J. Mater. Chem. C, 2015, 3, 9609–9614 RSC.
- L. Zheng, X. Huo, R. Wang, J. Wang, W. Jiang and W. Cao, CrystEngComm, 2013, 15, 7718–7722 RSC.
- B. Jaffe, W. R. Cook and H. Jaff, Piezoelectric Ceramics, Academic, New York, 1971 Search PubMed.
- D. A. Berlincourt, D. R. Curran and H. Jaffe, Physical Acoustics: Principle and Methods, Academic, New York, 1964 Search PubMed.
- Y. Kizaki, Y. Noguchi and M. Miyayama, Key Eng. Mater., 2007, 350, 85–88 CrossRef CAS.
- F. Z. Yao, K. Wang and J. F. Li, J. Appl. Phys., 2013, 113, 174105 CrossRef.
- Y. Inagaki and K. I. Kakimoto, Appl. Phys. Express, 2008, 1, 061602 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |