Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new potential energy surface for the ground state of the LiH2+ system and dynamic studies on LiH+(X2Σ+) + H(2S) → Li+(1S) + H2(X1Σ+g)
Man Dong,
Wentao Li,
Di He and
Maodu Chen *
*
Key Laboratory of Materials Modification by Laser, Electron, and Ion Beams, Ministry of Education, School of Physics and Optoelectronic Technology, Dalian University of Technology, Dalian 116024, PR China. E-mail: mdchen@dlut.edu.cn
First published on 20th January 2017
Abstract
The dynamic properties of the title reaction calculated by classical and quantum methods show large deviations from each other, whereas for the barrierless and exothermal reaction two methods should show good agreement. In order to further investigate the reaction mechanism of the title reaction, a global PES for the electronic ground state was constructed. The energy points are calculated by the multireference configuration interaction method with aug-cc-pVQZ and cc-pwCVQZ basis sets for H and Li atoms, respectively. The neural network approach is adopted in the fitting process. The classical and quantum methods are applied in the dynamic calculation based on the new PES. As expected, the dynamic properties obtained by these two methods are in good agreement with each other. In addition, two reaction mechanisms were found. When the energy is below 0.2 eV the insert reaction mechanism is dominant, and this changes to the abstract reaction mechanism as the energy increases.
1. Introduction
Lithium chemistry has received more and more attention in recent years because of its significant role in the evolution of the original universe. LiH and LiH+ are formed by the radiative association reactions of lithium chemistry. LiH molecule reacted with atomic hydrogen is recognized as an important pathway for the depletion of LiH. It is noted that LiH at low redshift is mainly ionized, therefore, for a normal lithium chemistry model the ionization process should be considered. LiH+ reacted with atomic hydrogen is recognized as an important pathway to effectually reduce the abundant LiH+. Because of the system's physical significance, lithium hydride and its ionic counterpart, LiH+, have attracted the attention of theorists and experimentalists for many years.The potential energy surfaces (PES) of the LiH2+ system have received extensive attention in recent years. Many groups1–11 have carried out lots of work both on the ground state and first excited state PES of the LiH2+ system. Among these groups, three-dimensional PES for the ground and first excited states, which were constructed by Martinazzo et al.,4 have been widely applied.12–28 The PES is based on 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ab initio points calculated using a multireference valence bond approach and extended with 600 points computed by multireference configuration interaction (MRCI) method in combination with a large basis set. Recently the PES of the LiH2+ system were reported by He et al.11 In their work, the ab initio points were calculated using the complete active space self-consistent field and MRCI method with the aug-cc-pVQZ basis set, and the dynamic calculations of the H+ + LiH ↔ H2+ + Li reactions were carried out based on the first excited state PES.
000 ab initio points calculated using a multireference valence bond approach and extended with 600 points computed by multireference configuration interaction (MRCI) method in combination with a large basis set. Recently the PES of the LiH2+ system were reported by He et al.11 In their work, the ab initio points were calculated using the complete active space self-consistent field and MRCI method with the aug-cc-pVQZ basis set, and the dynamic calculations of the H+ + LiH ↔ H2+ + Li reactions were carried out based on the first excited state PES.
With the aspect of dynamic calculations, the H+ + LiH ↔ H2+ + Li reactions based on the first excited state PES have received more attention than the reactions on the ground state PES. The H + LiH+ scattering reaction on the ground state PES may lead to the following products:
| H + LiH+ → H2 + Li+ (depletion, R1) |
| H + LiH+ → LiH+ + H (exchange, R2) |
| H + LiH+ → H + LiH+ (no reaction) |
| H + LiH+ → H + H + Li+ (collision induced dissociation, CID) |
The H + LiH+ scattering reaction is a barrierless and strongly exoergic process. Owing to the low binding energy of LiH+ molecular (D0 ≈ 0.112 eV) the three body break-up channel seems to make the primary contribution at moderate collision energies. However, the total CID probability was below 0.07 when the collision energy was below 1 eV as reported by Bodo et al.,22 and the branching ratio of H + H + Li+/H2 + Li+ reported by Yang et al.27 was below 1 in the low collision energy range. We can conclude that the H2 + Li+ channel plays a dominant role in the low collision energy range. Although the H + LiH+ reaction has been studied by quantum method (QM)22,25,28 and quasi-classical trajectory (QCT),23,24,26,27 as far as we know, there is no theoretical investigation of the H + LiH+ reaction at the state-to-state level of theory. The H + LiH+ reaction is essentially barrierless and exothermal. For such reactions, the QCT values should be closer to the QM results, especially in the high collision energy range. Whereas, the integral cross sections (ICS) obtained by Roy et al.25 (QM) and Pino et al.23 (QCT) show large deviations. So, to further understand the title reaction, it is necessary to check out both QCT and QM results. The ground state PES of Martinazzo et al.,4 which was adopted in the calculations of Roy et al.25 and Pino et al.,23 was without any correction for the basis set superposition error and the analytic fitting was globally optimized, meaning that the ground state PES has space to further improve. For the barrierless and highly exothermic reaction, the quantum wave packet may be more sensitive to the topography of the PES, especially in the low collision energy range. So, it is necessary to construct a new PES that is more accurate to further understand the reaction mechanism.
In this work, a new global PES for the ground state of the LiH2+ system was constructed and the time-dependent wave packet (TDWP) and QCT methods are employed for the dynamics study of the LiH+(X2Σ+) + H(2S) → Li+(1S) + H2(X1Σ+g) reaction based on the new PES. This article is organized as follows: the theoretical method will be introduced in Section 2; in Section 3, we will discuss the results; the conclusions are presented in Section 4.
2. Methods
2. 1. Potential energy surface
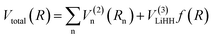 | (1) |
R is a collective variable of the internuclear distances, V(2)n (n = HH, LiHa, LiHb) is the diatomic potential, Rn is the bond length between the two atoms, and V(3)LiHH presents the three-body term. f(R) is a switch function, which is used for the purpose of having a better description for the PES in the asymptotic area, and it can be presented as below:
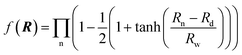 | (2) |
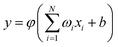 | (3) |
2. 2. Dynamic method
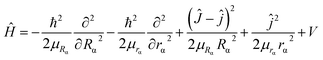 | (4) |
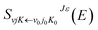
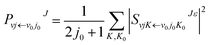 | (5) |
The state-to-state ICSs and differential cross sections (DCS) are calculated by:
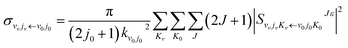 | (6) |
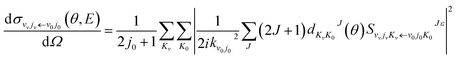 | (7) |
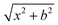 , where b is the impact parameter and x was set to 20.0 bohr. When the collision energy was below 0.3 eV, the maximum impact parameter (bmax) was set to 15.0 bohr and it was set to 12.0 bohr when the collision energy was larger than 0.3 eV. The orientation of the LiH+ ion was randomly sampled and b was selected randomly from the distribution
, where b is the impact parameter and x was set to 20.0 bohr. When the collision energy was below 0.3 eV, the maximum impact parameter (bmax) was set to 15.0 bohr and it was set to 12.0 bohr when the collision energy was larger than 0.3 eV. The orientation of the LiH+ ion was randomly sampled and b was selected randomly from the distribution 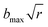 , where r is a random number uniformly distributed from 0 to 1. Roughly 3
, where r is a random number uniformly distributed from 0 to 1. Roughly 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600
600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run using the velocity-Verlet integration algorithm with a time step of 0.073 fs for a maximum time of 100 ps. The trajectories were terminated when the distance of the two fragments became larger than 20 bohr.
000 trajectories were run using the velocity-Verlet integration algorithm with a time step of 0.073 fs for a maximum time of 100 ps. The trajectories were terminated when the distance of the two fragments became larger than 20 bohr.3. Results and discussion
3. 1. Potential energy surface
The equilibrium position and dissociation energy for the ground electronic state of LiH+ and H2 molecules, which were obtained from the new PES, are displayed in Table 1. In order to compare with previous literature conveniently, the theoretical values obtained by Magnier,31 Page9 and Prudente et al.32 as well as the experimental data33 are also collected in Table 1.The spectroscopic constants of the diatomic molecules are calculated when the super-molecule is far from the other atom at a distance of 50 Å. As shown in Table 1, the equilibrium positions and dissociation energies of LiH+ and H2 molecules show good agreement with previous theoretical investigations. There is no experimental data for LiH+ ion as far as we know, so it is difficult to figure out whether the spectroscopic constants that were obtained in the present work are more accurate than previous reports or not. However, for H2 molecule, the present spectroscopic constants are more accurate than those of Page et al.9 and Prudente et al.32 The equilibrium position obtained by the present work is the same as the experimental data33 and the deviation of the dissociation energy from the experimental data33 is only 103.56 cm−1.
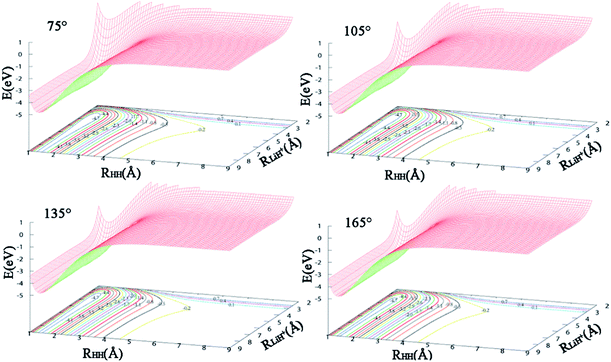
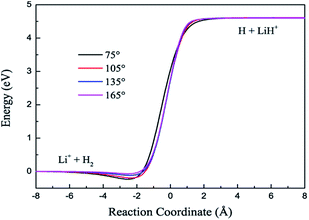
The contours of the ground state PES for the title reaction in internal coordinates at four fixed approaching angles (75°, 105°, 135°, 165°) are listed in Fig. 1. Two valleys exist in each figure: the Li+ + H2 product channel is in the left valley and the reactant channel of H + LiH+ is in the other valley. The left channel is deeper than the right one, so the LiH+(X2Σ+) + H(2S) → Li+(1S) + H2(X1Σ+g) reaction is exothermic and there are no barriers in these PESs. We also can see that the minimum energy paths (MEPs) from the LiH+ + H to the Li+ + H2 are smooth for different H–Li–H angles. In order to see clearly, Fig. 2 shows the MEPs at four approaching angles (75°, 105°, 135°, 165°). As shown in Fig. 2, the title reaction is exothermic and the exothermic energy is about 4.599 eV, which is consistent with previous theoretical literature.4 Besides, all the MEPs are exiting a well with depths of about 0.232, 0.195, 0.116 and 0.067 eV, which corresponds to 75°, 105°, 135°, and 165°, respectively.
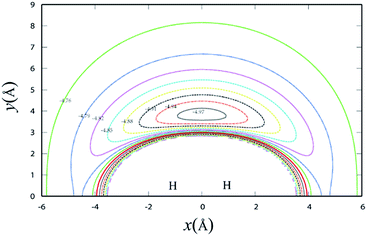
Fig. 3 shows the potential energy plot for the Li+ ion moving around the H2 molecule with a fixed bond length at the equilibrium distance RHH = 0.7414 Å. The energy is set as zero, when the H atom is far from the LiH+ molecule. For the title reaction, as the Li+ ion moves slowly to the H2 diatom, it is attracted to the well at about 0.23 eV, which is located at x = 0.0 Å, y = 3.83 Å. Therefore, it is expected that the insertion reaction plays an important role at the low collision energy range. Similar to Fig. 3, Fig. 4 shows the potential energy for the H atom moving around the LiH+ ion of which the bond length is fixed at the equilibrium distance. As shown in Fig. 4, it is apparent that the H + LiH+ reaction is an exothermal reaction and there is also a well located at about x = −2.4 Å, y = 0.5 Å and the depth of the well is about 0.35 eV.
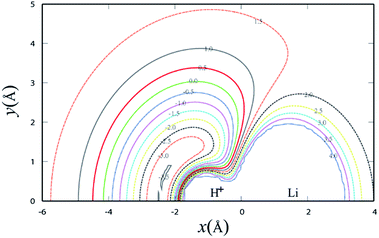 | ||
| Fig. 4 Contour plot for H atom moving around a fixed LiH+ diatom in equilibrium geometry RLiH = 2.196 Å. Contours are starting from −3.5 to 4.0 eV with equal energy spacing 0.5 eV. | ||
3. 2. Dynamic calculation
The reaction dynamics of the title reaction based on the new PES were determined by TDWP method with a second order split operator. The details of the TDWP method can be found in previous literature.34,35 Extensive convergence tests were carried out on the new PES with the total reaction probability of J = 0. The numerical parameters that were applied in the calculations are summarized in Table 2, and the same parameters were used for all J > 0 calculations. To get converged results, 205 translational basis functions were used covering the range 0.01 ≤ R/a0 ≤ 18, and 205 vibrational basis functions covering the range 0.01 ≤ r/a0 ≤15. The number of the rotational basis functions is 140. The propagation time was set to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. For the H + LiH+ reaction, the total angular momentum range is from 0 to 60.
000 a.u. For the H + LiH+ reaction, the total angular momentum range is from 0 to 60.
| Grid range and size | R ∈ [0.01, 18] | NtotR = 205 | NintR = 165 | ||
| r ∈ [0.01, 15] | Ntotr = 205 | Nintr = 139 | |||
| Angular basis j | [0, 140] | ||||
| Initial wave packet | E0 = 0.6 eV | δ = 0.4 | R0 = 14.0 | ||
| Matching plane | Rv0 = 12 | ||||
| Absorbing potential | C1R = 0.1 | C2R = 0.5 | C1r = 0.12 | C2r = 0.9 | |
| n = n′ = 2 | Ra = 14.5 | Rb = 17 | ra = 12 | rb = 14.5 | |
| Total propagation time | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
The total reaction probabilities of several selected angular momentum J are collected in Fig. 5 as a function of collision energy. The title reaction is an exothermic reaction, so there is no threshold exit for J = 0 and the threshold emerges as J increases, which can be attributed to the increasing centrifugation potential. As shown in Fig. 5, we also found that the larger J always have relative small reaction probabilities. We suppose that may be because the large centrifugation potential helps the H atom more easily overcome the well on the reaction path without collision with the LiH+ ions. There are some mild resonances that can be attributed to the shallow well on the reaction path when the collision energy is below 0.2 eV, whereas there are no resonance signals when the collision energy is above 0.2 eV. We suppose that there may be two different reaction mechanisms that are dominant in the reaction.
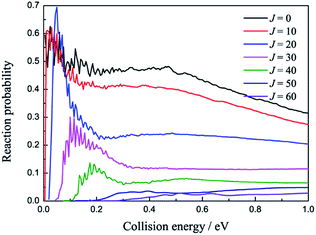 | ||
| Fig. 5 Reaction probabilities of several selected angular momentum J values as a function of collision energy. | ||
Because the title reaction is exothermic with a shallow well, the quantum effect will become apparent at the low collision energy range and it will become a direct type reaction for high collision energies. So, the QCT method will work well for such reactions. However, large deviations exist between the ICSs values obtained by Pino et al.23 (QCT) and Roy et al.25 (QM) and it is necessary to check out both QCT and QM results to further understand the reaction mechanism.
In this work we performed both QCT and TDWP calculations for the title reaction on the newly constructed PES and the ICSs obtained by these two methods, and the results reported by Pino et al.25 and Roy et al.27 are also listed in Fig. 6. As shown in Fig. 6, the QCT values obtained by Pino et al.23 are in good agreement with the present QCT values when the collision energy is below 0.1 eV. However, the deviations become larger as the collision energy increases. We suppose this can be attribute to the different PES adopted in the calculations. Comparing the results obtained by Roy et al.25 with the present TDWP and QCT values, large deviations exist. The ICS value of the H + LiH+ reaction is high at low collision energy, and then decreases as the collision energy increases. This feature is similar to the reaction of H + LiH.36–38 It is owing to the same mass of the atoms and similar PES. Like the H + LiH+ reaction, the H + LiH reaction is barrierless and exothermal.The possible reasons for this are as follows: firstly, different PESs were applied in the calculations. Secondly, the CS approximate theme was adopted in their work. Thirdly, different parameters were employed in the calculations, which may affect the calculated values greatly. As expected, the present QCT values are in good agreement with the TDWP values. However, there are also large deviations in the low collision energy region. This may be because a well exists and the quantum effect will be apparent in the low collision energy region and the QCT method cannot obtain accurate results.
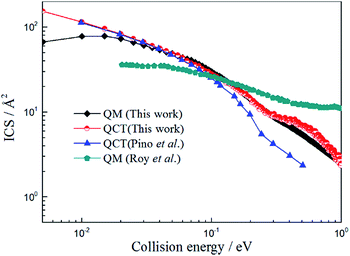 | ||
| Fig. 6 Total integral cross section of H + LiH+ reaction calculated by TDWP and QCT methods. To conveniently compare with previous theoretical studies, the values obtained by Pino et al.23 (QCT) and Roy et al.25 (QM) are also collected in the figure. | ||
The DCSs of the title reaction are displayed in Fig. 7 for some selected collision energies. As discussed above, there may be two reaction mechanisms in the reaction. So, we chose some collision energies below 0.2 eV in the left panel and some collision energies higher than 0.2 eV in the right panel. As shown in Fig. 7, the QCT results are in good agreement with the QM values. In the left panel, there is both forward and backward scattering, and bias to the forward scattering. It may indicate that the reaction is an insertion reaction and the complex has a short life. In the right panel, there are only forward scattering signals and the backward signals have almost disappeared. This may imply that the direct abstract mechanism dominates in the reaction. The H atom hit against the LiH+ ion, taking away the H atom and forming a H2 molecule directly.
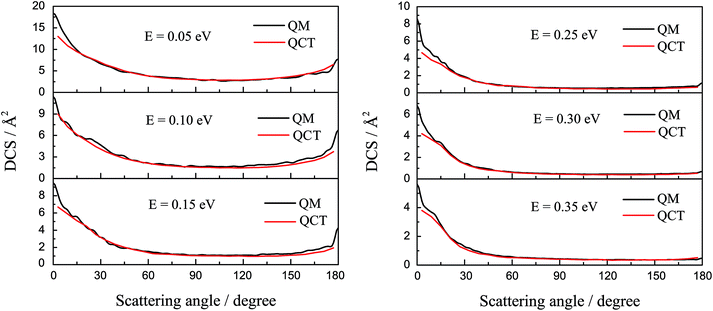 | ||
| Fig. 7 The differential cross section of the title reaction calculated by TDWP and QCT methods for some selected collision energies. | ||
To figure out the reaction mechanism of the title reaction, we plotted the forward scattering and backward scattering as a function of collision energy, which corresponded to 0° and 180°, respectively. As shown in Fig. 8, when the collision energy is below 0.2 eV, there is both forward scattering and backward scattering. Only forward scattering exists when the collision energy is above 0.2 eV. This may also indicate that the reaction mechanism changed from indirect to direct, which is consistent with the above discussion.
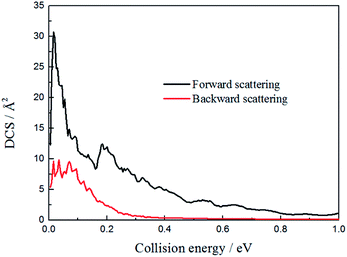 | ||
| Fig. 8 The forward and backward scattering for the H + LiH+ system as a function of collision energy. | ||
4. Conclusions
A global PES for the ground state of the H + LiH+ system was constructed. The topographical features of this new PES are discussed in detail through elaborating the PES at four different angles. The reaction dynamics calculations of the title reaction based on the new PES were also performed by QCT method and quantum TDWP approach with a second order split propagator. The reaction probability, ICSs and DCSs of the H + LiH+ reaction were calculated and the ICSs values obtained by the present work were compared with previous theoretical reports. The QCT results obtained by Pino et al. basically agree with the present QCT and TDWP values, whereas larger deviations exist between the present work and the results reported by Roy et al., maybe because of the CS approximate theme that was adopted in their work, or different PESs were used in the dynamic calculations leading to the deviations. The present values calculated by QCT and TDWP methods are in good agreement with each other, except for the low collision energy range in which the quantum effects are obvious. There are both forward and backward scattering signals when the collision energy is below 0.2 eV and only forward signals exist as the collision energy further increases. The results indicated that when the collision energy is below 0.2 eV, the reaction mechanism is dominated by the insert reaction type. When the collision is higher than 0.2 eV, the reaction mechanism changes from indirect to direct, and the abstract reaction type holds a dominant position in the reaction.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11374045), and Program for New Century Excellent Talents in University (Grant No. NCET-12-0077).Notes and references
- D. J. Searles and E. I. von Nagy-Felsobuki, Phys. Rev. A, 1991, 43, 3365–3372 CrossRef CAS.
- E. Bodo, F. A. Gianturco and R. Martinazzo, J. Phys. Chem. A, 2000, 104, 11972–11982 CrossRef CAS.
- E. Bodo, F. A. Gianturco, R. Martinazzo and M. Raimond, Chem. Phys., 2001, 271, 309–321 CrossRef CAS.
- R. Martinazzo, G. F. Tantardinibc, E. Bodo and F. A. Gianturco, J. Chem. Phys., 2003, 119, 11241–11248 CrossRef CAS.
- E. Bodo, F. A. Gianturco and R. Martinazzo, J. Phys. Chem. A, 2001, 105, 10994–11000 CrossRef CAS.
- R. Martinazzo, E. Bodo, F. A. Gianturco and M. Raimond, Chem. Phys., 2003, 287, 335–348 CrossRef CAS.
- C. Sanz, E. Bodo and F. A. Gianturco, Chem. Phys., 2005, 314, 135–142 CrossRef CAS.
- W. P. Kraemer and V. Spirko, Chem. Phys., 2006, 330, 190–203 CrossRef CAS.
- A. J. Page and E. I. von Nagy-Felsobuki, J. Phys. Chem. A, 2007, 111, 4478–4488 CrossRef CAS PubMed.
- W. P. Kraemer, J. Phys. Chem. A, 2011, 115, 11313–11320 CrossRef CAS PubMed.
- X. H. He, S. J. Lv, T. Hayat and K. L. Han, J. Phys. Chem. A, 2016, 120, 2459–2470 CrossRef CAS PubMed.
- F. Gogtas, Int. J. Quantum Chem., 2006, 106, 1979–1985 CrossRef CAS.
- W. F. D. Cunha, P. R. P. Barreto, G. M. E. Silva, J. B. L. Martins and R. Gargano, Int. J. Quantum Chem., 2010, 110, 2024–2028 Search PubMed.
- F. Gogtas, J. Chem. Phys., 2005, 123, 244301 CrossRef PubMed.
- N. Bulut, J. F. Castillo, L. Banares and F. J. Aoiz, J. Phys. Chem. A, 2009, 113, 14657–14663 CrossRef CAS PubMed.
- E. Aslan, N. Bulut, J. F. Castillo, L. Banares, O. Roncero and F. J. Aoiz, J. Phys. Chem. A, 2012, 116, 132–138 CrossRef CAS PubMed.
- N. Bulut, J. F. Castillo, F. J. Aoiz and L. Banares, Phys. Chem. Chem. Phys., 2008, 10, 821–827 RSC.
- S. Bovino, T. Stoecklin and F. A. Gianturco, Astrophys. J., 2009, 708, 1560–1565 CrossRef.
- S. Bovino, M. Tacconi, F. A. G ianturco and T. Stoecklin, Astrophys. J., 2010, 724, 126–130 CrossRef CAS.
- S. Bovino, M. Wernli, F. A. Gianturco, D. Galli and F. Palla, Astrophys. J., 2011, 731, 107 CrossRef.
- E. Aslam, N. Bulut, J. F. Castillo, L. Banares, F. J. Aoiz and O. Roncero, Astrophys. J., 2012, 759, 31 CrossRef.
- E. Bodo, F. A. Gianturco, R. Martinazzo and M. Raimond, J. Phys. Chem. A, 2001, 105, 10986–10993 CrossRef CAS.
- I. Pino, R. Martinazzo and G. F. Tantardinibc, Phys. Chem. Chem. Phys., 2008, 10, 5545–5551 RSC.
- X. H. Li, M. S. Wang, C. L. Yang, L. Z. Ma, N. Ma and J. C. Wu, Chin. Chem. Lett., 2010, 21, 376–378 CrossRef CAS.
- T. Roy, T. R. Rao and S. Mahapatra, Chem. Phys. Lett., 2011, 501, 252–256 CrossRef CAS.
- X. H. Li, M. S. Wang, I. Pino, C. H. Yang and J. C. Wu, Phys. Chem. Chem. Phys., 2012, 12, 7942–7949 RSC.
- T. G. Yang, J. C. Yuan, D. H. Cheng and M. D. Chen, Communications in Computational Chemistry, 2013, 1, 15–26 Search PubMed.
- T. Roy and S. Mahapatra, Chem. Phys., 2015, 448, 34 CrossRef CAS.
- W. L. Hase, in Classical Trajectory Simulations: Initial Conditions, a chapter in Encyclopedia of Computational Chemistry, Wiley, New York, 1998, vol. 1, pp. 402–407 Search PubMed.
- W. L. Hase, in Classical Trajectory Simulations: Final Conditions, a chapter in Encyclopedia of Computational Chemistry, Wiley, New York, 1998, vol. 1, pp. 399–402 Search PubMed.
- S. Magnier, J. Phys. Chem. A, 2004, 108, 1052–1056 CrossRef CAS.
- F. V. Prudente, J. M. C. Marques and A. M. Maniero, Chem. Phys. Lett., 2009, 474, 18–22 CrossRef CAS.
- K. P. Huber and G. Herzberg, Constants of diatomic molecules, Springer, 1979 Search PubMed.
- Z. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef PubMed.
- Z. Sun, S. Y. Lee, H. Guo and D. H. Zhang, J. Chem. Phys., 2009, 130, 174102 CrossRef PubMed.
- Y. F. Liu, X. H. He, D. H. Shi and J. F. Sun, Eur. Phys. J. D, 2011, 61, 349 CrossRef CAS.
- Y. F. Liu, X. H. He, D. H. Shi and J. F. Sun, Comput. Theor. Chem., 2011, 965, 107 CrossRef CAS.
- J. C. Yuan, D. He and M. D. Chen, Phys. Chem. Chem. Phys., 2015, 17, 11732 RSC.
| This journal is © The Royal Society of Chemistry 2017 |