Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A theoretical study on the electronic and photophysical properties of two series of iridium(III) complexes with different substituted N^N ligand†
Xiaohong Shang *a,
Deming Han
*a,
Deming Han b,
Mei Liua and
Gang Zhangc
b,
Mei Liua and
Gang Zhangc
aCollege of Chemistry and Life Science, Changchun University of Technology, Changchun 130012, P. R. China. E-mail: shangxiaohong58@aliyun.com; Tel: +86 186 8650 7982
bSchool of Life Science and Technology, Changchun University of Science and Technology, Changchun 130022, P. R. China
cInstitute of Theoretical Chemistry, Jilin University, Changchun 130023, P. R. China
First published on 17th January 2017
Abstract
A density functional theory/time-depended density functional theory has been applied to explore the geometrical, electronic and photophysical properties of the recently reported pyrazolyl-pyridine- or triazolyl-pyridine-containing iridium(III) complexes 1 and 2. The calculated absorption and emission wavelengths are in agreement with experimental data. Based on complexes 1 and 2, two series of Ir(III) complexes 1a–1c and 2a–2c with different N^N ligand have been designed. It is found that the photophysical properties of these complexes are greatly affected by the properties of the adopted ligands. From 2 to 2c, the ancillary ligands based on a bis(triazolyl-pyridine) moiety with a m-phenylene spacer group render an increase of the HOMO–LUMO energy gap, but relatively weak absorption intensities. It is believed that the larger 3MC/d–d → 3MLCT/π–π* energy gap, higher μS1 and MLCT % values, as well as the smaller ΔES1–T1 for 2b and 2c, are good indications for the higher quantum efficiency compared with that of experimental structure 2. Therefore, the newly designed complexes 2b and 2c are expected to be highly efficient deep-blue emitters for OLEDs application.
1. Introduction
In extensive and on-going research into the organic light-emitting diodes (OLEDs), particular focus has been directed towards phosphorescent emitting materials due to their potential 100% internal quantum efficiency and hence the strong possibility of developing more efficient OLEDs than fluorescent emitting material based OLEDs.1,2 Strong spin–orbit coupling induced by these central transition metal atoms promotes an efficient singlet/triplet intersystem crossing, and harnesses both the singlet and triplet excitons generated from electroluminescence excitation. Homoleptic and heteroleptic Ir(III) complexes bearing the main C^N ligand have attracted much attention due to their unique photophysical properties, such as higher phosphorescence quantum efficiency and easy tuning emission energies from blue to red through substituent changes of the main ligand.3,4 In particular, iridium compounds with green and red emission have been successful as triplet emitters in phosphorescence organic light-emitting diodes (PHOLEDs).5 Highly efficient blue phosphorescent iridium complexes are of particular importance because they are essential part in the development of energy-saving full-colour displays and solid state lighting.6–10 However, the number of suitable blue iridium compounds for OLEDs applications is very limited compared to green and red iridium phosphors.11The tuning of emission colors over the entire visible spectra has been achieved by ingenious modification of the cyclometalated and/or ancillary ligands.12–15 The representative blue Ir(III) phosphors include FIrpic,16 FIr6,17 and FIrtaz,18 which consist of at least one difluorophenyl-pyridine-based ligand (dfppy), one of the well-known ligands for providing short emission wavelengths. Although the modifications of ligands have produced a hypsochromic shift versus the emission of FIrpic, their significant lowering of the quantum yield has hampered the fabrication of the highly efficient, true-blue phosphorescent OLEDs.
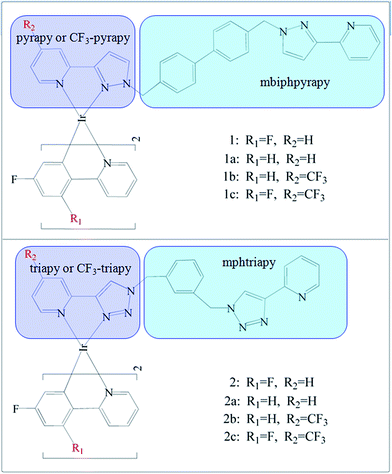
Recently, Sykes, D. et al. synthesized that blue Ir(III) complexes19 1 and 2 (Fig. 1).
The complexes form two pairs: in both 1 and 2, the phenyl-pyridine ligands are attached to Ir(III) contains two F atom substituents at positions 2 and 4 of the phenyl ring, but the bis-bidentate ligand contains pyrazolyl-pyridine chelating units in 1 is separated by a biphenyl spacer or based on a bis(triazolyl-pyridine) ligand with a m-phenylene spacer group in 2. In this work, based upon the experimental complexes 1 and 2, we designed two series of derivatives 1a–1c and 2a–2c by a systematic substitution by –F or –CF3 at “R1 and R2” positions on the ancillary (N^N) and cyclometalated (C^N) ligands, respectively. The spectroscopic properties and electron structures are crucial to gain insight into emission color change with different ancillary ligands. The main objective of this work is to explore the strategy of affecting the phosphorescent properties of these studied complexes. In particular, the influence of the employed ligands with the different electron-withdrawing abilities on quantum efficiency are also discussed, which will be of great benefit for designing novel, high efficient blue-emitting Ir(III) complexes.
2. Computational details
Density functional theory (DFT)20 method with hybrid Hartree–Fock/density functional model (PBE0) based on the Perdew–Burke–Erzenrhof (PBE)21,22 together with the 6-31G* basis set23,24 for C, H, N and F atoms and the “double-ζ” quality LANL2DZ basis set for the Ir element. An effective core potential (ECP) replaces the inner core electrons of Ir leaving the outer core [(5s)2(5p)6] electrons and the (5d)6 valence electrons of Ir(III). Singlet and triplet excitation energies have been obtained with the time dependent DFT (TDDFT) (TD-PBE0) formalism based on S0 geometries, while the S1–T1 energy gap (ΔES1–T1) was calculated considering the fixed triplet molecular geometry. Solvent effects were taken into account in DFT and TDDFT calculations using the polarized continuum model (PCM)25–28 in dichloromethane (CH2Cl2)19 media. All calculations were carried out with the default convergence criteria. The calculations mentioned above were done with the help of the D01 revision of the Gaussian 09 program package,29 Gausssum 2.5 (ref. 30) being used for UV/Vis spectra analysis and Gabedit 2.3.9 user interface31 for structures and orbitals manipulations.3. Results and discussion
3.1. Molecular geometries in ground and lowest triplet states
To investigate the solvent effect, the ground-state (S0) and triplet-state (T1) geometry optimization of all studied complexes were also performed within the self-consistent reaction field (SCRF) theory using the polarized continuum model (PCM) in dichloromethane (CH2Cl2) media to model the interaction with the solvent. Structural drawings of the investigated complexes 1–2c (1–2c indicates 1–1c and 2–2c, which are the same hereafter) are depicted in Fig. 1. Moreover, the optimized S0 geometrical structure of 1 is shown in Fig. 2, along with the numbering of some key atoms.To gain a better understanding of the structural relaxation from the S0 to T1 state, the selected optimized geometry parameters for the S0 and T1 states of 1–2c are summarized in Table 1 together with the X-ray crystal structure data of 1 and 2.
| 1 | 1a | 1b | 1c | |||||
|---|---|---|---|---|---|---|---|---|
| S0 exptl/PBE0/B3LYP | T1 | S0 | T1 | S0 | T1 | S0 | T1 | |
| a From ref. 19. | ||||||||
| Bond length/Å | ||||||||
| Ir–N1 | 2.053/2.057/2.085 | 2.031 | 2.059 | 2.055 | 2.060 | 2.052 | 2.058 | 2.050 |
| Ir–N2 | 2.047/2.054/2.079 | 2.062 | 2.054 | 2.042 | 2.055 | 2.052 | 2.053 | 2.045 |
| Ir–C1 | 1.991/1.995/2.012 | 1.978 | 1.996 | 1.991 | 1.996 | 1.978 | 1.995 | 1.983 |
| Ir–C2 | 2.008/2.005/2.021 | 2.002 | 2.005 | 2.001 | 2.005 | 1.983 | 2.004 | 1.999 |
| Ir–N3 | 2.169/2.196/2.240 | 2.213 | 2.198 | 2.161 | 2.195 | 2.170 | 2.194 | 2.152 |
| Ir–N4 | 2.158/2.196/2.252 | 2.201 | 2.199 | 2.149 | 2.202 | 2.178 | 2.201 | 2.174 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Bond angle/deg | ||||||||
| N1–Ir–C1 | 80.8/80.5/80.1 | 81.7 | 80.4 | 80.9 | 80.4 | 81.2 | 80.5 | 81.0 |
| N1–Ir–N2 | 175.2/173.4/173.4 | 174.1 | 173.3 | 175.4 | 173.1 | 177.2 | 173.3 | 176.0 |
| N1–Ir–N3 | 86.9/87.3/87.4 | 86.7 | 87.4 | 85.2 | 87.4 | 86.7 | 87.2 | 85.9 |
| 2 | 2a | 2b | 2c | |||||
|---|---|---|---|---|---|---|---|---|
| S0 exptl/PBE0/B3LYP | T1 | S0 | T1 | S0 | T1 | S0 | T1 | |
| Bond length/Å | ||||||||
| Ir–N1 | 2.044/2.053/2.080 | 2.027 | 2.055 | 2.033 | 2.056 | 2.053 | 2.055 | 2.051 |
| Ir–N2 | 2.059/2.057/2.081 | 2.066 | 2.057 | 2.065 | 2.057 | 2.052 | 2.055 | 2.051 |
| Ir–C1 | 2.005/1.997/2.015 | 1.977 | 1.999 | 1.976 | 2.000 | 1.974 | 2.000 | 1.974 |
| Ir–C2 | 2.002/2.000/2.015 | 1.996 | 2.000 | 1.996 | 2.001 | 1.987 | 1.999 | 1.989 |
| Ir–N3 | 2.176/2.209/2.261 | 2.233 | 2.209 | 2.232 | 2.206 | 2.152 | 2.204 | 2.143 |
| Ir–N4 | 2.116/2.158/2.192 | 2.164 | 2.158 | 2.164 | 2.151 | 2.144 | 2.147 | 2.145 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Bond angle/deg | ||||||||
| N1–Ir–C1 | 80.7/80.4/80.2 | 81.8 | 80.4 | 81.9 | 80.4 | 81.2 | 80.4 | 81.1 |
| N1–Ir–N2 | 171.9/173.5/173.7 | 174.4 | 173.2 | 174.3 | 173.1 | 177.1 | 173.3 | 176.9 |
| N1–Ir–N3 | 88.7/87.9/87.9 | 86.9 | 88.8 | 87.5 | 88.7 | 87.5 | 88.0 | 87.6 |
In order to check the reliability of the method used in the present calculation, B3LYP32,33 and PBE0 were also performed on the optimization of the S0 geometries for 1 and 2 based on their single-crystal X-ray structures,19 respectively. The results showed that the PBE0 functional has the best performance.
It can be seen that all complexes studied here adopt a pseudo-octahedral coordination geometry, similar to most reported Ir(III) complexes owing to the d6 configuration of the Ir(III) center. Table 1 also shows that the change of Ir–N3 and Ir–N4 bond lengths for complexes 1b, 1c, 2b and 2c has a significant influence on the ancillary ligand (N^N), which is probably due to the electron-withdrawing effect of –CF3 group and the extended π-conjugation. This may increase the π-accepting ability of pyridyl, and therefore, lead to the strengthened metal–ligand interaction. For all complexes, the metal–ligand bond distances (Ir–C1, Ir–C2, Ir–N1 and Ir–N2) show little change with the change of the cyclometalated ligands (C^N). Additionally, the Ir–C bonds lengths are generally shorter than the Ir–N ones, which can be attributed to the stronger ligand field of NHC ligands compared to the N^N ligand. Moreover, the Ir–C2 bond lengths are slightly changed (within 0.01 Å) compared with the Ir–C1 ones, while the Ir–N1 and Ir–N2 bond lengths are significantly shortened in comparison to those of Ir–N3 and Ir–N4. This indicates the strong interaction between the Ir(III) center and the C^N ligands, which may also increase the probability of charge transfer from metal to C^N ligands in 1–2c. The changes of the calculated coordination bond angle are minor (less than 1.0°) from 1 and 2 to 1a–1c and 2a–2c (Table 1).
Since both the S0 and T1 states are involved in the phosphorescence process, it is essential to discuss the geometric structures in the T1 state of the studied complexes. For the lowest lying excited state T1, a relatively large lengthening of 0.006–0.024 Å is detected for the Ir–N3 and Ir–N4 for 1, 2 and 2a in the T1 states corresponding to the S0 states, which weakens the interaction between the N^N ligand and metal. Meanwhile, the Ir–N1, Ir–N2 (except for 1, 2 and 2a), Ir–C1 and Ir–C2 bond lengths are significantly shortened compared with their corresponding ground state, resulting in the strengthened interaction between metal Ir and C^N ligands in T1 state, which suggests that the C^N ligands are more strongly bound to the Ir(III) than the N^N ligand, thus resulting in it having the most involvement in excited states and might consequently result in the decrease of metal-centered (MC) nonradiative emission and enhancement of radiative deactivation compared with 1, 2 and 2a.
3.2. Frontier molecular orbitals analysis
In order to gain in-depth information regarding the photophysical behavior of all the named complexes, it is imperative to further analyse the frontier molecular orbitals (FMOs), especially the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO). The contour plots of the HOMO and LUMO and energy levels for these complexes are shown in Fig. 3.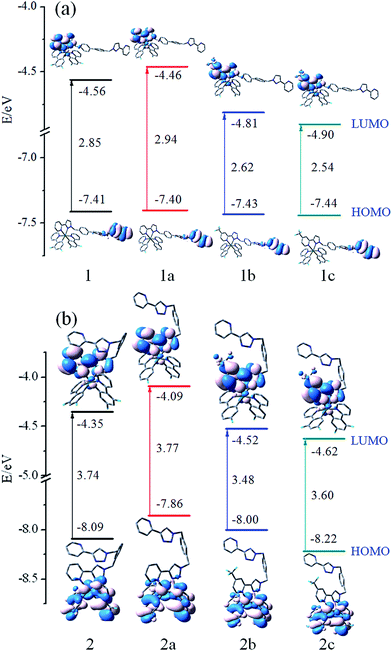 | ||
| Fig. 3 Energy level, energy gaps (in eV), and orbital composition distribution of HOMO and LUMO for the studied complexes. | ||
Furthermore, more detailed description of the molecular orbitals is collected in ESI Tables S1–S8.†
Fig. 3(a) shows that 1–1c have the similar FMOs. The HOMO is predominantly localized on π(mbiphpyrapy) moieties, while the LUMO is mainly contributed by π*(pyrapy) (for 1 and 1a) and π*(CF3-pyrapy) (for 1b and 1c). Taking 1 as an example, the HOMO is composed of 100% π(mbiphpyrapy), while the LUMO has 95% π*(CF3-pyrapy). However, the change of the ancillary ligands for complexes 2–2c has a significant influence on the electron density distributions and FMO energy levels as shown in Fig. 3(b). It can be seen from Fig. 3(b) that, for complexes 2–2c, the HOMO are both mainly localized on the π orbitals of the cyclometalated C^N ligands and d6 metal center of iridium, and the LUMO mainly reside on the π*(triapy) (for 2 and 2a) and π*(CF3-triapy) (for 2b and 2c) moieties. For the 2–2c complexes, d orbitals of Ir contribute much to the HOMO while contributing little to those LUMO, probably suggesting remarkable MLCT character for the excited states, whereas for 1–1c, the participation of the d(Ir) orbital to HOMO and LUMO is vanished (Tables S1–S4†), it is anticipated that 1–1c probably has obvious LLCT (ligand-to-ligand charge transfer) and ILCT (intraligand charge transfer) charge transfer character.
Fig. 3 shows that more –F and –CF3 groups on the complexes can efficiently stabilize the HOMO and LUMO energy levels and reduce the HOMO–LUMO energy gaps. The LUMO is destabilized more markedly than that of the HOMO. In addition, it is notable that the energy gap of 1–1c complexes are different from those of 2–2c, which is probably caused by the different degree of decrease in the HOMO and LUMO energy levels. Thus, making comparisons between 1–1c and 2–2c, it can be suspected that the change of the ancillary ligand for complexes 2–2c may make the emission band shift in the blue direction. This means that the selected ligand is very important because their HOMO and LUMO spatial distribution are closely related to the HOMO and LUMO energy levels of the complexes and will influence the emission spectra significantly. Besides, the energy gap of 2b is calculated to be 3.48 eV, which is about 0.29 eV lower than that of 2a. Simultaneously, 2c has the deepest HOMO and LUMO energy level among the studied complexes.
3.3. Absorption in dichloromethane
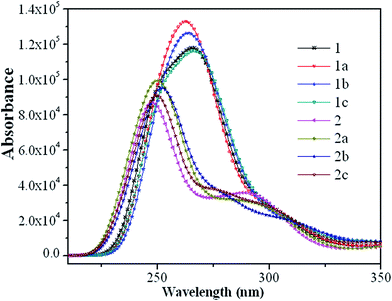
The absorption spectra of the eight guest complexes 1–2c in CH2Cl2 solvent through TDDFT/PBE0 methods have been investigated, and the corresponding results are sketched in Fig. 4.Additionally, to get the specific transition process, the related wavelengths, oscillator strengths, compositions, and transition natures of the main peaks for 1–2c are listed in Tables S9 and S10.†
As seen from Fig. 4, complexes 1–1c have the similar absorption curves in band locations in the ultraviolet region between 240–290 nm. The relatively weak absorption bands in the range 230–270 nm for 2–2c are blue-shifted by about 15 nm compared with that of 1–1c. It can also be seen from Fig. 4 that the most intense absorption bands of 1 is about 20 nm red-shifted compared with that of 2, which can be rationalized by the fact that it has the relatively small HOMO–LUMO energy gap. In the experimental spectra, lowest-lying singlet absorptions peaks for 1 and 2 are located at around 363 and 361 nm,19 respectively, while the TDDFT calculations at 366 and 371 nm (Tables S9 and S10†) agree well with the experimental data. Although, TDDFT is believed to give substantial errors for the excitation energies of charge-transfer excited states,34 in the present calculations, to a certain degree, it could predict the photophysical behavior of these Ir(III) complexes.
Complexes 1 and 1a (1b and 1c) show very similar patterns in their absorption curves, indicating that the addition of a fluoro-substituent in the phenyl of C^N ligands causes little influence on the absorption spectra of 1 and 1b, the same conclusion can also be applied to 2 and 2a (2b and 2c). Their lowest S0 → S1 excited states are mainly contributed by the transition HOMO → LUMO (96% in composition) and located at 366 and 371 nm for parent complexes 1 and 2 with negligible oscillator strengths, both of which are characterized as ILCT [π(mbiphpyrapy) → π*(pyrapy)] and MLCT(metal-to-ligand charge transfer)/LLCT [d(Ir) + π(C^N) → π*(triapy)] characters, respectively. The transition configuration of HOMO−7 → LUMO contributes to the 269 nm absorption with the largest oscillator strength for 1, which is described as the [π(C^N) → π*(pyrapy)] transition. The HOMO−1 → LUMO+2 excitation is the main configuration for 293 nm absorption of 2 with the mixed transition characters of LLCT/ILCT. For 1–1c, the transitions with the largest oscillator strengths are located at around 270 nm, and have the transition characters of [π(mbiphpyrapy) → π*(C^N)]/LLCT, with the exception of 1 and 1a, which is mainly the transition localized on the section [π(C^N) → π*(pyrapy)]/LLCT and [π(mbiphpyrapy) → π*(mbiphpyrapy)]/ILCT (Table S9, ESI†), respectively. Besides, 2–2c share the similar pattern in the absorption curves, which once again confirm that the introduction of different substituent causes little influence on the absorption properties.
3.4. Phosphorescence in CH2Cl2 media
In order to further confirm the nature of the lowest-lying emission transitions for the studied complexes, the phosphorescent emission energies at their optimized T1 geometries were calculated by the TDDFT/M062X method with PCM in the CH2Cl2 media. To obtain reliable results, six TDDFT functionals (M062X, M052X, PBE0, B3LYP, CAM-B3LYP and BP86) were examined here (Table S11†). Clearly, the emission wavelength are dramatically overrated when performed using M052X, PBE0, B3LYP, CAM-B3LYP and BP86 functionals, while the M062X gives more favorable results for parent complexes 1 and 2. The calculated lowest energy emissions for 1 and 2 at M062X level are localized at 479 and 466 nm, deviating from measured values by 25 and 22 nm. Hence, the M062X functional was employed to predict the emission spectra for other complexes.The calculated emission wavelength, configuration, transition nature, and the available experimental values are listed in Table 2.
| λ (nm) | Configuration | Character | Exptl | |
|---|---|---|---|---|
| a From ref. 19. | ||||
| 1 | 479 | L → H(81%) | π*(N^N) → π(N^N)/(ILCT) | 454 |
| 1a | 418 | L → H(90%) | π*(N^N) → π(N^N)/(ILCT) | |
| 1b | 404 | L → H(86%) | π*(N^N) → π(N^N)/(ILCT) | |
| 1c | 411 | L → H(92%) | π*(N^N) → π(N^N)/(ILCT) | |
| 2 | 476 | L → H(91%) | π*(N^N) → d(Ir) + π(C^N)/(MLCT/LLCT) | 454 |
| 2a | 487 | L → H(83%) | π*(N^N) → d(Ir) + π(C^N)/(MLCT/LLCT) | |
| 2b | 394 | L → H(87%) | π*(N^N) → d(Ir) + π(C^N)/(MLCT/LLCT) | |
| 2c | 384 | L → H(88%) | π*(N^N) → d(Ir) + π(C^N)/(MLCT/LLCT) | |
To conveniently discuss the transition property of emission, we list the partial compositions of FMO related to emission in Table S12.† The emission wavelengths are at 479 nm (for 1), 418 nm (1a), 476 nm (2) and 487 nm (2a), indicating that they are potential candidates for blue-emitting materials. A pronounced red-shift for 2a (487 nm) has been observed compared to 2 (476 nm), while a relatively larger blue-shift is detected for 2b (394 nm) and 2c (384 nm) compared to own parent. Therefore, 2b and 2c might be potential candidates for deep blue-emitting phosphorescent materials. Hence it is seen that the introduction stronger electron-withdrawing group may be an efficient strategy to tune the emitting color of 1 and 2.
Table 2 shows that the lowest-energy emissions of 1–1c originate mainly from LUMO → HOMO transition (81–92%) with characters of the π → π* intraligand (N^N) charge transfer (ILCT). Specifically, for 2–2c with two triazole ring N^N ligand, the lowest-energy emissions (476, 487, 394 and 384 nm, respectively, seen from the Table 2) originate mainly from the HOMO → LUMO transition consisting of the mixed MLCT (Ir metal to N^N ancillary ligand) and LLCT (C^N cyclometalated ligands to N^N ligand). Thus, the above-mentioned study indicated that either red or blue shifts can be observed by introducing the stronger electron-withdrawing group or changing the ancillary ligand.
3.5. Quantum efficiency
There are many parameters that can be used to evaluate the phosphorescent quantum efficiency, such as the d-orbital splitting values and radiative decay rates. In principle, the phosphorescence quantum yield ΦPL from an emissive excited state to the ground state is directly related to the radiative kr and nonradiative knr rate constants by eqn (1):
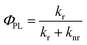 | (1) |
The knr from the T1 to the S0 states is usually expressed in the form of the energy law eqn (2),35 and the kr is given by eqn (3):36
knr ∝ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βET1) exp(−βET1)
| (2) |
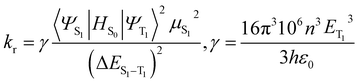 | (3) |
| ET1 (eV) | MLCT (%) | μS1 (Debye) | ΔES1–T1 (eV) | |
|---|---|---|---|---|
| 1 | 2.58 | 2.43 | 0.15 | 0.7691 |
| 1a | 2.96 | 2.70 | 0.30 | 0.1036 |
| 1b | 3.06 | 2.58 | 0.10 | 0.0539 |
| 1c | 3.01 | 2.76 | 0.20 | 0.0528 |
| 2 | 2.59 | 24.57 | 0.31 | 0.2192 |
| 2a | 2.54 | 21.58 | 0.31 | 0.1181 |
| 2b | 3.14 | 21.75 | 0.33 | 0.0413 |
| 2c | 3.22 | 23.76 | 0.32 | 0.0501 |
It is noted that the MLCT % is found to be affected by the different N^N ligand of these complexes. The change of N^N ligand, we found that the MLCT for 1–1c has almost vanished. The MLCT of 1 (2.43%) is relatively smaller than that in 2 (24.57%). The relatively large MLCT contribution is observed in 2 (24.57%), 2a (21.58%), 2b (21.75%) and 2c (23.76%).
On the other hand, the singlet–triplet energy gap ΔES1–T1 also is the factor that affects the SOC effects.39 According to eqn (3), transition moment may partially depend on the ΔES1–T1. The ISC rate decreases exponentially as the ΔES1–T1 increases,40–42 a minimal difference between the S1–T1 splitting energy ΔES1–T1 is favorable for enhancing the ISC rate, leading to an increased kr. Table 3 shows that the ΔES1–T1 for 2 is smaller, and the μS1 value, MLCT % are larger compared with 1. This behavior leads to the contribution to the total ISC rate in a photoluminescence process for complex 2, and thus a larger kr, which can also not explain their different ΦPL for 1 and 2, accordingly, the knr is also markedly affected. The designed complexes 2a, 2b and 2c have larger MLCT and smaller ΔES1–T1, and μS1 of 2a, 2b and 2c are comparable to that of other structures, therefore it was concluded that the designed complexes 2a, 2b and 2c have a favorable ISC rate which would lead to a higher kr for them. From the above discussion, it can be concluded that artificial complexes 2a, 2b and 2c with stronger SOC, better ISC rate, and faster radiative decay, may leads to the higher photoluminescent quantum yield ΦPL compared to others studied in this paper. However, besides the factors mentioned above, other factors may also play an important role for a high ΦPL, because ΦPL is the competition between kr and knr eqn (1). knr is also crucial in controlling a high quantum yield.
It's known that the higher-lying metal-centered (3MC d–d) triplet excited state is considered to be one of the most important deactivation pathways of the phosphorescent emission from T1 state.43–47 Theoretically, a larger energy separation between the 3MC d–d state and the corresponding 3MLCT/π–π* emissive state is regarded as an efficient way to reduce non-radiative transition. The 3MLCT/π–π* excited states were obtained by performing an unrestricted triplet optimization starting from the optimized ground-state geometries, while the electronic configurations of 3MC d–d state were calculated starting with a distorted molecular geometries by largely elongating the metal–ligand bonds lengths following the literature.48,49 The calculated results are shown in Fig. 5 with the normalized S0 levels.
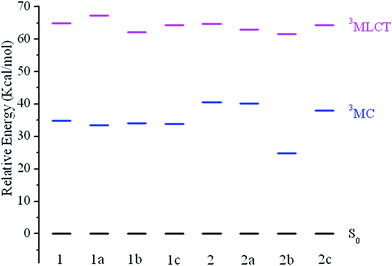 | ||
| Fig. 5 Energy level diagram of the studied complexes in 3MLCT and 3MC excited states, respectively, along with the normalized S0 levels. | ||
For all studied complexes, the 3MLCT/π–π* excited states are lying at a relatively higher energy than that of the 3MC/d–d states. This means upon excitation, the 3MC/d–d → 3MLCT/π–π* → S0 radiation less pathway is expected to be less efficient, which would result in a relatively low knr. A relationship between the –CF3 substituted R2-positions in N^N ligand and energy difference between 3MLCT/π–π* versus 3MC/d–d state can be observed (Fig. 5), in which –CF3 substitution remarkable stabilizes the 3MC/d–d states for 2b and 2c compared with 2. The energy of the 3MLCT/π–π* states only decrease slightly, while the 3MC/d–d and 3MLCT/π–π* states are hardly affected for 1b and 1c compared with 1a. As a result, 2b and 2c give a larger energy gap between 3MC/d–d and 3MLCT/π–π* states, which would lead to a lower knr, then a higher emission quantum yield.
4. Conclusions
In this article, we have carried out DFT and TDDFT investigations on the structures, spectral properties and phosphorescence efficiency of recently synthesized blue-emitting Ir(III) complexes 1 and 2 and newly designed complexes 1a–1c and 2a–2c. The calculated results showed that the substitution pattern does not have much influence on the absorption. It is found that the more –F and –CF3 groups introduced on the complexes can remarkably stabilize the LUMO energies and then lead to a smaller HOMO–LUMO energy gap. Compared with 1 and 2, the emission wavelength for 2a is red-shifted, while they are significantly blue-shifted for 1a–1c, 2b and 2c. Especially, the emission colour of the complexes 2b and 2c are in deep blue region. Apart from the lower S1–T1 energy gap (ΔES1–T1) and the larger MLCT contributions, the large transition dipole moment (μS1) and separation between 3MC/d–d → 3MLCT/π–π* states may also account for the larger kr values and are believed to play a key role in maintaining the phosphorescence quantum yield. Mentioned above, on closer inspection of the ΦPL, complexes 2b and 2c with relatively larger kr and smaller knr compared to the others can be attributed to its distinct indirect SOC paths. Thus, the assumed 2b and 2c are considered to be potential candidates of deep-blue emitting materials with high quantum efficiency.Acknowledgements
The authors thank the Science and Technology Research Project for the Twelfth Five-year Plan of Education Department of Jilin Province of China (Grant No. 2015110 and 201437) and the Program of Science and Technology Development Plan of Jilin Province of China (Grant No. 20140520090JH) and National Natural Science Foundation of China (No. 21401011).References
- W. Y. Wong and C. L. Ho, Coord. Chem. Rev., 2009, 253, 1709–1758 CrossRef CAS.
- Y. You and S. Y. Park, Dalton Trans., 2009, 1267–1282 RSC.
- S. Lamansky, P. Djurovich, D. Murphy, F. Abdel-Razaq, H.-E. Lee, C. Adachi, P. E. Burrows, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2001, 123, 4304–4312 CrossRef CAS PubMed.
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS.
- Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley-VCH, Weinheim, Germany, 2008 Search PubMed.
- B. W. D'Andrade and S. R. Forrest, Adv. Mater., 2004, 161, 585–1595 Search PubMed.
- J. Kido, M. Kimura and K. Nagai, Science, 1995, 267, 1332–1334 CrossRef CAS PubMed.
- Y. Sun, N. C. Giebink, H. Kanno, B. Ma, M. E. Thompson and S. R. Forrest, Nature, 2006, 440, 908–912 CrossRef CAS PubMed.
- K. T. Kamtekar, A. P. Monkman and M. R. Bryce, Adv. Mater., 2010, 22, 72–582 CrossRef PubMed.
- S. Reineke, F. Lindner, G. Schwartz, N. Seidler, K. Walzer, B. Lüssem and K. Leo, Nature, 2009, 459, 234–238 CrossRef CAS PubMed.
- C.-L. Ho and W.-Y. Wong, New J. Chem., 2013, 37, 1665–1683 RSC.
- A. B. Tamayo, S. Garon, T. Sajoto, P. I. Djurovich, I. M. Tsyba, R. Bau and M. E. Thompson, Inorg. Chem., 2005, 44, 8723–8732 CrossRef CAS PubMed.
- F.-M. Hwang, H.-Y. Chen, P.-S. Chen, C.-S. Liu, Y. Chi, C.-F. Shu, F.-I. Wu, P.-T. Chou, S.-M. Peng and G.-H. Lee, Inorg. Chem., 2005, 44, 1344–1353 CrossRef CAS PubMed.
- T. Matsushita, T. Asada and S. Koseki, J. Phys. Chem. C, 2007, 111, 6897–6903 CAS.
- G. J. Zhou, C. L. Ho, W. Y. Wong, Q. Wang, D. G. Ma, L. X. Wang, Z. Y. Lin, T. B. Marder and A. Beeby, Adv. Funct. Mater., 2008, 18, 499–511 CrossRef CAS.
- C. Adachi, R. C. Kwong, P. Djurovich, V. Adamovich, M. A. Baldo, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 2001, 79, 2082–2084 CrossRef CAS.
- R. J. Holmes, B. W. D'Andrade, S. R. Forrest, X. Ren, J. Li and M. E. Thompson, Appl. Phys. Lett., 2003, 83, 3818–3820 CrossRef CAS.
- S.-J. Yeh, W.-F. Wu, C.-T. Chen, Y.-H. Song, Y. Chi, M.-H. Ho, S.-F. Hsu and C.-H. Chen, Adv. Mater., 2005, 17, 285–289 CrossRef CAS.
- D. Sykes and M. D. Ward, Chem. Commun., 2011, 47, 2279–2281 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260 CrossRef CAS.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. K. Obayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision a 02, Gaussian, Inc, Wallingford CT, 2009 Search PubMed.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- A. R. Allouche, J. Comput. Chem., 2011, 32, 174–182 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Kohler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS PubMed.
- S. Haneder, E. D. Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. M€unster, C. Schildknecht and G. Wagenblast, Adv. Mater., 2008, 20, 3325–3330 CrossRef CAS.
- L. L. Shi, J. J. Su and Z. J. Wu, Inorg. Chem., 2011, 50, 5477–5484 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- I. Avilov, P. Minoofar, J. Cornil and L. De Cola, J. Am. Chem. Soc., 2007, 129, 8247–8258 CrossRef CAS PubMed.
- G. Gigli, F. Della Sala, M. Lomascolo, M. Anni, G. Barbarella, A. Di Carlo, P. Lugli and R. Cingolani, Phys. Rev. Lett., 2001, 86, 167–170 CrossRef CAS PubMed.
- D. Beljonne, J. Cornil, R. H. Friend, R. A. J. Janssen and J. L. Brédas, J. Am. Chem. Soc., 1996, 118, 6453–6461 CrossRef CAS.
- A. L. Burin and M. A. Ratner, J. Chem. Phys., 1998, 109, 6092–6102 CrossRef CAS.
- G. Treboux, J. Mizukami, M. Yabe and S. Nakamura, Chem. Lett., 2007, 36, 1344–1345 CrossRef CAS.
- F. Alary, J. L. Heully, L. Bijeire and P. Vicendo, Inorg. Chem., 2007, 46, 3154–3165 CrossRef CAS PubMed.
- J. Van Houten and R. J. Watts, J. Am. Chem. Soc., 1976, 98, 4853–4858 CrossRef CAS.
- T. Sajoto, I. Djurovich, A. B. Tamayo, J. Oxgaard, W. A. Goddard and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9813–9822 CrossRef CAS PubMed.
- D. M. Roundhill, Photochemistry and Photophysics of Metal Complexes, Plenum Press, New York, 1994 Search PubMed.
- T. Bark and R. P. Thummel, Inorg. Chem., 2005, 44, 8733–8739 CrossRef CAS PubMed.
- M. Abrahamsson, M. J. Lundqvist, H. Wolpher, O. Johansson, L. Eriksson, J. Bergquist, T. Rasmussen, H.-C. Becker, L. Hammarström, P.-O. Norrby, B. Åkermark and P. Persson, Inorg. Chem., 2008, 47, 3540–3542 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27631h |
| This journal is © The Royal Society of Chemistry 2017 |