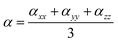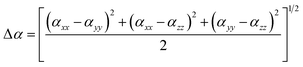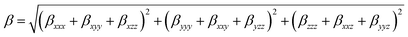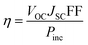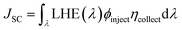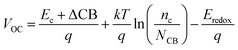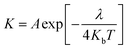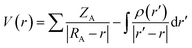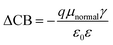DOI:
10.1039/C6RA28396A
(Paper)
RSC Adv., 2017,
7, 20520-20536
Screening and design of high-performance indoline-based dyes for DSSCs†
Received
19th December 2016
, Accepted 28th March 2017
First published on 10th April 2017
Abstract
The molecular structures and photophysical properties of three D–A–π–A dyes (WS-2, WS-92 and WS-95) were calculated based on density functional theory (DFT) and time-dependent DFT (TD-DFT). The results show that different donor (D) groups and π-spacer bridges affect the photophysical properties. WS-95 presents the highest light harvesting efficiency (LHE), maximum absorption peak, dipole moment (μnormal), electron affinity (EA), electrophilicity (ω) and electron accepting power (ω+), as well as a small natural bond orbital (NBO) charge of the electron acceptor, ionization potential (IP) and chemical hardness (h). These critical parameters have a close relationship with the open-circuit photo-voltage (VOC) and the short-circuit current density (JSC), and lead to WS-95 exhibiting higher efficiency. In order to obtain an efficient dye, we designed a series of dyes based on WS-95 and analyzed their optical and electronic properties. It was found that upon introducing a CN group into WS-95 (as in the designed molecules 1, 2, 3, 7, 8 and 9), the band gap energies of the dyes were decreased, leading to an absorption peak red-shift compared to WS-95. The structural modifications also result in an increase in the electrophilicity and electron accepting power, and a decrease in the chemical hardness. When –NH2 is introduced into WS-95 (4, 5, 6, 10, 11 and 12), the opposite trend is observed compared to dyes 1, 2, 3, 7, 8 and 9. We hope that these results will be helpful for experiments to synthesize new and highly efficient dyes.
1. Introduction
A dye-sensitized solar cell (DSSC) with a power conversion efficiency (PCE) of 7.1% was reported by Grätzel and O'Regan in 1991.1 DSSCs have received extensive attention due to their easy production, low price and flexibility, and are one of the most developed potential energy sources. DSSCs consist of a sensitizer, an electrolyte, and a photoanode and cathode. The performance of DSSCs is affected by all the components. The sensitizer is the core of the DSSC, and plays the role of absorbing photons and injecting electrons into the conduction band of the semiconductor, so its performance directly affects the PCE.
A good sensitizer should exhibit broad absorption of sunlight, and contain certain functional groups for chemical adsorption connected with the conduction band of the semiconductor (such as carboxyl groups and phosphoric acid groups, etc.). The types of sensitizers mainly include four kinds, which are synthetic organic dyes, solid dyes, natural dyes and ruthenium(II)-polypyridyl complexes.2,3 Ruthenium(II)-polypyridyl complexes exhibit a high PCE and good stability in DSSCs. For example, the PCEs of N3, N719 and black dye4 were more than 11% under air mass (AM) 1.5 irradiation. Ruthenium(II)-polypyridyl complexes also have some disadvantages, such as scarce resources of ruthenium, complex synthesis processes and relatively low yield, which are not conducive to large-scale industrial production.5 Researchers have found that ruthenium(II)-polypyridyl complexes can be replaced by metal-free organic dyes due to their environment-friendly characteristics, high molar extinction coefficient and tunable structures. A series of metal-free organic dyes such as indoline,6 the Ds series,7 cyanine,8 porphyrins,9,10 and merocyanine11 have been synthesized as photosensitizers for DSSCs. Recently, Wang et al. synthesized metal-free organic dyes, and achieved a PCE of 13%.12 At present, most of the metal-free organic dyes are donor–π spacer–acceptor (D–π–A) structures,13,14 with the donor part (D) of the molecule containing an electron-rich group. This kind of D–π–A structure can generate intramolecular charge transfer (ICT) after photoexcitation, which is beneficial for light trapping and accelerating electron injection into TiO2. A conjugation bridge is used to transfer electrons and broaden the absorption spectrum. The diversity of D–π–A structures is convenient for the design of molecules. The absorption spectra can be easily adjusted by introducing different substituents. Hosseinzadeh et al. synthesized and designed new bi-anchoring donor–π–acceptor metal-free organic dyes. Under AM 1.5 illumination (85 mW cm−2), the DSSC based on diphenylamine yielded a high PCE of 1.53% with an open-circuit photo-voltage (VOC) of 550 mV, a short-circuit current density (JSC) of 3.71 mA cm−2 and a fill factor (FF) of 0.75%.15 Lu et al. synthesized new DTP triarylamine-free organic dyes, where incorporation of 4-hexyloxyphenyl into DTP was beneficial to improving the performance of the dye. The DSSC based on X69 showed a higher PCE of 4.21% than DSSCs based on other dyes, with a corresponding short-circuit current density (JSC) of 12.1 mA cm−2, an open-circuit photo-voltage (VOC) of 0.52 V and a fill factor (FF) of 0.67.16 Ramamoorthy et al. used extracts from common pear and red tamarind and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of these as dyes. The main components of these dyes are betalain and anthocyanin. The photoelectric conversion efficiencies of betalain, anthocyanin and the mixture (1
1 mixture of these as dyes. The main components of these dyes are betalain and anthocyanin. The photoelectric conversion efficiencies of betalain, anthocyanin and the mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are 0.47%, 0.14% and 0.20%, respectively. Fourier transform infra-red, electrochemical impedance and ultraviolet-visible spectroscopy were used to analyze the photoelectric properties of the dyes.17 Ding et al. analyzed YA422, YA421 and IQ4 using DFT and TD-DFT, showing that Forster resonance energy transfer occurs only in YA422. The nearest position of every monomer in YA422 is separated by a row of Ti atoms, which is beneficial to the formation of ordered alignment. YA422 exhibits a faster electron injection rate, kinject (2.27 × 1015 s−1). Finally, they designed a promising candidate (DW1), which showed a larger kinject and strong absorption compared to YA422.18 Yang et al. designed and analyzed a series of SPL101–SPL108 dyes using DFT and TD-DFT, indicating that the π-spacer of SPL103–SPL104 is a promising functional group for D–π–A dyes. Compared with C217 dye, SPL106 and SPL108 not only have higher molar absorption coefficients and similar energy gaps, but also exhibit obvious red shifts (128 and 143 nm, respectively) and wide absorption spectra.19 Kwon et al. designed and investigated two novel D–A–π–A dyes (TICC and TICR) with ID6 dye as a reference using DFT and TD-DFT. The different LUMO levels affect the molar absorption coefficient and the absorption band of the molecule. Compared with other dyes, TICR exhibited a red shift and a broad absorption spectrum and had a higher molar extinction coefficient.20 Recently, Zhang et al. used WS-2 as a reference dye to design two novel indoline-based D–A–π–A dyes, WS-92 and WS-95 (Fig. 1). Solar cells based on WS-95 yielded a PCE of 7.69% (JSC = 16.87 mA cm−2, VOC = 696 mV, FF = 0.66).21
1) are 0.47%, 0.14% and 0.20%, respectively. Fourier transform infra-red, electrochemical impedance and ultraviolet-visible spectroscopy were used to analyze the photoelectric properties of the dyes.17 Ding et al. analyzed YA422, YA421 and IQ4 using DFT and TD-DFT, showing that Forster resonance energy transfer occurs only in YA422. The nearest position of every monomer in YA422 is separated by a row of Ti atoms, which is beneficial to the formation of ordered alignment. YA422 exhibits a faster electron injection rate, kinject (2.27 × 1015 s−1). Finally, they designed a promising candidate (DW1), which showed a larger kinject and strong absorption compared to YA422.18 Yang et al. designed and analyzed a series of SPL101–SPL108 dyes using DFT and TD-DFT, indicating that the π-spacer of SPL103–SPL104 is a promising functional group for D–π–A dyes. Compared with C217 dye, SPL106 and SPL108 not only have higher molar absorption coefficients and similar energy gaps, but also exhibit obvious red shifts (128 and 143 nm, respectively) and wide absorption spectra.19 Kwon et al. designed and investigated two novel D–A–π–A dyes (TICC and TICR) with ID6 dye as a reference using DFT and TD-DFT. The different LUMO levels affect the molar absorption coefficient and the absorption band of the molecule. Compared with other dyes, TICR exhibited a red shift and a broad absorption spectrum and had a higher molar extinction coefficient.20 Recently, Zhang et al. used WS-2 as a reference dye to design two novel indoline-based D–A–π–A dyes, WS-92 and WS-95 (Fig. 1). Solar cells based on WS-95 yielded a PCE of 7.69% (JSC = 16.87 mA cm−2, VOC = 696 mV, FF = 0.66).21
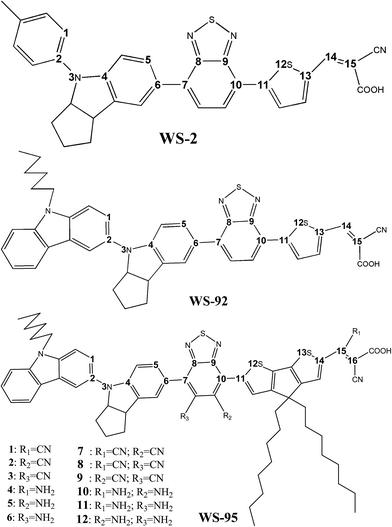 |
| | Fig. 1 Sketch map of the molecular structures. | |
In this work, in order to better explain the effects of different donor (D) units and π-spacers on the PCE. The HOMO, LUMO, energy gap, UV-Vis absorption spectra, light harvesting efficiency, ionization potential, electron affinity, reorganization energy, natural bond orbital, energy differences eVOC between ELUMO and ECB, dipole moment, chemical reactivity parameters, non-linear optical properties and injection driving force of three dyes (WS-2, WS-92 and WS-95) were studied using density functional theory (DFT) and time-dependent DFT (TD-DFT). The short-circuit current density (JSC) and open-circuit photo-voltage (VOC) were determined from these parameters. Higher JSC and VOC values are beneficial to improving the power conversion efficiency (PCE) of DSSCs. Theoretical results show that WS-95 has a high efficiency, which is in good agreement with the experimental results.21 On the basis of WS-95, we designed a series of dyes by introducing two types of electron-withdrawing group (–CN and –NH2) at different positions (R1, R2 and R3). The optical and electronic properties of all the dyes were calculated at the same level. The calculated results show that dyes with an inserted –CN group present lower band gaps and absorption spectra red-shifts, which is beneficial to improving the optoelectronic properties. We hope that our work will further help experimentalists to screen more efficient dyes.
2. Computational details
The ground state geometries of the three dyes in the gas phase and in dichloromethane solvent were fully optimized using Density Functional Theory (DFT)22 with B3LYP23–25 using the 6-31G(d) basis set. Frontier molecular orbitals are convenient to study intramolecular charge transfer (ICT).26–30 The excitation energies, oscillator strengths and UV-Vis absorption spectra of the three dyes in the gas phase and in dichloromethane solvent were simulated using Time-Dependent Density Functional Theory (TD-DFT)31 with the CAM-B3LYP32 functional using the 6-31G(d) basis set. The conductor-like polarized continuum model (C-PCM) was used to study the solvent effects, and is recognized as a reliable method to simulate the experimental values.33–35 The geometries, and optical and electrical properties of the dye/TiO2 systems were investigated using the same functional as used for the isolated dyes; here the 6-31G(d) basis set was used for C, H, O, N, and S atoms and the LANL2DZ basis set was used for Ti atoms. All calculations were performed with the Gaussian 09 package.36 The nonlinear optical properties (polarizability and hyperpolarizability) were computed using B3LYP/6-31G(d). Isotropic polarizability can be evaluated as:37| |
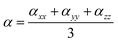 | (1) |
and the polarizability anisotropy is given by:| |
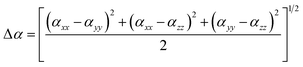 | (2) |
where αxx, αyy, and αzz are tensor components of the polarizability.The first hyperpolarizability can be calculated as:| |
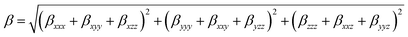 | (3) |
where βxxx, βxyy, βxzz, βyyy, βxxy, βyzz, βzzz, βxxz and βyyz are tensor components of the first hyperpolarizability. The polarizability and hyperpolarizability values have been converted into electrostatic units (esu) (α: 1 a.u. = 0.1482 × 10−24 esu; β: 1 a.u. = 8.6393 × 10−33 esu).
It is well-known that efficiency (η) is an important factor to determine the quality of a DSSC, and can be described by the following equation:38
| |
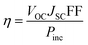 | (4) |
where
JSC is the short-circuit current density,
VOC is the open-circuit photo-voltage, FF is the fill factor and
Pinc is the incident solar power on the cell.The
JSC can be evaluated as:
39| |
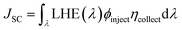 | (5) |
where
ηcollect is the charge collection efficiency;
ϕinject is the electron injection efficiency, which is related to Δ
Ginject; LHE is the light harvesting efficiency. A higher LHE is beneficial to improving the
JSC, and the LHE can be calculated as:
40where
f is the oscillator strength. According to
eqn (6), a dye with a larger
f has a higher LHE.The
VOC of a DSSC can be evaluated as:
41| |
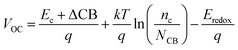 | (7) |
where
kT is the thermal energy,
Ec is the conduction band edge of the semiconductor substrate,
q is a unit of charge,
nc is the number of electrons in the conduction band,
NCB is the accessible density of conduction band (CB) states, and
Eredoox is the reduction–oxidation potential of the electrolyte.
The free energy change for electron injection (ΔGinject) affects the electron injection efficiency and JSC, and can be calculated as follows:40,42
| | |
ΔGinject = Edye* − ECB = Edye − E0–0 − ECB
| (8) |
where
Edye* is the oxidation potential of the excited state of the dye,
ECB is the conduction band (CB) edge of TiO
2 (
ECB = −4.00 eV),
Edye is the oxidation potential of the ground state of the dye, and
E0–0 is the vertical transition energy.
The reorganization energy can be used to represent the charge transfer characteristic based on the Marcus theory.43,44 The hole/electron transfer rate can be summarized as:45
| |
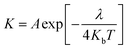 | (9) |
where
A is a pre-exponential factor,
Kb is the Boltzmann constant,
λ is the total reorganization energy and
T is the temperature. The reorganization energy can be divided into the intermolecular recombination energy and the intramolecular recombination energy.
46 The intermolecular recombination energy has no obvious effect on the charge transfer.
47 The energy of the neutral, cationic and anionic molecules can be used to calculate the reorganization energy. Hence, the intramolecular recombination energy for hole/electron (
λh/
λe) transfer can be estimated by:
48| λh = (E+0 − E+) + (E0+ − E0) = IP(v) − HEP |
| | |
λe = (E−0 − E−) + (E0− − E0) = EA(v) − EEP
| (10) |
As shown in
Fig. 2,
E0 represents the energy of the neutral molecule at the ground state,
E+0/
E−0 represents the energy of the cation/anion with the geometry of the neutral molecule, and
E0+/
E0− represents the energy of the neutral molecule with the geometry of the cationic/anionic state.
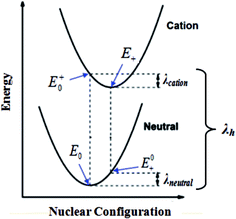 |
| | Fig. 2 Calculation of the hole reorganization energy. | |
3. Results and discussion
3.1 Geometric structures
A sketch map of the molecular structures is provided in Fig. 1, and the optimized ground-state geometries of all the studied dyes (WS-2, WS-92, WS-95) are shown in Fig. 3. Selected geometric parameters (bond lengths and bond angles) of the dyes in the ground state are listed in Table 1. For WS-2, the dihedral angles of the donor unit are very similar in the different phases (gas and solvent). WS-92 was obtained by substituting a carbazole group into the 4-methylphenyl unit of WS-2, and the dihedral angle (∠C1–C2–N3–C4) of the donor unit of WS-92 is small compared to that for WS-2. For WS-92, the dihedral angle (∠C1–C2–N3–C4) of the donor unit in the solvent is larger than that in the gas phase (by about 2.4°). The WS-95 molecule comes from the thiophene group of WS-92 being replaced with cyclopentadithiophene (CPDT). For WS-95, the dihedral angle (∠C1–C2–N3–C4) of the donor unit is larger than that of the other dyes; at the same time, the dihedral angle is decreased by 2.4° from the gas phase to the solvent. In addition, larger values of the dihedral angles (∠C5–C6–C7–C8) of all the dyes are found in the solvent. As shown in Table 1, the donor units of the three dyes exhibit distorted structures, which is beneficial for inhibiting dye aggregation on the semiconductor. The acceptor units of the three dyes have small dihedral angles, exhibiting a planar structure. The planar structure of the acceptor group is conducive to electron injection into the semiconductor conduction band. In Table 1, it can be observed that the bond lengths for the three dyes with different donor groups and π-spacers are very similar in the different phases (gas and solvent). The values of all bond lengths are smaller to the standard values (i.e. C–C: 1.530 Å (ref. 49) and N–C: 1.471 Å (ref. 50)).
 |
| | Fig. 3 Optimized molecular structures of the dyes. | |
Table 1 Selected critical bond lengths (in Å) and dihedral angles (in degrees) of WS-2, WS-92 and WS-95 in the ground state calculated using B3LYP/6-31G(d)
| |
WS-2 |
WS-92 |
WS-95 |
| Gas |
Solvent |
Gas |
Solvent |
Gas |
Solvent |
| ∠C1–C2–N3–C4 |
55.4 |
54.9 |
−24.5 |
−26.9 |
−61.9 |
−59.5 |
| ∠C5–C6–C7–C8 |
32.4 |
33.4 |
−31.6 |
−32.4 |
−33.1 |
−34.4 |
| ∠C9–C10–C11–S12 |
−0.5 |
0.7 |
−2.2 |
−2.4 |
3.0 |
2.9 |
| ∠S12–C13–C14–C15 |
179.9 |
179.8 |
179.9 |
−179.9 |
— |
— |
| ∠S13–C14–C15–C16 |
— |
— |
— |
— |
−0.5 |
−0.3 |
| C2–N3 |
1.412 |
1.413 |
1.413 |
1.413 |
1.419 |
1.418 |
| C6–C7 |
1.472 |
1.472 |
1.470 |
1.469 |
1.473 |
1.473 |
| C10–C11 |
1.456 |
1.455 |
1.455 |
1.454 |
1.455 |
1.456 |
| C13–C14 |
1.426 |
1.422 |
1.426 |
1.421 |
— |
— |
| C14–C15 |
— |
— |
— |
— |
1.423 |
1.416 |
3.2 Energy levels and frontier molecular orbital diagrams
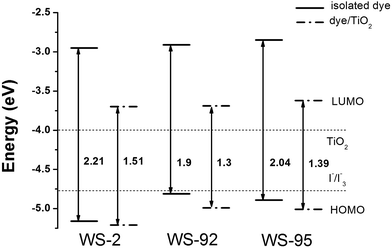
The HOMOs, LUMOs and band gap energies (ΔH–L) of the dyes and the dye/TiO2 systems are shown in Fig. 4 and 5, and the data are listed in Table S1 (see ESI Table S1).† The energy levels (HOMO and LUMO) of the dye sensitizers must match the redox potential of the I−/I3− couple and the conduction band edge level of TiO2.51,52 From Fig. 4 and 5, the LUMO levels of the dyes lie above the conduction band edge (CBE) of TiO2 (−4.0 eV), which indicates that electron injection can easily take place from the excited dyes to the TiO2 conduction band. Efficient and fast electron injection is beneficial to improving the performance of DSSCs. Meanwhile, the HOMO levels of the dyes lie below the redox potential of the I−/I3− couple (−4.80 eV),53 which ensures the charge regeneration of the dyes.
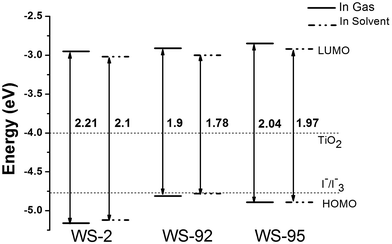 |
| | Fig. 4 The molecular energy level diagrams of the dyes in the gas and solvent phase. | |
 |
| | Fig. 5 The molecular energy level diagrams of the dyes and dye/TiO2 systems in the gas phase. | |
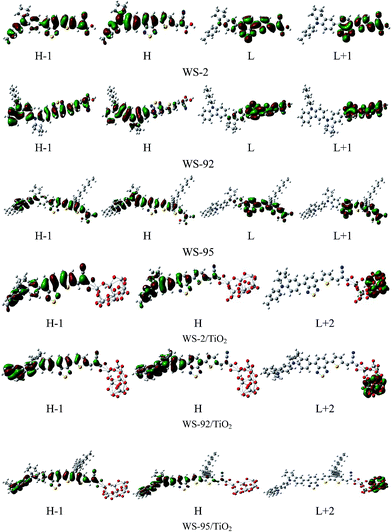
3.2.1 Isolated dyes under gas and solvent conditions. Intramolecular charge transfer (ICT) from the donor to the acceptor is a very important process that affects the performance of the whole cell device. We can understand the charge separated states by observing the frontier molecular orbitals. Frontier molecular orbital diagrams of the dyes and dye/TiO2 systems are presented in Fig. 6 (in the gas phase) and Fig. S1† (in the solvent phase). Under gas conditions, the HOMO energy level of WS-2 is −5.16 eV (see Table S1†), and the electron densities are focused over the whole dye. The HOMO−1 energy level of WS-2 is −5.88 eV below the HOMO, and has a similar electron distribution compared with the HOMO. From the character of the molecular orbitals, the HOMO and HOMO−1 are delocalized π orbitals. The LUMO energy level of WS-2 is −2.95 eV, and the electron densities of the LUMO are mostly located on the auxiliary acceptor, π-spacer and acceptor unit. The LUMO+1 lies at −2.18 eV above the LUMO, and the electron densities are concentrated on the auxiliary acceptor, π-spacer and acceptor unit. For WS-92, the HOMO energy level is −4.81 eV, which is a significant increase of 0.35 eV compared with the HOMO of WS-2. It is shown in Fig. 5 that the electron densities of the HOMO are mostly located on the donor and auxiliary acceptor unit. The HOMO−1 energy level is −5.59 eV below the HOMO, and the electron densities are concentrated over the whole dye. The LUMO energy level is −2.91 eV, and the electron densities of the LUMO are mostly located on the auxiliary acceptor, π-spacer and acceptor unit. The LUMO energies of WS-2 and WS-92 exhibit no obvious change, so it is found that enhancing the donor strength can only affect the HOMO energy level. The LUMO+1 of WS-92 has a similar electron distribution compared with the LUMO, lying at −2.14 eV above the LUMO. For WS-95, the HOMO and HOMO−1 energy levels are −4.89 and −5.31 eV, respectively, and the electron densities are both focused over the whole dye. The LUMO and LUMO+1 energy levels of WS-95 are −2.85 and −2.27 eV, respectively, and the electron densities are both focused on the auxiliary acceptor, π-spacer and acceptor unit. Compared with WS-92, the HOMO and LUMO energy levels of WS-95 exhibit no significant change, indicating that extending the π-spacer has no obvious effect on the energy levels. In conclusion, the HOMO energy levels are in the following order: WS-2 < WS-95 < WS-92, and the LUMO energy levels are in the following order: WS-2 < WS-92 < WS-95. A higher LUMO energy level will increase the open-circuit photo-voltage, leading to a higher efficiency of the DSSC. Hence, it is essential to screen the superior performance of the dye with a higher LUMO energy level.
 |
| | Fig. 6 The frontier molecular orbital diagrams of the dyes and dye/TiO2 systems in the gas phase. | |
The band gap energies (ΔH–L) are in the following order: WS-92 (1.90 eV) < WS-95 (2.04 eV) < WS-2 (2.21 eV). The band gap energy of WS-92 is smaller than that of the reference dye WS-2. Some reports show that dyes with a small energy gap exhibit better performance. For example, a dye with a small energy gap is beneficial for a maximum absorption peak red-shift and a relatively high light harvesting efficiency (LHE). From Table 2, we can see that WS-92 and WS-95 have obvious red-shifts and better LHEs compared with the reference dye WS-2.
Table 2 Computed excitation energy (Eg/eV), maximum absorption wavelength (λmax/nm), oscillator strength (f), electronic transition configuration and light harvesting efficiency (LHE) of the dyes and dye/TiO2 systems
| |
Dye |
State |
Eg/λmax |
f |
Main configuration |
LHE |
| Gas |
WS-2 |
1 |
2.571/482 |
1.2024 |
H → L/0.63819 |
0.9373 |
| 2 |
3.429/362 |
0.2491 |
H−1 → L/0.56622 |
| 3 |
3.633/341 |
0.1815 |
H → L+1/0.46443 |
| WS-92 |
1 |
2.422/512 |
1.2434 |
H → L/0.60830 |
0.9429 |
| 2 |
3.260/380 |
0.2636 |
H−1 → L/0.48947 |
| 3 |
3.507/354 |
0.2639 |
H → L+1/0.48934 |
| WS-95 |
1 |
2.395/518 |
1.7557 |
H → L/0.59868 |
0.9824 |
| 2 |
3.056/406 |
0.2120 |
H → L+1/0.44757 |
| 3 |
3.350/370 |
0.0771 |
H−1 → L/0.39667 |
| Solvent |
WS-2 |
1 |
2.456/505 |
1.4328 |
H → L/0.62034 |
0.9631 |
| 2 |
3.283/378 |
0.2340 |
H−1 → L/0.50088 |
| 3 |
3.568/348 |
0.0737 |
H → L+1/0.40612 |
| WS-92 |
1 |
2.303/538 |
1.4579 |
H → L/0.59682 |
0.9652 |
| 2 |
3.136/395 |
0.3020 |
H−1 → L/0.42328 |
| 3 |
3.403/364 |
0.0917 |
H → L+1/0.45406 |
| WS-95 |
1 |
2.288/542 |
2.0300 |
H → L/0.56468 |
0.9907 |
| 2 |
2.922/424 |
0.1329 |
H → L+1/0.45855 |
| 3 |
3.312/374 |
0.0569 |
H−1 → L+1/0.38645 |
| Gas |
WS-2/TiO2 |
1 |
2.345/529 |
1.6368 |
H → L+2/0.59591 |
0.9769 |
| 2 |
3.200/387 |
0.4725 |
H−1 → L+2/0.50278 |
| 3 |
3.315/374 |
0.0040 |
H → L/0.66319 |
| WS-92/TiO2 |
1 |
2.251/551 |
1.6082 |
H → L+2/0.57173 |
0.9754 |
| 2 |
3.088/402 |
0.4593 |
H−1 → L+2/0.33674 |
| 3 |
3.097/400 |
0.0541 |
H → L/0.65534 |
| WS-95/TiO2 |
1 |
2.250/551 |
2.4277 |
H → L+2/0.50629 |
0.9963 |
| 2 |
2.885/430 |
0.1567 |
H−1 → L+2/0.33627 |
| 3 |
3.202/387 |
0.0032 |
H → L/0.36233 |
Under solvent conditions, the energy levels have similar orbital distributions compared with those in the gas phase. As shown in Table S1,† the HOMO energy levels of WS-2, WS-92 and WS-95 are −5.12, −4.78 and −4.89 eV, respectively. There is little change in the HOMO energy levels compared with those in the gas phase. The LUMO energy levels of WS-2, WS-92 and WS-95 are −3.02, −3.00 and −2.92 eV, respectively. As shown in Fig. 4, the calculated LUMO energy levels are decreased slightly compared to those in the gas phase. Hence, the band gap energies (ΔH–L) of the dyes in the solvent are slightly lower than those in the gas phase.
3.2.2 Dye/TiO2 systems. The optimized structures of WS-2, WS-92 and WS-95 after binding the dyes onto the surface of TiO2 are listed in Tables S2–S4.† The HOMO energy levels of WS-2, WS-92 and WS-95 are −5.21, −4.99 and −5.01 eV, respectively (see Table S1†). It can be seen from Fig. 5 that the HOMO energy levels of the dye/TiO2 systems exhibit a slight decrease in comparison to the isolated dyes. The LUMO energy levels of WS-2, WS-92 and WS-95 are −3.70, −3.69 and −3.62 eV, respectively. Therefore, the LUMO energy levels are obviously decreased after the dyes are bound onto the surface of TiO2 (see Fig. 5). This shows that the LUMO energy levels of these dyes have a strong coupling with the TiO2, which is conducive to enhancing electron injection into TiO2. The band gap energies (ΔH–L) are obviously decreased after the dyes are bound onto the surface of TiO2 due to the relatively low LUMO energy level. The electron densities of the HOMO and HOMO−1 of the dye/TiO2 systems have a similar distribution compared to the isolated dyes, and the electron densities of the LUMO+2 of the dye/TiO2 systems are almost entirely concentrated on TiO2. This indicates that adsorbing the dyes onto TiO2 is beneficial to electron injection from the excited dye to the TiO2 conduction band, which leads to an increase in the short-circuit current density (JSC). The band gap energies of the dye/TiO2 systems are smaller than those of the isolated dyes, leading to the maximum absorption peaks of the dye/TiO2 systems exhibiting an obvious red-shift compared with the isolated dyes (see Table 2). A detailed discussion will be provided in the next section.Molecular electrostatic potential (MEP) is a very important tool to predict and explain chemical reactions (such as hydrogen bonding interactions), and it has a close relationship with the electron cloud. MEP and electrostatic potential are used to describe the nucleophilic and electrophilic reaction sites. As shown in Fig. 7, different colors represent different electrostatic potential values. Electrostatic potential can be calculated using the following formula:54
| |
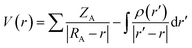 | (11) |
where
ZA is the charge of nucleus A located at
RA, and
ρ(
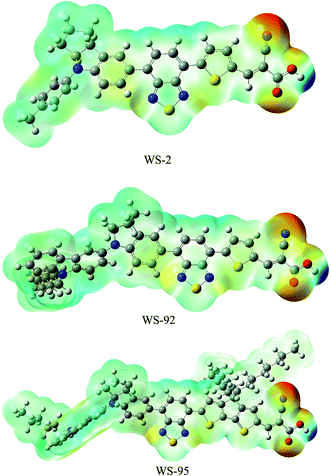
r′) is the electron density function of a molecule. It is found that the values of electrostatic potential increase in the following order: red < orange < yellow < green < blue. The red (negative) color area of the MEP implies electrophilic reactivity, and the blue (positive) color area implies nucleophilic reactivity. Negative and positive potential refer to electron-rich and electron-poor areas, respectively. The color code of the molecular electrostatic potential (MEP) maps ranges from −0.08 a.u. (deepest red) to 0.08 a.u. (deepest blue). The MEPs of the three dyes indicate that the most nucleophilic potential is found on the carboxyl hydrogen atom, with values of 0.0769, 0.0759 and 0.0735 a.u. for WS-2, WS-92 and WS-95, respectively. The greatest electrostatic potential is observed on the nitrogen atom of the –CN group, with values of −0.0655, −0.0665 and −0.0665 a.u. for WS-2, WS-92 and WS-95, respectively. Hydrogen atoms represent the strongest attraction, while nitrogen atoms represent the strongest repulsion.
 |
| | Fig. 7 Molecular electrostatic potential plots of the dyes. | |
3.3 UV-Vis absorption spectra and light harvesting efficiency (LHE)
In order to test the reliability of the theoretical results, three different functionals (CAM-B3LYP, BW97XD and LC-WPBE) combined with the 6-31G(d) basis set were used to simulate the UV-Vis absorption spectra, because the different functionals should affect the optoelectronic properties of the dyes. The conductor-like polarizable continuum model (CPCM) was selected to simulate solvent effects. The UV-Vis absorption spectra are shown in Fig. 8, and the data are listed in Table S5.† Compared with the experimental UV-Vis absorption spectra, the results show that the CAM-B3LYP functional is the closest to the experimental values (see Fig. 8 and Table S5†) among the different functionals. Kathiravan et al. used CAM-B3LYP to predict absorption maxima closer to the experimental absorption maxima values compared to other functionals.55 Many previous studies have shown that CAM-B3LYP can accurately characterize UV-Vis absorption spectra.33,56–58 Therefore, CAM-B3LYP can provide a more reliable and rational description of the UV-Vis absorption spectra, and was used to calculate the excited states of the isolated dyes and dye/TiO2 systems.
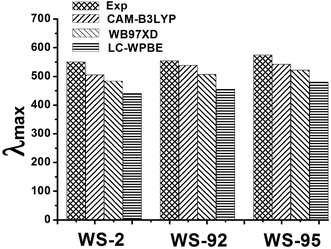 |
| | Fig. 8 The effects of different functionals on the absorption maxima (λmax/nm) of the dyes in CH2Cl2 solution. | |
3.3.1 Isolated dyes under gas and solvent conditions. The calculated oscillator strengths (f), transition energies, nature of the transitions and light harvesting efficiencies (LHEs) are listed in Table 2, and the UV-Vis absorption spectra are shown in Fig. 9 and 10. Photosensitizers with superior performances exhibit intense and wide absorption in the visible region (400–700 nm). As shown in Fig. S2,† WS-95 exhibits a broad absorption band and a high molar extinction coefficient compared with WS-2 and WS-92, resulting in the largest absorption ability for sunlight. The maximum absorption peaks of the dyes are found at 482–518 nm in the gas phase and 505–542 nm in the solvent phase. The maximum absorption peaks, oscillator strengths and light harvesting efficiencies in the gas and solvent phase are in the following order: WS-2 < WS-92 < WS-95. As shown in Table 2, the first excited states of all the dyes show a transition from the HOMO to the LUMO, and the corresponding electron transitions from the donor to the acceptor (see Fig. 6), and this is an intramolecular charge transfer (ICT). Under gas conditions, the maximum absorption peak of WS-92 red-shifts by 30 nm compared to that of WS-2, and that of WS-95 red-shifts by 6 nm compared to that of WS-92. The red-shift of the absorption peak is beneficial to increasing the open-circuit photo-voltage (VOC) and short-circuit current density (JSC), which leads to a higher photoelectric conversion efficiency (PCE) of the DSSC. Experimentally, WS-95 produced a relatively high PCE of 7.69%.21 The good optical response of WS-95 is beneficial for the improvement of the photoelectric properties of the solar cell, which supports the results of the experiment.
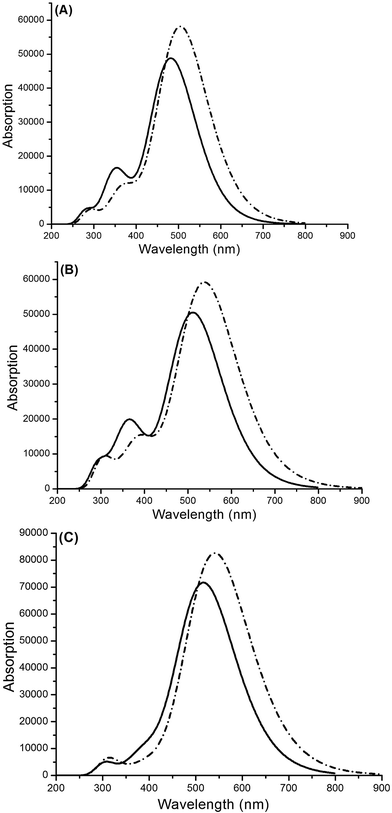 |
| | Fig. 9 Absorption spectra of (A) WS-2, (B) WS-92 and (C) WS-95 in the gas (solid line) and solvent (dotted line) phases. | |
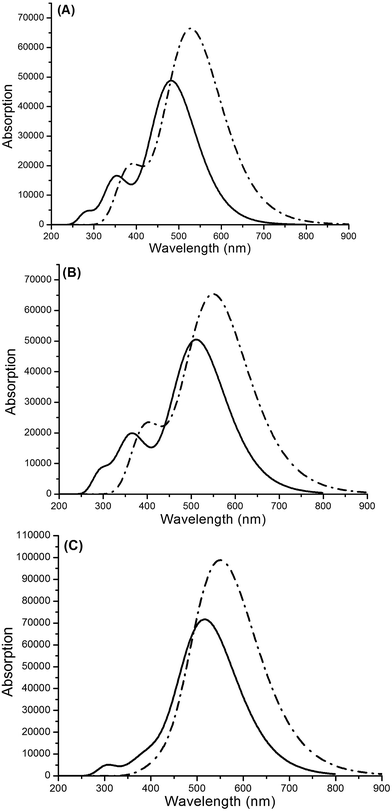 |
| | Fig. 10 Absorption spectra of (A) WS-2 (solid line) and WS-2/TiO2 (dotted line), (B) WS-92 (solid line) and WS-92/TiO2 (dotted line), and (C) WS-95 (solid line) and WS-95/TiO2 (dotted line) in the gas phase. | |
The oscillator strengths of WS-2, WS-92 and WS-95 are 1.2024, 1.2434 and 1.7557, respectively. The LHE can be calculated according to eqn (6), and the LHE values for WS-2, WS-92 and WS-95 are 0.9373, 0.9429 and 0.9824, respectively. WS-95 has the highest LHE value of all the dyes, which means that WS-95 can absorb more photons, leading to a higher JSC. The other major states (f > 0.1) of WS-2 are the S2 and S3 states, and the corresponding oscillator strengths are 0.2491 (electron transition: HOMO−1 → LUMO) and 0.1815 (electron transition: HOMO → LUMO+1), respectively. The other major states (f > 0.1) of WS-92 are the S2 and S3 states, and the corresponding oscillator strengths are 0.2636 (electron transition: HOMO−1 → LUMO) and 0.2639 (electron transition: HOMO → LUMO+1), respectively. The other major state (f > 0.1) of WS-95 is the S2 state, and the corresponding oscillator strength is 0.2120 (electron transition: HOMO → LUMO+1). As shown in Fig. 6 and Fig. S1,† for the above excited states, the electron transitions mainly include HOMO → LUMO, HOMO−1 → LUMO and HOMO → LUMO+1, and the change in electron density between the molecular orbitals shows that an electron moves from the donor to the acceptor unit, which is conducive to a high JSC. Under solvent conditions, the maximum absorption peaks are at 505, 538 and 542 nm for WS-2, WS-92 and WS-95, respectively. As shown in Fig. 9, we can see that the maximum absorption peaks of the dyes are obviously red-shifted compared with those in the gas phase, and the specific values are 23, 26 and 36 nm, respectively. As shown in Table 2, the dyes show larger oscillator strengths in the solvent phase than in the gas phase. Hence, relatively high light harvesting efficiencies of all the dyes from a solvent to a gas were found. However, solvent effects lead to a decrease in the excitation energies of all the dyes from a solvent to a gas. The other major state (f > 0.1) of the dyes is the S2 state, and the oscillator strengths are 0.2340 (HOMO−1 → LUMO), 0.3020 (HOMO−1 → LUMO) and 0.1329 (HOMO → LUMO+1) for WS-2, WS-92 and WS-95, respectively.
3.3.2 Dye/TiO2 systems under gas conditions. After the dyes were bound onto the surface of TiO2, the properties (such as maximum absorption peak, oscillator strength and LHE) of the dye/TiO2 systems were obviously changed, which may be attributed to the interaction between the dyes and the TiO2. The first excited states of all the dye/TiO2 systems show electron transfer from the HOMO to the LUMO+2. There is strong interaction between the dyes and TiO2, which facilitates electron injection from the excited dyes to the TiO2. The maximum absorption peaks of WS-2/TiO2, WS-92/TiO2 and WS-95/TiO2 are at 529, 551 and 551 nm, respectively, showing a significant red-shift compared to the isolated dyes. The oscillator strengths of the dye/TiO2 systems are in the following order: WS-92/TiO2 (1.6082) < WS-2/TiO2 (1.6368) < WS-95/TiO2 (2.4277). There is a direct relationship between the oscillator strength and the LHE. Therefore, the LHE values of all the dye/TiO2 systems follow the same trend (WS-92/TiO2 < WS-2/TiO2 < WS-95/TiO2). The oscillator strengths and LHEs of the dye/TiO2 systems are larger than those of the isolated dyes. A higher LHE facilitates the photocurrent response; therefore, WS-95/TiO2 should have a high performance. WS-95/TiO2 shows the highest oscillator strength, leading to the highest LHE (0.9963). The other major state (f > 0.1) of WS-2/TiO2, WS-92/TiO2 and WS-95/TiO2 is the S2 state, and the corresponding oscillator strengths are 0.4725, 0.4593 and 0.1567, respectively. All the dye/TiO2 systems show electron transitions from the HOMO−1 to the LUMO+2. As shown in Fig. 10, the maximum absorption peaks of all the dye/TiO2 systems show an obvious red-shift, and WS-95/TiO2 has a higher molar absorption coefficient and a broader absorption spectrum. In conclusion, the maximum absorption peaks, oscillator strengths and LHEs of all the dye/TiO2 systems present an increase after the dyes are bound onto the surface of TiO2. It should be noted that for the isolated dyes and the dye/TiO2 systems, WS-95 showed a better performance, including a higher molar absorption coefficient, oscillator strength and LHE, a broader absorption spectrum and an obviously larger red-shift of absorption. This result means that the substitution of a thiophene unit with a cyclopentadithiophene (CPDT) unit can improve the optical response and increase the utility of sunlight.
3.4 Non-linear optical (NLO) properties
In order to further study the relationship between NLO properties and efficiency, the polarizability and hyperpolarizability of the dyes were investigated, and the values are listed in Tables 3 and 4. Nonlinear optical properties characterize the response of a system to an applied electric field. Nonlinear optical properties have received wide attention owing to their larger number of applications in emerging technology areas, such as telecommunications, information storage, optical interconnections and signal processing.59,60 Generally, a dye with a higher polarizability will not only have strong interactions with surrounding species, but will also cause an increase in the local concentration of acceptor species.61 From Table 3, the isotropic polarizability values of the dyes are, in increasing order, WS-2 (65.046) < WS-92 (119.542) < WS-95 (166.860); the polarizability anisotropy values of the dyes follow a similar trend. Hence, the local concentration of acceptor species is increased at the TiO2 surface, which is beneficial for increasing the possibility that the acceptor species penetrate the dye adsorption layer. From Tables 3 and 4, WS-95 has the largest isotropic polarizability and polarizability anisotropy, which means that WS-95 is a better dye. Furthermore, the hyperpolarizability is closely related to the intramolecular charge transfer (ICT). From Table 4, we can see that the βtot values are in following order: WS-2 < WS-95 < WS-92, and the βxxx values of the dyes follow a similar trend. The value of βxxx is much larger than that of the next highest tensor. Hence, the βtot values are mainly determined by βxxx, which means that electron transfer from the donor to the acceptor is unidirectional. The βtot values of WS-92 and WS-95 are much larger than that of WS-2, indicating that they may produce more photoelectron-induced electron transfer in the excited state.
Table 3 Isotropic polarizability (α) and polarizability anisotropy (Δα) parameters of the dyes (1 × 10−24 esu)
| Dye |
αxx |
αxy |
αyy |
αxz |
αyz |
αzz |
α |
Δα |
| WS-2 |
89.746 |
2.413 |
65.599 |
0.5573 |
−1.785 |
39.793 |
65.046 |
43.269 |
| WS-92 |
231.940 |
−26.526 |
64.827 |
7.065 |
6.498 |
61.859 |
119.542 |
168.617 |
| WS-95 |
290.170 |
27.815 |
104.965 |
19.240 |
16.434 |
105.523 |
166.860 |
184.928 |
Table 4 Hyperpolarizability (β) of the dyes (1 × 10−30 esu)
| Dye |
βxxx |
βxxy |
βxyy |
βyyy |
βxxz |
βxyz |
βyyz |
βxzz |
βyzz |
βzzz |
βtot |
| WS-2 |
86.679 |
26.672 |
10.214 |
0.178 |
−0.896 |
0.255 |
−0.606 |
−0.190 |
−0.583 |
0.186 |
100.216 |
| WS-92 |
1313.217 |
−190.388 |
26.933 |
−3.912 |
−36.701 |
5.938 |
−1.278 |
−0.012 |
0.204 |
0.774 |
1354.632 |
| WS-95 |
992.267 |
181.562 |
29.670 |
5.125 |
179.352 |
34.751 |
8.066 |
33.917 |
7.315 |
8.266 |
1058.438 |
3.5 NBO analysis
Natural bond orbital (NBO) analysis based on the optimized structure of the ground state (S0) and the first excited state (S1) was performed in order to further understand the charge populations and the electron transfer from the donor and auxiliary acceptor to the acceptor via the π-spacer. The positive NBO value of the donor unit and π-spacer bridge indicates that they are effective electron-donor units. In contrast, the negative NBO value of the auxiliary acceptor and acceptor units indicates that the dye may trap electrons in the π-spacer. The calculated NBO values of the dyes are listed in Table 5. As shown, the NBO charges of the electron acceptors of WS-2, WS-92 and WS-95 are −0.131, −0.135 and −0.178 e in the ground state (S0), respectively. It can be seen that WS-2 and WS-92 have similar NBO charges, but the NBO charge of WS-95 is obviously changed in comparison with that of WS-92. This indicates that the electron acceptor of WS-95 with a larger π-spacer shows a strong electron-withdrawing ability and large charge polarization. The negative charge of the electron acceptor may be a factor leading to electron injection from the excited dye to the TiO2 conduction band. The Δq(D–A) values of the dyes in the ground state (S0) are, in increasing order, WS-2 (0.218 e) < WS-92 (0.237 e) < WS-95 (0.251 e). The values for the first excited state (S1) follow the same trend. This means that WS-95 exhibits the largest charge separation between the donor and acceptor unit. From Table 5, the incorporation of a larger π-spacer in WS-95 directly increases the charge variance on the donor unit between S0 and S1 in comparison with WS-92, which means that WS-95 has a strong electron-donating ability.
Table 5 The NBO (in e) analysis of the dyes in the ground state (S0) and excited state (S1)a
| Dye |
S0 |
Δq(D–A) |
S1 |
Δq(D–A) |
Δq(D)a |
| D |
A |
π |
A |
D |
A |
π |
A |
| Δq(D)a represents the charge variance on the donor unit between S0 and S1. |
| WS-2 |
0.087 |
−0.064 |
0.107 |
−0.131 |
0.218 |
0.614 |
−0.486 |
0.080 |
−0.209 |
0.823 |
0.527 |
| WS-92 |
0.102 |
−0.067 |
0.100 |
−0.135 |
0.237 |
0.615 |
−0.467 |
0.067 |
−0.215 |
0.830 |
0.513 |
| WS-95 |
0.073 |
−0.090 |
0.194 |
−0.178 |
0.251 |
0.684 |
−0.567 |
0.131 |
−0.247 |
0.931 |
0.611 |
3.6 Factors influencing VOC
According to eqn (7), in addition to the short-circuit current density (JSC), the open-circuit photo-voltage (VOC) is also an important factor affecting the overall power conversion efficiency (η) of DSSCs. The value of VOC is affected by the conduction band (CB), and ΔCB can be summarized as:| |
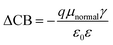 | (12) |
where q is the electron charge; μnormal is the dipole moment of an individual dye molecule perpendicular to the surface of the semiconductor substrate; γ is the molecular surface concentration; ε0 and ε are the vacuum permittivity and the dielectric permittivity, respectively. A higher μnormal of the dyes can improve charge the separation between the donor and acceptor units and further increase VOC. According to eqn (7) and (12), it is obvious that the larger μnormal, the higher VOC. As shown in Table 6, the μnormal values of the dyes are, in increasing order, WS-2 (−9.39) < WS-92 (10.47) < WS-95 (14.68). WS-95 has a larger μnormal than WS-92, which means that WS-95 has a larger VOC. This is in good agreement with the experimental results.21
Table 6 Computed free energy change for electron injection (ΔGinject/eV), oxidation potential of the excited state (Edye*/eV), oxidation potential of the ground state (Edye/eV), vertical dipole moment (μnormal) and open-circuit voltage (eVOC/eV) of the dyes
| Dye |
ΔGinject |
Edye* |
Edye |
μnormal |
eVOC |
| WS-2 |
−1.414 |
2.586 |
5.157 |
−9.39 |
1.05 |
| WS-92 |
−1.617 |
2.383 |
4.805 |
10.47 |
1.09 |
| WS-95 |
−1.504 |
2.496 |
4.891 |
14.68 |
1.15 |
In order to explore the relationship between the LUMO and VOC, VOC can be approximately expressed by the following formula:40
It can be seen that a higher
ELUMO will generate a larger
eVOC. As shown in
Table 6, the
eVOC values of the dyes are, in increasing order, WS-2 (1.05 eV) < WS-92 (1.09 eV) < WS-95 (1.15 eV). Certainly, the trend from WS-92 to WS-95 is in agreement with the experimental results.
21 Taking the
μnormal and
eVOC values into account, WS-95 should have a larger
VOC. Accordingly, the results indicate that substituting a CPDT unit in place of a thiophene unit can enhance
VOC. WS-95 showed a higher
VOC in both experimental and theoretical studies, which indicated that WS-95 is an outstanding dye.
According to the research of Islam, when the absolute value of ΔGinject > 0.2 eV, the electron injection efficiency is approximately equal to one.59 From Table 6, the injection driving force (ΔGinject) of WS-2, WS-92 and WS-95 is −1.414, −1.617 and −1.504 eV, respectively. The absolute values of ΔGinject for WS-2, WS-92 and WS-95 are much larger than 0.2 eV, which means that all the dyes show a sufficient driving force to inject electrons into TiO2. However, too large a value of ΔGinject can cause energy redundancy, leading to a smaller VOC.62,63 This is why WS-92 has a lower value of VOC than WS-95, despite it having a higher ΔGinject.
3.7 Chemical reactivity study
The chemical reactivity, including chemical hardness (h), electrophilicity index (ω) and electron accepting power (ω+), was investigated to further explain the molecular properties of the dyes. Chemical hardness represents the resistance of the dyes to intramolecular charge transfer (ICT);64,65 hence, the dyes should have a lower chemical hardness in order to increase charge transfer and separation. The calculated results are shown in Fig. 11. As shown, the chemical hardness values of the dyes are, in decreasing order, WS-2 (2.08 eV) > WS-92 (1.91 eV) > WS-95 (1.83 eV). WS-95 has the lowest chemical hardness; this leads to a higher short-circuit current density (JSC), and is in good agreement with the experimental results.21 Therefore, WS-95 is considered to be the best dye for intramolecular charge transfer (ICT).
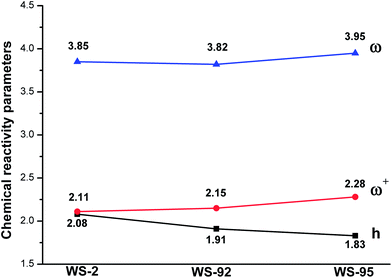 |
| | Fig. 11 Chemical hardness, electrophilicity index, and electron accepting power of the dyes. | |
Electrophilicity represents the stabilization energy of the dyes. WS-95 has the largest electrophilicity (3.95 eV), followed by WS-2 (3.85 eV) and WS-92 (3.82 eV). A higher electrophilicity represents a higher energetic stability. Therefore, WS-95 shows the highest stabilization energy. The electron accepting power represents electron-accepting ability, and a larger value is desirable. The electron accepting power values of the dyes are, in increasing order, WS-2 (2.11 eV) < WS-92 (2.15 eV) < WS-95 (2.28 eV). WS-95 has the highest electron-withdrawing ability. In conclusion, for indoline dyes, the photoactive layer has a higher stabilization energy and electron-withdrawing ability when the thiophene unit is substituted by a cyclopentadithiophene (CPDT) unit, which will lead to a higher short-circuit current density (JSC) and PCE.
3.8 Ionization potentials and electron affinities
Charge injection and balance affect the performance of DSSC devices. The ionization potential (IP) and electron affinity (EA) can depict the energy barrier of both holes and electrons. The IP, EA, hole extraction potential (HEP) and electron extraction potential (EEP) of the three molecules were calculated by DFT, and the results are listed in Table 7. IP(a)/EA(a) represents adiabatic excitations, IP(v)/EA(v) represents vertical excitations, and HEP/EEP represents the energy difference from the neutral molecule to cationic/anionic molecules with the same geometry.
Table 7 Ionization potentials, electron affinities, extraction potentials and reorganization energies (in eV) of the dyes
| Dye |
IP(v) |
IP(a) |
HEP |
EA(v) |
EA(a) |
EEP |
λh |
λe |
| WS-2 |
6.23 |
6.08 |
5.97 |
2.07 |
1.92 |
1.77 |
0.26 |
0.30 |
| WS-92 |
5.81 |
5.73 |
5.65 |
2.07 |
1.91 |
1.76 |
0.16 |
0.31 |
| WS-95 |
5.77 |
5.62 |
5.50 |
2.10 |
1.97 |
1.84 |
0.27 |
0.26 |
As shown in Table 7, the values of IP(v)/IP(a) for WS-95 (5.77/5.62 eV) are smaller than those of the other dyes. A lower IP is beneficial for promoting the hole-creating ability. The values of EA(v)/EA(a) for WS-95 (2.10/1.97 eV) are larger than those of the other dyes. A higher EA can improve the electron-accepting ability. Therefore, WS-95 has better hole-creating and electron-accepting abilities.
It is very important to maintain a balance between electron and hole transport. Furthermore, the more balanced the λh and λe values, the better the luminous efficiency. As shown in Table 7, the difference between λh and λe for WS-95 (0.01 eV) is smaller than that for WS-2 (0.04 eV) and WS-92 (0.05 eV), which means that WS-95 has more balanced transport rates. In addition, the λe (0.26 eV) is smaller than that for WS-2 (0.30 eV) and WS-92 (0.31 eV), which means that WS-95 has a better electron transfer rate than the other molecules.
3.9 Molecular design
In order to further screen the high efficiency sensitizers, a series of dyes (1, 2, 3…11 and 12) were obtained by introducing two types of electron-withdrawing group (–CN and –NH2) at different positions (R1, R2 and R3) based on WS-95. The chemical structures are shown in Fig. 1. Selected geometric parameters (bond lengths and bond angles) of the designed molecules in the ground state are listed in Table 8. As shown, when a –CN/–NH2 is introduced into the molecule, the dihedral angle (∠C1–C2–N3–C4) of 1 and 2 becomes smaller (by about 11°) than that of the reference dye WS-95. The dihedral angles (∠C5–C6–C7–C8) of 4 and 6 become larger, while the dihedral angles (∠C9–C10–C11–S12) of 2, 4 and 5 follow the same trend. The dihedral angle (∠S13–C14–C15–C16) of 4 exhibits a larger change. When two –CN/–NH2 groups are introduced into the molecule, it can be seen that the dihedral angles (∠C1–C2–N3–C4) of 9, 10, 11 and 12 are decreased, while the dihedral angles (∠C5–C6–C7–C8) of 8, 9, 11 and 12 as well as the dihedral angles (∠C9–C10–C11–S12) of 7, 9, 10 and 12 are increased. The dihedral angles (∠S13–C14–C15–C16) of 7 and 8 are slightly increased. For 10 and 11, the dihedral angle of the acceptor is obviously increased. From Table 8 it can be seen that the bond lengths exhibit no obvious change.
Table 8 Selected critical bond lengths (in Å) and dihedral angles (in degrees) of the designed molecules and the reference dye WS-95
| |
WS-95 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| ∠C1–C2–N3–C4 |
−61.9 |
−48.9 |
−49.3 |
−58.6 |
60.9 |
61.3 |
61.5 |
61.0 |
59.7 |
−50.3 |
−48.5 |
−45.1 |
−44.9 |
| ∠C5–C6–C7–C8 |
−33.1 |
34.3 |
33.8 |
−41.4 |
33.8 |
35.1 |
48.4 |
33.5 |
40.4 |
43.5 |
34.0 |
50.0 |
53.2 |
| ∠C9–C10–C11–S12 |
3.0 |
9.0 |
−21.0 |
−0.9 |
11.4 |
31.4 |
−5.3 |
25.9 |
−4.1 |
−28.5 |
−34.0 |
−171.2 |
−139.1 |
| ∠S13–C14–C15–C16 |
−0.5 |
−174.2 |
−179.2 |
−179.4 |
154.0 |
−178.9 |
−178.4 |
−171.0 |
−172.0 |
−179.4 |
−151.8 |
−31.4 |
−178.5 |
| C2–N3 |
1.419 |
1.434 |
1.434 |
1.417 |
1.418 |
1.419 |
1.418 |
1.419 |
1.419 |
1.434 |
1.435 |
1.434 |
1.4333 |
| C6–C7 |
1.473 |
1.472 |
1.473 |
1.470 |
1.474 |
1.475 |
1.483 |
1.472 |
1.469 |
1.434 |
1.476 |
1.484 |
1.485 |
| C10–C11 |
1.455 |
1.454 |
1.454 |
1.456 |
1.456 |
1.458 |
1.458 |
1.454 |
1.456 |
1.456 |
1.460 |
1.457 |
1.463 |
| C14–C15 |
1.423 |
1.454 |
1.421 |
1.420 |
1.454 |
1.418 |
1.419 |
1.438 |
1.437 |
1.422 |
1.453 |
1.459 |
1.419 |
It is well known that the band gap energy and frontier molecular orbitals have an important effect on electronic excitation (transition).66,67 A smaller band gap energy is beneficial for an absorption spectrum red-shift.68 The molecular energy level diagrams of all the dyes are shown in Fig. 12, and the HOMOs and LUMOs are listed in Table S6.† As shown in Fig. 12, the LUMO energy levels of 1, 2, 3, 7, 8 and 9 are lower than that of WS-95, with the values in the following order: WS-95 (−2.85 eV) > 3 (−3.09 eV) > 2 (−3.13 eV) > 1 (−3.15 eV) > 8 (−3.34 eV) > 9 (−3.35 eV) > 7 (−3.37 eV). It can be seen that the introduction of –CN leads to a lower LUMO energy level. Furthermore, upon the introduction of two –CN groups, the LUMO energy level further decreases. The HOMO energy levels of all the dyes are not changed significantly, except for that of 9, with the values in the following order: WS-95 (−4.89 eV) > 3 (−4.98 eV) > 7 (−5.06 eV) = 8 (−5.06 eV) > 1 (−5.07 eV) > 2 (−5.15 eV) > 9 (−5.31 eV). The results show that the HOMO energy levels are slightly reduced when –CN is introduced into the dyes. Therefore, the magnitude of the band gap energy is determined by the value of the LUMO energy level. The band gap energies of 1, 2, 3, 7, 8 and 9 are smaller than that of the reference dye WS-95 due to their lower LUMO energy levels, and the values are in the following order: WS-95 (2.04 eV) > 2 (2.02 eV) > 9 (1.96 eV) > 1 (1.92 eV) > 3 (1.89 eV) > 8 (1.72 eV) > 7 (1.69 eV). Hence, the introduction of –CN is beneficial to reducing the band gap energy, which may lead to the electrons being more easily excited and the dyes absorbing longer wavelength photons.
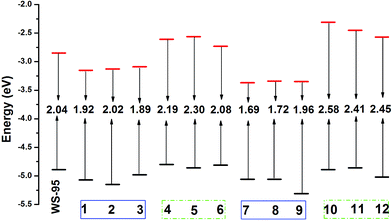 |
| | Fig. 12 Calculated energy levels of the designed molecules and the reference dye WS-95. | |
Compared with 1, 2 and 3, the band gap energies of the dyes containing two –CN groups are further reduced, except for that of 9 due to its lower HOMO energy level (−5.31 eV). Dye 7 exhibits the lowest band gap energy (1.69 eV) among these dyes. The LUMO energy levels of 4, 5, 6, 10, 11 and 12 are higher than that of the reference dye WS-95, and the values are in the following order: 10 (−2.31 eV) > 11 (−2.45 eV) > 5 (−2.56 eV) > 12 (−2.57 eV) > 4 (−2.61 eV) > 6 (−2.73 eV) > WS-95 (−2.85 eV). The results show that the insertion of –NH2 into the dyes is beneficial to increasing the LUMO energy level. When two –NH2 groups are introduced into the dyes, the dyes display a higher LUMO energy level in comparison with 4, 5 and 6, except for 12. There is no obvious change in the HOMO energy level (see Table S6†). The band gap energies of 4, 5, 6, 10, 11 and 12 with the insertion of –NH2 are higher than that of the reference dye WS-95 due to their higher LUMO energy levels, and the values are in the following order: 10 (2.58 eV) > 12 (2.45 eV) > 11 (2.41 eV) > 5 (2.30 eV) > 4 (2.19 eV) > 6 (2.08 eV). The introduction of two –NH2 groups (10, 11 and 12) at different positions (R1, R2 and R3) can increase the band gap energy compared to 4, 5, and 6. Dye 10 exhibits the highest band gap energy among these dyes. In conclusion, the introduction of –CN groups can decrease the band gap energy; meanwhile, the introduction of –NH2 groups can increase the band gap energy. When two –CN (–NH2) groups are introduced in the R1 and R2 positions, 7 (10) displays the lowest (highest) band gap energy. We know that a dye with a small band gap energy is advantageous for a red-shifted absorption spectrum and generates more electrons, and thus enhances the PCE in a DSSC. The photoelectric performance of the dyes will be discussed in detail in the next section.
Table 9 and Fig. 13 show the maximum absorption wavelengths of the synthesized series of dyes. As shown in Table 9, the first excited state of all the dyes shows an electron transition from the HOMO to LUMO. Compared with the reference dye WS-95, the dyes with the insertion of –CN have obvious red-shifts due to their smaller band gap energy as well as smaller excitation energies. The maximum absorption peaks are in the following order: 7 (553 nm) = 8 (553 nm) > 1 (543 nm) > 2 (537 nm) = 9 (537 nm) > 3 (535 nm) > WS-95 (518 nm), and the corresponding red-shift values are 35, 35, 25, 19, 19 and 17 nm, respectively. Among these dyes, dyes 7 and 8 exhibit superior performance, with the largest maximum absorption wavelength and the smallest excitation energy. It can be seen that the introduction of –CN is beneficial for an absorption spectrum red-shift. In particular, upon the introduction of two –CN groups, the absorption spectrum will be further red-shifted, except for 9. As shown in Fig. 13(A), the dyes with the insertion of –CN exhibit an obvious red-shift. On the contrary, dyes 4, 5, 6, 10, 11 and 12 with the insertion of –NH2 exhibit an obvious blue-shift (see Fig. 13(B)) due to their larger band gap energy, and the molar absorption coefficients of all the dyes are decreased, except for 5. The maximum absorption peaks are in the following order: WS-95 (518 nm) > 6 (497 nm) > 4 (495 nm) > 5 (478 nm) > 11 (469 nm) > 12 (456 nm) > 10 (453 nm), and the corresponding blue-shift values are 21, 23, 40, 48, 62 and 65 nm, respectively. The results show that the introduction of –NH2 is beneficial for an absorption spectrum blue-shift. Compared with dyes 4, 5 and 6, the absorption spectra of 10, 11 and 12 with the insertion of two –NH2 groups are blue-shifted. Therefore, the introduction of two –NH2 groups is more conducive to an absorption spectrum blue-shift. The excitation energies of these dyes are larger than that of the reference dye WS-95.
Table 9 Calculated transition properties of the designed molecules and the reference dye WS-95 using the TD-DFT method
| Dye |
State |
Eg/λmax |
f |
Main configuration |
| WS-95 |
1 |
2.40/518 |
1.7557 |
H → L/0.59868 |
| 1 |
1 |
2.29/543 |
1.8987 |
H → L/0.59718 |
| 2 |
2.90/428 |
0.0069 |
H → L+1/0.57293 |
| 3 |
3.31/374 |
0.0013 |
H−1 → L/0.36015 |
| 4 |
3.80/326 |
0.0078 |
H−1 → L+1/0.38500 |
| 5 |
3.92/317 |
0.0008 |
H−1 → L/0.46373 |
| 6 |
4.09/303 |
0.1752 |
H → L+2/0.52379 |
| 2 |
1 |
2.31/537 |
1.5435 |
H → L/0.64942 |
| 2 |
3.01/412 |
0.1677 |
H → L+1/0.38582 |
| 3 |
3.29/376 |
0.1881 |
H → L+1/0.43168 |
| 4 |
3.84/323 |
0.0009 |
H−1 → L/0.43290 |
| 5 |
4.02/309 |
0.0055 |
H−4 → L/0.37315 |
| 6 |
4.10/303 |
0.0016 |
H−7 → L/0.49167 |
| 3 |
1 |
2.32/535 |
1.5446 |
H → L/0.58958 |
| 2 |
2.89/429 |
0.2774 |
H−1 → L/0.49112 |
| 3 |
3.21/386 |
0.1759 |
H−1 → L+1/0.47607 |
| 4 |
3.80/326 |
0.0106 |
H−2 → L/0.42013 |
| 5 |
3.92/316 |
0.0084 |
H → L+1/0.43511 |
| 6 |
4.06/306 |
0.0564 |
H → L+4/0.49178 |
| 4 |
1 |
2.51/495 |
1.4514 |
H → L/0.61305 |
| 2 |
3.22/385 |
0.2331 |
H−1 → L/0.39088 |
| 3 |
3.48/357 |
0.1678 |
H−1 → L/0.40858 |
| 4 |
4.06/306 |
0.0533 |
H → L+2/0.44940 |
| 5 |
4.10/303 |
0.0089 |
H−3 → L/0.35272 |
| 6 |
4.19/296 |
0.0104 |
H → L+3/0.23839 |
| 5 |
1 |
2.59/478 |
1.8033 |
H → L/0.56841 |
| 2 |
3.09/401 |
0.0307 |
H → L+1/0.56783 |
| 3 |
3.52/352 |
0.1000 |
H−1 → L+1/0.42101 |
| 4 |
3.92/316 |
0.0325 |
H−4 → L/0.46424 |
| 5 |
4.07/305 |
0.0512 |
H−1 → L+3/0.42380 |
| 6 |
4.16/298 |
0.0678 |
H−1 → L+1/0.30184 |
| 6 |
1 |
2.49/497 |
1.5732 |
H → L/0.51858 |
| 2 |
3.09/401 |
0.2285 |
H → L+1/0.40811 |
| 3 |
3.45/359 |
0.0232 |
H−1 → L+1/0.40341 |
| 4 |
3.75/331 |
0.0543 |
H−4 → L/0.34397 |
| 5 |
4.04/307 |
0.0024 |
H−1 → L+1/0.35693 |
| 6 |
4.06/306 |
0.0543 |
H → L+1/0.51122 |
| 7 |
1 |
2.24/553 |
1.6770 |
H → L/0.49593 |
| 2 |
2.80/444 |
0.1114 |
H → L+1/0.39436 |
| 3 |
3.08/402 |
0.0085 |
H−1 → L/0.44698 |
| 4 |
3.58/346 |
0.0194 |
H → L+1/0.37731 |
| 5 |
3.67/338 |
0.0015 |
H−3 → L/0.36829 |
| 6 |
3.99/311 |
0.0089 |
H−2 → L/0.49322 |
| 8 |
1 |
2.24/553 |
1.7453 |
H → L/0.50225 |
| 2 |
2.74/452 |
0.1496 |
H → L+1/0.42316 |
| 3 |
3.09/401 |
0.0046 |
H−1 → L+1/0.46050 |
| 4 |
3.55/349 |
0.0134 |
H−1 → L+1/0.37419 |
| 5 |
3.70/335 |
0.0016 |
H−2 → L/0.37610 |
| 6 |
4.00/310 |
0.0089 |
H−2 → L/0.46476 |
| 9 |
1 |
2.31/537 |
1.3520 |
H → L/0.63133 |
| 2 |
2.88/431 |
0.1789 |
H−2 → L/0.42565 |
| 3 |
3.25/382 |
0.3067 |
H → L+1/0.43143 |
| 4 |
3.64/341 |
0.0039 |
H−1 → L/0.45128 |
| 5 |
3.84/323 |
0.0302 |
H → L+2/0.44811 |
| 6 |
3.93/315 |
0.0121 |
H−5 → L/0.42939 |
| 10 |
1 |
2.73/453 |
1.3804 |
H → L/0.65951 |
| 2 |
3.24/383 |
0.1929 |
H → L+1/0.59417 |
| 3 |
3.72/333 |
0.1467 |
H−1 → L/0.50919 |
| 4 |
4.08/304 |
0.0494 |
H−4 → L/0.50267 |
| 5 |
4.22/293 |
0.0543 |
H−5 → L/0.38925 |
| 6 |
4.28/290 |
0.0364 |
H−1 → L+2/0.50283 |
| 11 |
1 |
2.64/469 |
1.1763 |
H → L/0.61733 |
| 2 |
3.29/377 |
0.2961 |
H → L+1/0.42065 |
| 3 |
3.70/335 |
0.0457 |
H−1 → L/0.36039 |
| 4 |
3.91/317 |
0.0651 |
H−4 → L/0.50764 |
| 5 |
4.15/299 |
0.1828 |
H−5 → L/0.40007 |
| 6 |
4.26/291 |
0.0325 |
H−1 → L+3/0.47241 |
| 12 |
1 |
2.72/456 |
1.6245 |
H → L/0.58358 |
| 2 |
3.30/375 |
0.0040 |
H → L+1/0.58530 |
| 3 |
3.75/331 |
0.0691 |
H−1 → L+1/0.38091 |
| 4 |
3.93/316 |
0.0937 |
H−4 → L/0.48346 |
| 5 |
4.11/302 |
0.0816 |
H−4 → L+1/0.37872 |
| 6 |
4.26/291 |
0.0426 |
H−1 → L+3/0.46074 |
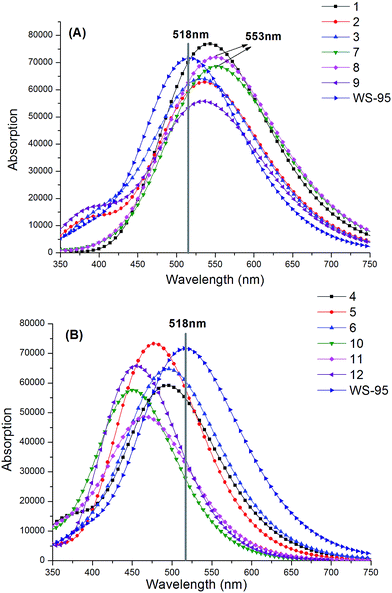 |
| | Fig. 13 Absorption spectra of the designed molecules and the reference dye WS-95 ((A) represents dyes with the insertion of –CN, (B) represents dyes with the insertion of –NH2). | |
Some other important parameters are listed in Table 10. It can be seen that the absolute values of ΔGinject for dyes 1, 2, 3, 7, 8 and 9 are smaller than that of the reference dye WS-95, and the absolute values are in the following order: WS-95 (1.51 eV) > 3 (1.34 eV) > 1 (1.22 eV) > 7 (1.18 eV) = 8 (1.18 eV) > 2 (1.16 eV) > 9 (1.00 eV), which means that the introduction of –CN at different positions can decrease the ΔGinject value. The absolute values of ΔGinject for 4, 5, 6, 10, 11 and 12 are higher than that of the reference dye WS-95, and the absolute values are in the following order: 10 (1.84 eV) > 11 (1.78 eV) > 5 (1.73 eV) > 4 (1.71 eV) > 12 (1.70 eV) > 6 (1.68 eV), which means that the introduction of –NH leads to an increase in ΔGinject. At the same time, the ΔGinject values of dyes 10 and 11 with the introduction of two –NH2 groups are higher than those of the dyes (4, 5 and 6) with the introduction of one –NH2 group. It is well-known that ΔGinject is an important factor affecting the JSC, and dye 10 with a larger ΔGinject will display a better performance. The eVOC values of the dyes are in the following order: 10 (1.69 eV) > 11 (1.55 eV) > 5 (1.44 eV) > 12 (1.43 eV) > 4 (1.39 eV) > 6 (1.27 eV) > WS-95 (1.15 eV) > 3 (0.91 eV) > 2 (0.87 eV) > 1 (0.85 eV) > 8 (0.66 eV) > 9 (0.65 eV) > 7 (0.63 eV). The results show that the eVOC values of dyes 1, 2 and 3 are lower than that of the reference dye WS-95, which means that the introduction of one –CN group into the molecule leads to a reduction in eVOC. Dyes 7, 8 and 9 with the introduction of two –CN groups show smaller values in comparison to dyes 1, 2 and 3 with one inserted –CN group. From this trend, it can be seen that the introduction of –NH is beneficial to an increase in eVOC. When two –NH2 groups are introduced into the R1/R3 and R1/R3 positions, 10 and 11 show higher eVOC values compared with 4, 5 and 6 with one inserted –NH2 group. As shown in Table 10, only 1 and 5 display higher LHEs compared to WS-95, while the other dyes show lower values due to their smaller oscillator strengths.
Table 10 LHE, injection driving force and open-circuit voltage of the designed molecules and the reference dye WS-95
| Dye |
ΔGinject |
Edye* |
Edye |
eVOC |
LHE |
| WS-95 |
−1.51 |
2.49 |
4.89 |
1.15 |
0.9824 |
| 1 |
−1.22 |
2.78 |
5.07 |
0.85 |
0.9874 |
| 2 |
−1.16 |
2.84 |
5.15 |
0.87 |
0.9714 |
| 3 |
−1.34 |
2.66 |
4.98 |
0.91 |
0.9715 |
| 4 |
−1.71 |
2.29 |
4.80 |
1.39 |
0.9646 |
| 5 |
−1.73 |
2.27 |
4.86 |
1.44 |
0.9843 |
| 6 |
−1.68 |
2.32 |
4.81 |
1.27 |
0.9733 |
| 7 |
−1.18 |
2.82 |
5.06 |
0.63 |
0.9790 |
| 8 |
−1.18 |
2.82 |
5.06 |
0.66 |
0.9820 |
| 9 |
−1.00 |
3.00 |
5.31 |
0.65 |
0.9555 |
| 10 |
−1.84 |
2.16 |
4.89 |
1.69 |
0.9587 |
| 11 |
−1.78 |
2.22 |
4.86 |
1.55 |
0.9334 |
| 12 |
−1.70 |
2.30 |
5.02 |
1.43 |
0.9763 |
The ionization potentials, electron affinities, reorganization energies, chemical hardness, electrophilicity index and electron accepting power of the dyes are listed in Table 11. The ionization potentials of the dyes are in the following order: 9 (5.96 eV) > 3 (5.84 eV) > 2 (5.82 eV) > 7 (5.81 eV) = 8 (5.81 eV) > 1 (5.76 eV) > 12 (5.70 eV) > WS-95 (5.62 eV) > 10 (5.60 eV) > 5 (5.58 eV) > 11 (5.57 eV) > 6 (5.54 eV) > 4 (5.52 eV). The results show that the IP values of dyes 1, 2, 3, 7, 8 and 9 are larger than that of the reference dye WS-95, and dye 9 displays the largest IP among these dyes. Therefore, the introduction of –CN is conducive to an increase in IP value. At the same time, when –NH2 is introduced into the dyes, the IP values of 4, 5, 6, 10, 11 and 12 (5.70 to 5.52 eV) exhibit no obvious change. Compared with the reference dye WS-95 (5.62 eV), only dye 12 exhibits a slightly increased IP value, while the other dyes (5, 6, 10 and 11) exhibit a slightly decreased value. The electron affinities of the dyes are in the following order: dye 7 (2.53 eV) > 9 (2.49 eV) > 8 (2.48 eV) > 1 (2.31 eV) > 3 (2.20 eV) > 2 (2.17 eV) > WS-95 (1.97 eV) > 6 (1.84 eV) > 4 (1.75 eV) > 5 (1.72 eV) > 12 (1.65 eV) > 11 (1.60 eV) > 10 (1.54 eV). This trend indicates that the introduction of –CN is conducive to an increase in EA value. Furthermore, upon the introduction of two –CN groups into the dyes, the EA will further increase. On the contrary, the introduction of –NH2 leads to a decrease in EA. When two –NH2 groups are introduced into the molecule, the EA will be further decreased. ω and ω+ follow the same trend as EA, and the values are listed in Table 11. Dye 7 has the largest ω and ω+, followed by dye 8. As discussed above, a larger ω and ω+ is expected, so the introduction of –CN will improve the performance of the dye to some degree. The chemical hardness values of the dyes are in the following order: 12 (2.03 eV) = 10 (2.03 eV) > 11 (2.02 eV) > 5 (1.93 eV) > 4 (1.89 eV) > 6 (1.85 eV) > WS-95 (1.83 eV) = 2 (1.83 eV) > 3 (1.82 eV) > 9 (1.74 eV) > 8 (1.67 eV) > 7 (1.64 eV). This trend shows that the introduction of –CN is conducive to a decrease in chemical hardness. Furthermore, the introduction of two –CN molecules into the dyes will lead to a further decrease in the chemical hardness. On the contrary, the introduction of –NH2 leads to an increase in chemical hardness. When two –NH2 groups are introduced into the molecule, the chemical hardness will be further increased. Dye 7 has the lowest chemical hardness, followed by 8. When –CN was introduced into the molecule, the chemical hardness was decreased with increasing values of ω and ω+ (see Fig. 14(a)). When –NH2 was introduced into the molecule, the chemical hardness was increased with decreasing values of ω and ω+ (see Fig. 14(b)). The λh and λe values of dye 8 are lower than those of the reference dye WS-95, while the other dyes all show comparable or even higher values, except for 3 (λh is 0.16 eV). The difference between λh and λe of 7 (0.02 eV) is the smallest among all the dyes, followed by 8 (0.03 eV).
Table 11 Ionization potentials, electron affinities, reorganization energies and chemical reactivity (in eV) of the designed molecules and the reference dye WS-95
| Dye |
IP |
EA |
λh |
λe |
ω |
ω+ |
h |
| WS-95 |
5.62 |
1.97 |
0.27 |
0.26 |
3.95 |
2.28 |
1.83 |
| 1 |
5.76 |
2.31 |
0.34 |
0.26 |
4.72 |
2.92 |
1.73 |
| 2 |
5.82 |
2.17 |
0.36 |
0.27 |
4.37 |
2.60 |
1.83 |
| 3 |
5.84 |
2.20 |
0.16 |
0.26 |
4.44 |
2.66 |
1.82 |
| 4 |
5.52 |
1.75 |
0.30 |
0.37 |
3.50 |
1.92 |
1.89 |
| 5 |
5.58 |
1.72 |
0.27 |
0.34 |
3.45 |
1.87 |
1.93 |
| 6 |
5.54 |
1.84 |
0.32 |
0.29 |
3.68 |
2.07 |
1.85 |
| 7 |
5.81 |
2.53 |
0.29 |
0.27 |
5.31 |
3.42 |
1.64 |
| 8 |
5.81 |
2.48 |
0.26 |
0.23 |
5.16 |
3.30 |
1.67 |
| 9 |
5.96 |
2.49 |
0.36 |
0.31 |
5.14 |
3.25 |
1.74 |
| 10 |
5.60 |
1.54 |
0.37 |
0.46 |
3.14 |
1.61 |
2.03 |
| 11 |
5.57 |
1.60 |
0.40 |
0.39 |
3.24 |
1.69 |
2.02 |
| 12 |
5.70 |
1.65 |
0.35 |
0.32 |
3.33 |
1.75 |
2.03 |
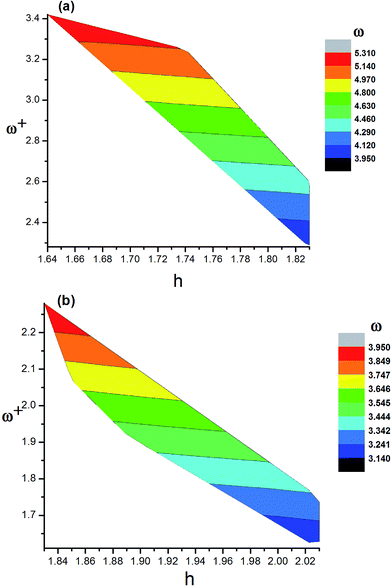 |
| | Fig. 14 Comparison graphs of h vs. ω+ for (a) dye molecules 1–3, 7–9 and (b) dye molecules 4–6, 10–12. The colors in the figure indicate the ω for the corresponding h and ω+. | |
4. Conclusions
The optical and electrical properties of three dyes (WS-2, WS-92 and WS-95) were investigated via DFT and TD-DFT methods. The results show that WS-95, with the thiophene unit substituted for a CPDT unit, exhibits a broad absorption band and a high molar extinction coefficient compared to WS-2 and WS-92, resulting in it exhibiting the largest absorption ability for sunlight. Importantly, the dipole moment and light harvesting efficiency of WS-95, which are closely related to the short-circuit current density (JSC) and open-circuit voltage (VOC), are superior to those of WS-2 and WS-92. Therefore, WS-95 exhibits superior performance in experiments.
On the basis of reference dye WS-95, a series of dyes were designed by introducing different functional groups (–CN/–NH2). When a –CN group was introduced into WS-95, the band gap energy and chemical hardness decreased, while the electrophilicity index, electron accepting power and electron affinity increased, and the absorption spectrum was red-shifted. The performance of dyes 1, 2, 3, 7, 8 and 9 is superior to that of WS-95, which will lead to a higher short-circuit current density (JSC). It was also found that upon introducing an –NH2 group into WS-95, the free energy change for electron injection and eVOC were increased. The performance of dyes 4, 5, 6, 10, 11 and 12 is superior to that of WS-95, which is beneficial to improving the short-circuit current density (JSC) and open-circuit voltage (VOC). Therefore, the introduction of different functional groups (–CN/–NH2) can improve the performance of different aspects of a molecule. Among all the designed dyes, dye 5 has the highest free energy change for electron injection, light harvesting efficiency, molar extinction coefficient and eVOC compared to WS-95, and may be regarded as an outstanding candidate for use in DSSCs.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11404055 and 11374353), the China Postdoctoral Science Foundation (2016M590270), a Heilongjiang Postdoctoral Grant (LBH-Z15002) and the Heilongjiang Provincial Youth Science Foundation (Grant No. QC2013C006).
References
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- C. Yang, G. Zhang, N. Xu and J. Shi, J. Membr. Sci., 1998, 142, 235–243 CrossRef.
- S. H. Lin and W. J. Lan, J. Hazard. Mater., 1998, 59, 189–199 CrossRef CAS.
- M. K. Nazeeruddin, P. Péchy, T. Renouard, S. M. Zakeeruddin, R. Humphry-Baker, P. Comte, P. Liska, L. Cevey, E. Costa, V. Shklover, L. Spiccia, G. B. Deacon, C. A. Bignozzi and M. Grätzel, J. Am. Chem. Soc., 2001, 123, 1613–1624 CrossRef CAS PubMed.
- P. Wang, S. M. Zakeeruddin, J. E. Moser, R. Humphry-Baker, P. Comte, V. Aranyos, A. Hagfeldt, M. K. Nazeeruddin and M. Grätzel, Adv. Mater., 2004, 16, 1806–1811 CrossRef CAS.
- D. Kuang, S. Uchida, R. Humphry-Baker, S. M. Zakeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2008, 47, 1923–1927 CrossRef CAS PubMed.
- D. P. Hagberg, J. H. Yum, H. Lee, F. De Angelis, T. Marinado, K. M. Karlsson, R. Humphry-Baker, L. Sun, A. Hagfeldt, M. Grätzel and M. K. Nazeeruddin, J. Am. Chem. Soc., 2008, 130, 6259–6266 CrossRef CAS PubMed.
- X. Chen, J. Guo, X. Peng, M. Guo, Y. Xu, L. Shi, C. Liang, L. Wang, Y. Gao, S. Sun and S. Cai, J. Photochem. Photobiol., A, 2005, 171, 231–236 CrossRef CAS.
- Z. S. Wang, Y. Cui, K. Hara, Y. Dan-oh, C. Kasada and A. Shinpo, Adv. Mater., 2007, 19, 1138–1141 CrossRef CAS.
- M. Urbani, M. Grätzel, M. K. Nazeeruddin and T. Torres, Chem. Rev., 2014, 114, 12330–12396 CrossRef CAS PubMed.
- K. Sayama, S. Tsukagoshi, K. Hara, Y. Ohga, A. Shinpou, Y. Abe, S. Suga and H. Arakawa, J. Phys. Chem. B, 2002, 106, 1363–1371 CrossRef CAS.
- Z. Yao, H. Wu, Y. Li, J. Wang, J. Zhang, M. Zhang, Y. Guo and P. Wang, Energy Environ. Sci., 2015, 8, 3192–3197 CAS.
- Y. Ooyama and Y. Harima, ChemPhysChem, 2012, 13, 4032–4080 CrossRef CAS PubMed.
- J. N. Clifford, E. Martinez-Ferrero, A. Viterisi and E. Palomares, Chem. Soc. Rev., 2011, 40, 1635–1646 RSC.
- B. Hosseinzadeh, A. Salimi Beni, A. Najafi Chermahini, R. Ghahary and A. Teimouri, Synth. Met., 2015, 209, 1–10 CrossRef CAS.
- Z. Lu, P. Dai, C. Wang, M. Liang, X. Zong, Z. Sun and S. Xue, Tetrahedron, 2016, 72, 3204–3212 CrossRef CAS.
- R. Ramamoorthy, N. Radha, G. Maheswari, S. Anandan, S. Manoharan and R. Victor Williams, J. Appl. Electrochem., 2016, 46, 929–941 CrossRef CAS.
- W. L. Ding, Q. S. Li and Z. S. Li, J. Mater. Chem. A, 2015, 3, 19948–19959 CAS.
- Z. Q. Yang, C. M. Liu, C. J. Shao, C. D. Lin and Y. Liu, J. Phys. Chem. C, 2015, 119, 21852–21859 CAS.
- D. Y. Kwon, D. M. Chang and Y. S. Kim, Mater. Res. Bull., 2014, 58, 93–96 CrossRef CAS.
- W. W. Zhang, Y. Z. Wu, H. B. Zhu, Q. P. Chai, J. C. Liu, H. Li, X. R. Song and W. H. Zhu, ACS Appl. Mater. Interfaces, 2015, 7, 26802–26810 CAS.
- J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- Y. Z. Li, F. C. Ma, B. Dong, J. Li and M. D. Chen, Dyes Pigm., 2012, 92, 1344–1350 CrossRef CAS.
- Y. Z. Li, D. W. Qi, P. Song and F. C. Ma, Materials, 2015, 8, 42–56 CrossRef.
- Y. Z. Li, H. X. Li, X. M. Zhao and M. D. Chen, J. Phys. Chem. A, 2010, 114, 6972–6977 CrossRef CAS PubMed.
- Y. Z. Li, C. F. Sun, D. W. Qi, P. Song and F. C. Ma, RSC Adv., 2016, 6, 61809–61820 RSC.
- P. Song, Y. Z. Li, F. C. Ma and M. T. Sun, J. Mater. Chem. C, 2015, 3, 4810–4819 RSC.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- K. Chaitanya, X. H. Ju and B. M. Heron, RSC Adv., 2014, 4, 26621–26634 RSC.
- W. L. Ding, D. M. Wang, Z. Y. Geng, X. L. Zhao and Y. F. Yan, J. Phys. Chem. C, 2013, 117, 17382–17398 CAS.
- S. Jungsuttiwong, R. Tarsang, T. Sudyoadsuk, V. Promarak, P. Khongpracha and S. Namuangruk, Org. Electron., 2013, 14, 711–722 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc, Wallingford, 2009 Search PubMed.
- R. Zhang, B. T. Du, G. Sun and Y. X. Sun, Spectrochim. Acta, Part A, 2010, 75, 1115–1124 CrossRef PubMed.
- J. Preat, D. Jacquemin and E. A. Perpete, Energy Environ. Sci., 2010, 3, 891–904 CAS.
- J. Zhang, H. B. Li, S. L. Sun, Y. Geng, Y. Wu and Z. M. Su, J. Mater. Chem., 2012, 22, 568–576 RSC.
- W. Sang-aroon, S. Saekow and V. Amornkitbamrung, J. Photochem. Photobiol., A, 2012, 236, 35–40 CrossRef CAS.
- Z. Ning, Y. Fu and H. Tian, Energy Environ. Sci., 2010, 3, 1170–1181 CAS.
- J. Preat, D. Jacquemin, C. Michaux and E. A. Perpète, Chem. Phys., 2010, 376, 56–68 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- N. A. Anderson and T. Q. Lian, Annu. Rev. Phys. Chem., 2004, 56, 491–519 CrossRef PubMed.
- Z. L. Zhang, L. Y. Zou, A. M. Ren, Y. F. Liu, J. K. Feng and C. C. Sun, Dyes Pigm., 2013, 96, 349–363 CrossRef CAS.
- J. Calvo-Castro, C. J. McHugh and A. J. McLean, Dyes Pigm., 2015, 113, 609–617 CrossRef CAS.
- J. L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350 CrossRef CAS PubMed.
- Y. R. Mo, Z. Y. Lin, W. Wu and Q. E. Zhang, J. Phys. Chem., 1996, 100, 11569–11572 CrossRef CAS.
- M. Krglewski, J. Mol. Spectrosc., 1989, 133, 10–21 CrossRef.
- P. Qin, X. C. Yang, R. K. Chen, L. C. Sun, T. Marinado, T. Edvinsson, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2007, 111, 1853–1860 CAS.
- J. Baldenebro-López, J. Castorena-González, N. Flores-Holguín, J. Almaral-Sánchez and D. Glossman-Mitnik, Int. J. Mol. Sci., 2012, 13, 4418–4432 CrossRef PubMed.
- G. L. Zhang, Y. Bai, R. Z. Li, D. Shi, S. Wenger, S. M. Zakeeruddin, M. Gratzel and P. Wang, Energy Environ. Sci., 2009, 2, 92–95 CAS.
- P. Politzer, P. R. Laurence and K. Jayasuriya, Environ. Health Perspect., 1985, 61, 191–202 CrossRef CAS PubMed.
- A. Kathiravan, V. Srinivasan, T. Khamrang, M. Velusamy, M. Jaccob, N. Pavithra, S. Anandan and K. Velappan, Phys. Chem. Chem. Phys., 2017, 19, 3125–3135 RSC.
- A. K. Biswas, A. Das and B. Ganguly, New J. Chem., 2016, 40, 9304–9312 RSC.
- K. Chaitanya, X. H. Ju and B. M. Heron, RSC Adv., 2015, 5, 3978–3998 RSC.
- W. Li, J. Wang, J. Chen, F. Q. Bai and H. X. Zhang, Spectrochim. Acta, Part A, 2014, 118, 1144–1151 CrossRef CAS PubMed.
- A. Islam, H. Sugihara and H. Arakawa, J. Photochem. Photobiol., A, 2003, 158, 131–138 CrossRef CAS.
- Z. J. Ning, Q. Zhang, W. J. Wu, H. C. Pei, B. Liu and H. Tian, J. Org. Chem., 2008, 73, 3791–3797 CrossRef CAS PubMed.
- J. Martínez, Chem. Phys. Lett., 2009, 478, 310–322 CrossRef.
- M. Nakano, H. Fujita, M. Takahata and K. Yamaguchi, J. Am. Chem. Soc., 2002, 124, 9648–9655 CrossRef CAS PubMed.
- V. M. Geskin, C. Lambert and J. L. Brédas, J. Am. Chem. Soc., 2003, 125, 15651–15658 CrossRef CAS PubMed.
- J. I. Nishida, T. Masuko, Y. Cui, K. Hara, H. Shibuya, M. Ihara, T. Hosoyama, R. Goto, S. Mori and Y. Yamashita, J. Phys. Chem. C, 2010, 114, 17920–17925 CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- Y. R. Fang, Y. Z. Li, H. X. Xu and M. T. Sun, Langmuir, 2010, 26, 7737–7746 CrossRef CAS PubMed.
- M. Sun, P. Kjellberg, W. J. D. Beenken and T. Pullerits, Chem. Phys., 2006, 327, 474–484 CrossRef CAS.
- T. T. Steckler, P. Henriksson, S. Mollinger, A. Lundin, A. Salleo and M. R. Andersson, J. Am. Chem. Soc., 2014, 136, 1190–1193 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28396a |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Yuanchao Lia,
Peng Songbcd,
Fengcai Mac,
Jianping Liange and
Mengtao Sun
*a,
Yuanchao Lia,
Peng Songbcd,
Fengcai Mac,
Jianping Liange and
Mengtao Sun *bcd
*bcd
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of these as dyes. The main components of these dyes are betalain and anthocyanin. The photoelectric conversion efficiencies of betalain, anthocyanin and the mixture (1
1 mixture of these as dyes. The main components of these dyes are betalain and anthocyanin. The photoelectric conversion efficiencies of betalain, anthocyanin and the mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are 0.47%, 0.14% and 0.20%, respectively. Fourier transform infra-red, electrochemical impedance and ultraviolet-visible spectroscopy were used to analyze the photoelectric properties of the dyes.17 Ding et al. analyzed YA422, YA421 and IQ4 using DFT and TD-DFT, showing that Forster resonance energy transfer occurs only in YA422. The nearest position of every monomer in YA422 is separated by a row of Ti atoms, which is beneficial to the formation of ordered alignment. YA422 exhibits a faster electron injection rate, kinject (2.27 × 1015 s−1). Finally, they designed a promising candidate (DW1), which showed a larger kinject and strong absorption compared to YA422.18 Yang et al. designed and analyzed a series of SPL101–SPL108 dyes using DFT and TD-DFT, indicating that the π-spacer of SPL103–SPL104 is a promising functional group for D–π–A dyes. Compared with C217 dye, SPL106 and SPL108 not only have higher molar absorption coefficients and similar energy gaps, but also exhibit obvious red shifts (128 and 143 nm, respectively) and wide absorption spectra.19 Kwon et al. designed and investigated two novel D–A–π–A dyes (TICC and TICR) with ID6 dye as a reference using DFT and TD-DFT. The different LUMO levels affect the molar absorption coefficient and the absorption band of the molecule. Compared with other dyes, TICR exhibited a red shift and a broad absorption spectrum and had a higher molar extinction coefficient.20 Recently, Zhang et al. used WS-2 as a reference dye to design two novel indoline-based D–A–π–A dyes, WS-92 and WS-95 (Fig. 1). Solar cells based on WS-95 yielded a PCE of 7.69% (JSC = 16.87 mA cm−2, VOC = 696 mV, FF = 0.66).21
1) are 0.47%, 0.14% and 0.20%, respectively. Fourier transform infra-red, electrochemical impedance and ultraviolet-visible spectroscopy were used to analyze the photoelectric properties of the dyes.17 Ding et al. analyzed YA422, YA421 and IQ4 using DFT and TD-DFT, showing that Forster resonance energy transfer occurs only in YA422. The nearest position of every monomer in YA422 is separated by a row of Ti atoms, which is beneficial to the formation of ordered alignment. YA422 exhibits a faster electron injection rate, kinject (2.27 × 1015 s−1). Finally, they designed a promising candidate (DW1), which showed a larger kinject and strong absorption compared to YA422.18 Yang et al. designed and analyzed a series of SPL101–SPL108 dyes using DFT and TD-DFT, indicating that the π-spacer of SPL103–SPL104 is a promising functional group for D–π–A dyes. Compared with C217 dye, SPL106 and SPL108 not only have higher molar absorption coefficients and similar energy gaps, but also exhibit obvious red shifts (128 and 143 nm, respectively) and wide absorption spectra.19 Kwon et al. designed and investigated two novel D–A–π–A dyes (TICC and TICR) with ID6 dye as a reference using DFT and TD-DFT. The different LUMO levels affect the molar absorption coefficient and the absorption band of the molecule. Compared with other dyes, TICR exhibited a red shift and a broad absorption spectrum and had a higher molar extinction coefficient.20 Recently, Zhang et al. used WS-2 as a reference dye to design two novel indoline-based D–A–π–A dyes, WS-92 and WS-95 (Fig. 1). Solar cells based on WS-95 yielded a PCE of 7.69% (JSC = 16.87 mA cm−2, VOC = 696 mV, FF = 0.66).21