Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sulfur doped graphene as a promising metal-free electrocatalyst for oxygen reduction reaction: a DFT-D study†
Zhansheng Lu ab,
Shuo Lia,
Chuang Liua,
Chaozheng Hec,
Xinwei Yanga,
Dongwei Mad,
Guoliang Xua and
Zongxian Yang*ae
ab,
Shuo Lia,
Chuang Liua,
Chaozheng Hec,
Xinwei Yanga,
Dongwei Mad,
Guoliang Xua and
Zongxian Yang*ae
aCollege of Physics and Materials Science, Henan Normal University, Xinxiang 453007, China. E-mail: yzx@henannu.edu.cn
bDepartment of Physics and Astronomy, University of California, Irvine, CA 92697-4575, USA
cCollege of Physics and Electronic Engineering, Nanyang Normal University, Nanyang 473061, China
dSchool of Physics, Anyang Normal University, Anyang 455000, China
eCollaborative Innovation Center of Nano Functional Materials and Applications, Kaifeng, China
First published on 7th April 2017
Abstract
As an efficient metal-free catalyst, graphene doped with heteroatoms is highly active in promoting electrochemical oxygen reduction reaction (ORR). The detailed kinetic and thermodynamic behaviors of the entire ORR process on sulfur doped monovacancy graphene (SGV), as well as the original mechanism are investigated by the dispersion-corrected density function theory (DFT-D) calculations. It is found that the SGV is rather stable and the sulfur dopant is probably the active center. There are two proposed ORR pathways by kinetic process: the dissociation of OOH and the hydrogenation of OOH with the rate-determining steps of 0.75 eV and 0.62 eV, respectively. And the Gibbs free energy diagram of the entire ORR indicates that the dissociation of OOH is precluded, because the process of reduction step of O into OH is endothermic, while the hydrogenation of HOOH is the most favorable pathway even at high potential of 0.86 V. Our DFT-D simulation suggests that the SGV would be an efficient electrocatalyst for ORR.
1. Introduction
The energy-conversion efficiency of low-temperature fuel cells (FCs) is mainly limited by the slow kinetics of the oxygen reduction reaction (ORR) on cathode.1,2 The most effective cathodes of the commercial FCs is Pt and its alloys.3 Given the high cost, low abundance and poor durability of the Pt-based catalysts in FCs, non-precious metals cathodes or metal-free carbon-based cathodes have sparked worldwide interest in very recent years owing to their low cost, environmental friendliness, outstanding activity and stability.4–9 The cheap and stable graphene-based materials doped with heteroatoms,10 such as nitrogen,11,12 phosphorus,13,14 and their mixtures,15–17 present high catalytic activity and selectivity for ORR. The detailed kinetic behaviors and mechanisms of the entire ORR process on the modified graphene, such as phosphorus doped graphene,18,19 nitrogen doped graphene,20,21 boron doped graphene,22 MnN4 embedded graphene,23 and FeN4 embedded graphene,24,25 have been revealed successfully through density functional theory (DFT) calculations.As one of the candidate for the metal-free cathode materials, the sulfur doped graphene (SG) is also reported to present high electrocatalytic activity for ORR.26–31 By replacing one C atom with sulfur, there are two kind of sulfur doped graphene, graphitic S and thiophene S: the thiophene S was found mainly at the edges of graphene bonding to C,28 and the graphitic S was found inside the lattice structure of the graphene.27,32 For ORR mechanism on the thiophene S doped graphene, Zhang et al.33 using several sulfur doped graphene clusters models demonstrated that the sulfur-doped graphene clusters with sulfur or sulfur oxide locating at graphene edges show electrocatalytic activity for ORR, and the zigzag edge or the neighboring carbon atoms of doped sulfur oxide atoms are the catalytic active sites. Summarily, from their reaction energy barrier calculation, Zhang et al.33 predicted that the (thiophene) sulfur-doped graphene could show ORR catalytic properties comparable to Pt.
On the other hand, as other important sulfur doping configuration, the graphitic sulfur doped graphene presents the great stability from our simulations presented below. Moreover, to the best of our knowledge, the theoretical studies on the electrocatalytic activity of the graphitic sulfur doped graphene is still lack, and the detailed kinetic behaviors, the catalytic active center and the catalytic mechanism for the ORR on the graphitic sulfur doped graphene remains unclear. Thus, in the current study, we have studied the entire ORR mechanisms on the graphitic sulfur doped graphene (SGV) using the first-principles method. The adsorption properties for all possible ORR involved species and the activation energies for all possible elementary reactions of the entire ORR on the SGV in acid environment. Furthermore, the most favorable pathway for ORR on SGV is identified based on the calculation of the transition states. Our current results not only show that the ORR on SGV proceeds more possibly via a direct hydrogenation of HOOH reaction pathway but also demonstrate that the SGV would be an efficient metal-free electrocatalyst for ORR.
2. Theoretical methods
All of the spin-polarized calculations were performed within dispersion-corrected density functional theory (DFT-D) computations as implemented in Dmol3 code embedded in Materials Studio (Accelrys, SanDiego, CA). The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) functional was employed using the DFT semi-core pseudopotential34 with long-range dispersion correction via Grimme approach35 to describe exchange and correlation effects,36 and the polarization p-function (DNP) as the basis set for the double numerical atomic orbital augmented was chosen. The convergence tolerances of the geometry optimization are set to 10−5 Ha (1 Ha = 27.21 eV) for the energy, 0.002 Ha Å−1 for the maximum force, and 0.005 Å for the maximum displacement. The electronic SCF tolerance is set to 10−6 Ha. In order to achieve accurate electronic convergence, we apply a smearing of 0.005 Ha to the orbital occupation. The k-points grid is set as 5 × 5 × 1 and the k-points are generated automatically using the Monkhorst–Pack method37 for the relaxation calculations. And denser meshes of 15 × 15 × 1 are used to calculate the density of states (DOS) for the electronic relaxation. The transition states are obtained by linear synchronous transit (LST)/quadratic synchronous transit (QST) method in Dmol3 code for ORR elemental steps. It is found that all the minima possess real frequencies, and the transition states have only one imaginary frequency.Gibbs free energy of the ORR intermediates can be calculated with the approach developed by Nørskov et al.38 The change in free energy for the elemental step is defined as ΔG = ΔE + ΔZPE + TΔS + ΔGU + ΔGPH + ΔGfield, where ΔE is the reaction energy based on DFT-D calculations, ΔZPE is the zero point energy, T is the temperature and equal to 300 K, ΔS is the change in the entropy. ZPE and S of the ORR intermediates are calculated based on the vibrational frequencies. ΔGU are the free energy contributions due to variations in the electrode potential U. ΔGU = −neU, where n is the number of electrons transferred and U is the electrode potential vs. the standard hydrogen electrode (SHE). In our system, ΔGPH isn't discussed. ΔGfield is normally ignored due to its small value.38 We set the reference potential to be that of the standard hydrogen electrode. The free energy of 1/2H2 can be used to instead of that of (H+ + e−). The free energy of H2O was calculated in the gas phase at 300 K and the free energy of O2 was obtained from the reaction O2 + 2H2 = 2H2O for which a free energy change is 4.92 eV.39
The adsorption energy (Ead) is defined as Ead = Eadsorbate + Esupport − Eadsorbate/support, where Eadsorbate, Esupport and Eadsorbate/support are the total energies of the free adsorbate, the corresponding support and the support with the adsorbate, respectively. With this definition, a positive value indicates an exothermic adsorption. We use the same periodic box dimensions and the same level of calculations to obtain all the energies for Eadsorbate, Esupport, and Eadsorbate/support.
3. Results and discussion
3.1. Properties of SGV
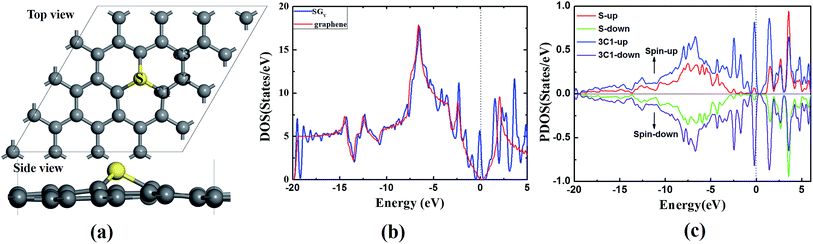
The SGV is modeled by replacing one of the lattice carbon atoms with a S atom from a 4 × 4 graphene supercell with the vacuum layer of 15 Å. According to our careful tests, the size of supercell is enough to study the ORR process. In the optimized SGV (as shown in Fig. 1a), the S atom protrudes out of the graphene plane forming three S–C1 bonds of 1.47 Å. The C1–C2 bond neighboring to the S dopant is 1.40 Å (see Fig. 1a). The formation energy (Ef) of the SGV given by Ef = Etotal(m, n) − Etotal(Gra) − mμS + nμC. In the formula, Etotal(S) is the total energy of the supercell with the defect complex, and Etotal(Gra) is the total energy of the pristine graphene. The symbols μS and μC are the chemical potentials of S and C and m and n is the number of S and the substituted C, respectively. μC is calculated as the carbon atom in the graphene. For the chemical potential of S, which is tunable in the experiments, we set the range from H2S to the free atomic sulfur. The Ef of the S doped graphene is from 3.68 to 0.45 eV. The increased μS is corresponding to the decreased Ef, indicating that S is able to dope into graphene at high S chemical potential. The Ef of S doped divacancy graphene with μS of the free atomic sulfur is 1.71 eV (higher 1.26 eV than SGV), because the formation of divacancy graphene is more difficult. Therefore, SGV is easier to form by thermodynamic standpoint.To understand the introduced changes of the SGV electronic structure upon sulfur doping, the calculated DOS of the SGV and the pure graphene are presented in Fig. 1b. Different from that of pure graphene, upon sulfur doping, some sharp peaks emerges at the Fermi level of the SGV. According to the partial density of states (PDOS) analysis (presented in Fig. 1c), the emerged peaks are mainly from the sulfur dopant and the its neighboring C atoms. As suggested in previous works, those kind of states near the Fermi level would facilitate to the charge transfer between the substrate and the adsorbed species,40,41 and the sulfur doping induced electronic states emerging near the Fermi level should play an important role in the enhanced chemical activity of graphene.
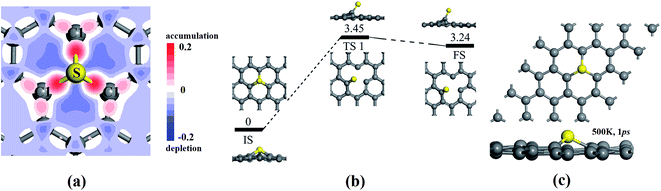
In addition to the novel catalytic activity of SGV with electronic structure analysis, on the other hand, the stability of SGV is a precondition for ORR. Fig. 2a presents the deformation charge density (DCD) map for the SGV, which confirms the formation of the stable covalent bond between sulfur atom and its neighboring C atoms, in line with the recent experimental results.27 According to the Mulliken atomic charges analysis, the atomic S is negatively charged by 0.09 |e|, the atomic C1 is negatively charged by 0.06 |e| and the atomic C2 is positively charged by 0.06 |e|, indicating a negligible charge transfer between the S and graphene sheet, due to the similar electronegativity of S and C.
The stability of the SGV model is further investigated from the mobility of the doping S and diffusion of the S dopant to its neighbor stable adsorption site. The various configurations of the S doped graphene or the adsorption of the S atom on the monovacancy-graphene support are presented in Fig. S1 in the ESI,† and it is turned out that SGV presented above is the most stable configuration from the rather strong interaction between the S atom and the defect-graphene support. The S atom adsorbed on one of C atoms around the defect is the second most stable configuration (see Fig. S1† and 2b). The extremely big diffusion barrier (marked as “TS 1” in Fig. 2b) of 3.45 eV for the mobility of the S dopant from the most stable adsorption configuration (the selected SGV model) to the second most stable adsorption configuration indicates the immobility of the atomic S anchored at the monovacancy-graphene and the great stability of the selected SGV model. To further confirm the thermodynamical stable of SGV, the first principles molecular dynamics calculations are performed in a period of 1000 fs at the temperature of 500 K. The final structure of SGV from the molecular dynamics calculations is presented in Fig. 2c, and it is turned out that the C and S atoms are almost in the same plane just with slight distortion.
3.2. The adsorption of various ORR involved species on SGV
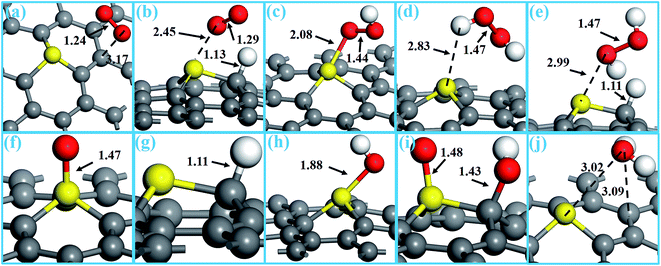
The most stable configurations of the various ORR involved species on SGV, including O2, OOH, HOOH, O, H, OH, and H2O, are presented in Fig. 3, and their corresponding adsorption properties are summarized in Table 1.| Reaction intermediates | Configurations | Bond lengths (Å) | Ead | Δq |
|---|---|---|---|---|
| a *represented that the reactant binds to the SGV surface. | ||||
| O2 | Top-C2 | d(O–O) = 1.24 | 0.25 | −0.21 |
| O2 + H* | Hollow | d(O–O) = 1.29 | 0.11 | −0.32 |
| d(H–C) = 1.13 | 1.64 | 0.24 | ||
| OOH* | Hollow | d(O–O) = 1.44 | 0.66 | −0.29 |
| HOOH | Hollow | d(O–O) = 1.47 | 0.34 | 0.03 |
| HOOH + H* | Hollow | d(O–O) = 1.47 | 0.49 | 0.03 |
| d(H–C) = 1.11 | 1.94 | 0.21 | ||
| O* | Top-S | d(O–S) = 1.47 | 5.06 | −0.35 |
| H* | Top-C1 | d(H–C) = 1.11 | 1.78 | 0.17 |
| OH* | Top-S | d(O–S) = 1.88 | 1.79 | −0.27 |
| O* + OH* | Top-S | d(O–S) = 1.48 | 4.49 | −0.35 |
| Top-C1 | d(O–C) = 1.43 | 1.22 | −0.09 | |
| H2O | Hollow | d(O–H) = 0.97 | 0.35 | 0.04 |
The adsorption of O2 is a prerequisite of the ORR proceeding on the catalyst, thus we firstly investigate the adsorption characters of O2. The most stable adsorption configuration of an O2 molecule is on a carbon (marked as “C2”) site with the Ead of 0.25 eV, the O–O bond length of 1.24 Å and the O and C2 distance of 3.17 Å (see Fig. 3a). Given the weak interaction together with the negligible charge transfer between the O2 molecule and the SGV support, this adsorption configuration (presented in Fig. 3a) would be a physisorption configuration without the formation of the chemical bond between O2 molecule and the SGV support.
The co-adsorption of O2 and H* (hereafter, “*” represents the reactant binding to the support) is an important intermediate product, where the O2 (the O–O bond of 1.29 Å) and H* is respectively adsorbed on the hollow site and the C1 site forming a C–H bond of 1.13 Å (see Fig. 3b). The Ead of O2 and H* is 0.11 eV and 1.64 eV, respectively. The adsorbed O2 is negatively charged by 0.32 |e|, and the H* is positively charged by 0.24 |e|.
It is found that the OOH species prefers to adsorb on sulfur dopant with the formation of the O–S bond of 2.08 Å (see Fig. 3c), and the O–O bond of the adsorbed OOH is 1.44 Å and the O–H bond is 0.98 Å. The Ead of OOH* is 0.66 eV and the OOH* is negatively charged by 0.29 |e|. The HOOH specie weakly adsorbs on SGV with the small Ead of 0.34 eV and the negligible charge transfer (0.03 |e|), and the distance between H and S is 2.83 Å (see Fig. 3d).
As one of the intermediate products, the most stable co-adsorption configuration of the HOOH and H* is presented in Fig. 3e: the HOOH stays above the sulfur dopant, and the H* adsorbed on C1 forming a C–H bond of 1.11 Å. The Ead of HOOH and H* is 0.49 eV and 1.94 eV, respectively. The adsorbed HOOH is negatively charged by 0.03 |e|. The H* is positively charged by 0.21 |e|.
As another ORR reactant, the atomic O is preferably adsorbed on S site with the rather big Ead of 5.06 eV, and the length of the formed S–O bond is 1.47 Å (see Fig. 3d). The atomic O is negatively charged by 0.35 |e|. The atomic H prefers to adsorb on C1 site (neighboring the S dopant) with an Ead of 1.78 eV, and the formed C–H bond is 1.11 Å (see Fig. 3g). The atomic H is positively charged by 0.17 |e|, confirming that H* could be taken as H+ in the calculations.
As an important intermediate product, OH is preferably adsorbed on S site forming an S–O bond of 1.88 Å with an Ead of 1.79 eV (see Fig. 3h). The OH* is negatively charged by 0.27 |e|. The co-adsorption of O and OH is other important intermediate product, where the O and OH adsorbs on the S site and the C1 site forming an S–O bond of 1.48 Å and a C–O bond of 1.43 Å, respectively (see Fig. 3i).
As the final product, H2O is weakly adsorbed on the SGV with the small adsorption energy of 0.35 eV (see Fig. 3j). The weak adsorption together with the long distance and the negligible charge transfer between H2O and the SGV support indicates that the formed H2O would be easily released as the final product of ORR.
3.3. Chemical behavior in various reaction pathways
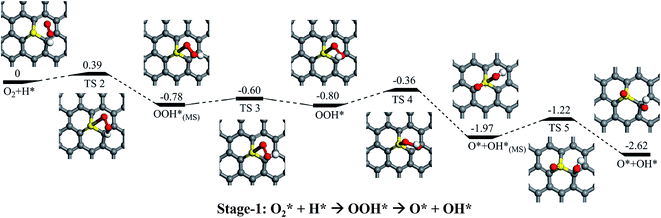
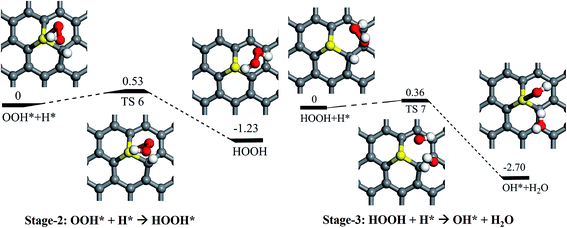
As mentioned above, it is found that the rather stronger adsorption of H than the O2 (1.78 eV vs. 0.25 eV), and the adsorption of H is greatly preferable than O2. Thus, the direct dissociation pathway of the adsorbed O2 on SGV support would not be further considered in here, and the H pro-adsorbed configuration would be focused. As shown in Fig. 4, it is found that the weakly adsorbed O2 is easily hydrogenated by the pre-adsorbed H into OOH* on SGV: firstly, the O2 + H* co-adsorbed configuration would form the metastable state (MS) of OOH* with a reaction barrier of 0.39 eV and an exothermic reaction energy of 0.78 eV. Then the metastable adsorbed OOH* convert into the most stable adsorbed OOH* with a small reaction barrier of 0.18 eV and a slight exothermic reaction energy of 0.02 eV. The most stable adsorbed OOH* is dissociated into the metastable co-adsorbed O + OH species via the activation barrier of 0.44 eV and an exothermic reaction energy of 1.17 eV. Finally, the formed OH* would diffuse from S site to C1 site via the diffusion barrier of 0.75 eV and an exothermic reaction energy of 0.65 eV. The above process is marked as Stage-1.In addition to the direct OOH* dissociation pathway, the hydrogenation of OOH* species is also considered, and the corresponding process is noted as “Stage-2” in Fig. 5. In Stage-2, upon the hydrogenation of the OOH* species by the co-adsorbed H*, the HOOH is formed via a reaction barrier of 0.53 eV and an exothermic reaction energy of 1.23 eV. We find that the formed HOOH is difficultly dissociated into two OH species due to the weak adsorption of HOOH on SGV. “Stage-3” in Fig. 5 is presented the hydrogenation of the HOOH by the co-adsorbed H*: the co-adsorbed OH* + H2O is formed via a reaction barrier of 0.36 eV and an exothermic reaction energy of 2.70 eV. As mentioned above, the formed H2O would easily release due to the weak interaction between H2O and SGV.
Following the formation of the O* + OH* species from the dissociation of OOH*, there are two possible pathways for their further hydrogenation: the O* hydrogenation or the OH* hydrogenation. On the one hand, we found that the hydrogenation of the OH would result in the formation of H2O via a reaction barrier of 0.68 eV and an exothermic reaction energy of 3.28 eV, respectively (see Stage-4 in Fig. 6). As the final product of the ORR process, the H2O molecule would be easily released due to the week interaction between H2O and SGV (with an adsorbed atomic O), which has a rather small Ead of 0.39 eV. On the other hand, the hydrogenation of the O* of the co-adsorbed O* + OH* is difficult because of the rather high reaction barrier (2.77 eV), and the pathway is not further considered.
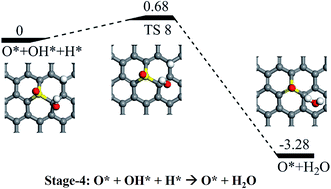 | ||
| Fig. 6 Schematic potential energy profiles for the formation of the H2O from the hydrogenation of the OH (Stage-4). The corresponding TS is denoted as “TS 8”. | ||
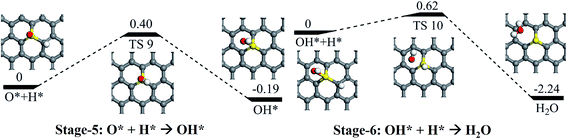
Following the release of the (first) formed H2O molecule, the left atomic O staying on sulfur will be hydrogenated into the OH species via a reaction barrier of 0.40 eV and an exothermic reaction energy of 0.19 eV (see Stage-5 in Fig. 7). Again, the formed OH would be further hydrogenated into H2O via the reaction barrier of 0.62 eV and an exothermic reaction energy of 2.24 eV (see Stage-6 in Fig. 7). The formed H2O would easily release due to the weak interaction between water and the support, resulting in the recovery of SGV.
3.4. The selectivity of two pathways with kinetics and thermodynamics
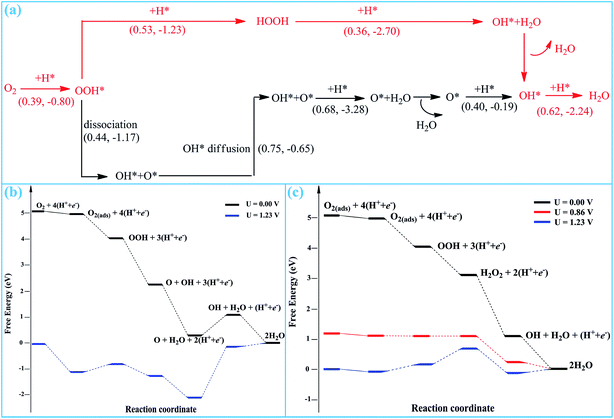
According to the reaction stages presented above, two possible pathways are proposed for the entire ORR process on SGV, which are summarized in Fig. 8a.Pathway I: Stage-1 (to form O + OH) → Stage-4 → Stage-5 → Stage-6
Pathway II: Stage-1 (to form OOH) → Stage-2 → Stage-3 → Stage-6
In pathway I (black lines in Fig. 8), the pathway starts from the direct hydrogenation of the adsorbed O2, resulting in the formation of the OOH* species. The form OOH* is dissociated into O* + OH*. Upon a diffusion process, the formed O* and OH* would be further hydrogenated into H2O. The rate-determining step of pathway I is the diffusion of OH* and the corresponding reaction barrier is 0.75 eV.
In pathway II (red lines in Fig. 8), the pathway starts from the co-adsorption of O2 + H*. The O2 will proceed with three sequential hydrogenation reactions to form OOH*, HOOH and the final ORR product of released H2O molecule, whereas the left OH* is chemisorbed on sulfur. Finally, the OH* is hydrogenated into the second H2O. The rate-determining step of this pathway is the formation of the second H2O with a reaction barrier of 0.62 eV.
According to the computed free energy diagram, all of the reduction steps of pathway I and pathway II are presented in Fig. 8b and c, respectively. In pathway I, all of the reduction steps except the O reduction are downhill at 0 potential, as shown in Fig. 8b. The reduction step of O into OH has a positive ΔG of 0.86 V at 0 potential, which is the thermodynamic rate-determining step. When the thermodynamic process is continuously exothermic, it can be favorably applicable to ORR. Therefore, pathway I is precluded by the Gibbs free energy calculation, because the process of reduction step of O into OH is endothermic at 0 potential. However, in pathway II, all of the reduction steps are downhill at 0 potential, indicating that the enter ORR process successfully occurs by thermodynamic calculations. And even the ORR process occurs at the high potential of 0.86 V. Therefore, the pathway II is the most possible for ORR on SGV.
4. Conclusions
DFT-D calculation is performed to investigate the detailed kinetic and thermodynamic behaviors of the entire ORR process on SGV. It is found that the SGV is rather stable due to the strong interaction between the sulfur and the defected-graphene. The O2 molecule prefers to form OOH* species on SGV with the co-adsorbed H*. There are two proposed pathways for the entire ORR process on SGV, i.e., the OOH* direct dissociation pathway and the OOH* hydrogenation pathway. The reaction barriers of the corresponding rate-determining steps of the two proposed pathways are 0.75 eV and 0.62 eV, respectively. According to the Gibbs free energy simulation at various potentials, the process of the OOH dissociation pathway is precluded, because the process of reduction step of O into OH is endothermic. While the process of the hydrogenation of HOOH species is effective at 0 potential, and it can occurs at a high potential of 0.86 V. It is expected that the SGV would be an efficient metal-free electrocatalyst for ORR.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 51401078, 11147006, and U1404216). Sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province (Grant No. 15HASTIT016), Foundation for the key Young Teachers of Henan Province and Key Technology Research and Development Program of Henan Province(Grant No. 152102210083 and 142102210455), Science Foundation for the Excellent Youth Scholars of Henan Normal University (Grant No. 14YQ005). Supported by The High Performance Computing Center of Henan Normal University. We are also grateful to the Computing Center of Jilin Province for essential support.References
- B. C. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed
.
- R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon and D. Wood, Chem. Rev., 2007, 107, 3904–3951 CrossRef CAS PubMed
.
- B. Lim, M. Jiang, P. H. Camargo, E. C. Cho, J. Tao, X. Lu, Y. Zhu and Y. Xia, Science, 2009, 324, 1302–1305 CrossRef CAS PubMed
.
- F. Jaouen, E. Proietti, M. Lefèvre, R. Chenitz, J.-P. Dodelet, G. Wu, H. T. Chung, C. M. Johnston and P. Zelenay, Energy Environ. Sci., 2011, 4, 114–130 CAS
.
- R. Bashyam and P. Zelenay, Nature, 2006, 443, 63–66 CrossRef CAS PubMed
.
- D. Yu, E. Nagelli, F. Du and L. Dai, J. Phys. Chem. Lett., 2010, 1, 2165–2173 CrossRef CAS
.
- Y. Zheng, Y. Jiao, J. Chen, J. Liu, J. Liang, A. Du, W. Zhang, Z. Zhu, S. C. Smith, M. Jaroniec, G. Q. Lu and S. Z. Qiao, J. Am. Chem. Soc., 2011, 133, 20116–20119 CrossRef CAS PubMed
.
- Z. Yang, H. Nie, X. A. Chen, X. Chen and S. Huang, J. Power Sources, 2013, 236, 238–249 CrossRef CAS
.
- Z. Lu, S. Li, D. Ma, Y. Zhang, X. Yang, C. He, X. Wang and Z. Yang, J. Mater. Sci., 2016, 51, 10400–10407 CrossRef CAS
.
- R. Ma, Y. Ma, Y. Dong and J.-M. Lee, Nano Adv., 2016, 1, 50–61 CrossRef
.
- J.-i. Ozaki, S.-i. Tanifuji, A. Furuichi and K. Yabutsuka, Electrochim. Acta, 2010, 55, 1864–1871 CrossRef CAS
.
- L. Qu, Y. Liu, J.-B. Baek and L. Dai, ACS Nano, 2010, 4, 1321–1326 CrossRef CAS PubMed
.
- Z. Liu, F. Peng, H. Wang, H. Yu, J. Tan and L. Zhu, Catal. Commun., 2011, 16, 35–38 CrossRef CAS
.
- D.-S. Yang, D. Bhattacharjya, S. Inamdar, J. Park and J.-S. Yu, J. Am. Chem. Soc., 2012, 134, 16127–16130 CrossRef CAS PubMed
.
- C. H. Choi, S. H. Park and S. I. Woo, J. Mater. Chem., 2012, 22, 12107–12115 RSC
.
- C. H. Choi, M. W. Chung, S. H. Park and S. I. Woo, Phys. Chem. Chem. Phys., 2013, 15, 1802–1805 RSC
.
- Y. Zhao, L. Yang, S. Chen, X. Wang, Y. Ma, Q. Wu, Y. Jiang, W. Qian and Z. Hu, J. Am. Chem. Soc., 2013, 135, 1201–1204 CrossRef CAS PubMed
.
- X. Zhang, Z. Lu, Z. Fu, Y. Tang, D. Ma and Z. Yang, J. Power Sources, 2015, 276, 222–229 CrossRef CAS
.
- X. Bai, E. Zhao, K. Li, Y. Wang, M. Jiao, F. He, X. Sun, H. Sun and Z. Wu, Carbon, 2016, 105, 214–223 CrossRef CAS
.
- L. Zhang and Z. Xia, J. Phys. Chem. C, 2011, 115, 11170–11176 CAS
.
- S. Ni, Z. Li and J. Yang, Nanoscale, 2012, 4, 1184–1189 RSC
.
- G. Fazio, L. Ferrighi and C. Di Valentin, J. Catal., 2014, 318, 203–210 CrossRef CAS
.
- Z. Lu, G. Xu, C. He, T. Wang, L. Yang, Z. Yang and D. Ma, Carbon, 2015, 84, 500–508 CrossRef CAS
.
- S. Kattel and G. Wang, J. Phys. Chem. Lett., 2014, 5, 452–456 CrossRef CAS PubMed
.
- J. Zhang, Z. Wang and Z. Zhu, J. Power Sources, 2014, 255, 65–69 CrossRef CAS
.
- Z. Yang, Z. Yao, G. Li, G. Fang, H. Nie, Z. Liu, X. Zhou, X. A. Chen and S. Huang, ACS Nano, 2011, 6, 205–211 CrossRef CAS PubMed
.
- H. L. Poh, P. Šimek, Z. K. Sofer and M. Pumera, ACS Nano, 2013, 7, 5262–5272 CrossRef CAS PubMed
.
- W. Kiciński, M. Szala and M. Bystrzejewski, Carbon, 2014, 68, 1–32 CrossRef
.
- S. Inamdar, H.-S. Choi, P. Wang, M. Y. Song and J.-S. Yu, Electrochem. Commun., 2013, 30, 9–12 CrossRef CAS
.
- Z. Ma, S. Dou, A. Shen, L. Tao, L. Dai and S. Wang, Angew. Chem., 2015, 127, 1908–1912 CrossRef
.
- J. Wang, R. Ma, Z. Zhou, G. Liu and Q. Liu, Sci. Rep., 2015, 5, 9304 CrossRef PubMed
.
- D. Higgins, M. A. Hoque, M. H. Seo, R. Wang, F. Hassan, J.-Y. Choi, M. Pritzker, A. Yu, J. Zhang and Z. Chen, Adv. Funct. Mater., 2014, 24, 4325–4336 CrossRef CAS
.
- L. Zhang, J. Niu, M. Li and Z. Xia, J. Phys. Chem. C, 2014, 118, 3545–3553 CAS
.
- B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef
.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- J. Zhang, L. Liu, W. Liu and M. Zhang, J. Electrochem. Soc., 2016, 163, F160–F165 CrossRef CAS
.
- X. Fan, W. Zheng and J.-L. Kuo, RSC Adv., 2013, 3, 5498–5505 RSC
.
- Y. Tang, Z. Yang, X. Dai, D. Ma and Z. Fu, J. Phys. Chem. C, 2013, 117, 5258–5268 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00632b |
| This journal is © The Royal Society of Chemistry 2017 |