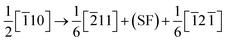Open Access Article
Open Access ArticleElectronic structure and multi-scale behaviour for the dislocation–doping complex in the gamma phase of nickel-base superalloys
Feng-Hua Liu a and
Chong-Yu Wang*ab
a and
Chong-Yu Wang*ab
aCentral Iron and Steel Research Institute, Beijing 100081, PR China. E-mail: cywang@mail.tsinghua.edu.cn
bDepartment of Physics, Tsinghua University, Beijing 100084, PR China
First published on 30th March 2017
Abstract
By using the lattice Green-function multiscale method, the equilibrium geometry of the edge dislocation in the γ matrix was obtained and the electronic structure changes due to the addition of refractory elements Re, W and Ta were analysed. The results indicate that the orbital hybridization takes place during the interaction between dislocation and doping atoms, among which the hybridization between dislocation and Re is the most complicated. On the macroscopic level, the critical resolved shear stress of the γ matrix containing dislocation–doping complex was predicted at T = 0 and 78 K from first-principles calculations. Considering the distribution of the doping elements between two phases, the remarkable strengthening effect of Re in Ni-base superalloys can be ascribed to a combination of the strong partitioning to the γ phase and the strong chemical interactions with dislocation.
1. Introduction
The nature of the dislocation–doping interaction is one of the important questions in the physics of the solid solution strengthening. An accurate configuration of the dislocation core structure is the key for understanding the mechanism of interaction between dislocation and the doping atoms in alloys. Atomic level studies by density functional theory (DFT) can precisely deal with a system containing hundreds of atoms,1–3 but are unable to address larger scale many-body problems. Continuum elasticity theory can deal with the long range stress field problem of material containing a dislocation–doping complex, but neglects the dislocation core structure.4–7 Therefore, the multi-scale modelling algorithm and bridging model are necessary and presented in this work. We hope that the multi-scale research for gaining the insight into the materials will promote the development of material science especially with the study of Materials Genomic Initiative (MGI).In the last twenty years, the multi-scale methods have been developed rapidly for probing the physical problems and exploring the intrinsic properties of material over multiple spacing and time scales in material science.8
To achieve seamless coupling between different length scales, various algorithms have been developed such as macroscopic atomistic ab initio dynamics,9 n-layered integrated molecular orbital and molecular mechanics,10 learn on the fly,11 quantum mechanics (QM)-coupled atomic discrete dislocation,12 constrained density functional theory13 and lattice Green-function (LGF).14 Among these methods, the LGF, which can bridge the gap in length scales between the DFT calculations on the atomic scale and the larger-scale continuum medium elasticity theory by an analytical formula, has been successfully applied to metallic systems to predict the dislocation core structure.14–16
Nickel-base superalloys possess outstanding high-temperature strength, low crack-growth rates and oxidation resistance and they have important applications in aircraft industry.17–19 Analysing the mechanical property of the material from the electronic structure with the multi-scale method has vast importance to the progress of nickel-base superalloys.20,21 In Ni-base single-crystal superalloys most of dislocations are present in the γ matrix, as indicated by experiments using scanning electron microscope (SEM).22,23 Huang et al. found by using energy dispersive X-ray spectroscopy (EDS)24 that refractory elements co-segregated at the dislocation core region, moreover other 3D atom probe tomography experiments also showed the partitioning of the solid solution strengtheners to the γ phase.25–27 In this regard, we will perform our study in the γ matrix containing dislocation–doping complex, where the doping atoms are refractory elements Ta, W and Re, respectively.
The paper is organized as follows: Section 2 presents the Phonon Green-function with lattice dynamics and bridging mode in multi-scale science; Section 3 outlines Electronic mechanism of dislocation–doping interaction in the γ matrix: Section 3.1 and 3.2 show computational model and methods respectively; the interaction energies between dislocation and doping atoms are to be presented in Section 3.3.1; in Section 3.3.2, we analyse the electronic structure of dislocation and dislocation–doping complex; Section 4 outlines the prediction of critical resolved shear stress on the dependence of temperature and concentration, including the corresponding first-principles calculations to obtain the parameters to carry out the prediction; Section 5 summarizes our work.
2. Phonon Green-function with lattice dynamics and bridging mode in multi-scale science
2.1 Theoretical background
The Hamiltonian of the lattice vibration system under the harmonic approximation is28
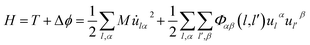 | (2-1) |
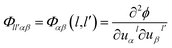 | (2-2) |
From canonical equation of classical mechanics, the equation of motion of the lattice vibration system28 can be written as
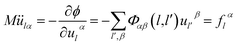 | (2-3) |
This is a linear coupling equation with 3N freedom.
2.2 Phonon Green-function29
The Green-function is defined as the solution of the operator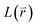 equation and
equation and 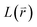 is a linear Hermitian and time independent differential operator. The equation is expressed as below
is a linear Hermitian and time independent differential operator. The equation is expressed as below
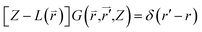 | (2-4) |
In the 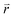 -representation, it can be written as
-representation, it can be written as
| [Z − L]G = 1 or G(ω2) = (ω2I − L)−1 | (2-5) |
Considering the phonon Green-function, one can have the expression as follows
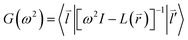 | (2-6) |
2.3 Green-function method for lattice statics30
The method is based on the Born–Von Kármán model30 of the lattice and take the zero frequency31 limit in the Born–Von Kármán equation for lattice dynamics. We can use the static Green-function for the imperfect lattice.Based on our design for computational model and the changing trend of structural energy El, the defect complex are only contained in the quantum mechanics area, which will result in the bridging area between the QM region and continuum medium region. Therefore we can use the static lattice Green-function treating the “bridging” problems of multi-scale spanning level.
Introducing 3N dimension column vectors u (displacement) and f (force acting on atoms), and the 3N × 3N square matrices Φ (force constant) and L (operator). Operator L is defined as
| L = Mü + Φ | (2-7) |
Correspondingly, the equation of motion for the lattice can be written in a matrix rotation as
| Lu = 0 | (2-8) |
| u = exp(iωt) | (2-9) |
Therefore we have
| L = −Mω2 + Φ | (2-10) |
If we take zero frequency limit, then the important expression is given as follows
| L = Φ | (2-11) |
From the eqn (2-5) and (2-11) we obtain
| G(ω2) = (ω2I − L)−1 = −(L)−1 = −(Φ)−1 | (2-12) |
2.4 Constructing the bridging mode for multi-scale science14
From the equation of lattice motion
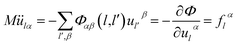 | (2-13) |
| G(ω2) = −[Φαβ(l − l′)]−1 | (2-14) |
We can obtain
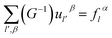 | (2-15) |
Utilizing operator performance, the expression is written as below:
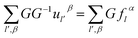 | (2-16) |
Based on the physics of force constant as well the translation symmetry of lattice, the equation of the bridging mode in the multi-scale science can be converted as
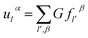 | (2-17) |
3. Electronic mechanism of dislocation–doping complex in the gamma phase
3.1 Computational model
An accurate atomic configuration of dislocation core is the key for understanding the electronic effect of the dislocation–doping complex in alloys. Generally, dislocations in a crystal are characterized by slip systems which consist of slip plane and direction. In a face-centred cubic (FCC) crystal, dislocations slip preferentially occurs on closed-packed (111) planes along [110] direction. In Ni matrix, an initial edge dislocation in the most observed slip system was constructed from the displacement field induced by dislocation in the crystal.32The model of the edge dislocation was along the x[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10], y[111] and z[1
10], y[111] and z[1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] directions, with the size of 50 Å × 50 Å × 4.311 Å containing 495 atoms. The dislocation line direction which consists of six non-equivalent (112) planes was in the z direction and periodic boundary condition was applied, while in the x and y directions vacuum boundary was introduced to separate the dislocation from its periodic images. The calculated model was divided into three regions, comprising a quantum mechanics (QM; region I) region containing 80 atoms near the core; a GF region (region II; 223 atoms) that can be treated as the bridging region between the two length scales and final continuum mechanics (CM; region III) region. The outermost layers of the model were contained in region III as if they were part of the infinite bulk.
] directions, with the size of 50 Å × 50 Å × 4.311 Å containing 495 atoms. The dislocation line direction which consists of six non-equivalent (112) planes was in the z direction and periodic boundary condition was applied, while in the x and y directions vacuum boundary was introduced to separate the dislocation from its periodic images. The calculated model was divided into three regions, comprising a quantum mechanics (QM; region I) region containing 80 atoms near the core; a GF region (region II; 223 atoms) that can be treated as the bridging region between the two length scales and final continuum mechanics (CM; region III) region. The outermost layers of the model were contained in region III as if they were part of the infinite bulk.
3.2 Computational methods
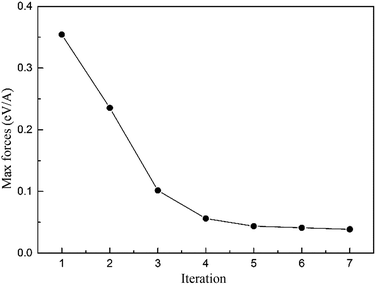
The DFT calculations were implemented by using the Vienna Ab initio Simulation Package (VASP),33,34 projector augmented wave method35,36 and the generalized gradient approximation (GGA) in the parameterization introduced by J. P. Perdew, K. Burke and M. Ernzerhof (PBE).37 The Fermi surface was smeared out using the Methfessel–Paxton smearing scheme38 taking σ = 0.2 eV. Plane waves have been included up to a cutoff energy of 300 eV. The convergence precision of the total energy was chosen as 10–5 eV in the relaxation of the electronic degrees of freedom, and a 1 × 1 × 4 Monkhorst–Pack k-mesh39 was used.The relaxation of the edge dislocation was carried out by combining first-principles calculation and the LGF multi-scale40 method. All atomic positions were optimized using the Hellmann–Feynman forces with the LGF method, which has been described previously.15 The LGF was applied to relax atoms throughout the entire region to minimize forces in the LGF region. Regarding the force-constant matrix used to obtain the LGF is derived from the perfect crystal, iterations between the VASP relaxation and the LGF optimization of the atomic positions are required. The maximum forces in the transition region in each iteration are shown in Fig. 1, where we can see that the maximum forces decrease with each iteration.
3.3 Results and discussion
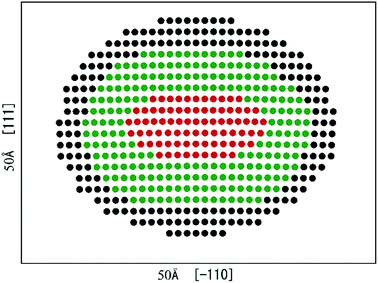
Fig. 2 presents the equilibrium dislocation core structure obtained in our calculation. The final equilibrium dislocation geometry has a core dissociated into two Shockley partials separated by approximately 15.4 Å, which is slightly larger than the value of 14.9 Å reported in ref. 41. We made dislocation analysis by Ovito software42 and the fragment of the central part of the dislocation core (atoms in red in Fig. 2) is shown in Fig. 3, in which atoms are coloured based on their local coordination structure. The stacking fault between two partial dislocations has HCP structure, and it is denoted by magenta atoms. Grey atoms represent the two Shockley partial dislocations and blue atoms represent FCC structure. The equilibrium dislocation core structure is the essential basis for the electronic structure calculations.
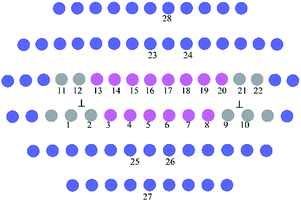 | ||
| Fig. 3 The fragment of the central dislocation core labelled with substitution sites (1−22) for solute atoms for interaction energies calculations. | ||
The interaction energy at site (xi,yj) was defined as the difference between the energy of the cell with a solute atom in dislocation core and the reference energy when the doping atom is located at infinity
| Einter(xi,yj) = Edis-doping(xi,yj) − Eref | (3-1) |
They were calculated when doping atoms occupy specific substitution positions in 〈110〉 (111) edge dislocation core in the γ phase. Doping atoms substitute for Ni atoms in different positions labelled 1−22 in Fig. 3, in both the compressed and the dilated regions of the dislocation. In the calculation only the central 80 atoms were relaxed with the surrounding atoms kept fixed.
In Fig. 4, the dislocation–doping interaction energies computed by DFT on both sides are shown for Re, W and Ta, respectively. As displayed in the plots, in dilated region the interaction energies are negative while in compressed region the energies turn out positive. We know that Ta, W and Re are bigger than the host Ni atoms, with atomic radii of 1.47, 1.39, 1.38 Å respectively. According to the continuum medium theory, the interaction energies are negative in the dilated region, which implies that our DFT calculations are in agreement with classical elastic theory. The negative interaction energies indicate that solute atoms prefer segregation in the dilated region; on the other hand, it can be characterized as friction forces when dislocation glide and therefore promote the strength of the alloy. For positions in compressed region, the interaction energies are positive which means the substitution positions in this region are energetically less favourable compared with positions in dilated region. Besides, simple symmetry can be seen in interaction energies from Fig. 4, which demonstrates the same symmetry in dislocation structure.
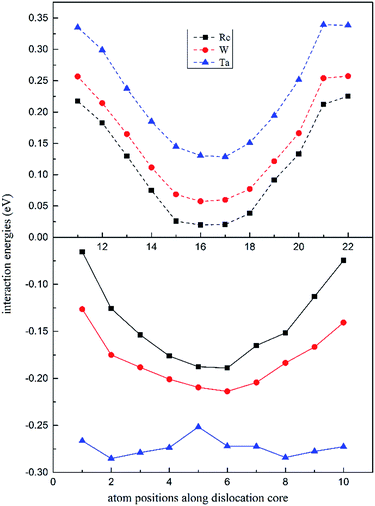 | ||
| Fig. 4 Position-dependent dislocation–doping interaction energies for Re (black), W (red) and Ta (blue) in both the compressed (dashed lines) and the dilated regions (solid lines) of the dislocation. | ||
It is noted that the magnitude of interaction energies caused by doping atoms in the dilated region obey the order: Ta > W > Re. To confirm this energy trend, the discrete variational method (DVM)43,44 was employed to calculate the interatomic energy (IE), which is an excellent quantity to represent the bonding strength between atoms and has been used successfully to study the electronic structure of metals and alloys.45,46 In the DVM frame, the molecular orbitals were expressed by a linear combination of atomic orbitals, and we used a single-site basis set with the frozen core mode in the atomic orbitals. The IE between atoms l and l′ is expressed as
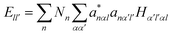 | (3-2) |
Based on the dislocation–doping interaction energies computed by VASP, we calculated the IE between impurity atom X (X = Ta, W or Re) (for W and Re locating at the Ni6 lattice site and for Ta at the Ni2 site) and its three first nearest-neighbour (FNN) Ni atoms and found that the absolute value of IE is in the same order such that Ta > W > Re. The obtained IE are shown in Fig. 5, together with the corresponding Ni–Ni atom pairs for comparison. This is in accordance with the trend of dislocation–doping interaction energies we computed by DFT and agrees well with the result obtained by Shinoda.48
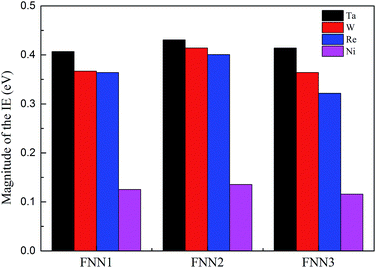 | ||
| Fig. 5 Magnitude of the interatomic energy between atom X (X = Ta, W, Re and Ni) and its three NN Ni atom pairs atoms by DVM calculations. | ||
As regards the most attractive positions, for W and Re they are located in the stacking fault region at the Ni6 site, while for Ta the binding is found to reach a maximum in the vicinity of the partial dislocation and the corresponding position locates at Ni2 site. Size misfit maybe the main factor for this discrepancy. Ta is more deformed relative to W and Re at the same position in stacking fault region, which will lead to a smaller probability of segregation and limited solubility in the γ phase.
From the calculated interaction energies, it is straightforward to see that when substituting for a host Ni atom, a larger solute atom will induce larger strain. Table 1 presents the dopant atomic radius values and their average NN distances in dislocation core. It is evident to show that Re introduces the smallest amount of relaxation among the three elements, from which we conclude that the larger size misfit between doping and bulk atoms, the larger magnitude of the dislocation–doping interaction energies are. To estimate the importance of the strain relaxation, we propose that the interaction energies for the dislocation–doping complex are the sum of strain energy and chemical energy, given as
| Einteraction = Estrain + Echem | (3-3) |
| Estrain = Erelaxeddoped-removal − Erelaxedclean | (3-4) |
| Element | Difference of radius between doping atom and Ni Δr (Å) | Average FNN distance in perfect lattice (Å) | Average 1st NN distance in dislocation core structure (Å) |
|---|---|---|---|
| Re | 0.134 | 2.504 | 2.520 |
| W | 0.144 | 2.511 | 2.533 |
| Ta | 0.224 | 2.537 | 2.587 |
To further understand the electronic mechanism of interaction of dislocation–doping complex, we consider the charge density difference (CDD), the local density of states (LDOS) and partial DOS (PDOS) for atoms in the dislocation core. We take the most stable structures which correspond to the minimum energy configurations to calculate the electronic structure for (i) pure Ni matrix, (ii) system containing dislocation only, and (iii) system containing dislocation–doping complex, to illustrate the electronic effect of dislocation–doping interaction.
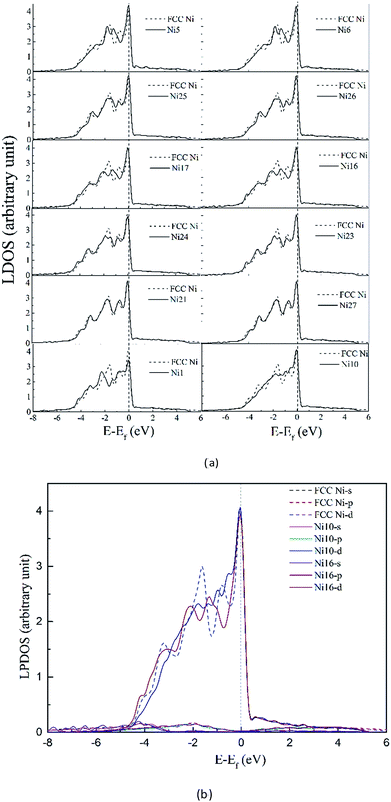
3.3.2.1 Density of states in dislocation core. To clarify the change of the electronic structure due to the presence of dislocation, we first consider the system containing dislocation only. In Fig. 7 the DOS for atoms (solid lines in Fig. 7) in the dissociated dislocation core are presented, along with the DOS for atoms in perfect crystal (dashed lines) given for comparison. The Fermi level of the clean dislocation system is −1.598 eV, and was shifted to zero in the DOS plots.
Comparison of the DOS with the perfect crystal establishes four points. First, dissociated dislocation does not bring significant changes at the Fermi level, except the decreased DOS of Ni1 atom which located around partial dislocation. Second, the DOS for atoms (Ni21 and Ni27 in Fig. 7) far from dislocation core are almost the same as that of perfect crystal. This implies that the electronic effect of dislocation is rather local in material. Third, little split can be found on DOS curves around −1.8 eV for atoms near the stacking fault region, and the electronic states become more extended and disperse. Fourth, PDOS analysis shows that s-states and p-states are almost unchanged with dislocation defect, only the d-states are influenced strongly below the Fermi level.
The analysis revealed that the electronic structure are sensitive to surrounding environment, even though the DOS didn't change significantly in dissociated dislocation.
3.3.2.2 Electronic structure of dislocation–doping complex system. As mentioned above, the most stable structures containing dislocation–doping complex correspond to configurations when Re (W) substitute Ni6 site while Ta substituting Ni2 site respectively. These most stable configurations were taken to calculate the electronic structure of the dislocation–doping effect.
Fig. 8 shows CDD contour maps on the (111) slip plane of dislocation doped with Re, W and Ta, respectively. In the plots, the red areas correspond to an increase in electron density. As shown in the CDD, the accumulation of charge has an order of Re–Ni > W–Ni > Ta–Ni. The orbital overlap is mainly contributed by doping atom localized 5d and Ni 3d orbitals in the interaction of dislocation and doping, therefore we deduce that it is small distance that facilitate orbital overlap and charge accumulation will be affected by the distance between atoms. Hence the charge accumulation is less pronounced between Ta–Ni, because of the larger atomic radii and less d electrons of Ta. To examine the range of the effect of doping atoms, we plot the LDOS of Re, W and Ta and their respective NN atoms (from 1st NN to 3rd NN, the interatomic distance are shown in Table 2) in dislocation core system in Fig. 9. The Fermi level of Re, W and Ta doped systems are −1.283 eV, −1.281 eV, and −1.284 eV respectively and they are all shifted to zero in the plots. It is found that, compared with the DOS of the 2nd NN and 3rd NN atoms, the LDOS of the 1st NN atoms at Ef are significantly affected, wherein the DOS decrease at Ef and peaks near Ef are shifted downward to lower energies. In the middle of the valence band, electronic states of 2nd NN and 3rd NN atoms can be found to contribute to hybridization in the three doped systems. However, in Re (W) doped dislocation, only the 1st NN atoms participate in hybrid with doping atoms at the lower edge of valence band, while in Ta doped dislocation, hybrid peaks can even be found on the 3rd NN Ni atom. This indicates that the electronic states of Re and W are more localized than that of Ta. Evident localized states are also be found for Ni5 atom in Re (W) doped dislocation, which can form strong hybrid states with doping atoms.
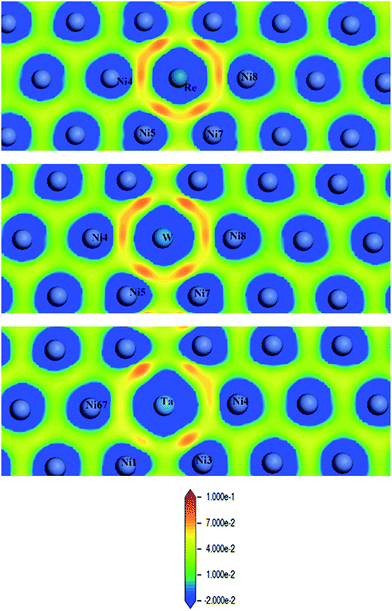 | ||
| Fig. 8 Charge density difference (in units of e per (a.u.)3) of Re (upper), W (middle) and Ta (lower) doped in γ phase dislocation core. | ||
| Re | W | Ta | |
|---|---|---|---|
| 1st NN | d(Re–Ni17) = 2.441 | d(W–Ni17) = 2.456 | d(Ta–Ni13) = 2.462 |
| d(Re–Ni5) = 2.518 | d(W–Ni5) = 2.534 | d(Ta–Ni3) = 2.545 | |
| 2nd NN | d(Re–Ni19) = 3.370 | d(W–Ni19) = 3.368 | d(Ta–Ni15) = 3.628 |
| 3rd NN | d(Re–Ni3) = 4.475 | d(W–Ni3) = 4.485 | d(Ta–Ni5) = 4.489 |
It has been testified that for 3d transition elements, the itinerant electrons are essentially 3di electrons with very few 4s electrons at the Fermi surface.50 Therefore, the reduction of states at the Ef and the shift of the main peaks to lower energies suggest that itinerant electrons on Fermi surface have been transferred to a deeper valence band, which result in less chemical activity and a low excitation transition probability to ensure the increased stability of the system.51 Hence, conclusions are obtained that the interaction between dislocation and doping atoms can stabilize the dislocation structure.
To further investigate the chemical interaction between dislocation and doping atoms, detailed analysis on the PDOS is necessary. We plot the PDOS of Re, W and Ta and their respective 1st NN atoms (Ni5 for Re and W, Ni3 for Ta) in dislocation core (in solid lines) in Fig. 10–12, along with the corresponding PDOS in bulk Ni (in dashed lines) for comparison. The DOS curves of atoms in dislocation core are shown in solid lines, while in perfect crystal they are shown in dashed lines. It is noted that s and p states exhibit extended character while d electronic states are more localized. Taking into consideration of the local effect of doping defect, there are no significant changes on the s and p states of Ni atom and changes mainly take place on d electronic states. Although Re, W and Ta have similar electronic configuration only with one valance electron difference on d-orbitals, the d-DOS of their surrounding 1st NN Ni atoms are influenced to varying degrees, among which the effect of Re is the most dramatic. Due to the delocalized nature of s and p states, their contribution to hybrid is minor. Therefore, focus will be put on d-orbitals analysis.
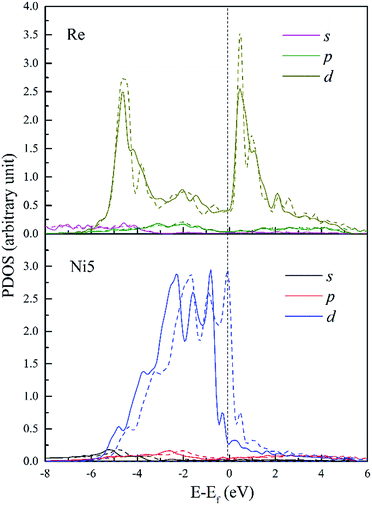 | ||
| Fig. 10 PDOS of Re and its 1st NN Ni5 atoms in bulk Ni (dashed lines) and in dislocation core (solid lines). | ||
In Fig. 10, d-DOS of Re atom in dislocation from E = −6 to −4.6 eV remain nearly unaffected and minor differences mainly occur in the energy range from −4.6 eV to Fermi level. Whereas, d-DOS of FNN Ni5 atom are significantly changed both near the Fermi level and in the lower bound of the valance band. It's notable that the chemical interaction between dislocation and Re results in an increase of 0.18 states for Ni5 atom and a decrease of 0.18 states for Re atom in the same energy range E = −6 to −4.0 eV. Moreover the valley appears on Ni5 d-DOS between E = −1.56 eV and Fermi level with a decrease of 0.13 states, which means the electrons in the upper part of the valence band are transferred to the deeper energy levels and make the structure more stable. From the fivefold d-orbital PDOS (not shown), it is indicated that the additional electronic states of Ni5 between the energy E = −6 and −4.0 eV have t2g (dxy, dyz and dxz) character, on the other hand t2g states decrease in the energy range from −3.9 to −2.2 eV. This implies that, the interaction between Re and dislocation made t2g states move from the energy between E = −3.9 and −2.2 eV to deeper energies, forming the hybrid peaks at around −4.6 eV and resulting in a lowering of the energy. Therefore, the bonding states around −4.6 eV can be further assigned to the ddδ (Re 5d t2g–Ni 3d t2g) states. Moreover, ddδ (Re 5d t2g–Ni 3d t2g) and ddπ (Re 5d eg–Ni 3d eg) hybrid states can also be found at −2.0 eV and −1.5 eV, respectively. From −1.5 eV to the Fermi level, it is indicated that there are nonbonding states between Re and Ni5. Besides, detailed analysis indicates that compared with the PDOS in doped bulk Ni (shown in dashed lines), there is an increase of 0.16 states occupying Ni5 d-t2g, this suggests that charge transfer into Ni t2g orbitals along [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1] and [
1] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01] directions in which the atom pairs Re–Ni5 and Re–Ni7 are aligned respectively. It should be noticeable that the interatomic distance of Re–Ni5 and Re–Ni7 are relatively smaller among Re and its FNN atoms, thus the decreased bond length will facilitate the orbitals overlap. Meanwhile, the increase of 0.16 states for Re 5d-eg states implies that charge also accumulate along [
01] directions in which the atom pairs Re–Ni5 and Re–Ni7 are aligned respectively. It should be noticeable that the interatomic distance of Re–Ni5 and Re–Ni7 are relatively smaller among Re and its FNN atoms, thus the decreased bond length will facilitate the orbitals overlap. Meanwhile, the increase of 0.16 states for Re 5d-eg states implies that charge also accumulate along [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] directions. Therefore, electrons will redistribute to increase interatomic bond strength with the effect of interaction between dislocation and doping Re atom. In summary, on the microscopic level, we attribute the strengthening effect to the chemical interaction of dislocation–Re, forming hybrid peaks at lower energy levels and making charge redistribute.
10] directions. Therefore, electrons will redistribute to increase interatomic bond strength with the effect of interaction between dislocation and doping Re atom. In summary, on the microscopic level, we attribute the strengthening effect to the chemical interaction of dislocation–Re, forming hybrid peaks at lower energy levels and making charge redistribute.
The PDOS of W and its FNN Ni5 atoms are shown in Fig. 11. Compared with Re doped system, Ni5 d-DOS is relatively little changed only with hybrid peaks shifting to higher energies in both the upper bound and lower bound of the valence band. The intensity of hybrid peak of 0.90 eV−1 at E = −4.43 eV in W doped dislocation is smaller than the corresponding peak with maximum 0.92 eV−1 at E = −4.6 eV in Re doped dislocation.
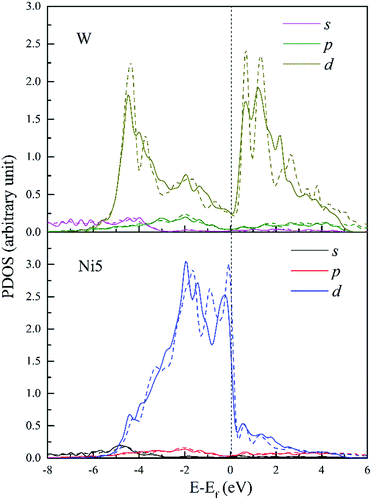 | ||
| Fig. 11 PDOS of W and its 1st NN Ni5 atoms in bulk Ni (dashed lines) and in dislocation core (solid lines). | ||
Therefore, the hybrid between W–Ni5 is weaker compared to Re–Ni5 interaction due to the hybridization peaks shifting to higher energy levels and the decreased intensity. However, in W doped dislocation, s and p states are found to participate in hybrid with Ni5 3d states. This will decrease the directivity of covalent-like bonding of atom pairs between Ni and W.
Fig. 12 shows the PDOS of Ta and its FNN Ni atoms. It is found that d-DOS of Ni3 in Ta doped dislocation core is markedly different from that in Re or W doped conditions. As shown in Fig. 12, Ni3 d-DOS peaks at around −4.5 eV and −1.5 eV almost disappear, suggesting that the hybrid between Ta 5d–Ni 3d is the weakest among the three doped systems. However, several small hybrid peaks appeared, forming ssσ (Ta 6s–Ni 4s) bond below the energy −5.6 eV, which are absent in Re and W doped systems. Moreover, contribution of p states of Ta to hybrid at around −2 eV should not be neglected. All these reveal that the s and p states of Ta are more extended than that of Re and W due to the weak attraction between Ta ion core and valence electrons. Therefore, there will be more s and p states participating in bonding when Ta interact with its NN Ni atoms in dislocation core, and the directivity of covalent-like bonding between FNN Ni and Ta is the weakest among the three doped system.
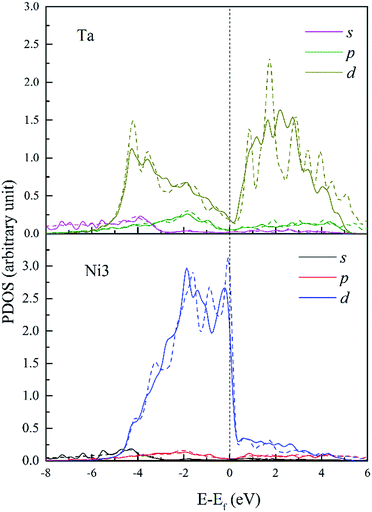 | ||
| Fig. 12 PDOS of Ta and its 1st NN Ni3 atoms in bulk Ni (dashed lines) and in dislocation core (solid lines). | ||
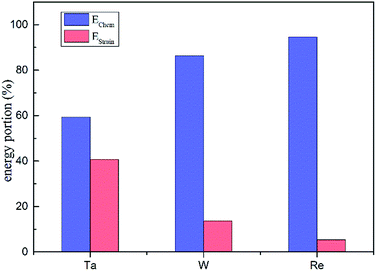
Overall, based on the above analysis of electronic structure, orbital hybridization was found in the interaction between dislocation and doping atom. This was the major contributor to the increase of bond strength by optimizing the direction and overlap of the atomic orbitals. Thus charge transfer corresponding to the changes of t2g and eg states in d-DOS, will be along the optimized direction for which the distance between Ni and doping atoms is smallest as shown in CDD map in Fig. 8. The orbital hybridization and charge transfer can be taken as electronic effect of dislocation–doping interaction and be attributed to the increased bond strength and structure stabilization on microscopic level. Among the three refractory elements, Re has half-filled 5d valence electrons while with the smallest radii, therefore, the local Re 5d–Ni 3d interaction will predominate in the hybrid and make the hybrid the most complicated. This is in accordance with our calculation that found, in Re-doped system the chemical contribution accounts for the vast majority of the interaction energy. In Ta doped system, more s-states participate in hybrid, which are absent in Re and W doped systems. Therefore, the directivity of covalent-like bonding between FNN Ni and Ta is the weakest.
4. Prediction of resolved shear stress from first-principles calculation
In Section 3, we have analysed the electronic structure of dislocation–doping complex and explained the stabilization mechanism on microscopic level. It is generally accepted that the macroscopic physical properties are affected by atomic-level electronic interactions. The yield strength is a critical parameter in the mechanics performance. Therefore, prediction of the yield strength from electronic level will be necessary to explore the effect of the alloying elements. In this section, we adopt the method proposed by Leyson52 to calculate the resolved shear stress (CRSS) of γ phase containing dislocation–doping complex. More details about the method can be found in ref. 52 and 53.The method covers the interaction energy across multiple length scales by combining first-principles calculations
| Einter(xi,yj) = Edis-doping(xi,yj) − Eref | (4-1) |
| Uelastic = −pΔV | (4-2) |
With the introduce of statistical model, total energy change ΔEtot(ξ,w) due to the spatial fluctuations of doping concentration can be written as
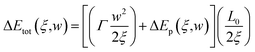 | (4-3) |
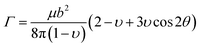 | (4-4) |
Minimizing the total energy change, the energy barrier can be expressed
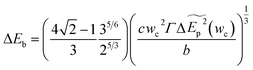 | (4-5) |
The zero-temperature yield strength τy0 corresponds to the stress at which the dislocation escapes from the energy barrier, and it can be predicted as
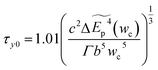 | (4-6) |
4.1 First-principles calculations of the parameters for the elasticity computation
In this portion, the elastic parameters and misfit volume are obtained from DFT calculations, they are necessary mechanics parameters for the doping systems and will be essential in the continuum elasticity theory calculations.The models adopted are 2 × 2 × 2 supercells with one doping atom substituting one bulk Ni atom. A 11 × 11 × 11 Monkhorst–Pack k-mesh39 and a kinetic energy cutoff of 500 eV were used in the elastic moduli calculations. The bulk modulus was obtained by fitting the Murnaghan equation of state54 and elastic constants were obtained by using the energy-strain approach.55 The shear modulus μ and Poisson's ratio υ were calculated according to the equations of linear elasticity for isotropic materials,56 given as
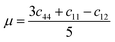 | (4-7) |
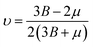 | (4-8) |
Good agreement is obtained between our DFT calculations and the available data from other calculations.56 The values of the bulk and shear moduli and Poisson's ratio obtained are given in Table 3.
| Doping element | Bulk modulus (B) | Shear modulus (μ) | Poisson's ratio (υ) |
|---|---|---|---|
| Ni | 193.0 | 101 | 0.28 |
| Re | 198.4 | 88.69 | 0.31 |
| W | 197.9 | 87.22 | 0.31 |
| Ta | 197 | 84.38 | 0.32 |
With the calculated elastic parameters, the line tension of the dislocation in expression (4-4) can be obtained as 0.19 eV Å−1.
The misfit volume ΔV, which is the volume difference between doping and bulk atoms, is another parameter obtained from the DFT calculation. The calculation is based on the definition of the bulk modulus B, given as
| B = dp/(−dV/V0) | (4-9) |
Eqn (4-9) expresses that the system is under a pressure P0 with its volume V0, and if the pressure increases by the amount dp (P0 → P0 + dp) then the corresponding volume will decrease by an amount dV (V0 → V0 − dV). From eqn (4-9), the volume change can be derived by dV = −(dp/B)V0. To ensure precision, we used the method described in ref. 7 and 57 to compute the misfit volume ΔV
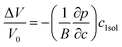 | (4-10) |
4.2 Resolved shear stress at 0 K and finite temperatures
By using the elastic parameters and misfit volume from DFT calculations, together with the interaction energies from two length scales as input to the strengthening model, the critical resolved shear stress (CRSS) of Ni–Ta, Ni–W and Ni–Re at T = 0 K and T = 78 K can be predicted. In general, the single-phase solid-solution model yield stress is a combination of lattice frictional stress and the additional strengthening contributed by doping atoms. The lattice frictional stress is intrinsic resistance to dislocation movement and can be taken as Peierls stress,58 given as
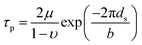 | (4-11) |
| τ = τp + Δτss ≈ Δτss | (4-12) |
In the fragment of Labush's theory,60 the CRSS is proportional to solute concentration to the power of 2/3 for dislocation-mediated plasticity, and to a certain degree it also depends on the temperature and strain rate. Fig. 13 shows the theoretically predicted τc values vs. the solute concentration (at%) at T = 0 and 78 K under the strain rate of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 6.67 × 10−5 s−1. As illustrated in Fig. 13, among the three refractory elements, Ta increases τc of the γ phase most significantly.
= 6.67 × 10−5 s−1. As illustrated in Fig. 13, among the three refractory elements, Ta increases τc of the γ phase most significantly.
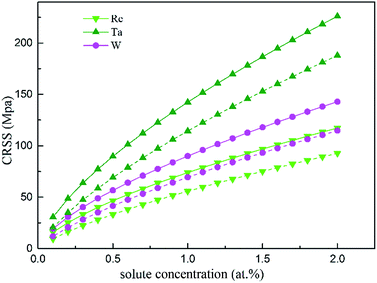 | ||
| Fig. 13 CRSS as a function of the atomic fraction at the temperatures 0 K (solid line) and 78 K (dashed line). | ||
Considering that in Ni-base single superalloys, Ta is a strong γ′-forming element that preferentially partitions into the γ′ phase and exhibits limited solubility in γ-FCC Ni (only 0.6 wt% (ref. 61)), the data will be considered up to a maximum concentration of 2 at%. Compared with the results from solid solution strengthening experiments,62,63 our calculation obtains the same trends and order of magnitude for different solutes strengthening effect. Re mainly partitions to the γ phase, therefore it may be one reason for the remarkable strengthening effect of Re in Ni-base superalloys.64
The temperature and strain rate dependence of the CRSS when solute concentration is 1 at% are shown in Fig. 14, where it is obvious to see that the CRSS increase with the strain rate. In addition, the CRSS is sensitive to temperature under different strain rates, just as shown in the plot, at low temperature there is a period of slow increase for the CRSS with the increased strain rate, but this increase accelerates at higher temperature. Campbell65 classified the τ vs. temperature curve into four temperature regimes. Based on the classification, high stress will be needed to aid the dislocation to pass through an array of solute atoms under the non-thermal activated regime; but the dislocation can be more easily thermally activated over the energy barrier resulting in a decreasing CRSS with increasing temperature.
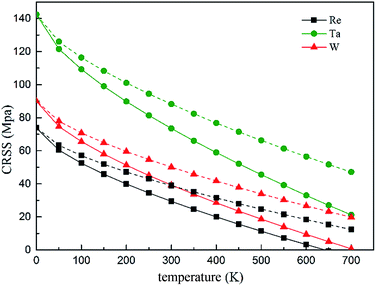 | ||
| Fig. 14 Temperature and strain rate dependence of CRSS under the strain rate of 6.67 × 10−5 s−1 (solid line) and 2 × 10−2 s−1 (dashed line), respectively. | ||
On the basis of our calculated results, Ta exhibits a high solid solution strengthening ability. However, the influence of Ta on the CRSS of γ-FCC Ni is restricted because of its limited solubility in the Ni matrix. On the other hand, Re exhibits remarkable strengthening effect in real Ni-base superalloys with respect to W and Ta, which maybe the results of the complex chemical interaction between Re and dislocation and the strong partitioning of Re to γ phase.
5. Conclusions
Based on the lattice Green-function and first principles, we performed the continuum mechanics (CM)/quantum mechanics (QM) multi-scale simulation of dislocation in the γ phase of Ni-base superalloys and analysed the electronic effect of interaction between dislocation and doping atoms. The calculations indicated that the chemical contribution accounts for nearly the whole interaction energy in dislocation–Re complex. This signifies that Re is more chemically active than W and Ta. Furthermore, electronic structure analysis demonstrated that hybrid take place during the interaction between dislocation and doping atoms (Ta, W and Re) in the γ phase, among which the hybridization between dislocation and Re is the most complicated. This also implies that the chemical interaction plays an important role in the bonding states. On the macroscopic level, we predicted the critical resolved shear stress of dislocation–doping complex at T = 0 and 78 K respectively and found that Ta is the most potent element for strengthening. However, Ta mainly partials to γ′ phase and the solubility is quite limited in the γ matrix, hence the strengthening of γ phase is restricted. Based on the distribution of solute elements between two phases in Ni-base superalloys, we conclude that the remarkable strengthening effect of Re in Ni-base superalloys may be ascribed to a combination of the strong partitioning of Re to the γ phase and the strong chemical interactions when Re interacts with defects in the dislocation core.Acknowledgements
This work was supported by the National Basic Research Program of China (Grant no. 2011CB606402) and Beijing Municipality Science & Technology Commission (Grant no. D161100002416001). The simulations were performed using the “Explorer 100” cluster system at Tsinghua National Laboratory for Information Science and Technology, Beijing, China.References
- J. A. Yan, C. Y. Wang, W. H. Duan and S. Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1681 Search PubMed.
- Y. Niu, S. Y. Wang, D. L. Zhao and C. Y. Wang, J. Phys.: Condens. Matter, 2001, 13, 4267 CrossRef CAS.
- L. Q. Chen, C. Y. Wang and T. Yu, Comput. Mater. Sci., 2006, 38, 39 CrossRef CAS.
- L. E. Shilkrot, R. E. Miller and W. A. Curtin, Phys. Rev. Lett., 2002, 89, 207 CrossRef PubMed.
- H. M. Zbib, M. Rhee and J. P. Hirth, Int. J. Mech. Sci., 1998, 40, 113 CrossRef.
- L. P. Kubin and G. Canova, Scr. Metall. Mater., 1992, 27, 957 CrossRef CAS.
- E. V. D. Giessen and A. Needleman, Modell. Simul. Mater. Sci. Eng., 1995, 3, 689 CrossRef.
- M. Rieth and W. Schommers, Handbook of Theoretical and Computational Nanotechnology, American Scientific Publishers, California, 2006 Search PubMed.
- J. Q. Broughton and F. F. Abraham, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2391 CrossRef CAS.
- S. Ogata, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 5348 CrossRef.
- G. Csányi, T. Albaret, M. C. Payne and V. A. De, Phys. Rev. Lett., 2004, 93, 175503 CrossRef PubMed.
- A. K. Nair, D. H. Warner and R. G. Hennig, J. Mech. Phys. Solids, 2011, 59, 2476 CrossRef CAS.
- X. Zhang, G. Lu and W. A. Curtin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 178 Search PubMed.
- C. Woodward and S. I. Rao, Phys. Rev. Lett., 2002, 88, 177 CrossRef PubMed.
- C. Woodward, D. R. Trinkle, H. L. Jr and D. L. Olmsted, Phys. Rev. Lett., 2008, 100, 045507 CrossRef CAS PubMed.
- M. Ghazisaeidi and D. R. Trinkle, Acta Mater., 2012, 60, 1287 CrossRef CAS.
- R. Schafrik and R. Sprague, Adv. Mater. Processes, 2004, 162, 33 Search PubMed.
- D. Furrer and H. Fecht, JOM, 1999, 51, 14 CrossRef CAS.
- R. C. Reed, The superalloys: fundamentals and applications, Cambridge University Press, New York, 2006 Search PubMed.
- X. Zhang, C. Y. Wang and G. Lu, Phys. Rev. B: Condens. Matter, 2008, 78, 235119 CrossRef.
- X. X. Yu and C. Y. Wang, Acta Mater., 2009, 57, 5914–5920 CrossRef CAS.
- J. X. Zhang, H. Harada, Y. Ro, Y. Koizumi and T. Kobayashi, Acta Mater., 2008, 56, 2975 CrossRef CAS.
- C. P. Liu, X. N. Zhang, L. Ge, S. H. Liu, C. Y. Wang, T. Yu, Y. F. Zhang and Z. Zhang, Mater. Sci. Eng., A, 2016, 682, 90 CrossRef.
- M. Huang, Z. Cheng, J. Xiong, J. Li, J. Hu, Z. Liu and J. Zhu, Acta Mater., 2014, 76, 294 CrossRef CAS.
- M. Pröbstle, S. Neumeier, P. S. Feldner, R. Rettig, H. E. Helmer, R. F. Singer and M. Göken, Mater. Sci. Eng., A, 2016, 676, 411 CrossRef.
- J. S. V. Sluytman, A. L. Fontaine, J. M. Cairney and T. M. Pollock, Acta Mater., 2010, 58, 1952 CrossRef.
- Y. Amouyal, Z. Mao and D. N. Seidman, Acta Mater., 2010, 58, 5898 CrossRef CAS.
- J. Callaway, Quantum Theory of the Solid State, Academic Press, New York, 1974 Search PubMed.
- E. N. Economou, Green's Functions in Quantum Physics, Springer-Verlag Berlin Heidelberg, New York, 1979 Search PubMed.
- V. K. Tewary, Adv. Phys., 1973, 22, 757 CrossRef CAS.
- M. Born, K. Huang and M. Lax, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954 Search PubMed.
- J. P. Hirth and J. Lothe, Theory of Dislocations, McGraw-Hill, New York, 2nd edn, 1982 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. E. Sinclair, P. C. Gehlen, R. G. Hoagland and J. P. Hirth, J. Appl. Phys., 1978, 49, 3890 CrossRef CAS.
- X. Li, J. Z. Yang and E. Weinan, J. Comput. Phys., 2010, 229, 3970 CrossRef CAS.
- A. Stukowski, V. V. Bulatov and A. Arsenlis, Modell. Simul. Mater. Sci. Eng., 2012, 20, 85007 CrossRef.
- D. E. Ellis and G. S. Painter, Phys. Rev. B: Solid State, 1970, 2, 2887–2898 CrossRef.
- B. Delley, D. E. Ellis, A. J. Freeman, E. J. Baerends and D. Post, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2132 CrossRef CAS.
- J.-X. Shang and C.-Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 184105 CrossRef.
- C. Y. Wang, Acta Metall. Sin., 1997, 33, 54 CAS.
- W. Fuhe and W. Chongyu, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 289 CrossRef.
- T. Shinoda, K. Masuda-Jindo and T. Suzuki, Philos. Mag. B, 1990, 62, 289 CAS.
- C. T. Sims, N. S. Stoloff and W. C. Hagel, Superalloys II, John Wiley and Sons Ltd, New York 1987 Search PubMed.
- M. B. Stearns, Phys. Today, 1978, 31, 34 CrossRef CAS.
- W. Fuhe, W. Chongyu and Y. Jinlong, J. Phys.: Condens. Matter, 1998, 8, 5527 CrossRef.
- G. P. Leyson, W. A. Curtin, H. L. Jr and C. F. Woodward, Nat. Mater., 2010, 9, 750 CrossRef CAS PubMed.
- G. P. M. Leyson, L. G. Hector and W. A. Curtin, Acta Mater., 2012, 60, 5197 CrossRef CAS.
- F. D. Murnaghan, PNAS, 1944, 30, 244 CrossRef CAS.
- P. Söderlind, O. Eriksson, J. M. Wills and A. M. Boring, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 5844 CrossRef.
- D. E. Kim, S. L. Shang and Z. K. Liu, Comput. Mater. Sci., 2009, 47, 254 CrossRef CAS.
- S. Vannarat, M. H. F. Sluiter and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 224203 CrossRef.
- G. E. Dieter, Mechanical metallurgy, Mc Graw-Hill Book Co, New York, 3rd edn, 1986 Search PubMed.
- Z. Wu, H. Bei, G. M. Pharr and E. P. George, Acta Mater., 2014, 81, 428 CrossRef CAS.
- R. Labusch, Acta Metall., 1972, 20, 917 CrossRef.
- E. Fleischmann, M. K. Miller, E. Affeldt and U. Glatzel, Acta Mater., 2015, 87, 350 CrossRef CAS.
- Y. Mishima, S. Ochiai, N. Hamao, M. Yodogawa and T. Suzuki, Trans. Jpn. Inst. Met., 1986, 27, 656 CrossRef CAS.
- B. Gan and S. Tin, Mater. Sci. Eng., A, 2010, 527, 6809 CrossRef.
- S. Neumeier, F. Pyczak and M. Göken, Philos. Mag., 2011, 91, 4187 CrossRef CAS.
- W. G. Ferguson, Philos. Mag. A, 1970, 21, 63 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |