DOI:
10.1039/C7RA01237C
(Paper)
RSC Adv., 2017,
7, 29815-29820
Rapid and facile chemical actinometric protocol for photo-microfluidic systems using azobenzene and NMR spectroscopy†
Received
28th January 2017
, Accepted 27th May 2017
First published on 7th June 2017
Abstract
In this study, the photon flux inside a photomicroreactor was determined using chemical actinometry via the photoisomerization of azobenzene at 365 nm. For this purpose, a differential equation, in which the only external data are the tabulated absorption coefficient and the quantum yield of the E isomer, was derived enabling the use of concentrated solutions of azobenzene needed for simple NMR spectroscopy analysis. The developed protocol is shown to be efficient when working using different concentrations, light intensities and solvents.
Introduction
There is a strong revival of organic photochemistry pushed by new photocatalytic systems, new irradiation sources based on light emitting diodes (LEDs) and new experimental designs based on photomicroreactors.1–5 Such reactors range between simple transparent and inexpensive FEP tubing to chips that are designed for specific applications. The fundamental parameter to characterize both the irradiation source and the photomicroreactor system is the number of photons received by the flowing liquid per unit of time. An external measurement by a radiometer gives only a coarse approximation due to the incomplete transmission of light by the photomicroreactor's material and to its geometric form.6 In batch, the classical way to rule out these uncertainties is to perform in situ chemical actinometry measurements. Despite the growing interest for organic photochemistry in flow, only two chemical actinometry protocols have been described. A chemical actinometry method based on the benzophenone-benzhydrol system in benzene was described in the early 90s but has never been revisited.1,7 Recently a system based on potassium ferrioxalate has been reported however this system has several drawbacks: it only works in water and the low absorption of ferrioxalate in thin microsystems cannot be overcome by increasing its concentration as the formed ferrous oxalate precipitates following irradiation.8 (E)-Azobenzene is listed as a “well established” photochromic actinometer in the IUPAC report on chemical actinometry9 as it presents a lot of advantages: (i) it is commercially available and stable on storage; (ii) it may be used from 245 to 440 nm; (iii) it is soluble in a broad range of organic solvents; (iv) it is easily dosed by UV spectroscopy without the need of complexation or titration or any additional treatments and (v) it is reversible and reusable. Its main drawback when using the classical UV measurement is the requirement to determine the photochemical parameters for the Z isomer. Herein, we describe the use of (E)-azobenzene as a chemical actinometer for photoflow chemistry using NMR spectroscopy which needs no photochemical information from (Z)-azobenzene.
Upon exposure to UV irradiation, (E)-azobenzene isomerizes to (Z)-azobenzene. However, reverse thermal and photoisomerization of (Z)-azobenzene also takes place leading to the regeneration of the (E) form (Fig. 1). Thus, an equilibrium state, the photostationary state (PSS) whose composition varies depending on wavelength and solvent, is established.10 The thermal isomerization, that follows first order kinetics, can be neglected however since it is much slower than photoisomerization.10 In the standard protocol for batch, UV/Vis spectroscopy is used for monitoring the evolution of the photoisomerization.11–15 The photokinetic equations used for measuring the photon flux from these data, depend on the quantum yields φ of both forward and reverse photoisomerizations and on the extinction coefficients ε of both isomers. One of the major limitations of this protocol is the need for the quantum yield of the reverse isomerization φZ and the molar extinction coefficient εZ of (Z)-azobenzene. Though extensively studied, φZ is reported in literature for limited wavelengths, solvents and temperatures in contrast to that of the E to Z isomerization φE.16 Furthermore UV/Vis spectroscopy requires the calibration with pure solutions of the two isomers as their spectra are overlapping in both the UV and visible regions and thus need to be deconvoluted.17 Moreover, (Z)-azobenzene is not commercially available, is thermally unstable and obtaining pure (Z)-azobenzene to determine εZ for specific conditions is challenging. Previously described methods for its purification from an irradiated sample of (E)-azobenzene, require working with g scale and involve tedious recrystallizations.10 1H NMR spectroscopy can be used for monitoring the photoisomerization reaction when using more concentrated solutions of azobenzene. Both isomers can be easily distinguished from each other and the fraction of each isomer can be directly determined by integration (ESI Fig. S8 and S9†). So we decided to derive a photokinetic equation that depends on fractions of isomers rather than absorbance, applicable for concentrated solutions and that can provide reliable actinometric measurements without the need of neither the quantum yield nor the extinction coefficient of (Z)-azobenzene.
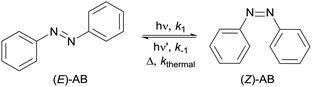 |
| | Fig. 1 Photochemical isomerization reaction of azobenzene. | |
Derivation of the photokinetic equation
When performing chemical actinometry in batch reactors, the photokinetic factor, given in eqn (1), where I is the light intensity, V is the volume and a, b are the path length limits must be estimated:| |
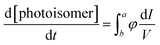 | (1) |
This evaluation implies to use very low concentration in batch to minimize the variation of absorption along the path length. However, this is not the case when working with microfluidic devices whose path lengths are less than 1 mm. In our case, for 10−2 M of (E)-azobenzene (εE = 95 L mol−1 cm−1) and a path length of 500 μm, the absorbance is only 9.5 × 10−3 and the transmission is nearly 100%. The small path length favours homogeneous penetration of light throughout the reaction mixture and thus gives eqn (2):
| |
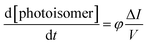 | (2) |
Using Beer Lambert's law for (E) and (Z) isomers (eqn (3) and (4) respectively) and Taylor series expansion of the absorbance and the photokinetic factor (eqn (5) and (2)), eqn (6) that corresponds to the rate of formation of the (Z)-azobenzene can be derived.
| |
ΔI = I0(1 − 10−ΔA) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10ΔA 10ΔA
| (5) |
| |
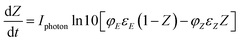 | (6) |
Given that Z is the fraction of (Z)-azobenzene isomer, (1 − Z) is the fraction of the (E)-azobenzene isomer, εE and εZ are the extinction coefficient (L mol−1 cm−1) of the E and Z isomers respectively and 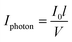 (ein s m−2) is the intensity of light received by the irradiated solution per surface area.
(ein s m−2) is the intensity of light received by the irradiated solution per surface area.
At the photostationary state, 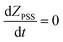 thus giving eqn (7):
thus giving eqn (7):
| |
Iphoton![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10[φEεE(1 − ZPSS) − φZεZZPSS] = 0 10[φEεE(1 − ZPSS) − φZεZZPSS] = 0
| (7) |
By rearrangement, φZ can be expressed as in eqn (8)
| |
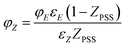 | (8) |
Substituting eqn (8) in (6) will give eqn (9)
| |
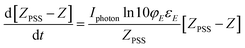 | (9) |
So plotting the graph of ln(ZPSS − Z) vs. time will exhibit a linear relationship whose the slope is used to determine the value of Iphoton and thus to calculate the irradiance (Fig. 3). The variation of (Z)-azobenzene and (E)-azobenzene with time is determined from kinetic eqn (10) which leads to eqn (11) after integration respectively having k1 the rate constant of (E) → (Z), k−1 the rate constant of (Z) → (E) and KPSS the equilibrium constant where  .
.
| |
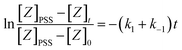 | (10) |
| |
|
[Z]t = [Z]PSS(1 − e−(k1+k−1)t)
| (11Z) |
| |
|
[E]t = [E]PSS(1 + KPSSe−(k1+k−1)t)
| (11E) |
Similarly, the evolution of the thermal isomerization was translated into kinetic equations that follow first order with a rate constant kthermal (eqn (12)). The ESI† contains all the details of the settings of the equations derived and used.
| |
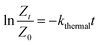 | (12) |
Experimental section
Reagents
(E)-Azobenzene (98%) and dry isooctane, methanol and acetonitrile were purchased from Sigma Aldrich (St. Louis, MO, USA) and used as received.
Microfluidic set up
The microfluidic set up is composed by an injection system, delivering the studied solution to a Mikroglas Dwell Device® [1.15 m × 2 mm × 0.5 mm, Invenios Europe, Langen, Germany, ESI Fig. S1†] made of Foturan® glass18 as micro-photoreactor illuminated by high power UV LEDs-A [18 HP UV LEDs assembled on an electronic printed board, 10 × 5.5 cm, 365 ± 15 nm, Roithner Lasertechnik, Vienna, Austria, ESI Fig. S2†] or HP UV LEDs-B [365 nm, Omnicure® AC475 equipped with an optical adaptor, Excelitas Technologies, Waltham, MA, USA, ESI Fig. S3†] as light source. The injection system can be either a Smartline pump 100 [Knauer, Berlin, Germany] connected to a 6 port medium pressure injection valve [V-451, IDEX, Illinois USA] equipped with a ten meters FEP tubing loop [800 μm ID] or a syringe pump [Harvard Apparatus, Holliston, MA, USA]. To avoid any deviation caused by the natural light the flow microreactor system was enclosed in a box. The Dwell device® was kept at a constant temperature of 20 °C by circulating a cooled fluid in the dedicated Dwell Device channel using a cryostat (GE Healthcare, Pittsburgh, PA, USA).
Photoisomerization experiment
A solution of (E)-azobenzene of concentration 6.4 × 10−4 M in isooctane was injected into the microphotoreactor and irradiated at various flow rates (Fig. 2). The flow rates were chosen depending on the desired irradiation times ranging between 9 s and 140 s. The solvent of irradiated samples was evaporated and the residue was then dissolved in 500 μl of CDCl3 for analysis by 1H NMR spectrometry (Bruker AVANCE 300 MHz, Wissembourg, France). The degree of conversion was calculated by integrating the peaks that correspond to the (Z)-azobenzene and (E)-azobenzene isomers in the 1H spectrum (ESI Fig. S9†).
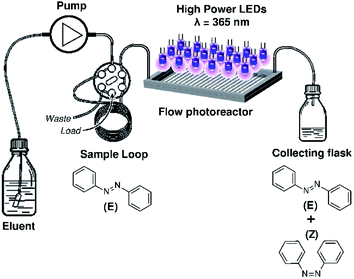 |
| | Fig. 2 Experimental set-up of the photoisomerization of azobenzene under flow conditions. It comprises an injection system, a photo-microreactor and a light source. | |
The obtained results were then used to determine the photon flux inside the microreactor. More concentrated solutions of (E)-azobenzene (0.01 M) in isooctane, acetonitrile and methanol were also assessed. The same protocol with 0.01 M of (E)-azobenzene was then performed in isooctane but with changing the HP UV LEDs-A source to UV LEDs-B (365 nm, Omnicure® AC475) at 30% (Qemitted = 70 mW cm−2) and 100% (Qemitted = 230 mW cm−2) power. The composition at the photostationary state was determined by the irradiation of a sample for an extended time (around 2 h).
Thermal isomerization
A photostationary state sample was kept in the dark at room temperature and the variation in its composition was then monitored by 1H NMR during the following 48 hours. This experiment was done to determine the value of kthermal to verify the exclusion of this factor in the calculations mentioned in the kinetics section.
External irradiance
An X9-2 radiometer coupled with an irradiance detector (Gigahertz-Optik, Türkenfeld, Germany, ESI Fig. S4†) was used to measure the irradiance of light delivered to the microreactor. The light detector is placed in contact to the surface of the reactor that was illuminated by different UV LEDs and the corresponding irradiances (Qemitted radio) were directly recorded.
Physical constants
Refractive indices and quantum yields were obtained from literature (ESI Table S1†).10,16 The absorption coefficients of (E)-azobenzene in isooctane (ESI Table S2, Fig. S5†), acetonitrile (ESI Table S3, Fig. S6†) and methanol (ESI Table S4, Fig. S7†) were determined using Beer Lambert's law in a 1 cm cuvette on a UV/Vis spectrometer (PerkinElmer). The transmittance (Tx), needed to determine the experimental Qemitted to compare it to that given by the radiometer, was calculated using Fresnel's law of reflectance (R) (eqn (13), T = 1 − R and total transmittance Ttotal = T1 × T2) (Table 1).19 Given that nx is the refractive index of medium (x).| |
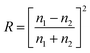 | (13) |
Table 1 The total transmittance of light in the used solvents
| Solvent |
Tair-Foturan |
TFoturan-solvent |
Ttotal |
| Isooctane |
0.958 |
0.998 |
0.956 |
| Acetonitrile |
0.958 |
0.996 |
0.955 |
| Methanol |
0.958 |
0.996 |
0.954 |
Results and discussion
The calculations will be exemplified referring to the results of a solution of 6.4 × 10−4 M of (E)-azobenzene in isooctane injected in the photomicroreactor at various flow rates and irradiated by HP UV LEDs-A (90 mW cm−2) (ESI, Table S5†). The given data was then used to plot the graph of ln(ZPSS − Z) vs. time (Fig. 3).
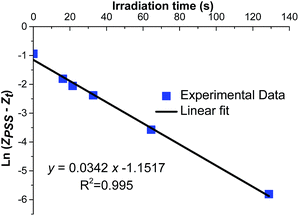 |
| | Fig. 3 Graph of ln(ZPSS − Zt) vs. time (s) for a 6.4 × 10−4 M of (E)-azobenzene in isooctane injected within the microfluidic system irradiated by 365 nm HP UV LEDs-A (Qemitted = 90 mW cm−2). | |
The corresponding graph exhibits a linear relationship with a good squared correlation coefficient (R2 = 0.995) which was maximized using ZPSS as a parameter. The slope of the graph (0.0342 s−1) corresponds to that represented in eqn (9). Substituting the values of ZPSS (0.208), φE (0.12)15 and εE, in isooctane at 365 nm (95 L mol−1 cm−1) affords Iphoton (2.71 × 10−3 ein s m−2). The experimental photon flux Qinside exp. (W m−2) is obtained by multiplying Iphoton by the energy of 1 mole of photons: 2.71 × 10−3 × 327![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 = 887.4 W m−2 = 88.7 mW cm−2. In order to compare our experimental values to those given by the radiometer, Qemitted exp. that corresponds to the experimental value for the photon flux outside the reactor is determined by dividing the Qinside by the total transmittance T (Table 1). Using the eqn (10) and (11), KPSS = 0.208/0.792 = 0.263, k1 = 0.008 s−1, k−1 = 0.030 s−1 and the plots of Fig. 4 are obtained.
500 = 887.4 W m−2 = 88.7 mW cm−2. In order to compare our experimental values to those given by the radiometer, Qemitted exp. that corresponds to the experimental value for the photon flux outside the reactor is determined by dividing the Qinside by the total transmittance T (Table 1). Using the eqn (10) and (11), KPSS = 0.208/0.792 = 0.263, k1 = 0.008 s−1, k−1 = 0.030 s−1 and the plots of Fig. 4 are obtained.
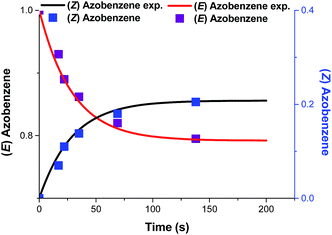 |
| | Fig. 4 Evolution of (E)-azobenzene and (Z)-azobenzene with the time of irradiation by 90 mW cm−2 UV LEDs in flow square: experimental points, line fitted values. | |
Table 2 includes all of the experimental data for the chemical actinometry of azobenzene at two different concentrations 6.4 × 10−4 M (entry 1) and 1.0 × 10−2 M (entries 2–6). HP UV LEDs-A (90 mW cm−2) was used to irradiate entries 1–4 whereas entries 5 and 6 were irradiated using HP UV LEDs-B regulated to provide 30% (70 mW cm−2) and 100% power (230 mW cm−2) respectively. All data are fitted with good linear correlation coefficients (R2 > 0.99) which is not easily achievable when working under batch conditions (ESI Fig. S10 to S14†). It must be noted that ZPSS may be estimated from the data without reaching the photostationary state by maximizing the standard deviation. The k−1 values of all entries in Table 2 were greater than those of k1 which is justified by the fact that the (Z) to (E) isomerization more favored as the (E) isomer is more stable. The experiment described in entry 2 was realized in triplicate and gave very close (ZPSS)-azobenzene isomer photostationary state amount (0.192, 0.188, 0.195) and slope values (3.43, 3.50, 3.28 × 10−2) which demonstrates the stability of the actinometric measurement. Furthermore, when working in isooctane (entries 1, 2a, b, c, 5 and 6), the photostationary state had approximately the same amount of the (Z)-azobenzene isomer (0.208, 0.192, 0.188, 0.195, 0.203 and 0.210) in very different conditions. So the same KPSS was obtained regardless the azobenzene concentrations or the irradiation source which confirms the stability of the actinometric measurement over a broad range of conditions. When using the same light source and the same concentration of azobenzene (entries 2–4) but in different solvents, varying from strongly apolar (isooctane) to dipolar aprotic (acetonitrile) and protic (methanol), very different photostationary states were obtained. Nevertheless the Qinside exp. values are almost equal (80 to 85 mW cm−2). By comparing entries 1 and 2, only a slight variation between the two experimental photon fluxes Qinside exp. was observed (88.7 vs. 84.6 mW cm−2). This shows that the approximation taken when using Taylor series expansion is valid even when working with relatively concentrated solutions (entry 2: 1.0 × 10−2 M) due to the small path length and the small absorption coefficient of (E)-azobenzene. This method provides an advantage of using the rapid and straightforward 1H NMR for monitoring the experiments rather than using UV spectrometry followed by data deconvolution which is complicated by the overlapping of the (E) and (Z)-azobenzene spectra. The impact of the intensity of the light source is seen in the difference in the values of the slopes, k1 and k−1 between entries 2, 5 and 6 (Table 2). By increasing the power of the light source, the system reached the plateau more rapidly (entry 2 ≈ 60 s vs. entry 6 ≈ 25 s). This can lead to a limitation, as a full kinetic assessment cannot be performed when working at elevated light intensity. For example in our case, the maximum flow rate that could be used was 14 mL min−1 that corresponds to a residence time of 5 s. Experiments which require data at shorter irradiation times cannot be performed.
Table 2 Results of chemical actinometry assessment using (E)-azobenzene in flow
| Entrya |
[(E)-Azobenzene] mol L−1 |
Solvent |
ZPSSb |
Slopec × 102 s−1 |
KPSSd |
k1e × 102 s−1 |
k−1e × 102 s−1 |
Qinside exp.f mW cm−2 |
Qemitted exp.g mW cm−2 |
Qemitted radiog mW cm−2 |
| Solution of (E)-azobenzene was injected within the Mikroglas Dwell Device® whose temperature was kept at 20 °C and the composition of the irradiated mixture was determined by 1H NMR. Obtained following 2 h of irradiation in flow. Slope of plot ln(ZPSS − Zt) vs. t. Ratio ZPSS/EPSS. Refer to eqn (10). Refer to eqn (9). Refer to eqn (S34). Experiment realized in triplicate, mean value for ZPSS and slope; refer to Table S6 and Fig. S10a–d. |
| 1 |
6.4 × 10−4 |
Isooctane |
0.208 |
3.42 |
0.263 |
0.71 |
2.71 |
88.7 |
92.8 |
90 |
| 2 |
1.0 × 10−2 |
Isooctaneh |
0.192 |
3.41 |
0.237 |
0.66 |
2.75 |
87.1 |
91.5 |
90 |
| 3 |
1.0 × 10−2 |
CH3CN |
0.315 |
7.42 |
0.459 |
2.33 |
5.09 |
80.1 |
83.9 |
90 |
| 4 |
1.0 × 10−2 |
MeOH |
0.382 |
7.03 |
0.618 |
2.69 |
4.34 |
81.6 |
85.5 |
90 |
| 5 |
1.0 × 10−2 |
Isooctane |
0.203 |
2.55 |
0.255 |
0.52 |
2.03 |
64.6 |
67.5 |
70 |
| 6 |
1.0 × 10−2 |
Isooctane |
0.210 |
7.99 |
0.266 |
1.68 |
6.31 |
209.0 |
218.9 |
230 |
Thermal isomerization
By plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z vs. time (h), the linear graph with a squared correlation coefficient R2 = 0.998, was obtained (Fig. 5). The slope of this straight line corresponds to kthermal = 0.0035 h−1 or 0.97 × 10−6 s−1. Comparing the values of k1 and k−1 of Table 1, entry 2 to that of kthermal validates the assumption of neglecting the thermal isomerization effect in the actinometric calculations (k1 = 7.8 × 10−3 s−1, k−1 = 2.98 × 10−2 s−1 vs. kthermal = 0.97 × 10−6 s−1).
Z vs. time (h), the linear graph with a squared correlation coefficient R2 = 0.998, was obtained (Fig. 5). The slope of this straight line corresponds to kthermal = 0.0035 h−1 or 0.97 × 10−6 s−1. Comparing the values of k1 and k−1 of Table 1, entry 2 to that of kthermal validates the assumption of neglecting the thermal isomerization effect in the actinometric calculations (k1 = 7.8 × 10−3 s−1, k−1 = 2.98 × 10−2 s−1 vs. kthermal = 0.97 × 10−6 s−1).
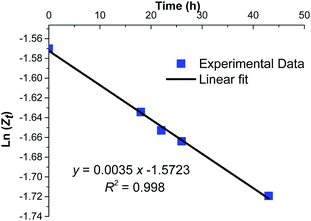 |
| | Fig. 5 Evolution of the thermal isomerization of a solution of azobenzene at photostationary state. | |
Conclusions
The photon flux received in a photomicroreactor was measured by actinometry using azobenzene. Different solvents and irradiation powers were assessed showing that this method is general, accurate and rapid especially when using a concentration of azobenzene suitable for a rapid 1H NMR analysis. Due to its nearly ideal geometry the photomicroreactor allowed us to compare internal actinometric measurement with external measurement. The two measurements were in agreement whatever the solvents and the irradiation powers used, validating the use of this new method for flow system with more complex geometries. Once established by NMR, these measurement can be performed by HPLC coupled with UV detection since the (E) and (Z)-azobenzene isomers are easily separated on a reverse phase column.20 This work can be further extended by assessing the same protocol at different irradiation wavelengths in the visible region and even in the red using newly developed azobenzene sensors.21,22
Acknowledgements
The authors gratefully acknowledge the LASeR Association – Lebanon for the financial support. The NMR and Mass Spectrometry facilities used in this study were funded by the European Community (FEDER), Région Haut de France (France), the CNRS, and the Université de Lille, Sciences et Technologies.
References
- E. E. Coyle and M. Oelgemöller, Photochem. Photobiol. Sci., 2008, 7, 1313 CAS.
- J. P. Knowles, L. D. Elliott and K. I. Booker-Milburn, Beilstein J. Org. Chem., 2012, 8, 2025 CrossRef CAS PubMed.
- D. Cambié, C. Bottecchia, N. J. Straathof, V. Hessel and T. Noël, Chem. Rev., 2016, 116, 10276 CrossRef PubMed.
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075 CrossRef CAS PubMed.
- I. Rodriguez-Ruiz, T. N. Ackermann, X. Muñoz-Berbel and A. Llobera, Anal. Chem., 2016, 88, 6630 CrossRef CAS PubMed.
- C. S. Zalazar, M. D. Labas, C. A. Martin, R. J. Brandi, O. M. Alfano and A. E. Cassano, Chem. Eng. J., 2005, 109, 67 CrossRef CAS.
- B. Borderie, D. Lavabre, G. Levy, J. P. Laplante and J. C. Micheau, J. Photochem. Photobiol., A, 1991, 56, 13 CrossRef CAS.
- T. Aillet, K. Loubiere, O. Dechy-Cabaret and L. Prat, Int. J. Chem. React. Eng., 2014, 12, 257 Search PubMed.
- H. J. Kuhn, S. E. Braslavsky and R. Schmidt, Pure Appl. Chem., 2004, 76, 2105 CrossRef CAS.
- G. Zimmerman, L.-Y. Chow and U.-J. Paik, J. Am. Chem. Soc., 1958, 80, 3528 CrossRef CAS.
- E. Fischer, J. Am. Chem. Soc., 1960, 82, 3249 CrossRef CAS.
- G. Gauglitz, J. Photochem., 1976, 5, 41 CrossRef CAS.
- G. Gauglitz and S. Hubig, J. Photochem., 1981, 15, 255 CrossRef CAS.
- G. Gauglitz and S. Hubig, J. Photochem., 1985, 30, 121 CrossRef CAS.
- N. Siampiringue, G. Guyot, S. Monti and P. Bortolus, J. Photochem., 1987, 37, 185 CrossRef CAS.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of photochemistry, CRC press, Boca Raton, 3rd edn, 2006 Search PubMed.
- E. Pretsch, P. Bühlmann, C. Affolter, E. Pretsch, P. Bhuhlmann and C. Affolter, Structure determination of organic compounds, Springer, Berlin, 2009, vol. 13 Search PubMed.
- The transmission of Foturan® glass is approximately 92% at 365 nm and the refractive index is around 1.53. For detail see: http://www.us.schott.com/advanced_optics/english/products/optical-materials/thin-glass/foturan-2/index.html.
- L. Vincze, T. J. Kemp and P. R. Unwin, J. Photochem. Photobiol., A, 1999, 123, 7 CrossRef CAS.
- S. Ahuja, G. Thompson and J. Smith, J. Chromatogr. A, 1989, 471, 443 CrossRef CAS.
- A. A. Beharry, O. Sadovski and G. A. Woolley, J. Am. Chem. Soc., 2011, 133, 19684 CrossRef CAS PubMed.
- S. Samanta, A. A. Beharry, O. Sadovski, T. M. McCormick, A. Babalhavaeji, V. Tropepe and G. A. Woolley, J. Am. Chem. Soc., 2013, 135, 9777 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed derivation of the photokinetics equation used, experimental protocol including NMR data, data and graph for all the kinetics measurements (PDF). See DOI: 10.1039/c7ra01237c |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
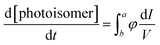
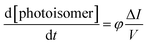
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10ΔA
10ΔA
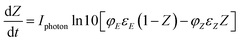
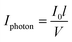 (ein s m−2) is the intensity of light received by the irradiated solution per surface area.
(ein s m−2) is the intensity of light received by the irradiated solution per surface area.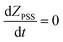 thus giving eqn (7):
thus giving eqn (7):![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10[φEεE(1 − ZPSS) − φZεZZPSS] = 0
10[φEεE(1 − ZPSS) − φZεZZPSS] = 0
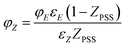
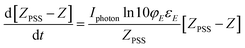
 .
.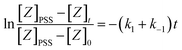
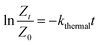

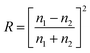

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 = 887.4 W m−2 = 88.7 mW cm−2. In order to compare our experimental values to those given by the radiometer, Qemitted exp. that corresponds to the experimental value for the photon flux outside the reactor is determined by dividing the Qinside by the total transmittance T (Table 1). Using the eqn (10) and (11), KPSS = 0.208/0.792 = 0.263, k1 = 0.008 s−1, k−1 = 0.030 s−1 and the plots of Fig. 4 are obtained.
500 = 887.4 W m−2 = 88.7 mW cm−2. In order to compare our experimental values to those given by the radiometer, Qemitted exp. that corresponds to the experimental value for the photon flux outside the reactor is determined by dividing the Qinside by the total transmittance T (Table 1). Using the eqn (10) and (11), KPSS = 0.208/0.792 = 0.263, k1 = 0.008 s−1, k−1 = 0.030 s−1 and the plots of Fig. 4 are obtained.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z vs. time (h), the linear graph with a squared correlation coefficient R2 = 0.998, was obtained (Fig. 5). The slope of this straight line corresponds to kthermal = 0.0035 h−1 or 0.97 × 10−6 s−1. Comparing the values of k1 and k−1 of Table 1, entry 2 to that of kthermal validates the assumption of neglecting the thermal isomerization effect in the actinometric calculations (k1 = 7.8 × 10−3 s−1, k−1 = 2.98 × 10−2 s−1 vs. kthermal = 0.97 × 10−6 s−1).
Z vs. time (h), the linear graph with a squared correlation coefficient R2 = 0.998, was obtained (Fig. 5). The slope of this straight line corresponds to kthermal = 0.0035 h−1 or 0.97 × 10−6 s−1. Comparing the values of k1 and k−1 of Table 1, entry 2 to that of kthermal validates the assumption of neglecting the thermal isomerization effect in the actinometric calculations (k1 = 7.8 × 10−3 s−1, k−1 = 2.98 × 10−2 s−1 vs. kthermal = 0.97 × 10−6 s−1).


