The effect of vacancies and the substitution of p-block atoms on single-layer buckled germanium selenide

Abstract

Single-layer GeSe is a new candidate in the two-dimensional family of materials. In our recent study, we showed that GeSe can form a stable buckled honeycomb structure (b-GeSe) and is a semiconductor with a 2.29 eV band gap. This paper investigates the effect of point defects of both hole (Ge, Se) and substitution doping of p-block elements, in single-layer b-GeSe, based on first principles plane wave calculations within spin-polarized density functional theory. In the case of the substitution process, we present an extensive analysis of the effects of substituting atoms (Al, As, Cl, P, C, N, Ge or Se, Si, B, F, Ga and S) on the electronic and magnetic properties of the b-GeSe phase. Our results show that nonmagnetic and semiconducting b-GeSe can be half-metallized by Ge vacancies, while it remains a semiconductor with Se vacancies with a decreasing band gap value. The results of the substitution process can be categorized by the group number in the periodic table. b-GeSe remains a nonmagnetic semiconductor upon the substitution of defects with group IVA and VIA atoms on either the Ge or Se position of the b-GeSe structure. On the other hand, the results show that the influence of group IIIA and VIIA atoms is obvious, as these atoms raise the net magnetic moments (1 μ_B to 3 μ_B) of the new b-GeSe system. In particular, the system shows half-metallicity when the Se atoms are replaced with group IIIA atoms. The system has a net magnetic moment when substituting group VA atoms for Se atoms, whereas it does not when substituting them for Ge atoms (except for N). We believe that these results are useful for the further functionalization of b-GeSe with point defects.

---

1 Introduction

The two dimensional single-layer (SL) hexagonal structures of group IV or V elements^1–10 and other hexagonal boron nitride analogs of group IV–IV, III–V and II–VI compounds^11–14 have unusual electronic, mechanical and thermal properties. The search for a contender for graphene has led to the prediction/synthesis of new single-layer, crystalline nanostructures which do not exist in nature. In contrast to the zero band gap of the honeycomb lattices of group IV elements, the single-layer structures of group V elements such as nitrogene,¹⁵ phosphorene,^16–18 arsenene,^19–21 antimonene²² and bismuthene²³ are semiconductors, and they were found to be stable and the optical, mechanical and electronic^23,24 properties were investigated. Owing to the direct or indirect band gap properties, these single-layer structures can be promising materials for digital circuits and light emitting diodes. Recently, GeSe and GeS nanosheets were synthesized, and GeS nanoribbons were also fabricated.^25,26 Theoretical studies show that these nanostructures are similar in structure to phosphorene, and they have semiconducting behaviour.²⁷ However, F. O. von Rohr et al. obtained a new form of the GeSe nanostructure, labeled as β-GeSe.²⁸ This new structure has an uncommon boat conformation, and has a 0.5 eV band gap for its bulk form and 0.9 eV for its monolayer.²⁸ Furthermore, in our recent study, the hexagonal structure of stable b-GeSe²⁹ was predicted by means of first principles calculations.

Recent experimental and computational studies have demonstrated that the interesting properties of bare SL structures can be modified through adsorption and substitution processes.^14,30–33 The band gap of single-layers can be controlled through the substitution of subatoms, and more importantly, it can be tuned for different nanoscale applications.^34–37 In this respect, the substitution of atoms in SL-GeSe is highly attractive and gives rise to important changes. Phosphorene-like GeSe and GeS structures (aw-GeS/Se) can exhibit metallic behaviour when substituted with light, non-metallic atoms.³⁸ While aw-GeSe has a 0.99 eV indirect band gap, b-GeSe has a 2.29 eV indirect band gap. This new form of GeSe and its new electronic structure may be useful for future electronic devices. With this motivation, in this manuscript, we investigated the effects of the substitution process on the physical properties of buckled single-layer GeSe. We found that single atom substitution changed the bare single-layer properties significantly. Nonmagnetic b-GeSe gains a net magnetic moment from the substitution of certain atoms. Nonmagnetic and semiconducting b-GeSe can be half-metallized, and it also gains magnetization with Ge vacancies of 2 μ_B per unit cell, whereas it remains a semiconductor with Se vacancies. In addition, the results of the substitution process can be categorized by the group number of the substituted atoms. We believe that the functionalization of b-GeSe with point defects appears to be a promising way to extend the applications of single-layer GeSe.

2 Computational methodology

Our predictions were obtained from first principles plane-wave calculations within density functional theory (DFT) using projector augmented wave (PAW) potentials.³⁹ The exchange–correlation potential was approximated with the generalized gradient approximation (GGA) using Perdew–Burke–Ernzerhof (PBE) parametrization.⁴⁰ All numerical results were obtained using Quantum Espresso software.⁴¹ A plane-wave basis set with the kinetic energy cutoff ħ²(k + G)²/2m = 500 eV was used. Pseudopotentials with 4s²3d¹⁰4p⁴ and 4s²3d¹⁰4p² valence electron configurations were used for the Se and Ge atoms, respectively. All structures were treated using periodic boundary conditions. The Brillouin zone (BZ) was sampled in k-space within the Monkhorst–Pack scheme⁴² using the (25 × 25 × 1) and (9 × 9 × 1) special mesh points for the (1 × 1) and (4 × 4) b-GeSe cells, respectively. All atomic positions and lattice constants were optimized using the BFGS quasi-Newton algorithm,⁴³ where the total energy and forces are minimized. The convergence criteria for energy was chosen as 10⁻⁶ eV between two consecutive steps. The maximum Hellmann–Feynman forces acting on each atom were less than 0.01 eV Å⁻¹ upon ionic relaxation. The maximum pressure on the unit cell was less than 0.5 kbar. The Gaussian-type Fermi-level smearing method was used with a smearing width of 0.01 eV. To prevent interaction between the periodically repeating b-GeSe layers, a vacuum spacing of 20 Å was chosen. On-site Coulomb interactions were neglected in the present work, but due to the d-orbitals in the valence electron configurations, the inclusion of the Hubbard-U parameter in the calculations may have an influence on the electronic structures. We also performed a band structure calculation for bare b-GeSe using the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional.⁴⁴ For this calculation we used norm conserving-type pseudopotentials, and the electronic exchange–correlation functional was simulated using the GGA with Becke–Lee–Yang–Parr parametrisation.⁴⁵ The mixing rate of the HF exchange potential was 0.25 and the screening length of HSE was 0.106 Å⁻¹. We considered the spin–orbit coupling (SOC) effect of the electronic structure of b-GeSe, and the calculated results indicate that the SOC effect has a negligible impact on the energy band structure of b-GeSe. Therefore, our following calculations do not include the SOC effect.

3 Results and discussion

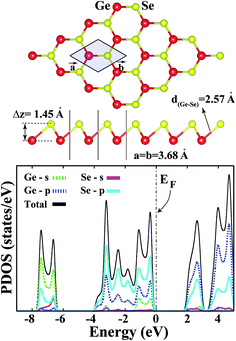
3.1 Bare single-layer b-GeSe

For the sake of comparison, we first present a brief discussion on the structural and electronic properties of single-layer buckled germanium selenide. To prove the stability of SL-GeSe, we calculated its cohesive energies per pair of atoms, defined as follows:

E_coh = E_Ge + E_Se − E_GeSe, (1)

where E_Ge, E_Se and E_GeSe are the total energies of an isolated single Ge atom, an isolated single Se atom and a Ge–Se pair in b-GeSe, respectively. The cohesive energy of b-GeSe was calculated as 4.02 eV per Ge–Se pair, and this value is very similar for other single-layer structures which are stable and manufactured successfully, including its asymmetric washboard counterpart, aw-GeSe, which has a cohesive energy of 4.37 eV. These values are clear evidence that b-GeSe is also a strongly bonded network. Additionally, phonon dispersion calculations were carried out in our recent study to show the stability of b-GeSe.²⁹ The lattice constants of the optimized hexagonal structure in equilibrium are a = b = 3.68 Å and the bond distance between Ge and Se atoms is d_Ge–Se = 2.57 Å. The atomic configuration of b-GeSe and the total and orbital projected partial density of states (PDOS) in a wide energy range are depicted in Fig. 1. The ground state of the b-GeSe phase was found to be a nonmagnetic semiconductor, with an indirect band gap of E_g = 2.29 eV, calculated using the PBE functional. After SOC correction of the PBE results, the band gap became 2.33 eV, which increased to 3.36 eV in the HSE calculations. The energy bands of pristine b-GeSe near the Fermi level region are largely dominated by the p-states of the Ge and of Se atoms. The s-states of Ge are also remarkable, around 1.7 eV below the Fermi level. The Ge-4p orbitals give rise to a pronounced peak above the Fermi level, whereas the Ge-4p orbitals decrease below the Fermi level and the Se p-states become dominant. According to Löwdin⁴⁶ analysis, 0.11 electrons transfer from Ge to Se.

Fig. 1 Top and side views of the atomic configuration of the (4 × 4) supercells of the b-GeSe phase, considered for vacancies and the substitution process, and the corresponding projected density of states for the pristine b-GeSe single-layer. Zero energy is set to the Fermi level, shown by a dashed line.

3.2 Substitutions in single-layer b-GeSe

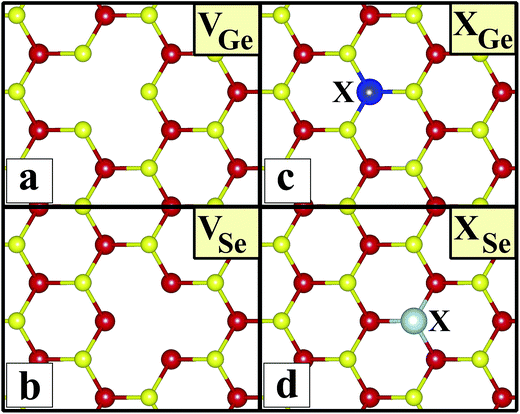
In this paper, we consider the effect of single Al, As, Cl, P, C, N, Ge or Se, Si, B, F, Ga and S atoms, which were found to modify the properties of different 2D materials: graphene,⁴⁷ silicene,⁴⁸ antimonene,⁴⁹ arsenene³¹ and phosphorene.^50,51 From these studies, it can be concluded that introducing intrinsic and extrinsic point defects is an effective method for modulating the properties for diverse applications. The vacancy and substitutional defects of a single atom in b-GeSe were studied using a supercell geometry with periodic boundary conditions. We chose a (4 × 4) supercell containing 32 atoms, 16 Ge atoms and 16 Se atoms, with a lattice constant of a = 14.72 Å. This supercell size was chosen to avoid defect–defect interactions with neighboring cells, so we could investigate the effects of the point defects themselves on the electronic properties. An atom was initially placed instead of a Ge or Se atom in the SL. The various defects considered and their labels are given as follows.

Vacancy (intrinsic). An atom of Ge(Se) subtracted from its position in the single-layer network, labelled as V_Ge(V_Se).

Substitution (extrinsic). An atom of X placed instead of a Ge(Se) atom, labeled as X_Ge(X_Se). The X atoms chosen were Al, As, Cl, P, C, N, Se or Ge, Si, B, F, Ga and S.

All atomic positions, including those of the subatom and the remaining substrate atoms, were relaxed to find the ground state energy for the new geometric configuration. After geometrical optimization, we calculated their cohesive energies using the equation above, and the formation energy for the substitution of defect X_Y, where atom X occupies the site of atom Y, using the equation below:

E_form = E_substrate+XY − E_substrate + E_Y − E_X. (2)

We also used this equation to determine the vacancy formation energy by using the term E_{substrate–Ge(Se)} instead of E_substrate+XY and omitting the E_X term.

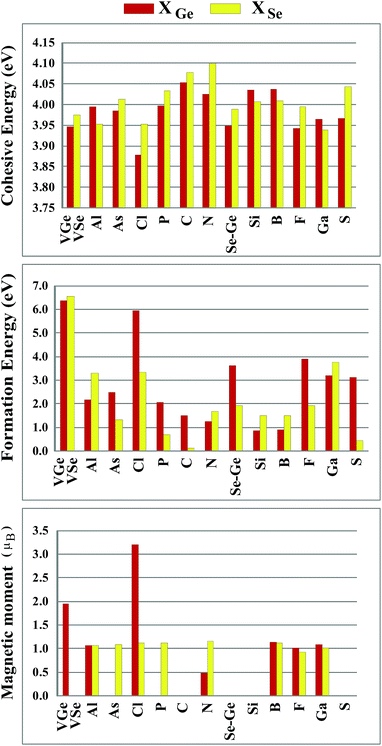
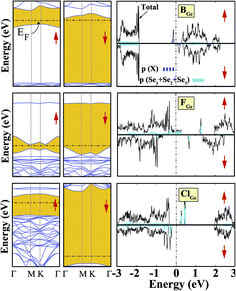
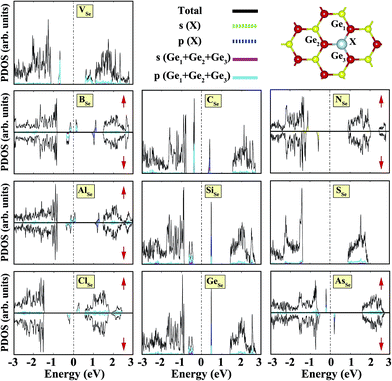
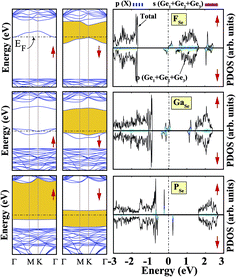
Sketches for each system considered in this study are given in Fig. 2(a)–(d) in detail. The charge at the substituted atom (X), ρ_L, was obtained by Löwdin charge analysis. The excess charge of atom X was calculated as ρ* = Z_A − ρ_L. Here, Z_A is the valance charge of atom X and ρ_L is the charge at atom X. In Tables 1 and 2, we present the relevant structural parameters, such as the length of the X–Ge and X–Se bonds and the lattice constant, and energetic values, such as the cohesive energy and defect formation energy, magnetic moments and excess charge on the subatom, for the defected structures built by substitution in the Ge and Se positions of the SL-GeSe network, respectively. The calculated cohesive energies of the intrinsic and extrinsic point defects are almost equal and interchangeable in the small range of 3.9 eV to 4.1 eV, while the formation energies for the vacancies and Cl_Ge are two to three times higher than those for the other atom substitutions. Based on the formation energy equation without van der Waals (vdW) correction, we obtained values of 6.354 eV and 6.543 eV for the required energy to form V_Ge and V_Se, respectively, indicating that the Ge vacancy is more easily formed in SL-GeSe, while an anion (S or Se) vacancy is more favorable for SL-GaS and -GaSe.^52,53 The Ge vacancy does not change the supercell lattice constant, while the Se vacancy causes a small structural shrink. Upon Ge vacancy formation, three dangling bonds remain surrounding the vacancy, with 0.07 Å smaller Ge–Se bond lengths than those in the bare single-layer. Because of these dangling bonds, three unpaired electrons exist in the atoms surrounding the vacancy, and they form one bonding and one antibonding orbital. Due to spin-polarization, unoccupied antibonding states occur above the Fermi level, as illustrated in Fig. 4. The new system has a local magnetic moment of 2 μ_B, in addition to ferromagnetism, and half-metallicity occurs upon Ge vacancy formation. In contrast to the Ge vacancy, after relaxation, the GeSe lattice constant of the supercell becomes 0.14 Å smaller than that of the bare one. This atomic replacement is called the pseudo Jahn–Teller effect,⁵⁴ and it induces a nonmagnetic system, whereas the system has a magnetic moment before relaxation according to Liebs theorem. Another way to tune the electronic and magnetic properties of the system is to change the carrier density by creating impurities in the bare system. For this investigation we chose p-block elements. These atoms can be categorized for the Ge(Se) host atom as follows: (1) fewer p electrons than the Ge(Se) atom, (2) isovalency with Ge(Se) and (3) more p electrons than Ge(Se).

Fig. 2 Sketches of the systems considered in this study in the (4 × 4) supercell of the b-GeSe phase. (a) Ge vacancy, V_Ge. (b) Se vacancy, V_Se. (c) Substitution of atom X in the Ge position, X_Ge, where atom X is Al, As, Cl, P, C, N, Se, Si, B, F, Ga or S. (d) Substitution of atom X in the Se position, X_Se, where atom X is Al, As, Cl, P, C, N, Ge, Si, B, F, Ga or S.

Table 1 Calculated parameters for atom substitutions in the (4 × 4) supercells of GeSe in the Ge position. E_coh is the cohesive energy; E_form is the formation energy; a is the lattice constant (NC indicates that the lattice constant is not changed), which is the same as in the bare single-layer; d_(X–Ge) and d_(X–Se) are the bond distances between the substituted (X) and Ge and Se atoms in b-GeSe, respectively (for V_Ge, the bond distances are given for Se–Ge and Se–Se); μ is the local magnetic moment (NM indicates a nonmagnetic system); ρ* is the excess charge on the substituted atom, obtained by subtracting the charge on the substituted atom from its valence charge (a negative sign indicates excess electrons). For V_Ge, the excess charges on the atoms around the vacancy are given in the table

System	Ecoh (eV)	Eform (eV)	a (Å)	d(X–Ge) (Å)	d(X–Se) (Å)	μ (μB)	ρ* (e)
VGe	3.946	6.354	NC	2.50	3.67	2.00	−0.05
BGe	4.037	0.895	14.62	3.83	1.99	1.00	−0.37
AlGe	3.995	2.170	NC	3.68	2.45	1.00	0.22
GaGe	3.965	3.211	NC	3.74	2.51	1.00	0.04
CGe	4.053	1.496	14.52	3.52	2.08	NM	−0.58
SiGe	4.036	0.856	14.67	3.65	2.47	NM	0.10
NGe	4.026	1.268	14.58	3.58	2.07	0.48	−0.57
PGe	3.998	2.073	NC	3.63	2.39	NM	0.07
AsGe	3.985	2.497	NC	3.64	2.54	NM	0.13
SGe	3.967	3.127	14.65	3.36	2.26	NM	−0.04
SeGe	3.949	3.632	NC	3.44	2.40	NM	0.08
FGe	3.943	3.903	14.66	3.14	1.84	1.00	−0.41
ClGe	3.879	5.934	NC	3.68	3.01	3.00	−0.33

---

Table 2 Calculated parameters for atom substitutions in the (4 × 4) supercells of GeSe in the Se position. E_coh is the cohesive energy; E_form is the formation energy; a is the lattice constant (NC indicates that the lattice constant is not changed), which is the same as in the bare single-layer; d_(X–Ge) and d_(X–Se) are the bond distances between the substituted (X) and Ge and Se atoms in b-GeSe, respectively (for V_Se, the bond distances are given for Ge–Ge and Se–Ge); μ is the local magnetic moment (NM indicates a nonmagnetic system); ρ* is the excess charge on the substituted atom, obtained by subtracting the charge on the substituted atom from its valence charge (a negative sign indicates excess electrons). For V_Se, the excess charges on the atoms around the vacancy are given in the table

System	Ecoh (eV)	Eform (eV)	a (Å)	d(X–Ge) (Å)	d(X–Se) (Å)	μ (μB)	ρ* (e)
VSe	3.975	6.543	14.58	2.94	2.59	NM	0.08
BSe	4.010	1.458	14.65	2.10	3.66	1.00	−0.36
AlSe	3.912	3.284	NC	2.59	3.84	1.00	0.28
GaSe	3.939	3.743	NC	2.60	3.86	1.00	0.09
CSe	4.078	0.136	14.62	2.03	3.66	NM	−0.46
SiSe	4.007	1.519	NC	2.45	3.77	NM	0.19
GeSe	3.990	1.927	NC	2.52	3.79	NM	0.14
NSe	4.099	1.676	14.60	2.02	3.66	1.00	−0.58
PSe	4.033	0.696	NC	2.42	3.70	1.00	−0.03
AsSe	4.013	1.335	NC	2.52	3.72	1.00	0.04
SSe	4.043	0.439	14.65	2.45	3.64	NM	−0.15
FSe	3.996	1.939	14.64	2.37	3.61	1.00	−0.44
ClSe	3.953	3.325	NC	2.49	3.56	1.00	−0.16

---

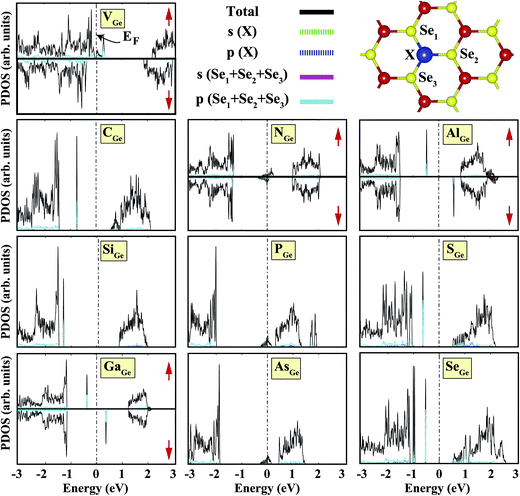
We started our investigation on substituted atoms in the Ge position. After optimization following substitutional doping, local defects and reconstructions occur in single-layer b-GeSe. Some of the substituted atoms change the lattice constant and create new bond lengths around the defects, and these values are given in Table 1. The cohesive energies and formation energies for all of the considered systems are given in Fig. 3. As evident in Fig. 3 and Table 1, the cohesive energies decrease with an increase in period for the same group number, while the formation energies increase. These results are as expected, as with an increasing atomic radius and decreasing electronegativity of the dopant atoms, the doping feasibility becomes harder with the increasing period, and binding will be weaker and the cohesive energy will decrease. In accordance with these results, the formation energies of defects with atoms B, C, N and Si in the Ge position in the network are lower than those of the other atoms and vacancies. These differences can indicate that these point defects may be more dominant defects during the fabrication of single-layer b-GeSe. To investigate the change in the electronic structure of the new systems, we calculated their electronic partial density of states (PDOS) and their band structures, as illustrated in Fig. 4 and 5. According to our extensive calculations, the substitution of group IIIA atoms on Ge sites yields a magnetic semiconductor material (μ = 1 μ_B), as seen in Fig. 4 and 5. By increasing the atomic radius, impurity states in the spin-up channel slip below the Fermi level, and also the conduction bands move to the upper energy levels. As seen in the figures, the impurity states are composed of the p-orbitals of the dopants (B, Al, Ga, etc.) and the p-orbitals of the Se atoms, which are around the defects. All group IIIA dopant systems show n-type semiconductor properties for the spin-down channels, therefore charge transfer becomes easier than in the bare GeSe state. When C or Si are substituted on a Ge site, as seen in Table 1, the cohesive energies of the system are closest to the cohesive energy of bare GeSe, because they have the same number of valence electrons. If we compare the total density of states of GeSe with that of C_Ge and Si_Ge, we can see similarities in the general trends of the DOS, and also their band structures are the same except for the impurity states. Again, with an increase in the atomic radius, the impurity states go to deeper energy levels. Although the atomic radii are changing, the nonmagnetic semiconductor properties are conserved because C and Si possess the same number of valence electrons as the Ge atom. For example, when the dopants have three more electrons from the host Ge atom, such as in group VIIA, the system attains a magnetic moment and GeSe becomes a magnetic semiconductor. As seen in the F_Ge part of Fig. 5, there is one shallow state in both of the spin-up and down states, which lies near the conduction band minimum (CBM). For F_Ge and Cl_Ge, there are donor bands instead of donor states in the spin-up states in the vicinity of the Fermi level. If the first Bohr radius is large, these kinds of band occur due to the donor orbital overlapping, even though the doping ratio is low. Different to the other mentioned dopants, GeSe can show metallic behavior with a doped atom in the Ge position which has one more valence electron than the Ge atom, such as atoms from group VA. By substituting N, P or As atoms into a Ge site, impurity bands occur in the Fermi level due to the p-orbitals of the dopants and Se atoms around the defect. In addition, N doping on a Ge site raises the magnetic moment of the system by 0.5 μ_B.

Fig. 3 Cohesive energy, defect formation energy and magnetic moments for the vacancy systems (V_Ge and V_Se) and X atom substituted systems (X = Al, As, Cl, P, C, N, Se or Ge, Si, B, F, Ga and S) in the Ge position and Se position in the (4 × 4) supercell of the b-GeSe phase.

Fig. 4 Total (shown by black lines), subatom and atoms around the defect projected density of states for a single atom, substituted in the Ge position, in the (4 × 4) supercell of the b-GeSe phase. Zero energy is set to the Fermi level, E_F, shown by dashed dotted lines.

Fig. 5 Total (shown by black lines), subatom and atoms around the defect projected density of states for a single atom, substituted in the Ge position, in the (4 × 4) supercell of the b-GeSe phase. Band structures are also illustrated in the vicinity of the Fermi level. Zero energy is set to the Fermi level, E_F, shown by dashed dotted lines.

We also investigated the substitution of the same atoms in the Se position. As seen in Fig. 3, similar trends for the formation (cohesive) energy values are valid for the X_Se structures. Their values increase (decrease) with an increasing period. The most dominant defect is the C_Se defect, and the substitution of an S atom instead of a Se atom is another favorable defect type with a lower formation energy. Similar to the X_Ge defect, some of the X_Se structures have smaller lattice constants than that of the bare GeSe structure. We did not encounter a structure that was larger than bare GeSe. This situation can be attributed to our selection of dopant atoms, which are all light elements. We suppose that the GeSe structure will be enlarged with heavy elements. Similar to X_Ge, substituted atoms in the Se position change the electronic structure and cause localized states in the fundamental band gap or resonance states in the band continua of b-GeSe. However, different to X_Ge, there are many half metallic systems for the X_Se defect type. Group IIIA doping gives rise to localized states in the fundamental band gap of GeSe. B, Al and Ga doping yields similar band structures with different band gap values, so we only give the Ga_Se band structure (see Fig. 6). As seen in Fig. 7, there are half-occupied acceptor bands in the Fermi level, and one unoccupied acceptor state near the VBM for the spin-up channel. These acceptor bands and state become nearly 0.1 eV lower in energy, and the system shows semiconductor properties for the spin-down channel. C, Si or Ge doping in the Se position gives similar electronic structures to each other, and the new systems display p-type nonmagnetic semiconductor properties due to the shallow states near the CBM. When we substituted group VA atoms in the Se position, we attained magnetic (μ = 1 μ_B) semiconductor materials resulting from the one extra hole in the crystals. PDOS are given in Fig. 6, and we also plot the band structure of P_Se and illustrate it in Fig. 7. N_Se and As_Se also have similar bands. As is evident in Fig. 7, there is one occupied and unoccupied impurity state in the spin-up and spin-down channels, respectively. All group VA doped systems are p-type semiconductors for the spin-down state. Replacing Se with S atoms almost does not change the electronic structure of GeSe, and only the degeneracy decreases due to a very small structural shrink. If we add dopants which have one more electron than Se, such as F and Cl, the systems have a 1 μ_B magnetic moment and show half-metallicity properties for F doping, while remaining a semiconductor for Cl doping.

Fig. 6 Total (shown by black lines), subatom and atoms around the defect projected density of states for a single atom, substituted in the Se position, in the (4 × 4) supercell of the b-GeSe phase. Zero energy is set to the Fermi level, E_F, shown by dashed dotted lines.

Fig. 7 Total (shown by black lines), subatom and atoms around the defect projected density of states for a single atom, substituted in the Se position, in the (4 × 4) supercell of the b-GeSe phase. Band structures are also illustrated in the vicinity of the Fermi level. Zero energy is set to the Fermi level, E_F, shown by dashed dotted lines.

4 Conclusions

In conclusion, we present a theoretical study on the effects of point defects in single-layer b-GeSe, systematically studied by means of first principles plane-wave calculations within density functional theory. On the basis of the DFT results, bare SL-GeSe is a stable buckled honeycomb structure with semiconducting behavior and is nonmagnetic. Our calculations show that a magnetism of 2 μ_B can be induced by a single Ge vacancy in the b-GeSe phase, but a Se vacancy does not induce any magnetization in the system. After the substitution process, some of the atoms give rise to magnetic states, so b-GeSe can attain magnetism and can have a half-metallic, metallic or semiconductor character. The calculated cohesive energies range from 3.9 eV to 4.1 eV, which shows that all of the considered dopants can strongly interact with SL-GeSe. Our results show that the group number is the most important factor to determine the magnetic and electronic structure of doped GeSe. If we doped b-GeSe with atoms which have odd numbers of valence electrons, the doped GeSe would attain a magnetic moment resulting from the remaining one unpaired electron or hole in the crystal. If we doped b-GeSe with even valence number dopants, the doped GeSe would remain a semiconductor, but would show a p- or n-type character. We believe that these results are useful for the further functionalization of b-GeSe with point defects.

References

1. K. S. Novoselov, Science, 2004, 306, 666–669.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
3. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
4. S. Ghosh, I. Calizo, D. Teweldebrhan, E. P. Pokatilov, D. L. Nika, A. A. Balandin, W. Bao, F. Miao and C. N. Lau, Appl. Phys. Lett., 2008, 92, 151911.
5. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204.
6. E. Durgun, S. Tongay and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075420.
7. S. Cahangirov, M. Topsakal, E. Aktürk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
8. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501.
9. V. O. Özçelik, E. Durgun and S. Ciraci, J. Phys. Chem. Lett., 2014, 5, 2694–2699.
10. Y. Xu, B. Yan, H.-J. Zhang, J. Wang, G. Xu, P. Tang, W. Duan and S.-C. Zhang, Phys. Rev. Lett., 2013, 111, 136804.
11. H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
12. M. Topsakal, S. Cahangirov, E. Bekaroglu and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235119.
13. J. N. Coleman, M. Lotya, A. O’Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De and R. J. E. A. Smith, Science, 2011, 331, 568–571.
14. C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999.
15. V. O. Özçelik, O. Ü. Aktürk, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125420.
16. Z. Zhu and D. Tomanek, Phys. Rev. Lett., 2014, 112, 176802.
17. Y. Aierken, D. Çakir, C. Sevik and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081408.
18. D. Çakir, C. Sevik and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165406.
19. C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423.
20. D. Kecik, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 205409.
21. D. Kecik, E. Durgun and S. Ciraci, Phys.Rev. B: Condens. Matter Mater. Phys., 2016, 94, 205410.
22. O. Ü. Aktürk, V. O. Özҫelik and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235446.
23. E. Aktürk, O. Ü. Aktürk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 014115.
24. S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115.
25. B. Mukherjee, Y. Cai, H. R. Tan, Y. P. Feng, E. S. Tok and C. H. Sow, ACS Appl. Mater. Interfaces, 2013, 5, 9594–9604.
26. C. Lan, C. Li, Y. Yin, H. Guo and S. Wang, J. Mater. Chem. C, 2015, 3, 8074–8079.
27. Y. Hu, S. Zhang, S. Sun, M. Xie, B. Cai and H. Zeng, Appl. Phys. Lett., 2015, 107, 122107.
28. F. O. von Rohr, H. Ji, F. A. Cevallos, T. Gao, N. P. Ong and R. J. Cava, J. Am. Chem. Soc., 2017, 139, 2771–2777.
29. H. Arkin and E. Aktürk, Appl. Surf. Sci., 2016, 390, 185–189.
30. C. Ataca and S. Ciraci, J. Phys. Chem. C, 2011, 115, 13303–13311.
31. F. Ersan, E. Aktürk and S. Ciraci, J. Phys. Chem. C, 2016, 120, 14345–14355.
32. E. Bekaroglu, M. Topsakal, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075433.
33. B. Xu, J. Yin, Y. D. Xia, X. G. Wan and Z. G. Liu, Appl. Phys. Lett., 2010, 96, 143111.
34. A. Gökҫe and E. Aktürk, Appl. Surf. Sci., 2015, 332, 147–151.
35. M.-Y. Liu, Y. Huang, Q.-Y. Chen, C. Cao and Y. He, Sci. Rep., 2016, 6, 29114.
36. F. Ersan, A. G. Gökҫe and E. Aktürk, Appl. Surf. Sci., 2016, 389, 1–6.
37. F. Ersan, G. Gökoglu and E. Aktürk, J. Phys.: Condens. Matter, 2014, 26, 325303.
38. Y. Ding and Y. Wang, Phys. Chem. Chem. Phys., 2016, 18, 23080–23088.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
41. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. E. A. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
43. C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90.
44. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
45. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
46. P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375.
47. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
48. X. Lin and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075440.
49. O. Üzengi Aktürk, E. Aktürk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035450.
50. G. Wang, R. Pandey and S. P. Karna, Appl. Phys. Lett., 2015, 106, 173104.
51. H. Zheng, H. Yang, H. Wang, X. Du and Y. Yan, J. Magn. Magn. Mater., 2016, 408, 121–126.
52. L. Ao, H. Y. Xiao, X. Xiang, S. Li, K. Z. Liu, H. Huang and X. T. Zu, Phys. Chem. Chem. Phys., 2015, 17, 10737–10748.
53. T. Cao, Z. Li and S. G. Louie, Phys. Rev. Lett., 2015, 114, 236602.
54. B. Bersuker, J. Phys.: Conf. Ser., 2017, 833, 012001.

---