First-principles calculation of lithium insertion into homogeneous a-SiC_2/5O_6/5 as high performance anode

Abstract

Amorphous silicon oxycarbide is considered as a promising anode material for new generation of lithium-ion batteries, and figuring out the lithiation mechanism is crucial for its application. In this work, first principle calculations are performed to study the atomic structures, formation energy and lithiation voltage of homogeneous SiC_2/5O_6/5. The interpretation of radial distribution, angular distribution and coordinate number suggests that the Si–O bond tends to break and the Li₂O will form at the beginning of lithiation, then the Li_xO and the Li_ySi form with increasing Li concentration, which makes a major contribution to the capacity of SiC_2/5O_6/5. By the Li content dependence of the formation energies curve, the theoretical specific capacity of SiC_2/5O_6/5 is predicted as 1415 mA h g⁻¹, which is comparable to the reversible capacity of 900 mA h g⁻¹ in experiments. Both the formation energies and the voltage curves suggest lithium is preferable in incorporation with SiC_2/5O_6/5, and this is attributed to the formation of Li_xO and Li_ySi.

---

1. Introduction

Graphite is widely used as an anode material for commercial lithium-ion batteries (LIBs), however, the low capacity (372 mA h g⁻¹) has limited its further applications. Silicon is a promising material to replace graphite with lower cost and around 10 times the gravimetric capacity.^1,2 But silicon exhibits about a 300% volume expansion during cycling, which will lead to mechanical failure, poor cycling performance and irreversible capacity.^3,4 Therefore, research efforts are being made to search for new anode materials with high capacities and long life cycle.

Amorphous silicon oxycarbide (a-SiCO) presents a high reversible capacity (larger than 800 mA h g⁻¹) and is a promising anode material for LIBs.^5–12 Amorphous SiCO ceramics generally include SiCO glass and SiCO glass with free carbon phase, corresponding to homogeneous structure and inhomogeneous structure respectively. Current experiments¹³ suggested that both the SiCO structures have a very high first insertion capacity, the concentration of lithium residing at the mixed bonds is much greater than the concentration sequestered in the free carbon,⁷ and the reversible capacity of these mixed bonds is severely diminished when oxygen is substituted by nitrogen.⁶ Although the experiments provide some information on how the nano-structure influences the electrochemical properties of SiCO, the mechanism for lithium insertion into a-SiCO is still not clearly understood. More insight needs to be gained in terms of atomistic structure and energy, which could be very challenging for current experimental technologies.

First principles calculations can obtain the atomic structure, electronic properties and lithiation characters of anode materials, and were successfully used in analyzing LIB electrodes such as Si,¹⁴ SiO,¹⁵ Nb₂C ¹⁶ and graphene sheets.³ In our previous studies,^17,18 SiCO models containing mixed-bond tetrahedron were proposed based on crystalline SiO₂ configuration,¹⁷ the influence of tetrahedron on the performance of SiCO was studied. Moreover, in order to gain deeper insight into amorphous SiCO structure, a more realistic model was established by molecular dynamics simulation of melt-quench, and the effect of carbon segregation on performance of inhomogeneous SiCO was studied.¹⁸ In this work, the performance of homogeneous a-SiCO is investigated by first principles calculations, the atomic structures, formation energy and lithiation voltage of SiC_2/5O_6/5 are calculated and discussed.

2. Methods

Classical molecular dynamics (CMD) based melt quench simulations were used to obtain the initial structures of SiC_2/5O_6/5. Tersoff potential¹⁹ and the potential parameters for SiC¹⁹ and SiO₂ (ref. 20) were used to describe the atomic interaction in SiC_2/5O_6/5. The melt-quench procedure proposed in our previous study²¹ was used to generate the amorphous structures of SiC_2/5O_6/5 from random atomic configuration, the system temperature was adjusted by velocity scaling and canonical ensemble (NVT) using a Nosé–Hoover thermostat. The CMD simulations were implemented by LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code.²²

The first principles simulations were then performed to optimize the SiC_2/5O_6/5 structures further. The systems were annealed at 1800 K by 8 ps of NVT simulations, and were then quenched to 300 K at a rate of 0.3 K fs⁻¹ by NPT simulations. Finally the amorphous structures are relaxed fully by geometry optimization of lattice parameters and atomic position. A plane-wave cut-off of 300 eV and a 2 × 2 × 2 κ-points mesh were found to give sufficient convergence. The geometry optimization was conducted by: residual force < 0.01 eV Å⁻¹, convergence of energy change per atom < 2 × 10⁻⁶ eV, stress < 0.01 GPa. The electronic broadening width was 0.1 eV in a variable occupancy calculation, and the same orbitals for alpha and beta spins were used. The generalized gradient approximation following the Perdew–Bueke–Ernzerhof scheme (GGA-PBE)²³ was used. The first principles simulations according to the density functional theory (DFT) ultra-soft pseudo-potential method were conducted in CASTEP code^24,25 in Materials Studio 5.5.

The SiC_2/5O_6/5 studied here refers to the stoichiometric glass composed of 1/3(SiC) and 2/3(SiO₂). The formation energy of Li_xSiC_2/5O_6/5 is obtained by subtracting the reference energies of SiC_2/5O_6/5 and Li from the energy of Li_xSiC_2/5O_6/5 model. The formation energy per Si atom is given by:¹⁵

E_f = E(Li_xSiC_2/5O_6/5) − (xE(Li) + E(SiC_2/5O_6/5)) (1)

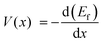where x is the ratio of number of Li atoms per Si atoms, E(Li_xSiC_2/5O_6/5) and E(SiC_2/5O_6/5) are the per Si atom energies for the lithiated SiC_2/5O_6/5 and the original SiC_2/5O_6/5, and E(Li) is the per Li atom energy of bcc-Li. The average intercalation voltage V(x) is the chemical potential of Li ion in electrodes and is calculated by ¹⁵

3. Results and discussion

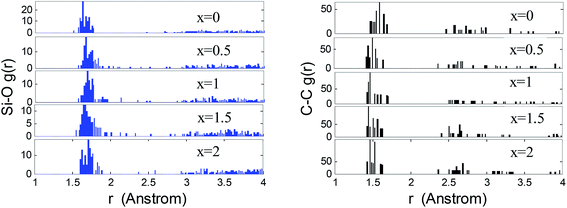
The calculated properties of SiC_2/5O_6/5 are listed in Table 1 and compared to the experimental data. The peaks values in radial distribution functions (RDFs) and angular distribution are obtained by Gaussian multi-peak fitting.²⁶ The bond length of Si–O, Si–C and C–C are obtained by the sharp peaks of RDFs, observed at r_SiO = 1.64 Å, r_SiC = 1.89 Å and r_CC = 1.51 Å respectively, correspond to the experimental data of r_SiO = 1.62 Å, r_SiC = 1.88 Å and r_CC = 1.49 Å.^27,28 The tetrahedrons are mainly linked to each other by vertex and form a broad angular distribution Si–O–Si, centered approximately at 146°, it corresponds to the peak of 140–144° in experiments.²⁷ The Young's modulus (E) of SiC_2/5O_6/5 is 99 GPa and within the range of 90–110 GPa in experiments.^29,30 The glass transition temperature (T_g) is determined by the temperature corresponds to the change in slope of temperature-dependent Young's modulus curve. The obtained T_g of SiC_2/5O_6/5 is 1460 K and is closed to the range of 1573–1673 K in experiments.^31–33

Table 1 Computed properties compared to reported experimental data

	This work	Experimental results^27,28,30–36
Si–O [Å]	1.64	1.62
Si–C [Å]	1.89	1.88
C–C [Å]	1.51	1.49
Si–O–Si [deg]	146	140–144
E [GPa]	99	90–110
Tg [K]	1460	1573–1673
Density [g m^−3]	2.58	2.4–2.64

---

In order to describe the structural evolution of SiC_2/5O_6/5 under Li insertion, a series of configuration snapshots of Li_xSiC_2/5O_6/5 are presented in Fig. 1. At low Li concentration, the Si atoms are slightly displaced from their tetrahedral positions, and formation of Li_xSiO_y-like structures can be observed. With increasing Li concentration, some of the silicon-centered tetrahedrons are destroyed, which leads to the breaking of Si–O bonds and the formation of Li_xO.

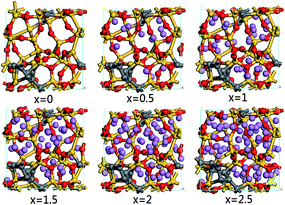Fig. 1 Atomic configurations of Li_xSiC_2/5O_6/5 with increasing Li concentration. The yellow, grey, red and purple spheres represent the silicon, carbon, oxygen and lithium atoms respectively.

The atomic correlations of the lithiated SiC_xO_6/5 are inferred by means of RDFs, as shown in Fig. 2. The bond length of Si–O and C–C for lithiated SiC_2/5O_6/5 are determined by the first peaks of RDFs around 1.64 Å and 1.51 Å respectively. With increasing Li concentration, the first peak of Si–O slightly shift to a larger value and its long distance correlation becomes more predominate, this is an indicative of stretched Si–O bonds and rupture of Si–O–Si units, which is accorded with the above observations. The small peak of Si–O around 1.85 Å corresponds to the Si–O bond near the edge of free carbon. The C–C network tends to be more close together after the rupture of Si–O–Si units, it results in a very slight decrease on C–C bond length, which proves the structural stability of free carbon during lithiation.

Fig. 2 Calculated Si–O and C–C RDFs of a-SiC_2/5O_6/5 at several degrees of lithiation.

The coordination numbers are obtained by integrating the first peak of radial distribution function, as shown in Fig. 3. Based on the average bond length of O–Si, Si–Li and O–Li,^15,37–40 1.85 Å, 3.08 Å and 2.16 Å are chosen as maximum cutoff radii for the calculations of CN_O–Si, CN_Si–Li and CN_O–Li respectively. Consisting with the above results, with increasing concentration of lithium atoms in the mixture, a quasi-linear drop of CN_O–Si from 1.9 to 1.4 confirm the disintegration of Si–O bonds. The increasing of CN_Si–Li and CN_O–Li is attributed to increasing Li atoms surround the Si and O atoms, it indicates the formation of Li_xO and Li_ySi structures. The Si and O atoms prefer to interact with the Li atoms rather than with each other, specially at high Li concentration. When x = 2, the insertion of Li gradually disintegrates the a-SiC_2/5O_6/5 host mixture with O and Si atoms coordinating to 2.8 and 3.5 Li atoms.

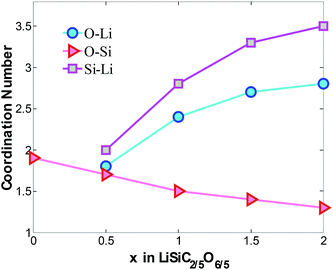Fig. 3 Average coordinate number of O–Li, O–Si and Si–Li atom pairs in Li_xSiC_2/5O_6/5. The cutoff radii for CN_O–Si, CN_Si–Li and CN_O–Li are 1.85 Å, 3.08 Å and 2.16 Å respectively.

Detailed views on formation of Li_xO and Li_ySi complexes in lithiated SiC_2/5O_6/5 (x = 2) are shown in Fig. 4. As the Li concentration increases, more O atoms are involved in formation of Li_xO (x = 2, 3, 4) and Li_ySi (y = 3, 4, 5) complexes. Stable formation of both Li_xO and Li_ySi complexes in high Li concentration structure is attributed to the Si–C/O mixed-bond tetrahedrons in the original structure. According to the first-principle calculation of silicon dioxide,⁴¹ after lithiation and some of the Si–O bonds broke, only Li_xO was found in the lithiated structure, indicating the broken Si atoms still connected with other O atoms and could not form Li_ySi compound in silicon dioxide. While the mixed bond tetrahedrons in SiCO provide the possibility to generate broken Si and O for the formation of Li_xO and Li_ySi complexes.

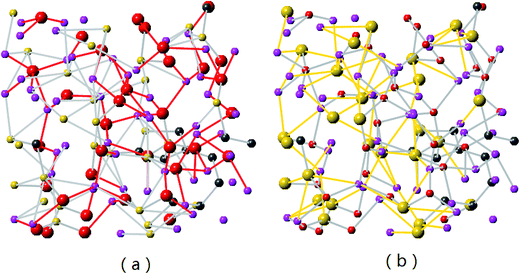Fig. 4 Formation of Li_xO and Li_ySi in Li₂SiC_2/5O_6/5 (the Li–O and Li–Si bonds are presented by red and yellow colors respectively).

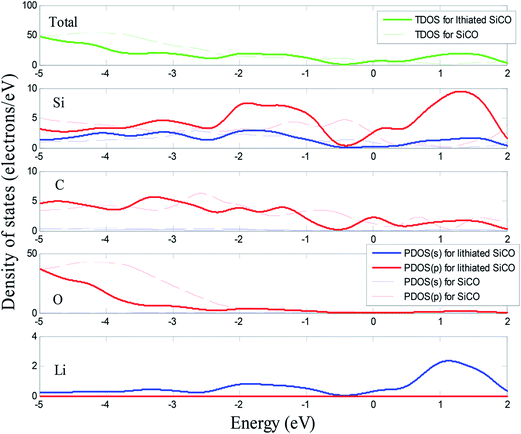
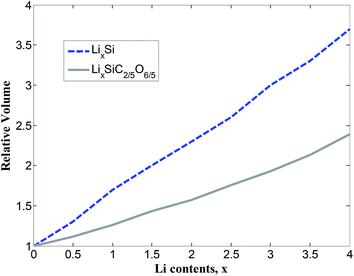
The total density of states (TDOS) and partial density of states (PDOS) of SiC_2/5O_6/5 and lithiated SiC_2/5O_6/5 around the Fermi level are shown in Fig. 5. The insertion of Li makes two main contributions to the TDOS: one is located at around −4 eV while the other is near 1.2 eV, which can be viewed as bonding and anti-bonding states introduced by Li insertion. The TDOS around the Fermi level is mainly composed of Si-s, Si-p, C-p, O-p and a little Li-p components. In particular, the non-zero s component of Li PDOS is almost the same as the p orbit of Si atoms. Above Fermi level, Si-p makes a major contribution to TDOS with some Li-s, Si-s and C-p components, it means that the bond of Li–Si is mainly covalency with little ionicity. The relative volumes of SiC_2/5O_6/5 with different degree of lithiation were calculated and compared with those of Si,¹⁴ as shown in Fig. 6. The results show that the profile of relative volume for Li_xSiC_2/5O_6/5 is considerably lower compared to the value of Li_xSi, SiC_2/5O_6/5 presented a better expansion performance than Si.

Fig. 5 Calculated total and partial density of states of SiC_2/5O_6/5 and lithiated SiC_2/5O_6/5.

Fig. 6 Evolution of relative volume of Li_xSiC_2/5O_6/5 and Li_xSi 14.

Fig. 7 showed the formation energies of Li_xSiC_2/5O_6/5 as a function of x. The formation energies decrease with increasing Li concentration and reach the minimum when the structure is fully lithiated. The lithiation is favorable until a Li concentration of x = 2.75, an additional Li insertion is thermodynamically unfavorable. It corresponds to a specific capacity of 1415 mA h g⁻¹, considering that the ratio of irreversible and reversible capacity is about 1/3 for the SiCO with similar composition,⁴² a reversible capacity of 1061 mA h g⁻¹ is expected and this is comparable to reversible capacity of 900 mA h g⁻¹ in experiments.⁴² The composition–voltage curve if Li_xSiC_2/5O_6/5 is also calculated and compared to the experimental data.⁵ The lithiation voltage relative is given by the negative of the reaction free energy per Li.⁴³ The lithiation voltage for SiC_2/5O_6/5 is predicted to be around 0.42 to 1.12 V.

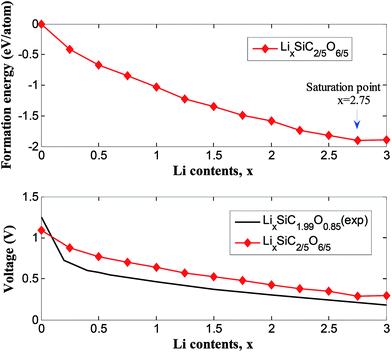Fig. 7 Formation energy and voltage profiles for Li_xSiC_2/5O_6/5 in comparison to experimental results of Li_xSiC_1.99O_0.85 (ref. 5).

4. Conclusions

The present first-principle simulations offer an insights into the lithiated structures and lithiation mechanism of a-SiC_2/5O_6/5. Our interpretation of radial distribution, angular distribution and coordinate number suggests that the Si–O bond tends to break and the Li₂O will forms at the beginning of lithiation, then Li_xO and Li_ySi form with increasing of Li concentration, which make major contribution to the capacity of the a-SiC_2/5O_6/5. The Li concentration dependent of formation energies curve indicates that the lithiation of SiC_2/5O_6/5 is favorable until a Li concentration of x = 2.75, which corresponds to a specific capacity of 1415 mA h g⁻¹. Both the formation energies and the voltage curves suggest lithium is preferable in incorporation with SiC_2/5O_6/5, and this is attributed to the formation of Li_xO and Li_ySi.

Acknowledgements

The authors would like to acknowledge the support of the National Natural Science Foundation of China (51675384), Public Welfare Science and Technology Project of Wenzhou City (G20160011) and High Performance Computing System of Wenzhou University.

References

1. C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35.
2. Y. Bie, J. Yang, Y. Nuli and J. Wang, RSC Adv., 2016, 6, 97084–97088.
3. Y. J. Cho, H. S. Kim, H. Im, Y. Myung, G. B. Jung, C. W. Lee, J. Park, M.-H. Park, J. Cho and H. S. Kang, J. Phys. Chem. C, 2011, 115, 9451–9457.
4. A. G. Kannan, S. H. Kim, H. S. Yang and D.-W. Kim, RSC Adv., 2016, 6, 25159–25166.
5. D. Ahn and R. Raj, J. Power Sources, 2010, 195, 3900–3906.
6. D. Ahn and R. Raj, J. Power Sources, 2011, 196, 2179–2186.
7. P. E. Sanchez-Jimenez and R. Raj, J. Am. Ceram. Soc., 2010, 93, 1127–1135.
8. R. Bhandavat and G. Singh, J. Phys. Chem. C, 2013, 117, 11899–11905.
9. H. Fukui, Y. Harimoto, M. Akasaka and K. Eguchi, ACS Appl. Mater. Interfaces, 2014, 6, 12827–12836.
10. S. Choi, D. S. Jung and J. W. Choi, Nano Lett., 2014, 14(12), 7120–7125.
11. M. Wilamowska-Zawlocka, P. Puczkarski, Z. Grabowska, J. Kaspar, M. Graczyk-Zajac, R. Riedel and G. D. Sorarù, RSC Adv., 2016, 6, 104597–104607.
12. M. Ma, H. Wang, M. Niu, L. Su, X. Fan, J. Deng, Y. Zhang and X. Du, RSC Adv., 2016, 6, 43316–43321.
13. V. Pradeep, M. Graczyk-Zajac, R. Riedel and G. Soraru, Electrochim. Acta, 2014, 119, 78–85.
14. M. K. Chan, C. Wolverton and J. P. Greeley, J. Am. Chem. Soc., 2012, 134, 14362–14374.
15. C.-Y. Chou and G. S. Hwang, Chem. Mater., 2013, 25, 3435–3440.
16. J. Hu, B. Xu, C. Ouyang, Y. Zhang and S. A. Yang, RSC Adv., 2016, 6, 27467–27474.
17. N. Liao, B. Zheng, H. Zhou and W. Xue, J. Mater. Chem. A, 2015, 3, 5067–5071.
18. N. Liao, B. Zheng, H. Zhou and W. Xue, J. Power Sources, 2016, 334, 39–43.
19. J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566.
20. S. Munetoh, T. Motooka, K. Moriguchi and A. Shintani, Comput. Mater. Sci., 2007, 39, 334–339.
21. N. Liao, W. Xue and M. Zhang, J. Eur. Ceram. Soc., 2012, 32, 1275–1281.
22. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
24. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
25. S. J. Clark, M. D. Segall and C. J. Pickard, Z. Kristallogr., 2005, 220, 567–570.
26. W.-S. Feng, Y. Fang, J.-X. XU, C.-H. Fang, Q.-J. Jia, H.-H. Wang and X.-M. Jiang, Acta Phys.-Chim. Sin., 2008, 24, 497–501.
27. H. Bréquel, J. Parmentier, S. Walter, R. Badheka, G. Trimmel, S. Masse, J. Latournerie, P. Dempsey, C. Turquat and A. Desmartin-Chomel, Chem. Mater., 2004, 16, 2585–2598.
28. H. Brequel, G. Soraru, L. Schiffini and S. Enzo, Mater. Sci. Forum, 2000, 343, 677–682.
29. G. D. Sorarù, G. D'Andrea and A. Glisenti, Mater. Lett., 1996, 27, 1–5.
30. C. Moysan, R. Riedel, R. Harshe, T. Rouxel and F. Augereau, J. Eur. Ceram. Soc., 2007, 27, 397–403.
31. M. G. Segatelli, A. T. N. Pires and I. V. P. Yoshida, J. Eur. Ceram. Soc., 2008, 28, 2247–2257.
32. B. Papendorf, E. Ionescu, H. J. Kleebe, C. Linck, O. Guillon, K. Nonnenmacher and R. Riedel, J. Am. Ceram. Soc., 2013, 96, 272–280.
33. T. Rouxel, G. D. Soraru and J. Vicens, J. Am. Ceram. Soc., 2001, 84, 1052–1058.
34. G. D. Sorarù, E. Dallapiccola and G. D'Andrea, J. Am. Ceram. Soc., 1996, 79, 2074–2080.
35. G. D. Soraru, G. D'andrea, R. Campostrini, F. Babonneau and G. Mariotto, J. Am. Ceram. Soc., 1995, 78, 379–387.
36. R. Angel, D. Allan, R. Miletich and L. Finger, J. Appl. Crystallogr., 1997, 30, 461–466.
37. B. Schiemenz and P. P. Power, Angew. Chem., Int. Ed. Engl., 1996, 35, 2150–2152.
38. M. M. Islam, T. Bredow and P. Heitjans, J. Phys. Chem. C, 2011, 115, 12343–12349.
39. E. Martinez, J. Plans and F. Yndurain, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 8043.
40. H. Chen, P. Jutzi, W. Leffers, M. Olmstead and P. Power, Organometallics, 1991, 10, 1282–1286.
41. S. Perez-Beltran, G. E. Ramírez-Caballero and P. B. Balbuena, J. Phys. Chem. C, 2015, 119, 16424–16431.
42. X. Liu, K. Xie, C.-m. Zheng, J. Wang and Z. Jing, J. Power Sources, 2012, 214, 119–123.
43. M. Aydinol, A. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354.

---