Open Access Article
Open Access ArticleEfficient removal of Pb(II) ions using manganese oxides: the role of crystal structure
Haipeng Zhang,
Anbang Wu,
Heyun Fu,
Ling Zhang,
Hui Liu,
Shourong Zheng,
Haiqin Wan and
Zhaoyi Xu *
*
State Key Laboratory of Pollution Control and Resource Reuse, Jiangsu Key Laboratory of Vehicle Emissions Control, School of the Environment, Nanjing University, Nanjing 210023, China. E-mail: zhaoyixu@nju.edu.cn; Fax: +86-25-89680596; Tel: +86-25-89680370
First published on 23rd August 2017
Abstract
Manganese oxides have been proven to be promising adsorbents to capture Pb(II) from wastewaters. In nature, MnO2 can be found in different crystalline structures, while the effect of crystal structure on their adsorption performance remains unclear. In this study, five manganese oxides with different crystallographic phases, α-, β-, γ-, δ-, and λ-MnO2 were prepared and characterized by X-ray diffraction (XRD), transmission electron microscopy (TEM), X-ray photoelectron spectroscopy (XPS), N2 adsorption–desorption, Fourier transform infrared (FT-IR) spectroscopy and zeta potential measurements. The adsorptive removal of aqueous Pb(II) was investigated using these manganese oxides as adsorbents. The results showed that the adsorption capacities of manganese oxides for Pb(II) varied with BET surface area and crystalline structure, following the order of δ-MnO2 > α-MnO2 > λ-MnO2 > γ-MnO2 > β-MnO2. δ-MnO2 displayed the highest capacity for Pb(II), and the adsorption was scarcely influenced by the presence of the coexisting Na+ cation. The surface complexation model was used to describe the Pb(II) adsorption on the MnO2 adsorbents. In a column adsorption test δ-MnO2 was capable of continuously treating 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bed volumes synthetic wastewater stream with an influent concentration of 20 mg L−1 Pb(II) and an effluent concentration below 0.5 mg L−1. This work indicates that δ-MnO2 has great potential to be used as an effective adsorbent for Pb(II) removal.
000 bed volumes synthetic wastewater stream with an influent concentration of 20 mg L−1 Pb(II) and an effluent concentration below 0.5 mg L−1. This work indicates that δ-MnO2 has great potential to be used as an effective adsorbent for Pb(II) removal.
1. Introduction
Water pollution by Pb(II) is a serious environmental problem. Wastewaters from various industrial activities usually contain considerable amounts of Pb(II) which can be a severe threat to public health.1 Toxicity studies have demonstrated that Pb(II) can be accumulated in human body because of its high volatility and non-biodegradability, causing neurological, reproductive and immunological pathologies.2,3 Therefore, a simple and cost-effective treatment technique to remove Pb(II) from the environment is recognized as a top priority by the World Health Organization (WHO).4Adsorption is considered as an effective and economic technology to remove Pb(II) from water prior to its discharge into the natural environment. A variety of materials have been explored for adsorptive removal of Pb(II) from water, including carbon materials,5 clay minerals6,7 and metal oxides (e.g. Fe2O3, Al2O3 and MnO2),8 and MnO2 was found to be the one of the most active species for Pb(II) removal.9 Wang et al.10 prepared layered birnessite type MnO2 and found that the adsorbent was effective for the removal of Pb(II) at pH 4.5. In parallel, Maliyekkal et al. synthesized cellulose–manganese oxide hybrid material for adsorptive removal of Pb(II) in water.11 It should be emphasized that manganese oxides are suitable for Pb(II) adsorption because of the high specific surface area, low isoelectric point (IEP) and negatively charged surface over a wide pH range.12 Tonkin et al.13 reported that Pb(II) could be effectively adsorbed on δ-MnO2 within the pH range of 2–9. Moreover, manganese oxides have attracted special attention because of their outstanding structural flexibility, low-cost and environmental friendliness, which have been widely applied in adsorbents,9 catalysts14 and cathodes.15
Manganese oxides are widely used in adsorption of removing Pb(II) from aqueous solutions. However, according to some recent studies, the adsorption affinity of MnO2 towards Pb(II) was highly related to the structures and surface properties of MnO2. Luo et al.16 studied adsorptive removal of lithium by 3D-MnO2 from wastewater and found that 3D-MnO2 with high degree of porosity and large pores exhibited a higher adsorption capacity than 1D-MnO2. Kozlova et al.17 prepared complex manganese oxides with different sizes of structural tunnels, and concluded that the tunnel size was the determining factor for the sorption of heavy metal cations. In addition, Korshin et al.18 and Abdullah et al.19 found that heavy metal ions could be complexed at different adsorption sites on birnessite and α-MnO2 using EXAFS spectroscopy. Wang et al.10 studied the adsorption mechanisms of Pb(II) onto varied birnessite type MnO2 and found that the adsorption capacities were largely controlled by the Mn average oxidation states and type of sorption sites on the MnO2 surface. Notably, MnO2 exists in five main crystallographic forms in nature: α-, β-, γ-, δ-, and λ- types, as the basic structure unit, [MnO6] octahedron, links in different conditions.20 The crystalline structures are generally believed to be responsible for their chemical and physical properties.21 The influence of crystal forms on MnO2 catalytic performance has been extensively studied.22,23 Different crystallographic MnO2 materials were also prepared for pollutants adsorption, and MnO2 adsorbents showed varying adsorption performance depending on the surface area and crystalline structure. Zhang et al. investigated the effect of the crystallographic structure of MnO2 on Li+ adsorption, and found that MnO2 ion sieve with λ-crystallographic structure exhibited higher capacity for Li(I) selective adsorption.24 Kanungo and Parida prepared MnO2 adsorbents with different crystallographic forms (α-, β-, γ- and δ-MnO2), and adsorption of Cu(II) on those adsorbents were studied. They found the layered δ-MnO2 showed the highest adsorption capacity and the adsorption capacity was directly related to BET surface area.25 To gain a better understanding of the effect of MnO2 structure on adsorption behaviors, the adsorption comparison of Pb(II) on α-, β-, γ-, δ-, and λ-MnO2 were made in our experiments. However, to the best of our knowledge, no attempt has been made.
In this study, α-, β-, γ-, δ-, and λ-MnO2 were prepared and characterized by X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), transmission electron microscopy (TEM), Fourier transform infrared (FT-IR), N2 adsorption/desorption and zeta potential measurements. The adsorption properties of the adsorbents toward Pb(II) in aqueous solution were systematically examined for adsorption capacity and effect of water chemistry. The influence of crystal forms of MnO2 on their adsorption performance was investigated in conjunction with important physicochemical parameters. Column adsorption tests were also carried out to elucidate the applicability of δ-MnO2 in Pb(II) removal from synthetic wastewater effluent.
2. Experimental section
2.1 Materials and reagents
Chemicals used in the experiments were of analytical grade and were used without further purification. All chemicals including manganese sulfate (MnSO4·H2O), ammonium persulfate ((NH4)2S2O8), potassium hypermanganate (KMnO4), lead nitrate (Pb(NO3)2), sodium nitrate (NaNO3), magnesium nitrate (Mg(NO3)2), calcium nitrate (Ca(NO3)2) were purchased from Nanjing Chemical Reagents Co., Ltd. Stock solutions of Pb(II) was prepared by dissolving appropriate amount of Pb(NO3)2 in deionized (DI) water.2.2 Preparation of manganese oxides
The α-MnO2, β-MnO2, and γ-MnO2 were prepared by the hydrothermal method according to the literature.20 In brief, 2.4 g of MnSO4·H2O and appropriate amount of (NH4)2S2O8 (5.3 g for α-MnO2, and 3.7 g for β-MnO2 and γ-MnO2) were put into DI water at room temperature to form a homogeneous solution, which was then transferred into a 40 mL Teflon-lined stainless steel autoclave and heated for 12 h. The hydrothermal temperature was set at 90 °C for γ-MnO2, and 140 °C for α-MnO2 and β-MnO2. After the reaction was completed, the resulting solid product was filtered and washed with DI water, drying at 110 °C for 12 h.To prepare δ-MnO2, 1.8 g of KMnO4 was dissolved in 100 mL DI water, then 30 mL H2O2 (30%) was added dropwise to the solution under fast stirring. The solution pH was kept at 7.0 ± 0.2 using 0.1 mol L−1 HNO3 and/or KOH. After continuously stirring for another 30 min, the suspension was aged at room temperature for 3 h. Then the aged precipitate was filtered and washed with DI water and dried at 110 °C for 12 h.
The λ-MnO2 was prepared using LiMn2O4 as the precursor. Four grams of KMnO4, 1.5 g of NaCl and 4.5 g of LiCl were grinded thoroughly and transferred to ceramic crucible, followed by a heat-treatment at 600 °C for 5 h.26 The resulting solid product was added in 200 mL 0.1 mol L−1 HNO3 solution under fast stirring for 12 h. After the acid treatment, the suspension was filtered and the solid product was washed with DI water and dried at 110 °C for 12 h.
2.3 Characterization of manganese oxides
Powder XRD patterns of the samples were collected on a Rigaku D/max-RA powder diffraction meter with Cu Kα radiation (Rigaku, Japan). TEM images of the samples were collected on a Hitachi H-800 transmission electron microscope (Hitachi, Japan). The specific surface areas of the adsorbents were measured by N2 adsorption/desorption after pretreated at 200 °C under vacuum (1.33 Pa) for 4 h on a Micrometrics ASAP 2020 analyzer (Micromeritics ASAP 2020, USA) at −196 °C (77 K) and were calculated by the Brunauer–Emmett–Teller (BET) method. FT-IR spectra of the samples were recorded on a Nicolet Nexus 870 FT-IR spectrometer (Nicolet, USA) with the KBr pellet technique. An XPS spectrometer (Perkin Elmer PHI 550 ESCA/SAM, USA) equipped with a monochromatized Al Kα X-ray source (hv = 1486.6 eV) and a hemispherical electron analyzer was used to analyze the surface properties of the samples. The C 1s peak (284.6 eV) was used for the calibration of binding energy values. Surface zeta potentials (ζ) of the materials were measured using a zeta potential analyzer (Zeta PALS, Brookhaven Instruments Co., USA). Briefly, 0.01 g of materials were dispersed in 100 mL of 1 mmol L−1 NaCl with varied pH adjusted using 0.1 mol L−1 HCl or NaOH, and the suspension was allowed to settle for 24 h before zeta-potential measurement.2.4 Adsorption kinetics
To examine the adsorption kinetic of Pb(II) to the adsorbent, 0.25 g of adsorbent was added into a 500 mL round-bottom flasks containing 500 mL of Pb(II) solution with varied initial concentrations under vigorous magnetic stirring. The initial Pb(II) concentrations were 45.0 mg L−1 for α-, β-, γ- and λ-MnO2, and 150.0 mg L−1 for δ-MnO2. The samples were taken from the flasks at preset time intervals and the adsorbent was removed by fast filtration. The concentration of Pb(II) in the filtrate was determined by AAS, and the adsorption amount was calculated according to the following equation:
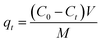 | (1) |
2.5 Adsorption isotherms
Adsorption isotherms of Pb(II) on the adsorbents were obtained from batch experiments by placing 20.0 mg of adsorbent in 40 mL polytetrafluoroethylene-lined screw cap glass tubules receiving 40 mL of Pb(NO3)2 aqueous solutions with varied initial concentrations. The pH of the aqueous solutions was adjusted to 4.0 ± 0.2 using 0.1 mol L−1 HNO3 or NaOH. Then, the samples were shaken at room temperature for 24 h in an orbital shaker. The time period was sufficient to reach apparent adsorption equilibrium based on preliminarily determined adsorption kinetics. After shaking, the sample was filtrated using a 0.45 μm filter, and Pb(II) concentration in the was filtrate determined by AAS. The adsorbed amount of Pb(II) at equilibrium was calculated according to the following equation:
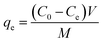 | (2) |
The impact of ionic strength and pH on Pb(II) adsorption was tested in the presence of NaNO3 solutions with varied concentrations (0.001, 0.01, and 0.10 mol L−1) in a pH range of 2.5–10.0. The initial Pb(II) concentrations were 45.0 mg L−1 for α-, β-, γ- and λ-MnO2, and 150.0 mg L−1 for δ-MnO2. The initial pH of Pb(II) solution was adjusted using 0.1 mol L−1 HNO3 or NaOH, and the pH of all samples was measured after adsorption equilibrium. All adsorption experiments were conducted in duplicate.
2.6 Fixed-bed column adsorption
The experiments of column adsorption were carried out in a polyethylene column (1.78 mm internal diameter, 130 mm in length) equipped at room temperature. The wet δ-MnO2 (bed volume = 2.0 mL, M = 3.27 g) or silica sand was packed within the columns before operation. A control of only silica sand was also tested and the results revealed that the silica sand did not adsorb Pb(II) (data not shown). A synthetic influent solution containing Pb(II) (20.0 mg L−1), Na(I) (100.0 mg L−1), Mg(II) (100.0 mg L−1) and Ca(II) (150.0 mg L−1) was pumped upflow through the column at flow rate of 15.0 mL h−1 using a Lange-580 pump (Baoding, China). The effluent was collected regularly by a BSZ-100 programmable fraction collector (Shanghai, China) and measured by AAS. As for the regeneration test, a mixed solution containing 0.1 mol L−1 HNO3 and 5 wt% Ca(NO3)2 was used as the regenerant and the flow rate was 7.5 mL h−1.3. Results and discussion
3.1 Characterization of adsorbents
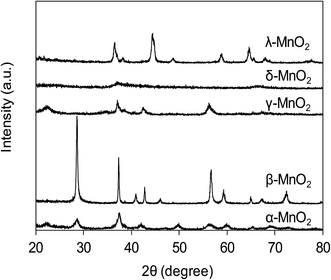
The XRD patterns of varied MnO2 adsorbents are compiled in Fig. 1. For α-MnO2, diffraction peaks were identified with 2θ at 22.5°, 28.7°, 37.5°, 42.0°, 49.9°, 56.6°, 59.9°, 65.3° and 68.9°, indicative of the presence of manganese oxide with a tetragonal structure.20 As for β-MnO2, diffraction peaks were observed with 2θ at 28.6°, 37.3°, 40.9°, 42.8°, 46.1°, 56.7°, 59.3° and 64.9°, assigned to rutile structure.20 The XRD pattern of γ-MnO2 displayed four distinct diffraction peaks at 22.2°, 37.6°, 42.5° and 56.2°, corresponding to manganese oxide resulted from a random intergrowth of blocks of the rutile-type structural units within the Ramsdellite structure.20 Two low intensity and broad diffraction peaks at 37.0° and 67.5° were observed for δ-MnO2, characteristic of hexagonal randomly-stacked and single phased birnessite-type MnO2.27 The diffraction peaks of λ-MnO2 were identified with 2θ at 36.5°, 38.2°, 44.4°, 48.8°, 58.9°, 64.6°, 65.6° and 67.9°, indicative of cubic spinel structure for λ-MnO2.26 The XRD results clearly revealed the successful preparation of varied MnO2 crystallographic forms.The TEM images of the five MnO2 adsorbents are compared in Fig. 2 α-MnO2 (Fig. 2a) was shown to be ribbon-like nanowires with diameters around 10 nm and lengths ranging between 0.06 and 0.4 μm. β-MnO2 (Fig. 2b) and γ-MnO2 (Fig. 2c) were observed to be nanorods with average diameters of 100 and 20 nm, respectively. As for δ-MnO2 (Fig. 2d), the layered structure was clearly identified, which was commonly formed by MnO2 nanosheets organizing in layer-by-layer structure for multilayer systems. The λ-MnO2 (Fig. 2e) had a cubic structure with a size about 20 nm, which was consistent with the XRD results. The BET surface areas were 97.5, 14.2, 71.4, 270.8 and 36.6 for α-, β-, γ-, δ-, and λ-MnO2, respectively. The δ-MnO2 with a layered structure exhibited a highest BET surface area, which was likely because the layer spacing of δ-MnO2 was large enough to host N2 molecules. As for α-, β-, γ- and λ-MnO2, N2 molecules were mainly adsorbed on the external surface.23
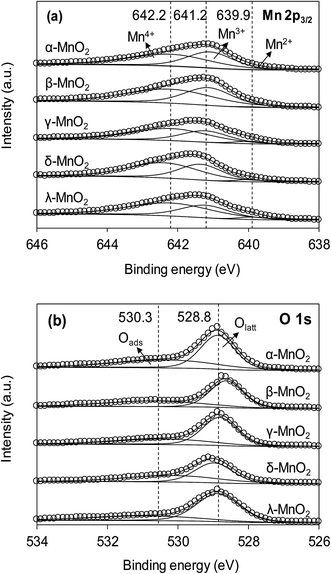
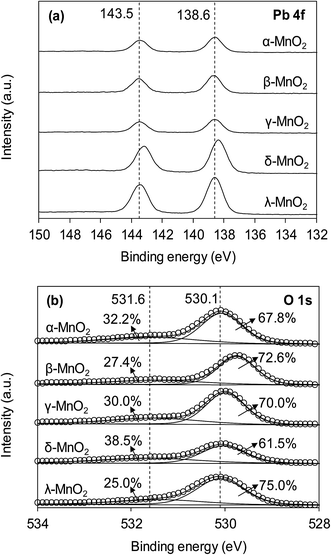
The XPS spectra of the adsorbents in the Mn 2p3/2 and O 1s regions are compared in Fig. 3a and b, respectively. As can be seen in Fig. 3a, the Mn 2p3/2 spectrums were asymmetrical and could be divided into three peaks at 639.9, 641.2 and 642.2 eV, assigned to Mn2+, Mn3+ and Mn4+, respectively.10,28 To obtain the relative quantity of Mn2+, Mn3+ and Mn4+ in the adsorbents, the Mn 2p3/2 spectrums were fitted according to the literature,10,29 and the fitting results are listed in Table 1. The content of Mn3+ in α- and β-MnO2 were higher than others. According to literature, the higher Mn3+ content led to fewer cationic vacancies because the Mn3+ site binding might involve additional complexes when compared to Mn4+.10 The O 1s spectrums (Fig. 3b) of the adsorbents were highly asymmetrical and were divided into two peaks at 528.6–529.0 eV and 530.9–531.0 eV, assigned to oxygen containing species of lattice oxygen and adsorbed oxygen, respectively.30 The contents of lattice oxygen and adsorbed oxygen in the adsorbents are listed in Table 1. As for δ-MnO2, the content of adsorbed oxygen was the highest among the adsorbents, revealing an abundance of surface hydroxyl groups.
| Sorbents | Mn4+ | Mn3+ | Mn2+ | Olatt | OHads | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BEa (eV) | FWHMb (eV) | At.c (%) | BE (eV) | FWHM (eV) | At. (%) | BE (eV) | FWHM (eV) | At. (%) | BE (eV) | FWHM (eV) | At. (%) | BE (eV) | FWHM (eV) | At. (%) | |
| a Binding energy.b The FWHM of all peaks were constrained.c At. represents the percentage of the contribution for each peak to the total number of counts under the Mn 2p3/2 or O 1s peak, and all peaks modeled as 70% Gaussian–30% Lorentzian. | |||||||||||||||
| α-MnO2 | 642.22 | 2.72 | 56.1 | 641.08 | 1.57 | 43.9 | 639.02 | 1.18 | 0.0 | 528.62 | 1.10 | 61.7 | 530.67 | 3.29 | 38.3 |
| β-MnO2 | 642.21 | 2.93 | 58.3 | 641.13 | 1.62 | 41.1 | 639.91 | 0.91 | 0.6 | 528.87 | 1.15 | 58.9 | 530.31 | 3.40 | 41.1 |
| γ-MnO2 | 642.18 | 2.64 | 60.1 | 641.21 | 1.61 | 35.2 | 639.96 | 0.96 | 4.7 | 528.82 | 1.15 | 64.0 | 530.37 | 3.17 | 36.0 |
| δ-MnO2 | 642.29 | 2.38 | 58.9 | 641.35 | 1.46 | 38.1 | 639.99 | 0.85 | 3.0 | 528.97 | 1.26 | 55.7 | 530.10 | 3.20 | 44.3 |
| λ-MnO2 | 642.21 | 2.78 | 60.5 | 641.22 | 1.63 | 35.6 | 639.87 | 0.90 | 3.9 | 528.86 | 1.43 | 71.0 | 530.86 | 3.53 | 29.0 |
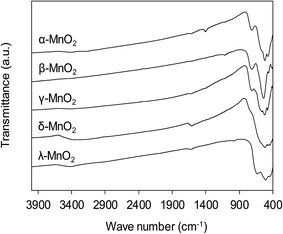
The functional groups on MnO2 surface were studied by FT-IR, and the FT-IR spectra of the adsorbents are compiled in Fig. 4. The broad band appearing at around 3400 cm−1 was assigned to O–H stretching and the band at 1610 cm−1 was attributed to O–H bending vibration.31 For all MnO2 adsorbents, the characteristic bands at 400–800 cm−1 were observed, corresponding to the Mn–O lattice vibration.27 For the layered δ-MnO2 and cubic spinel λ-MnO2, the bands around 416, 441 and 512 cm−1 were recorded, which is in good agreement with reported FT-IR characteristic bands in literature.27 However, as for the tunnel α-, β- and γ-MnO2 the position of those characteristic bands displayed some obvious changes. A weak band around 711 cm−1 was observed, corresponding to the manganese oxides with tunnel structure.32,33 Additionally, the band at 1106 cm−1 was also recorded in the FT-IR spectra of α- and γ-MnO2, characteristic of the vibration of the Mn3+–O bond.27 This observation suggests that some Mn3+ occupies the Mn4+ sites in the frameworks of α- and γ-MnO2. These results implied that the crystal structure of MnO2 played a key role in affecting the Mn–O lattice vibration as well as the nature of surface hydroxyl groups.
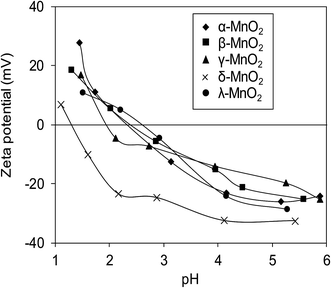
Surface zeta potentials of the varied crystallographic MnO2 as a function of solution pH are compared in Fig. 5. Within the test pH range, surface zeta potentials of all adsorbents monotonically decreased due to the continuous deprotonation effect of surface hydroxyl groups. The isoelectric points (IEP) of α-, β-, γ-, δ-, and λ-MnO2 were found to be 2.4, 2.4, 2.0, 1.3 and 2.6, respectively, similar to those reported in literatures.12,21,26,34 Additionally, negative surface zeta potentials were observed on the five adsorbents over a wide pH range, suggesting the potential for adsorptive removal of Pb(II) in water. Notably, much lower ζ potential was observed in δ-MnO2 than in others in the test pH range of 1.0–6.0.
3.2 Adsorption kinetics
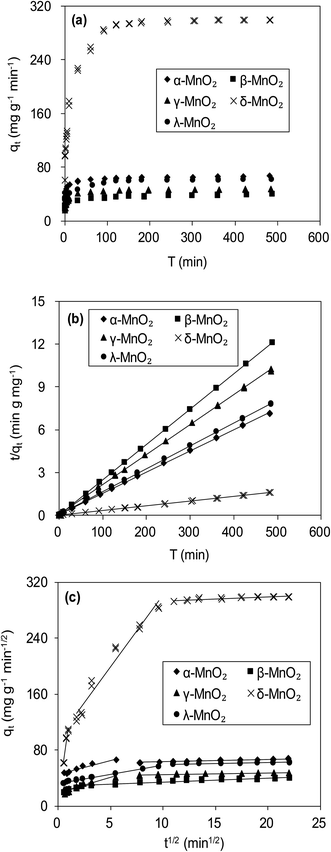
Fig. 6a compares the kinetics of Pb(II) adsorption onto the five MnO2 adsorbents. It was shown that the adsorption of Pb(II) on MnO2 adsorbents were very fast. The Pb(II) adsorption amounts increased sharply within 20 min and reached equilibrium at about 150 min. The kinetic data were fitted using the pseudo-second-order kinetic model as follow:21
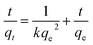 | (3) |
| Sorbents | qexp, mg g−1 | Pseudo second-order | Weber–Morris model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k, mg g−1 min−1 | qcal, mg g−1 | R2 | k1, mg g−1 min−1/2 | C1 | R2 | k2, mg g−1 min−1/2 | C2 | R2 | ||
| α-MnO2 | 67.6 | 4.40 × 10−3 | 67.1 | 0.99 | 3.63 | 40.75 | 0.94 | |||
| β-MnO2 | 40.3 | 3.42 × 10−3 | 39.7 | 0.99 | 3.78 | 18.82 | 0.85 | |||
| γ-MnO2 | 47.9 | 5.94 × 10−3 | 47.6 | 0.99 | 4.44 | 18.42 | 0.90 | |||
| δ-MnO2 | 299.2 | 6.07 × 10−4 | 303.0 | 0.99 | 36.67 | 1.65 | 0.92 | 20.51 | 97.27 | 0.96 |
| λ-MnO2 | 62.4 | 3.31 × 10−3 | 62.5 | 0.99 | 2.59 | 32.33 | 0.99 | |||
To further verify the controlling mechanism involved in the adsorption process, Weber–Morris model was used to fit the kinetic adsorption data. The model is expressed as follows:21
| qt = kit1/2 + Ci | (4) |
Fig. 6c presents the plots of qt versus t1/2 for adsorption of Pb(II) onto the five adsorbents, and the fitting parameters are listed in Table 2. The qt–t1/2 relations clearly exhibited multilinearity, reflecting that the adsorption process appeared to be controlled by more than one step. According to Weber–Morris model, the adsorption process is only controlled by intraparticle diffusion when Ci = 0. For δ-MnO2, the qt–t1/2 plots consisted of three linear portions, and the first linear portion did not pass through the origin, suggesting the involvement of external diffusion.21 Therefore, the first linear portion was attributed to the fast lead adsorption onto δ-MnO2 external surface and the second one was indicative of Pb(II) diffusion into the interlayer space of the adsorbent, and the third one was characteristic of the final equilibrium step. Notably, the majority of Pb(II) adsorption onto δ-MnO2 was observed in second linear portion and the intraparticle diffusion was slower than the external surface diffusion. In contrast, the Weber–Morris plots of α-, β-, γ- and λ-MnO2 consisted of two linear portions, in which the first linear portion was Pb(II) diffusion to the sorbents external surfaces and the second one was the final equilibrium stage.
3.3 Adsorption isotherms
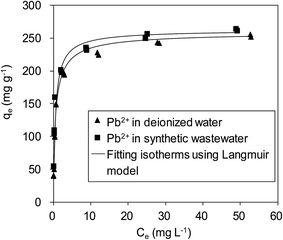
The adsorption isotherms of Pb(II) onto various MnO2 adsorbents are compared in Fig. 7a. For δ-MnO2, Pb(II) adsorption amount was 242.6 mg g−1 at an equilibrium concentration of 28.2 mg L−1, which was significantly larger than that for α-, β-, γ- and λ-MnO2 (84.4, 58.9, 62.1 and 61.9 mg g−1, respectively). To analyze the adsorption behavior of the adsorbents, the adsorption isotherms were further modeled using Langmuir and Freundlich models. The Langmuir isotherm model is expressed as follows:
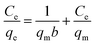 | (5) |
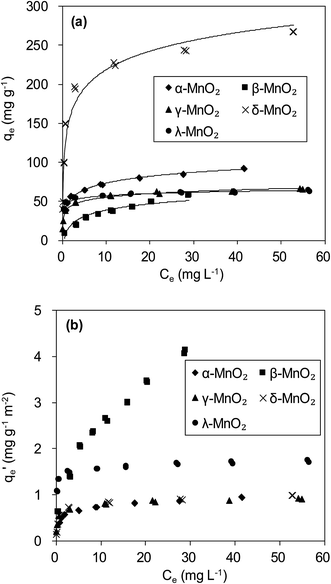 | ||
| Fig. 7 (a) Pb(II) adsorption isotherms and (b) BET surface area normalized Pb(II) adsorption isotherms on MnO2 adsorbents. | ||
The Freundlich isotherm model can be described as:
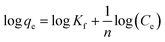 | (6) |
The fitting parameters are summarized in Table 3. High correlation coefficients (R2) were achieved for the Langmuir and Freundlich models, indicating that Pb(II) adsorption onto the adsorbents could be well described by these two models. The maximum adsorption capacity qm value and Freundlich coefficient Kf value for δ-MnO2 were both higher in comparison with the other MnO2, confirming the largest adsorption capacity of δ-MnO2. This can be explained by different BET surface area of the five MnO2 adsorbents. Among the five MnO2 adsorbents, δ-MnO2 exhibited the largest BET surface area with abundant hydroxyl groups as observed in XPS and FT-IR spectra.30 Compared with the other three MnO2 adsorbents, γ- and λ-MnO2 had larger b values in Langmuir model, suggesting their high affinity for Pb(II). This is likely due to the high contents of Mn4+ in γ- and λ-MnO2. The charge imbalance on Mn4+ sites is much higher than on Mn3+ and Mn2+ sites and the former sites exhibit higher affinity for metal binding. Thus, structural forms of MnO2 had great impact on its Pb(II) adsorption performance.
| Sorbents | Langmuir model | Freundlich model | ||||
|---|---|---|---|---|---|---|
| b (L g−1) | qm (mg g−1) | R2 | Kf (mg1−n L−1 g−1) | n | R2 | |
| α-MnO2 | 1.08 | 84.0 | 0.97 | 45.4 | 5.08 | 0.96 |
| β-MnO2 | 0.55 | 42.4 | 0.93 | 12.5 | 2.20 | 0.99 |
| γ-MnO2 | 12.93 | 51.6 | 0.92 | 34.6 | 5.35 | 0.94 |
| δ-MnO2 | 3.57 | 200.0 | 0.92 | 112.2 | 3.68 | 0.87 |
| λ-MnO2 | 6.92 | 60.2 | 0.96 | 47.5 | 13.02 | 0.91 |
The interaction of Pb(II) with surface hydroxyl groups was confirmed by the XPS results of MnO2 after Pb(II) adsorption. Fig. 8 displays the XPS spectra of Pb 4f and O 1s of the MnO2 after Pb(II) adsorption. The MnO2 adsorbents displayed two peaks with Pb 4f7/2 and Pb 4f5/2 derived from spin–orbit splitting. The binding energy of Pb 4f7/2 core level was observed at around 138.6 eV, reflecting the orthorhombic PbO compound and no hydroxides or carbonates precipitation of Pb during adsorption.21 As for O 1s spectra, after Pb(II) adsorption the ratio of Oads decreased in all MnO2 adsorbents. This was likely due to the complexation interactions between surface –OH and Pb(II). The increase of Olatt ratio in Pb(II)-loaded MnO2 was attributed to the formation of Pb–O–Mn bond and the higher binding energy of O 1s in Pb(II)-loaded MnO2 confirmed the covalent of Pb–O–Mn linkage.
More insight into the structural properties of the adsorbents with varied crystallographic forms could be gained by comparing the surface area normalized adsorption isotherms, and the results are shown in Fig. 7b. Among the tested adsorbents, the normalized adsorption capacity of β-MnO2 was much higher. This could be well explained by the interface reaction mechanism inferred from adsorbate–adsorbent polyhedral linkage. Previous studies found that the [MnO6] octahedral structure units of the manganese dioxide were connected with the edge and double-corner linkages, and concluded that Pb(II) was adsorbed at double-corner-sharing (DCS) and double-edge-sharing (DES) sites.35 Notably, β- and λ-MnO2 is composed of single strands of edge-sharing [MnO6] octahedral with 1 × 1 tunnels, while α- and γ-MnO2 are constructed from the chains of 2 × 2, 1 × 1 and 1 × 2 tunnels, respectively.20,36 Thus, more DCS and DES adsorption sites per unit area were observed on β- and λ-MnO2 surfaces, making them showed higher surface area normalized adsorption capacities of Pb(II). Additionally, δ-MnO2 exhibited nearly identical normalized adsorption capacity to that of α- and γ-MnO2. These results further implied that crystal structure confinement effect was the main factor that affected the adsorption capacity.
The qm value for δ-MnO2 (200.0 mg g−1) synthesized in this study was also markedly larger than the values reported for many other adsorbents such as coconut shell carbon (26.5 mg g−1),37 amino-functionalized Fe3O4@SiO2 (76.7 mg g−1),38 montmorillonite (158.5 mg g−1)7 and nanoscale organo-functionalized SiO2–Al2O3 (183.0 mg g−1).39 Hence, the δ-MnO2 exhibited a significantly higher adsorption capacity than these other adsorbents. Additionally, the synthesis cost of δ-MnO2 was much less than amino-functionalized Fe3O4@SiO2, which was feasible for industrial Pb(II) recycling.
3.4 Effect of pH and ionic strength
The effects of pH and ionic strength on Pb(II) adsorption to the adsorbents were examined, and the results are presented in Fig. 9. For the five adsorbents, Pb(II) adsorption was significantly affected by the solution pH, which increased continuously in the experimental pH range of 2.5–5.5. It should be noted that Pb(II) would precipitate under high pH (e.g. pH > 7.0) conditions. The effect of pH on Pb(II) adsorption on MnO2 could be well explained by the electrostatic interaction mechanism. Because surface hydroxyl groups were the adsorption sites, the impact of solution pH on Pb(II) adsorption predominantly depending on the protonation–deprotonation transition of surface hydroxyl groups.13,21 The results of zeta potential showed that the isoelectric points (IEP) of α-, β-, γ-, δ-, and λ-MnO2 were found to be 2.4, 2.4, 2.0, 1.3 and 2.6, respectively, indicated that MnO2 was negatively charged at pH values above the IEP and electrostatic attractive interaction was expected at high pH, resulting in increased Pb(II) adsorption. When the solution pH values below IEP, MnO2 was positively charged and repulsive interaction occurred at low pH between Pb(II) and MnO2, thus displaying lowered Pb(II) adsorption. The ζ potential analysis showed that MnO2 surface became more negative charged with increasing solution pH, which would enhance the attraction of Pb(II). The nearly negligible Pb(II) adsorption on the sorbents at pH 2.0 suggested that the saturated adsorbent could be regenerated under acidic conditions.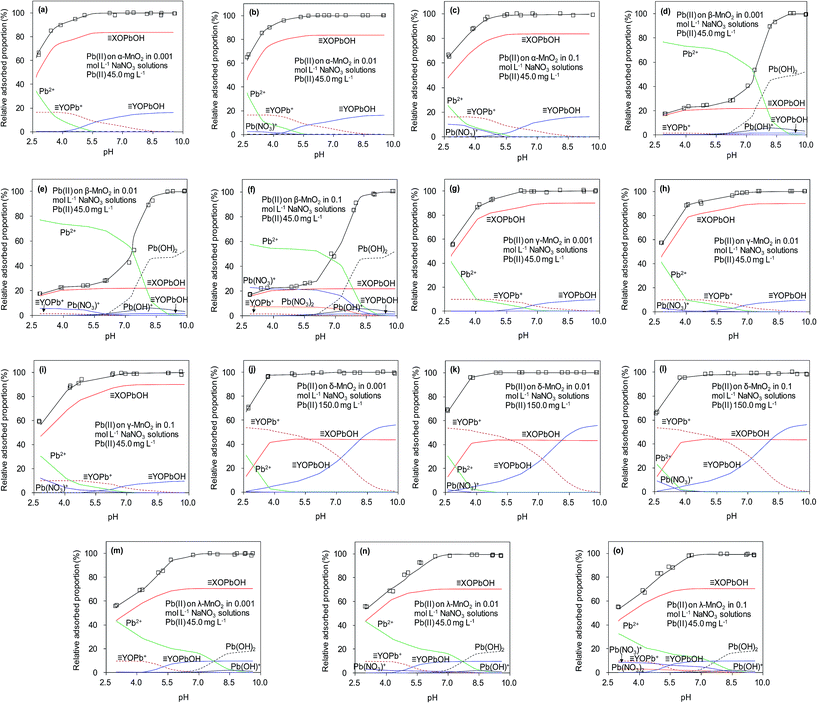 | ||
| Fig. 9 Surface binding species for Pb(II) adsorbed on the five MnO2 adsorbents at different solution pH and ionic strengths. | ||
In NaNO3 solutions, the formation of aqueous Pb(II) complexes with NO3− and OH− species might affect the Pb(II) adsorption on MnO2 as reported in previous work.41 The aqueous speciation reactions of Pb(II) with the electrolyte anions (OH− and NO3−) were described as follows:40,41
Pb2+ + H2O = Pb(OH)+ + H+, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = −6.19 K = −6.19
| (7) |
Pb2+ + 2H2O = Pb(OH)2(s) + 2H+, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = −8.15 K = −8.15
| (8) |
Pb2+ + NO3− = PbNO3+, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.1 K = 1.1
| (9) |
Pb2+ + 2NO3− = Pb(NO3)2, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.4 K = 1.4
| (10) |
The equilibrium protonation constants and complexation constants with OH− and NO3− were calculated at the ionic strength of 0.01 mol L−1 NaNO3, and these constants were also used for the higher ionic strengths. The predicted aqueous complexation of Pb(II) in 0.001, 0.01 and 0.1 mol L−1 NaNO3 solutions was performed using the computer program FITEQL 3.2, and the results are shown in Fig. 9. The amount of Pb(OH)+ species increased with the solution pH, while the amount of PbNO3+ species increased with ionic strength. According to the literature, the increase of ionic strength facilitated the formation of the Pb(NO3)+ and Pb(NO3)2 species,40 whose amounts increased at higher ionic strength at low pH conditions (<5.0). Moreover, the stability of aqueous Pb(II) complexes was enhanced at high ionic strength, which might suppress the adsorption of Pb(II) on the adsorbents. However, due to the high adsorption capacity of α-, γ-, δ- and λ-MnO2, the PbNO3+ and Pb(OH)+ species could also be adsorbed on the negative charged MnO2 in the tested pH range, suggesting the negligible effect of speciation on Pb(II) adsorption onto α-, γ- and δ-MnO2. As for β- and λ-MnO2, the poor Pb(II) adsorption capacity within the pH range of 2.5–5.0 implied that a large amount of PbNO3+ and Pb(OH)+ complexes remained in the solutions. The residual PbNO3+ and Pb(OH)+ complexes would precipitate at high pH conditions (>6.0), which was in line with the results of pH effect. Additionally, the observed effect of ionic strength on Pb(II) adsorption on MnO2 was negligible over the pH range of 2–10, indicating that Pb(II) was adsorbed predominantly via inner-sphere complexation. Similar results were also observed by Al Degs et al.42 and Han et al.43 This could be ascribed to the fact that the five MnO2 adsorbents possessed excellent adsorption selectivity for Pb(II) under the interference of Na(I). Moreover, δ-MnO2 exhibited a high adsorption capacity of Pb(II) with outstanding selectivity under high ionic strength, indicating a promising potential for Pb(II) adsorptive removal from wastewaters.
To verify the efficiency of using δ-MnO2 to remove Pb(II) from real wastewater, Pb(II) adsorption on δ-MnO2 in a synthetic wastewater containing Na(I) (100.0 mg L−1), Mg(II) (100.0 mg L−1) and Ca(II) (150.0 mg L−1) was studied, and the results are shown in Fig. 10. It is shown that Pb(II) adsorption on the δ-MnO2 adsorbent slightly increased with the co-existing ions in synthetic wastewater at pH 4.0, further indicating that Pb(II) adsorption was mainly driven by the strong inner-sphere complexation interactions between Pb(II) and the hydroxyl groups on δ-MnO2.21 The observed effects of coexisting alkaline/earth metal ions on Pb(II) adsorption to δ-MnO2 in synthetic wastewater clarified the validity of using δ-MnO2 as an efficient adsorbent for Pb(II) removal from actual wastewater.
 | ||
| Fig. 10 Adsorption isotherms of Pb(II) on δ-MnO2 in a synthetic wastewater containing 100 mg L−1 of Na(I), 100 mg L−1 Mg(II) and 150 mg L−1 Ca(II). | ||
3.5 Modeling the adsorption of Pb(II) onto MnO2
A number of previous researchers have used the diffuse double layer surface complexation model (SCM) to predict the adsorption of Pb(II) on manganese oxides at different ionic strengths.44,45 The SCM assumes that only surface complexation occurs on the charged surfaces, consistent with the adsorption mechanism of Pb(II) adsorption to the five MnO2 adsorbents. Thus, the SCM was chosen to be used in this study to describe the adsorption of Pb(II) to the surface sites on the five MnO2 adsorbents. The determination of surface equilibrium constants from experimental data was performed using the computer program FITEQL 3.2. The surface hydroxyl groups, including DCS and DES sites, at the five MnO2 adsorbents surface were determined according to the literature,44 and the results are listed in Table 4. The content of hydroxyl groups on δ-MnO2 was observed to be much higher than those of other MnO2 adsorbents, which resulted from its largest BET surface area. Manganese oxides with a larger BET surface area possessed more site vacancies, resulting in more surface hydroxyl groups. These results suggested that the BET surface area was the predominant factor affecting the content of hydroxyl groups on manganese oxides.| Sorbents | SBET (m2 g−1) | ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH (mmol g−1) XOH (mmol g−1) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH (mmol g−1) YOH (mmol g−1) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XO− XO− |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YO− YO− |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH2+ YOH2+ |
|---|---|---|---|---|---|---|
| α-MnO2 | 97.5 | 0.1996 | 0.0355 | −0.86 | −1.45 | 4.35 |
| β-MnO2 | 14.2 | 0.0477 | 0.0333 | −1.24 | −1.91 | 4.61 |
| γ-MnO2 | 71.4 | 0.1993 | 0.0214 | −1.25 | −2.67 | 4.71 |
| δ-MnO2 | 270.8 | 0.7093 | 0.4090 | −1.76 | −4.52 | 2.57 |
| λ-MnO2 | 36.6 | 0.1528 | 0.0208 | −1.44 | −1.28 | 4.28 |
A two-site model is employed to describe the reactions at manganese oxides surface, and the following reactions were used in FITEQL 3.2 to model Pb(II) adsorption on the five MnO2 adsorbents surface.
On the DCS sites:
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH + H+ = XOH + H+ = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH2+ XOH2+
| (11) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH = XOH = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XO− + H+ XO− + H+
| (12) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH2+ + Pb2+ = XOH2+ + Pb2+ = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPb+ + 2H+ XOPb+ + 2H+
| (13) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XO− + Pb2+ + H2O = XO− + Pb2+ + H2O = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPbOH + H+ XOPbOH + H+
| (14) |
On the DES sites:
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH + H+ = YOH + H+ = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH2+ YOH2+
| (15) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH = YOH = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YO− + H+ YO− + H+
| (16) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH2+ + Pb2+ = YOH2+ + Pb2+ = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ + 2H+ YOPb+ + 2H+
| (17) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YO− + Pb2+ + H2O = YO− + Pb2+ + H2O = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPbOH + H+ YOPbOH + H+
| (18) |
The FITEQL failed to simulate the surface species on the five MnO2 adsorbents because the species ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH2+ did not exist below the IEP of MnO2.42 The zeta potential analysis showed that the IEP values of the five MnO2 adsorbents were all below tested solution pH, suggesting that the
XOH2+ did not exist below the IEP of MnO2.42 The zeta potential analysis showed that the IEP values of the five MnO2 adsorbents were all below tested solution pH, suggesting that the ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH2+ and
XOH2+ and ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPb+ would not be significant species in the present study. Thus, the reaction
XOPb+ would not be significant species in the present study. Thus, the reaction ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOH2+ + Pb2+ =
XOH2+ + Pb2+ = ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPb+ + 2H+ was ignored in this study. All the parameters used to simulate the acid–base chemistry of the five MnO2 adsorbents are summarized in Table 4.
XOPb+ + 2H+ was ignored in this study. All the parameters used to simulate the acid–base chemistry of the five MnO2 adsorbents are summarized in Table 4.
Fig. 9 presents predicted the surface binding species for Pb(II) adsorbed onto the five MnO2 adsorbents in 0.001, 0.01 and 0.1 mol L−1 NaNO3. It is apparent that the fitted curves provided a close description of Pb(II) adsorption on the five MnO2 adsorbents over the tested pH range. Within the pH range of 2.5–10.0, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPbOH was the predominant species on α-, β-, γ- and λ-MnO2 surfaces, while
XOPbOH was the predominant species on α-, β-, γ- and λ-MnO2 surfaces, while ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ made insignificant contributions to adsorption at acidic to neutral pH conditions. The
YOPb+ made insignificant contributions to adsorption at acidic to neutral pH conditions. The ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ species decreased with the increase of solution pH, probably because the OH− species increased at higher pH conditions and would bind to the
YOPb+ species decreased with the increase of solution pH, probably because the OH− species increased at higher pH conditions and would bind to the ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+, resulting in the increase of
YOPb+, resulting in the increase of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPbOH species on α-, β-, γ- and λ-MnO2 surfaces. For δ-MnO2,
YOPbOH species on α-, β-, γ- and λ-MnO2 surfaces. For δ-MnO2, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ was the predominant species over the pH range of 2.5–5.8, likely due to the large amount of
YOPb+ was the predominant species over the pH range of 2.5–5.8, likely due to the large amount of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOH groups on the layered structural surfaces. Notably, Pb(OH)2 species appeared on the surface of β- and λ-MnO2 at high pH conditions, suggesting the Pb(II) had precipitated. This is conceivably attributed to the insufficient hydroxyl groups on β- and λ-MnO2 surfaces for Pb(II) adsorption.
YOH groups on the layered structural surfaces. Notably, Pb(OH)2 species appeared on the surface of β- and λ-MnO2 at high pH conditions, suggesting the Pb(II) had precipitated. This is conceivably attributed to the insufficient hydroxyl groups on β- and λ-MnO2 surfaces for Pb(II) adsorption.
The adsorption isotherm data were reproduced by using parameters estimated from SCM, and the results are shown in Fig. 11. According to the fitting results from SCM, Pb(OH)+ and Pb(OH)2 precipitate did not present at low pH conditions (<6.0) (Fig. 9). The aqueous Pb(II) species were Pb2+ and Pb(NO3)+. For α-, β-, γ- and λ-MnO2, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPbOH was the dominant species contributing to Pb(II) adsorption at the tested Pb(II) concentration in deionized water. This is likely due to the high Pb(II) concentration in the adsorption isotherm experiment. Similar results were also reported by Usiyama and Fukushi.41 As for δ-MnO2, prediction of surface speciation showed that the
XOPbOH was the dominant species contributing to Pb(II) adsorption at the tested Pb(II) concentration in deionized water. This is likely due to the high Pb(II) concentration in the adsorption isotherm experiment. Similar results were also reported by Usiyama and Fukushi.41 As for δ-MnO2, prediction of surface speciation showed that the ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ was the dominant species at various Pb(II) concentrations. The difference of dominant surface speciation between δ-MnO2 and other MnO2 adsorbents was possibly attributed to the high content of DES adsorption sites and high cation exchange capacity on layered manganese oxides.
YOPb+ was the dominant species at various Pb(II) concentrations. The difference of dominant surface speciation between δ-MnO2 and other MnO2 adsorbents was possibly attributed to the high content of DES adsorption sites and high cation exchange capacity on layered manganese oxides.
 | ||
| Fig. 11 Modeling Pb(II) adsorption isotherms using diffuse double layer surface complexation model (SCM). | ||
3.6 Fixed-bed adsorption
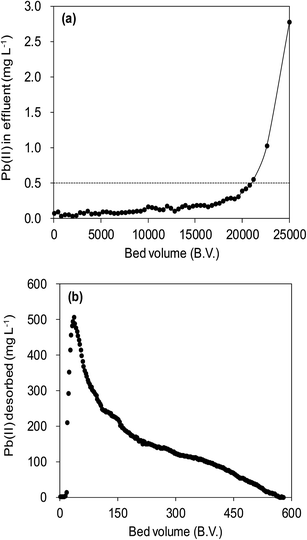
Fig. 12a illustrated an effluent history of δ-MnO2 fixed-bed column adsorption experiment, which was carried out to evaluate the sorbent applicability in wastewater treatment. The breakthrough point was set as 0.5 mg L−1 for Pb(II), as the regulated maximum concentration level by the mining industry emission standard of China.46 The sorbent exhibited a breakthrough at the point of ∼25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bed volume (BV) under the experimental conditions, indicated that Pb(II) could be efficiently removed by δ-MnO2 till the significant breakthrough occurs. The column adsorption behavior of Pb(II) on δ-MnO2 could be further quantified by the Thomas model and Yoon–Nelson model. The Thomas model can be expressed as follows:47
000 bed volume (BV) under the experimental conditions, indicated that Pb(II) could be efficiently removed by δ-MnO2 till the significant breakthrough occurs. The column adsorption behavior of Pb(II) on δ-MnO2 could be further quantified by the Thomas model and Yoon–Nelson model. The Thomas model can be expressed as follows:47
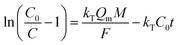 | (19) |
The Yoon–Nelson model is given in eqn (20).48
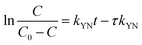 | (20) |
The fitting parameters of experimental data are summarized in Table 5. From the regression coefficients it could be concluded that the Thomas and Yoon–Nelson models fitted the experimental data accurately. As was not observed in the present study, the column breakthrough capacity was estimated using the Thomas model according to the literature.48 The Pb(II) adsorption capacity at the breakthrough point was 6.27 × 105 mg g−1, which was much higher than the values reported for hydrous Zr(IV) oxide-based nanocomposite (319.4 mg g−1) and polyacrylamide–hydrated ferric oxide hybrid material (211.4 mg g−1).48,49 Considering the structure of δ-MnO2, the higher adsorption capacity was likely due to the capillary condensation, which was used advantageously as universal functionalization strategy in nanoparticle thin films assembled layer-by-layer.49 The value of τ was as large as 7.32 × 103 h, also remarkably larger than the reported values.50,51 These results indicate that δ-MnO2 is highly effective for removal of Pb(II) from water in both batch and fixed-bed mode. Notably, the synthetic method of δ-MnO2 in this study was simple, economic, environmentally friendly, and was suitable for large-scale production. Therefore, δ-MnO2 could be applied as a cost-effective adsorbent for the adsorptive removal of Pb(II) from wastewater.
| C0 (mg L−1) | Flow rate (mL h−1) | Thomas model | Yoon–Nelson model | ||||
|---|---|---|---|---|---|---|---|
| kT (L mg−1 h−1) | Qm (mg g−1) | R2 | kYN (min−1) | τ | R2 | ||
| 20.0 | 15.0 | 4.26 × 10−5 | 6.27 × 105 | 0.82 | 8.52 × 10−4 | 7.32 × 103 | 0.82 |
The suppressed adsorption of Pb(II) on δ-MnO2 observed at low pH implied that acidic treatment was a feasible approach to regenerating the Pb(II)-loaded adsorbent. The mixed regenerant of 0.1 mol L−1 HNO3 and 5 wt% wt Ca(NO3)2 was used for the exhausted δ-MnO2 column regeneration at room temperature, and the results are showed in Fig. 12b. The cumulative desorption efficiency was around 20%, and about 80% of Pb(II) preloaded by δ-MnO2 could not be effectively desorbed by the regeneration solution. Such low desorption ratio suggested that the adsorption sites of δ-MnO2 were irreversible and could not be reused. Li et al.35 and Pan et al.52 investigated the adsorption sites of δ-MnO2 by EXAFS and found two distinct sites of δ-MnO2 for heavy metal ions adsorption. They concluded that the edge-linkage inner-sphere complexation were irreversible, while the corner-linkage mode was reversible. Additionally, the ionic strengths effects proved surface complexes were formed by Pb(II) and surface adsorption sites. Thus, we suggested that the edge-linkage inner-sphere complexes were responsible for the irreversible Pb(II) adsorption by δ-MnO2. Moreover, the ability of δ-MnO2 fixed-bed column to efficiently remove Pb(II) from synthetic wastewaters makes it a good system for large-scale application.
4. Conclusions
In this work, we investigated the adsorption behavior of Pb(II) on five manganese oxides with different crystallographic phases. δ-MnO2 showed the highest adsorption capacity due to its high BET surface area and layered structure which was fully accessible for Pb(II). Additionally, the large interlayer spacing and high amount of surface chemisorbed oxygen enhanced the Pb(II) adsorption on δ-MnO2. On the contrary, adsorption capacities of porous α-, β-, γ- and λ-MnO2 were constrained by the low efficiency of pores and Pb(II) was mainly adsorbed on the external surfaces. The adsorption kinetics of Pb(II) on MnO2 adsorbents followed the pseudo-second-order model, and the adsorption of δ-MnO2 was no affected by coexisting cations in water. The hydroxyl groups on the MnO2 surface undergo pH dependent inner-sphere surface complexation reactions. The predominant species on α-, β-, γ- and λ-MnO2 surfaces was![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) XOPbOH, while the
XOPbOH, while the ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) YOPb+ species was the predominant species on δ-MnO2 surface over the pH range of 2.5–5.8. Column test verified the high working adsorption capacity and durability of δ-MnO2 and therefore highlighted its promising potential as an effective adsorbent for the removal of heavy metal ions in water.
YOPb+ species was the predominant species on δ-MnO2 surface over the pH range of 2.5–5.8. Column test verified the high working adsorption capacity and durability of δ-MnO2 and therefore highlighted its promising potential as an effective adsorbent for the removal of heavy metal ions in water.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support from the Special S&T Project on Treatment and Control of Water Pollution of China (No. 2017ZX07201005) is gratefully acknowledged.References
- M. Liu, Y. Wang, L. Chen, Y. Zhang and Z. Lin, ACS Appl. Mater. Interfaces, 2015, 7, 7961–7969 CAS.
- C. H. Yan, J. Xu and X. M. Shen, Environ. Health Perspect., 2013, 121, A294–A295 CrossRef PubMed.
- S. Hou, L. Yuan, P. Jin, B. Ding, N. Qin, L. Li, X. Liu, Z. Wu, G. Zhao and Y. Deng, Theor. Biol. Med. Modell., 2013, 10, 13 CrossRef CAS PubMed.
- World Health Organization, Guidelines for Drinking-water Quality, Incorporating The First and Second Addenda, 3rd edn, 2008, vol. 1, http://www.who.int/water_sanitation_health/dwq/fulltext.pdf Search PubMed.
- Z. X. Wu and D. Y. Zhao, Chem. Commun., 2011, 47, 3332–3338 RSC.
- X. Gu, L. J. Evans and S. J. Barabash, Geochim. Cosmochim. Acta, 2010, 74, 5718–5728 CrossRef CAS.
- C. C. Wang, L. C. Juang, C. K. Lee, T. C. Hsu, J. F. Lee and H. P. Chao, J. Colloid Interface Sci., 2004, 280, 27–35 CrossRef CAS PubMed.
- D. Dong, Y. M. Nelson, L. W. Lion, M. L. Shuler and W. C. Ghiorse, Water Res., 2000, 34, 427–436 CrossRef CAS.
- L. D. Puppa, M. Komárek, F. Bordas, J. C. Bollinger and E. Joussein, J. Colloid Interface Sci., 2013, 399, 99–106 CrossRef PubMed.
- Y. Wang, X. Feng, M. Villalobos, W. Tan and F. Liu, Chem. Geol., 2012, 292–293, 25–34 CrossRef CAS.
- S. M. Maliyekkal, K. P. Lisha and T. Pradeep, J. Hazard. Mater., 2010, 181, 986–995 CrossRef CAS PubMed.
- R. M. McKenzie, Soil Res., 1981, 19, 41–50 CrossRef CAS.
- J. W. Tonkin, L. S. Balistrieri and J. W. Murray, Appl. Geochem., 2004, 19, 29–53 CrossRef CAS.
- Y. C. Son, V. D. Makwana, A. R. Howell and S. L. Suib, Angew. Chem., Int. Ed., 2001, 40, 4280–4283 CrossRef CAS.
- M. Yano, S. Suzuki, M. Miyayama and M. Ohgaki, Solid State Ionics, 2013, 233, 32–37 CrossRef CAS.
- X. B. Luo, K. Zhang, J. M. Luo, S. L. Luo and J. Crittenden, Environ. Sci. Technol., 2016, 50, 13002–13012 CrossRef CAS PubMed.
- M. G. Kozlova, S. V. Balakhonov, E. A. Goodilin, B. R. Churaulov, A. G. Veresov and Y. D. Tret'yakov, Russ. Chem. Bull., 2008, 57, 1151–1156 CrossRef CAS.
- G. V. Korshin, H. S. Chang, A. I. Frenkel and J. F. Ferguson, Environ. Sci. Technol., 2007, 41, 2560–2565 CrossRef CAS PubMed.
- J. Al Abdullah, A. G. Al Lafi, W. Al Masri, Y. Amin and T. Alnama, Water, Air, Soil Pollut., 2016, 227, 1–14 CrossRef CAS.
- X. Wang and Y. D. Li, Chemistry, 2003, 9, 300–306 CrossRef CAS PubMed.
- H. P. Zhang, L. Q. Gu, L. Zhang, S. R. Zheng, H. Q. Wan, J. Y. Sun, D. Q. Zhu and Z. Y. Xu, Appl. Surf. Sci., 2017, 406, 330–338 CrossRef CAS.
- H. Chen, Y. Wang and Y. K. Lv, RSC Adv., 2016, 6, 54032 RSC.
- H. M. Xu, Z. Qu, S. J. Zhao, J. Mei, F. Q. Quan and N. Q. Yan, J. Hazard. Mater., 2015, 299, 86–93 CrossRef CAS PubMed.
- Q. H. Zhang, S. Sun, S. Li, H. Jiang and J. G. Yu, Chem. Eng. Sci., 2007, 62, 4869–4874 CrossRef CAS.
- S. B. Kanungo and K. M. Parida, J. Colloid Interface Sci., 1984, 98, 245–251 CrossRef CAS.
- D. M. Robinson, Y. B. Go, M. Greenblatt and G. C. Dismukes, J. Am. Chem. Soc., 2010, 132, 11467–11469 CrossRef CAS PubMed.
- L. P. Kang, M. M. Zhang, Z. H. Liu and K. Ooi, Spectrochim. Acta, Part A, 2007, 67, 864–869 CrossRef PubMed.
- W. A. Jefferson, C. Hu, H. Liu and J. Qu, Chemosphere, 2015, 119, 1–7 CrossRef CAS PubMed.
- H. W. Nesbitt, G. W. Canning and G. M. Bancroft, Geochim. Cosmochim. Acta, 1998, 62, 2097–2110 CrossRef CAS.
- S. M. Ponder, J. C. Darab and T. E. Mallouk, Environ. Sci. Technol., 2000, 34, 2564–2569 CrossRef CAS.
- Z. Rao, K. Feng, B. Tang and P. Wu, ACS Appl. Mater. Interfaces, 2017, 9, 2594–2605 CAS.
- D. C. Golden, C. C. Chen and J. B. Dixon, Clays Clay Miner., 1987, 35, 271–278 CAS.
- H. S. Kim and P. C. Stair, J. Phys. Chem. B, 2004, 108, 17019–17026 CrossRef CAS.
- K. D. Kwon, K. Refson and G. Sposito, Geochim. Cosmochim. Acta, 2010, 74, 6731–6740 CrossRef CAS.
- X. Li, G. Pan, Y. Qin, T. Hu, Z. Wu and Y. Xie, J. Colloid Interface Sci., 2004, 271, 35–40 CrossRef CAS PubMed.
- A. Perner, K. Holl, D. Ilic and M. Wohlfahrt-Mechrens, Eur. J. Inorg. Chem., 2002, 5, 1108–1114 CrossRef.
- M. Sekar, V. Sakthi and S. Rengaraj, J. Colloid Interface Sci., 2004, 279, 307–313 CrossRef CAS PubMed.
- J. Wang, S. Zheng, Y. Shao, J. Liu, Z. Xu and D. Zhu, J. Colloid Interface Sci., 2010, 349, 293–299 CrossRef CAS PubMed.
- M. B. Jazi, M. Arshadi, M. J. Amiri and A. Gil, J. Colloid Interface Sci., 2014, 422, 16–24 CrossRef PubMed.
- T. Usiyama and K. Fukushi, Geochim. Cosmochim. Acta, 2016, 190, 134–155 CrossRef CAS.
- A. M. Puziy, O. I. Poddubnaya, V. N. Zaitsev and O. P. Konoplitska, Appl. Surf. Sci., 2004, 221, 421–429 CrossRef CAS.
- Y. Al Degs, M. A. M. Khraisheh and M. F. Tutunji, Water Res., 2001, 35, 3724–3728 CrossRef CAS PubMed.
- R. Han, W. Zou, Z. Zhang, J. Shi and J. Yang, J. Hazard. Mater., 2006, 137, 384–395 CrossRef CAS PubMed.
- P. J. Pretorius and P. W. Linder, Appl. Geochem., 2001, 16, 1067–1082 CrossRef CAS.
- J. W. Tonkin, L. S. Balistrieri and J. W. Murray, Appl. Geochem., 2004, 19, 29–53 CrossRef CAS.
- Integrated Water Discharge Standard, Ministry of the People's Republic of China, Beijing, 1996 Search PubMed.
- H. C. Thomas, J. Am. Chem. Soc., 1944, 66, 1664–1666 CrossRef CAS.
- J. F. Costa, V. J. Vilar, C. M. Botelho, E. A. Da Silva and R. A. Boaventura, Water Res., 2010, 44, 3946–3958 CrossRef CAS PubMed.
- M. Hua, Y. N. Jiang, B. Wu, B. C. Pan, X. Zhao and Q. X. Zhang, ACS Appl. Mater. Interfaces, 2013, 5, 12135–12142 CAS.
- F. Fu and Q. Wang, J. Environ. Manage., 2011, 92, 407–418 CrossRef CAS PubMed.
- H. L. Lu, W. H. Zhang, Y. X. Yang, X. F. Huang, S. Z. Wang and R. L. Qiu, Water Res., 2012, 46, 854–862 CrossRef CAS PubMed.
- G. Pan, Y. Qin, X. Li, T. Hu, Z. Wu and Y. Xie, J. Colloid Interface Sci., 2004, 271, 28–34 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |