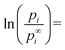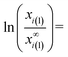Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new paradigm on the chemical potentials of components in multi-component nano-phases within multi-phase systems†
George Kaptay *abc
*abc
aUniversity of Miskolc, Department of Nanotechnology, Miskolc, 3525 Hungary. E-mail: kaptay@hotmail.com; Tel: +36 304150002
bMTA-ME Materials Science Research Group, Miskolc, 3525 Hungary
cBay Zoltan Nonprofit Ltd for Applied Research, BAY-ENG, Miskolc, 3519 Hungary
First published on 24th August 2017
Abstract
The chemical potentials of components in nano-phases determine the equilibrium of nano-materials. In this paper the difference between the equilibrium of a nano-phase and the equilibrium of an analogous macro-phase under the same constraints is called a “nano-effect”. Historically the first paper to describe the nano-effect was published by Kelvin (1871), claiming that it is due to the increased curvature of the nano-phase. This approach forms the basis of the Kelvin paradigm, still widely used in chemistry, biology and materials science (but not in physics). The Kelvin paradigm is the basis of the Kelvin equation, the Gibbs–Thomson equation and the Ostwald–Freundlich equation for the vapor pressure, melting point and solubility of nano-phases, respectively. The Kelvin paradigm is also successful in the interpretation of more complex phenomena, such as capillary condensation. However, the Kelvin paradigm predicts no nano-effect for not curved nano-phases, such as crystals and thin films, contradicting experimental facts. Moreover, it wrongly predicts that a cubic (or any other crystal-shaped) nano-droplet is more stable than a spherical nano-droplet of the same volume (this contradiction is shown here for the first time). In addition to its positive features, these and other shortcomings of the Kelvin paradigm call for a paradigm shift. A new paradigm is presented in this paper, claiming that the nano-effect is due to the increased specific surface area of the nano-phase. Chemical potentials of components in multi-component phases are derived in this paper within this new paradigm. These equations are extended for nano-phases in multi-phase situations, such as liquids confined within nano-capillaries, or nano-sized sessile drops attached to flat solid substrates. The new paradigm leads to similar results compared to the Kelvin paradigm for the case of capillary condensation into capillaries (this is because the specific surface area of a cylindrical wall is the same as the curvature of the spherical phase: 2/r). However, the new paradigm is able to provide meaningful solutions also for problems, not tractable by the Kelvin equation, such as the case of crystals and thin films having no curvature.
1. Introduction
The steady development of nano-technologies1–17 requires a solid theoretical basis and clear techniques to calculate the equilibrium of nano-systems. Nano-systems contain at least one phase with at least one of its dimensions below 100 nm. Phase equilibria, and thus all properties of such systems are functions of the nano-dimensions. Similarly to macro-systems, the equilibrium in nano-systems is also calculable through the chemical potentials of the components.18–32 Therefore, the knowledge of accurate equations describing the chemical potential of components in nano-phases is of primary importance. Unfortunately, this subject is far from being clear today, despite its 146 years history. The goal of this paper is to review the subject and to offer a new solution to this old problem.For brevity, the expression “nano-effect” will be used in this paper, meaning the difference between the equilibrium of a nano-phase and the equilibrium of an analogous macro-phase under the same constraints. Examples of nano-effect include the increased vapor pressure around a liquid nano-droplet, a solid nano-crystal or a solid thin film, an increased solubility of a nano-crystal, a nano-droplet or a thin film in a solution, a decreased (or sometimes increased) melting point of a nano-crystal and a thin solid film inside or outside capillaries, a decreased vapor pressure above the liquid confined in well wetted capillaries and in nano-bubbles, etc. A successful paradigm should be able to explain all these phenomena not only in qualitative, but also in a quantitative way.
Historically the first equation on nano-equilibria was due to Kelvin (W. Thomson, 1871), who claimed that the increased vapor pressure around a liquid nano-droplet is due to its increased curvature.33 This very first attempt to describe equilibrium in nano-systems is still in use today. Adamson34 even calls the Kelvin equation one of the three fundamental equations of surface science (the other two being the Laplace equation35 and the Gibbs adsorption equation36). The Kelvin equation is a basis to form a current paradigm (called here the “Kelvin paradigm”) for equilibrium of nano-materials. This paradigm is followed in chemistry,34,37–45 biology,46–49 materials science50–67 and even in microelectronics.68 The Kelvin equation was extended later to describe the size dependence of the melting point and the solubility of the nano-particles. The size dependence of the melting point is described by the so-called Gibbs–Thomson equation, derived not by Gibbs, rather by J. J. Thomson,69 while the size dependence of solubility was described by the so-called Freundlich–Ostwald equation, originally derived by Ostwald70 and corrected later by Freundlich71 to bring it to agreement with the Kelvin paradigm. The success of the Kelvin paradigm is due to the fact that it describes well the equilibrium of curved fluid nano-systems, including nano-droplets and liquids confined in nano-capillaries.34,72–76
Although the Kelvin equation does not predict any nano-effect for not curved phases such as crystals and thin films, this situation was partly “resolved” by treating crystals as spheres of inscribed radius within cubes.34 The limit of such a “flexible” interpretation of a curvature was reached when the behavior of thin films was studied, as it is really hard to inscribe a sphere within a thin film. This is the main reason why the Kelvin paradigm and its analogues are not used in physics (another reason is that physics developed independently of chemistry).
In addition to the problem describing equilibrium of non-curved nano-phases, the Kelvin paradigm has further hidden flaws, discussed in the present paper. All this is an indication that the general validity of the Kelvin paradigm can be questioned. This is not surprising, as the science on equilibrium of nano-materials should have been created as an extension of the science on equilibrium of macro-materials. However, the Kelvin equation was published in 1871,33 before Gibbs published in 1875–1878 his monumental work on the equilibrium of heterogeneous (macroscopic) substances.36 In his work, Gibbs added a surface term to his bulk Gibbs energy term, as we call it today. Later in this paper it will be shown that the new paradigm is based on this part of Gibbs' work. Looking at the publication dates above, one can ask why Gibbs did not correct the Kelvin equation similarly as it is offered here? At this point let us mention that Gibbs actually referred to the Kelvin equation in his work, but did not comment on it. One possible explanation is that Gibbs did not want to enter into an open conflict with an elder and well (much better than himself at the time) established fellow-scientist. A second explanation is that Gibbs might have supposed that what is written by him is obvious, anyway. If any, it was Gibbs' most important mistake: supposing that whatever was written by him was so obvious to all of his readers.
Recently an alternative approach was partly developed on the equilibrium of nano-systems. This new paradigm claims that the nano-effect is due to the increased specific surface area of a nano-phase.77–79 This new approach treats successfully the problems of one-component not curved nano-phases, such as nano-crystals and thin films, without any need to draw artificial inscribed spheres into them. It should be mentioned that the same approach was first used by Ostwald70 (who not only translated Gibbs into the German language, but also “interpreted” his writings and got a Nobel prize in chemistry in 1909). Unfortunately, the Ostwald equation was soon “corrected” by Freundlich71 from the Gibbs-type equation to the Kelvin-type equation, and thus the original Ostwald approach is lost/forgotten. Now it is time to correct it back.
It is also important to realize that the new paradigm has been developed only partly; today it can tackle only the simplest one-component and two-phase problems. The goal of this paper is to fill this knowledge gap and to extend the ability of the new paradigm to describe the equilibrium of nano-materials in multi-component and multi-phase nano-systems. The subject will be put into a wider historical perspective in this paper: the general framework of equilibrium of nano-materials and the Kelvin paradigm will be also discussed in details.
2. The general framework for the equilibrium of nano-systems
Before we start let us state that the surface term to the chemical potential will have a significant effect only if at least one of the sizes of the phase is below 100 nm. On the other hand, if the size of the phase is below 1 nm or so, the meaning of the phase becomes questionable. Therefore, all the equations which follow will be valid only for those phases, which have at least one of their dimensions below 100 nm, but have all of their dimensions above 1 nm.2.1. The chemical potential
The condition of equilibrium of heterogeneous substances including nano-phases is formally the same as given by Gibbs for macro-phases:36| μi(α) = μi(β) | (1) |
| μi(α) = μbi(α) + z·Vm,i(α)·σα/β | (2) |
As follows from the unit of parameter z, it is inversely proportional to the characteristic size of the phase (radius for a sphere or a cylinder, side length of a cube, thickness of a thin film, etc.). For free standing phases (such as a spherical liquid droplet levitating in a vapor phase) parameter z is only size- and shape-dependent. However, for more difficult situations, such as a nano-sized liquid sessile droplet attached to a solid slab, parameter z will also depend on the contact angle of the liquid on the solid slab. Different approaches existing in the literature differ in how this parameter z is interpreted, defined and calculated. The goal of this paper is to derive proper expressions for parameter z for free standing nano-phases and also for nano-phases attached to other phases.
2.2. The integral molar Gibbs energy of a nano-phase
Now, let us derive the integral molar Gibbs energy of a nano-phase α using the following generally valid equation:
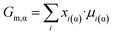 | (3a) |
| Gm,α = Gbm,α + z·Vm,α·σα/β | (3b) |
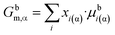 | (3c) |
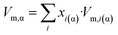 | (3d) |
The integral molar Gibbs energy of phase α written by (eqn (3b)) takes into account the surface effect, similarly to the original equation of Gibbs, written for the absolute Gibbs energy of phase α as:36
| Gα = Gbα + Aα·σα/β | (4) |
2.3. The chemical potential of a one-component nano-phase
As a first simplest approach let us apply eqn (4) of Gibbs for a one-component phase:| Goi(α) = Go,bi(α) + Aα·σoi(α)/β | (4a) |
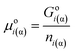 | (4b) |
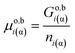 | (4c) |
Thus, dividing eqn (4a) by the amount of matter within this phase, the following is obtained:
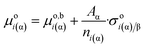 | (4d) |
The amount of matter can be written as the ratio of the volume (Vα, m3) and the molar volume (Vom,i(α), m3 mol−1) of the phase:
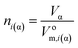 | (4e) |
Now, let us define the specific surface area of the phase (Asp,α, m−1) as the ratio of its surface area to its volume:
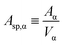 | (4f) |
Substituting eqn (4e) into eqn (4d) and taking into account eqn (4f), the following final equation is obtained for the standard chemical potential of a one-component nano-phase:
| μoi(α) = μo,bi(α) + Asp,α·Vom,i(α)·σoi(α)/β | (4g) |
According to eqn (4g), the standard chemical potential of a one-component nano-phase is proportional to the specific surface area of the phase. Comparing eqn (2) and (4g), parameter z for the free standing one-component nano-phase is identical to the specific surface area of the phase:
| z = Asp,α | (4h) |
The same result of eqn (4g) was achieved by the author before77–79 for 1-component and 2-phase situations. This paper is devoted to the extension of eqn (4h) to multi-component and multi-phase situations.
2.4. A validity test for models on equilibrium of nano-materials
The molar Gibbs energy of the system, containing a nano-phase is generally written as:
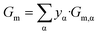 | (5) |
3. The approach based on the curvature of the nano-phase (the Kelvin paradigm)
3.1. The derivation of the key equations for the Kelvin paradigm
The chemical potential is usually written using the following three terms:| μi(α) = Ubi(α) + p·Vm,i(α) − T·Sbi(α) | (6a) |
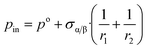 | (6b) |
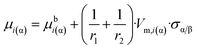 | (6c) |
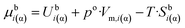 | (6d) |
Comparing eqn (2) and (6c) the requested equation for parameter z:
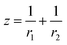 | (6e) |
Eqn (2) and (6e) form the basis of the Kelvin paradigm. Using these equations, the classical Kelvin, Ostwald–Freundlich and Gibbs–Thomson equations are derived for spherical nano-phases (see ESI A†). When phase α is a sphere of radius r, then r1 = r2 = r and thus parameter z of the general eqn (2) equals: z = 2/r. When phase α is a cylinder of radius r then r1 = r, r2 = ∞ and thus parameter z of the general eqn (2) equals: z = 1/r. The curvature can also have a negative sign, for example for a liquid meniscus within a well wetted solid capillary, or within a bubble. The curvature of the spherical cap at the end of the liquid cylinder within a cylindrical solid capillary is written as:
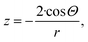 | (6f) |
Whichever is the right numerical coefficient in eqn (6f), it indeed provides a negative curvature for well wetting liquids (Θ < 90°). This makes the Kelvin paradigm very versatile as it can predict accurately both the increase and the decrease of the chemical potential within curved nano-phases. Eqn (6f) is also the basis to interpret capillary condensation.
3.2. The list of reasons why the Kelvin paradigm is not acceptable
Although the derivation of eqn (6e) is perfect mathematically, this equation and the following Kelvin paradigm are connected with the following contradictions:i. Eqn (6e) was derived by substituting the inner pressure to replace the state parameter (=the outside pressure), which is theoretically incorrect,
ii. when eqn (6e) is derived, it is done from the understanding that the inner pressure within the nano-phase is higher than the outer pressure around this phase, and so it seems to lead to higher activity (escaping tendency, after Lewis) of the components of this nano-phase. However, this increased activity is compensated by the same Laplace pressure by which it was created, as the vector of the Laplace pressure points perpendicular to the curved surface from outside towards inside of the nano-phase (this is how the inner phase of higher pressure is in mechanical equilibrium with an outer phase of lower pressure). Thus, the extra activity inside the nano-phase is also compensated by the Laplace pressure, thus it has no influence outside the nano-phase, i.e. it cannot lead to increased vapor pressure, or to increased solubility in any outer phase.
iii. Eqn (6e) predicts that any nano-phase surrounded by flat (not curved) planes (such as crystals, or thin films) has no nano-effect; however, this prediction contradicts the experimental observations. Particularly, it follows that for a nano-phase of given volume, a cube (or any other not curved phase such as a thin film) has a lower integral Gibbs energy compared to a sphere, so a liquid droplet would prefer a crystal shape, such as a cube or thin film: this is certainly non-sense and contradicts experimental observations. This contradiction proves further that eqn (6e) is wrong. At this point let me mention that one can consider the atoms/molecules along the edges or the corners of the cube to provide the missing curvature for the cube. However, it is not the curvature of the cubic phase, it is rather the curvature of the atoms/molecules. Furthermore, if the curvature of the atoms/molecules is taken into account to calculate the nano-effect, then this effect would be size-independent, as small and large cubes have equally small atoms/molecules. This conclusion on the size-independent nano-effect also contradicts experimental facts.
iv. The curvature effect is actually used in another aspect of chemical thermodynamics: already Gibbs,36 and later Tolman80 showed that the surface tension of small curved phases is curvature dependent. Using the same effect twice is not reasonable.
v. The curvature induced interfacial (Laplace) pressure can be derived from the interfacial term of the Gibbs energy,81,82 so it is not reasonable to substitute this effect back into the same Gibbs energy (chemical potential) again, while forgetting at the same time about the surface term of the Gibbs energy (see eqn (4)), as was done when eqn (6e) was derived,
vi. the equilibrium size of the nano-particle as follows from eqn (6e) for a spherical nano-nucleus coincides with the critical size of the nucleus; however, the later corresponds to the maximum of the Gibbs energy and not to its minimum (as we expect for an equilibrium size). Thus, eqn (6e) contradicts the nucleation theory of Gibbs (for details see ref. 79).
vii. Eqn (6e) is principally different from eqn (4h) obtained for a one-component case. This principal difference between a one-component and multi-component phases shows that something must be wrong. As nothing is wrong (to our opinion) with eqn (4h) then (6e) must be wrong.
Based on the above seven reasons, the validity of the Kelvin paradigm is under question. Thus, it is subject to the paradigm shift, supposing that a new and better paradigm is developed.
4. A possible approach, based on the definition of the chemical potential
The chemical potential of component i in a macroscopic phase α is defined as:36
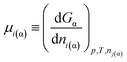 | (7a) |
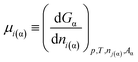 | (7b) |
If eqn (4) is substituted into eqn (7b), the following equation is obtained:
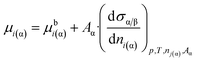 | (7c) |
From comparison of eqn (2) and (7c) one can obtain the expression for parameter z:
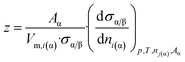 | (7d) |
Let us note that ni(α) = nα·xi(α) (where xi(α) is the mole fraction of component i in phase α) and so: dni(α) = nα·dxi(α). Also remember that (see eqn (4e)): nα = Vα/Vm,α. Substituting these equations into eqn (7d) and taking into account eqn (4f), the following equation is found:
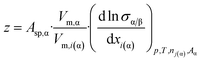 | (7e) |
As follows from eqn (7e), parameter z is proportional to the specific surface area of the phase, which is in agreement with eqn (4h), obtained above for one-component phases. The value of Vm,α/Vm,i(α) of eqn (7e) is around unity. However, different components of the solution can have different values and even different signs of (d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σα/β/dxi(α))p,T,nj(α),Aα of eqn (7e) leading to different signs of parameter z. On the other hand, parameter z is expected to have only positive values. The possible negative value of parameter z proves that eqn (7b) is not a proper basis to derive the chemical potential for nano-phases and so this approach is not considered here further.
σα/β/dxi(α))p,T,nj(α),Aα of eqn (7e) leading to different signs of parameter z. On the other hand, parameter z is expected to have only positive values. The possible negative value of parameter z proves that eqn (7b) is not a proper basis to derive the chemical potential for nano-phases and so this approach is not considered here further.
5. The approach based on the specific surface area of nano-phases (the new paradigm)
5.1. Derivation of the key equation for the new paradigm
Let us re-write the classical eqn (4) of Gibbs for a multi-component nano-phase in a somewhat different form:
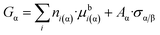 | (8a) |
Now, let us express Aα from eqn (4f) and let us substitute this equation into eqn (8a):
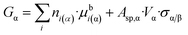 | (8b) |
The absolute volume of the nano-phase can be written as:
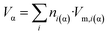 | (8c) |
Now, let us substitute eqn (8c) into eqn (8b) and note that the number of moles is a common multiplicator of both terms in the right hand side:
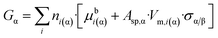 | (8d) |
On the other hand, the following equation is also valid, by definition:36
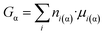 | (8e) |
Comparing eqn (8d) and (e), the following equation is obtained for the chemical potential of component i in a free standing nano-phase α:
| μi(α) = μbi(α) + Asp,α·Vm,i(α)·σα/β | (8f) |
From the comparison of eqn (2) and (8f), the final equation is obtained for parameter z for free standing nano-phases:
| z = Asp,α | (8g) |
One can see that eqn (4h) and (8g) are identical, so our result for parameter z is identical for one-component and multi-component phases. Thus, although eqn (8f) is obtained using an independent derivation, it is a natural and logical extension of eqn (4g) from a one-component system to multi-component systems. In other words, eqn (4g) is a boundary case of a more general eqn (8f). Eqn (8f) is practically more useful compared to the equations of the Kelvin paradigm, because it provides some nano-effect not only for nano-phases surrounded by curved surfaces, but also for nano-phases surrounded by flat (not curved) surfaces, such as crystals and thin films. This approach is also free from the failure of the Kelvin approach, as it predicts that liquid droplets will gain spherical shapes (and not cubic shapes, as predicted by the Kelvin approach – see above). This is because a sphere provides a minimum specific surface area among all 3-dimensional bodies of the same volume (see also Table 1).
| Description of the nano-phase α | Number of sides | Asp,α | Asp,α/Asp,sphere |
|---|---|---|---|
| a When the end walls of the cylinder are neglected, a cylinder seems to provide smaller specific surface area compared to the sphere of the same volume, but for a 3-dimensional cylinder (with its end walls) this is never the case. | |||
| Sphere of radius r | ∞ | 3/r | 1.000 |
| Tetrahedron of side length a | 4 | 14.70/a | 1.490 |
| Cube of side length a | 6 | 6/a | 1.241 |
| Octahedron of side length a | 8 | 7.348/a | 1.183 |
| Dodecahedron of side length a | 12 | 2.694/a | 1.098 |
| Icosahedron of side length a | 20 | 3.970/a | 1.065 |
| Nano-sheet of thickness t | 2 | 2/t | Undefined (≫1) |
| A long wire/cylinder with radius rcap | 1 | 2/rcap | Undefineda |
| A long nano-tube with inner and outer radii ri and ro | 2 | 2/ri + 2/ro | Undefined (≫1) |
Eqn (8f) is also in agreement with a wide-spread interpretation of why nano-phases have size-dependent properties: it is because the ratio of their surface atoms/molecules among all atoms/molecules within the nano-phase is significant and varies with the size of the nano-phase. As this surface ratio of atoms/molecules is proportional to the specific surface area of the phase (see ESI B† and eqn (9)), it is reasonable that the surface term of the chemical potential is also proportional to the same physical quantity.
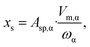 | (9) |
5.2. Application of the new paradigm to free standing nano-phases
For free standing nano-phases eqn (8f) can be coupled with the equations of ESI A† to obtain expressions for phase equilibria.In Table 1, equations for the specific surface areas of different simple shapes of free standing nano-phases are summarized (“free standing” means here that a given phase is fully surrounded only by one macroscopic phase, usually a vapor phase, or a macroscopic liquid or solid phase). In the last column of Table 1 the ratio of the specific surface area of the given phase to that of a sphere of the same volume is shown. As follows from this comparison, the specific surface area of all polyhedra are larger than that of a sphere, but these values gradually approach the specific surface area of a sphere of the same volume as the number of sides of the polyhedron increases. This is because a sphere can be considered as a polyhedron with infinite number of sides.
In Table 2 equations for vapor pressure, solubility and melting point of different free standing nano-phases are collected. For this purpose, equations of Table 1 are substituted into eqn (8g), and the result is substituted into eqn (A1b), (A2c), (A3c) of ESI A.† These equations are similar (although not identical) to the equations of the Kelvin paradigm for the curved phases. These equations are also similar (although not identical) to the equations of the Kelvin paradigm, if the crystals are replaced by inscribed spheres. The equations provided in Table 2 for thin solid films are missing from the subjects covered by the Kelvin paradigm due to the difficulty to replace a thin solid film by an inscribed sphere.
| Shape of the phasea | Tm,i − T∞m,i= | ||
|---|---|---|---|
| a The sphere is characterized by its radius r, the thin film by its thickness t, the long cylinder by its radius rcap, the long tube with its inner and outer radii ri and ro, other bodies by their side lengths a.b For simplicity the same phase is supposed on both sides of the nano-sheet and inside/outside of the nano-tube. | |||
| Sphere | 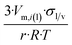 |
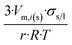 |
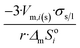 |
| Tetrahedron | 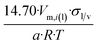 |
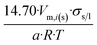 |
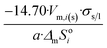 |
| Cube | 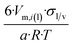 |
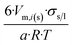 |
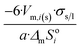 |
| Octahedron | 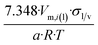 |
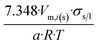 |
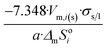 |
| Dodecahedron | 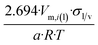 |
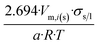 |
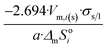 |
| Icosahedron | 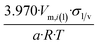 |
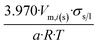 |
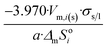 |
| Nano-sheetb | 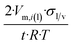 |
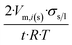 |
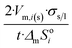 |
| Long wire/cylinder | 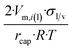 |
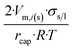 |
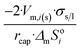 |
| Long nano-tubeb | 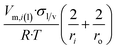 |
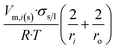 |
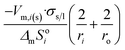 |
It should be noted that in a given nano-system usually a large amount of similar, but not identical nano-phases are present. This dispersity of nano-phases can be handled, if the minimum, average and maximum sizes of the nano-phase are known and correspondingly the maximum, average and minimum chemical potentials are calculated through their specific surface areas. This feature will definitely lead to uncertainty in nano-thermodynamics, but this uncertainty is an inherent property of the nano-system and is not a consequence of the present model.
5.3. Extension of the new paradigm to multi-phase situations
So far, the new paradigm was worked out only for free standing nano-phases, i.e. for 2-phase systems. However, the Kelvin paradigm is also able to explain more complex phenomena, such as capillary condensation, involving more than two phases. Herewith the new paradigm is extended to treat these more complex problems.To calculate phase equilibria for nano-phases attached to other phases, eqn (8f) should be modified. For this purpose, a third term should be added to eqn (8f) as:
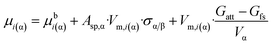 | (10) |
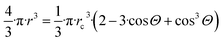 | (11a) |
The total interfacial energy (Gfs, J) of the system containing a free standing spherical nano-droplet and a free standing solid slab is written as:
| Gfs = 4·π·r2·σlv + Aosv·σsv | (11b) |
| Gatt = Alv·σlv + (Aosv − Asl)·σsv + Asl·σsl | (11c) |
Alv = 2·rc2·π·(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ) Θ)
| (11d) |
Asl = rc2·π·(1 − cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ) Θ)
| (11e) |
Now, let us express rc from eqn (11a), substitute this expression into eqn (11d) and (e), and substitute the resulting expressions together with eqn (11c) into eqn (10), taking into account the left-hand side of eqn (11a) for Vα and also the Young equation (σlv·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = σsv − σsl). The final equation for the chemical potential of a component within a sessile nano-drop follows as:
Θ = σsv − σsl). The final equation for the chemical potential of a component within a sessile nano-drop follows as:
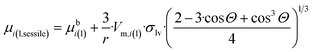 | (11f) |
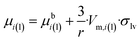 | (11g) |
Comparing eqn (11f) and (g) one can see that the expression of the chemical potential within a sessile drop is very similar to that within a free standing droplet, the only difference being the correcting parenthesis at the end of eqn (11f). Naturally, eqn (11f) simplifies back to eqn (11g) at Θ = 180°, which is a reasonable boundary condition for eqn (11f). Another boundary condition of eqn (11f) is that at Θ = 0° the expression in parenthesis of eqn (11f) becomes nil, and so the chemical potential of components in a perfectly wetting nano-droplet becomes identical to the bulk chemical potential of the same component (μi(l,sessile) = μbi(l)). It means that the solid slab perfectly wetted by the nano-droplet perfectly stabilizes the nano-droplet (as much as if it was a macro-phase).
Comparing eqn (2) and (11f), the following expression is obtained for parameter z for the nano-sized sessile droplet:
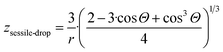 | (11h) |
It is important to underline that even in this complex 3-phase situation the chemical potential is proportional to the specific surface area of the nano-droplet, although corrected by a complex expression containing the contact angle.
Now, let us substitute eqn (11h) into eqn (A1b)† to get the equilibrium vapor pressure of component i above a nano-sized sessile droplet:
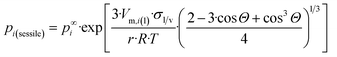 | (11i) |
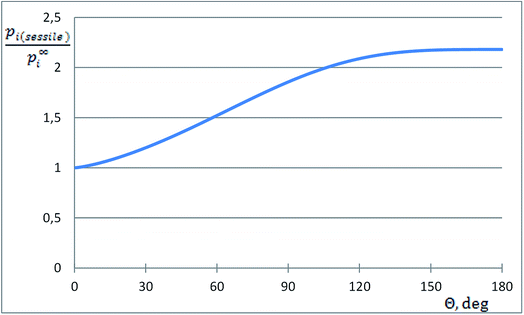
The dimensionless ratio 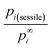 is shown in Fig. 1 as function of the contact angle of the sessile drop on the solid slab. It shows a steady increase of the vapor pressure above a nano-sized sessile droplet with increasing its contact angle, which is a reasonable result. For the sessile drop perfectly wetting the slab: pi(sessile) = p∞i.
is shown in Fig. 1 as function of the contact angle of the sessile drop on the solid slab. It shows a steady increase of the vapor pressure above a nano-sized sessile droplet with increasing its contact angle, which is a reasonable result. For the sessile drop perfectly wetting the slab: pi(sessile) = p∞i.
| A = Asv = Alv = N·2·π·rcap·h | (12a) |
| Vl = Vpore = N·π·rcap2·h | (12b) |
For long cylinders the specific surface area:
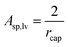 | (12c) |
The total surface Gibbs energy of the free standing liquid nano-cylinders and that of the porous body with the empty nano-cylinders is written as:
| Gfs = A·(σlv + σsv) | (12d) |
The total surface Gibbs energy of the system with the liquid fully filling the nano-capillaries in the porous body is written as:
| Gatt = A·σsl | (12e) |
Let us substitute eqn (12a) into eqn (12d) and (e). Further, let us substitute the resulting equations, together with eqn (12b) and (c) into eqn (10), taking into account the Young equation (σlv·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = σsv − σsl). Finally, the chemical potential of a component in a liquid, confined within long nano-capillaries of radius rcap follows as:
Θ = σsv − σsl). Finally, the chemical potential of a component in a liquid, confined within long nano-capillaries of radius rcap follows as:
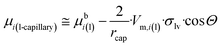 | (12f) |
From the comparison of eqn (2) and (12f) the expression for parameter z is obtained as:
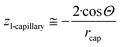 | (12g) |
Let us mention that the expression 2/rcap in eqn (12g) is the specific surface area of the nano-capillary (see eqn (12c)). Thus, even in this complex 3-phase situation the chemical potential is proportional to the specific surface area of the cylindrical capillaries, although corrected by a complex expression containing the contact angle. Let us also mention that eqn (12g) is the same as eqn (6f), which followed from the Kelvin equation. Thus, the Kelvin paradigm and the new paradigm provide identical results for some of the problems. It is good news for a new paradigm, as in this particular case the validity of the Kelvin equation was experimentally validated.72–76 This coincidence is due to the fact that the curvature of the sphere and the specific surface area of the cylindrical wall is described by the same expression 2/r (if r denotes both the radius of the sphere and the radius of the cylinder).
Now, let us substitute eqn (12g) into eqn (A1b)† to get the equilibrium vapor pressure of component i above a liquid, confined within long nano-capillaries:
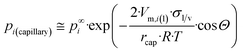 | (12h) |
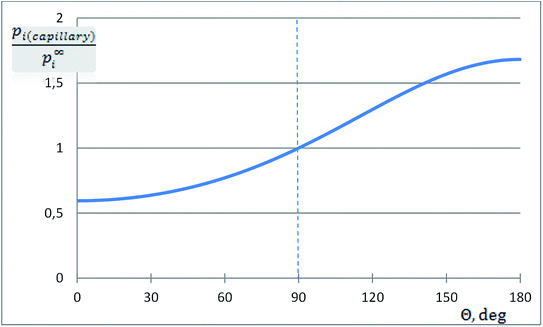
The dimensionless ratio 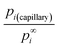 is shown in Fig. 2 as function of the contact angle. It shows the stabilization of the liquid within well wetted capillaries (Θ < 90°) and de-stabilization of the liquid within poorly wetted capillaries (Θ > 90°). The behavior of the liquid within neutrally wetted capillaries (Θ = 90°) is the same as that of the macro-liquid. Fig. 2 is in agreement with the well-known experimental fact that capillary condensation takes place only at Θ < 90°. Eqn (12h) and Fig. 2 are identical to the results obtainable using the Kelvin paradigm, at least, if coefficient 2 of eqn (12h) is not corrected to coefficient 1, as explained in ref. 39 and 43. This coincidence is due again to the fact that the curvature of the sphere and the specific surface area of the cylindrical wall is described by the same expression 2/r (if r denotes both the radius of the sphere and the radius of the cylinder).
is shown in Fig. 2 as function of the contact angle. It shows the stabilization of the liquid within well wetted capillaries (Θ < 90°) and de-stabilization of the liquid within poorly wetted capillaries (Θ > 90°). The behavior of the liquid within neutrally wetted capillaries (Θ = 90°) is the same as that of the macro-liquid. Fig. 2 is in agreement with the well-known experimental fact that capillary condensation takes place only at Θ < 90°. Eqn (12h) and Fig. 2 are identical to the results obtainable using the Kelvin paradigm, at least, if coefficient 2 of eqn (12h) is not corrected to coefficient 1, as explained in ref. 39 and 43. This coincidence is due again to the fact that the curvature of the sphere and the specific surface area of the cylindrical wall is described by the same expression 2/r (if r denotes both the radius of the sphere and the radius of the cylinder).
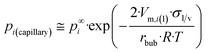 | (13a) |
If eqn (13a) is coupled with eqn (A1b),† parameter z can be obtained for the liquid phase in the vicinity of the nano-bubble as:
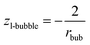 | (13b) |
Although this result is derived from the new paradigm, it is in full agreement with the Kelvin paradigm.34,43 Again, this coincidence is due to the fact that the curvature of the sphere and the specific surface area of the cylindrical wall is described by the same expression 2/r (if r denotes both the radius of the sphere and the radius of the cylinder).
6. Discussion
The most important result of this paper is that the new paradigm (=the nano-effect is due to the increased specific surface area of the nano-phase) is extended to multi-component nano-solutions and also to multi-phase situations including nano-phases. The new paradigm is found applicable and successful in all cases, where the Kelvin paradigm (=the nano-effect is due to the increased curvature of the nano-phase) was applicable and successful. However, the new paradigm is successful also in areas, where the Kelvin paradigm provided a practical failure (or when it was pushed to draw artificial inscribed spheres): this is the equilibrium of nano-crystals and thin films. Moreover, the new paradigm is free of those contradictions (see above), which lead to the criticism of the Kelvin paradigm.Summarizing the above, the present author thinks that the new paradigm is ready to replace the Kelvin paradigm. This paradigm shift, however, will not happen by the publication of this paper. Many further discussions are ahead before the community can accept or reject this new paradigm.86
7. Conclusions
1. The chemical potential of component i in a nano-phase α is generally written as:| μi(α) = μbi(α) + z·Vm,i(α)·σα/β | (2) |
2. The molar Gibbs energy of a nano-phase α is generally written as:
| Gm,α = Gbm,α + z·Vm,α·σα/β | (3b) |
3. Following Kelvin, parameter z of eqn (2) and (3b) is derived as the curvature of the nano-phase, using the Laplace pressure. This result is found wrong for many different reasons (see above). Thus, the Kelvin paradigm should be replaced by a new paradigm.
4. The application of the formal definition of chemical potential under proper constraints does not lead to a meaningful result in this case, as the constancy of the surface area (as a new state parameter for nano-phases) should be guaranteed when the derivative of the Gibbs energy is taken as function of the amount of matter of the component in question.
5. Parameter z of eqn (2) and (3b) is derived here as the specific surface area for free standing one-component and multi-component nano-phases:
| z = Asp,α | (8g) |
6. A general method is developed here to derive equations for parameter z for nano-phases in multi-phase situations. The following expression is obtained for a nano-sized sessile drop, attached to a solid slab with a contact angle of Θ:
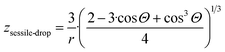 | (11i) |
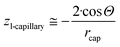 | (12g) |
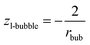 | (13b) |
As a result, the chemical potentials of components will be different within the same nano-phase, if this nano-phase is surrounded by different phases, i.e. if it is involved in different multi-phase situations. This is demonstrated here by the differences in eqn (11i), (12g) and (13b). Eqn (12g) and (13b) are the same in the framework of the Kelvin paradigm and in the framework of this new paradigm. This is because te curvature of a sphere coincides with the specific surface area of a cylinder wall.
7. Summarizing: the new paradigm states that nano-effects are due to the increased specific surface areas of the nano-phases. The new paradigm offers a theoretically coherent method to describe multi-component and multi-phase equilibria of nano-materials in all areas covered and by the Kelvin paradigm and beyond. Thus, the new paradigm is ready to replace the Kelvin paradigm.
8. It should be noted that the present model does not take into account the size-dependence of various physico-chemical properties of nano-phases, such as the size dependence of surface tension, etc. These effects should be added to the major effect connected with specific interfacial area, considered here in details.
Conflicts of interest
The author declares no conflict of interest.Acknowledgements
The author acknowledges the financial support from GINOP-2.3.2-15-2016-00027 and is grateful for Agnes K. Sandor for motivating discussions and for ref. 86.References
- D. S. Lee, S. Park, Y. D. Han, J. E. Lee, H. Y. Jeong, H. C. Yoon, M. Y. Jung, S. O. Kim and S. Y. Choi, Selective protein transport through ultra-thin suspended reduced graphene oxide nanopores, Nanoscale, 2017 10.1039/c7nr01889d.
- E. Varga, P. Pusztai, A. Oszkó, K. Baán, A. Erdőhelyi, Z. Kónya and J. Kiss, Stability and temperature-induced agglomeration of Rh nanoparticles supported by CeO2, Langmuir, 2016, 32, 2761–2770 CrossRef CAS PubMed.
- E. Tombacz, R. Turcu, V. Socoliuc and L. Vekas, Magnetic iron oxide nanoparticles: recent trends in design and synthesis of magnetoresponsive nanosystems, Biochem. Biophys. Res. Commun., 2015, 468, 442–453 CrossRef CAS PubMed.
- E. Alber, N. Cotolan, N. Nagy, G. Safran, G. Szabo, L. M. Muresan and Z. Horvolgyi, Mesoporous silica coatings with improved corrosion protection properties, Microporous Mesoporous Mater., 2015, 206, 102–113 CrossRef.
- Z. Wei, J. H. Yang, J. Zhou, F. Xu, M. Zrinyi, P. H. Dussault, Y. Osada and Y. M. Chen, Self healing gels based on constitutional dynamic chemistry and their potential applications, Chem. Soc. Rev., 2014, 43, 8114–8131 RSC.
- A. Majzik, V. Hornok, N. Varga, R. Tabajdi and I. Dekany, Functionalized gold nanoparticles for 2-napthol binding and their fluorescence properties, Colloids Surf., A, 2015, 481, 244–251 CrossRef CAS.
- G. Levai, M. Godzsák, T. I. Török, J. Hakl, V. Takáts, A. Csik, K. Vad and G. Kaptay, Designing the color of hot-dip galvanized steel sheet through destructive light interference using a Zn-Ti liquid metallic bath, Metall. Mater. Trans. A, 2016, 47, 3580–3596 CrossRef CAS.
- N. Shardt and J. A. W. Elliott, Thermodynamic study of the role of interface curvature on multicomponent vapor-liquid phase equilibrium, J. Phys. Chem. A, 2016, 120, 2194–2200 CrossRef CAS PubMed.
- T. Solymosi, R. Angi, O. Bassa-Denes, S. Ranky, Z. Otvos, H. Glavinas, G. Filipcsei and G. Heltovics, Sirolimus formulation with improved pharmacokinetic properties produced by a continuous flow method, Eur. J. Pharm. Biopharm., 2015, 94, 135–140 CrossRef CAS PubMed.
- K. S. Kontturi, K. W. Biegaj, A. Mautner, R. T. Woodward, B. P. Wilson, L. S. Johansson, K. Y. Lee, J. Y. Y. Heng, A. Bismarck and E. Kontturi, Non-covalent surface modification of cellulose nanopapers by adsorption of polymers from alrotic solvents, Langmuir, 2017, 33(23), 5707–5712 CrossRef CAS PubMed.
- N. Oláh, Zs. Fogarassy, A. Sulyok, M. Veres, G. Kaptay and K. Balázsi, TiC crystallite formation and the role of interfacial energies on the composition during the deposition process of TiC/a:C thin films, Surf. Coat. Technol., 2016, 302, 410–419 CrossRef.
- L. Naszalyi Nagy, J. Mihaly, A. Polyak, B. Debreczeni, B. Csaszar, I. C. Szigyarto, A. Wacha, Z. Czegeny, E. Jakab, S. Klebert, E. Drotar, G. Dabasi, A. Bota, L. Balogh and E. Kiss, Inherently fluorescent and porous zirconia colloids preparation, characterization and drug adsorption studies, J. Mater. Chem. B, 2015, 3, 7529–7537 RSC.
- G. Bournival, S. Ata and E. J. Wanless, The roles of particles in multiphase processes: particles on bubble surfaces, Adv. Colloid Interface Sci., 2015, 225, 114–133 CrossRef CAS PubMed.
- A. Yakymovych, G. Kaptay, A. Roshanghias, H. Falndorfer and H. Ipser, Enthalpy effect of adding cobalt to liquid Sn-3.8Ag-0.7Cu lead-free solder alloy: difference between bulk and nanosized cobalt, J. Phys. Chem. C, 2016, 120, 1881–1890 CAS.
- S. Barany, Polymer adsorption and electrokinetic potential of dispersed particles in weak and strong electric fields, Adv. Colloid Interface Sci., 2015, 222, 58–69 CrossRef CAS PubMed.
- U. Wais, A. W. Jackson, Y. Zuo, Y. Xiang, T. He and H. Zhang, Drug nanoparticles by emulsion-freeze-drying via the employment of branched block copolymer nanoparticles, J. Controlled Release, 2016, 222, 141–150 CrossRef CAS PubMed.
- L. Vanyorek, F. Kristaly, A. Mihalko, O. Banhidi, A. Kukovecz, Z. Konya and J. Lakatos, Synthesis and 1-butene hydrogenation activity of platinum decorated bamboo-shaped multiwall carbon nanotubes, React. Kinet., Mech. Catal., 2015, 116, 371–383 CrossRef CAS.
- K. K. Nanda, Size-dependent melting of nanoparticles: hundred years of thermodynamic model, Pramana, 2009, l72, 617–628 CrossRef.
- J. Lee and K. J. Sim, General equations of CALPHAD-type thermodynamic description for metallic nanoparticle systems, Calphad, 2014, 44, 129–132 CrossRef CAS.
- A. Junkaew, B. Ham, X. Zhang and R. Arróyave, Tailoring the formation of metastable Mg through interfacial engineering: a phase stability analysis, Calphad, 2014, 45, 145–150 CrossRef CAS.
- F. Eslami and J. A. W. Elliott, Role of Precipitating Solute Curvature on Microdrops and Nanodrops during Concentrating Processes: The Nonideal Ostwald–Freundlich Equation, J. Phys. Chem. B, 2014, 118, 14675–14686 CrossRef CAS PubMed.
- A. R. Kalidini, T. Chookajorn and C. A. Schuh, Nanocrystalline materials at equilibrium: a thermodynamic review, JOM, 2015, 67, 2834–2843 CrossRef.
- G. Guenther, R. Theissmann and O. Guillon, Size-dependent phase transformations in bismuth oxide nanoparticles. Part II: melting and stability diagram, J. Phys. Chem. C, 2014, 118, 27020–27027 CAS.
- G. Kaptay, J. Janczak-Rusch, G. Pigozzi and L. P. H. Jeurgens, Theoretical analysis of melting point depression of pure metals in different initial configurations, J. Mater. Eng. Perform., 2014, 23, 1600–1607 CrossRef CAS.
- J. Gubicza, Z. Hegedűs, J. L. Lábár, A. Kauffmann, J. Freudenberger and J. S. Sarma, Solute redistribution during annealing of a cold rolled Cu–Ag alloy, J. Alloys Compd., 2015, 623, 96–103 CrossRef CAS.
- J. Sopousek, O. Zobac, J. Bursık, P. Roupcova, V. Vykoukal, P. Broz, J. Pinkas and J. Vrestal, Heat-induced spinodal decomposition of Ag–Cu nanoparticles, Phys. Chem. Chem. Phys., 2015, 17, 28277–28285 RSC.
- S. Bajaj, M. G. Haverty, R. Arróyave, W. A. Goddard III and S. Shankar, Phase stability in nanoscale material systems: extension from bulk phase diagrams, Nanoscale, 2015, 7, 9868–9877 RSC.
- V. M. Samsonov and O. A. Malkov, Thermodynamic model of crystallization and melting of small particles, Cent. Eur. J. Phys., 2004, 2, 1895–1902 Search PubMed.
- T. Wejrzanowski, M. Lewandowska, K. Sikorski and K. J. Kurzydlowski, Effect of grain size on the melting point of confined thin aluminum films, J. Appl. Phys., 2014, 116, 164302 CrossRef.
- G. Kaptay, J. Janczak-Rusch and L. P. H. Jeurgens, Melting Point Depression and Fast Diffusion in Nanostructured Brazing Fillers Confined Between Barrier Nanolayers, J. Mater. Eng. Perform., 2016, 25, 3275–3284 CrossRef CAS.
- J. Zhu, Q. Fu, Y. Xue and Z. Cui, Comparison of different models of melting transformation of nanoparticles, J. Mater. Sci., 2016, 51, 4462–4469 CrossRef CAS.
- A. Dezso and G. Kaptay, On the configurational entropy of nanoscale solutions for more accurate surface and bulk nano-thermodynamic calculations, Entropy, 2017, 19, 248 CrossRef.
- W. Thomson, On the equilibrium of vapour at a curved surface of liquid, Philos. Mag., 1871, 42, 448–452 Search PubMed.
- A. W. Adamson, Physical Chemistry of Surfaces, 5th edn, John Wiley and Sons Inc., NY, 1990 Search PubMed.
- de Laplace P. S., Mechanique Celeste, Supplement to Book 10, 1806.
- J. W. Gibbs, On the Equilibrium of Heterogenous Substances, Trans. Conn. Acad. Arts Sci., 1875, 3, 108–248 Search PubMed.
- J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon Press, Oxford, 1982 Search PubMed.
- J. M. Coulson and J. F. Richardson, Chemical Engineering, 4th edn, Bath: Butterworth Heinemann, 1991 Search PubMed.
- D. J. Shaw, Introduction to Colloid & Surface Chemistry, 4th edn, Bath: Butterwoth – Heinemann, 1992 Search PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, London, 1992 Search PubMed.
- G. A. Somorjai, Introduction to Surface Chemistry and Catalysis, Wiley, Weinheim, 1994 Search PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, 7th edn, Oxford University Press, Oxford, 2002 Search PubMed.
- H.-N. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley, Weinheim, 2003 Search PubMed.
- D. Myers, Surfactant Science and Technology, Wiley, Weinheim, 2006 Search PubMed.
- K. S. Birdi, Handbook of Surface and Colloid Chemistry, 3rd edn, CRC Press, New York, 2009 Search PubMed.
- U. Wais, A. W. Jackson, T. He and H. Zhang, Nanoformulation and encapsulation approaches for poorly water-soluble drug nanoparticles, Nanoscale, 2016, 8, 1746–1769 RSC.
- G. Wang, J. J. Wang, W. Wu, S. Shun, T. To, H. F. Zhao and J. Wang, Advances in lipid-based drug delivery: enhancing efficiency for hydrophobic drugs, Expert Opin. Drug Delivery, 2015, 12, 1475–1499 CrossRef PubMed.
- J. H. Min, H. K. Kwon and B. I. Kim, Prevention of dental erosion of a sports drink by nano-sized hydroxyapatite in situ study, Int. J. Paediatr. Dent., 2015, 25, 61–69 CrossRef PubMed.
- J. K. Schluesener and H. J. Schluesener, Nanosilver: application and novel aspects of toxicology, Arch. Toxicol., 2013, 87, 569–576 CrossRef CAS PubMed.
- J. D. Verhoeven, Fundamentals of physical metallurgy, Wiley, New York, 1975 Search PubMed.
- W. Kurz and D. J. Fisher, Fundamentals of Solidification, 3rd edn, Trans Tech Publ, Lausanne, 1989 Search PubMed.
- E. Budevski, G. Staikov and W. J. Lorenz, Electrochemical phase formation and growth, VCH, New York, 1996 Search PubMed.
- N. Eustathopoulos, M. G. Nicholas and B. Drevet, Wettability at High Temperatures, Pergamon, New York, 1999 Search PubMed.
- D. M. Stefanescu, Science and Engineering of Casting Solidification, Kluwer Academic, New York, 2002 Search PubMed.
- G. L. Hornyak, J. Dutta, H. F. Tibbals and A. K. Rao, Introduction to Nanoscience, CRC Press, New York, 2008 Search PubMed.
- J. A. Dantzig and M. Rappaz, Solidification, EPFL Press, Lausanne, 2009 Search PubMed.
- C. Zou, Y. Gao, B. Yang and Q. Zhai, Synthesis and DSC study on Sn3.5Ag alloy nanoparticles used for lower melting temperature solder, J. Mater. Sci.: Mater. Electron., 2010, 21, 868–874 CrossRef CAS.
- S. Ananiev, P. Nikrityuk and K. Eckert, Dendrite fragmentation by catastrophic elastic remelting, Acta Mater., 2009, 57, 657–665 CrossRef CAS.
- K. Leskovics, M. Kollár and P. Bárczy, A study of structure and mechanical properties of welded joints in polyethylene pipes, Mater. Sci. Eng., A, 2006, 419, 138–143 CrossRef.
- T. Tanaka and S. Hara, Thermodynamic evaluation of binary phase diagrams of small particle system, Z. Metallkd., 2001, 92, 467–472 CAS.
- M. Hillert and J. Argen, Effect of surface free energy and surface stress on phase equilibria, Acta Mater., 2002, 50, 2429–2441 CrossRef CAS.
- J. G. Lee and H. Mori, In-situ observation of alloy phase formation in nanometre-sized particles in the Sn-Bi system, Philos. Mag., 2004, 84, 2675–2686 CrossRef CAS.
- X. J. Liu, C. P. Wang, J. Z. Jiang, I. Ohnuma, R. Kainuma and K. Ishida, Thermodynamic calculation of phase diagram and phase stability with nano-size particle, Int. J. Mod. Phys. B, 2005, 19, 2645–2650 CrossRef CAS.
- J. Lee, J. Lee, T. Tanaka, H. Mori and K. Penttilá, Phase diagrams of nano-metre sized particles in binary systems, JOM, 2005, 56–59 CrossRef.
- N. Braidy, G. R. Purdy and G. A. Botton, Equilibrium and stability of phase-separating Au–Pt nanoparticles, Acta Mater., 2008, 56, 5972–5983 CrossRef CAS.
- J. Lee, J. Park and T. Tanaka, Effects of interaction parameters and melting points of pure metals on the phase diagrams of the binary alloy nanoparticle systems: a classical approach based on the regular solution model, Calphad, 2009, 33, 377–381 CrossRef.
- G. Kaptay, The Extension of the Phase Rule to Nano-Systems and on the Quaternary Point in One-Component Nano Phase Diagrams, J. Nanosci. Nanotechnol., 2010, 10, 8164–8170 CrossRef CAS PubMed.
- K. J. Bachmann, The materials science of microelectronics, VCH, New-York, 1995 Search PubMed.
- J. J. Thomson, Application of dynamics to physics and chemistry, MacMillan, London, 1888 Search PubMed.
- W. Ostwald, Über die vermeintliche Isomerie des roten und gelben Quescksilberoxyds und die Oberflachenspannung fester Körper, Z. Phys. Chem., 1900, 34, 495–503 Search PubMed.
- H. Freundlich, Kolloidchemie, Akademischer Verlag, Leipzig 1909, English translation: 1923, E. P. Dutton Co Publ., New York.
- L. R. Fisher and J. N. Israelachvili, Experimental studies on the applicability of the Kelvin equation to highly curved concave menisci, J. Colloid Interface Sci., 1981, 80, 528–541 CrossRef CAS.
- H. K. Christenson, Capillary condensation in systems of immiscible liquids, J. Colloid Interface Sci., 1985, 104, 234–249 CrossRef CAS.
- T. Takei, M. Chikazawa and T. Kanazawa, Validity of the Kelvin equation in estimation of small pore size by nitrogen adsorption, Colloid Polym. Sci., 1997, 275, 1156–1161 CAS.
- M. M. Kohonen and H. K. Christenson, Capillary condensation of water between rinsed mical surfaces, Langmuir, 2000, 16, 7285–7288 CrossRef CAS.
- A. C. Mitropoulos, The Kelvin equation, J. Colloid Interface Sci., 2008, 317, 643–648 CrossRef CAS PubMed.
- G. Kaptay, Nano-Calphad: extension of the Calphad method to systems with nano-phases and complexions, J. Mater. Sci., 2012, 47, 8320–8335 CrossRef CAS.
- G. Kaptay, On the size and shape dependence of the solubility of nano-particles in solutions, Int. J. Pharm., 2012, 430, 253–257 CrossRef CAS PubMed.
- G. Kaptay, The Gibbs equation versus the Kelvin and the Gibbs–Thomson equations to describe nucleation and equilibrium of nano-materials, J. Nanosci. Nanotechnol., 2012, 12, 2625–2633 CrossRef CAS PubMed.
- R. C. Tolman, The effect of droplet size on surface tension, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS.
- G. Kaptay, Classification and general derivation of interfacial forces, acting on phases, situated in the bulk, or at the interface of other phases, J. Mater. Sci., 2005, 40, 2125–2131 CrossRef CAS.
- G. Kaptay, Interfacial Forces in Dispersion Science and Technology, J. Dispersion Sci. Technol., 2012, 33, 130–140 CrossRef CAS.
- P. Letellier, A. Mayaffre and M. Turmine, Solubility of nanoparticles: nonextensive thermodynamic approach, J. Phys.: Condens. Matter, 2007, 19, 436229 CrossRef.
- P. Letellier, A. Mayaffre and M. Turmine, Melting point depression of nanosolids: nonextensive thermodynamic approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045428 CrossRef.
- Zi-X. Cui, M.-Z. Zhao, W.-P. Lai and Y.-Q. Xue, Thermodynamics of Size Effect on Phase Transition Temperatures of Dispersed Phases, J. Phys. Chem. C, 2011, 115, 22796–22803 CAS.
- T. S. Kuhn, The structure of scientific revolutions, The University of Chicago Press, 1962 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07911g |
| This journal is © The Royal Society of Chemistry 2017 |