Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sequence dependency of the thermodynamic properties of long DNA double-strands
Jabbar Khodadadi a,
Kavoos Mirabbaszadeh
a,
Kavoos Mirabbaszadeh *a and
Mohsen Yarmohammadi
*a and
Mohsen Yarmohammadi b
b
aDepartment of Energy Engineering and Physics, Amirkabir University of Technology, Tehran, Iran. E-mail: mirabbas@aut.ac.ir; Fax: +98 21 6454 5248; Tel: +98 21 6454 5248
bYoung Researchers and Elite Club, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran
First published on 24th October 2017
Abstract
Using the Green’s function technique and tight-binding (TB) Hamiltonian method for π-electrons within a ladder model of long DNA double-strands acting as semiconducting nanowires, the temperature and sequence dependency of the Pauli paramagnetic susceptibility (PMS) and electronic heat capacity (EHC) of some selected configurations are investigated. The results show the explicit reliance of the two quantities on the arrangement of the DNA base-pairs (BPs). The notable result of this study is the appearance of three temperature points for which the EHC (PMS) curves of the ordered systems converge (diverge) at the lowest and highest points, while they diverge (converge) at the middle point. Disordered systems exhibit a deviation from the trend of the ordered ones and this is more significant around the higher temperature points. Over a wide range of temperatures, the responses of the poly(GC) and poly(AT) double-helices limit the behavior of the random DNA chains. Our finding could inspire the design of experiments to assess the order of randomness in BP sequencing and also to better set the TB parameters of the model.
1 Introduction
DNA, famed in biology as the carrier of the genetic code, has attracted enormous attention from physics communities in recent years. A better insight into the physical behavior of these mysterious building blocks would provide more knowledge about their biological function and thus more possibilities for medical manipulation. Moreover, studies on DNA behavior offer hope for future molecular electronics by designing high-speed miniaturized circuits with self-organizing components.1–6 DNA may be handled as a wire, transistor, switch or rectifier, depending on its electronic properties,7,8 and therefore, a comprehensive understanding of the electronic structure of these creations is vital. This need is felt particularly strongly while determining physical quantities such as the thermodynamic and transport properties, most of which depend on the electronic structure. However, various intrinsic and extrinsic complexities have rendered the complete achievement of this objective impossible. This contradiction has also persevered in the experimental domain. Natural DNA in solution has highly supported charge transfer rates,9–12 but dried single DNA molecules have shown diverse insulating,13,14 semiconducting,15,16 and metallic12,17,18 behavior.Further to this background, no comprehensive theory relating to the electronic structure and transport mechanisms through DNA strands has been proposed so far. Nonetheless, tremendous effort is still being made in this area of research.
The thermodynamic properties of DNA and relevant structures have long been under consideration.19–27 For example, the thermodynamic parameters of DNA sequences with dangling ends and the contribution of these terminations to the duplex stability were inspected by Bommarito et al. via enthalpy and entropy changes extracted from UV melting curves of the synthesized oligonucleotides on solid supports.19 Using finite-difference Poisson–Boltzmann methods, Gallagher and Sharp determined the contribution of electrostatics to the changes of heat capacity of DNA binding reactions involving the ligands DAPI, netropsin and lexitropsin, and the λ repressor binding domain.20 Based on the enthalpy and heat capacity changes, Holbrook et al. investigated the thermodynamics of the self-assembly of a DNA duplex with 14 BPs from complementary strands, using titration and differential scanning calorimetry along with van’t Hoff analysis of the UV thermal scans.21 Using the same method, Bergqvist et al. probed the local effects of water molecules and ions on the heat capacity changes of a protein–DNA interaction.22 They found that although changes in the local ion binding capacity influenced the enthalpic and entropic contributions to the free energy of the interaction, there was no overall effect of ionic strength on the heat capacity changes. However, remarkable impacts were observed which originated from two particular symmetry-related mutations. An interesting case of the TB approach to be pointed out is the study conducted by Roche and Maciá who considered the genomic sequences of the chromosome 22, λ-bacteriophage and D1s80 genes of humans and pygmy chimpanzees and compared these with both periodic and quasiperiodic sequences of nucleotides.23
The magnetic properties of DNA have also been under consideration and reported in the literature, particularly during the last two decades. Yan et al. developed a near-field magnetic-tweezer for micromanipulation of single DNA molecules consisting of a small permanent magnet which can move to as close as 10 μm from the particle and generate forces much larger than those generated by previous instruments.24 By means of molecular dynamics simulations and quantum chemistry methods, Berashevich and Chakraborty investigated the effect of humidity on the transport and magnetic properties of DNA. They concluded that the interaction of water molecules with nucleobases leads to the breaking of some π bonds and the appearance of unbound π electrons which could then participate considerably, up to 103 times more, in the conductivity at room temperature, while at low temperature the efficiency of charge transfer is determined by the spin interaction of two unbound electrons on the intrastrand nucleobases.25
Scanning the literature for experimental and computational studies on the thermodynamic properties of DNA during the last few decades shows that the majority of them are carried out by chemists and biologists, but those by physicists are far fewer. In this study, we try to draw a theoretical picture of the EHC and PMS of the DNA double-strands with respect to the temperature and BP sequencing, using the Green’s function technique and the TB Hamiltonian model.
In Section 2 we review a semiconducting ladder model with the corresponding Hamiltonian for long DNA double-strands, using the Green’s function approach28,29 and related formulas for the physical quantities. Section 3 includes the calculations, results and the related discussions. Finally, Section 4 presents the summary and conclusion of all the results.
2 Model and approach
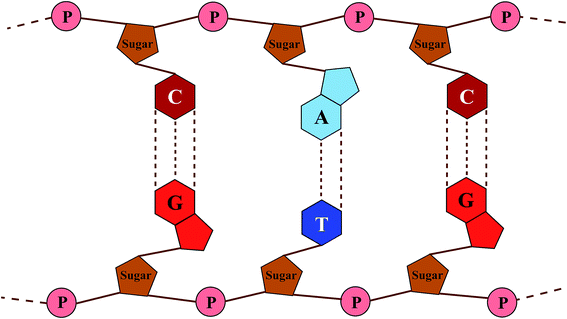
DNA (deoxyribonucleic acid) macro-molecules are twisted double-helix structures composed of repeated stacks of either adenine–thymine (A–T) or guanine–cytosine (G–C) BPs with an intimate sugar–phosphate (S–P) backbone, being coupled with hydrogen bonds (the Watson–Crick model).30 Fig. 1 shows a schematic view of the DNA structure with the simplifications used: firstly to untwist it to achieve a planar shape and secondly not to include the internal details of the constituents with respect to scale, spacing and position.In general, the theoretical studies on DNA can be classified into two main groups of ab initio calculations31–37 and the model-based Hamiltonian approach.38–49 Although the former method operates in a more fundamental way and provides more detail, it is very time-consuming for systems that are not small. The latter technique is generally favored when dealing with large systems wherein optimizing a few parameters can reproduce experimental results and reliable data. In this light, various TB models with proper on-site and hopping parameters have already been introduced with the aim of giving results compatible with experimental or ab initio reports.47–52 These models have mostly evolved around the important finding that overlapping of π orbitals, particularly those of the stacked BPs, can create a π pathway for the migration of electrons.2,10,11,24
In this work, we proceed by means of a disordered ladder model proposed by Yamada,42 constructed by repetition of the S–P sites with interchain hoppings at the S sites which come from the attached BPs. This model is shown in Fig. 2; in fact it is an oversimplified representation of Fig. 1 obtained by ignoring the migration of electrons along successive BPs. As marked in the figure, t1 and t2 indicate the hopping amplitudes of a π-electron from a P site to the left and right attached S sites, respectively, while WGC and WAT indicate the same quantity but between the BPs on complementary strands. It is assumed that no hopping exists between the P sites. Additionally, the BPs with permuted nucleotides are equivalent, namely WCG = WGC and WTA = WAT.
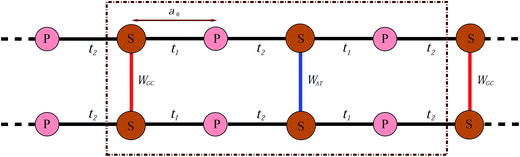 | ||
| Fig. 2 Simplified model of a two-channel periodic DNA with the appropriate parameter sets to attain semiconductivity. | ||
The second quantized Hamiltonian of this model reads as:46
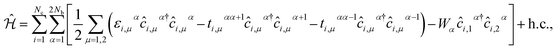 | (1) |
The aim of this study is to make a comparison between the EHC and PMS of long DNA semiconducting nanowires with respect to their dependence on the temperature and BP sequencing. We start with three specific ordered chains, namely poly(GC), poly(AT) and poly(GC–AT) double-strands, defined as an infinite arrangement of the GC, AT and alternating GC–AT pairs. We then move towards more realistic states of randomly arranged chains by considering periodic one-dimensional systems composed of big unit cells with many BPs arranged randomly inside. It is obvious from Fig. 2 that the length of such a unit cell with n BPs is a = 2na0, where a0 is the distance between a P site and a proximate S site. From our previous work,46 larger unit cells lead to a better resemblance of natural DNA and even medium-sized cells (for example those with a couple of hundred BPs) bring about acceptable outcomes.
It is convenient to continue in a system of units in which most of the physical constants, such as ħ and kB, are equal to one. Recalling from the Green’s function approach,53–56 the matrix elements are generally expressed by Gμναβ(i,j;τ) = −〈Τĉi,μα(τ)ĉj,νβ†(0)〉, where τ = it is the imaginary time, Τ is the time ordering operator, and 〈…〉 is a symbol for ensemble averaging over the ground state of the system. Calculation of the dynamical equations for the operators, dĉi,μα(τ)/dτ = 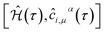 , results in:
, results in:
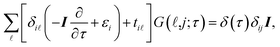 | (2) |
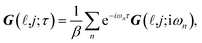 | (3a) |
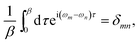 | (3b) |
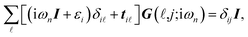 | (4) |
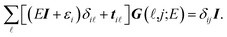 | (5) |
In the last step, applying the k-space Fourier transform is helpful:
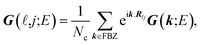 | (6a) |
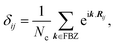 | (6b) |
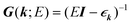 | (7) |
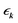 denotes the Fourier transform of tij,
denotes the Fourier transform of tij,
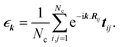 | (8) |
Regarding the relationship between the total DOS and the imaginary part of the Green’s function, D(ε) = −ImTrG(E)/π,54 by summing over the quantum numbers which label the Hamiltonian, the DOS of the system takes the form of:
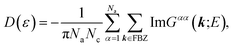 | (9) |
Now we are sufficiently equipped to extract the desired physical quantities. The electronic heat capacity could be calculated by:55–57
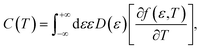 | (10) |
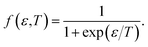 | (11) |
Likewise, recalling the definition of static susceptibility,58
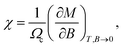 | (12) |
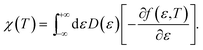 | (13) |
Finally, from the combination of eqn (9)–(13), the following forms for the EHC and PMS of our systems are derived:
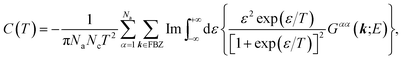 | (14) |
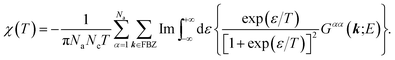 | (15) |
3 Calculations and results
By rescaling all energies to that of t1 for further simplification, we adapt the subsequent TB parameters from the model given by Yamada. The parameters were extracted while investigating the long-range correlation effects on the localization property of the one-electron states in such disordered models via the DOS and Lyapunov exponents of the wave functions:42
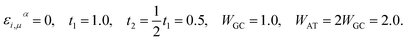 | (16) |
Perhaps these parameters, particularly the fixing of all the on-site energies to zero, seem unsound and different to some other works,35–38,50–52 however, this simple model with the above set of parameters has succeeded in reproducing the semiconductivity of DNA double-strands.42,43,46
For the simple case of the poly(GC) duplex, as a practical example, the orthogonal basis kets of the Hilbert space corresponding to four sites within the unit cell (two coupled strands of G–P and C–P) are as follows:
| {|ΦG1〉,|ΦP1〉,|ΦC2〉,|ΦP2〉}, | (17) |
 | (18) |
For the corresponding unit cell of length a = 2a0 with the nearest neighbor vectors Ri,i+1 = −Ri.i−1 = aex, the FBZ interval would be −π/a ≤ k ≤ π/a, and hence by inserting the parameters of eqn (16) into eqn (8), we are led to:
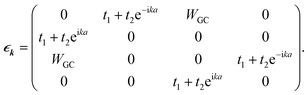 | (19) |
Diagonalizing the above matrix through some calculations determines the band structure (BS) of the system as below:
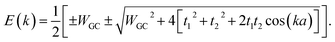 | (20) |
The energy gap of the system can be extracted directly as the minimum difference between the mid-upper and mid-lower bands,
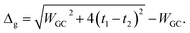 | (21) |
Obviously these results hold true for poly(AT) DNA as well, however, WGC should be replaced with WAT. Substituting the numerical values of the parameters generates values of 0.414t1 and 0.236t1 for the energy gaps of the poly(GC) and poly(AT) chains, respectively. The results indicate the typical dependence of the band gap and electrical profile of such systems on their geometry and TB parameters.
For the case of the poly(GC–AT) duplex, which includes eight sites within its unit cell (two coupled strands of G–P–A–P and C–P–T–P), the orthogonal basis kets of the Hilbert space are:
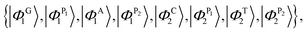 | (22) |
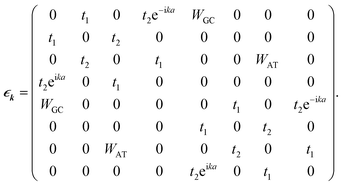 | (23) |
Numerically solving the above matrix and reiterating for all k vectors of the FBZ determines the BS of this case. The acquired results have found 0.30t1 to be the value of the band gap. Furthermore, substitution of eqn (23) in eqn (7) and (9) specifies the profile and details of the DOS.
Similarly, larger calculations are carried out to extract the DOS of bigger duplexes. Fig. 3 shows the results for the three mentioned ordered systems. Panel (a) for poly(GC) DNA shows the greatest band gap at the Fermi level, εF = 0, and mini-gaps between the subbands on both sides. In contrast, in panel (b), poly(AT) DNA appears to have the smallest band gap at εF with widely separated subbands. Principally, van Hove singularities directly relate to the number of atoms in the unit cell and address the regions in which the eigenstates are larger. In both systems, van Hove singularities occur at the edges of the bands and subbands, implying that the eigenstates are denser in these vicinities. The emergence of central gaps and the observed discrepancies for different systems can be explained by symmetry breaking, that is asymmetry of the hopping terms from a typical site to either the left or right neighbor, which resembles the picture of a molecule located between two other molecules of different types. If the neighbors on both sides of a typical molecule are different, they have different energy levels, leading to the opening of a gap in the energy band. The noticeable point in panel (c) for poly(GC–AT) is a band gap of medium size compared to the two other cases. Moreover, there are higher numbers of allowed bands and van Hove singularities due to its larger unit cell that has a larger number of atoms inside. Therefore, it might be speculated that poly(GC) and poly(AT) DNA chains can set the limits and confine the curves of all other double-strands. This could be supported by more inspection of the plots (a)–(c) of Fig. 4, representing the DOS of the three disordered chains with unit cells including 20, 100 and 200 randomly arranged BPs. Details of the sequencing have not been demonstrated except to consider only one constraint: that every case is composed of equal numbers of G–C and A–T pairs but in a random arrangement. It can be clearly seen that the different shapes of the DOS corresponding to unit cells of different sizes are in agreement with ref. 46 where this result is verified not only for this condition but also for different configurations of BPs within a fixed size unit cell.
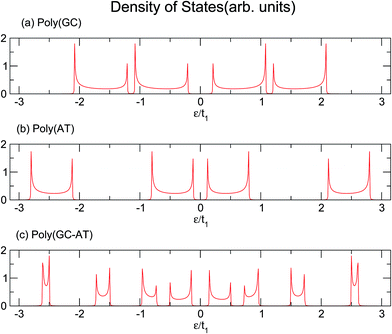 | ||
| Fig. 3 The DOS of three ordered chains of (a) poly(GC), (b) poly(AT) and (c) poly(GC–AT) double-strands, based upon the parameter sets of eqn (16). | ||
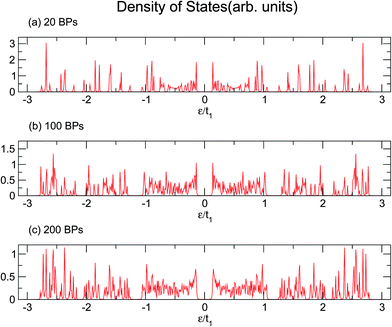 | ||
| Fig. 4 The DOS of three disordered double-strands with (a) 20, (b) 100, and (c) 200 randomly arranged BPs. | ||
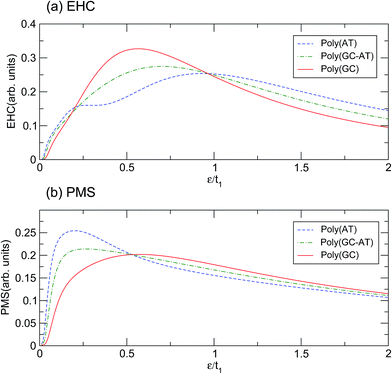
Illustrated in panels (a) and (b) of Fig. 5 are the EHC and PMS of the ordered chains with respect to the dimensionless temperature (ε = kBT)/t1. The behavior of the curves in the limit of very high and very low temperatures can be explained because the thermal effects are dominant in the upper limit and overcome all other mechanisms, while in the lower extreme the thermal energy is not sufficient to excite the electrons to cross the energy gap. There are two mechanisms governing the systems: the temperature gradient as a driving agent and the scattering of electrons from the site potentials as a disturbing factor. For different systems both mechanisms are locally of different strengths and their competition dictates the overall behavior. The confluence points of the curves are quite salient. Concerning the EHC, there are three special temperatures of about ε1 = 0.20t1, ε2 = 0.53t1 and ε3 = 0.96t1. For the points ε1 and ε3, all the ordered systems are almost coincident, while for ε2 they diverge significantly. In addition, the poly(GC) and poly(AT) curves cross, and thus which case is higher alternates, at ε1 and ε3. Every system exhibits an unsteady increasing trend until it reaches its peak, after which the figures steadily decline. The poly(GC) DNA curve reaches its peak at about 0.56t1 with the least degree of fluctuation, while the poly(AT) DNA curve has the lowest peak among all the systems, reaching its peak at 0.93t1 with the most recognizable fluctuations among all the systems. The existence of another extreme at 0.27t1 in the latter case may provide enough evidence to consider a double-crossover. As expected based on the above interpretation, the curve of the poly(GC–AT) DNA resides between those of the other two, with the exception of a meagre departure at about ε1. This is clearer than the peak at 0.7t1, in terms of both its position and height.
Similar description emerges with obvious discrepancies for the PMS of the systems. As panel (b) of Fig. 5 shows, the PMS of poly(AT) DNA reaches its peak abruptly at 0.2t1 and decreases much slowly after that, without any considerable fluctuation. However, the curve for poly(GC) DNA reaches its maximum at about 0.57t1 after a noticeable deviation from the initial trend. Again, the poly(GC–AT) DNA curve stays between the two other curves and has a peak at about 0.26t1. In contrast to those of the EHC, the curves of the PMS of the ordered chains meet at ε2 and show a distinguishable divergence at ε1 and ε3.
According to the results based on this model, perhaps it can be claimed that the physical properties of the poly(GC) and poly(AT) DNA nanowires delineate the boundaries which enclose the graphs of other double-strands. Of course, any extension must be inferred from more work on more systems of other types, including periodic, quasi-periodic, and natural DNA structures.59–63 This idea has been assessed further, within the scope of our results, by comparing the mentioned quantities calculated for such systems with different random DNA chains whose DOS is plotted in Fig. 4. The outcomes, as portrayed in Fig. 6, are moderately distributed around the poly(GC–AT) DNA, giving further evidence to support our first speculation. We observe that these random systems disobey the trend of the ordered chains, i.e. they diverge around the points where the ordered systems converge and vice versa. Furthermore, this discrepancy is more noticeable around the higher coincidence temperatures. For instance, the EHC curves of the random chains deviate from being coincident at ε1 and ε3, with more divergence around ε3. They also don’t show a severe divergence at ε2, as opposed to what was previously observed for the ordered systems. Likewise, the PMS curves of the random chains deviate from divergence at ε1 and ε3 and coincidence at ε2. Moreover, this deviation from the behavior of the ordered systems is greater around the higher temperature points.
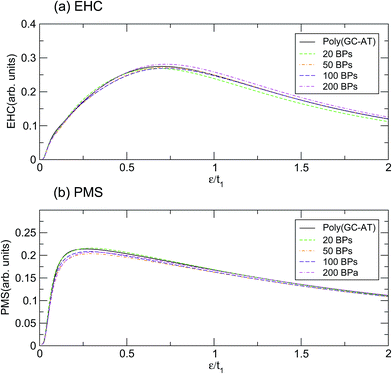 | ||
| Fig. 6 The (a) EHC and (b) PMS of a few disordered double-strands including different numbers of BPs with equal contributions of both types. | ||
This behavior holds even for disordered systems of the same unit cell size but with different arrangements of BPs. Fig. 7 depicts the calculation for a few configurations of such a unit cell with 200 BPs which have been labelled by their respective number of GC pairs. The first two double-strands both contain 100 GCs but they are arranged in different ways, labelled I and II. Obviously, the mentioned discrepancy is still present but it is not as severe. The dependence of EHC and PMS of the DNA on temperature and sequencing, along with the particular temperatures at which the ordered chains exhibit exclusive behavior, can inspire the design of experiments for the investigation of BP arrangement and the order of randomness in random DNA double-strands. The outcomes of these investigations would be helpful for regulating and quantifying the TB parameters of the model applied here.
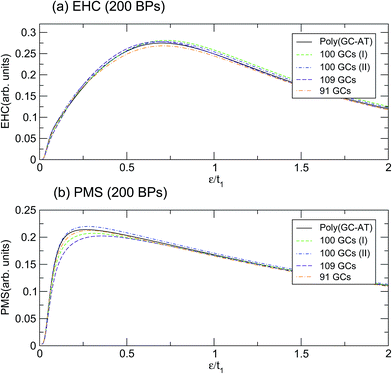 | ||
| Fig. 7 The (a) EHC and (b) PMS of the three different configurations of disordered double-strands with 200 BPs, labelled by their GC numbers. | ||
4 Summary and conclusion
Using a proper TB Hamiltonian model and the Green’s function method, the EHC and PMS of some selected ordered and disordered DNA double strands have been studied. The main finding from our calculations using this model is that the EHC and PMS of poly(GC) and poly(AT) DNA draw the boundaries which enclose these graphs for the other disordered chains. Additionally, for each of the mentioned quantities, there exist particular temperature points at which the EHC curves of the ordered double-strands coincide (diverge) while their PMS curves diverge (coincide). Interestingly, these are the points where disordered systems exhibit the most discrepancy with respect to the ordered systems, and the deviation is more significant for points of higher temperature. Therefore, the deviation from these points can be considered as a criterion for evaluating the degree of randomness in BP sequencing of random DNA chains. Furthermore, they allow the possibility to better quantify the TB parameters of the model.Conflicts of interest
There are no conflicts to declare.References
- K. Keren, R. S. Berman, E. Buchstab, U. Sivan and E. Braun, Science, 2003, 302, 1380 CrossRef CAS PubMed.
- R. Gutiérrez, S. Mohapatra, H. Cohen, D. Porath and G. Cuniberti, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 235105 CrossRef.
- V. Bhalla, R. P. Bajpai and L. M. Bharadwaj, Eur. Mol. Biol. Organ. J., 2003, 4, 442 CAS.
- M. Mertig, R. Kirsch, W. Pompe and H. Engelhardt, Eur. Phys. J. D, 1999, 9, 45 CrossRef CAS.
- D. B. Hall, R. E. Holmlin and J. K. Barton, Nature, 1996, 382, 731 CrossRef CAS PubMed.
- E. Meggers, M. E. Michel-Beyerle and B. Giese, J. Am. Chem. Soc., 1998, 120, 12950 CrossRef CAS.
- E. M. Conwell and S. V. Rakhmanova, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 4556 CrossRef CAS PubMed.
- G. Cuniberti, L. Craco, D. Porath and C. Dekker, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 241314 CrossRef.
- S. O. Kelley and J. K. Barton, Science, 1999, 283, 375 CrossRef CAS PubMed.
- C. J. Murphy, M. A. Arkin, Y. Jenkins, N. D. Ghatlia, S. Bossman, N. J. Turro and J. K. Barton, Science, 1993, 262, 1025 CAS.
- C. R. Treadway, M. G. Hill and J. K. Barton, Chem. Phys., 2002, 281, 409 CrossRef CAS.
- E. Braun, Y. Eichen, U. Sivan and G. B. Yoseph, Nature, 1998, 391, 775 CrossRef CAS PubMed.
- A. J. Storm, J. van Noort, S. de Vries and C. Dekker, Appl. Phys. Lett., 2001, 79, 3881 CrossRef CAS.
- J. P. Lewis, T. E. Cheatham, E. B. Starikov, H. Wang and O. F. Sankey, J. Phys. Chem. B, 2003, 107, 2581 CrossRef CAS.
- D. Porath, A. Bezryadin, S. Vries and C. Dekker, Nature, 2000, 403, 635 CrossRef CAS PubMed.
- H. Cohen, C. Nogues, R. Naaman and D. Porath, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11589 CrossRef CAS PubMed.
- H. W. Fink and C. Schonenberger, Nature, 1999, 398, 407 CrossRef CAS PubMed.
- B. Xu, P. Zhang, X. Li and N. Tao, Nano Lett., 2004, 4, 1105 CrossRef CAS.
- S. Bommarito, N. Peyret and J. SantaLucia Jr, Nucleic Acids Res., 2000, 28, 1929 CrossRef CAS PubMed.
- K. R. Gallagher and K. R. Sharp, Biophys. J., 1998, 75, 769 CrossRef CAS PubMed.
- J. A. Holbrook, M. W. Capp, R. M. Saecker and M. T. Record, Biochemistry, 1999, 38, 8409 CrossRef CAS PubMed.
- S. Bergqvist, M. A. Williams, R. O’Brien and J. E. Ladbury, J. Mol. Biol., 2004, 336, 829 CrossRef CAS PubMed.
- S. Roche and E. Maciá, Mod. Phys. Lett. B, 2004, 18, 847 CrossRef CAS.
- J. Yan, D. Skoko and J. F. Marko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 011905 CrossRef PubMed.
- J. Berashevich and T. Chakraborty, J. Phys. Chem. B, 2008, 112, 14083 CrossRef CAS PubMed.
- J. Zenk, D. Scalise, K. Wang, P. Dorsey, J. Fern, A. Cruz and R. Schulman, RSC Adv., 2017, 7, 18032 RSC.
- C. G. Evans and E. Winfree, Chem. Soc. Rev., 2017, 46, 3808 RSC.
- H. Bruus and K. Flensberg, Many-Body Quantum Theory in Condensed Matter Physics: An Introduction, 2nd edn, Oxford University Press, UK, 2004 Search PubMed.
- H. Mousavi and J. Khodadadi, Superlattices Microstruct., 2015, 88, 434 CrossRef CAS.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737 CrossRef CAS PubMed.
- F. Bogar, A. Bende and J. Ladik, Phys. Lett. A, 2014, 378, 2157 CrossRef CAS.
- R. Di Felice, A. Calzolari and H. Zhang, Nanotechnology, 2004, 15, 1256 CrossRef CAS.
- Q. Cui and M. Elstner, Phys. Chem. Chem. Phys., 2014, 16, 14368 RSC.
- M. Elstner and G. Seifert, Philos. Trans. R. Soc., A, 2014, 372, 20120483 CrossRef PubMed.
- H. Mehrez and M. P. Anantram, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115405 CrossRef.
- A. Migliore, S. Corni, D. Varsano, M. L. Klein and R. Di Felice, J. Phys. Chem. B, 2009, 113(28), 9402 CrossRef CAS PubMed.
- A. Ivanova, P. Shushkov and N. Rösch, J. Phys. Chem. A, 2008, 112(30), 7106 CrossRef CAS PubMed.
- L. G. D. Hawke, G. Kalosakas and C. Simserides, Eur. Phys. J. E, 2010, 32, 291 CrossRef CAS PubMed.
- C. J. Paez, P. A. Schulz, N. R. Wilson and R. A. Römer, New J. Phys., 2012, 14, 093049 CrossRef.
- F. Palmero, J. F. R. Archilla, D. Hennig and F. R. Romero, New J. Phys., 2004, 6, 13 CrossRef.
- O. R. Davies and J. E. Inglesfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195110 CrossRef.
- H. Yamada, Int. J. Mod. Phys. B, 2004, 18, 1697 CrossRef CAS.
- H. Yamada and K. Iguchi, Adv. Condens. Matter Phys., 2010, 380710 Search PubMed.
- A. Kole and K. Radhakrishnan, RSC Adv., 2017, 7, 8474 RSC.
- C. Simserides, Chem. Phys., 2014, 440, 31 CrossRef CAS.
- H. Mousavi, J. Khodadadi and M. Grabowski, Solid State Commun., 2015, 222, 42 CrossRef CAS.
- K. Iguchi, Int. J. Mod. Phys. B, 2003, 17, 2565 CrossRef CAS.
- K. Iguchi, Int. J. Mod. Phys. B, 2004, 18, 1845 CrossRef CAS.
- D. Klotsa, R. A. Römer and M. S. Turner, Biophys. J., 2005, 89, 2187 CrossRef CAS PubMed.
- T. Kubar, P. B. Woiczikowski, G. Cuniberti and M. Elstner, J. Phys. Chem. B, 2008, 112(26), 7937 CrossRef CAS PubMed.
- K. Senthilkumar, F. C. Grozema, C. F. Guerra, F. M. Bickelhaupt, F. D. Lewis, Y. A. Berlin, M. A. Ratner and L. D. Siebbeles, J. Am. Chem. Soc., 2005, 127 42, 14894 CrossRef PubMed.
- A. A. Voityuk, J. Jortner, M. Bixon and N. Rösch, J. Chem. Phys., 2001, 114 13, 5614 CrossRef.
- E. N. Economou, Green’s Functions in Quantum Physics, 3rd edn, Springer-Verlag, Berlin-Heidelberg, 2006 Search PubMed.
- G. Grosso and G. P. Parravicini, Solid State Physics, 2nd edn, Academic Press, 2014 Search PubMed.
- H. Mousavi, M. Bagheri and J. Khodadadi, Phys. E, 2015, 74, 135 CrossRef CAS.
- H. Mousavi and J. Khodadadi, Appl. Phys. A, 2016, 122, 14 CrossRef.
- C. Kittel, Introduction to SolidState Physics, 8th edn, Wiley, New York, 2004 Search PubMed.
- W. Nolthing and A. Ramakanth, Quantum Theory of Magnetism, Springer, New York, 2009 Search PubMed.
- K. Lambropoulos, M. Chatzieleftheriou, A. Morphis, K. Kaklamanis, M. Theodorakou and C. Simserides, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032725 CrossRef CAS PubMed.
- K. Lambropoulos, M. Chatzieleftheriou, A. Morphis, K. Kaklamanis, R. Lopp, M. Theodorakou, M. Tassi and C. Simserides, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 94, 062403 CrossRef CAS PubMed.
- E. L. Albuquerque, U. L. Fulco, V. N. Freire, E. W. S. Caetano, M. L. Lyra and F. A. B. F. de Moura, Phys. Rep., 2014, 535(4), 139 CrossRef.
- R. G. Sarmento, G. A. Mendes, E. L. Albuquerque, U. L. Fulco, M. S. Vasconcelos, O. Ujsághy, V. N. Freire and E. W. S. Caetano, Phys. Lett. A, 2012, 376, 2413 CrossRef CAS.
- C. T. Shih, Y. Y. Cheng, S. A. Wells, C. L. Hsu and R. A. Römer, Comput. Phys. Commun., 2011, 182, 36 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |