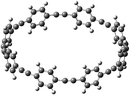
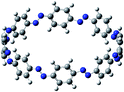
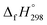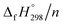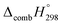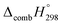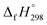Open Access Article
Open Access ArticleTheoretical studies on the structure and thermochemistry of cyclicparaphenylenediazenes†
Mohamad Akbar Ali *a and
Mohammad A. Alam
*a and
Mohammad A. Alam *b
*b
aDepartment of Chemistry, Sejong University, Seoul, 143-747, Republic of Korea. E-mail: akbar256@sejong.ac.kr
bDepartment of Chemistry and Physics, College of Science and Mathematics, Arkansas State University, Jonesboro, AR 72467, USA. E-mail: malam@astate.edu
First published on 16th August 2017
Abstract
Cyclicparaphenylenediazenes (CPPDs) have drawn great attention due to their potential applications in molecular electronics and solar energy. However, to date, there have been no detailed structure and thermochemistry investigations on CPPDs. Herein, we used an integrated computational approach aimed at providing reliable structural and thermochemical information on novel CPPDs based photoswitchable molecular rings. The approach involves hybrid density functional theory calculation at the B3LYP/6-31+G(d,p) level coupled with homodesmotic reaction approach to calculate strain energies (SE) and standard enthalpies of formation 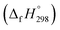 of all cis and all trans isomers of [n]CPPDs (n = 2 to 8). The results show that strain energies and
of all cis and all trans isomers of [n]CPPDs (n = 2 to 8). The results show that strain energies and 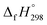 per-unit monomer of all cis-[n]CPPDs (n = 4 to 8) increase with increasing the numbers of Ph–N
per-unit monomer of all cis-[n]CPPDs (n = 4 to 8) increase with increasing the numbers of Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N linkages. However, an opposite trend was observed for all trans-[n]CPPDs (n = 4 to 8). The results were also compared with carbon nanoring structures i.e., cyclicparaphenyleneacetylenes (CPPAs) and cycloparaphenylenes (CPPs). The calculated highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) energy gaps are in the range of 1.98 eV to 2.36 eV, indicating potential material for the construction of solar cells. The reported structures, SE,
N linkages. However, an opposite trend was observed for all trans-[n]CPPDs (n = 4 to 8). The results were also compared with carbon nanoring structures i.e., cyclicparaphenyleneacetylenes (CPPAs) and cycloparaphenylenes (CPPs). The calculated highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) energy gaps are in the range of 1.98 eV to 2.36 eV, indicating potential material for the construction of solar cells. The reported structures, SE, 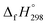 , and electronic properties of CPPDs can be also helpful to synthesize these novel materials.
, and electronic properties of CPPDs can be also helpful to synthesize these novel materials.
1. Introduction
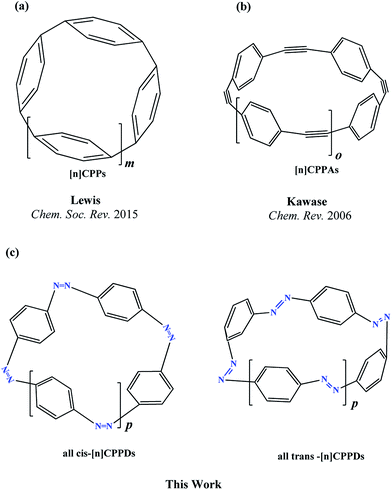
Nitrogen-doped cyclic oligomers including cyclic azobenzenophanes (CABPs) have received great attention1,2 due to their potential applications in semiconductor devices,3 high-performance catalytic reactions,4,5 Li-ion batteries,6 ultracapacitors, optomechanical devices,7–9 biochemical applications,10 photoswitches in photopharmacology,11–13 and molecular motors in drug delivery.14,15 These attractive properties of CABPs are all due to their cis–trans photo and thermal isomerization, and due to their molecular strain.16–19CABPs, in which two, three, and four azobenzene (AB) units are connected by –CH2–CH2– and –CH2–S–CH2– chains at the meta and para positions have been studied by various research groups.16,17 Nagamani et al.17 have reported CABPs, in which two AB are connected by –CH2–CH2– group at the para positions. They suggested trans, trans (t,t) isomers are more stable than the trans, cis (t,c) and cis, cis (c,c) isomers. In another study, Rau and Lueddecke18 have prepared an azobenzenophane (ABP), in which two AB are connected by –CH2–S–CH2– chains at the para positions. They found photoisomerization of ABP was based on a rotation/inversion mechanism from the state of AB, which was inhibited due to the ring strain. In 2013, Durgun and Grossman19 performed the density functional theory (DFT) calculations on the structure and enthalpies of reaction of cis and trans-[n]azobenzenophanes (n = 2 to 6). In their study, the effect of steric distortion on photoisomerization and thermal stability [n]azobenzenophanes (n = 2 to 6)19 with –CH2– linkage were calculated. These CABPs has been suggested for the construction of solar thermal fuel,20 and photoswitchable devices.12,13
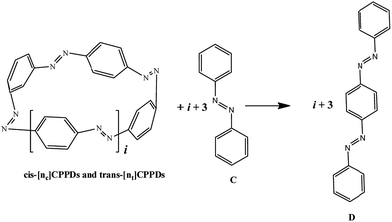
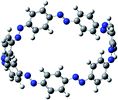
The next challenging target in the research field is another important class of CABPs, so called cyclicparaphenylenediazenes (CPPDs). CPPDs are obtained by connecting phenyldiazene (Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) unit through para linkage as shown in Fig. 1. CPPDs can be constructed by replacing acetylenic bond (–C
N–) unit through para linkage as shown in Fig. 1. CPPDs can be constructed by replacing acetylenic bond (–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–) with an azo group (–N
C–) with an azo group (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) on cyclicparaphenyleneacetylenes (CPPAs) oligomer21,22 and can be formed by inserting an azo group between two benzene rings of cycloparaphenylenes (CPPs)23–25 (Fig. 1). Very few theoretical studies have been carried out on CPPDs.19,26 As far as we know Durgun and Grossman reported the structure and enthalpies of all cis and all trans isomer of cyclic[6]paraphenylenediazenes ([6]CPPD).19 Recently, Van Raden et al.27 have synthesized highly strained nitrogen-doped cyclicparaphenylenes i.e., aza[6]CPP. They calculated highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy gap level using hybrid DFT at B3LYP/6-31G(d) level. In another study, Yuan et al.26 have predicted the host–guest interaction between [6]CPPD and [7]CPPD with fullerene (C60) using hybrid DFT at M06-L and M06-2X levels. They reported the relative stabilities of host–guest interactions between fullerene C60 and [6]CPPD and [7]CPPD by varying nitrogen atoms in the ring.
N–) on cyclicparaphenyleneacetylenes (CPPAs) oligomer21,22 and can be formed by inserting an azo group between two benzene rings of cycloparaphenylenes (CPPs)23–25 (Fig. 1). Very few theoretical studies have been carried out on CPPDs.19,26 As far as we know Durgun and Grossman reported the structure and enthalpies of all cis and all trans isomer of cyclic[6]paraphenylenediazenes ([6]CPPD).19 Recently, Van Raden et al.27 have synthesized highly strained nitrogen-doped cyclicparaphenylenes i.e., aza[6]CPP. They calculated highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy gap level using hybrid DFT at B3LYP/6-31G(d) level. In another study, Yuan et al.26 have predicted the host–guest interaction between [6]CPPD and [7]CPPD with fullerene (C60) using hybrid DFT at M06-L and M06-2X levels. They reported the relative stabilities of host–guest interactions between fullerene C60 and [6]CPPD and [7]CPPD by varying nitrogen atoms in the ring.
Over the years, many hypothetical chemical reactions have been proposed in an effort to predict the thermochemistry of organic and inorganic molecules. Since Baeyer's28 classic strain theory from 1885 and Bredt's rule almost 100 years ago, strained hydrocarbons have aroused considerable interest to chemists and material scientists. Efforts of chemists to bend and break Bredt's rule have generated a great variety of interesting molecules. Angle strained cyclic oligomer i.e., CPPAs, CPPs, and CPPDs are the important class of strained hydrocarbons that are attractive to both experimental and theoretical chemists.19,22,25 Some of these molecules are useful in photovoltaic cells because they have strong electron withdrawing character of the triple bond and their rod-like structure.29
The group equivalent method, Westheimer bond angle method,30 Dudev ring fragment method,31 Wiberg heats of reaction method, isodesmic,32–37 connectivity-based hierarchy,38 and homodesmotic reaction approaches, etc.,21,32,39–41 are a few widely used methods in literature for calculating strain energies (SE) and standard enthalpies of formation 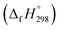 of cyclic and acyclic molecules. In this paper, we have used similar approaches i.e., isodesmic and homodesmotic reaction schemes coupled with density functional theory to analyze the trends of SE and
of cyclic and acyclic molecules. In this paper, we have used similar approaches i.e., isodesmic and homodesmotic reaction schemes coupled with density functional theory to analyze the trends of SE and 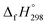 of CPPDs.
of CPPDs.
To the best of our knowledge, there have been no experimental and theoretical studies on structure, thermochemistry, and electronic properties of all cis and all trans isomers of cyclic [n]paraphenylenediazenes ([n]CPPDs) (n = 2 to 8). The synthesis of angle-strained [n]CPPDs is highly desirable due to their potential application in π-conjugated organic materials. In this paper we attempt to quantify this synthetic challenge, by applying an integrated computational strategy aimed at providing reliable structure, molecular orbitals, SE, and 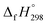 for all cis and all trans-CPPDs. The SE of highly strained CPPDs and weakly strained CPPDs molecules have a significant impact on their stability and reactivity, were calculated using hybrid density functional methods in combination of homodesmotic reaction approach.39 The SE of CPPDs was also compared with its analogous π-conjugated oligomer (Fig. 1) i.e., CPPs and CPPAs, which have been suggested for the model compounds for carbon nanotube and carbon nanobelt.21,22,25,40 To further explore the structure of novel CPPDs and its applications in molecular electronics and in solar energy, we calculated the energies of HOMO, LUMO, and HOMO–LUMO gap.
for all cis and all trans-CPPDs. The SE of highly strained CPPDs and weakly strained CPPDs molecules have a significant impact on their stability and reactivity, were calculated using hybrid density functional methods in combination of homodesmotic reaction approach.39 The SE of CPPDs was also compared with its analogous π-conjugated oligomer (Fig. 1) i.e., CPPs and CPPAs, which have been suggested for the model compounds for carbon nanotube and carbon nanobelt.21,22,25,40 To further explore the structure of novel CPPDs and its applications in molecular electronics and in solar energy, we calculated the energies of HOMO, LUMO, and HOMO–LUMO gap.
2. Theoretical methodology
The geometrical, energetical, vibrational, and electronic properties of all cis-[n]CPPDs (designated as [nc]CPPDs) (n = 2 to 8) and all trans-[n]CPPDs isomer of [n]CPPDs (designated as [nt]CPPDs) (n = 2 to 8) were performed using hybrid DFT; B3LYP42 in conjunction with 6-31+G(d,p) basis set as implemented in the Gaussian 09 (Rev. D.01) and Gaussian 09 (Rev.E.01) program suites.43,44 No symmetry constraint was applied during geometry optimization. Optimized geometries and vibrational frequencies are tabulated in the ESI (Tables S1–S4†). The nature of all stationary points on the potential energy surface (PES) (minimum) was checked by diagonalizing the corresponding Hessians. The absence of imaginary frequency confirms that the obtained structure corresponds to a true minimum on the potential energy surface. The zero-point energy (ZPE), and thermal correction (ΔHT) were calculated from vibrational frequency analysis. We have chosen the B3LYP model, since it produces reasonably good π-conjugated structures, and appropriate for the prediction of electronic structure of polycyclic hydrocarbons and their energies.21,27,34,35,40,45–48 The combination of B3LYP42 with 6-31G(d) and 6-31+G(d,p) basis sets has been tested by other groups and results were found to be in good agreement with experimental values.21,40,46,48 Therefore, we believe the same combination will provide reasonably accurate geometrical parameters and vibrational frequencies for [n]CPPDs.Some calculations were also carried out using high-level quantum composite Gaussian-4 (G4) method49 as implemented in the Gaussian 09 (Rev. D.01)43 and Gaussian 09 (Rev.E.01)44 program suites. The G4 theory49 is the fourth in the Gaussian-n series of quantum chemical methods, which is based on geometry optimization as well vibrational analysis of molecules at the B3LYP/6-31G(2df,p). This calculation is followed by a series of single-point energy calculations with higher level of theory: CCSD(T,FC)/6-31G(d), MP4 (FC)/6-31G(d), MP4(FC)/6-31+G(d), MP4 (FC)/6-31G(2df,p), and MP2(FU)/G3LargeXP.49 The G4 method produces approximate energy accuracy of ±1 kcal mol−1.49
The calculation of SE and 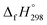 of [n]CPPDs were carried out using similar homodesmotic reaction approach39 as discussed in previous works.21,24 The SE and
of [n]CPPDs were carried out using similar homodesmotic reaction approach39 as discussed in previous works.21,24 The SE and 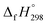 of a hypothetical isodesmic or homodesmotic reaction schemes of unknown molecule A of reaction type nA + mB → rC + sD were calculated using;
of a hypothetical isodesmic or homodesmotic reaction schemes of unknown molecule A of reaction type nA + mB → rC + sD were calculated using;
| Strain energy = ∑ΔEproducts0 K − ∑ΔEreactants0 K | (1) |
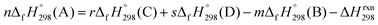 | (2) |
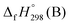 ,
, 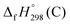 , and
, and 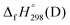 are enthalpies of formation of species B, C, and D, respectively and ΔHrxn298 is the enthalpies of reaction for reaction nA + mB → rC + sD.
are enthalpies of formation of species B, C, and D, respectively and ΔHrxn298 is the enthalpies of reaction for reaction nA + mB → rC + sD.
All the optimized geometrical parameters and vibrational frequencies are given in the ESI.† Strain energies, enthalpies of reaction, enthalpies of formation, and enthalpies of combustion are expressed in kJ mol−1, vibrational frequencies in cm−1 and HOMO, LUMO, and HOMO–LUMO gap energies in eV.
3. Results and discussion
3.1 Structure of [n]CPPDs
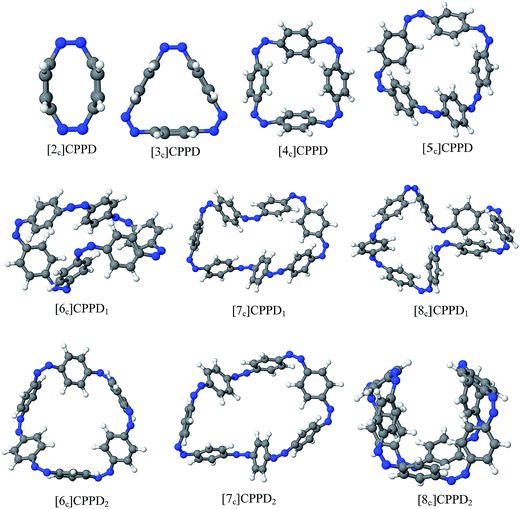
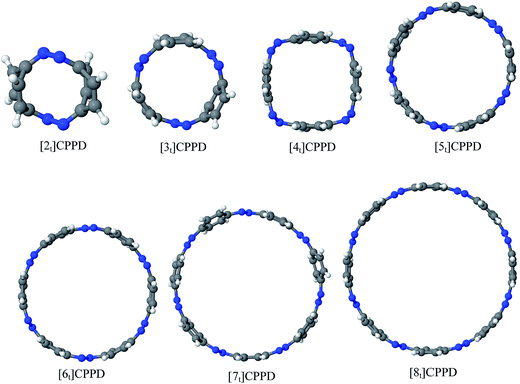
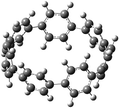
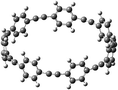
Before discussing thermochemistry and electronic properties, it is necessary to examine the molecular geometries of CPPDs, since they are closely related to physical and chemical properties. Structure of all cis-[nc]CPPDs (n = 2 to 8) and all trans-[nt]CPPDs (n = 2 to 8) were optimized using at B3LYP/6-31+G(d,p) level of theory. Optimized structures of all cis and all trans-CPPDs are shown in Fig. 2 and 3, respectively. To find out the different conformations of all trans-CPPDs and all cis-CPPDs, we have carried out many geometry optimizations. For example, in the case of all trans-[6t]CPPD, we started different orientation of phenyl group in [6t]CPPD and in all cases, we have obtained a stable circular structure as shown in the ESI Fig. S1.† Therefore, we believe that the possibilities of other stable structures are negligible for all trans-CPPDs. However, in case of all-cis CPPDs, we have found the different conformation of [6c]CPPD, [7c]CPPD, and [8c]CPPD as shown in the Fig. 2. The mix combination of cis and trans isomers may be important and but is not the focused of the current study. In previous reports, researchers have shown the importance all cis and trans isomers of CPPDs.19,26 For example; Durgun and Grossman have shown the photoisomerization of all cis and all trans isomers of OH-substituted 3-azobenzenophanes and 4-AB azobenzenophanes.19 In another study, Yuan et al.26 have predicted the host–guest interaction between only all trans-[6]CPPD and all-trans-[7]CPPD with fullerene (C60). In the present study, we focused only on all cis and all trans form of [n]CPPDs, but in future, we plan to examine combination of cis and trans isomers of [n]CPPDs.ESI Table S5† lists some selected bond lengths and bond angles of [nc]CPPDs (n = 2 to 8) and [nt]CPPDs (n = 2 to 8) at the B3LYP/6-31+G(d,p). This table also includes the calculated bond lengths and bond angles of reference compounds i.e., cis and trans 1,4-bis(diazenyl)benzene (bDB), and cis and trans azobenzene (AB) and experimentally reported value for AB.50 The C–N and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond distance and bond angle in [2c]CPPD and [3c]CPPD are quantitatively similar to bDB and AB. These values are in very good agreement with reported experimental values.50 The CNNC angles of [2t]CPPD (∼85.6°), [3t]CPPD (104.9°) and [4t]CPPD (134.9°) are smaller than strain free bDB and trans AB (∼180°). The higher deviation of angle shows maximum angle strain in the trans CPPDs series (Table S5†). As shown in the Table S5,† large bond distortion and dihedral angle of [2t]CPPD, [3t]CPPD, and [4t]CPPD may destabilize the structures through maximizing the molecular strain energy. The C–N and N
N bond distance and bond angle in [2c]CPPD and [3c]CPPD are quantitatively similar to bDB and AB. These values are in very good agreement with reported experimental values.50 The CNNC angles of [2t]CPPD (∼85.6°), [3t]CPPD (104.9°) and [4t]CPPD (134.9°) are smaller than strain free bDB and trans AB (∼180°). The higher deviation of angle shows maximum angle strain in the trans CPPDs series (Table S5†). As shown in the Table S5,† large bond distortion and dihedral angle of [2t]CPPD, [3t]CPPD, and [4t]CPPD may destabilize the structures through maximizing the molecular strain energy. The C–N and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond lengths and C–N
N bond lengths and C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond angle of cis-[4c]CPPD are different from its trans-[4t]CPPD isomers. This is due to the fact that cis isomer was found to be a stable boat form and trans isomer was found as a ring type structure (Fig. 2 and 3). The bond length and bond angle of higher members show a little variation compared to those cis–trans bDBs and cis–trans ABs. The dihedral angle of trans-[n]CPPDs (n = 4 to 8) approaches ∼180° as the number of n increases, which may stabilize the structures. The calculated values of cis and trans isomers of AB are also in very good agreement with reported experimental values.50 The point group symmetry of [n]CPPDs (n = 2 to 8) has been listed in Table S5.† The point group symmetry of [2c]CPPD is D2h which is similar to the point group symmetry of highly strained cyclic[2]paraphenyleneacetylenes ([2]CPPA) in the [n]CPPAs series. However, the point group symmetry of [2t]CPPD is C2h. The point group symmetry of [3c]CPPD (Cs) and [3t]CPPD (C2) is different from [3]CPPA (D3h). The generalized point group for the higher member of trans-[n]CPPDs (n > 3) is Dn. The point group of all cis isomers varies as n increases (Table S5†). The predicted point group symmetry of cis and trans isomers of CPPDs are different from its analogous oligomer i.e., cyclicparaphenyleneacetylenes (CPPAs) and cycloparaphenylenes (CPPs).21–24
N bond angle of cis-[4c]CPPD are different from its trans-[4t]CPPD isomers. This is due to the fact that cis isomer was found to be a stable boat form and trans isomer was found as a ring type structure (Fig. 2 and 3). The bond length and bond angle of higher members show a little variation compared to those cis–trans bDBs and cis–trans ABs. The dihedral angle of trans-[n]CPPDs (n = 4 to 8) approaches ∼180° as the number of n increases, which may stabilize the structures. The calculated values of cis and trans isomers of AB are also in very good agreement with reported experimental values.50 The point group symmetry of [n]CPPDs (n = 2 to 8) has been listed in Table S5.† The point group symmetry of [2c]CPPD is D2h which is similar to the point group symmetry of highly strained cyclic[2]paraphenyleneacetylenes ([2]CPPA) in the [n]CPPAs series. However, the point group symmetry of [2t]CPPD is C2h. The point group symmetry of [3c]CPPD (Cs) and [3t]CPPD (C2) is different from [3]CPPA (D3h). The generalized point group for the higher member of trans-[n]CPPDs (n > 3) is Dn. The point group of all cis isomers varies as n increases (Table S5†). The predicted point group symmetry of cis and trans isomers of CPPDs are different from its analogous oligomer i.e., cyclicparaphenyleneacetylenes (CPPAs) and cycloparaphenylenes (CPPs).21–24
3.2 Reaction energies
Before considering ring systems, we first calculated ΔE (at 0 K), ΔH (at 298 K), and ΔG (at 298 K) for the cis → trans photo isomerization of open azobenzene (AB) and 1,4-bis(diazenyl)benzene (bDB) using G4 method (Fig. 4). The trans isomer of AB is found to be more stable than cis isomer of AB by ∼46.1 kJ mol−1, which is in good agreement with reported experimental value (48.5 kJ mol−1). The G4 enthalpy (46.1 kJ mol−1) were also compared with theoretically calculated value (55.9 kJ mol−1) by Durgun and Grossmann.19 Their calculated value (8–9 kJ mol−1) using hybrid DFT functional is higher than that of our calculated value (46.1 kJ mol−1) and experimentally reported one (48.5 kJ mol−1). In case of bDB, cis → trans photo isomerization is (∼41 kJ mol−1), this value is ∼5 kJ mol−1 lower than AB.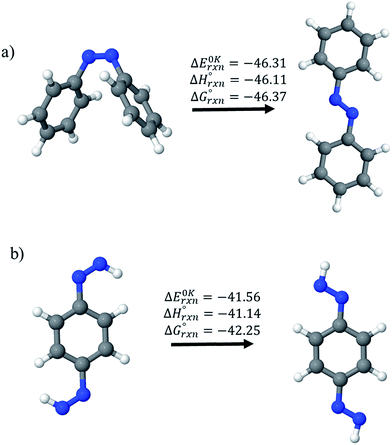 | ||
| Fig. 4 Enthalpies of reaction (at 0 K and 298 K) and Gibbs free energies (at 298 K) of cis → trans isomerization of (a) azobenzene and (b) 1,4-bis(diazenyl)benzene computed using G4 method. | ||
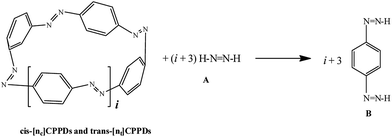
AB has most often served as a model system for the study of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N based cis and trans isomerization in CPPDs, because it absorbs light and experimentally convenient to study. Therefore, we believe that CPPDs, which contain 2 to 7 azobenzene units have been of interest in studying the steric distortion on the photochemical cis and trans isomerization. Because strain-free oligomers of CPPDs have not been reported so far, we have applied two different hypothetical homodesmotic reaction Scheme 1 (based on Ali and Krishnan study),21 and Scheme 2 (based on Segwa et al.),24 to calculate the strain energies (SE) of CPPDs.
N based cis and trans isomerization in CPPDs, because it absorbs light and experimentally convenient to study. Therefore, we believe that CPPDs, which contain 2 to 7 azobenzene units have been of interest in studying the steric distortion on the photochemical cis and trans isomerization. Because strain-free oligomers of CPPDs have not been reported so far, we have applied two different hypothetical homodesmotic reaction Scheme 1 (based on Ali and Krishnan study),21 and Scheme 2 (based on Segwa et al.),24 to calculate the strain energies (SE) of CPPDs. 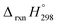 calculated using both schemes are shown in Fig. 5 and tabulated in Table 1. The
calculated using both schemes are shown in Fig. 5 and tabulated in Table 1. The 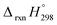 of both schemes is lower for smaller members and increases as the number of Ph–N
of both schemes is lower for smaller members and increases as the number of Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N linkages increase. The bar diagram (Fig. 5) shows that
N linkages increase. The bar diagram (Fig. 5) shows that 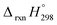 of Scheme 1 is lower than Scheme 2, indicating HD Scheme 1 has less error compared to HD Scheme 2.
of Scheme 1 is lower than Scheme 2, indicating HD Scheme 1 has less error compared to HD Scheme 2.
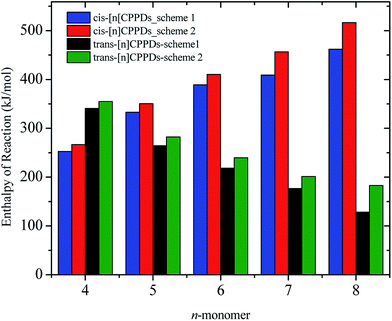 | ||
| Fig. 5 Enthalpies of reaction calculated using Schemes 1 and 2. Only stable conformation of all cis of [nc]CPPDs (n = 6 to 8) are shown. | ||
| Homodesmotic reaction schemes | |||||
|---|---|---|---|---|---|
| All-cis CPPDs | ΔHrxn298 | SE | All-trans CPPDs | ΔHrxn298 | SE |
a ΔHrxn298 and SE calculated based on Scheme 1.b ΔHrxn298 and SE calculated based on Scheme 2.c Calculated using B3LYP/6-31G(d) level. A: HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH; B: HN NH; B: HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Ph–N N–Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH; C: Ph–N NH; C: Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Ph; D: Ph–N N–Ph; D: Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Ph–N N–Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Ph; Ph: phenyl ring,1,2 different conformation of cis-CPPD. N–Ph; Ph: phenyl ring,1,2 different conformation of cis-CPPD. |
|||||
| [2c]CPPD + 2A → 2Ba | −353.3 | 351.5 | [2t]CPPD + 2A → 2Ba | −403.3 | 401.8 |
| [2c]CPPD + 2C → 2Db | −360.4 | 364.6 | [2t]CPPD + 2C → 2Db | −410.5 | 414.9 |
| [3c]CPPD + 3A → 3Ba | −230.6 | 226.3 | [3t]CPPD + 3A → 3Ba | −299.4 | 295.7 |
| [3c]CPPD + 3C → 3Db | −241.3 | 246.0 | [3t]CPPD + 3C → 3Db | −310.1 | 315.4 |
| [4c]CPPD + 4A → 4Ba | −252.5 | 245.8 | [4t]CPPD + 4A → 4Ba | −340.9 | 334.7 |
| [4c]CPPD + 4C → 4Db | −266.8 | 272.0 | [4t]CPPD + 4C → 4Db | −355.2 | 361.0 |
| [5c]CPPD + 5A → 5Ba | −332.7 | 323.3 | [5t]CPPD + 5A → 5Ba | −264.5 | 255.6 |
| [5c]CPPD + 5C → 5Db | −350.5 | 356.0 | [5t]CPPD + 5C → 5Db | −282.3 | 288.4 |
| 1[6c]CPPD1 + 6A → 6Ba | −401.0 | 388.9 | [6t]CPPD + 6A → 6Ba | −218.5 | 206.4 |
| 2[6c]CPPD2 + 6A → 6Ba | −389.0 | 377.1 | |||
| 1[6c]CPPD1 + 6C → 6Db | −422.4 | 428.2 | [6t]CPPD + 6C → 6Db | −239.9 | 245.7 |
| 2[6c]CPPD2 + 6C → 6Db | −410.4 | 416.5 | |||
| 1[7c]CPPD1 + 7A → 7Ba | −408.9 | 394.1 | [7t]CPPD + 7A → 7Bb | −176.5 | 161.8 |
| 2[7c]CPPD2 + 7A → 7Ba | −420.6 | 405.5 | |||
| 1[7c]CPPD1 + 7C → 7Da | −456.6 | 679.1 | [7t]CPPD + 7C → 7Da | −201.4 | 207.7 |
| 2[7c]CPPD2 + 7C → 7Da | −468.2 | 690.6 | |||
| 1[8c]CPPD1 + 8A → 8Ba,c | −463.1 | 445.7 | [8t]CPPD + 8A → 8Bb,c | −128.4 | 110.0 |
| 2[8c]CPPD2 + 8A → 8Ba,c | −462.0 | 445.6 | |||
| 1[8c]CPPD1 + 8C → 8Da,c | −517.6 | 771.4 | [8t]CPPD + 8C → 8Da,c | −182.9 | 435.8 |
| 2[8c]CPPD2 + 8C → 8Da,c | −516.5 | 771.4 | |||
The SE at 0 K (i.e., with the zero-point correction included) for the all cis and all trans isomer of [n]CPPDs (n = 2 to 8) were calculated using both schemes are listed in Table 1. The difference in SE using Schemes 1 and 2 for lower members are smaller. However, for the higher member of CPPDs these values are larger. The SE of [2c]CPPD and [2t]CPPD has the highest SE in [nc]CPPDs (n < 5) series, and [nt]CPPD series, respectively. This is mostly due to its distorted sp2–sp2–sp2 angle (117.2°) in [2c]CPPD and (85.6°) [2t]CPPD. The SE of [nc]CPPDs (n = 5 to 8) is higher than all trans-[nt]CPPDs (n = 5 to 8), which may be attributed to the higher dihedral angle of cis isomer than that of trans isomer (Table S5†). The SE of all cis isomer increases linearly with adding each Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. The SE of trans isomer decreases linearly with increasing Ph–N
N unit. The SE of trans isomer decreases linearly with increasing Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. The higher SE of [8c]CPPD, [7c]CPPD, [2t]CPPD, [6c]CPPD, [2c]CPPD, [3t]CPPD, [4t]CPPD, and [5c]CPPD may not favour their synthesis. However, the lower SE of [4c]CPPD, [3c]CPPD, [5t]CPPD, [6t]CPPD, [7t]CPPD, and [8t]CPPD may favour the synthesis of these molecules.
N unit. The higher SE of [8c]CPPD, [7c]CPPD, [2t]CPPD, [6c]CPPD, [2c]CPPD, [3t]CPPD, [4t]CPPD, and [5c]CPPD may not favour their synthesis. However, the lower SE of [4c]CPPD, [3c]CPPD, [5t]CPPD, [6t]CPPD, [7t]CPPD, and [8t]CPPD may favour the synthesis of these molecules.
Fig. 6 details the thermodynamic stability i.e., enthalpies and Gibbs free energies of [nc]CPPDs and [nt]CPPDs (n = 4 to 8) and isolated AB and bDB. Positive values of ΔHrxn0 K and 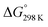 indicate all the cis-CPPDs is more stable, whereas negative values indicate all trans-CPPDs are more stable. In all cases (n = 5 to 8), trans isomers are more stable than cis isomers, however, for n = 4, cis isomer is more stable than the trans isomer. This is due to the fact that [4c]CPPD is less strained compared to [4t]CPPD (see Fig. 2 and Table S5†). The computed ZPE, thermal correction (HT), and entropy of all cis and all trans isomers are in tabulated in the ESI (Table S6†). The ΔZPE, ΔHT, and ΔS of cis → trans transformation isomers are very small. The relatively smaller value of ΔS can be explained by assuming that the isomerization of cis-CPPDs or trans-CPPDs can start from a structure that has the smaller degree of freedom because of the strain caused by a cyclic structure.
indicate all the cis-CPPDs is more stable, whereas negative values indicate all trans-CPPDs are more stable. In all cases (n = 5 to 8), trans isomers are more stable than cis isomers, however, for n = 4, cis isomer is more stable than the trans isomer. This is due to the fact that [4c]CPPD is less strained compared to [4t]CPPD (see Fig. 2 and Table S5†). The computed ZPE, thermal correction (HT), and entropy of all cis and all trans isomers are in tabulated in the ESI (Table S6†). The ΔZPE, ΔHT, and ΔS of cis → trans transformation isomers are very small. The relatively smaller value of ΔS can be explained by assuming that the isomerization of cis-CPPDs or trans-CPPDs can start from a structure that has the smaller degree of freedom because of the strain caused by a cyclic structure.
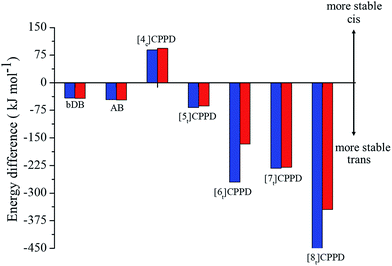 | ||
Fig. 6 Enthalpy difference (ΔHrxn0 K) and Gibbs free energy  change between cis and trans isomers. Blue line corresponds to ΔHrxn0 K and red line corresponds to change between cis and trans isomers. Blue line corresponds to ΔHrxn0 K and red line corresponds to  . . | ||
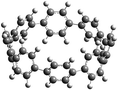
The calculated SE of [n]CPPDs (n = 4 to 8) are compared with previously calculated SE of [n]CPPs and [n]CPPAs (n = 4 to 8) as shown in Fig. 7. The SE of [nt]CPPDs decreases with increasing Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N units, which is consistent with [n]CPPAs (strain energies decreases linearly as Ph–C
N units, which is consistent with [n]CPPAs (strain energies decreases linearly as Ph–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) and CPPs (SE decreases linearly as Ph– unit increases). The SE of [4c]CPPD, [5c]CPPD, and [6c]CPPD are lower than that of [4]CPP, [5]CPP, and [6]CPP respectively. The SE value for [7c]CPPD and [8c]CPPD are higher than that of respective [7]CPP and [8]CPP. This effect is due to the twisted structure, which imposes higher dihedral angle in the higher member of CPPDs. If we compare the SE of trans isomer of CPPDs with CPPAs and CPPs, the order of SE of these oligomer are [n]CPPs > [nt]CPPDs > [n]CPPAs (n = 4 to 7).
C) and CPPs (SE decreases linearly as Ph– unit increases). The SE of [4c]CPPD, [5c]CPPD, and [6c]CPPD are lower than that of [4]CPP, [5]CPP, and [6]CPP respectively. The SE value for [7c]CPPD and [8c]CPPD are higher than that of respective [7]CPP and [8]CPP. This effect is due to the twisted structure, which imposes higher dihedral angle in the higher member of CPPDs. If we compare the SE of trans isomer of CPPDs with CPPAs and CPPs, the order of SE of these oligomer are [n]CPPs > [nt]CPPDs > [n]CPPAs (n = 4 to 7).
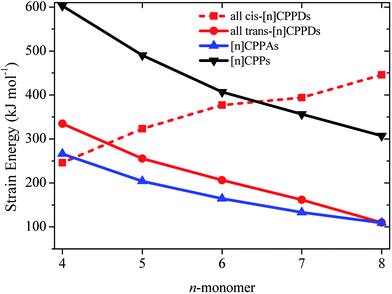 | ||
| Fig. 7 Comparison of SE calculated using homodesmotic Scheme 1 for [n]CPPDs (n = 4 to 8) and the SE value of [n]CPPAs (n = 4 to 8)21 and [n]CPPs (n = 4 to 8).23,24 | ||
SE is a good indicator in the feasibility of synthesis process. Some of the carbon nanoring structure i.e., [5]CPP (490.5 kJ mol−1), [6]CPP (406.8 kJ mol−1), [7]CPP (356.5 kJ mol−1), [8]CPP (307.1 kJ mol−1), [9]CPP (274.5 kJ mol−1), [12]CPP (201.3 kJ mol−1), [18]CPP (132.6 kJ mol−1), [6]CPPA (164.4 kJ mol−1), [7]CPPA (133.3 kJ mol−1), and [8]CPPA (109.4 kJ mol−1) have already been synthesized by various research groups.22,23,51–53 Therefore, we believe the same synthetic strategies may also be applied for the synthesis of all cis and all trans isomers of CPPDs with lower SE values.
The standard enthalpies of formation 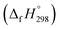 is a fundamental quantity in the estimation of the energy stored in [n]CPPDs (n = 2 to 8).
is a fundamental quantity in the estimation of the energy stored in [n]CPPDs (n = 2 to 8). 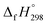 is calculated using the combination of homodesmotic reactions (Schemes 3a and b). The
is calculated using the combination of homodesmotic reactions (Schemes 3a and b). The 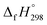 of cis and trans isomers of CPPDs are shown in Table 2. The experimental
of cis and trans isomers of CPPDs are shown in Table 2. The experimental 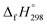 of 1,4-bis(diazenyl)benzene (bDB) is unknown. Therefore, our calculation of
of 1,4-bis(diazenyl)benzene (bDB) is unknown. Therefore, our calculation of 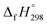 of bDB is based on another homodesmotic approach (Scheme 3b). The
of bDB is based on another homodesmotic approach (Scheme 3b). The 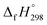 of bDB is calculated using high-level quantum composite Gaussian-4 method.49 The experimental gas-phase
of bDB is calculated using high-level quantum composite Gaussian-4 method.49 The experimental gas-phase 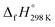 of benzene (82.8 kJ mol−1)54 and ethylene (20.4 kJ mol−1) is used to obtain the value of bDB (522.9 kJ mol−1). However, the experimental
of benzene (82.8 kJ mol−1)54 and ethylene (20.4 kJ mol−1) is used to obtain the value of bDB (522.9 kJ mol−1). However, the experimental 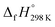 of reference HN
of reference HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH
NCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 is not known. Therefore, our calculation of
CH2 is not known. Therefore, our calculation of 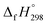 for HN
for HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH
NCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 is based on another hypothetical isodesmic reaction (HN
CH2 is based on another hypothetical isodesmic reaction (HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH
NCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 + CH4 → H3CN
CH2 + CH4 → H3CN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH + C2H4). The experimental
NH + C2H4). The experimental 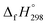 for CH3N
for CH3N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH is taken from Matus et al. study55 for the calculation of
NH is taken from Matus et al. study55 for the calculation of 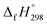 for HN
for HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH
NCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2. The calculated
CH2. The calculated 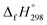 of HNNCH
of HNNCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 using isodesmic reaction approach is 266.8 kJ mol−1. The
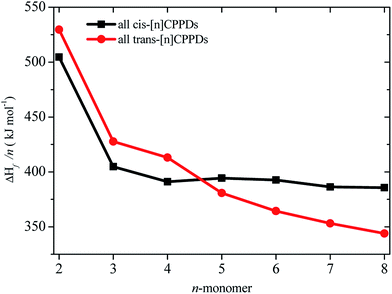
CH2 using isodesmic reaction approach is 266.8 kJ mol−1. The 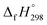 per-unit monomer of all cis and all trans isomers of [n]CPPDs (n = 2 to 8) are shown in Fig. 8. The
per-unit monomer of all cis and all trans isomers of [n]CPPDs (n = 2 to 8) are shown in Fig. 8. The 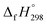 per-unit monomer of all cis isomer is higher than that of all trans isomers indicating the higher strain and less stable compared to trans isomers. The
per-unit monomer of all cis isomer is higher than that of all trans isomers indicating the higher strain and less stable compared to trans isomers. The 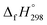 per-unit monomer of cis isomer reaches to the plateau for n = 7 and 8. However, for the trans isomer
per-unit monomer of cis isomer reaches to the plateau for n = 7 and 8. However, for the trans isomer 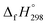 per-unit monomer decreases linearly. We have also calculated energy difference between
per-unit monomer decreases linearly. We have also calculated energy difference between 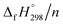 – SE/n for [n]CPPDs (Table 2). The average
– SE/n for [n]CPPDs (Table 2). The average 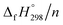 – SE/n value for all cis and all trans-[n]CPPDs is ∼330 kJ mol−1. This value is very close to
– SE/n value for all cis and all trans-[n]CPPDs is ∼330 kJ mol−1. This value is very close to 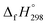 of strain free Ph–N
of strain free Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–H (334 kJ mol−1).
N–H (334 kJ mol−1).
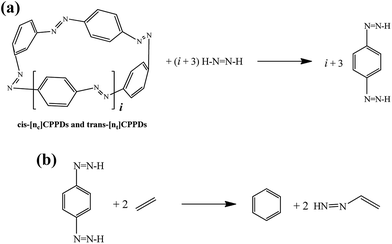 | ||
Scheme 3 Hypothetical homodesmotic reactions for the calculation of 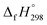 of all cis and all trans-[n]CPPDs. of all cis and all trans-[n]CPPDs. | ||
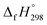 (kJ mol−1),
(kJ mol−1), 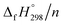 – SE/n (kJ mol−1) and enthalpies of combustion (kJ mol−1) for [n]CPPDs (n = 2 to 8)
– SE/n (kJ mol−1) and enthalpies of combustion (kJ mol−1) for [n]CPPDs (n = 2 to 8)
| [n]CPPDs | – SE/n | a | b | |
|---|---|---|---|---|
| a A generalised combustion reaction of [n]CPPDs: [n]CPPDs + 7nO2 → 6nCO2 + 2nH2O + nN2.b Molar enthalpy of combustion (in kJ g−1). | ||||
| [2c]CPPD | 1009 | 328.8 | −6698.1 | −32.2b |
| [2t]CPPD | 1059.1 | 328.7 | −7722.6 | −37.1 |
| [3c]CPPD | 1214.3 | 329.6 | −9747.9 | −31.2 |
| [3t]CPPD | 1283.1 | 320.1 | −10794.6 | −34.6 |
| [4c]CPPD | 1564.1 | 329.6 | −12942.2 | −31.1 |
| [4t]CPPD | 1652.5 | 329.4 | −13044.8 | −31.3 |
| [5c]CPPD | 1972.2 | 329.8 | −16194.7 | −31.1 |
| [5t]CPPD | 1904.0 | 329.7 | −16144.3 | −31.0 |
| [6c]CPPD1 | 2368.4 | 329.9 | −19435.5 | −31.1 |
| [6c]CPPD2 | 2356.4 | 329.9 | −19423.4 | −31.1 |
| [6t]CPPD | 2185.9 | 329.9 | −19274.3 | −30.8 |
| [7c]CPPD1 | 2704.2 | 330.0 | −22615.7 | −31.1 |
| [7c]CPPD2 | 2715.9 | 330.1 | −22627.4 | −31.1 |
| [7t]CPPD | 2471.8 | 330.0 | −22408.3 | −30.7 |
| [8c]CPPD1 | 3086.3 | 330.1 | −25842.4 | −31.0 |
| [8c]CPPD2 | 3085.2 | 330.0 | −25841.3 | −31.0 |
| [8t]CPPD | 2751.6 | 330.2 | −25562.1 | −30.6 |
Table 2 also contains the enthalpies of combustion 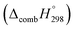 and molar enthalpy of combustion. It can be seen that absolute value for CPPDs is ∼−(30–32) kJ g−1 indicating the release a large amount of energy during the combustion of CPPDs. Moreover, the replacement of N
and molar enthalpy of combustion. It can be seen that absolute value for CPPDs is ∼−(30–32) kJ g−1 indicating the release a large amount of energy during the combustion of CPPDs. Moreover, the replacement of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond by C
N bond by C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond in CPPDs results in increasing the C atoms, leading to a relatively higher absolute value of
C bond in CPPDs results in increasing the C atoms, leading to a relatively higher absolute value of 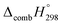 for CPPAs. This indicates that C atoms contribute ∼8–9 kJ g−1 energy through the formation of carbon dioxide during combustion, which can explain the higher
for CPPAs. This indicates that C atoms contribute ∼8–9 kJ g−1 energy through the formation of carbon dioxide during combustion, which can explain the higher 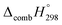 of CPPAs than that of CPPDs.
of CPPAs than that of CPPDs.
3.3 Electronic properties of [n]CPPDs
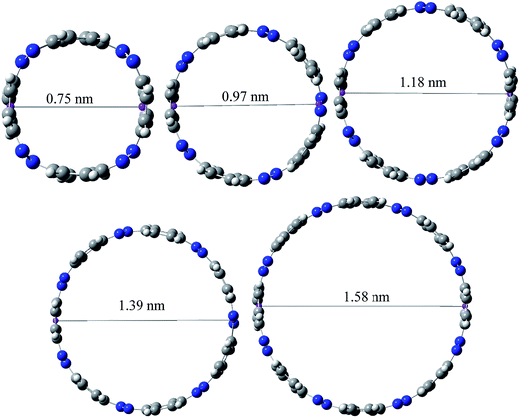
Ring diameter is good indicator of host–guest chemistry26 of [n]CPPDs and it is estimated as the distance between the centres of mass of the opposite benzene ring for the even member of all trans CPPDs i.e., [4t]CPPD, [6t]CPPD, and [8t]CPPD and the distance between the nitrogen atom and the center of mass of the opposite benzene ring for the odd number of trans CPPDs i.e., [5t]CPPD and [7t]CPPD (see Fig. 9). As expected, when azo groups are all in trans configuration, the nanorings are in open state in which the cavities are available and when the azo groups are all in cis forms, they are in the closed state in which the cavities are deformed or collapsed. The cavity diameter (Dn) from [4t]CPPD to [8t]CPPD evolves linearly with increasing phenylenediazene units (n); for example, the B3LY/6-31+G(d,p) results can be described by equation (the regression coefficient is 0.99968)| Dn (nm) = −0.074 + n × 0.208. |
The trend of ring diameters is similar to SE of [nt]CPPDs (n = 4 to 8). When the size of the system increases, SE decreasing with increasing the ring diameter. The calculated ring diameter of [6t]CPPDs (1.18 nm) and [7t]CPPDs (1.39 nm) are also in very good agreement with the values reported by Yuan et al.26 for [6t]CPPD (1.19 nm) and [7t]CPPD (∼1.39 nm) calculated using M06-2X/6-31G(d) level of theory. Moreover, comparing the diameter of [nt]CPPDs (n = 4 to 8) with their analogous [n]CPPAs (n = 4 to 8) and [n]CPPs (n = 4 to 8) nanorings (ESI Table S7†). The values of [nt]CPPDs (n = 4 to 8) are lower than those of corresponding [n]CPPAs and [n]CPPs.
The cavity size of [6t]CPPD (1.18 nm) is almost comparable to that of (1.01 nm) carbon nanotube, and it appears to be suitable for the inclusion of C60 (0.7 nm in diameter). In the previous study, Zhao and Truhlar56 have calculated the interaction energies of guest molecules such as three arm-chair-type nanotubes; (3, 3), (4, 4), and (5, 5) with the host molecules such as [6]CPPA, (3,3) [6]CPPA, (4,4) [6]CPPA, and (5,5) [6]CPPA using the density functional theory. In another study, Bachrach and Zayat57 have calculated binding free energies of host [14]CPP and guest molecule [n]CPP (n = 6 to 10), [14]CPP [6]CPP, [14]CPP [7]CPP, [14]CPP [7]CPP, [14]CPP [8]CPP, [14]CPP [9]CPP, and [14]CPP [10]CPP using ωB97X-D/6-31G(d) level calculation. In 2015, Yuan et al.26 have predicted the host–guest interaction between [6]CPPD nanoring with C60. Recently, Lee et al.58 have synthesized [3]CPP C70 and [3]CPPA C70 and calculated cavity diameter using B3LYP/6-31G(d) level of theory. A similar approach can be applied to design host–guest systems with host CPPDs and guest molecules such as C60, C70, (3,3), (4,4) and (5,5), CPPs, and CPPAs to understand the chemical and electronic properties.
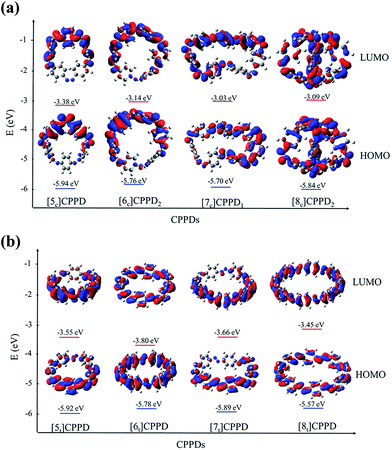
Molecular orbital is an important parameter, which can provide useful information on the electronic structure and a decisive factor indicating potential material for the construction of solar cells. The calculated highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO) are provided in ESI Table S7† and their spatial distribution are shown in Fig. 10. The HOMO and LUMO of [6c]CPPD1, [6t]CPPD, and [8t]CPPD show the uniform orbital density located at all atoms in the skeleton, whereas the HOMO and LUMO of [5c]CPPD, [6c]CPPD2, [5t]CPPD, and [7c]CPPD1, [7t]CPPD have non-uniform orbital density on Ph–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. The HOMO and LUMO levels of [5t]CPPD and [7t]CPPD are 2-fold degenerate, which indicate that the removal of an electron from the HOMO level or addition of an electron to the LUMO level could weaken the skeleton framework.59 The values of HOMOs and LUMOs of the odd trans-CPPDs are higher than that of even trans-CPPDs. However, the odd-even trend was not observed in cis-CPPDs. This is probably due to conformational differences of the odd and even CPPDs as described above. The spatial distribution of HOMO–LUMO gap for CPPDs were also compared with CPPs and CPPAs. As for CPPDs, the HOMO and LUMO distribution are quite different from CPPAs and CPPs.
N unit. The HOMO and LUMO levels of [5t]CPPD and [7t]CPPD are 2-fold degenerate, which indicate that the removal of an electron from the HOMO level or addition of an electron to the LUMO level could weaken the skeleton framework.59 The values of HOMOs and LUMOs of the odd trans-CPPDs are higher than that of even trans-CPPDs. However, the odd-even trend was not observed in cis-CPPDs. This is probably due to conformational differences of the odd and even CPPDs as described above. The spatial distribution of HOMO–LUMO gap for CPPDs were also compared with CPPs and CPPAs. As for CPPDs, the HOMO and LUMO distribution are quite different from CPPAs and CPPs.
Table S7† also includes the HOMO–LUMO gap values for CPPAs and CPPs. The HOMO–LUMO gap of CPPDs is in between 1.98 and 2.85 eV, for CPPAs (2.99 to 3.05 eV) and for CPPs (2.55–3.41 eV). The predicted HOMO–LUMO gap of all cis-CPPDs and all trans CPPDs have smaller values than that of CPPAs and CPPs. Our calculations also suggest that adding nitrogen atoms in CPPs decreases the HOMO–LUMO gap, which is in consistent with the data reported by Van Raden et al.,27 who have also predicted the decreasing value of HOMO–LUMO gap of nitrogen doped CPP i.e., azo[6]CPP. The predicted HOMO–LUMO gap of CPPDs are in the range of the material used in the construction of solar cells. The results suggest that CPPDs oligomer are better candidate for building solar cells than CPPAs and CPPs.
3.4 Comparison of CPPDs with carbon nanorings (CNRs)
The structure, electronic properties, and thermochemistry of all trans-[n]CPPDs (n = 6 to 8) were compared with its analogous carbon nanoring structure i.e., [n]CPPs and [n]CPPAs (n = 6 to 8) are given in Table 3. Results indicate that nitrogen substituted cyclic para phenyl oligomer have higher strain energies compared to acetylene substituted cyclic paraphenyl oligomer. However, strain energies of CPPs are higher than the strain energies of CPPAs and CPPDs. The ring diameter of all three species are also correlated with molecular strain. The lower value of diameter of nanoring has higher strain energies and higher value of diameter has lower strain energies. The HOMO–LUMO gap of these nanorings suggests that CPPDs could be the good material for the construction of solar cells. In addition, it may be possible to design host–guest systems with hosts; [6]CPPD, [7]CPPD, and [8]CPPD with guest molecules; C60, C70, CPPs (3,3), (4,4) and (5,5), CPPAs and carbon nanotubes to understand their chemistry. The predicted structure, SE, and electronic properties of CPPDs with carbon nanoring structure (CPAs and CPPAs) (Table 3), suggest that [6t]CPPD, [7t]CPPD, and [8t]CPPD can be synthesized in the laboratory.4. Conclusions
We have provided the theoretical calculation related to the structure, strain energies (SE), standard enthalpies of formation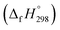 , and electronic properties of the novel structures of all cis and all trans isomers of [n]CPPDs (n = 2 to 8). The calculations of SE and
, and electronic properties of the novel structures of all cis and all trans isomers of [n]CPPDs (n = 2 to 8). The calculations of SE and 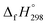 are based on homodesmotic reaction approach and B3LYP hybrid DFT method with 6-31+G(d,p) basis set. The SE and ring diameter of CPPDs indicate [6t]CPPD, [7t]CPPD, and [8t]CPPD are the ideal molecules for the future experimental study. The unique behaviour of HOMO and LUMO of CPPDs compared to CPPAs and CPPs opens a new possibility of CPPDs for applications in optoelectronics. The trends observed for ring systems presented here are not just limited to CPPDs but rather applicable to a wide range of photo convertible molecules. Our campaign toward the design of mix combination of CPPDs is underway and will be reported in future. We believe that the ring effect uncovered in this study may find uses in the emerging field of organic electronics. The present study should help us not only to plan a new synthetic strategy but also to understand the structural, electronic, physical properties, and the host-guest chemistry of other nitrogen doped cyclic oligomer.
are based on homodesmotic reaction approach and B3LYP hybrid DFT method with 6-31+G(d,p) basis set. The SE and ring diameter of CPPDs indicate [6t]CPPD, [7t]CPPD, and [8t]CPPD are the ideal molecules for the future experimental study. The unique behaviour of HOMO and LUMO of CPPDs compared to CPPAs and CPPs opens a new possibility of CPPDs for applications in optoelectronics. The trends observed for ring systems presented here are not just limited to CPPDs but rather applicable to a wide range of photo convertible molecules. Our campaign toward the design of mix combination of CPPDs is underway and will be reported in future. We believe that the ring effect uncovered in this study may find uses in the emerging field of organic electronics. The present study should help us not only to plan a new synthetic strategy but also to understand the structural, electronic, physical properties, and the host-guest chemistry of other nitrogen doped cyclic oligomer.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Author gratefully acknowledge the computational resources at KISTI super computer facility in the South Korea. MAA thanks Sejong University Seoul for the research support. MAA thanks Professor John R. Barker from University of Michigan for useful suggestions. We thank the anonymous reviewers for helpful suggestions, including the suggestion to find out other conformations of cis and trans-CPPDs. M. A. Alam thanks, ABI-A-State (Grant number: Start-up 200127) for supporting.References
- C. Pu, D. Zhou, Y. Li, H. Liu, Z. Chen, Y. Wang and Y. Ma, J. Phys. Chem. C, 2017, 121, 2669–2674 CAS.
- Y. Liu, A. Singharoy, C. G. Mayne, A. Sengupta, K. Raghavachari, K. Schulten and A. H. Flood, J. Am. Chem. Soc., 2016, 138, 4843–4851 CrossRef CAS PubMed.
- X. Wang, X. Li, L. Zhang, Y. Yoon, P. K. Weber, H. Wang, J. Guo and H. Dai, Science, 2009, 324, 768–771 CrossRef CAS PubMed.
- T. Cui, R. Lv, Z.-H. Huang, H. Zhu, J. Zhang, Z. Li, Y. Jia, F. Kang, K. Wang and D. Wu, Carbon, 2011, 49, 5022–5028 CrossRef CAS.
- L. Qu, Y. Liu, J. B. Baek and L. Dai, ACS Nano, 2010, 4, 1321–1326 CrossRef CAS PubMed.
- A. L. M. Reddy, A. Srivastava, S. R. Gowda, H. Gullapalli, M. Dubey and P. M. Ajayan, ACS Nano, 2010, 4, 6337–6342 CrossRef CAS PubMed.
- W. R. Browne and B. L. Feringa, Nat. Nanotechnol., 2006, 1, 25–35 CrossRef CAS PubMed.
- T. Hugel, N. B. Holland, A. Cattani, L. Moroder, M. Seitz and H. E. Gaub, Science, 2002, 296, 1103–1106 CrossRef PubMed.
- H. M. Jeong, J. W. Lee, W. H. Shin, Y. J. Choi, H. J. Shin, J. K. Kang and J. W. Choi, Nano Lett., 2011, 11, 2472–2477 CrossRef CAS PubMed.
- A. Khan, C. Kaiser and S. Hecht, Angew. Chem., Int. Ed., 2006, 45, 1878–1881 CrossRef CAS PubMed.
- K. K. Cotí, M. E. Belowich, M. Liong, M. W. Ambrogio, Y. A. Lau, H. A. Khatib, J. I. Zink, N. M. Khashab and J. F. Stoddart, Nanoscale, 2009, 1, 16–39 RSC.
- Y. Yang, R. P. Hughes and I. Aprahamian, J. Am. Chem. Soc., 2014, 136, 13190–13193 CrossRef CAS PubMed.
- W. A. Velema, W. Szymanski and B. L. Feringa, J. Am. Chem. Soc., 2014, 136, 2178–2191 CrossRef CAS PubMed.
- D. Hoersch, S.-H. Roh, W. Chiu and T. Kortemme, Nat. Nanotechnol., 2013, 8, 928–932 CrossRef CAS PubMed.
- J. E. Koskela, V. Liljeström, J. Lim, E. E. Simanek and R. H. Ras, J. Am. Chem. Soc., 2014, 136, 6850–6853 CrossRef CAS PubMed.
- Y. Norikane, K. Kitamoto and N. Tamaoki, J. Org. Chem., 2003, 68, 8291–8304 CrossRef CAS PubMed.
- S. A. Nagamani, Y. Norikane and N. Tamaoki, J. Org. Chem., 2005, 70, 9304–9313 CrossRef CAS PubMed.
- H. Rau and E. Lueddecke, J. Am. Chem. Soc., 1982, 104, 1616–1620 CrossRef CAS.
- E. Durgun and J. C. Grossman, J. Phys. Chem. Lett., 2013, 4, 854–860 CrossRef CAS PubMed.
- J. Olmsted III, J. Lawrence and G. G. Yee, Sol. Energy, 1983, 30, 271–274 CrossRef.
- M. A. Ali and M. S. Krishnan, Mol. Phys., 2009, 107, 2149–2158 CrossRef CAS.
- T. Kawase and H. Kurata, Chem. Rev., 2006, 106, 5250–5273 CrossRef CAS PubMed.
- E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410 RSC.
- Y. Segawa, H. Omachi and K. Itami, Org. Lett., 2010, 12, 2262–2266 CrossRef CAS PubMed.
- S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304 RSC.
- K. Yuan, J.-S. Dang, Y.-J. Guo and X. Zhao, J. Comput. Chem., 2015, 36, 518–528 CrossRef CAS PubMed.
- J. M. Van Raden, E. R. Darzi, L. N. Zakharov and R. Jasti, Org. Biomol. Chem., 2016, 14, 5721–5727 CAS.
- A. von Baeyer, Ber. Dtsch. Chem. Ges., 1885, 18, 2278 Search PubMed.
- F. Klappenberger, Y.-Q. Zhang, J. Bjork, S. Klyatskaya, M. Ruben and J. V. Barth, Acc. Chem. Res., 2015, 48, 2140–2150 CrossRef CAS PubMed.
- F. H. Westheimer, Special Publication No. 8, The Chemical Society, London, 1957, p. 1 Search PubMed.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120, 4450–4458 CrossRef CAS.
- W. J. Hehre, R. Ditchfield, L. Radom and J. A. Pople, J. Am. Chem. Soc., 1970, 92, 4796–4801 CrossRef CAS.
- O. V. Dorofeeva and O. N. Ryzhova, J. Phys. Chem. A, 2016, 120, 2471–2479 CrossRef CAS PubMed.
- P. Wessig, M. Czarnecki, D. Badetko, U. Schilde and A. Kelling, J. Org. Chem., 2016, 81, 9147–9157 CrossRef CAS PubMed.
- R. V. Williams, A. G. Al-Sehemi, A. K. Meier, Z. Z. Brown and J. R. Armantrout, J. Org. Chem., 2017, 82, 4136–4147 CrossRef CAS PubMed.
- R. Notario, M. V. Roux and O. Castano, Phys. Chem. Chem. Phys., 2011, 3, 3717–3721 RSC.
- N. Sebbar, H. Bockhorn and J. W. Bozzelli, Phys. Chem. Chem. Phys., 2002, 4, 3691–3703 RSC.
- R. O. Ramabhadran and K. Raghavachari, Acc. Chem. Res., 2014, 47, 3596–3604 CrossRef CAS PubMed.
- S. E. Wheeler, K. N. Houk, P. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560 CrossRef CAS PubMed.
- M. A. Ali and M. S. Krishnan, J. Org. Chem., 2010, 75, 5797–5809 CrossRef CAS PubMed.
- P. Nava and Y. Carissan, Phys. Chem. Chem. Phys., 2014, 16, 16196–16203 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. Moral, A. Pérez-Guardiola, E. San-Fabián, A. J. Pérez-Jiménez and J. C. Sancho-García, J. Phys. Chem. C, 2016, 120, 22069–22078 CAS.
- M. R. Golder, C. E. Colwell, B. M. Wong, L. N. Zakharov, J. Zhen and R. Jasti, J. Am. Chem. Soc., 2016, 138, 6577–6582 CrossRef CAS PubMed.
- D. Vijay, E. Varathan and V. Subramanian, J. Mater. Chem. A, 2013, 1, 4358–4369 CAS.
- M. A. Ali and S. Sen, Thermochim. Acta, 2017, 654, 146–156 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- J. A. Bouwstra, A. Schouten and J. Kroon, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1121–1123 CrossRef.
- Y. Segawa, A. Fukazawa, S. Matsuura, H. Omachi, S. Yamaguchi, S. Irle and K. Itami, Org. Biomol. Chem., 2012, 10, 5979–5984 CAS.
- T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361 CrossRef CAS PubMed.
- E. Kayahara, V. K. Patel and S. Yamago, J. Am. Chem. Soc., 2014, 136, 2284–2287 CrossRef CAS PubMed.
- H. Y. Afeefy, J. F. Liebman and S. E. Stein, MD, 2017, http://webbook.nist.gov, retrieved 03.28.2017.
- M. H. Matus, A. J. Arduengo III and D. A. Dixon, J. Phys. Chem. A, 2006, 110, 10116–10121 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Am. Chem. Soc., 2007, 129, 8440–8442 CrossRef CAS PubMed.
- S. M. Bachrach and Z. C. Zayat, J. Org. Chem., 2016, 81, 4559–4565 CrossRef CAS PubMed.
- S. Lee, E. Chénard, D. L. Gray and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 13814–13817 CrossRef CAS PubMed.
- C. Shen, P. Wang and M. Lu, J. Phys. Chem. A, 2015, 119, 8250–8255 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables of optimized geometries, vibrational frequencies, ZPEs, thermal correction, entropy for CPPDs. Table of ring diameter of CPPDs, CPPAs, and CPPs and figures showing HOMO, LUMO and HOMO–LUMO gap of CPPDs. See DOI: 10.1039/c7ra06409h |
| This journal is © The Royal Society of Chemistry 2017 |