Open Access Article
Open Access ArticleArtificial neural network analysis of the catalytic efficiency of platinum nanoparticles†
Michael Fernandez *,
Hector Barron and
Amanda S. Barnard
*,
Hector Barron and
Amanda S. Barnard
Molecular and Materials Modelling, Data61 CSIRO, Door 34 Goods Shed, Village St, Docklands, VIC 3008, Australia. E-mail: michael.fernandezllamosa@data61.csiro.au
First published on 17th October 2017
Abstract
Even using high throughput methods, data-driven predictions of nanomaterials properties from first principles simulations can be impractical. In this work, machine learning models are developed to map the catalytic efficiency of Pt nanocrystals to structural features, such as nanoparticle diameter, surface area, sphericity, facet configuration and type of surface defects, using a theoretically derived big data set of over three hundred thousand nanoparticles. Artificial Neural Networks (ANNs) were calibrated with 50% of a data set including structural features of symmetric Pt nanoparticles; and catalytic activity, selectivity and thermodynamic stability. Surface response analysis was applied to two-inputs ANNs with squared correlation coefficient > 0.9, yielding a region of optimal catalytic efficiency for the less spherical nanocatalysts and {110} facets lower than 20%. Binary decision tree models reveal the optimal three-property combinations for high catalytic efficiency. In addition, ANN models built for non-symmetric nanoparticles predict the catalytic efficiency and stability with accuracy >0.93. In general, we show the combination of machine learning models can rapidly estimate functional properties of hypothetical nanomaterials at a resolution that is inaccessible to both computation and experimental methods, as well as identifying principles or rules that could guide rational nanomaterial design in the near future.
1 Introduction
The move from nanoscience to nanotechnology is underpinned by a detailed and reliable understanding of structure–property relationships, but this can be extremely difficult to obtain due to the lack of systematic experimental data correlating nanomaterial structure and performance. In turn, high-throughput (HT) computer simulations of virtual nanomaterial libraries provide an alternative to explore how structural diversity can affect nanomaterial behaviour. HT computational characterization of relevant nanomaterials using proven computational methods such as density functional theory (DFT) have been reported on multicomponent crystals1–3 and alloys,4 lithium-based batteries,5–7 optically-active organic molecules,8 photovoltaic materials,9 graphene nanoflakes10 and metal–organic frameworks (MOFs).11 However, electronic structure stimulations can be computationally costly, and subject to numerous practical limitations that inhibit their widespread use in big data studies.For example, an extensive computational screening of surface structures for new nanocatalysts has been performed for the methanation reaction,12 but the computational cost of the electronic structure calculations using DFT was a bottleneck that limited the number of data points to only a few dozen. This problem is not unique to metallic nanoparticles, but is particularly poignant in cases (such as these) where the wide variety of shapes, facets, and fraction of different types of surface atoms, directly impact the catalytic efficiency in organic and inorganic reactions. An alternative approach aimed at reducing the computational load was proposed by Barnard et al.13 This study demonstrated how restricting the diversity of the ensemble can be used to improve or retard the catalytic performance, while avoiding computationally intense electronic structure calculations. Taking this type of theoretical screening analysis even further to identify correlations that underpin these relationships using more sophisticated statistical and data mining techniques would be advantageous in many ways, the most obvious of which is the speed at which predictions could be made to guide more detailed analyses. However, an entirely theoretical data set will only be useful if each unique configuration can be represented by a set of structural features14 which can be used to measure similarity among individual nanoparticles or to build predictive machine learning (ML) models,15 and systematically relate the structural features of samples to their functional properties in quantitative terms. It has been well established that ML can produce parametric functions of structural features capable of yielding accurate predictions of functional properties of different nanoparticle10 and nanoporous16,17 systems without the requirement of any atomistic simulations, but in these cases the atomistic structure was explicitly defined. To the best of our knowledge the ability of simple structural features that pertaining the nanoparticle as a whole (i.e. diameter, surface area, sphericity and facet configuration) to predict the catalytic efficiency of nanoparticles remains unknown.
In this paper, we investigate the correlations between structural features of a theoretical data set of 8517 Pt nanoparticles and the molar catalytic activity, selectivity and thermodynamic stability. Using decision tree (DT) regression and artificial neural networks (ANNs) we explore the most significant combinations of only two or three features that impact catalytic efficiency. In addition, when all features are simultaneously used to train ANNs models, we obtain outstandingly accurate predictions of how these nanoparticles could be engineered. The effect of the temperature in the catalytic efficiency is also accurately predicted for more than 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples by adding an additional input neuron to the network architecture. As we will show, this approach of mapping the performance of nanoparticles into its feature space identifies significant structure–function relationship principles, while yielding efficient predict models that can be developed with minimal (or no) reliance on high performance supercomputers.
000 samples by adding an additional input neuron to the network architecture. As we will show, this approach of mapping the performance of nanoparticles into its feature space identifies significant structure–function relationship principles, while yielding efficient predict models that can be developed with minimal (or no) reliance on high performance supercomputers.
2 Data preparation and computational methods
2.1 Pt nanoparticle data set
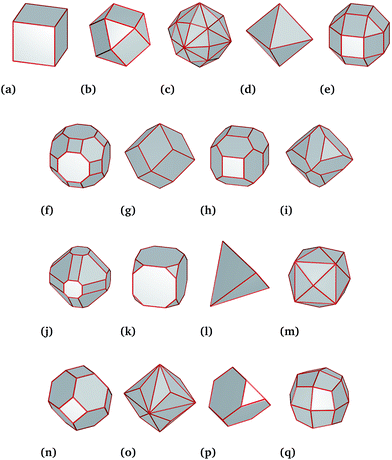
For this work, we generated a theoretical data set of 8517 Pt nanoparticles spanning a large range of diameters from 3 nm to 100 nm and including a diverse mixture of shapes consistent with experimental observations18–20 (Fig. 1). Theoretical predictions of the molar catalytic activity and stability were generated in a temperature range from 0 °C to 200 °C. The molar catalytic activity was obtained by using a surface coordination number (SCN) classification scheme published elsewhere.13,21 In that study the SCN is linked to functional similarities in the nanoparticles. Under this scheme all Pt atoms with SCN of 1, 2 or 3 are classified as “surface defects” (where adatoms are placed on “top”, “bridge” and “hollow” sites); atoms with SCN of 4, 5, 6 or 7 are termed “surface microstructures” (corresponding to kinks/steps-like features); and atoms with SCN of 8, 9, 10 or 11 are termed “surface facets” (corresponding to surface-like features that includes any planar configuration). The coordination number of Pt atom in the bulk is 12. Each of these groups are linked to a specific catalytic reaction,22–27 where the total number of atoms in the surface is defined as the number of atoms with SCN less than that of the bulk. For example, facet-driven catalytic activity is suitable for hydrogenation reactions, whilst nanoparticles with microstructure-driven activity are more efficient to catalyse combustion reactions.22–27 Therefore, a theoretical hydrogenation/combustion selectivity can be defined as the ratio between facet-driven catalytic activity and microstructure-driven catalytic activity.While the SCN provides specific details of the local disorder and faceting, a more global measure of “sphericity” provides valuable information of the structural features of the particles as a whole. We define this term as the shape surface-to-volume ratio divided by the surface-to-volume ratio of a sphere of equivalent volume.
The molar thermodynamic stability was derived from a shape-dependent thermodynamic model for nanostructures reported in ref. 28 and 29. It is based on a summation of the Gibbs free energy Gx(T) of a nanoparticle of material in phase x, and includes contributions from the bulk and surface of the structure, as well as from the edges and the corners. This approach was extended to include planar defects such as twin planes or stacking faults:
| Gx(T) = Gbulkx(T) + Gsurfacex(T) + Gedgex(T) + Gcornerx(T) + Gpdx(T) + … | (1) |
Each structure in the data set is unique and was characterised by the set of structural features in Table 1. From this point on, using this data set, all manipulation, pre-processing, calibration, testing and analysis of machine learning models was done in Python programming language.
| Variable | Structural feature |
|---|---|
| D | Spherically averaged particle diameter (nm) |
| NPt | Number of Pt atoms |
| A | Molar surface area (m2 mol−1) |
| S | Sphericity |
| f111 | Fractional area associated with {111} facets |
| f110 | Fractional area associated with {110} facets |
| f100 | Fractional area associated with {100} facets |
| f331 | Fractional area associated with {331} facets |
| f210 | Fractional area associated with {210} facets |
| f113 | Fractional area associated with {113} facets |
| f123 | Fractional area associated with {123} facets |
| Surface defects | Atoms with surface coordination number 1, 2 and 3 |
| Surface microstructures | Atoms with surface coordination number 4, 5, 6 or 7 |
| Surface facets | Atoms with surface coordination number 8, 9, 10 or 11 |
| Nsurface | Total surface sites |
| ΔG | Free energy (kJ mol−1) |
| X | Total molar activity (site per mol) |
| Y | Hydrogenation/combustion selectivity |
2.2 Machine learning modeling
To correlate the stability and catalytic activity, we used correlation techniques, that includes multiple linear regression (MLR), decision tree (DT)30 and artificial neural networks (ANNs).31 Decision trees are binary rule-based modeling technique that typically uses an attribute selection search to construct binary rules of different combinations of attributes. Our decision tree model approximates the stability and catalytic activity of the metallic nanoparticles as rudimentary decision rules based on the values of a number of attributes, with the number and specific types of attributes varying to suit the needs of the task. Despite their simplicity, decision trees have been shown to yield accurate predictions with the added value of ease interpretation given the number of rules are not very large.30 In this case the catalytic activity, hydrogenation/combustion selectivity and the thermodynamic stability of the metallic nanoparticles are approximated as simple combination of three binary rules since too many rules would compromise the interpretation of the tree model. DTs were implemented using the scikit-learn machine learning library in Python programming language.32ANNs are computer-based models in which a number of processing elements, also called neurons, units or nodes are interconnected by links in a net-like structure forming “layers”,31 that can approximate any nonlinear relationship, according to Kolmogorov's theorem.33 In back-propagation ANNs, a variable value is assigned to every neuron, which can be one of three different kinds. The input neurons form the input layer, which are directly assigned and are associated with independent variables, with the exception of the bias neuron. The hidden neurons collect values from the input neurons, giving a result that is passed to a non-input neuron. Finally, the output neurons collect values from other units and correspond to different dependent variables, forming the output layer. The links between units have associated values, known as weights that condition the values assigned to the neurons. There exist additional weights assigned to bias values that act as neuron value offsets. The weights are adjusted through a training process in order to minimize network error. Commonly neural networks are adjusted, or trained, so that a particular input leads to a specific target output. The ANNs models of the catalytic activity, selectivity and the stability of Pt nanocatalysts were implemented in Python programming language using the FANN package.34
3 Results and discussion
A quick inspection of the generated data set reveals that catalytic activity, hydrogenation/combustion selectivity and the thermodynamic stability strongly depend on the configuration of the nanoparticle facets, with the most catalytically active facets ({111}, {110} and {100}) also corresponding to the more selective and stable configurations according to our thermodynamic model. However, small nanoparticles with large surface area per mole of Pt atoms (>10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m2 mol−1) are the most catalytically active but display the lowest selectivity and thermodynamic stability (see Fig. S1 in the ESI†). This suggests that more than one structural feature needs to be simultaneously controlled to activate high performance nanocatalysts.
000 m2 mol−1) are the most catalytically active but display the lowest selectivity and thermodynamic stability (see Fig. S1 in the ESI†). This suggests that more than one structural feature needs to be simultaneously controlled to activate high performance nanocatalysts.
To identify the best correlation models of the stability, catalytic activity and selectivity, we explored different machine learning techniques. Learning curves of the regression models, as described by Hansen et al.,35 appear in Fig. S2 in the ESI,† which includes mean predictor (meanp), multilinear regression (MLR), ridge regression (Ridge), decision tree regression along with ANNs. As described in ref. 35, the lower prediction errors of the ANN models, suggest that optimum regressions can be achieved when training ANNs with structural features of 50% of data set, whilst the remaining 50% is used to test the prediction ability of the models (see ESI† for details). Readers will note from the ESI† that learning curves generated from 0.1–0.9 fractions of data are flat because the models learn very quickly from very few examples, meaning that this type of data set is easy to approximate using a nonlinear predictor because it was artificially generated from an analytic expression without noise (as is expected from this type of theoretical data set). This is an advantage of using theoretical data, provided it is well tested. One should not be confused by small variations in RMSE in the learning curves; these are not relevant in this case, since the correlations are already on the order of 0.95 to 0.99. We can see that over-fitting has been avoided because the R2 of the training, cross-validation and test sets are very high and similar.
3.1 Two-inputs artificial neural networks (ANNs) models of the catalytic efficiency of symmetric Pt nanoparticles
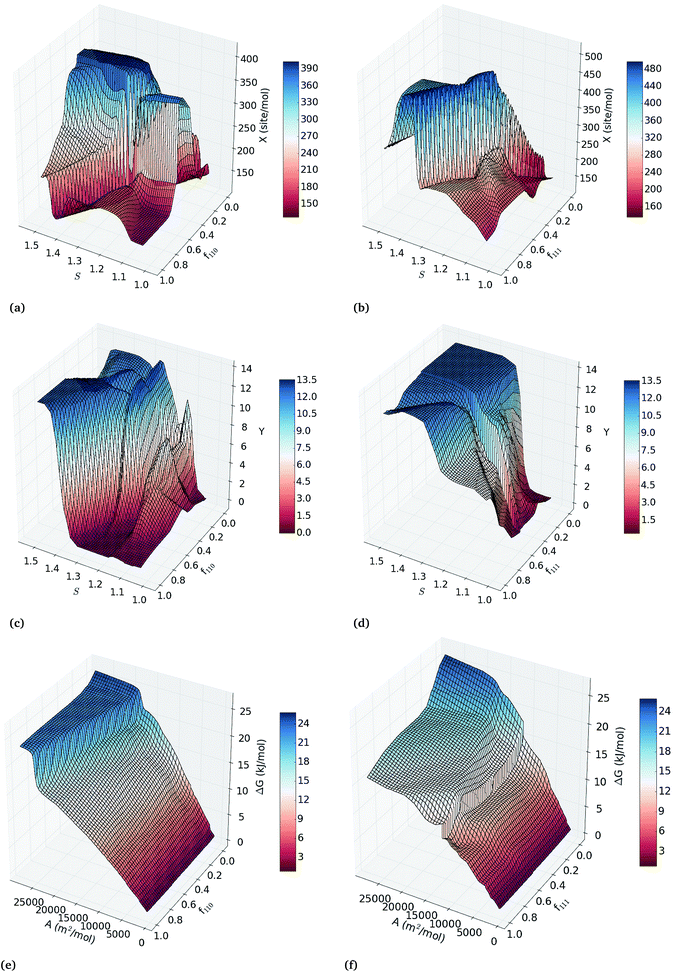
To explore all binary correlation patterns across the entire range of nanoparticle sizes, shapes and surface defects, we use two-inputs ANN models. Each pair of structural features was used as inputs of back-propagated ANN models for the calibration of regression models of the catalytic activity, hydrogenation/combustion selectivity and thermodynamic stability of the Pt nanocatalysts. The efficacy of each combination of two variables to describe these properties is depicted in Fig. S4 in the ESI† as heatmaps of the squared correlation coefficient of three-fold-out cross-validation (RTFO2) of the two-inputs ANN models. Combining sphericity with fraction of {111} facets, {110} facets or molar surface area, exhibits the highest correlations with the catalytic activity and selectivity (RTFO2 > 0.92); whereas the correlations for thermodynamic stability are higher than 0.9 for all the variable pairs that include the diameter or molar surface area. This fact confirms that simultaneously controlling the overall shape and size of the nanoparticles, without directly constraining the facet configuration, can improve catalytic efficiency. This prediction supports the experimental evidence that the tunability of the catalytic properties depends on the full control over the nanoparticle size and morphology.36–38The two-inputs ANN models that predict catalytic activity, hydrogenation/combustion selectivity and the stability of Pt nanocatalysts with high accuracy represent robust parametric functions of these properties. These models can be used to further explore the response surfaces of these properties within the variables ranges in the data set (see ESI† for details). Fig. 2(a–d) depicts the response surface analysis of the two-inputs ANN models of sphericity and fraction of {110} facets; and sphericity and fraction of {111} facets. In general, the response surfaces in Fig. 2 depicts both maximum catalytic activity and hydrogenation/combustion selectivity for the less spherical Pt nanocatalysts with low and high fractions of {110} and {111} facets, respectively, with the exception of the least spherical nanoparticles (S > 1.4) that display very high hydrogenation/combustion selectivity regardless of the facet configuration. This result suggests that optimal catalytic efficiency occurs for less spherical nanoparticles, where the contributions of more edges and corners can compensate each other. As it can be expected, Fig. 2(e) and (f) illustrates that nanoparticles with smaller molar surface area (the larger particles) are more stable regardless of their facet configuration, where high fraction of active {111} facets contributes to lower the ΔG values increasing the stability.
3.2 Multiple linear regression models of the catalytic efficiency of symmetric Pt nanoparticles
The response surface analysis of the two-inputs ANN modes provides valuable insights into the mutual correlations of structural features and the catalytic efficiency and stability of the Pt nanoparticles. However, this analysis can overlook relevant interactions between more than two variables, which could be essential for a more comprehensive understanding of Pt nanoparticle structure–property relationships.MLR analysis is a convenient approach to correlate structure and properties due to its easy implementation and straightforward interpretation. MLR models of the catalytic efficient of symmetric Pt nanoparticles trained with the variables in Table 1 appear in eqn (2)–(4).
| ΔG = 2.473 + 2.523 × 10−2 × D − 4.012 × 10−8 × NPt + 1.058 × 10−3 × A − 7.463 × 10−1 × S − 1.390 × f111 + 6.108 × 10−2 × f110 + 3.686 × 10−2 × f100 + 7.644 × 10−1 × f331 + 1.339 × f210 + 9.321 × 10−1 × f113 + 7.306 × 10−1 × f123 − 2.615 × 10−4 × surface defects − 1.781 × 10−6 × surface microstructures + 1.021 × 10−8 × surface facets + 4.712 × 10−7 × Nsurface, | (2) |
| X = −110.510 + 7.203 × 10−1 × D − 3.362 × 10−6 × NPt + 7.116 × 10−3 × A + 2.347 × 102 × S + 2.868 × 101 × f111 − 3.562 × 101 × f110 + 1.024 × 101 × f100 + 9.098 × f331 − 5.235 × 10−1 × f210 − 4.379 × 10−1 × f113 − 2.677 × 10−1 × f123 + 2.451 × 10−3 × surface defects − 9.723 × 10−6 × surface microstructures + 7.302 × 10−6 × surface facets + 8.394 × 10−6 × Nsurface, | (3) |
| Y = −20.961 − 1.883 × 10−2 × D + 2.812 × 10−7 × NPt − 2.178 × 10−4 × A − 2.542 × 10−1 × S − 3.900 × 10−1 × f111 − 5.280 × f110 + 5.948 × 10−1 × f100 − 4.210 × f331 − 4.612 × f210 − 3.774 × f113 − 3.289 × f123 − 2.568 × 10−4 × surface defects + 7.762 × 10−6 × surface microstructures − 1.683 × 10−6 × surface facets + 8.814 × 10−7 × Nsurface, | (4) |
In each case R2, RTFO2 and RTest2 are square Pearson's correlation coefficient of the training, three-fold-out cross-validation and test set predictions, respectively, with corresponding standard deviation values σ, σTFO and σTest, whilst N and NTest are the number of structures used for training and testing the models, respectively. These amenable linear combinations of structural features provide good prediction accuracies and are also interesting mathematical expressions due to their simplicity and easy application.
3.3 Decision tree models of the catalytic efficiency of symmetric Pt nanoparticles
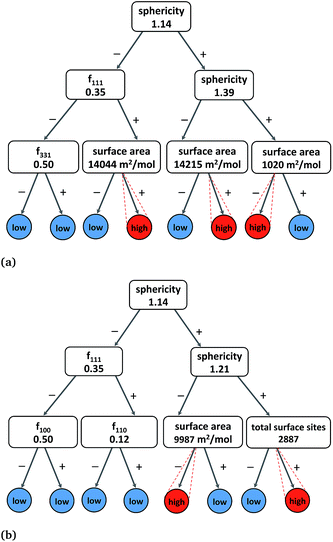
In addition to MLR models, simple binary rules (e.g., fraction of {111} facets must be greater than 0.5), such as in DT30 predictions, can provide reliable information on how Pt nanocatalysts exhibit a desired range of catalytic activity, selectivity and stability. In comparison to multiple decision levels, three rules yield more practical models at the expense of lower accuracy but are more amenable to interpretation.Therefore, we built three-levels DT models of the molar catalytic activity, hydrogenation/combustion selectivity and stability using all the structural features, and produced a satisfactory cross-validation correlation accuracies of ∼0.93. Fig. 3(a) depicts the binary decision tree graph with the “rules-of-thumb” principles to exhibit high catalytic activity that include sphericity, surface and the fraction of {111} facets. We found two combinations of two-rules and one combination of three-rules that characterize high catalytic activity as it is indicated by the similar high values in the lowest branches in Fig. 3(a). Therefore, the “rules-of-thumb” for high catalytic activity values are to have sphericity lower than 1.39 (morphologies different from tetrahedron and truncated tetrahedron) and surface area higher than 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 m2 mol−1 (D > 10 nm); or sphericity higher than 1.39 and surface area lower than 1020 m2 mol−1 (D < 60 nm). In addition, another more specific rule suggests that nanoparticles with higher degree of sphericity (S < 1.14 and octahedron morphologies) can also be catalytically active given that the molar surface area is higher than 14
215 m2 mol−1 (D > 10 nm); or sphericity higher than 1.39 and surface area lower than 1020 m2 mol−1 (D < 60 nm). In addition, another more specific rule suggests that nanoparticles with higher degree of sphericity (S < 1.14 and octahedron morphologies) can also be catalytically active given that the molar surface area is higher than 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044 m2 mol−1 (D > 10 nm) and, more importantly, the fraction of {111} facets higher than 0.35 (no cubic nanoparticles).
044 m2 mol−1 (D > 10 nm) and, more importantly, the fraction of {111} facets higher than 0.35 (no cubic nanoparticles).
In the case of hydrogenation/combustion selectivity, Fig. 3(b) depicts a binary decision tree with “rules-of-thumb” principles that include sphericity, surface area and the total number of surface sites or dangling bonds. We found two combinations of two-rules that characterize nanoparticles with selectivity of approximately or higher than 10, which would guarantee a 10-fold product enrichment, in the lowest branches in Fig. 3(b). One “rule-of-thumb” characterises less spherical nanoparticles (S > 1.21) with an average of more than 2900 surface sites, whilst another rule accounts for more spherical nanoparticles (S < 1.21) but with average molar surface area of less than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m2 mol−1 (D < 10 nm). Interestingly, both rules corroborate that nanoparticles with diameter higher than 7 nm exhibit high selectivity. The DT analysis clearly illustrate a trade-off between activity and selectivity that usually govern the selection of an efficient catalysts for a given chemical reaction, i.e. hydrogenation or combustion.
000 m2 mol−1 (D < 10 nm). Interestingly, both rules corroborate that nanoparticles with diameter higher than 7 nm exhibit high selectivity. The DT analysis clearly illustrate a trade-off between activity and selectivity that usually govern the selection of an efficient catalysts for a given chemical reaction, i.e. hydrogenation or combustion.
The DT analysis yields a simpler model of molar stability with only one fundamental rule accounting for the low thermodynamic stability of nanoparticles with less than 9000 total atoms in the surface (D < 5 nm) (see Fig. S4 in the ESI†). Owing to the fact that the total number of atoms in the surface (SCN < 12) is the result of the combination of the nanoparticle size, shape and facet configuration, this rule illustrates a consolidated structural requirement for stable nanocatalysts, that implicitly considers the geometrical constrains resulting in the subsequent formation of active facets and its contributions to the overall particle-free energy according to the thermodynamic model.
3.4 ANN models of the catalytic efficiency of symmetric Pt nanoparticles
In addition to providing useful insights into the intrinsic structural–property relationship of Pt nanocatalyst systems, machine learning models can yield accurate predictive models of the molar catalytic activity, selectivity and stability. For this purpose, we implemented back-propagated ANNs that are suitable for data processing, in which the functional relationship between the inputs variables is complex and the output is not previously defined. ANNs are able to approximate any kind of analytical continuous function, as complex structure–property relationships, by adding sufficient processing units or neurons. Back-propagated ANNs were designed with one input layer of 15 neurons fully connected to one hidden layer with variable number of neuron that transmitted the signal to the single neuron in the one output layer. The learning curves in Fig. S2 of the ESI† showed optimum training set size of 50% of the data set. Therefore, ANNs are trained with the structural features of 50% of the data set, while the remaining 50% was used to test the predictive power of the neural networks.The optimum ANN regressions were selected based on cross-validation accuracy using early stopping criteria (see ESI† for details). Table 2 shows the details and statistics of the optimum ANNs of molar catalytic activity, selectivity and stability, which outclass MLR models with extremely high accuracies of ∼0.99 using 20, 20 and 30 neurons in the hidden layer, respectively. In addition to the molar thermodynamic stability at 25 °C, we also trained ANNs to predict the stability of the Pt nanoparticles at different temperatures, by adding an extra input neuron to the network architecture. For training these ANNs the data set was extended to include the molar free energy (ΔG in kJ mol−1) at temperature values in the range from 0 °C to 200 °C and a temperature increment of 5 °C. In this case the calibration was performed with ∼10% of the extended data set of 349![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 for a total of 34
197 for a total of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 training samples that combine structural features and temperature values. Table 2 shows that an optimum ANN model of more complex architecture with 40 hidden neurons is capable of handling the influence of temperature on the thermodynamic stability with extremely high accuracy ∼0.99.
919 training samples that combine structural features and temperature values. Table 2 shows that an optimum ANN model of more complex architecture with 40 hidden neurons is capable of handling the influence of temperature on the thermodynamic stability with extremely high accuracy ∼0.99.
| Property | Training set size | Parametersb | RTFO2a | RTest2a |
|---|---|---|---|---|
| a Square Pearson's correlation coefficient of the training set cross-validation and test set prediction.b e, h and α are the number of epochs, hidden neurons and weighting smoothing parameters of the ANN model, respectively. | ||||
| X | 4258 | h = 20, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.996 | 0.993 |
| Y | 4258 | h = 20, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.996 | 0.999 |
| ΔG at 25 °C | 4258 | h = 30, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.993 | 0.999 |
| ΔG from 0 °C to 200 °C | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
h = 40, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.996 | 0.999 |
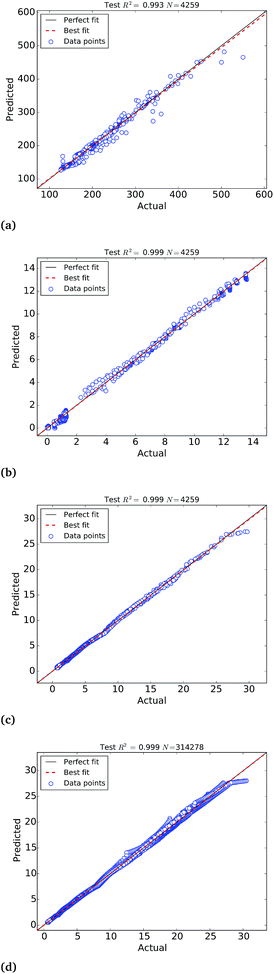
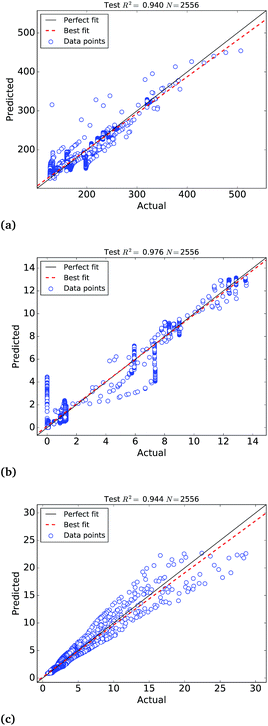
The calibration of the ANNs yielded outstanding accuracies but the predictions need further evaluation on an external test set of samples not used to calibrate the models. For this purpose, we have selected a test set of 4259 Pt nanoparticles that were not used to calibrate the machine learning models of the molar catalytic activity and stability at 25 °C. The scatter plots of the predicted values in this test set are depicted in Fig. 4, where “actual” refers to the values calculated theoretically and “predicted” corresponds to the ANNs predictions, as highlighted in Table 2. In addition to this we use a test set of 314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 samples to test the larger ANN model of stability at different temperatures that also yields extremely high R2 ∼ 0.999. Fig. 4(c) depicts the scatter plots of the predictions, where it can be observed that the ANN model successfully approximate the molar stability in the entire temperature range, with the exception of the highest free energy values that are slightly underestimated by the models. In order to improve the fitting of large free energy values, we added extra neurons to the hidden layer but this caused overfitting of the ANN model. It is worth mentioning that, in addition to the good approximation provided by ANNs, the theoretical nature and the completeness of the big data set also contribute to the exceptionally high correlation coefficients.
278 samples to test the larger ANN model of stability at different temperatures that also yields extremely high R2 ∼ 0.999. Fig. 4(c) depicts the scatter plots of the predictions, where it can be observed that the ANN model successfully approximate the molar stability in the entire temperature range, with the exception of the highest free energy values that are slightly underestimated by the models. In order to improve the fitting of large free energy values, we added extra neurons to the hidden layer but this caused overfitting of the ANN model. It is worth mentioning that, in addition to the good approximation provided by ANNs, the theoretical nature and the completeness of the big data set also contribute to the exceptionally high correlation coefficients.
3.5 Application of ANNs models to predict the catalytic efficiency of non-symmetric Pt nanoparticles
ANN models in Table 2 were trained with numerically derived catalytic activities, selectivity and stability of a theoretical data set of symmetric Pt nanoparticles. However, these models use facet configuration information, which may not be available for non-symmetric nanoparticles. Therefore, by training new ANNs without facet configuration inputs we build structure–efficiency relationship models suitable to predict catalytic efficiency and stability of more complex non-symmetric nanoparticles.The optimum ANN regressions of non-symmetric nanoparticles appear in Table 3, where models are less accurate than in Table 2. In this case, the scatter plots of the predicted values of the test set depicted in Fig. 5, also exhibit larger errors in comparison to the ANNs for symmetric Pt nanoparticles in Fig. 4. However, the agreeable correlation coefficient scores higher than 0.93 reveal that accurate predictions can also be made without detailed characterisation of the facet configurations.
| Property | Training set size | Parametersb | RTFO2a | RTest2a |
|---|---|---|---|---|
| a Square Pearson's correlation coefficient of the training set cross-validation and test set prediction.b e, h and α are the number of epochs, hidden neurons and weighting smoothing parameters of the ANN model, respectively. | ||||
| X | 4258 | h = 10, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.937 | 0.937 |
| Y | 4258 | h = 10, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.971 | 0.976 |
| ΔG at 25 °C | 4258 | h = 10, e = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, α = 0.25 000, α = 0.25 |
0.940 | 0.947 |
The new ANN models were applied to predict the catalytic efficiency and stability of an external dataset of 521 non-symmetric Pt nanoparticles generated by molecular dynamics simulations as described elsewhere.39 The tri-dimensional structures of the nanoparticles with the highest catalytic activity, selectivity and thermodynamic stability according to ANN predictions appear in Fig. 6. As we can observed, lower coordinated atoms are localised on the tips and edges while higher coordinated atoms occupy planar areas over the surface. The nanoparticle with 662 atoms exhibits high catalytic activity that is linked to a highly irregular morphology, where low coordinates sites can be noticeable (atoms in red in Fig. 6). The nanoparticle with 1554 atoms has localised atomic distribution of atoms with SCN of 8, 9, 10 and 11 (atoms in blue Fig. 6) covering larger extensions on the surface. Meanwhile, lower coordinated atoms can not be distinguished and atoms with SCN of 4, 5, 6 and 7 that appear in green in Fig. 6 are randomly distributed forming “chains”. These structural features enhance the selectivity through surface microstructure defects. The rise of surface defects and the subsequent development of surface facets increases the thermodynamic stability of the nanoparticles with 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 atoms in Fig. 6, where regardless the sphericity of the structure, we can observe “patches” of SCN of 8, 9, 10 and 11; and SCN of 4, 5, 6 and 7; and developed facets.
600 atoms in Fig. 6, where regardless the sphericity of the structure, we can observe “patches” of SCN of 8, 9, 10 and 11; and SCN of 4, 5, 6 and 7; and developed facets.
Our models have shown that simple global features of these nanoparticles, of the type routinely characterized using electron microscopy,20 can be used to screen large configuration spaces. These models can, of course, be used to predict the structure–property relationships of more complicated nanoparticle system upon previous characterization using the structural features in Table 1. The ANN predictors can be extended to handle other nanocatalysts by adding more processing neurons to account for the chemical diversity and retraining the models with additional data on different nanoparticle systems.
4 Conclusion
The use of theoretical representations of nanoparticle systems has intrinsic advantages, such as the reduced computational cost of representing each unique configuration as a set of structural features, but this requires careful consideration. Pattern recognition techniques can reveal which structural features are important, and to what degree; and can provide unprecedented insights into physical phenomena while still being consistent with intuitive assumptions. Simple models can be used to develop large exhaustive data sets ideal for data-driven screening prior to a deeper commitment of computational and experimental resources.In the case of Pt nanocatalysts, two main strategies to increase the catalytic efficiency are revealed by our machine learning models. The DT predicts that the insertion of low-index facets and the manipulation of the ratio between molar surface area and sphericity, possibly mediated by the diameter of the nanoparticle, would increase the catalytic activity, whilst the hydrogenation/combustion selectivity could be improved for nanoparticles with diameter higher than 7 nm. Meanwhile, the structural requirements for stable nanoparticles are reduced to the simple principle of more than 9000 atoms in the nanoparticle surface, which condenses all the geometrical constrains and contributions of the different facets to the overall particle-free energy. Furthermore, the flexibility of ANNs to approximate complex structure–property relationship is demonstrated by correlation coefficients higher than 93% of models suitable for non-symmetric nanoparticles.
To the best of our knowledge this is the first demonstration of using structural data on nanoparticles derived from a thermodynamic model to calibrate machine learning predictors of their functional properties. The present methodology is a sound and relatively inexpensive approach to rapidly explore hypothetical structure–property spaces of nanomaterials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computational resources for this project have been supplied by the Australian National Computing Infrastructure facility under Grant q27.References
- S. Curtarolo, A. N. Kolmogorov and F. H. Cocks, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2005, 29, 155–161 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- D. Morgan, G. Ceder and S. Curtarolo, Meas. Sci. Technol., 2005, 16, 296–301 CrossRef CAS.
- K. Kang, Y. S. Meng, J. Bréger, C. P. Grey and G. Ceder, Science, 2006, 311, 977–980 CrossRef CAS PubMed.
- H. Chen, G. Hautier, A. Jain, C. Moore, B. Kang, R. Doe, L. Wu, Y. Zhu, Y. Tang and G. Ceder, Chem. Mater., 2012, 24, 2009–2016 CrossRef CAS.
- G. Hautier, A. Jain, T. Mueller, C. Moore, S. P. Ong and G. Ceder, Chem. Mater., 2013, 25, 2064–2074 CrossRef CAS.
- S. Keinan, M. J. Therien, D. N. Beratan and W. Yang, J. Phys. Chem. A, 2008, 112, 12203–12207 CrossRef CAS PubMed.
- R. Olivares-Amaya, C. Amador-Bedolla, J. Hachmann, S. Atahan-Evrenk, R. S. Sánchez-Carrera, L. Vogt and A. Aspuru-Guzik, Energy Environ. Sci., 2011, 4, 4849 CAS.
- M. Fernandez, H. Shi and A. S. Barnard, J. Chem. Inf. Model., 2015, 55, 2500–2506 CrossRef CAS PubMed.
- C. E. Wilmer, O. K. Farha, Y.-S. Bae, J. T. Hupp and R. Q. Snurr, Energy Environ. Sci., 2012, 5, 9849–9856 CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- H. Barron and A. S. Barnard, Catal. Sci. Technol., 2015, 5, 2848–2855 CAS.
- K. T. Schütt, H. Glawe, F. Brockherde, a. Sanna, K. R. Müller and E. K. U. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205118 CrossRef.
- M. Fernandez, N. R. Trefiak and T. K. Woo, J. Phys. Chem. C, 2013, 117, 14095–14105 CAS.
- M. Fernandez, P. G. Boyd, T. D. Daff, M. Z. Aghaji and K. Tom, J. Phys. Chem. Lett., 2014, 5, 3056–3060 CrossRef CAS PubMed.
- C. M. Simon, R. Mercado, S. K. Schnell, B. Smit and M. Haranczyk, Chem. Mater., 2015, 27, 4459–4475 CrossRef CAS.
- A. Mayoral, H. Barron, R. Estrada-Salas, A. Vazquez-Duran and M. Jose-Yacaman, Nanoscale, 2010, 2, 335–342 RSC.
- Y. Tang and M. Ouyang, Nat. Mater., 2007, 6, 754–759 CrossRef CAS PubMed.
- Z. L. Wang, J. Phys. Chem. B, 2000, 104, 1153–1175 CrossRef CAS.
- H. Barron, G. Opletal, R. D. Tilley and A. S. Barnard, Catal. Sci. Technol., 2016, 6, 144–151 Search PubMed.
- K. J. J. Mayrhofer, M. Arenz, B. Blizanac, V. Stamenkovic, P. N. Ross and N. M. Markovic, Electrochim. Acta, 2005, 50, 5144–5154 CrossRef CAS.
- Q.-S. Chen, J. Solla-Gullon, S.-G. Sun and J. M. Feliu, Electrochim. Acta, 2010, 55, 7982–7994 CrossRef CAS.
- N. P. Lebedeva, M. T. M. Koper, J. M. Feliu and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 12938–12947 CrossRef CAS.
- G. Garcia and M. T. M. Koper, Phys. Chem. Chem. Phys., 2008, 10, 3802–3811 RSC.
- G. Garcia and M. T. M. Koper, J. Am. Chem. Soc., 2009, 131, 5384–5385 CrossRef CAS PubMed.
- Q.-S. Chen, F. J. Vidal-Iglesias, J. Solla-Gullon, S.-G. Sun and J. M. Feliu, Chem. Sci., 2012, 3, 136–147 RSC.
- A. S. Barnard and P. Zapol, J. Chem. Phys., 2004, 121, 4276–4283 CrossRef CAS PubMed.
- A. S. Barnard, J. Phys. Chem. B, 2006, 110, 24498–24504 CrossRef CAS PubMed.
- J. R. Quinlan, C4.5: Programs for Machine Learning, Morgan Kaufmann Publishers, San Mateo, California, 1993 Search PubMed.
- C. M. Bishop, Neural Networks for Pattern Recognition, Oxford University Press, USA, 1995 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Kolmogorov, Dokl. Akad. Nauk SSSR, 1957, 114, 953–956 Search PubMed.
- S. Nissen, Ph.D. thesis, University of Copenhagen (DIKU), 2003.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko and K.-R. Muller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- M. Grzelczak, J. Pérez-Juste, B. Rodríguez-González, M. Spasova, I. Barsukov, M. Farle and L. M. Liz-Marzán, Chem. Mater., 2008, 20, 5399–5405 CrossRef CAS.
- C. T. Campbell, S. C. Parker and D. E. Starr, Science, 2002, 298, 811–814 CrossRef CAS PubMed.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS PubMed.
- H. Barron, G. Opletal, R. D. Tilley and A. S. Barnard, Catal. Sci. Technol., 2015, 6, 144–151 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the single scatter plots, heatmaps of the two-inputs ANNs cross-validation accuracy and decision tree model of the thermodynamic stability. See DOI: 10.1039/c7ra06622h |
| This journal is © The Royal Society of Chemistry 2017 |