Theoretical and kinetic study of the reaction of C₂H₃ + HO₂ on the C₂H₃O₂H potential energy surface

Abstract

The potential energy surface (PES) for reaction of C₂H₃ + HO₂ was examined by using high-level quantum chemical methods. Conventional transition state theory (TST) was used to determine the rates where the reaction has a tight transition state; variable reaction coordinate transition-state theory (VRC-TST) was used for rate constant calculations corresponding to the barrierless reactions. And Rice–Ramsberger–Kassel–Marcus/Master-Equation (RRKM/ME) theory was used to calculate the pressure-dependent rate constants of these channels. The major product channel of the reaction C₂H₃ + HO₂ is the formation of C₂H₃O₂H via a highly vibrationally excited product. Thermochemical properties of the species involved in the reactions were determined using the QCISD(T)/CBS//M062X/6-311++G(d,p) method and enthalpies of formation of species were compared with literature values. The calculated rate constants are in good agreement with limited data from the literature and are given in modified Arrhenius equation form, which are useful in combustion modeling of hydrocarbons. Finally, in order to investigate the effect of the calculated parameters on ignition delay, they were used to simulate ignition delay with the current mainstream mechanism. It is shown that these parameters have improved the mechanism and that the simulation results for ethylene ignition in a shock tube are similar to the observed values.

---

1 Introduction

The vinyl radical (C₂H₃) has received increasing attention in recent years, since it is a key intermediate in combustion and pyrolysis of hydrocarbon fuels.^1,2 And it is an important species in planetary atmospheres,^3–5 and hydrocarbon plasma chemistry.⁶ At high temperatures, alkyl radicals rapidly fragment to yield smaller radicals and a corresponding alkene. At moderate temperature and high pressure, bimolecular reactions involving the hydroperoxyl radical (HO₂) and other radicals are critically important in ignition chemistry. Reactions of HO₂ are typically slow. However, because of its high concentration in the low temperature preignition regime, even relatively slow reactions involving HO₂ can have a significant effect on the combustion process, especially in low-temperature combustion chemistry.^7–10 Furthermore, R + HO₂ reactions can promote ignition by converting less reactive radicals into more reactive radicals OH. Similar to the reaction type of C₂H₃ + HO₂, Petersen et al.¹¹ studied that, in the modeling of CH₄/O₂, the CH₃ + HO₂ reaction was found to be an important source of OH during ignition which needed to be further studied. And the reaction CH₃ + HO₂ is among the most important reactions in methane ignition which is confirmed by Liu et al.¹² Similarly, allyl + HO₂ reaction also has been confirmed with of great effect on the combustion of propene. Heyberger et al.¹³ demonstrated that the induction period of propene ignition in the temperature range of 500–800 K is highly sensitive to allyl + HO₂ kinetics, and that omitting this reaction increased the induction period by an order of magnitude. What is more, Goldsmith et al.¹⁴ studied the kinetics of the allyl + HO₂ bimolecular reaction at the level of QCISD(T)/CBS//B3LYP/MG3S, which found that the reaction of allyl + HO₂ will promote chain branching significantly more than previous models suggest. But to the best of our knowledge, there has not been comprehensively studied about the reaction between C₂H₃ and HO₂ which would have a big effect on the combustion of ethylene. And their kinetics will also be important for many larger hydrocarbons. Accurate measurements or high-level quantum chemistry calculations of these rate constants are urgently needed to develop and refine core mechanisms of combustion chemistry.

In the recombination reaction of two radicals, chemical energy is released and a highly vibrationally excited (HVE) product may be formed and this HVE molecule is capable of further decomposition, isomerization, or collisional stabilization.^15–17 In this paper, the recombination reaction of C₂H₃ and HO₂ is studied and the possible reaction pathways considered as detail in the following.

There are three possible H-transfer reactions corresponding to the bimolecular reactions. The C₂H₃ radical can abstract the H-atom from HO₂ radical, forming ethylene (C₂H₄) and either singlet or triplet molecular oxygen; alternatively, HO₂ can abstract the H-atom from C₂H₃, forming H₂O₂ and triplet H₂CC:

HO₂ can add to the end of the C₂H₃ on the radical side to produce a highly vibrationally excited state, which can be stabilized by collisions with a third body M, as well as isomerization of the intermediate to HOCH₂CHO, CH₃CHOO and CH₃COOH or decomposition to the bimolecular products:

The resulting intermediate HOCH₂CHO and CH₃CHOO can furthermore decompose to small products:

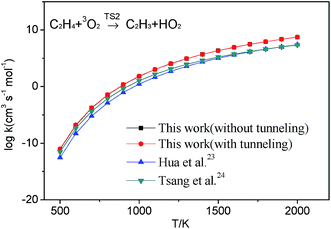
Although these reactions may be important in the modeling of the combustion of hydrocarbon fuels, however, the literature on these reactions is sparse and only a few of them are contained in the popular combustion mechanism.^18–22 The reaction between C₂H₃ and HO₂ has not been comprehensively studied. The existent reactions involving C₂H₃ + HO₂ system in the popular core mechanisms are shown in Table 1. There are only four kinds of reactions appeared in these mechanisms and each of them contains the reverse reaction (2a). To the best of our knowledge, for these reactions, the only available data comes from the work of Hua et al.,²³ in which this reaction was calculated at the QCISD(T)/6-311++G(3df,2p)//MP2(full)/6-311G(d,p) level and compared with an estimate value from Tsang et al.²⁴ in 1983. And this rate constant of reaction C₂H₄ + O₂ → C₂H₃ + HO₂ in these mechanisms all adopted the estimate value from the Tsang et al.²⁴ except the mechanism developed by Konnov²¹ who derived a new rate constant expression by adjusting the A and E_a and the mechanism developed by Lopez²² who adopted the theoretical values from Hua et al.²³ The rate coefficients of reaction C₂H₃ + HO₂ → CH₂CHO + OH contained in the USC-Mech II¹⁸ was estimated. And the rate constant values for the same reaction in the Lopez mechanism was adopted the estimate values from Tsang et al.²⁴ The rate coefficients values of reaction C₂H₃ + HO₂ → CH₃ + CO + OH contained in the Konnov mechanism²¹ was also from Tsang et al.²⁴ The rate coefficients of reaction C₂H₃OOH → CH₂CHO + OH contained in the AramcoMech 1.3 (ref. 19) was also estimated because there were no measurements on the rate constants for this process.

Table 1 Summary of the reactions involved to C₂H₃ + HO₂ system contained in the popular core mechanisms

Mechanism	Reaction numbers	Reactions
USC-Mech II^18	2	C2H4 + O2 → C2H3 + HO2, C2H3 + HO2 → CH2CHO + OH
AramcoMech 1.3 ^19	2	C2H4 + O2 → C2H3 + HO2, C2H3OOH → CH2CHO + OH
UCSD model^20	1	C2H4 + O2 → C2H3 + HO2
Konnov mechanism^21	2	C2H4 + O2 → C2H3 + HO2, C2H3 + HO2 → CH3 + CO + OH
Lopez mechanism^22	2	C2H4 + O2 → C2H3 + HO2, C2H3 + HO2 → CH2CHO + OH

---

Moreover, detailed kinetic model is a valuable design tool to describe the oxidation of hydrocarbon fuels, which can be used to improve the efficiency and emissions of internal combustion engines. Therefore, it is necessary to make a detailed investigation for C₂H₃ + HO₂ system. In this paper, ab initio calculations were performed for all reactants, transition states, and products. The rate constants for these reaction channels were calculated by applying transition state theory and variable reaction coordinate transition-state theory along with appropriate quantum-mechanical tunneling corrections, and the dominant channel was determined.

2 Computational details

2.1 Potential energy surface calculations

The potential energy surface and molecular properties of stationary points were performed by the Gaussian 09 quantum chemistry package.²⁵ Comparing with our previous work⁹ via density functional theory employing the B3LYP level, which is not very accurate for barrier heights,²⁶ we obtained more accurate imaginary frequencies at the M062X/6-311++G(d,p) level (scaled by a factor 0.97).²⁷ All the transition-state structures were confirmed with one and only one single imaginary frequency. Moreover, intrinsic reaction coordinate (IRC)²⁸ calculations were carried out in all case to verify that the transition-state structure connected with the corresponding reactant and product. Higher level single point energy were obtained from QCISD(T) (quadratic configuration interaction with singles doubles and perturbative inclusion of triples) method in complete basis set (CBS) limit.^29,30 In previous studies for a similar albeit smaller molecular system,³¹ the QCISD(T) energies were extrapolated to the complete basis set (CBS) limit³² with the correlation-consistent, polarized-valence, triple-f (cc-pVTZ, denoted by TZ) and quadruple-ζ (cc-pVQZ, denoted QZ) basis sets of Dunning.^33,34 This calculation approach was deemed to be too computationally intensive for the present study.

In the present study, the QCISD(T) energies are extrapolated to the complete basis set limit (CBS) according to the following expression:

E[QCISD(T)/CBS] = E[QCISD(T)/CBS]_DZ→TZ + {E[MP2/CBS]_TZ→QZ − E[MP2/CBS]_DZ→TZ} (1)

which avoids the most time-consuming QCISD(T)/QZ calculation and so are considerably more computationally efficient. The method has been recently examined by Zhang et al.²⁹ for C₄H₉O system and Zhang et al.³⁰ for methylbutanoate system, which was proved to be an efficient and accurate method for high-level energy estimation.²⁹

T1 diagnostic is a measure to gain an insight on the significance of the multireference effects. In general, the multireference wave function is significant only if the T1 diagnostic value is greater than 0.02 for a closed-shell species.³⁵ In the case of open-shell species, it has been suggested that a higher threshold for the T1 diagnostic may be more appropriate, T1 diagnostic values for open-shell systems of up to ∼0.045 may be acceptable.^36–38 For the barrierless reactions, conventional single-reference ab initio methods fail to accurately predict the potential when distance between pivot points on each of the reacting fragments exceeds a certain value.¹⁷ For this reason, multi-reference CASPT2 method^39,40 is used to study the barrierless reactions.

In order to correctly describe the association between two separated fragments, the CASPT2 (8e, 6o)/aug-cc-pVTZ calculation is chosen for association process involving the HO₂ and C₂H₃ radical recombination (HO₂ + C₂H₃ = C₂H₃OOH). The active space includes the π and π* orbital of C=C double bond, two lone pair orbitals of the terminal oxygen, and two O lone pair orbitals of hydroxyl radical, and two radical orbitals. All CASPT2 calculations were done by using MPLPRO.⁴¹

2.2 Thermochemical properties

Standard enthalpies of formation (Δ_fH^θ (298 K), kcal mol⁻¹) have been calculated for all minima and transition states in this paper. The values of Δ_fH^θ (298 K) are determined at the QCISD(T)/CBS//M062X/6-311++G(d,p) level using atomization method. The experimental values of Δ_fH^θ (0 K) are 169.98, 51.63, and 58.99 kcal mol⁻¹ for the elements C, H, and O, respectively.⁴² Thermochemical properties (Δ_fH^θ, Δ_fS^θ, and C_p) are evaluated from standard enthalpies of formation, vibrational frequencies, and moments of inertia, according to statistical mechanical principles employing the ChemRate program.⁴³ Usually, low-frequency internal rotations treated by the harmonic oscillator (HO) approximation can lead to significant errors in the partition function. Vansteenkiste et al.⁴⁴ found that treating hindered internal rotations is crucial to get accurate entropies and heat capacities. Therefore, the one-dimensional (1-D) hindered internal rotor method⁴⁵ was applied to estimate the contributions of low-frequency torsional motions in the partition functions calculation. Internal rotor potentials were calculated by relaxed scans of the dihedral angle with an interval of 10° at the M062X/6-311++G(d,p) level, to determine the barrier height of rotation, number of rotational minima, and symmetry number. In this study, the low-frequency vibrational modes corresponding to internal rotation around the breaking bonds for barrierless reactions were assumed as free rotors. The method proposed by Pitzer and Gwinn⁴⁵ in ChemRate was applied to compute reduced moments of inertia rotations for each species using the geometries calculated at the M062X/6-311++G(d,p) level.

2.3 Rate constant calculations

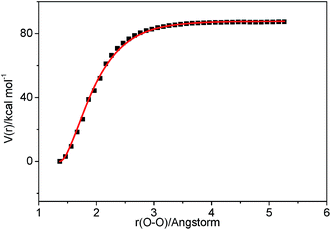
Although some work found that taking into the variational effects in the calculation of pressure-dependent rate constants are helpful to improve the accuracy of rate.^46–48 Due to the huge amount of computation in this work, this paper mainly dealt with the calculations as following. The high-pressure-limit (HPL) rate constants for reactions with pronounced barriers were calculated according to canonical transition state theory (TST) and HPL rate constants for barrierless reactions were treated using variable reaction coordinate transition state theory (VRC-TST) which was shown to be efficient with estimated accurate rate constant errors of less than 20% for a series of hydrocarbon barrierless radical–radical association reactions.^49,50 The pressure-dependent rate constants were computed with the time-dependent RRKM/ME method at the pressures varying from 0.01 to 100 atm. All barrierless reactions were calculated using the VARIFLEX code⁵¹ and others were dealt with ChemRate program.⁴³

The rate constant for the barrierless reactions (reaction (4a) and reaction (13a) in this work), employing in the VARIFLEX code,⁵¹ was calculated based on the VRC-TST theory. The basis of this theory involves a separation of the vibrational modes into conserved and transitional modes. The conserved modes correspond to the vibrational modes, which have little changes from reactants to products, and they are treated as harmonic vibrators employing the frequencies and geometries of the isolated fragments. The transitional modes are typically the bending and rotational modes of the reactant and rotational modes of the products. And the rotational modes of the reactant and rotational modes of the product are treated via Monte Carlo integration of a classical phase space representation. For the barrierless transition state process, the Morse functional

E(R) = De{1 − exp[−β(R − Re)]}² (2)

was used to represent the minimum potential energy path for the association reaction. In the above equation, De is the bonding energy excluding zero-point vibrational energy for an association reaction, R is the reaction coordinate (i.e., the distance between the two bonding atoms), and Re is the equilibrium value of R at the stable intermediate structure.

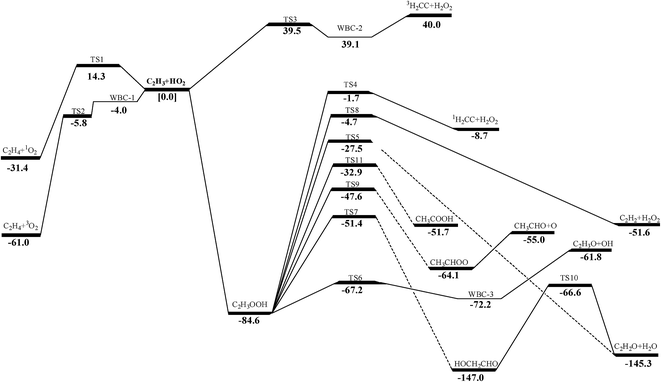
The pressure-dependent rate constants were computed with the time-dependent RRKM/ME method at the pressures varying from 0.01 to 100 atm. Basing on RRKM theory implemented in VARIFLEX program, the component rates were evaluated at the E/J (energy E and total angular momentum J) resolved level and the pressure dependence was treated by solving the one-dimensional master equation calculations using the Boltzmann probability of the complex for the J-distribution and inversion-based approach for single channel calculations.^52,53 The number of a variational transition quantum states, N(E,J), is the sum of states of the transition state to energy E with angular momentum J, and it is a function of the bond length along the reaction coordinate R. N(E,J) is computed by using the Beyer–Swinehart algorithm.⁵⁴ In E/J-resolved calculation, the range of E and J should be adjusted until obtaining converged results. The zero-point corrected binding energy (D₀), which represents the energy to go from the ground state of the desired electronic state of the complex to the ground states of the fragment for the first channel is 29589.3 cm⁻¹ (corresponding to 84.6 kcal mol⁻¹ of the C–O bond cleavage in Fig. 1). The range and step sizes for J are system dependent (i.e., due to variation in the rotational constants), but steps of 5 to 20 and maximum values of 100 to 400 are fairly typical. Generally, the minimum J value should be near zero.⁵⁵ One can evaluate the number of states by Monte Carlo integration for the convolution of the sum of the vibrational quantum states for the conserved modes and the classical phase space density of states for the transitional modes.⁵⁶ Convergences of the Variflex calculations must be carefully tested. The errors of Monte Carlo integrations are less than 5% for the considered temperature.⁵⁷

Fig. 1 Schematic energy profile for C₂H₃ + HO₂ reaction system. Relative energies are those at the QCISD(T)/CBS//M062X/6-311++G(d,p) level, or QCISD(T)/CBS//MP2(full)/6-311++G(d,p) level if no M062X/6-311++G(d,p) calculations are available.

For those reactions except barrierless reactions, the ChemRate program⁴³ was used, which provides the computational means, based on energy conserved one-dimensional master equation, coupling chemical activation, isomerization, decomposition and collisional energy transfer processes involved in the reactions. The rate constants for reactions with pronounced barriers were calculated according to canonical transition state theory (TST), and the pressure-dependent rate constants were computed with the time-dependent RRKM/ME method at the pressures varying from 0.01 to 100 atm. The calculated theory are the same as our previous work for dealing with the C₂H₄OOH system.⁹ The one-dimensional Eckart transmission coefficients have been calculated for those reactions involved in H atom transfer by using ChemRate program to estimate quantum mechanical tunneling corrections. The tunneling corrections will be the main factor to cause the error bar which determine the reliability of the kinetic data.^58,59 In this work, the characteristic length of the Eckart function was obtained using the equations reported by Johnston and Heicklen⁶⁰ with the parameters such as the imaginary frequency of the transition state and barrier height. Considering the Eckart tunneling for the bimolecular reaction is unavailable in the ChemRate, the tunneling effect is roughly estimated by the Wigner method⁶¹ used in these H-abstractions reactions and the method of detailed calculations can be found in our previous work.⁶² The Eckart tunneling correction depends on three main factors, i.e., the imaginary frequency (v*) of the transition state, the forward barrier height (E₁) and the reverse barrier height (E₋₁).^61,63 Calculated barrier width L, as well as E₁, E₋₁, and v*, are listed in the ESI Table S1.†

Lennard–Jones parameters σ and ε are used to estimate the collision frequency between reactant and bath gas, which are taken from the JetSurF version 1.1 transport database⁶⁴ and literature data reported by Hippler et al.⁶⁵ Argon is used as a bath gas collider with values of σ = 3.47 Å, and ε = 114 K. The collision energy transfer is applied using a single-parameter exponential down model⁶⁶ with 〈ΔE_down〉 = 0.35 T cm⁻¹ K⁻¹ for all the calculations. This function form is reasonable, and similar form has been used in previous study of Gong et al.,⁶³ Manion et al.,⁶⁷ and Zhao et al.⁶⁸

Rate constants from 500 to 2000 K were fit to a modified empirical three-parameters form of the Arrhenius equation (eqn (3)) to obtain the elementary rate parameters A, n, and E_a

k = ATⁿ(−E_a/RT) (3)

All pre-exponential terms (ATⁿ) quoted in this study are in units of s⁻¹ (first order) or cm³ mol⁻¹ s⁻¹ (second order), with all temperatures in K.

3 Results and discussion

3.1 C₂H₃O₂H potential energy surface

The schematic potential energy surface (PES) of C₂H₃ + HO₂ reaction at the QCISD(T)/CBS//M062X/6-311++G(d,p)level is displayed in Fig. 1 and the geometrical parameters of the transition states in this work can be found in the ESI Fig. S1.† In the present study, the QCISD(T)/CBS method is used for single-point energy calculations in the subsequent calculation of reaction energies, energy barriers and rate constants unless otherwise mentioned. For practical applications in hydrocarbon combustion, the enthalpies of formation, entropies and heat capacities of species involved in C₂H₃ + HO₂ reaction are presented in ESI Table S2.† As in the present calculation reported above, internal rotations in all species were treated as hindered rotors rather than harmonic oscillators in the calculations of standard entropies and heat capacities. Enthalpies of formation of species in this work show good agreement with literature values.^9,63,69,70 The energies and T1 diagnostic values calculated in this paper are presented in the ESI Table S3 and S4.†

3.2 Reaction mechanism and rate constants

3.2.1 H-abstraction. As shown in Fig. 1, there are three different H-abstraction pathways of C₂H₃ by the HO₂ radical. A comparison of the energy values shows that vinyl radical abstracting the H-atom forming ethylene and triplet molecular oxygen is the most thermodynamically and kinetically favorable pathway. The energy of this transition state (TS2) for this reaction lower than those of the reactants with a value of −5.8 kcal mol⁻¹ which is in good agreement with that from Hua et al. (−6.2 kcal mol⁻¹ at the QCISD(T)/6-311++G(3df,2p)//MP2(full)/6-311G(d,p) level). Both they have a weakly bonded complex (WBC) with minus energy with −4.0 and −3.6 kcal mol⁻¹ comparing to that of reactants, respectively. The detailed illustration of TS2 is provided in Fig. S2 (ESI†), where intrinsic reaction coordinate calculation is presented to show the reactants conversion into weakly bonded complex. For the reaction (1a), a tight transition state TS1 is located for this channel at the MP2(full)/6-311++G(d,p) level, which cannot be found at the M062X/6-311++G(d,p) level. Because the T1 diagnostic for TS1 (0.142) is large, which implies that this transition states are ill-described by single-reference methods. At the same time, the barrier of this reaction is a little high than those of other channels, so this reaction would be negligible in this paper. The reaction (3a) is also negligible because its barrier (39.5 kcal mol⁻¹) is by far higher than others'. Because the H-abstraction reaction (2a) has pronounced barrier, conventional transition state theory is used to calculate the rate constants using the calculated geometrical parameters, vibrational frequencies, and energy of transition state. Considering the Eckart tunneling for the bimolecular reaction is unavailable in the ChemRate, the tunneling effect is roughly estimated by the Wigner method^61,62 used in the H-abstraction reaction. The tunneling effect nearly has no effect on the rate constants for the reaction as plotted in Fig. 2. At present, popular core mechanisms such as USC-Mech II, the UCSD model and AramcoMech 1.3 involving in C₂H₃ + HO₂ system is reaction (2a). And the kinetic data of this reaction are all using the values from Tsang et al.²⁴ who estimated the rate constant according to the work of Walker et al.⁷¹ It can be noted that, in the low-temperature range, a rather good agreement between our values and those from literatures at HPL as presented in Fig. 2. In the high-temperature range, our calculation values are a little higher than other data. As the computational accuracy is much higher, the rate constants calculated in this work should be regarded much more accurate. High-pressure limit rate parameters for the H-abstraction reaction in the temperature range 500–2000 K are given in ESI Table S5.† All other reaction rate parameters in this work are given in ESI Table S6.†

Fig. 2 High-pressure limit rate constants of reaction C₂H₄ + ³O₂ → C₂H₃ + HO₂ on triplet potential surface from the calculated results in this work, Hua et al.,²³ and Tsang et al.²⁴

3.2.2 Association reaction. C₂H₃ radical and the HO₂ radical can directly combine to form a highly vibrationally excited C₂H₃OOH adduct and it can be stabilized by colliding with a third body M. Because this association reaction does not have a well-defined transition state, the rate constants are computed with VCR-TST and RRKM/ME theory using VARIFLEX code. As illustrated in Fig. 3, the dissociation potential function was calculated, which covered the range of C–O separations varying from 1.364 to 5.264 Å at the M062X/6-311++G(d,p) level. During this calculation, relaxed potential energy scan was performed. The resultant M062X/6-311++G(d,p) PES was then scaled to provide a more accurate single energy at the CASPT2 (8e, 6o)/aug-cc-pVTZ level. The plot shown in Fig. 4 illustrates the C₂H₃ + HO₂ interaction energy along the reaction coordinate. This potential energy curve can be fitted to the Morse function with parameters De = 87.7 kcal mol⁻¹, β = 2.177 Å⁻¹, Re = 1.364 Å. The calculated forward and reverse rate constants were plotted in Fig. 5, which cover the temperature range from 500 K to 2000 K, and the pressure varying from 0.01 atm to HPL. The results show that both the forward and reverse reaction rate constants are extremely sensitive to pressure. And the forward rate constants nearly remain unchanged at HPL.

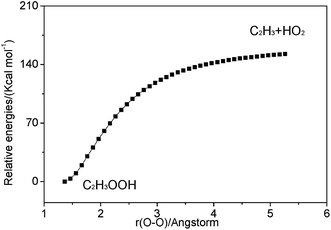Fig. 3 Relaxed potential energy surface scan for C–O bond cleavage of C₂H₃OOH at the M062X/6-311++G(d,p) level.

Fig. 4 Morse curve for the association process C₂H₃ + HO₂ → C₂H₃OOH. Points are computed at the CASPT2 (8e, 6o)/aug-cc-pVTZ//M062X/6-311++G(d,p) level, and the solid curve is the fitted Morse function.

Fig. 5 Calculated rate constants at different pressures for reaction (a) C₂H₃ + HO₂ → C₂H₃OOH and (b) C₂H₃OOH → C₂H₃ + HO₂ in this work.

3.2.3 Decomposition or isomerize of C₂H₃OOH. Aside from dissociation back to the reactants, C₂H₃OOH can directly decompose into ¹H₂CC + H₂O₂, C₂H₂ + H₂O₂, C₂H₂O + HO₂ and C₂H₃O + OH products, or isomerize to CH₃OOH or CH₃CHOO intermediate and then decompose or HOCH₂CHO intermediate and then decompose. The reactions involved in the direct decomposition and isomerization/decomposition are discussed in details respectively in the follows.
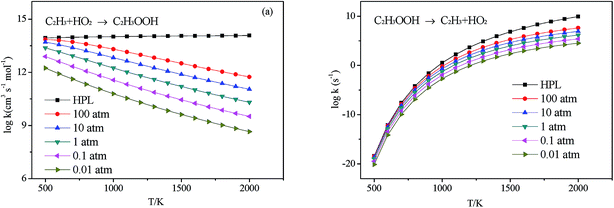
3.2.3.1 Decomposition of C₂H₃OOH. In the present work, C₂H₃OOH is the main reaction intermediate on the C₂H₃ + HO₂ reaction PES. There are four dissociation channels for C₂H₃OOH reactions. As shown in Fig. 1, the most energetic reaction channel for C₂H₃OOH is broken down into C₂H₃O + OH products via TS6. It reacts through the hemolysis of the O–OH bond, which is thought to be the major direct source of the OH in ozonolysis.⁷² This reaction has 17.4 kcal mol⁻¹ barrier height, which is agreement with that from Kurtén et al.⁷³ (15.7 kcal mol⁻¹ at the MRCISD(4,4)/CC-PVTZ//MRCI(4,4)/CC-PVTZ level). There is nearly no other available researchs about dissociation reactions involving in C₂H₃OOH. The most difficult step for C₂H₃OOH channels is broking C–C and C–H bond on the same side to decompose into ¹H₂CC + H₂O₂ via TS4 with a barrier height of 82.9 kcal mol⁻¹. It also can break C–C and C–H bond on different sides to decompose into C₂H₂+H₂O₂ via TS8 with a barrier height of 79.9 kcal mol⁻¹. Although each of these two channels has a high barrier, they are quite important for temperature above 900 K, which the products H₂O₂ undertaking a quick chain-branching reaction H₂O₂ = OH + OH have a large effect on the ignition for hydrocarbon combustion. C₂H₃OOH can also directly decompose to C₂H₂O + H₂O, via TS5, by H₂O-elimination reaction, which has 57.1 kcal mol⁻¹ barrier height. There is nearly no theoretical calculation or experimental rate constants available for reaction involving in C₂H₃OOH. The only kinetic data for reaction C₂H₃OOH → C₂H₃O + OH in some mechanisms are estimated, which are not accurate for combustion modeling. These reactions correspond to C₂H₃OOH decomposition are all pressure-dependent as shown in Fig. 6, especially for reaction C₂H₃OOH → C₂H₃O + OH. It also can be found that the reaction C₂H₃OOH → C₂H₂O + H₂O, pictured in Fig. 6(b), has a greater pressure effect on the reaction constants than those of others such as reaction C₂H₃OOH → ¹H₂CC + H₂O₂ and C₂H₃OOH → C₂H₂ + H₂O₂.

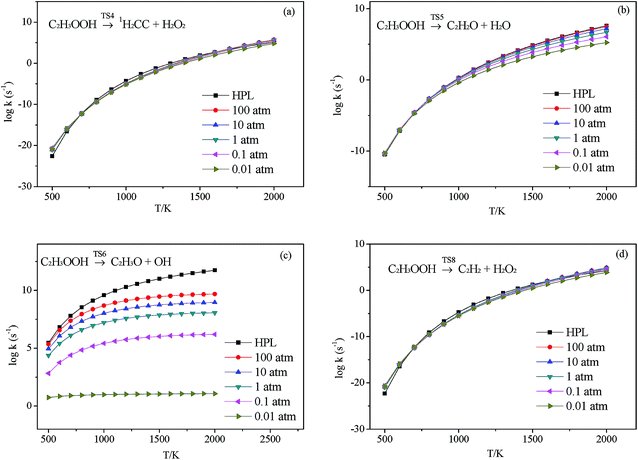Fig. 6 Calculated rate constants at different pressures for reaction (a) C₂H₃OOH → ¹H₂CC + H₂O₂, (b) C₂H₃OOH → C₂H₂O + H₂O, (c) C₂H₃OOH → C₂H₃O + OH and (d) C₂H₃OOH → C₂H₂ + H₂O₂ in this work.

3.2.3.2 Isomerize of C₂H₃OOH. Aside from directly decompose into small fragments, C₂H₃OOH can isomerize to form other products listed as following: it can reaction through TS7, by the terminal OH group rotation and transfer to the second C atom, to produce intermediate HOCH₂CHO with a barrier height of 33.2 kcal mol⁻¹. HOCH₂CHO can then directly decompose into C₂H₂O + H₂O products via a H₂O-elimination reaction. The calculated reaction barrier is 80.4 kcal mol⁻¹. C₂H₃OOH can also isomerize to give CH₃CHOO through a 5-member ring transition state (TS9) with a barrier height of 37.0 kcal mol⁻¹. The most difficult step for C₂H₃OOH isomerization is to form CH₃COOH by the terminal OH group rotation and transfer the H atom of the same side to the second C atom via TS11 with a barrier height of 51.7 kcal mol⁻¹. These reactions are all have a well-defined transition state. To the best of our knowledge, there is no theoretical calculation or experimental data available for comparison of these reactions as mentioned above. These reactions show significant pressure-dependent impact, especially for reactions plotted in Fig. 7(a), (c) and (d). And the pressure effect becomes significant as the temperature increases. The reaction HOCH₂CHO → C₂H₂O + H₂O shown in Fig. 7(b) is not sensitive to the pressure.

Fig. 7 Calculated rate constants at different pressures for reaction (a) C₂H₃OOH → HOCH₂CHO, (b) HOCH₂CHO → C₂H₂O + H₂O, (c) C₂H₃OOH → CH₃CHOO and (d) C₂H₃OOH → CH₃COOH in this work.

3.2.4 Decomposition of CH₃CHOO. CH₃CHOO can directly undergo O–O heterolysis into CH₃CHO + O products. Because this reaction is also a barrierless process, the pressure-dependent rate constants for this reaction were also computed with VCR-TST and RRKM/ME theory using VARIFLEX code. This potential energy curve can be fitted to the Morse function with parameters De = 54.8 kcal mol⁻¹, β = 2.982 Å⁻¹, Re = 1.358 Å. The calculated forward and reverse rate constants were plotted in Fig. 8, which cover the temperature range from 500 K to 2000 K, and the pressure varying from 0.01 atm to HPL. Both the forward and reverse reaction rate constants are extremely sensitive to pressure. And the forward rate constants nearly remain unchanged at HPL.

Fig. 8 Calculated rate constants at different pressures for reaction (a) C₂H₃ + HO₂ → C₂H₃OOH and (b) C₂H₃OOH → C₂H₃ + HO₂ in this work.

3.3 Kinetic modeling

At present, main core mechanisms for C₂H₄ combustion are not afford to reproduce the ignition delay in a wide range of temperatures, pressures and equivalence ratios such as USC-Mech II,¹⁸ UCSD model²⁰ and AramcoMech 1.3.¹⁹ To illustrate the effect for ignition of our new rate constants, we have implemented them into the existing mechanism. The USC-Mech II¹⁸ was chosen as our title mechanism, which has been validated against a wide range of experimental data.⁷⁴ In this part, the USC-Mech II-2nd is the revised mechanism basing on USC-Mech II by adding our previous work for the C₂H₄ + HO₂ reaction on the C₂H₃O₂H potential energy surface.⁹ The USC-Mech II-3rd is the revised mechanism basing on the USC-Mech II-2nd mechanism by adding the work of this paper. The simulations for ignition delay in shock tube were carried out by using the CHEMKIN-PRO software package.⁷⁵ All simulations presented in this section were performed under the assumption of constant-volume, homogeneous and adiabatic conditions.

Liang et al.⁷⁶ have systematic studied the ignition delay of ethylene/O₂/Ar in a shock tube covering a temperature range of 800–1650 K and with equivalence ratios of 0.5, 1.0 and 2.0. The comparison of ignition delay time calculated using the original and revised mechanisms mentioned above and the experimental data from Liang et al. are presented in Fig. 9 and 10. As can be seen from the results, the original mechanisms could not reproduce the C₂H₄ ignition in low temperature, the revised mechanism USC-Mech II-3rd which add the new rate constants calculated in this work could have a better performance on ignition. As plotted in Fig. 9(a) and (b) and Fig. 10(a) and (b), the simulation results of USC-Mech II-3rd show faster ignition delay time. But the discrepancies still are large which need to be further study. Furthermore, a detailed mechanism usually consists of hundreds of species and thousands of reactions. The revised mechanism cannot obtain good performance on predicting the characteristics of fuel combustion by simply adding several reactions. Thus, in order to improve the prediction of ignition delay under a wide range of conditions, it is important to develop a detailed and comprehensive mechanism.

Fig. 9 Comparison of experimental data of ignition delay time and calculated results using different mechanisms under 7 × 10⁵ Pa and (a) Φ = 0.5 and (b) Φ = 1.0 (symbols are experimental data, lines are the simulation results of different mechanisms).

Fig. 10 Comparison of experimental data of ignition delay time and calculated results using different mechanisms under 1.2 × 10⁶ Pa and (a) Φ = 0.5 and (b) Φ = 1.0 (symbols are experimental data, lines are the simulation results of different mechanisms).

4 Conclusions

In this paper, the mechanism and kinetics of bimolecular association reaction C₂H₃ + HO₂ and subsequent reactions by quantum chemical calculations have been investigated over a wide range of temperatures and pressures relevant for combustion modeling. Thermochemical properties of the species involved in the reactions are performed using the QCISD(T)/CBS//M062X/6-311++G(d,p) method and enthalpies of formation of species in this work are in good agreement with available literature values. The reaction rate constants calculated using the TST method for reactions with pronounced barriers are expected to be of high accuracy, in which the tunneling effect has been taken into account. The barrier heights, heat of reaction and rate constants that we calculated agree well with those presented by previous studies. The VRC-TST calculations on barrierless associations are carried out to obtain rate constants. Furthermore, rate constants of pressure-dependent reactions in the three-parameter modified Arrhenius expression are derived in the temperature range of 500–2000 which can be used to simulate conditions encountered in a real combustion environment. Finally, the revised mechanisms by adding the kinetic calculation proposed in this paper can improve the ignition performance in modeling ethylene combustion characteristics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Dr Long Li with China University of Mining and Technology for his help. We are also thankful to Shenzhen Cloud Computing Center, for providing us computational resources. This work is supported by the National Natural Science Foundation of China (No. 91441132) and S&T Plan Project Approving in Guizhou (No. Guizhou branch in LH word [2016] 7104).

References

1. B. K. Carpenter, J. Phys. Chem., 1995, 99, 9801–9810.
2. J. A. Miller, R. J. Kee and C. K. Westbrook, Annu. Rev. Phys. Chem., 1990, 41, 345–387.
3. A. Fahr, P. S. Monks, L. J. Stief and A. H. Laufer, Icarus, 1995, 116, 415–422.
4. G. R. Gladstone, M. Allen and Y. L. Yung, Icarus, 1996, 119, 1–52.
5. W. H. Ip, Astrophys. J., 1990, 362, 354–363.
6. R. K. Janev and D. Reiter, Phys. Plasmas, 2004, 11, 780–829.
7. K. Kumar, G. Mittal, C. J. Sung and C. K. Law, Combust. Flame, 2008, 153, 343–354.
8. J. Zádor, S. J. Klippenstein and J. A. Miller, J. Phys. Chem. A, 2011, 115, 10218–10225.
9. J. J. Guo, J. Q. Xu, Z. R. Li, N. X. Tan and X. Y. Li, J. Phys. Chem. A, 2015, 119, 3161–3170.
10. Q. D. Wang, RSC Adv., 2014, 4, 4564–4585.
11. E. L. Petersen, D. F. Davidson and R. K. Hanson, Combust. Flame, 1999, 117, 272–290.
12. W. Liu, C. K. Law and T. F. Lu, Int. J. Chem. Kinet., 2009, 41, 764–776.
13. B. Heyberger, F. Battin-Leclerc, V. Warth, R. Fournet, G. M. Come and G. Scacchi, Combust. Flame, 2001, 126, 1780–1802.
14. C. F. Goldsmith, S. J. Klippenstein and W. H. Green, Proc. Combust. Inst., 2011, 33, 273–282.
15. J. R. Barker and D. M. Golden, Chem. Rev., 2003, 103, 4577–4592.
16. A. Maranzana, J. R. Barker and G. Tonachini, Phys. Chem. Chem. Phys., 2007, 9, 4129–4141.
17. S. Z. Xiong, Q. Yao, Z. R. Li and X. Y. Li, Combust. Flame, 2014, 161, 885–897.
18. H. Wang, X. Q. You, A. V. Joshi, S. G. Davis, A. Laskin, F. N. Egolfopoulos and C. K. Law, USC Mech Version II.High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds, http://ignis.usc.edu/USC_Mech_II.htm, accessed 2007.
19. W. K. Metcalfe, S. M. Burke, S. S. Ahmed and H. J. Curran, Int. J. Chem. Kinet., 2013, 45, 638–675.
20. UCSD, The San Diego Mechanism, Version 20141004, 2014, http://maeweb.ucsd.edu/combustion/.
21. A. A. Konnov, Combust. Flame, 2009, 156, 2093–2105.
22. J. G. Lopez, C. L. Rasmussen, M. U. Alzueta, Y. Gao, P. Marshall and P. Glarborg, Proc. Combust. Inst., 2009, 32, 367–375.
23. H. Hua, B. Ruscic and B. Wang, Chem. Phys., 2005, 311, 335–341.
24. W. Tsang and R. F. Hampson, J. Phys. Chem. Ref. Data, 1986, 15, 1087–1279.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, A. Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
26. J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808–821.
27. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
28. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
29. P. Zhang, S. J. Klippenstein and C. K. Law, J. Phys. Chem. A, 2013, 117, 1890–1906.
30. L. Zhang, Q. Chen and P. Zhang, Proc. Combust. Inst., 2015, 35, 481–489.
31. J. Zádor, A. W. Jasper and J. A. Mille, Phys. Chem. Chem. Phys., 2009, 11, 11040–11053.
32. J. M. L. Martin and O. Uzan, Chem. Phys. Lett., 1998, 282, 16–24.
33. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
34. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
35. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, 23, 199.
36. I. M. Alecu and D. G. Truhlar, J. Phys. Chem. A, 2011, 115, 2811–2829.
37. J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2000, 104, 9823–9840.
38. J. Peiro-Garcia and I. Nebot-Gil, J. Comput. Chem., 2003, 24, 1657–1663.
39. J. M. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856.
40. S. Parthiban and J. M. Martin, J. Chem. Phys., 2001, 114, 6014–6029.
41. H. J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schὒtz, P. Celani and A. Berning, MOLPRO, Version 2010.1, A Package of Ab initio Programs, 2010.
42. L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079.
43. V. Mokrushin and W. Tsang, ChemRate, v.1.5.8., National Institue of Standards and Technology, Gaithersburg, MD, 2009.
44. P. Vansteenkiste, V. Van Speybroeck, G. B. Marin and M. Waroquier, J. Phys. Chem. A, 2003, 107, 3139–3145.
45. K. S. Pitzer and W. D. Gwinn, J. Chem. Phys., 1942, 10, 428–440.
46. J. L. Bao, J. Zheng and D. G. Truhlar, J. Am. Chem. Soc., 2016, 2690–2704.
47. B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422.
48. B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100.
49. L. B. Harding, Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2005, 109, 4646–4656.
50. S. J. Klippenstein, Y. Georgievskii and L. B. Harding, Phys. Chem. Chem. Phys., 2006, 8, 1133–1147.
51. S. J. Klippenstein, A. F. Wagner, R. C. Dunbar, D. M. Wardlaw and S. H. Robertson, VariFlex, Version 1.0,Argonne National Laboratory, Argonne, IL, 1999.
52. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Scientific, Carlton, Australia, 1990.
53. K. A. Holbrook, K. J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, UK, 1996.
54. T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379.
55. S. J. Klippenstein, Y. C. Yang, V. Ryzhov and R. C. Dunbar, J. Chem. Phys., 1996, 104, 4502–4516.
56. R. S. Zhu and M. C. Lin, Comput. Theor. Chem., 2011, 965, 328–339.
57. H. B. Ning, C. M. Gong, Z. R. Li and X. Y. Li, J. Phys. Chem. A, 2015, 119, 4093–4107.
58. B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422.
59. B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100.
60. H. S. Johnston and J. Heicklen, J. Chem. Phys., 1962, 66, 532–533.
61. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, New York, 2nd edn, 1999.
62. S. H. Li, J. J. Guo, R. Li, F. Wang and X. Y. Li, J. Phys. Chem. A, 2016, 120, 3424–3432.
63. C. M. Gong, H. B. Ning, Z. R. Li and X. Y. Li, Theor. Chem. Acc., 2015, 134, 1–14.
64. B. Sirjean, E. Dames, D. A. Sheen, F. N. Egolfopoulos, H. Wang, D. F. Davidson, R. K. Hanson, H. Pitsch, C. T. Bowman, C. K. Law, W. Tsang, N. P. Cernansky, D. L. Miller, A. Violi and R. P. Lindstedt, A High-Temperature Chemical Kinetic Model of n-Alkane, Cyclohexane, and Methyl-, Ethyl-, n-Propyl and n-Butyl-cyclohexane Oxidation at High Temperatures, JetSurF version 1.1, September 15, 2009, http://melchior.usc.edu/JetSurF/JetSurF1.1.
65. H. Hippler, J. Troe and H. J. Wendelken, J. Chem. Phys., 1983, 78, 6709–6717.
66. D. C. Tardy and B. S. Rabinovitch, Chem. Rev., 1977, 77, 369–408.
67. J. A. Manion and I. A. Awan, Proc. Combust. Inst., 2013, 34, 537–545.
68. L. Zhao, L. Ye, F. Zhang and L. Zhang, J. Phys. Chem. A, 2012, 116, 9238–9244.
69. C. Y. Sheng, J. W. Bozzelli, A. M. Dean and A. Y. Chang, J. Phys. Chem. A, 2002, 106, 7276–7293.
70. NIST, Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, 2013, available at http://webbook.nist.gov/.
71. R. W. Walker, React. Kinet., 1975, 1, 161.
72. K. T. Kuwata, K. L. Templeton and A. S. Hasson, J. Phys. Chem. A, 2003, 107, 11525–11532.
73. T. Kurtén and N. M. Donahue, J. Phys. Chem. A, 2012, 116, 6823–6830.
74. S. G. Davis, C. K. Law and H. Wang, Combust. Flame, 1999, 119, 375–399.
75. Chemkin-Pro Release 15101, Reaction Design, 2010.
76. J. H. Liang, H. H. Hu, S. Wang, S. T. Zhang, B. C. Fan and J. P. Cui, Chin. J. Theor. Appl. Mech., 2014, 1, 155–159.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07734c

---