Open Access Article
Open Access ArticleDensity functional theory study on the boron and phosphorus doping of germanium quantum dots
Zhenyi Ni ,
Hui Jia,
Xiaodong Pi* and
Deren Yang
,
Hui Jia,
Xiaodong Pi* and
Deren Yang
State Key Laboratory of Silicon Materials, School of Materials Science and Engineering, Zhejiang University, Hangzhou, Zhejiang 310027, China. E-mail: xdpi@zju.edu.cn
First published on 1st November 2017
Abstract
Doping is a crucial way of tuning the properties of semiconductor quantum dots (QDs). As one type of important semiconductor QDs, germanium (Ge) QDs have been recently doped with boron (B) and phosphorus (P) through a gas-phase synthesis approach successfully. However, theoretical understanding about the structural and electronic properties of doped Ge QDs remains rather limited. Here we investigate the doping of Ge QDs with B and P in the framework of density functional theory. The formation energies and electronic structures of singularly B- or P-doped Ge QDs and B/P-codoped Ge QDs are systematically studied. It is found that both B and P prefer the near-surface region of Ge QDs. The electronic structures of Ge QDs can be effectively tuned by B and P doping. The B/P codoping may facilitate the incorporation of B and P into Ge QDs, resulting in the further modification of the electronic structures of Ge QDs.
Introduction
Semiconductor quantum dots (QDs) have exhibited great potential in the applications of various fields including electronics,1–4 photovoltaics,5–8 optoelectronics9–15 and bioimaging.16–18 It is of significant current interest that semiconductor QDs are doped to obtain desirable properties.19–24 For example, doping has extended the wavelength of the light emission from silicon (Si) QDs beyond 1.1 μm.25,26 Novel localized surface plasmon resonance (LSPR) has been demonstrated in all kinds of doped semiconductor QDs.24,27–33 The conductivity of semiconductor-QD films is clearly improved after semiconductor QDs are doped.34,35 Compared with the doping of other semiconductor QDs, the doping of germanium (Ge) QDs has not been systematically investigated despite the fact that Ge QDs are a type of important elemental semiconductor QDs. Up to now, most of the research have been focused on the Ge-based-alloy nanostructures (e.g., germanium tin (GexSn1−x) nanocrystals).36–40 It is only recently that Ge QDs have been doped with boron (B) and phosphorus (P) by using a gas-phase synthesis approach.41,42 It is found that both B and P atoms prefer occupying the near-surface region of Ge QDs, rather than the core of the QDs. The conductivity of Ge-QD films may be effectively modulated by the doping of Ge QDs with B and P.41,42It is well known that theoretical simulation is critical to understanding on the doping mechanism of semiconductor QDs. As a powerful theory for the investigation on the structural and electronic properties of materials, density functional theory (DFT) has been extensively employed to study the doping of a variety of semiconductor QDs such as the group IV counterpart of Ge QDs—silicon (Si) QDs.43–49 With the development of the experimental study on the doping of Ge QDs, it is now imperative that theoretical work such as DFT investigation ought to be carried out to explain the experimental findings on the doping of Ge QDs and predict the properties of doped Ge QDs.
In this work, we construct hydrogen (H)-passivated Ge-QD models with a diameter of 1.4 nm to investigate the B and P doping of Ge QDs within the framework of DFT. The formation energies of dopants in Ge QDs are calculated. The electronic structures of singularly B- or P-doped Ge QDs and B/P-codoped Ge QDs are systematically studied. It is found that B or P is the most likely incorporated in the near-surface region of Ge QDs. B is more likely doped than P. B introduces deep energy levels in the bandgap of a Ge QD whether it is inside or in the near-surface region of the QD. In contrast, P gives rise to deep energy levels only when it is incorporated inside a Ge QD. It is interesting that the deep energy levels induced by P are deeper than those induced by B. The B/P codoping may promote the incorporation of B and P into Ge QDs. The Ge-QD bandgap is effectively reduced by the B/P codoping.
Method
The optimization of structures and the calculation of total energies are performed at 0 K by using the all-electron DFT modeling package DMol3.46,50,51 The Becke–Lee–Yang–Parr (BLYP) exchange–correlation functional at the generalized gradient approximation (GGA) level is used. Double numerical basis sets augmented with p-polarization functions (DNP basis sets) are employed as the atomic orbital basis functions. To ensure accurate calculation, a high self-consistent field (SCF) convergence threshold of 10−6 and a large orbital cutoff of 4.6 Å are employed. The maximum energy change and forces on all of the atoms in the optimized structures are less than 10−5 Ha and 0.002 Ha Å−1, respectively. To prevent the optimizer from taking unreasonable steps, the maximum allowed change of any cartesian coordinate during the structural relaxation is less than 0.3 Å. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are sampled on a grid with a spacing of 0.2 Å.Results and discussion
B or P doping
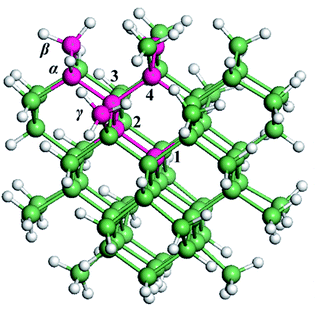
Fig. 1 shows the model of a 1.4 nm Ge QD, which is constructed by cutting out a spherical portion in an optimized bulk Ge model. H atoms are used to passivate the dangling bonds of Ge atoms at the surface of the QD. Three types of hydrides (GeH, GeH2 and GeH3) are at the QD surface, consistent with experimental observation.42 The obtained Ge QD is in the form of Ge71H84. When a substitutional B (P) atom moves along the path of 1 → 2 → 3 → 4 in a Ge QD (from the center toward the surface of a Ge QD), it is denoted as B1 (P1), B2 (P2), B3 (P3) or B4 (P4). When a B (P) atom replaces a Ge atom that is originally connected to one, two or three H atoms at the surface, it is denoted as Bα (Pα), Bβ (Pβ) or Bγ (Pγ), respectively. Bα (Pα), Bβ (Pβ) and Bγ (Pγ) are passivated by zero (zero), one (one) and zero (two) H atoms, respectively. Therefore, no dangling bonds are associated with B or P. We should point out that defects like dangling bonds often exist at the surface of as-synthesized QD-materials including Ge QDs.26,41 By carrying out appropriate surface modification and annealing processes, we may obtain defect-free Ge QDs, akin to that for Si QDs52,53 and two-dimensional materials.54,55We calculated the formation energy (Ef) of a B or P atom in Ge QD by using56,57
| Ef = E(Gex′Hy′X) − E(GexHy) − μX − (x′ − x)μGe − (y′ − y)μH, | (1) |
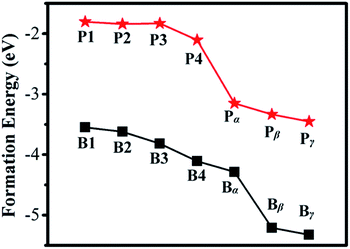
The calculated Ef for B or P in a Ge QD is shown in Fig. 2. It is seen that the values of Ef for B doping are smaller than those for P doping in all the configurations, indicating that B is more likely to be incorporated into a Ge QD than P in term of thermodynamics. This is in contrast with the doping of B and P in H-passivated Si QDs where on average P exhibits a lower Ef than B.59 For both B and P doping, the values of Ef at the surface of the QD (α, β and γ) are smaller than those inside the QD (1, 2, 3 and 4), validating a preference of the near-surface region for B and P. The calculated results are in good agreement with experimental observations carried out on the doping of Ge QDs with B and P.41,42 As a B or P atom moves from the center to the sub-surface of the Ge QD (i.e., from 1 → 4), the Ef shows a trend of decrease. Similar results have been obtained by B- or P-doped Si QD.43,44,59 This is mainly due to the self-purification nature of QDs for impurities. We should mention that the lattice constant of the B- or P-doped Ge QD is basically equal to that of undoped Ge QD. This may because that the current value of the dopant concentration of 1.4% is too small to significantly affect the lattice constant of the Ge QD. With the increase of the concentration of the dopant, we may expect a decrease of the lattice constant of the Ge QD according to the Vegard's law, similar to what has been observed in B-doped Si QDs60 and carbon- and germanium-doped silicene.61
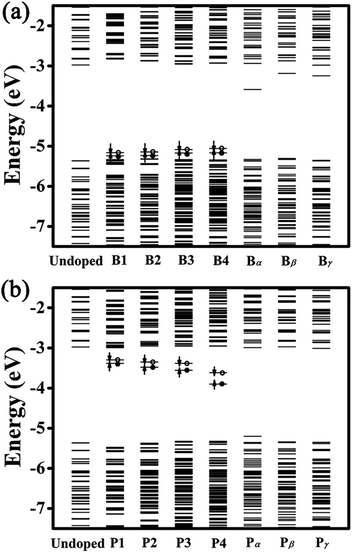
Fig. 3 presents the energy-level diagrams for undoped, B- and P-doped Ge QDs. It is seen that an undoped Ge QD with a diameter of 1.4 nm shows a bandgap of 2.39 eV, which is larger than that of bulk Ge, consistent with the quantum confinement effect.62 Similar to carbon- and germanium-doped silicene,61 Ge QDs doped with B or P in different configurations show different band structures. For B-doped Ge QDs, the bandgaps of the QDs are hardly affected (<5%) while deep energy levels are introduced in the bandgap (Fig. 3(a)). This is akin to H-passivated Si QDs when they are doped with B via first-principles calculations.44
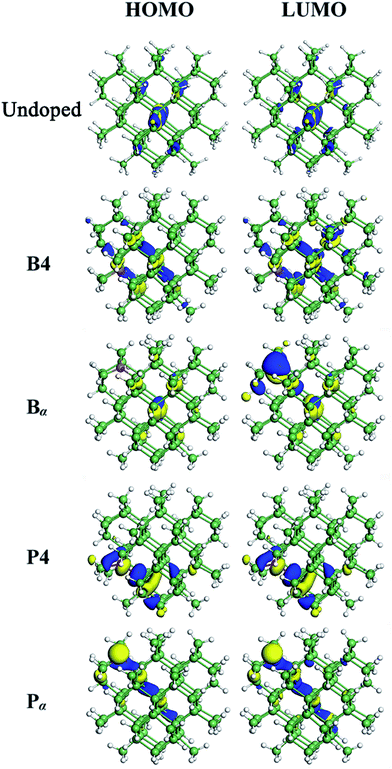
When a B atom is in the configurations of B1, B2, B3 or B4, deep energy levels are close to the valence band with a small spin splitting, verifying a p-type characteristic of B-doped Ge QD. This is mainly due to the B-doping-induced extra hole in a Ge QD. In these cases, the electron densities of the HOMO and LUMO (here the HOMO and LUMO are deep energy levels) are mainly located at the B and neighboring Ge atoms with similar distributions (representatively shown for B4-doped Ge QD in Fig. 4). Since the spin splitting of the deep energy levels is associated with the polarizability of bonds,45 as the B atom moves from the isotropic configuration of B1 to the anisotropic configuration of B4, the spin splitting of the deep energy levels slightly increases from 78 to 107 meV. When a B atom is incorporated in the configuration of Bα, Bβ or Bγ, a deep energy level with empty electronic states is introduced near the conduction band of the Ge QD. The electron density of this energy level (LUMO) is mainly located at the B atom, while the electron density of the HOMO is dislocated among the Ge atoms (representatively shown for Bα-doped Ge QD in Fig. 4). Similar to B-doped H-passivated Si QDs with B atoms at the QD surface,44 these deep energy levels are induced by the empty 2pz orbitals of B. Since an empty 2pz orbital is a good electron-acceptor, the electron cloud of an unconnected nearest-neighboring atom may shift to the empty 2pz orbital of the B atom. This makes B-doping-induced energy levels to move close to the conduction band of a Ge QD.
For P-doped Ge QDs, deep energy levels are introduced into the bandgap when P is in the configurations of P1, P2, P3 and P4. The P-doping-induced deep energy levels are close to the conduction band with a spin-splitting, proving the n-type characteristic of P-doped Ge QDs. This is caused by an extra electron induced by P doping in a Ge QD. In these cases, the electron densities of the HOMO and LUMO (deep energy levels) are mainly located at the P and neighboring Ge atoms with similar distributions (representatively shown for P4-doped Ge QD in Fig. 4). As a P atom moves from the center (P1) to the sub-surface (P4) of the Ge QD, the deep energy levels step deeper into the middle of the bandgap while the spin splitting gradually increases from 88 to 280 meV. The former is due to the enhanced structural distortion induced by P doping from P1 to P4 (e.g., the bond length of a Ge–P bond is compressed by 15.9% and that of the adjacent Ge–P bond is stretched by 4.6%) that causes a more localized electron density distribution of the deep energy levels, while the latter is due to the anisotropic transition of the polarizability of the Ge–P bonds from P1 to P4. We observe that the P-doping-induced energy levels are deeper than those induced by B doping, which is analogous to the results obtained on the doping of B and P in both hydrogen-passivated Si QDs43,44 and Si QDs that embedded in a SiO2 matrix.45,46 This infers the similarity of the electronic structures between Ge and Si QDs after B and P doping. When a P atom is incorporated in the configuration of Pα, Pβ or Bγ, no deep energy levels are introduced into the bandgap due to the threefold coordination of the electrons. The electron densities of both the HOMO and LUMO are located around P and neighboring Ge atoms. Again, this is similar to P-doped Si QDs.43
B/P codoping
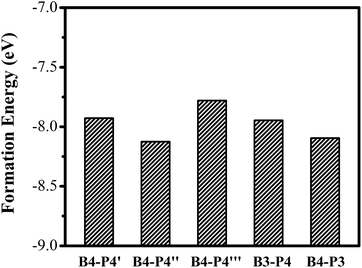
We further investigate the effect of B/P codoping for Ge QDs. As discussed above, a B (P) atom at the surface of a Ge QD does not act as an effective acceptor (donor). Thus, we only focus on the codoping of B and P when they are both incorporated inside a Ge QD. Under this condition, the configurations in which B and P are both incorporated in their energetically favored locations of 4 at the sub-surface of the QD are first considered. Depending on the distance between the B and P atoms, there exist three types of B/P-codoping configurations when both of them are doped at the locations of 4. As the B–P distance increases, these three types of B/P-codoping configurations are denoted as B4–P4′, B4–P4′′ and B4–P4′′′. To figure out the influence of a dipole (i.e., a B–P pair) on the electronic properties of a Ge QD, we have considered the configurations in which B and P form a B–P pair, namely B3–P4 and B4–P3. Fig. 5 shows the models of (a) B4–P4′′ and (b) B4–P3 codoped Ge QDs.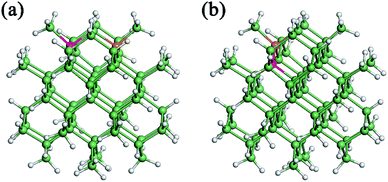 | ||
| Fig. 5 Model of a Ge QD codoped with (a) B4–P4′′ or (b) B4–P3. Ge, H, B and P atoms are denoted by green, grey, orange and pink balls, respectively. | ||
The Ef of the dopants in a Ge QD is calculated by using56,57
| Ef = E(Gex′Hy′BP) − E(GexHy) − μB − μP − (x′ − x)μGe − (y′ − y)μH, | (2) |
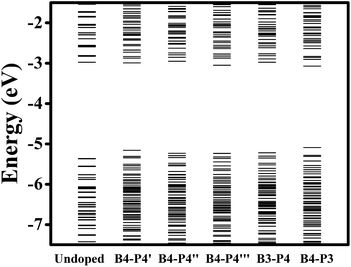
The energy-level diagrams for undoped and B/P codoped Ge QDs are shown in Fig. 7. Similar to B/P codoped H-passivated Si QDs,63 B/P codoping reduces the bandgaps of Ge QDs by 0.11–0.37 eV. This highlights the tunability of band structures of Ge QDs upon B/P codoping. The reduction of the bandgaps of Ge QDs is mainly due to the rise of the HOMO levels towards the middle of the bandgaps (Fig. 7). For B/P codoped Ge QDs, the electron densities of the HOMO are localized at the B and neighboring Ge atoms, while those of the LUMO are distributed around B, P and Ge atoms (Fig. 8). It is the localization of the electron density of the HOMO on B that contributes to the uplift of the HOMO level. It is interesting that the formation of a B–P pair does not distinctly affect the band structures of B/P codoped Ge QDs. This is again quite different from Si QDs embedded in a SiO2 matrix, in which a B–P pair alters the band structure of codoped Si QDs by forming a static electric dipole that radially points toward the QD core.46
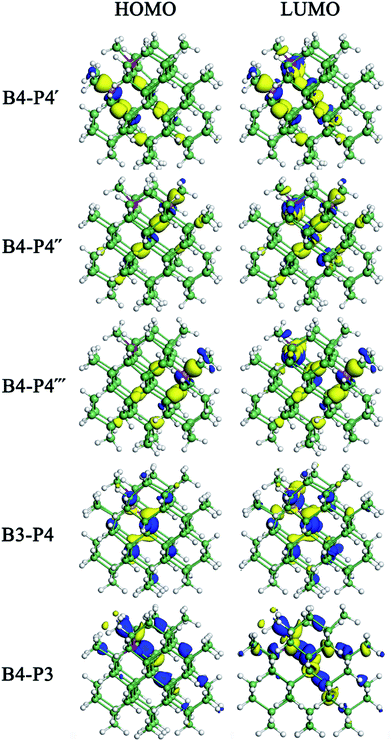 | ||
| Fig. 8 Distribution of the isosurface for the electron density of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for B/P-codoped Ge QDs. | ||
Conclusions
We have studied the doping of Ge QDs with B and P by means of density functional theory. The current results show that B or P is the most likely incorporated at the near-surface region of Ge QDs. B doping introduces deep energy levels in the bandgap of a Ge QD whether it is inside or at the surface of the QD. In contrast, P doping causes deep energy levels only when it is incorporated inside the Ge QD. The codoping of B and P may promote the incorporation of B and P into Ge QDs, given a lower formation energy of B/P dopants. After B/P codoping, the bandgap of a Ge QD is reduced. Considering the moderate bandgaps (∼2.02 to 2.52 eV) and suitable band alignment with water, B- and P-doped Ge QDs may have the potential applications in photocatalytic water splitting.64 Our calculated results inspire the modulation of the band structures of Ge QDs for desirable applications by B and P doping in the future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Shanghai Supercomputer Center is acknowledged for providing computation resources. This study is mainly supported by the National Key Research and Development Program of China (Grant No. 2017YFA0205700), Natural Science Foundation of China (NSFC) (Grant No. 61774133 and 6147409), NSFC-FWO program (Grant No. 61411130229 and 61511130264) and Program for Innovative Research Team in University of Ministry of Education of China (IRT13R54).References
- J. Zhu and M. C. Hersam, Adv. Mater., 2017, 29, 1603895 CrossRef PubMed.
- D. K. Kim, Y. Lai, B. T. Diroll, C. B. Murray and C. R. Kagan, Nat. Commun., 2012, 3, 1216 CrossRef PubMed.
- Q. B. Luan, Z. Y. Ni, S. Koura, T. J. Zhu, D. Yang and X. D. Pi, AIP Adv., 2014, 4, 127108 CrossRef.
- M.-S. Yeh, Y.-C. Wu, M.-H. Chung, Y.-R. Jhan, K.-S. Chang-Liao, K.-C. Liu, M.-H. Wu and M.-F. Hung, Appl. Phys. Lett., 2014, 105, 042109 CrossRef.
- M. Yuan, M. Liu and E. H. Sargent, Nat. Energy, 2016, 1, 16016 CrossRef CAS.
- S. Y. Zhao, X. D. Pi, C. Mercier, Z. C. Yuan, B. Q. Sun and D. Yang, Nano Energy, 2016, 26, 305–312 CrossRef CAS.
- X. D. Pi, L. Zhang and D. R. Yang, J. Phys. Chem. C, 2012, 116, 21240–21243 CAS.
- J. Xu, S. H. Sun, Y. Q. Cao, P. Lu, W. Li and K. J. Chen, Part. Part. Syst. Charact., 2014, 31, 459–464 CrossRef CAS.
- Z. Y. Ni, L. L. Ma, S. C. Du, Y. Xu, M. Yuan, H. H. Fang, Z. Wang, M. S. Xu, D. S. Li, J. Y. Yang, W. D. Hu, X. D. Pi and D. Yang, ACS Nano, 2017, 11, 9854–9862 CrossRef CAS PubMed.
- V. Adinolfi and E. H. Sargent, Nature, 2017, 542, 324–327 CrossRef CAS PubMed.
- T. Yu, F. Wang, Y. Xu, L. L. Ma, X. D. Pi and D. Yang, Adv. Mater., 2016, 28, 4912–4919 CrossRef CAS PubMed.
- F. P. García de Arquer, A. Armin, P. Meredith and E. H. Sargent, Nat. Rev. Mater., 2017, 2, 16100 CrossRef.
- L. Yao, T. Yu, L. X. Ba, H. Meng, X. Fang, Y. L. Wang, L. Li, X. Rong, S. Wang, X. Q. Wang, G. Z. Ran, X. D. Pi and G. G. Qin, J. Mater. Chem. C, 2016, 4, 673–677 RSC.
- F. Maier-Flaig, J. Rinck, M. Stephan, T. Bocksrocker, M. Bruns, C. Kubel, A. K. Powell, G. A. Ozin and U. Lemmer, Nano Lett., 2013, 13, 475–480 CrossRef CAS PubMed.
- W. Gu, X. K. Liu, X. D. Pi, X. L. Dai, S. Y. Zhao, L. Yao, D. S. Li, Y. Z. Jin, M. S. Xu, D. Yang and G. G. Qin, IEEE Photonics J., 2017, 9, 1–10 Search PubMed.
- X. Cheng, S. B. Lowe, P. J. Reece and J. J. Gooding, Chem. Soc. Rev., 2014, 43, 2680–2700 RSC.
- Y. L. Zhong, X. T. Sun, S. Y. Wang, F. Peng, F. Bao, Y. Y. Su, Y. Y. Li, S.-T. Lee and Y. He, ACS Nano, 2015, 9, 5958–5967 CrossRef CAS PubMed.
- J. Kang, J. Joo, E. J. Kwon, M. Skalak, S. Hussain, Z. G. She, E. Ruoslahti, S. N. Bhatia and M. J. Sailor, Adv. Mater., 2016, 28, 7962–7969 CrossRef CAS PubMed.
- L. Jing, S. V. Kershaw, Y. Li, X. Huang, Y. Li, A. L. Rogach and M. Gao, Chem. Rev., 2016, 116, 10623–10730 CrossRef CAS PubMed.
- C. R. Kagan and C. B. Murray, Nat. Nanotechnol., 2015, 10, 1013 CrossRef CAS PubMed.
- Z. Y. Ni, X. D. Pi, M. Ali, S. Zhou, T. Nozaki and D. R. Yang, J. Phys. D: Appl. Phys., 2015, 48, 314006 CrossRef.
- D. Mocatta, G. Cohen, J. Schattner, O. Millo, E. Rabani and U. Banin, Science, 2011, 332, 77–81 CrossRef CAS PubMed.
- A. Sahu, M. S. Kang, A. Kompch, C. Notthoff, A. W. Wills, D. Deng, M. Winterer, C. D. Frisbie and D. J. Norris, Nano Lett., 2012, 12, 2587–2594 CrossRef CAS PubMed.
- B. L. Greenberg, S. Ganguly, J. T. Held, N. J. Kramer, K. A. Mkhoyan, E. S. Aydil and U. R. Kortshagen, Nano Lett., 2015, 15, 8162–8169 CrossRef CAS PubMed.
- M. Fujii, H. Sugimoto and K. Imakita, Nanotechnology, 2016, 27, 262001 CrossRef PubMed.
- P. Lu, W. Mu, J. Xu, X. Zhang, W. Zhang, W. Li, L. Xu and K. Chen, Sci. Rep., 2016, 6, 22888 CrossRef CAS PubMed.
- J. M. Luther, P. K. Jain, T. Ewers and A. P. Alivisatos, Nat. Mater., 2011, 10, 361–366 CrossRef CAS PubMed.
- S. W. Hsu, K. On and A. R. Tao, J. Am. Chem. Soc., 2011, 133, 19072–19075 CrossRef CAS PubMed.
- S. Zhou, X. D. Pi, Z. Y. Ni, Y. Ding, Y. Y. Jiang, C. H. Jin, C. Delerue, D. R. Yang and T. Nozaki, ACS Nano, 2015, 9, 378–386 CrossRef CAS PubMed.
- S. Zhou, Z. Y. Ni, Y. Ding, M. Sugaya, X. D. Pi and T. Nozaki, ACS Photonics, 2016, 3, 415–422 CrossRef CAS.
- Z. Y. Ni, X. D. Pi, S. Zhou, T. Nozaki, B. Grandidier and D. Yang, Adv. Opt. Mater., 2016, 4, 700–707 CrossRef CAS.
- X. D. Pi and C. Delerue, Phys. Rev. Lett., 2013, 111, 177402 CrossRef PubMed.
- M. Kanehara, H. Koike, T. Yoshinaga and T. Teranishi, J. Am. Chem. Soc., 2009, 131, 17736–17737 CrossRef CAS PubMed.
- A. R. Stegner, R. N. Pereira, K. Klein, R. Lechner, R. Dietmueller, M. S. Brandt, M. Stutzmann and H. Wiggers, Phys. Rev. Lett., 2008, 100, 026803 CrossRef CAS PubMed.
- R. Gresback, N. J. Kramer, Y. Ding, T. Chen, U. R. Kortshagen and T. Nozaki, ACS Nano, 2014, 8, 5650–5656 CrossRef CAS PubMed.
- D. A. Ruddy and N. R. Neale, ACS National Meeting, 2012, INOR-1288 Search PubMed.
- L. Men, M. A. White, H. Andaraarachchi, B. A. Rosales and J. Vela, Chem. Mater., 2017, 29, 168–175 CrossRef CAS.
- B. W. Boote, L. Men, H. P. Andaraarachchi, U. Bhattacharjee, J. W. Petrich, J. Vela and E. A. Smith, Chem. Mater., 2017, 29, 6012–6021 CrossRef CAS.
- K. Ramasamy, P. G. Kotula, A. F. Fidler, M. T. Brumbach, J. M. Pietryga and S. A. Ivanov, Chem. Mater., 2015, 27, 4640–4649 CrossRef CAS.
- R. J. A. Esteves, M. Q. Ho and I. U. Arachchige, Chem. Mater., 2015, 27, 1559–1568 CrossRef CAS.
- T. H. Yuan, X. D. Pi and D. Yang, IEEE J. Sel. Top. Quantum Electron., 2017, 23, 4800205 CrossRef.
- Y. Gao, X. D. Pi, X. H. Wang, T. H. Yuan, Q. J. Jiang, R. Gresback, J. G. Lu and D. Yang, Part. Part. Syst. Charact., 2016, 33, 271–278 CrossRef CAS.
- X. B. Chen, X. D. Pi and D. Yang, J. Phys. Chem. C, 2011, 115, 661–666 CAS.
- X. D. Pi, X. B. Chen and D. Yang, J. Phys. Chem. C, 2011, 115, 9838–9843 CAS.
- Z. Y. Ni, X. D. Pi and D. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035312 CrossRef.
- Z. Y. Ni, X. D. Pi, S. Cottenier and D. Yang, Phys. Rev. B, 2017, 95, 075307 CrossRef.
- A. Puzder, A. Williamson, J. Grossman and G. Galli, Phys. Rev. Lett., 2002, 88, 097401 CrossRef PubMed.
- L. Ramos, E. Degoli, G. Cantele, S. Ossicini, D. Ninno, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235310 CrossRef.
- R. Guerra and S. Ossicini, J. Am. Chem. Soc., 2014, 136, 4404–4409 CrossRef CAS PubMed.
- X. D. Pi, R. Wang and D. Yang, Chin. Phys. B, 2014, 23, 076102 CrossRef.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- X. Liu, Y. Zhang, T. Yu, X. Qiao, R. Gresback, X. Pi and D. Yang, Part. Part. Syst. Charact., 2016, 33, 44–52 CrossRef CAS.
- S. Niesar, R. N. Pereira, A. R. Stegner, N. Erhard, M. Hoeb, A. Baumer, H. Wiggers, M. S. Brandt and M. Stutzmann, Adv. Funct. Mater., 2012, 22, 1190–1198 CrossRef CAS.
- S. M. Pratik, A. Nijamudheen and A. Datta, Chemistry, 2015, 21, 18454–18460 CrossRef CAS PubMed.
- A. Nijamudheen, R. Bhattacharjee, S. Choudhury and A. Datta, J. Phys. Chem. C, 2015, 119, 3802–3809 CAS.
- E. Degoli, S. Ossicini, G. Cantele, E. Luppi, R. Magri, D. Ninno and O. Bisi, Phys. Status Solidi C, 2005, 2, 3354–3358 CrossRef CAS.
- A. Carvalho, S. Öberg, M. J. Rayson and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045308 CrossRef.
- L. G. Wang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 161202 CrossRef.
- X. D. Pi, J. Nanomater., 2012, 2012, 912903 Search PubMed.
- S. Zhou, X. D. Pi, Z. Y. Ni, Q. B. Luan, Y. Y. Jiang, C. H. Jin, T. Nozaki and D. R. Yang, Part. Part. Syst. Charact., 2015, 32, 213–221 CrossRef CAS.
- T. Teshome and A. Datta, J. Phys. Chem. C, 2017, 121, 15169–15180 CAS.
- E. G. Barbagiovanni, D. J. Lockwood, P. J. Simpson and L. V. Goncharova, J. Appl. Phys., 2012, 111, 034307 CrossRef.
- Y. S. Ma, X. B. Chen, X. D. Pi and D. Yang, J. Nanopart. Res., 2012, 14, 802 CrossRef.
- C. Chowdhury, S. Karmakar and A. Datta, J. Phys. Chem. C, 2017, 121, 7615–7624 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |