Open Access Article
Open Access ArticleMolecular dynamics and charge transport in organic semiconductors: a classical approach to modeling electron transfer†
Kenley M.
Pelzer
 *ab,
Álvaro
Vázquez-Mayagoitia
c,
Laura E.
Ratcliff
c,
Sergei
Tretiak
d,
Raymond A.
Bair
efg,
Stephen K.
Gray
af,
Troy
Van Voorhis
h,
Ross E.
Larsen
i and
Seth B.
Darling
*ab,
Álvaro
Vázquez-Mayagoitia
c,
Laura E.
Ratcliff
c,
Sergei
Tretiak
d,
Raymond A.
Bair
efg,
Stephen K.
Gray
af,
Troy
Van Voorhis
h,
Ross E.
Larsen
i and
Seth B.
Darling
 aj
aj
aCenter for Nanoscale Materials, Argonne National Laboratory, 9700 Cass Ave., Lemont, IL 60439, USA. E-mail: kpelzer@anl.gov; Tel: +1-630-252-7020
bMaterials Science Division, Argonne National Laboratory, 9700 Cass Ave, Lemont, IL 60439, USA
cArgonne Leadership Computing Facility, Argonne National Laboratory, 9700 Cass Ave., Lemont, IL 60439, USA
dTheoretical Division, Center for Nonlinear Studies, Center for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
eMathematics and Computer Science Division, Argonne National Laboratory, 9700 Cass Ave., Argonne, IL 60439, USA
fComputation Institute, University of Chicago, 5735 S. Ellis Ave., Chicago, IL 60637, USA
gComputer, Environment, and Life Sciences, Argonne National Laboratory, 9700 Cass Ave., Lemont, IL 60439, USA
hDepartment of Chemistry, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA
iComputational Science Center, National Renewable Energy Laboratory, 15301 Denver W. Parkway, Golden, CO 80401, USA
jInstitute for Molecular Engineering, University of Chicago, 5747 S. Ellis Ave., Chicago, IL 60637, USA
First published on 11th January 2017
Abstract
Organic photovoltaics (OPVs) are a promising carbon-neutral energy conversion technology, with recent improvements pushing power conversion efficiencies over 10%. A major factor limiting OPV performance is inefficiency of charge transport in organic semiconducting materials (OSCs). Due to strong coupling with lattice degrees of freedom, the charges form polarons, localized quasi-particles comprised of charges dressed with phonons. These polarons can be conceptualized as pseudo-atoms with a greater effective mass than a bare charge. We propose that due to this increased mass, polarons can be modeled with Langevin molecular dynamics (LMD), a classical approach with a computational cost much lower than most quantum mechanical methods. Here we present LMD simulations of charge transfer between a pair of fullerene molecules, which commonly serve as electron acceptors in OSCs. We find transfer rates consistent with experimental measurements of charge mobility, suggesting that this method may provide quantitative predictions of efficiency when used to simulate materials on the device scale. Our approach also offers information that is not captured in the overall transfer rate or mobility: in the simulation data, we observe exactly when and why intermolecular transfer events occur. In addition, we demonstrate that these simulations can shed light on the properties of polarons in OSCs. Much remains to be learned about these quasi-particles, and there are no widely accepted methods for calculating properties such as effective mass and friction. Our model offers a promising approach to exploring mass and friction as well as providing insight into the details of polaron transport in OSCs.
Introduction
Since the discovery of high electrical conductivity in organic materials in the 1970s,1 organic semiconductors have been a focus of intense research, with applications ranging from field-effect transistors (FETs) to light-emitting diodes (LEDs) and organic photovoltaics (OPVs). In addition to the advantages of light weight, flexibility, and transparency, organic semiconductors have a relatively low-energy production process and are composed of abundant materials, offering the low cost of production needed for economic viability of widespread use.2–15 While some organic semiconductors such as LEDs for displays have already been successfully commercialized, other technologies struggle with low efficiencies that limit integration into the mass market. A major factor limiting the efficiency of OPVs is the inefficiency of charge transport, with charge mobilities much lower than those of their inorganic photovoltaic counterparts.16 Development of theoretical methods that accurately model charge transport would represent a major contribution to the optimization of this promising renewable energy technology.Because of the relatively large size of OPV systems (with a typical active layer >100 nm in thickness), modeling of charge transport on the device scale presents a daunting problem in terms of computational cost. Although there have been major developments in linear-scaling density functional theory (DFT),17 the tens of millions of atoms in a representative volume are prohibitively costly for dynamical methods such as time-dependent DFT. Even the simpler ground state calculations would be prohibited by memory issues on most supercomputers. Here, we propose a simplified approach in which charge transport is modeled with Langevin molecular dynamics (LMD).18 LMD is fundamentally a classical method, while charges are traditionally assumed to require quantum mechanical treatment. However, we argue that in some organic semiconductors, the unique properties of charges in these materials permit an accurate classical treatment.
In many organic electronic materials, charges are coupled to surrounding nuclei. The Coulombic interaction between the negative charge of an excess electron and the positive charge of surrounding nuclei pulls nuclei toward the charge (or in the case of a positively charged hole, repels the nuclei). This interaction with the nuclei creates a “polaron,” a charge dressed with phonons, which then transfers between molecules via a thermally activated hopping process. Understanding the electronic structure of these charges and their coupling to molecular motions presents a major challenge in theoretical modeling.15,19–25 However, in this challenge there may also lie an opportunity for simplified modeling. We argue that because of the mass of the nuclei to which charges are coupled, polarons can be treated as localized quasi-particles with an effective mass greater than that of bare charges. With this greater mass, a classical treatment can be applied in which the polaron acts as a pseudo-atom obeying Newton's laws. Moreover, if the dynamics of the polaron pseudo-atoms can be modeled on a potential energy surface defined by the atoms in the OPV active layer (allowing the properties of the active layer atoms to be considered without explicit treatment of their dynamics), the scale of the problem is drastically reduced. The typical OPV charge density of 1021 to 1023 polarons per m3 indicates that a 100 nm thick region would only contain 1–100 polarons.16,26–28 Here, we present a multiscale approach grounded in constrained density functional theory (CDFT)29 calculations. We demonstrate that once a set of CDFT calculations are conducted to build a potential energy surface (PES) for LMD charge transfer, the transfer process itself can be modeled at an almost negligible computational cost.
In this work, we do not tackle the full challenge of modeling a large region of an OPV, but rather we present the building blocks of such a method by studying the charge transfer properties of a pair of fullerenes. We apply our model to phenyl-C61-butyric acid methyl ester (PCBM) molecules, with the crystal structure shown in the upper part of Fig. 1.30 Fullerenes are widely used in organic semiconductors, with PCBM being one of the most commonly used electron acceptors in OPVs. PCBM is also a convenient choice for developing our model due to recent work suggesting that excess charges are mostly localized to a single molecule in PCBM materials,31 allowing a straightforward application of our model in which charges are assumed to hop from one molecule to the next in localized states. Defining the extent of delocalization of a charge in a given material is a challenge in itself (and in fact there is conflicting literature regarding PCBM, with ref. 32 suggesting that the charge tends to delocalize over multiple molecules). If a polaron is delocalized over multiple molecules but still moves via thermally activated hopping, our model is still in principle applicable. However, the computational cost would increase, as a more delocalized state would require a larger number of atoms in each CDFT calculation. Here for convenience we work with a small polaron restricted to a single PCBM molecule.
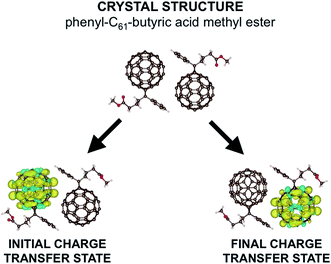 | ||
| Fig. 1 Here we show the crystal structure of two PCBM molecules as obtained by ref. 29. Below we show the difference in α and β spin densities for the two constrained structures used to construct the reaction coordinate. We see that CDFT produces an anionic electronic state in which one excess charge with α spin is constrained to a chosen set of atoms. | ||
We emphasize that the model we present of a polaron traveling via hopping is not an accurate description of charges in every organic semiconductor. The nature of charge transfer in these materials is a very active area of research. Dynamics of polaron transport derived from a master equation approach demonstrate that polarons may exhibit hopping or band-like transport depending on parameters such as system-phonon coupling strength and temperature.33 Some materials have shown signs of band-like transport, while other literature suggests that charge transport in organic semiconductors is not fully described by a hopping or band-like transport model.34–36 Our description of the charge as a classical particle governed by the dynamics of LMD is not appropriate for these cases. Rather, our model provides an effective description for the case of polaronic charges that transfer between molecules via a hopping process and are effectively weighed down by their coupling to nuclei. We argue that in such cases, the polaron can be conceptualized a classical pseudo-atom with unique opportunities for theoretical modeling.
The use of CDFT to produce diabatic PESs, and, via diagonalization of the resulting Hamiltonian, produce adiabatic PESs, is well established. For example, this method has been used to calculate charge transfer rates via Marcus theory.29,37–42 In 2000, Kim et al. suggested that a charge could be treated via the Langevin equation.43 Beyond CDFT and LMD, many other models of charge transport in organic semiconductors have been proposed (see ref. 14, 19, 35 and 44–47 for thorough discussions of previous work). However, to our knowledge no one has conducted molecular dynamics simulations of polaron dynamics using CDFT PESs. Here we present such simulations and the resulting predictions of transfer rates. Going beyond transfer rates that describe charge transfer in a material with a single number, we also show how the simulation data provide insight into exactly when and how individual transfer events occur. We demonstrate that the LMD simulation approach is unique both in the information that can be incorporated into the model and the information that can be extracted from the results.
The model and its application to PCBM
First, we give a brief overview of the concept of pseudo-atom charge transfer. We then summarize the fundamental steps in building this pseudo-atom model, conducting simulations, and analyzing the results. The subsequent sections each correspond to one of these steps. Each section corresponding to a given step will first present the formalism in general terms and then describe its application to PCBM charge transfer.Overview of the pseudo-atom approach
Henceforth we will use the phrases “polaron” and “pseudo-atom” interchangeably to emphasize that within our model, the charge along with its coupling to nuclear positions together form a quasi-particle or “pseudo-atom.” It is with this pseudo-atom that classical dynamics are applied. In this approach the pseudo-atom is not described by the charge alone, but rather by a composite degree of freedom which is a combination of the positions of the nuclei that then determine the location of the charge. This definition of a polaron as a charge coupled to nuclei describes the nature of small polarons in organic semiconductors, and captures the entangled nature of the charge and its influence on its surroundings.Our PES describes the energy of the pseudo-atom as it moves from one molecule to another (the process of polaron transfer). Because our pseudo-atom describes a charge coupled to nuclei, this transfer process is described by the gradual change in the positions of the PCBM atoms that occurs as the charge moves in space from the initial state to the final state. We can think of this gradual change in nuclear positions as the “reaction coordinate” for polaron transfer. The PES is created as a function of this reaction coordinate. The PES as a function of the reaction coordinate can then be transformed to a PES as a function of a spatial coordinate, which is then utilized in LMD simulations. This derivation of the PES is discussed in detail below.
The propagation of a particle in one dimension in the LMD formalism is described by the Langevin equation:18
| mẍ = −∇U(x) − γmẋ + R(t) | (1) |
Summary of formalism and its implementation
Before discussing the details of the model, we pause here to give a step-by-step summary of the seven fundamental steps of this formalism. Each of these steps (described only briefly in the summary below) will be presented in detail in the following sections.(1) Perform CDFT calculations, as well as unconstrained DFT calculations, to find the optimized geometries of the initial state, final state, and transition state. These three optimized structures are used to form a “reaction coordinate”, where the reaction coordinate describes the gradual change in nuclear positions as the system moves from the initial state optimized geometry to the final state optimized geometry.
(2) Perform single-point CDFT calculations for a series of geometries along the reaction coordinate. There are two sets of single-point CDFT calculations. In one, the charge is constrained to a single fullerene (the initial state). In the next, the charge is constrained to the other fullerene (the final state). By implementing these constraints while gradually changing the geometries, we obtain diabatic PESs for charge transfer.
(3) Use diabatic PESs to compute the adiabatic PESs. The lower adiabat is then used to create our PES for LMD.
(4) This adiabatic PES, like the diabatic PESs, is a function of the reaction coordinate. However, we wish to obtain a pseudo-atom PES as a function of the spatial coordinate: the movement of the pseudo-atom in space as it travels over a distance of several angstroms from one fullerene to the next. In this fourth step, we convert the PES from a reaction coordinate to a spatial coordinate.
(5) Effective mass and friction are assigned (for PCBM, we will explore a range of values).
(6) The spatial-coordinate PES, the effective mass, and the friction are then used as input for our LMD simulations. Because the LMD equation involves a random force term (representing the thermal effects of the environment), many simulations should be performed to obtain an appropriate sampling of trajectories. Here we perform 500 simulations for each point in our parameter space (where the effective mass and friction terms are varied).
(7) LMD results are then analyzed to compute charge transfer rates and examine the details of polaron movement through space.
We describe this procedure in detail in the following sections, with each section presenting a given step in formalism and then discussing its application to PCBM.
As discussed above, it is also possible to use initial and final states in which a more delocalized charge is constrained to a set of several molecules. In this article, for the sake of simplicity, our language will refer to bimolecular systems in which a charge is constrained to a single molecule.
The optimized geometries are represented with arrays R, where each array contains the xyz coordinates of each atom in the PCBM molecules. The geometries corresponding to the reaction coordinate Rq are then extracted from the optimized geometries of the initial state (R1), transition state (RT), and final state (R2) for the charge transfer event. This gradual change can be described by the following interpolation suggested by Wu et al.:40
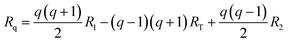 | (2) |
In implementing step #1 for the PCBM dimer, the crystal structure of two PCBM molecules shown in the upper part of Fig. 1 is used as the starting structure for all optimizations. Although the disordered nature of OPVs almost certainly leads to significant variability in the relative orientations of PCBM molecules, here for simplicity we work only with the crystal structure. Other work applying DFT to the PCBM crystal structure shows that use of this geometry produces efficiency results consistent with experimental observations of charge mobility in PCBM.48 The parameters of the DFT calculations are described in the ESI.† Due to the difficulty of defining an implicit solvent that represents a solid state OPV environment, the DFT calculations are conducted in the gas phase (with effects of the environment inherently included in the mass and friction of the LMD formalism).
A full-dimensional LMD calculation would obviously require a full-dimensional PES, which, although in principle possible, would be a major endeavor to derive from a set of CDFT calculations. Here we suggest a simpler approach: we perform LMD for a charge transfer event in which the charge is assumed to move in a straight line from one molecule to another, allowing a one-dimensional (1D) PES to be used. A 1D approach to modeling polaron transfer has been successfully applied in other work studying organic semiconductors, where a master equation approach to modeling polaron transfer demonstrated good agreement with experimental charge transfer rates when applied to a 1D model system.33
In applying steps #2 and #3 to PCBM, some experimentation (including the variation of density functional models, constraints, and omission of outlying points) was necessary to obtain physically reasonable PESs. We describe this process in detail in the ESI,† noting that such careful treatment of CDFT results may frequently be necessary to create appropriate PESs for this model. Ultimately we obtained the diabats and adiabats shown in Fig. 2, which give energies as a function of the reaction coordinate. These diabats are obtained from 17 points along the reaction coordinate; because a continuous adiabat is needed for LMD, all simulations employed a cubic spline interpolation to create a continuous PES. As discussed above, this reaction coordinate describes the change in positions of the atoms in the PCBM molecules as a polaronic charge moves from one molecule to another. As described in eqn (2), this reaction coordinate is a function of the interpolation parameter q, which is shown on the x-axis of Fig. 2. (While a range of −1 ≤ q ≤ 1 is used in the creation of the reaction coordinate, the omission of outlying points described in the ESI† leaves the range of −1 ≤ q ≤ 0.6 shown in Fig. 2.) This charge transfer event is illustrated by the CDFT spin density images shown below the plot.
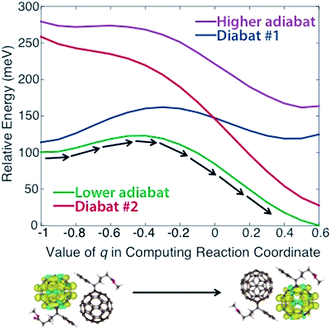 | ||
| Fig. 2 Diabatic and adiabatic PESs obtained from CDFT calculations. These PESs are a function of reaction coordinate rather than space. The x-axis shows the value of the interpolation parameter q of eqn (2) that is used to derive the reaction coordinate. Diabat #1/2 corresponds to constraint of the charge to fullerene #1/2 as referenced in the text. Images of the initial and final spin densities are shown to represent the change in the system as it moves along the reaction coordinate. As indicated by the black arrows, transport in our model represents movement along the lower energy adiabat. | ||
We note that the PES used for the calculations is asymmetric, with an adiabatic final state energy 100.4 meV lower than the adiabatic initial state energy, as shown in Fig. 2. This deviation will lead to somewhat higher transfer rates relative to a symmetric PES. The asymmetry of the PES is partly an artifact of the removal of outlying points, as discussed in the ESI.† However, we also found that the CDFT calculations consistently produced different diabatic energies for the initial and final states, in spite of the dimer system having Ci symmetry. This deviation reflects the challenge of performing geometry optimizations for the large systems involved in OPVs, where geometries are prone to become trapped in local minima. One could force symmetry into the reaction coordinate by performing a single CDFT calculation and applying the result to both the initial and final states via symmetry operations; however, there is nothing especially desirable about a symmetric PES for methods development purposes. An asymmetric PES would actually be the norm in real organic semiconductors because they frequently are disordered, so we view the convergence-based asymmetry as an asset for testing the overall LMD approach. Of course, the disordered nature of OPVs must lead to great variation in the PESs between different pairs of molecules, and we wish to be clear that the goal of this work is not to explore the vast array of geometries and PESs that are present in a disordered OPV. We simply seek one reasonable PES for the purpose of developing and testing the LMD model.
The conversion to a spatial coordinate is straightforward, using the variables c1 and c2 that describe the contribution of each diabat to the adiabat at a given point on the reaction coordinate. The variables c1 and c2 are calculated when converting diabats to adiabats following ref. 40. With the positions of the fullerenes denoted as x1 and x2, the spatial coordinate of each adiabatic energy point is calculated as:
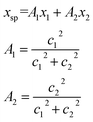 | (3) |
We thus obtain an adiabatic PES describing the energy of our pseudo-atom as it moves through space.
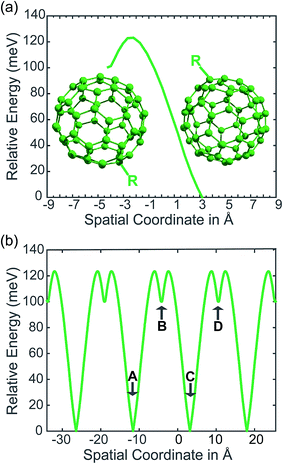
In our PCBM calculations, x1 and x2 are set 10 Å apart in accordance with the center-to-center distance in PCBM crystals.30Fig. 3a shows the lower adiabat converted from a reaction coordinate to a spatial coordinate as described by eqn (3). C60 cages are added to show the approximate location and size of the fullerenes. To create a complete PES for our LMD simulations, the PES was mirrored around the starting point and then expanded in space with periodic boundary conditions, as shown in Fig. 3b. Our LMD simulations begin with the pseudo-atom at point B, and we consider transfer to have occurred if the pseudo-atom reaches point A or C.
The creation of the PES described by steps #1–4 is summarized by the flow chart in Fig. 4. Beginning at the top of the flow chart, we see that the geometries of the initial, final, and unconstrained states are calculated, where yellow ovals indicate the atoms over which the charge is allowed to delocalize. These geometries are then applied viaeqn (2) to create a reaction coordinate Rq, using the interpolation parameter q that varies from −1 to 1. The coloring of the arrays R1, RT, and R2 shown in cyan, magenta, and purple in eqn (2) correspond to the coloring of the optimized geometries in the top panel. We then compute diabatic and adiabatic PESs as a function of this reaction coordinate, shown in this figure by a simplified representation of Fig. 2. Eqn (3) is then applied to convert the lower adiabatic PES from a reaction coordinate to a spatial coordinate xsp, with A1 and A2 giving the contributions of diabats #1 and #2 to the adiabat at each point on the reaction coordinate. The coloring of the variables x1 and x2 shown in red and blue correspond to the coloring of the diabats in the representation of Fig. 2. The adiabat as a function of spatial coordinate is then shown by a simplified representation of Fig. 3a. This adiabat as a function of space is expanded in one dimension to provide a PES that can be used for LMD, as shown by a simplified representation of Fig. 3b.
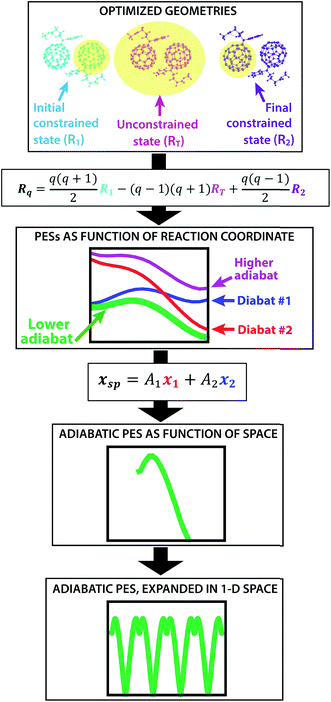 | ||
| Fig. 4 From top to bottom, a flow chart summarizes the procedure (described by steps #1–4 in the text) for creating a PES suitable for LMD simulations. First, we compute CDFT geometries of the initial and final states for charge transfer, as well as an unconstrained DFT geometry. In this top panel, we show these geometries with yellow ovals indicating the atoms over which the charge is allowed to delocalize. Eqn (2) converts this information to a reaction coordinate Rq using the interpolation parameter q that varies from −1 to 1. We then create diabatic and adiabatic PESs as a function of this reaction coordinate. Eqn (3) converts the lower adiabat from a reaction coordinate to a spatial coordinate xsp, with A1 and A2 giving the contributions of diabats #1 and #2 to the adiabat at each point on the reaction coordinate. This adiabat as a function of space is then expanded in one dimension to create a full PES for LMD. | ||
In our PCBM calculations, for simplicity we hold meff constant throughout the simulation. However, there is no reason why meff could not be varied as the pseudo-atom moves along the spatial coordinate, and this may in fact be more accurate and offer an advantage to the LMD simulation approach. In regions corresponding to a steeper diabat (reflecting a sharp increase in energy with movement of the nuclei), an increased effective mass may be appropriate. Friction seems more likely to be constant for a given temperature because it is a manifestation of the disordered vibrations of many atoms, but within our formalism both mass and friction can easily be varied as a function of space or time.
For our simulations we choose a wide range of trial values of meff that vary over several orders of magnitude from 7.22 × 10−2 to 7.22 × 103 amu, where the mass of an electron is 5.49 × 10−4 amu. We emphasize that this effective mass is neither the mass of the electron nor the mass of the nuclei to which is it coupled, but rather describes the properties of the quasi-particle that is defined by the coupling between charges and nuclei. In the wide range that we use in our calculations, it is unlikely that the polaron effective mass is well described by either the highest or lowest values. However, exploring results over a wide range of masses is interesting for the purposes of model development and comparison to experimental benchmarks. The variation in γ is more complex, as γ is a function of meff, with a heavier particle influenced less by random fluctuations in the environment. For our calculations a friction γ = pγD was utilized, with γD as a function of meff derived as shown in the ESI.† This γD is proportional to the square root of meff, and friction was varied over three orders of magnitude with p values of 0.036, 0.36, and 3.6. We found that this method optimized transfer rates, as discussed below.
 that it takes for a transfer event to occur. For example, in our system, this is the average amount of time it takes for a pseudo-atom beginning at point B to reach point A or C. We then calculate the rate as
that it takes for a transfer event to occur. For example, in our system, this is the average amount of time it takes for a pseudo-atom beginning at point B to reach point A or C. We then calculate the rate as  .
.
In our calculations of PCBM, all simulations are conducted at room temperature, with an initial random velocity assigned from a normal distribution with a mean of 0 and standard deviation of 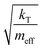 . For each point in the meff/γ parameter space, 500 calculations were performed, all with the pseudo-atom beginning at point B of Fig. 3b. For all values of meff and γ presented here, the simulation times tmax were long enough to allow all 500 simulations to achieve transfer to point A or C. We do not present data for meff/γ values for which all 500 runs did not achieve transfer within 5 ns—in such cases, it is not straightforward to calculate a transfer rate that is an appropriate comparison to the
. For each point in the meff/γ parameter space, 500 calculations were performed, all with the pseudo-atom beginning at point B of Fig. 3b. For all values of meff and γ presented here, the simulation times tmax were long enough to allow all 500 simulations to achieve transfer to point A or C. We do not present data for meff/γ values for which all 500 runs did not achieve transfer within 5 ns—in such cases, it is not straightforward to calculate a transfer rate that is an appropriate comparison to the 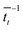 rates described above. Regardless, a system in which no transfer occurs within 5 ns would, by the Einstein relation discussed immediately below, correspond to a charge mobility several orders of magnitude lower than that needed for a functional OPV device, and therefore is not of practical interest.
rates described above. Regardless, a system in which no transfer occurs within 5 ns would, by the Einstein relation discussed immediately below, correspond to a charge mobility several orders of magnitude lower than that needed for a functional OPV device, and therefore is not of practical interest.
7.1 Experimental rate estimates. Before presenting our results, it is useful to define an estimate of transfer rates that can be used to benchmark the accuracy of our model. Although there is no direct way of experimentally measuring the rate of a fullerene-to-fullerene transfer, we can derive a reasonable value of the rate constant k from experimental estimates of charge mobilities. In one dimension, the diffusion constant of a material is calculated as
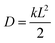 , where L is the mean length of particle movements. The Einstein relation gives the mobility
, where L is the mean length of particle movements. The Einstein relation gives the mobility 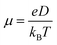 . Estimates of mobility in PCBM range from 0.001–0.08 cm2 V−1 s−1,69–73 and L is taken to be the PCBM crystal center-to-center distance of about 10 Å. This gives a range of k values from k = 5.14 × 109 s−1 to k = 4.11 × 1011 s−1. Below we demonstrate that our model produces results in reasonable agreement with these estimated values.
. Estimates of mobility in PCBM range from 0.001–0.08 cm2 V−1 s−1,69–73 and L is taken to be the PCBM crystal center-to-center distance of about 10 Å. This gives a range of k values from k = 5.14 × 109 s−1 to k = 4.11 × 1011 s−1. Below we demonstrate that our model produces results in reasonable agreement with these estimated values.
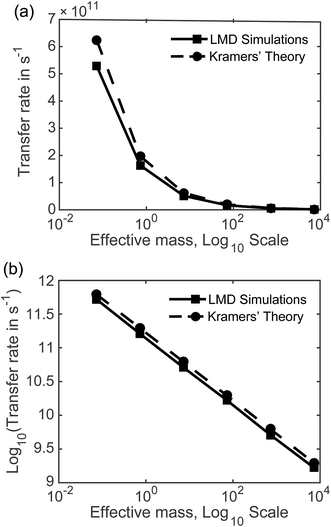
7.2 Rates as a function of mass and friction. Fig. 5 displays the mass dependence of k, where the rate in s−1 calculated from our LMD simulations is shown with the solid black line and meff is shown on a logarithmic scale. While mass is varied, friction was held constant at p = 3.6. Fig. 5a shows k as a function of meff and Fig. 5b shows the (base 10) logarithm of k, which shows a clear linear relationship between log[k] and log[meff] that is consistent over several orders of magnitude. We also note consistency with experimental estimates of rate, with values that are mostly in the 109 to 1011 s−1 range. Below we will compare our result to other theoretical calculations of transfer rate. However, we note that with an assignment of the mean length of particle movements L, the equalities presented in the previous paragraph can be used to convert our rates to mobilities or diffusion constants when these quantities are more convenient for comparison.
With the dashed line we show the Kramers' theory rate, a rate that is derived from the Langevin equation not via simulation but via an analytical derivation that is valid given the assumption of moderate to strong friction.74 We adapt the rate equation of Ensing:75
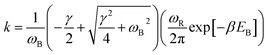 | (4) |
The frequencies ωR/B are derived from a harmonic oscillator treatment of the PES in the region of the reactants and the barrier, with 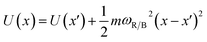 for the reactants and
for the reactants and 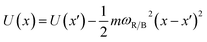 for the barrier. γ is a function of meff as described in the ESI.†EB corresponds to the difference in U between the reactants and the energy peak of the adiabat and β = 1/kBT. In this work we seek a method that is robust over a broad range of friction values and provides trajectories in addition to just a single rate. However, the Kramers' theory rates are a useful check to ensure that our application of LMD gives proper functional dependence.
for the barrier. γ is a function of meff as described in the ESI.†EB corresponds to the difference in U between the reactants and the energy peak of the adiabat and β = 1/kBT. In this work we seek a method that is robust over a broad range of friction values and provides trajectories in addition to just a single rate. However, the Kramers' theory rates are a useful check to ensure that our application of LMD gives proper functional dependence.
The simulation data and Kramers' theory results show almost exactly the same relationship between pseudo-atom effective mass and transfer rate. It is not obvious why the Kramers' theory rates are shifted a bit higher than the LMD simulation rates, and we suggest two explanations. One is the fact that Kramers' theory relies on assumptions about friction, while our simulations work directly with the LMD equation without simplifying premises. The other limitation of Kramers' theory is that it does not contain complete information on the PES; rather, the frequencies that enter the equation are derived from information on the PES only in the close proximity of the reactants and the barrier. In contrast, the complete shape of all regions of the PES is incorporated into the LMD simulations.
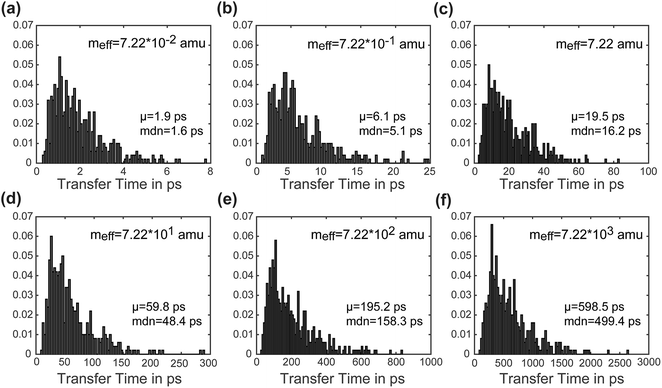
Another advantage of our simulation approach is that we can observe the distribution of rates in an ensemble of systems, rather than just observing a single rate that provides only averaged information. In Fig. 6, we present normalized histograms of transfer time tt in ps for all 500 calculations, where the y-axis gives the probability density of a particular transfer time. The mean and median of the transfer times are noted for each mass. For all masses the histograms show a long right tail and a mean transfer time that exceeds the median transfer time by about 20%. These results demonstrate that although the majority of the calculations achieve transfer in a relatively short period of time, a few outlying cases exhibit high transfer times. The ease of obtaining such information on ensemble distributions is a useful feature of our model.
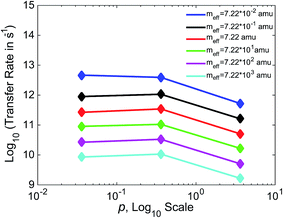
In Fig. 7, we show the relationship between γ and k for three values of γ, varying γ by an order of magnitude with each data point. Separate lines are shown for varying values of meff. For values of meff from 7.22 × 10−1 to 7.22 × 103 amu, we see a non-monotonic relationship between friction and efficiency, with the highest efficiency found at the intermediate value of p = 0.36. This non-monotonic relationship (“Kramers turnover”) is expected, having been predicted as early as 1940 by Kramers for the movement over a barrier of a particle subject to friction.74 We again see results consistent with experimental estimates, with rates in the 109 to 1012 s−1 range for these boundaries. The case that varies slightly from the others, with higher rates and a monotonic decrease in this range of meff, is that with the lowest meff of 7.22 × 10−2 amu.
As mentioned above, CDFT diabats can be easily used to calculate rates of charge transfer at the level of Marcus theory.76 Comparing the LMD rates to Marcus theory sheds some light on the challenge of defining meff. In Marcus theory the rate is:
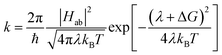 | (5) |
While Marcus theory is more effective in modeling a system at low friction, the Kramers' rate of eqn (4), in contrast, is valid only in the limit of moderate to high friction. The fact that the Kramers' rates of Fig. 5 are very close to the results of the LMD simulations (and experimental predictions) suggests that the moderate-to-high friction assumption is appropriate for this problem of polaron transfer (at least in PCBM). A key advantage of our LMD simulation approach is the fact that we are not constrained to simulating systems in either the low- or high-friction limit; we are free to choose any values of friction and meff that are appropriate for the system of interest. Higher friction can be explicitly included, and a relatively high effective mass can incorporate the sluggish nature of reorganization, offering an advantage to Marcus theory. However, we are also free to simulate low friction systems, where simulations do not suffer from the invalidation of eqn (4) that occurs at lower frictions. This provides a major advantage in terms of the flexibility of our model in simulating a variety of systems.
Another key distinction between the Marcus and Kramers' theory models is the question of their appropriateness in modeling an adiabatic transfer process. As noted in Section 3, previous work suggests that systems in which V ≪ kBT should exhibit nonadiabatic charge transfer. V > kBT in our PCBM simulations, consistent with adiabatic charge transfer. Cao and Jung apply a two-state diffusion equation modeling charge transfer to demonstrate that the nonadiabatic limit of charge transfer can be used to derive the Marcus rate expression, while the adiabatic limit can be used to derive the strong-friction limit of the Kramers’ rate.49 Thus, the fact that our simulations provide V > kBT is consistent with the fact that our rates differ greatly from Marcus rates and are much closer to the Kramers' rate of eqn (4).
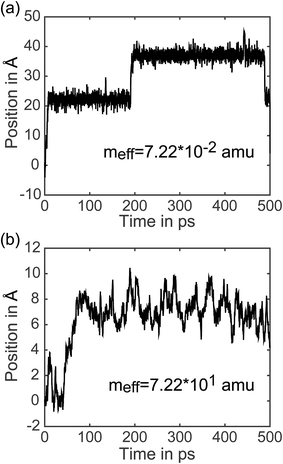
7.3 Analysis of individual trajectories. In addition to representing the properties of charge transfer with a single rate, LMD simulations can also provide information on when and why transfer events occur. (Did the charge have high velocity when passing through the well? Was the charge stuck in the well and kicked out by an energy perturbation from R(t)? What is the exact length of time between transfer events, and how long does it take the pseudo-atom to climb up one side of the PES peak?) We do not present results addressing all of these questions here, but to demonstrate the capabilities of our model, we present the full trajectory of positions for two arbitrary single simulations in Fig. 8. We show meff = 7.22 × 10−2 amu in (a) and meff = 7.22 × 101 amu in (b), where a distance shift of 7.4 Å represents a complete transfer event. (This deviation in distance from the 10 Å center-to-center distance of PCBM is a result of the spatial coordinate of our CDFT calculations described in eqn (3), which demonstrate that the pseudo-atom transport is best represented by a transfer event over this distance.) In Fig. 8, the pseudo-atom begins at point B of Fig. 3b, which is set to 0 on the y-axis. Observing movement along the spatial coordinate, there is a qualitative difference in transfer events. At lower mass the pseudo-atom lingers in the region of the well for some time and then hops quickly over the barrier, sometimes achieving two or three hops in a short period of time. With larger mass, in contrast, we see that the pseudo-atom not only experiences longer periods of time between transfer events, but also climbs up one side of the PES much more slowly compared to the quick hops we see with lighter mass. The ability to easily record and analyze these dynamical data is an important feature of our approach.
Discussion
Application to large-scale simulations
Before closing, we will discuss how this model can be applied to the simulation of large regions of an organic semiconducting device. Although such large-scale simulations are beyond the scope of this paper, a major advantage of this LMD model is that it can simulate transport at a very low computational cost, allowing simulation of large material volumes in a way that is intractable for other methods.Here we have presented one-dimensional PESs. Derivation of a three-dimensional PES from a series of one-dimensional intermolecular PESs would be difficult. We suggest an alternative in which transport over a sizable, three-dimensional region is simulated by patching together a series of one-dimensional transport events such as those that we present in this paper. It would be possible and valuable to calculate different PESs for different intermolecular orientations, thus representing the disordered nature of an organic semiconductor. (There would be an added computational cost in performing CDFT calculations for distinct orientations, but not at a prohibitive level.) Because there would be discontinuities in the PES as different curves were patched together, it would not be possible to smoothly continue the LMD simulations in time. Instead, after the completion of a transfer event, the simulation would pause to recalculate velocity based on the change in direction of the pseudo-atom as it proceeds to the next transfer event. Then the process would begin anew with an LMD simulation of transport to the next molecule. Of course, there are multiple molecules adjacent to the molecule on which the charge resides, so there are multiple transfer events that are possible. However, this does not significantly complicate things: the code can simply perform a simulation of transfer to each of the possible acceptors utilizing the same set of random numbers R(t), and the accepting molecule that attains transfer most quickly will then be selected as the new position of the pseudo-atom. We note that consideration of re-crossing is inherent in this approach.
As mentioned above, the small polaron description of a charge is not appropriate for all organic semiconductors, and on a device scale one must carefully consider whether this model is suitable for a given morphology. One challenge faced by theoretical modeling of organic semiconductors is the variation of morphology within a given device: many devices contain some combination of disordered regions and more ordered, crystalline regions. Because our potential energy surface is constructed solely based on the orientation between two molecules, information on overall morphology of a region is not considered in the PES. Intuitively, effective mass and friction are influenced by a region's morphology, and exploration of this relationship is an important direction for future work.
Conclusions
Here we have presented a Langevin molecular dynamics approach to modeling polaron motions in organic semiconductors. While charges are generally assumed to require a quantum mechanical treatment, we argue that a small polaron defined as a charge coupled to nuclei can be treated as a pseudo-atom that is appropriate for classical dynamics. We demonstrate that for the test case of polaron motion between two PCBM molecules, this method shows promising quantitative accuracy in predicting charge transfer rates. This LMD approach allows polaron motion to be considered in terms of dynamical trajectories, giving details on polaron transport that are not captured in a single inter-site transfer rate. The low cost of the simulations allows ensembles of hundreds of simulations to be easily performed, allowing a direct assessment of the variation in transfer rates that is caused by the random nature of environmental perturbations. It is also straightforward to record the polaron's position, velocity, and environmental perturbations R(t) over long periods of time, providing a clear view of when and why crossings and re-crossings occur. A challenge in this approach is the accurate definition of effective mass and friction, which are both complex functions of the polaron's interaction with the surrounding environment. We note that the interaction of charges with surrounding vibrations is a very active area of theoretical research20 that will hopefully lead to clarifications regarding the mass, friction, and other properties of polarons in organic semiconductors.A major advantage of this classical model is computational cost: by reducing a problem of millions of atoms to a calculation treating a small number of pseudo-atoms, the length and time scales of OPV charge transport are accessible. The greatest computational cost lies in the construction of an accurate PES, which requires atomistic CDFT calculations of large molecules. Many OPVs contain molecules larger than PCBM, and given the disordered nature of these systems, calculations would ideally use PESs built from CDFT calculations for many different inter-molecular orientations. Fortunately, recent improvements in linear-scaling DFT have dramatically decreased the cost of treating large molecules. With CDFT now available in linear-scaling DFT software packages,17,78–81 PES development for a few dozen possible orientations is feasible and the disordered nature of these systems can be captured.
The slow rate of charge transport in organic photovoltaics and other semiconductors presents a major challenge in the development of viable technologies. The charge transport model we present here is essentially a multiscale method in which atomistic ab initio calculations of a small bimolecular system serve as a foundation for classical dynamics over large distances. This method is not only computationally affordable but also unique in the information that can be incorporated into the model and the information that is provided by the results. We emphasize that although the low computational cost makes simulation of large regions tractable, we have demonstrated here that simulating even a single transfer event provides substantial insight into the polaron and its transfer process. The use of this model at any scale is expected to provide multiple insights into charge transfer dynamics that may facilitate the development of the next generation of organic electronics.
Acknowledgements
This work was performed at the Center for Nanoscale Materials, a U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences User Facility under Contract No. DE-AC02-06CH11357. This work employed resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. T. Van Voorhis was supported by NSF grant CHE-1464804. S. Tretiak acknowledges support of the Center for Integrated Nanotechnology (CINT), a U.S. Department of Energy and Office of Basic Energy Sciences User Facility, at Los Alamos National Laboratory (LANL). K. Pelzer was supported by the Aneesur Rahman Fellowship of Argonne National Laboratory. R. Larsen acknowledges support by the U.S. Department of Energy under Contract No. DE-AC36-08-GO28308 with the National Renewable Energy Laboratory.References
- J. Ferraris, D. O. Cowen, V. Walatka and J. H. Perlstein, J. Am. Chem. Soc., 1973, 95, 948–949 CrossRef CAS.
- N. S. Lewis, Science, 2007, 315, 798–801 CrossRef CAS PubMed.
- A. J. Heeger, Adv. Mater., 2014, 26, 10–28 CrossRef CAS PubMed.
- C. W. Lee, O. Y. Kim and J. Y. Lee, J. Ind. Eng. Chem., 2014, 20, 1198–1208 CrossRef CAS.
- H. D. d. Gier, F. Jahani, R. Broer, J. C. Hummelen and R. W. A. Havenith, J. Phys. Chem. A, 2016, 120, 4664–4671 CrossRef PubMed.
- L. Li, W. Niu, X. L. Zhao, X. N. Yang and S. W. Chen, Sci. Adv. Mater., 2015, 7, 2021–2036 CrossRef CAS.
- L. Y. Lu, M. A. Kelly, W. You and L. P. Yu, Nat. Photonics, 2015, 9, 491–500 CrossRef CAS.
- H. Youn, H. J. Park and L. J. Guo, Small, 2015, 11, 2228–2246 CrossRef CAS PubMed.
- I. Etxebarria, J. Ajuria and R. Pacios, Org. Electron., 2015, 19, 34–60 CrossRef CAS.
- I. Etxebarria, J. Ajuria and R. Pacios, J. Photonics Energy, 2015, 5, 057214 CrossRef.
- S. B. Darling and F. You, RSC Adv., 2013, 3, 17633 RSC.
- K. A. Mazzio and C. K. Luscombe, Chem. Soc. Rev., 2015, 44, 78–90 RSC.
- M. V. Jacob, Electronics, 2014, 3, 594–597 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. D. S. Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- I. H. Nayyar, E. R. Batista, S. Tretiak, A. Saxena, D. L. Smith and R. L. Martin, J. Phys. Chem. Lett., 2011, 2, 566–571 CrossRef CAS.
- C. G. Shuttle, R. Hamilton, J. Nelson, B. C. O'Regan and J. R. Durrant, Adv. Funct. Mater., 2010, 20, 698–702 CrossRef CAS.
- D. R. Bowler and T. Miyazak, Rep. Prog. Phys., 2012, 75, 036503 CrossRef CAS PubMed.
- T. Schlick, Molecular modeling and simulation: an interdisciplinary guide, Springer-Verlag, New York, 2002 Search PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003 CrossRef PubMed.
- A. Zhugayavych and S. Tretiak, Annu. Rev. Phys. Chem., 2015, 66, 305–330 CrossRef PubMed.
- I. H. Nayyar, E. R. Batista, S. Tretiak, A. Saxena, D. L. Smith and R. L. Martin, J. Chem. Theory Comput., 2013, 9, 1144–1154 CrossRef CAS PubMed.
- I. Nayyar, E. Batista, S. Tretiak, A. Saxena, D. L. Smith and R. L. Martin, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 935–942 CrossRef CAS.
- Y. Jiang, X. Zhong, W. Shi, Q. Peng, H. Geng, Y. Zhao and Z. Shuai, Nanoscale Horiz., 2016, 1, 53–59 RSC.
- Y. Jiang, Q. Peng, H. Geng, H. Ma and Z. Shuai, Phys. Chem. Chem. Phys., 2015, 17, 3273–3280 RSC.
- J. Xi, D. Wang and Z. Shuai, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 215–227 CrossRef CAS.
- C. G. Shuttle, A. Maurano, R. Hamilton, B. O'Regan and J. C. d. Mello, Appl. Phys. Lett., 2008, 93, 183501 CrossRef.
- D. Rauh, D. Carsten and V. Dyakonov, Adv. Funct. Mater., 2012, 22, 3371–3377 CrossRef CAS.
- K. M. Pelzer, M. K. Y. Chan, S. K. Gray and S. B. Darling, J. Phys. Chem. C, 2014, 118, 21785–21797 CAS.
- Q. Wu and T. V. Voorhis, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 024502 CrossRef.
- M. T. Rispens, A. Meetsma, R. Rittberger, C. J. Brabec, N. S. Sariciftci and J. C. Hummelen, Chem. Commun., 2003, 2116–2118 RSC.
- G. D'Avino, Y. Olivier, L. Muccioli and D. Beljonne, J. Mater. Chem. C, 2016, 4, 3747–3756 RSC.
- D. L. Cheung and A. Troisi, J. Phys. Chem. C, 2010, 114, 20479–20488 CAS.
- C. K. Lee, J. Moix and J. Cao, J. Chem. Phys., 2015, 142, 164103 CrossRef PubMed.
- A. Troisi and G. Orlandi, Phys. Rev. Lett., 2006, 96, 086601 CrossRef PubMed.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347–2358 RSC.
- S. Fratini and S. Ciuchi, Phys. Rev. Lett., 2009, 103, 266601 CrossRef CAS PubMed.
- S. Difley and T. V. Voorhis, J. Chem. Theory Comput., 2011, 7, 594–601 CrossRef CAS PubMed.
- B. Kaduk, T. Kowalczyk and T. V. Voorhis, Chem. Rev., 2012, 112, 321 CrossRef CAS PubMed.
- T. V. Voorhis, T. Kowalczyk, B. Kaduk, L.-P. Wang, C.-L. Cheng and Q. Wu, Annu. Rev. Phys. Chem., 2010, 61, 149–170 CrossRef PubMed.
- Q. Wu and T. V. Voorhis, J. Chem. Phys., 2006, 125, 164105 CrossRef PubMed.
- Q. Wu and T. V. Voorhis, J. Phys. Chem. A, 2006, 110, 9212 CrossRef CAS PubMed.
- S. Difley, L. P. Wang, S. Yeganeh, S. R. Yost and T. V. Voorhis, Acc. Chem. Res., 2010, 43, 995 CrossRef CAS PubMed.
- S. H. Kim, T. Zyung, H. Y. Chu, L.-M. Do and D.-H. Hwang, Phys. Rev. B: Condens. Matter, 2000, 61, R854–857 CrossRef.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeler and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- A. Massé, P. Friederich, F. Symalla, F. Liu, R. Nitsche, R. Coehoorn, W. Wenzel and P. A. Bobbert, Phys. Rev. B, 2016, 93, 195209 CrossRef.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- S. Stafström, Chem. Soc. Rev., 2010, 39, 2484–2499 RSC.
- J. C. Aguirre, C. Arntsen, S. Hernandez, R. Huber, A. M. Nardes, M. Halim, D. Kilbride, Y. Rubin, S. Tolbert, N. Kopidakis, B. Schwartz and D. Neuhauser, Adv. Funct. Mater., 2014, 24, 784–792 CrossRef CAS.
- J. Cao and Y. Jung, J. Chem. Phys., 2000, 112, 4716–4722 CrossRef CAS.
- S. Chakravarty and A. J. Leggett, Phys. Rev. Lett., 1984, 52, 5–8 CrossRef.
- A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fisher, A. Garg and W. Zwerger, Rev. Mod. Phys., 1987, 59, 1–85 CrossRef CAS.
- J. E. Straub and B. J. Berne, J. Chem. Phys., 1987, 87, 6111–6116 CrossRef CAS.
- J. Cao and G. A. Voth, J. Chem. Phys., 1997, 106, 1769–1779 CrossRef CAS.
- J. Cao, Chem. Phys. Lett., 1999, 312, 606–612 CrossRef CAS.
- D. Y. Yang and R. I. Cukier, J. Chem. Phys., 1989, 91, 281–292 CrossRef CAS.
- A. Lucke, C. H. Mak, R. Egger, J. Ankerhold, J. Stockburger and H. Grabert, J. Chem. Phys., 1997, 107, 8397–8408 CrossRef CAS.
- D. G. Evans, A. Nitzan and M. A. Ratner, J. Chem. Phys., 1998, 108, 6387–6393 CrossRef CAS.
- L. D. Zusman, Chem. Phys., 1980, 49, 295–304 CrossRef CAS.
- L. D. Zusman and D. N. Beratan, J. Chem. Phys., 1999, 110, 10468–10481 CrossRef CAS.
- J. Moix, M. Khasin and J. Cao, New J. Phys., 2013, 15, 085010 CrossRef.
- D. P. S. McCutcheon and A. Nazir, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 165101 CrossRef.
- H.-T. Chang and Y.-C. Cheng, J. Chem. Phys., 2012, 137, 165103 CrossRef PubMed.
- P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, New J. Phys., 2009, 11, 033003 CrossRef.
- M. B. Plenio and S. F. Huelga, New J. Phys., 2008, 10, 113019 CrossRef.
- J. Singh, E. R. Bittner, D. Beljonne and G. D. Scholes, J. Chem. Phys., 2009, 131, 194905 CrossRef PubMed.
- T. E. Dykstra, E. Hennebicq, D. Beljonne, J. Gierschner, G. Claudio, E. R. Bittner, J. Knoester and G. D. Scholes, J. Phys. Chem. B, 2009, 113, 656–667 CrossRef CAS PubMed.
- K. M. Pelzer, A. F. Fidler, G. B. Griffen, S. K. Gray and G. S. Engel, New J. Phys., 2013, 15, 095019 CrossRef.
- A. J. C. Ladd, Numerical methods for molecular and continuum dynamics. Lectures at the 3rd Warsaw School of Statistical Physics, Kazimierz, Poland, 2009 Search PubMed.
- A. M. Nardes, A. J. Ferguson, P. Wolfer, K. Gui, P. L. Burn, P. Meredith and N. Kopidakis, ChemPhysChem, 2014, 15, 1539–1549 CrossRef CAS PubMed.
- S. Günes, H. Neugebauer and N. S. Sariciftci, Chem. Rev., 2007, 107, 1324–1338 CrossRef PubMed.
- A. M. Nardes, A. L. Ayzner, S. R. Hammond, A. J. Ferguson, B. J. Schwartz and N. Kopidakis, J. Phys. Chem. C, 2012, 116, 7293–7305 CAS.
- A. J. Ferguson, N. Kopidakis, S. E. Shaheen and G. Rumbles, J. Phys. Chem. C, 2011, 46 Search PubMed.
- W. J. Grzegorczyk, T. J. Savenije, T. E. Dykstra, J. Piris, J. M. Schins and L. D. A. Siebbeles, J. Phys. Chem. C, 2010, 114, 5182–5186 CAS.
- H. A. Kramers, Physica, 1940, 7, 284–304 CrossRef CAS.
- B. Ensing, Ph.D., VU University Amsterdam, 2003.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- H. Sumi and R. A. Marcus, J. Chem. Phys., 1986, 84, 4894 CrossRef CAS.
- L. E. Ratcliff, L. Genovese, S. Mohr and T. Deutsch, J. Chem. Phys., 2015, 142, 234105 CrossRef PubMed.
- L. E. Ratcliff, L. Grisanti, L. Genovese, T. Deutsch, T. Neumann, D. Danilov, W. Wenzel, D. Beljonne and J. Cornil, J. Chem. Theory Comput., 2015, 11, 2077–2086 CrossRef CAS PubMed.
- D. H. P. Turban, G. Teobaldi, D. D. O'Regan and N. D. M. Hine, Phys. Rev. B, 2016, 93, 165102 CrossRef.
- A. M. P. Sena, T. Miyazaki and D. R. Bowler, J. Chem. Theory Comput., 2011, 7, 884–889 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc04547b |
| This journal is © The Royal Society of Chemistry 2017 |