The limitation of electrode shape on the operational speed of a carbon nanotube based micro-supercapacitor

Abstract

In order to establish design rules for micro-supercapacitors (micro-SCs), the influence of electrode shape, specifically aspect ratio, was investigated on the operational speed of micro-SCs. The operational speed, as characterized by the relaxation time constant, was found to nonlinearly decrease (85 to ∼0.5 ms) as the electrode aspect ratio increased (0.2 to 7). This was achieved by simplifying the electrode design to a basic parallel electrode geometry. In so doing, all factors, such as electrode height, volume, electrolyte volume, inter-electrode separation, etc. could be maintained while adjusting the electrode aspect ratio (AR). In addition, the results showed that the relaxation time constant showed only moderate improvement for aspect ratios above 1, illustrating the limitation on this single shape parameter. Investigation into the underlying reasons for this behavior showed that the observed dependence of the relaxation time constant with the electrode AR originated from differences in the electrolyte resistance within the electrode for each electrode shape as determined by electrochemical impedance spectroscopy. Although these results demonstrate that the operational speed of a micro-SC can be improved by increasing the electrode AR, our results also show that this factor alone is insufficient to improve the speed into the microsecond regime within our experimental scope.

---

Introduction

Micro-supercapacitors (micro-SCs) have received increased attention over the past few years due to their combination of size and performance and from the availability of new materials.¹ Numerous groups have reported the fabrication of devices exemplified by their small size (micro-scale), high capacitance, design-ability, and importantly their compatibility with portable and wearable electronics.^2,3 For example, Pech et al. reported the fabrication of planar micro-SCs of 25 mm² order, which demonstrated a 100-fold decrease in volume while showing performance similar to conventional capacitors.⁴ In addition, Gao et al. reported the fabrication of micro-SCs possessing capacitance nearly twice that of macro-scale supercapacitors.⁵ Further, Tian et al. demonstrated a complex micro-SC circular design using standard lithographic processing.⁶ These advances demonstrate that micro-SCs can possess higher performance than commercial capacitors and advance micro-SCs closer to industry.^7,8

From a practical standpoint, applications, for which micro-SCs are particularly well-suited due to their size, are rectifiers⁹ and mobile power devices.^10,11 Therefore, in addition to the capacitance, the operational speed represents a critically important property as it is directly related to deliverable power. Therefore, limitations in operational speed results in the failure of the capacitor, i.e. drop on capacitance, at high operational speeds.¹² Several general factors affect the operational speed, such as electrolyte,^13–15 electrode material,^16,17 and electrode design.^4,7,18 Electrode design is the most common approach, because it does not require changes of the used materials and technology. While aqueous electrolytes benefit from the fast ions (one order higher diffusivity in water¹⁹) but their operational voltage range is limited. Further, new electrode materials run the risk of incompatible processing with the existing device components. Most reports investigating the effect of electrode shape on the operational speed use an interdigitated electrode design in order to maximize the ion accessibility by maximizing the length of the inter-electrode separation.²⁰ Unfortunately, due to the geometrical complexity of the interdigitated electrode design, a change in one aspect, i.e. number, width, length of fingers, will lead to a change in others. For example, an increase in the electrode interdigitated finger length can lead to an increase in volume, i.e. surface area, or a decrease in number of fingers. Further, an increase to the finger width can lead to changes in volume, inter-electrode separation distance, as well as its length. Due to this geometrical cross-talk, elucidation of the dominant electrode design feature is intrinsically difficult. Furthermore, differences in fabrication processes and materials in the current reports make the extraction of a common set of design rules difficult.

In this communication, we report a study revealing the influence of electrode shape, in particular aspect ratio, on the operational speed of micro-SCs. This study was made possible by simplifying the electrode design to a parallel electrode geometry to maintain all factors, such as electrode height, volume, electrolyte volume, inter-electrode separation, etc. while only modulating the aspect ratio (AR) of the electrodes. Our results demonstrate that the AR of the electrodes have a nonlinear dependence on the operational speed, as defined by the relaxation time constant. Additional examination of the rate limiting processes showed that the observed dependence of the relaxation time constant with the electrode AR originates from the difference in the electrolyte resistance between the respective electrode designs as determined by electrochemical impedance spectroscopy (EIS). Our results further show that despite the nonlinear relationship between the aspect ratio and operational speed, a limitation does exist for the improvement of operational speed through the electrode shape.

Results and discussion

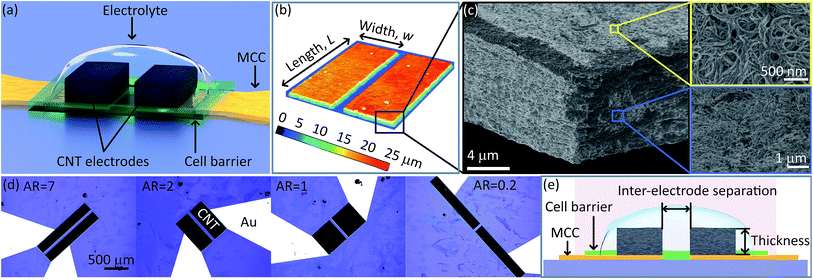
To begin, we fabricated micro-SCs with a simplified electrode design composed of a set of two opposing, parallel rectangular electrodes in order to examine the influence of the electrode shape on the operational speed (Fig. 1a). In general, the devices consisted of a metal current (MC) pathways, aqueous electrolyte, epoxy cell barrier to confine the electrolyte, and electrodes patterned from a high concentrated dispersion of single wall carbon nanotubes (SWCNTs; Fig. 1a and b). Standard lithographic processes were utilized to pattern the CNT film made from the dispersion for ensure high accuracy (Fig. 1c). We fabricated four different micro-SCs, which were identical in every way (e.g. electrode material, electrode volume, electrode thickness, inter-electrode separation, electrolyte amount, etc.) with the exception of the electrode length and width (Fig. 1d and e, Table S1 and Fig. S1†). In fact, to ensure consistency in fabrication, the set of capacitors were fabricated in parallel and with the same CNT film for the electrodes²¹ (Fig. 1c). The pore structure of the CNT film was carried out using the Barrett–Joyner–Halenda (BJH) analysis from nitrogen adsorption/desorption isotherm. The pore size distribution fell within the range between 2 nm and 50 nm (Fig. S2a and b†). SEM observation of the cross-section for each of the configurations showed the apparent pore structures is similar, which is reasonable as they were fabricated from the same CNT film (Fig. 1b and e, inset). The aqueous electrolyte (35 wt% H₂SO₄) was used for allowing the optimum high rate performance with fast ion diffusion (Fig. S1 and S3†).

Fig. 1 One-dimensional solvable approach to define the relationship of the electrode shape vs. the operational speed: (a) a digital illustration of the micro-supercapacitor; (b) a laser scanning microscopy (LSM) digital image – the uniformity and structure of electrodes and (c) SEM images, respectively; (d) optical microscopy (OM) images of a set of electrodes with the various electrode aspect ratios (AR); (e) a schematic illustration – a side of the micro-SC cell.

Maintaining an identical electrode volume was important as the capacitance is directly related to the amount of the electrode material (e.g. surface area). As the set of designs were made from the same CNT film, the film thickness was nearly identical, simplifying the consideration of our capacitor from 3-D to 2-D. Thusly, the total volume could be simply ensured by maintaining a constant lateral area (i.e. L × w) for each electrode pair (Fig. 1b). Further, because of the geometric condition of fixed lateral area (L × w), our capacitor could be further simplified to 1-D, where each electrode configuration could be completely described by a single numerical value. For this, we chose the electrode aspect ratio (AR) being defined as the electrode width to length ratio (AR = L/w). Therefore, the AR in our study spanned from 7, 2, 1, and 0.2, respectively.

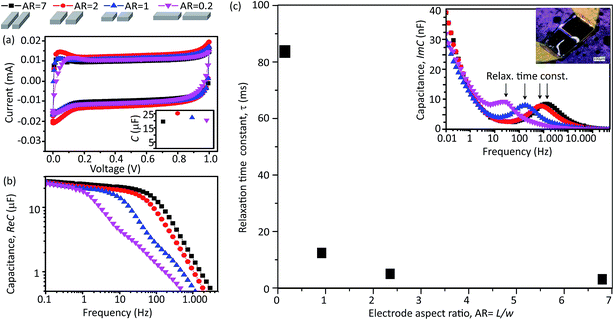
The capacitance for each micro-SC in our series was evaluated. Capacitance was evaluated by cyclic voltammetry (CV) using a VMP3 (Bio-Logic Instruments, US) potentiostat in a neutral gas environment at a rate of 0.5 V s⁻¹. The capacitance was characterized by a nearly an ideal rectangular shape indicating the efficient formation of the electric double layer (EDL) capacitance and the absence of parasitic reactions. The capacitance was estimated by calculating the enclosed area of the CV (AR = 7) and found to be ∼22 μF (Fig. 2a). CV characterization performed for the remaining electrode configurations showed nearly identical CV profiles. Furthermore, estimated capacitance for each of the electrode AR was nearly identical at 22.1, 25.0, 21.8, and 21.2 μF, for the AR of 7, 2, 1, and 0.2, respectively. This similarity in capacitance is direct confirmation on the accuracy on our ability to fabricate electrodes of identical volume. Importantly, this also represents an essential starting point for our study.

Fig. 2 The results of the electrode shape vs. the micro-SC's performance – the graphs comparing electrodes with various electrode ARs: (a) cyclic voltammograms, voltage vs. current, the inset – capacitance; (b) frequency vs. capacitance (real part); (c) the AR, vs. the relaxation time const., the inset – frequency vs. capacitance (imaginary part) and a LSM photo of micro-SC electrodes with the electrolyte.

To examine the differences in the operational speed, we used electrochemical impedance spectroscopy (EIS) as it affords evaluation of the charge–discharge cycling at higher rates than cyclic voltammetry.²² Through this method, we could evaluate our series of micro-SCs across a frequency range spanning four orders of magnitude (0.1 to over 1000 Hz). Each micro-SC was evaluated, and capacitance as a function of charge–discharge frequency was plotted for each of the four capacitor designs (Fig. 2b). From the comparison of the four capacitance–frequency profiles, we made several observations: (1) the initial capacitances at low frequency for each electrode AR were nearly identical and agreed well with the CV results; (2) the profile for each electrode AR was found to be quite similar as characterized by two regions: a nearly plateau region followed by a sharply decreasing region (decaying capacitance; the frequency at which this transition from the plateau region to the decaying capacitance region is called the “cut-off frequency”, which is typical of any capacitor and describes the maximum speed at which the device can operate while maintaining its capacitance²³); (3) the cut-off frequency, at which the decay began, differed for each electrode AR; (4) the slope of the capacitance decay differed for the different electrode AR. Specifically, AR = 7 showed the highest cut-off frequency ∼50 Hz and the steepest capacitance decay, followed in order by the aspect ratio, (AR = 2, 1, and 0.2, with the decrease up to 30, 4, and 0.9 Hz, respectively). A steep decaying capacitance behavior is expected for an ideal capacitor, which is indicative of the absence of side phenomena, such as the distributed charge storage.¹² To highlight the difference in operational performance, at ∼200 Hz, AR = 7 showed a ∼50% decrease in its initial capacitance, while AR = 1 and 0.2 showed a ∼85 and ∼95% decrease, respectively. Essentially, ARs = 1 and 0.2 failed to operate as supercapacitors.

To elucidate the impact of the electrode shape on the operational speed, we estimated the relaxation time constants (τ) for each design and plotted them as a function of the electrode AR. Conceptually, τ is defined as the inverse of the frequency at which the capacitor retains 50% of its full capacitance, and can be estimated from the location of the peak in a plot of the imaginary capacitance vs. frequency (Fig. 2c inset – right corner). From this plot, we made several observations. First, τ exhibited a nearly two-order, nonlinear decrease with asymptotic approach towards zero as the electrode AR increased 46-times. Second, a small increase in the AR from 0.2 to 1 resulted in a nearly one order drop in the relaxation time constant. Third, τ showed much weaker dependence on the aspect ratio (AR > 1) as evidenced by the mere 12 to 5 ms decrease. These results are clear evidence of the strong influence of the electrode aspect ratio, alone, on the operational speed of the micro-SC.

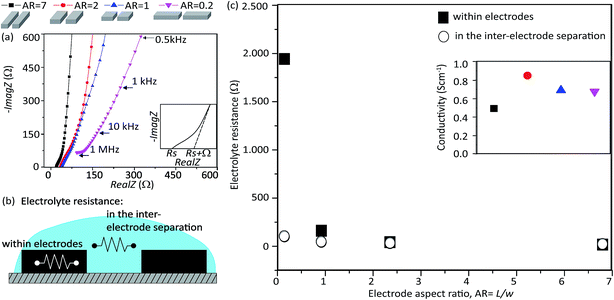
To investigate the underlying mechanism governing the dependence of τ and the electrode shape, we examined the electrolyte resistance for each supercapacitor design in our series. The electrolyte resistance, both within the electrodes and between the electrodes, has been reported to govern the operational speed as it describes the limitation of the electrolyte ions movement.²⁴ The electrolyte resistance was estimated from the Nyquist plot (complex plot of the real and imaginary components of the impedance) of the impedance spectra for each micro-SC in our series. It should be noted that EIS allows for the investigation of both bulk and interfacial processes down to the microsecond level.²⁵ The shape of the Nyquist plot for AR = 7 was characterized by three sections: a gradual incline, a sharp upswing transition, (related to the charge transfer at electrolyte/electrode interface) and a nearly linear, steep incline (related to the mass transport of electrolyte ions) and is typical for carbon-based electrodes using EDL storage mechanism (Fig. 3a).²⁶ Each of the electrode designs shared these general features, yet differed by the slopes of their respective nearly linear, steep sections. The x-intercept of a gradual incline section represents the sum of the ohmic resistance (equivalent series resistance) of the entire cell and the electrolyte resistance between the electrodes (i.e. in the inter-electrode separation), denoted as a series resistance, R_s. Following this procedure, the R_s for the electrode ARs, from 7, 2, 1, and 0.2, were found to be 20, 30, 43, and 99 Ω, respectively. In addition, the x-intercept of the linear extension of the nearly linear, steep section (depicted as Ω) represents the sum of R_s and the electrolyte resistance within the electrodes. Following this procedure, the x-intercepts (R_s + electrolyte resistance within the electrodes) for the electrode ARs, from 7, 2, 1, and 0.2, were found to be 17, 42, 161, and 2 k Ω, respectively. Therefore, from these two intercept values, the electrolyte resistances within the electrodes were estimated and plotted as a function of the electrode AR (Fig. 3c). The electrolyte resistance within the electrodes showed a strong, asymptotic behavior with increased electrode AR as observed for the relaxation time constant (Fig. 2c). Specifically, the electrolyte resistance dropped 114-times as the electrode AR increased from 0.2 to 1. Beyond the electrode AR of 1, the difference was significantly less.

Fig. 3 The results of the electrode shape vs. the electrolyte resistance – the graphs: (a) the Nyquist plot at high frequencies, realZ vs. imagZ, inset – the model used to estimate the resistances of the entire cell of the micro-SC (R_s) and inside the pores (Ω); (b) the schematic illustration – the electrolyte resistance within electrodes and in the inter-electrode separation; (c) the electrode aspect ratio vs. the electrolyte resistance, the inset – electrolyte conductivity in the inter-electrode separation.

We further examined the electrolyte resistance between the electrodes. Estimation was performed as follows. In general, R_s is a sum of the resistances of the MCC, CNT, MCC/CNT and electrolyte, as denoted, R_s = R_MCC + R_CNT + R_MCC/CNT + R_el. R_MCC and R_CNT were estimated using the actual dimensions of the device and were found to be insignificant compared to the intercept value. Specifically, the values for R_MCC and R_CNT were 0.2–1.1 and ∼0.02 Ω, respectively. Although the MCC/CNT resistance was unknown, the value was assumed to be a constant for all cases as the surface contact area was the same. Therefore, we could conclude that observed changes in the electrolyte + MCC/CNT resistance resulted from changes in the electrolyte resistance. These values were plotted as a function of the electrode AR (Fig. 3c). In contrast to the behavior observed for the electrolyte resistance within the electrodes, the electrolyte resistance in the inter-electrode separation exhibited no significant dependence on the electrode AR. The difference between the highest and lowest values were a ∼5 times difference. Furthermore, unlike the asymptotic behavior observed previously, the relative drop from each electrode AR was similar. It should be noted that to confirm the data are correct, we estimated the ionic conductivity (eqn (S1)–(S3)†) to be the same order for various designs with a good agreement to the referred value.^27,28 From these results, we conclude that the observed dependence of τ with the electrode AR originates from the difference in the electrolyte resistance within the respective electrode shapes. As the electrolyte resistance within the electrode depends on a number complex parameters, such as an electrolyte, pores size and shape, we cannot determine the specific rate limiting mechanisms with our experimental arrangement. It should be noted that within our scope of experiments, the pore structure was fixed, but previous reports have shown the strong effect of pore structure on the micro-super-capacitor operational speed.^29,30

Conclusions

We performed a study to clarify the relationship between the electrode aspect ratio on the micro-supercapacitor operational speed. This study was made possible by simplifying the electrode design to a parallel electrode geometry to maintain all factors, such as electrode height, volume, electrolyte volume, inter-electrode separation, etc. while only modulating the electrode AR. Our results showed that the dependence on the electrode shape, within our scope of length scale and nanoporous electrode materials, was surprisingly slight particularly for high electrode ARs. It indicates that increasing the aspect ratio follows a law of decreasing returns for high electrode ARs. Specifically, the improvement in the relaxation time constant was found to be most significant at ARs below 1 and significantly less significant for ARs above 1. The observed dependence of the relaxation time constant with the electrode AR originates from the difference in the electrolyte resistance within the respective electrode shapes as determined by the electrochemical impedance spectroscopy. Taken together, the results also show that although the operational speed of a micro-SC can be improved by increasing the AR, this factor alone is insufficient to improve the speed into the microsecond regime. Other design considerations, such as electrolyte, electrode material, electrode pore structure, etc. must also be considered for improving the operational speed into the microsecond regime. We believe that these results are completely applicable to the more complex interdigitated electrode design which is commonly used and hope that these results contribute to the development of general design rules for micro-supercapacitors.

Acknowledgements

The authors thank H. Hatori, Y. Soneda and Y. Kado from Energy Technology Research Institute, for discussion on electrochemistry. M. Fujii, R. Hikosaka, and M. Suzuki for assistance in making CNT ink. M. Fujii and H. Jinping for assistance in the porosity and BET measurements and analysis. The authors also thank I. Laszczyk for his contribution to 2D and 3D figures. This paper is based on results obtained from a project commissioned by the New Energy and Industrial Technology Development Organization (NEDO). K. U. L. designed the study and analyzed the data, designed, fabricated, and measured cells, K. K. provided assistance in making CNT ink, porosity and BET measurements, and their analysis. D. N. F., K. U. L., and A. S. co-wrote the paper, A. S., T. Y. and K. H. supervised the project.

References

1. P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845.
2. M. Beidaghi and Y. Gogotsi, Energy Environ. Sci., 2014, 7, 867.
3. American Chemical Society, https://www.acs.org/content/acs/en/pressroom/newsreleases/2016/august/stretchy-supercapacitors-power-wearable-electronics.html, accessed: September 2016.
4. D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P.-L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651.
5. W. Gao, N. Singh, L. Song, Z. Liu, A. L. M. Reddy, L. Ci, R. Vajtai, Q. Zhang, B. Wei and P. M. Ajayan, Nat. Nanotechnol., 2011, 6, 496.
6. X. Tian, M. Shi, X. Xu, M. Yan, L. Xu, A. Minhas-Khan, C. Han, L. He and L. Mai, Adv. Mater., 2015, 27, 7476.
7. M. F. El-Kady and R. B. Kaner, Nat. Commun., 2013, 4, 1.
8. Z.-S. Wu, K. Parvez, X. Feng and K. Mullen, Nat. Commun., 2013, 4, 1.
9. M. Zhang, Q. Zhou, J. Chen, X. Yu, L. Huang, Y. Li, C. Li and G. Shi, Energy Environ. Sci., 2016, 9, 2005.
10. Z. L. Wang, Adv. Mater., 2012, 24, 280.
11. B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928.
12. J. R. Miller, R. A. Outlaw and B. C. Holloway, Science, 2010, 329, 1637.
13. A. Jänes, H. Kurig, T. Romann and E. Lust, Electrochem. Commun., 2010, 12, 535.
14. G. Ma, E. Feng, K. Sun, H. Peng, J. Li and Z. Lei, Electrochim. Acta, 2014, 135, 461.
15. M. K. Singh, M. Suleman, Y. Kumar and S. A. Hashmi, Energy, 2015, 80, 465.
16. X. Wang, Y. Zhang, C. Zhi, X. Wang, D. Tang, Y. Xu, Q. Weng, X. Jiang, M. Mitome, D. Golberg and Y. Bando, Nat. Commun., 2013, 4, 1.
17. J. Chang, S. Adhikari, T. H. Lee, B. Li, F. Yao, D. T. Pham, V. T. Le and Y. H. Lee, Adv. Eng. Mater., 2015, 5, 1.
18. M. Beidaghi and C. Wang, Adv. Funct. Mater., 2012, 22, 4501.
19. W. Liu, C. Lu, X. Wang, R. Y. Tay and B. K. Tay, ACS Nano, 2015, 9, 1528.
20. L. Pilon, H. Wang and A. d'Entremont, J. Electrochem. Soc., 2015, 162, A5158.
21. K. Laszczyk, K. Kobashi, S. Sakurai, A. Sekiguchi, D. Futaba, T. Yamada and K. Hata, Adv. Eng. Mater., 2015, 5, 1.
22. Gamry Instruments, http://www.gamry.com/application-notes/battery-research/testing-electrochemical-capacitors-cyclic-voltammetry-leakage-current/, accessed: September 2016.
23. Y. Wada, J. Pu and T. Takenobu, Appl. Phys. Lett., 2015, 107, 1.
24. D. Pech, M. Brunet, T. M. Dinh, K. Armstrong, J. Gaudet and D. Guay, J. Power Sources, 2013, 230, 230.
25. S. Srivastav and R. Kant, J. Phys. Chem. C, 2011, 115, 12232.
26. R. Kötz and M. Carlen, Electrochim. Acta, 2000, 45, 2483.
27. K. Lota, A. Sierczynska, I. Acznik and G. Lota, Chemik, 2013, 67, 1138.
28. M. Latifatu, H. S. Lee, C. S. Yoon, J. Oh, J. H. Park, J. W. Park and J. M. Ko, Int. J. Electrochem. Sci., 2016, 11, 5353.
29. M. Zhang, Q. Zhou, J. Chen, X. Yu, L. Huang, Y. Li, C. Li and G. Shi, Energy Environ. Sci., 2016, 9, 2005.
30. A. C. Forse, C. Merlet, J. M. Griffin and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 5731.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, electrode design, electrode material, characterization, Table S1, Fig. S1–S3. Eqn (S1)–(S3). See DOI: 10.1039/c7se00101k

---