The effect of Mg-doping and Cu nonstoichiometry on the photoelectrochemical response of CuFeO2†
Anna
Wuttig
,
Jason W.
Krizan
,
Jing
Gu
,
Jessica J.
Frick
,
Robert J.
Cava
and
Andrew B.
Bocarsly
*
Department of Chemistry, Princeton University, Princeton, NJ 08544, USA. E-mail: bocarsly@princeton.edu; Fax: +1-609-258-2902; Tel: +1-609-258-3888
First published on 14th November 2016
Abstract
We report the tuning of CuFeO2 photoelectrodes by Mg doping and Cu deficiency to demonstrate the effects of carrier concentration on the photoresponse. Carrier type and concentration were quantitatively assessed using the Hall effect on pure, Mg-incorporated, and Cu-deficient pellets (CuFe1−xMgxO2 and Cu1−yFeO2, x = 0, 0.0005, 0.005, 0.02, and y = 0.005, 0.02) over the range of thermodynamic stability achievable using solid-state synthesis. The same samples were used in a photoelectrochemical cell to measure their photoresponse. We find that the material with the lowest p-type carrier concentration and the highest carrier mobility shows the largest photoresponse. Furthermore, we show that increasing the p-type carrier concentration and thus the conductivity to high levels is limited by the delafossite defect chemistry, which changes the majority carrier type from p-type to n-type near the Mg solubility limit (x = 0.05) and at high Cu defect concentrations.
1 Introduction
Semiconductor oxides offer unique advantages as photoelectrodes in photoelectrochemical cells (PEC). Unlike III–V semiconductors, which can degrade easily,1–5 oxide materials have been shown to exhibit long-term stability and easy processability.6–8 The oxides that yield photoreduced products from water or dissolved CO2, indicating alignment of solid/liquid electronic energies, tend to have wide band gaps,9–11 and thus they are not optimal materials for PEC applications. Their large band gaps and consequently lower absorption in the solar spectral region lead to decreased photoactivity and, ultimately, lower product yields.12While chemical doping has been employed as an avenue to reduce the band gap,13–16 this strategy shows discrepant results. Both increased17,18 and unchanged18–20 photoresponse with doping have been reported. A rarely approached avenue to optimize materials for photoelectrochemical applications is to use doping to interrogate the influence of a semiconductor photoelectrode's carrier concentration on its photoresponse. Here, we examine the influence of changing the carrier concentration on the photoresponse of the emergent photoelectrode CuFeO2.
Doping is known to increase a material's carrier concentration (N), and thus enhance its conductivity. When BiVO4 was doped with Mo17 or W,21 for example, enhancement in photoactivity was explained by a dramatic increase in the electron concentration. Similarly, doped Fe2O3 showed an increase in photoresponse that was attributed to greater conductivity.18 Conversely, increasing N can also hinder the performance of a photoelectrode. Large N can reduce photocurrents because the depletion width (WSC) is inversely proportional to N. Smaller WSC allows for a lesser volume from which photogenerated carriers can be formed, reducing the photoeffect.22,23
Thus, an optimal carrier concentration for photoresponse is expected. Here, we investigate this balance point for CuFeO2, a promising photoelectrode, by systematically changing the carrier concentration with doping. CuFeO2 is currently of interest due to its relatively small bandgap (Eg = 1.15 eV),24,25 favorable band structure for hydrogen production,26 thermodynamic stability, and fabrication from earth-abundant, nontoxic constituents. In addition, CuFeO2 has recently been reported to reduce CO2 to formate under illumination at an underpotential.27 Despite these properties, the reported photocurrents are low, 0.16 mA cm−2 at 100 W cm−2.26 Although photoelectrochemical evaluation of intrinsic CuFeO2 has been conducted,28,29 the effect of dopants on its photoresponse have not been investigated.
In the CuFeO2 delafossite, a layer of FeO2 is formed by edge-sharing FeO6 octahedra that are separated by monovalent copper sticks.30 The intrinsic material is p-type, and the reported electrical conductivities are low.31 Although the conductivity has been reported to improve for non-stoichiometric CuFeO2+x,31 the room temperature value was reported to be 2 S cm−1, only a ∼1.5-fold improvement from the intrinsic material.32 It has been shown that substituting a divalent metal (i.e. Mg2+) for the trivalent metal (i.e. Fe3+) renders CuFeO2 more p-type and increases its conductivity.24,33,34 p-Type electrodes are useful photocathodes for reduction reactions, particularly for CO2 reduction and H2 evolution, further supporting interest in CuFeO2.26,35,36
Here, within range of thermodynamic stability achievable using solid-state synthesis, we show that the photoresponse of Mg-doped CuFeO2 varies with both p-type carrier concentration and mobility. For comparison, a second source of p-type carriers, Cu-deficiency, is explored to garner information about the correlation of the hole mobility to the material's defect chemistry, and ultimately its photoresponse. We find that increasing the impurity concentration by either Mg doping or Cu deficiency decreases the photoeffect in CuFeO2, accompanied by lower majority carrier mobilities, and that the system eventually crosses over from p-type to n-type at high defect concentrations.
2 Experimental
CuFe1−xMgxO2 (x = 0, 0.0005, 0.005, 0.02) powder was prepared by grinding stoichiometric amounts of CuO (Sigma Aldrich 99.999%), Fe2O3 (Alfa Aesar 99.99%), and MgO (Alfa Aesar 99.99%), according to previously reported procedures.24,37,38 Roughly 10 g of sample was prepared for samples with lower concentrations of Mg (x = 0.0005, 0.005). The ground powder was heated to 950 °C in a covered alumina crucible under flowing Ar atmosphere for 192 hours with intermittent grinding for x = 0, 0.0005, and 0.005 samples. The x = 0.02 sample was heated to 850 °C under the same reaction conditions. The resultant pellets were black. The reaction progress was monitored using powder X-ray diffraction (XRD) on a Rigaku Miniflex equipped with a Cu Kα X-ray source and a diffracted beam graphite monochromator. After CuFe1−xMgxO2 showed a single delafossite phase in the XRD pattern, the samples were filtered through a 325 mm sieve, and ground with stearic acid in a 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio. Addition of ethanol under low heat dissolved the stearic acid in the mixture, which was then dried, reground, and pressed into a pellet (0.4 mm thickness, 0.785 cm2 area) with 4 tons of pressure. The pellets were first heated at 500 °C in air for 4 hours and then sintered for 96 hours under Ar atmosphere at 925 °C. The obtained pellets (≥85% of theoretical density30) were then used for subsequent characterization. Cu1−yFeO2 pellets were synthesized using the same methodology with CuO and Fe2O3 as starting materials.
1 mole ratio. Addition of ethanol under low heat dissolved the stearic acid in the mixture, which was then dried, reground, and pressed into a pellet (0.4 mm thickness, 0.785 cm2 area) with 4 tons of pressure. The pellets were first heated at 500 °C in air for 4 hours and then sintered for 96 hours under Ar atmosphere at 925 °C. The obtained pellets (≥85% of theoretical density30) were then used for subsequent characterization. Cu1−yFeO2 pellets were synthesized using the same methodology with CuO and Fe2O3 as starting materials.
A Quanta 200 Field Emission Gun Environmental-Scanning Electron Microscope (SEM) equipped with an integrated Oxford System was employed for Energy Dispersive X-ray (EDX) analysis. The X-ray penetration depth was 1–2 mm. X-ray photoelectron spectroscopy (XPS) spectra were collected under 10−9 Torr using an electron spectrometer (VG ESCALAB MkII) in constant hemispherical energy analyzer mode with pass energies of 50 and 20 eV for survey and detailed scans, respectively. A Mg Kα X-ray source centered at 1.254 keV was employed. The C 1s peak at 285 eV of adventitious hydrocarbon was used as an internal binding energy reference.
Hall effect data and electrical resistivities were collected using a Quantum Design Physical Property Measurement System. The samples were cut from the pellets into 0.4 mm-thick rectangles, measuring approximately 1.9 mm by 0.6 mm. Hall effect data were obtained at 300 K by sweeping the magnetic field from a negative value to the equivalent positive value at a constant current of 0.1 mA through the sample. The carrier concentration, N, was estimated by assuming a single dominant carrier type and the relationship,
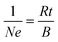 | (1) |
Photocurrent density measurements were carried out using the delafossite pellets as the working electrode, Pt mesh (Sigma Aldrich) as the counter electrode and standard calomel electrode (SCE, Accument) as the reference electrode in 0.1 M NaHCO3 (≥99%, Fisher) aqueous electrolyte, pH 8.1. In the photoelectrochemical cell (PEC), constant incident light (75 W Xe-arc lamp, USHIO UXL 151H, 350 nm-1350 nm) was illuminated onto the working electrode at a fixed distance (∼9 cm) and monitored using a CdS photocell (100 W readout, corresponding to 700 ± 50 mW cm−2, PerkinElmer) 6.7 mm below the working electrode. The PEC was open to air. The PEC cell was made out of Teflon, and quartz windows were secured opposite to the working electrode, which was fitted in a 0.7 cm diameter slot created to fit synthesized delafossite pellets after protecting the edges with Teflon tape to prevent leakage of the electrolyte. The delafossite pellets were 0.4 mm thick, and they were back-side Au-sputtered (100 nm, Angstrom Metal Sputter), attached to Teflon-coated copper leads using Ag epoxy, and secured with water-tight epoxy (Epoxy Technology H31). The contacts were ohmic (Fig. S1†), and the PEC design allowed for only the front side of the pellet to contact the electrolyte and to be illuminated.
The chopped light experiments were performed using the above experimental setup and carried out using a CHI760 Electrochemical Potentiostat in linear sweep voltammetry mode with a scan rate of 100 mV s−1. The sweep was performed at reducing potentials (0 V vs. SCE to −1.5 V vs. SCE) for p-type samples and at oxidizing potentials (0 V vs. SCE to 1.5 V vs. SCE) for n-type samples. The frequency of the chopped light was monitored using a Thorlabs-Optical Chopper MC1000A at 198 Hz. Shorter chopping frequencies did not give a detectable measure of the photocurrent, and longer chopping frequencies did not change the amount or yield of the photocurrent.
3 Results and discussion
3.1 CuFe1−xMgxO2
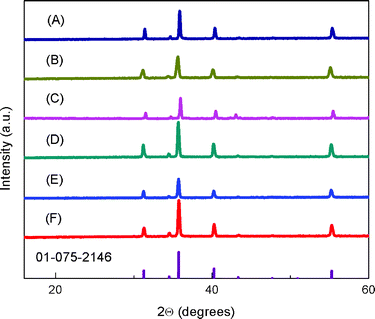
Fig. 1 shows the powder X-ray diffraction (XRD) patterns for the sintered CuFe1−xMgxO2 pellets. The samples show pure delafossite patterns. Samples for x = 0.05 and 0.07 were also prepared; the higher Mg-doped samples contained Cu2O impurities in agreement with previous studies.24 Thus, x = 0, 0.0005, 0.005 and 0.02 samples were used for subsequent characterization. The EDX analysis of the as-synthesized CuFeO2 pellet, Fig. S2,† shows roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu to Fe and did not yield any other elements besides O (in anticipated 2
1 ratio of Cu to Fe and did not yield any other elements besides O (in anticipated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with both Cu and Fe) and adventitious carbon, suggesting that impurities below the detection limit of EDX (up 0.05%) are not present in the material and that the delafossite stoichiometry is preserved. Furthermore, additional EDX analysis of CuFe1−xMgxO2, Table S1,† display incorporation of Mg content ranging from 0 to 1 atomic%, mirroring the increasing amount of prepared dopant from sample to sample. For x = 0.0005, the Mg content was not visible because the doping amount was below the detection limit of the instrument (0.05%). For x = 0.005 and 0.0005, it is noted that the dopant amount may be equal to that of the impurity of the precursor (Fe3O4, 99.99% metal basis), however possible impurities present in the precursor material itself were not detectable in the pure x = 0 sample. Significant changes observed in transport properties, shown below, suggest that Mg-doping is present in the lowest doped sample. XPS analyses were performed to probe Mg on the surface: no detectable precipitates or other inhomogeneities in Mg distribution were seen at the surface (Fig. S3†).
1 ratio with both Cu and Fe) and adventitious carbon, suggesting that impurities below the detection limit of EDX (up 0.05%) are not present in the material and that the delafossite stoichiometry is preserved. Furthermore, additional EDX analysis of CuFe1−xMgxO2, Table S1,† display incorporation of Mg content ranging from 0 to 1 atomic%, mirroring the increasing amount of prepared dopant from sample to sample. For x = 0.0005, the Mg content was not visible because the doping amount was below the detection limit of the instrument (0.05%). For x = 0.005 and 0.0005, it is noted that the dopant amount may be equal to that of the impurity of the precursor (Fe3O4, 99.99% metal basis), however possible impurities present in the precursor material itself were not detectable in the pure x = 0 sample. Significant changes observed in transport properties, shown below, suggest that Mg-doping is present in the lowest doped sample. XPS analyses were performed to probe Mg on the surface: no detectable precipitates or other inhomogeneities in Mg distribution were seen at the surface (Fig. S3†).
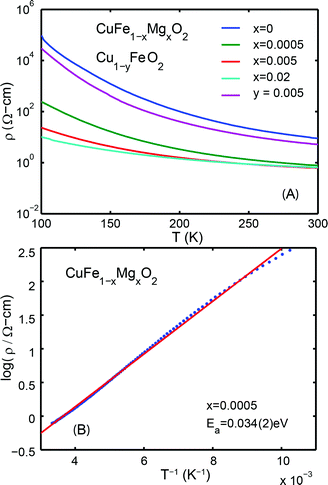
Representative Hall resistivities of CuFe1−xMgxO2, x = 0.005 and x = 0.02 at 300 K are shown in Fig. 2. The pellets synthesized by our method produced a reliable linear fit of the Hall data (R2 ≥ 0.92) to applied field, allowing for carrier concentration to be determined. The hole and electron concentrations are listed in Table 1.
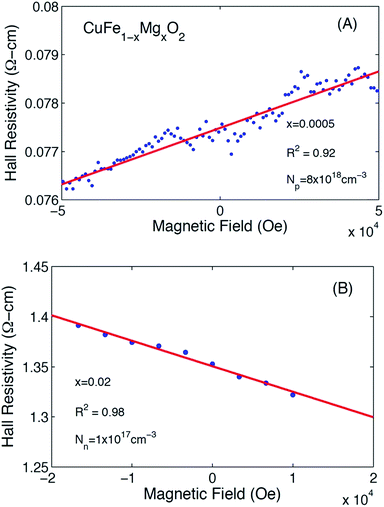 | ||
| Fig. 2 Hall resistivity data for CuFe1−xMgxO2. (A) x = 0.0005 depict a positive slope, indicating p-type majority carriers. (B) x = 0.02 depict a negative slope, indicating n-type majority carriers. | ||
| Sample | x = 0 | x = 0.0005 | x = 0.005 | x = 0.02 | Cu deficient, y = 0.005 | Cu deficient, y = 0.02 |
| N (cm−3) | (8 ± 2) × 1015 | (8 ± 2) × 1018 | (1 ± 0.2) × 1018 | (1 ± 0.3) × 1017 | (2.2 ± 0.6) × 1016 | (2 ± 0.5) × 1018 |
| Carrier type | p | p | p | n | p | n |
| ρ at 300 K (Ω cm) | 9 ± 3 | 0.8 ± 0.3 | 0.6 ± 0.1 | 0.2 ± 0.05 | 5 ± 1 | 5 ± 2 |
| σ (S cm−1) | 0.1 ± 0.04 | 1 ± 0.5 | 2 ± 0.4 | 6 ± 2 | 0.2 ± 0.05 | 0.2 ± 0.05 |
| μ n, μp (cm2 V−1 s−1) | 90 ± 40 | 1 ± 0.4 | 10 ± 3 | 400 ± 100 | 50 ± 20 | 60 ± 15 |
| j ph,c (mA cm−2) | 0.43 ± 0.01 | 0.20 ± 0.01 | 0.16 ± 0.01 | NA | 0.19 ± 0.01 | NA |
The Hall effect measurements show that substituting x = 0.0005 Mg to nominally replace an equivalent amount of Fe in pure CuFeO2 leads to increased hole doping over the undoped material. Assuming that Mg2+ substitutes for Fe3+ (see section 3.3), more p-type carriers are expected as the Mg content increases. We find that at x = 0.005, however, the increased Mg content leads to compensation of the p-type carriers by the introduction of n-type carriers. Eventually, in the vicinity of the solubility limit at x = 0.02, the material crosses over to n-type, consistent with the trend suggested by the x = 0.005 sample. This observation indicates the existence of a more complex underlying defect chemistry in this compound.
The temperature dependencies of the electrical resistivities are plotted in Fig. 3A. The exponentially decreasing resistivities with increasing temperature indicate that CuFe1−xMgxO2, x = 0, 0.0005, 0.005, 0.02 are semiconducting. The room temperature (300 K) resistivities are listed in Table 1. Significant differences from previously reported resistivities24 are noted; these differences may be attributed to variations in sample preparation. All measurements reported here are made on the same set of samples, and thus the data are self consistent.
Based on the equation,
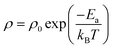 | (2) |
As a useful further characterization, the mobilities of the majority carriers were estimated by assuming a single dominant carrier and band-like carrier motion. Using the measured quantities and the relationship
| σ = Neμ | (3) |
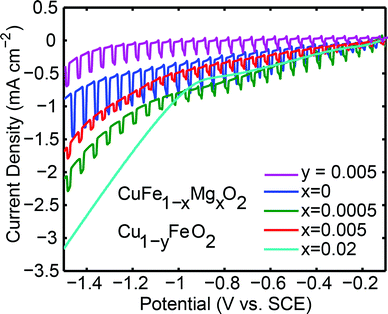
With the electronic characterization in hand, the pellets were used as photoelectrodes in an aqueous PEC. Under similar conditions to those employed in this work, this system has been reported to reduce water to H2 under illumination.26,35Fig. 4 shows the behavior of CuFe1−xMgxO2x = 0, x = 0.0005, x = 0.005, x = 0.02, and Cu deficient samples under chopped light illumination at reducing potentials. Reducing potentials, 0 ≥ E ≥ −1.5 V vs. SCE, were chosen because most of the prepared samples exhibited p-type behavior, a key characteristic of photocathodes. The n-type material x = 0.02 does not display a photoresponse at reducing potentials.
The Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe 1
Fe 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry is preserved even after multiple linear sweep voltammetry measurements, as shown by EDX analyses (Fig. S5A†), with only detectable oxygen and carbon as additional elements. These data, combined with the lack of observable Cu nanoparticles shown in the SEM data after polarization (Fig. S5B†), suggest that corrosive formation of metallic copper does not occur over the short timescale of linear sweep voltammetry measurements and simultaneously collected during electrode illumination. In addition, we note that electrolyses occurring over 8 hours
1 stoichiometry is preserved even after multiple linear sweep voltammetry measurements, as shown by EDX analyses (Fig. S5A†), with only detectable oxygen and carbon as additional elements. These data, combined with the lack of observable Cu nanoparticles shown in the SEM data after polarization (Fig. S5B†), suggest that corrosive formation of metallic copper does not occur over the short timescale of linear sweep voltammetry measurements and simultaneously collected during electrode illumination. In addition, we note that electrolyses occurring over 8 hours![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 has shown to give rise to XRD diffraction patterns indicative of metallic Cu formation, illustrating that the corrosion processes of CuFeO2 under reductive potential bias occurs over timescale of several hours.
27 has shown to give rise to XRD diffraction patterns indicative of metallic Cu formation, illustrating that the corrosion processes of CuFeO2 under reductive potential bias occurs over timescale of several hours.
The observed photoresponse of intrinsic CuFeO2 is consistent with the presence of the optical direct band gap of 0.9 ± 0.2 eV (Fig. S4†). We report the photocurrent densities from the seventh scan at −0.7 V vs. SCE. This potential value is the thermodynamic reduction potential for water reduction under these pH and electrolyte conditions. Beyond the thermodynamic potential, the observed photocurrent is assisted by an electrode bias. The same number of scans was performed on each electrode sample, and the appearance of significant dark current at −0.9 V vs. SCE remained constant with successive scans.
To a first approximation, the difference in dark and photocurrent with increasing cathodic polarization remains constant beyond −0.7 V vs. SCE, indicative of a saturation photocurrent regime, i.e. the electronic properties of the material govern the observed photocurrent rather than the interfacial electrochemical reaction kinetics. Therefore, while the end point electrochemical reaction remains ambiguous, the nature of the electrochemical reaction at the interface should not be different for the varying dopant concentrations in the current samples, and therefore is not further discussed. Furthermore, the band edge positions of the materials, as examined by the flat band potential and the dark open circuit voltage potential, do not depend on the dopant concentration (Fig. S6†). Because a material's photocurrent depends on the nature of the electrochemical reaction occurring at the interface,26 electrokinetic studies to elucidate the reactions by using varying electrolyte media and atmosphere may be of future interest.
The undoped sample, x = 0, yields the highest photocurrent at 0.43 ± 0.01 mA cm−2, comparable to that previously reported for undoped thin film and bulk p-type CuFeO2,26,27 although direct comparison is not possible because photocurrents and illuminated light intensity do not scale linearly due to recombination effects and varying kinetics of the electrochemical reaction at the interface.26,44 At the dopant concentrations x = 0.0005 and x = 0.005 lower photocurrents of 0.20 ± 0.01 mA cm−2 and 0.16 ± 0.01 mA cm−2, respectively, are observed. We note that the photocurrents of the CuFeO2 pellets used in this study are lower than prior reports,7,20,35 which could reflect differences in grain boundary densities between differently prepared materials. The dark currents of the samples increase with doping, which is attributed to their higher conductivities. The n-type x = 0.02 sample is conducting, but lacks a photoresponse at all negative potentials.
As seen in Fig. 4, there is a significant difference between the maximum photocurrent obtained from p-type samples (x = 0, 0.0005, and 0.005) and the maximum dark current of about 3 mA cm−2 passed through the n-type (x = 0.02) sample. This limited photocurrent of the p-type samples, is attributed to surface recombination processes. Assuming that enough light intensity was applied, a photon-limited current can be ruled out. Additionally, x = 0.0005 and x = 0.005 materials have similar resistivities to that of x = 0.02, so the efficiency of charge mobility is not the contributing factor restricting the photocurrent.
For the CuFe1−xMgxO2 system, we observe no correlation between the mobility of the majority carriers and the photocurrents. Even though doping increases the conductivity of the material, e.g. for x = 0.0005 and x = 0.005, these materials exhibit significantly reduced photocurrents. The p-type carriers for x = 0 are more mobile than those introduced by Mg-dopant in the x = 0.0005 and 0.005 samples. Comparison, however, of these latter two samples to make a correlation of photocurrent with carrier mobility is complicated by the fact that some n-type carrier compensation may already be present for x = 0.005, evidenced by its lower net p-type carrier concentration. To determine the influence of the mobility of the photogenerated minority carriers on the photocurrent density, experiments should be done to determine the mobility of the photogenerated minority carriers by measuring their diffusion lengths and lifetimes.
3.2 Cu1−yFeO2
An alternative way to introduce holes in CuFeO2 is by incorporating Cu deficiency. Cu1−yFeO2, y = 0.005 and 0.02, were therefore tested for their electronic and photoactive properties (Table 1). The XRD patterns and the temperature dependent resistivity measurements are shown in Fig. 1 and Fig. 3, respectively. Cu1−yFeO2, y = 0.0005, did not yield a detectable slope in the Hall data and was therefore omitted from the analysis. The y = 0.02 sample showed n-type behavior, and consequently was not tested for photoactivity at reducing potentials. For y = 0.005, the p-type carrier concentration was larger than that of the stoichiometric material, while the mobility of the majority carriers decreased slightly. This sample showed a decrease in photoactivity (Fig. 4).3.3 Defect chemistry of doped and nonstoichiometric CuFeO2
Many theoretical studies have been undertaken to understand the underlying defect chemistry45–47 in p-type conductive oxides based on Cu2O and the related CuMO2 (M = trivalent metal) delafossites.13,48,49 Using Kröger–Vink notation50 the possible point defects within the CuFeO2 lattice are: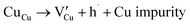 | (4) |
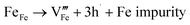 | (5) |
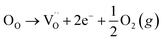 | (6) |
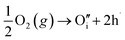 | (7) |
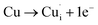 | (8) |
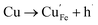 | (9) |
Of these proposed mechanisms, four ((4), (5), (7) and (9)) give rise to p-type behavior. Two key energies are involved: (1) the formation energy of the point defects; and (2) the ionization energy of the defects. A theoretical treatment by Raebiger et al. found, for systems with O–Cu(I)–O coordination (also found in delafossites), that copper vacancies (VCu) exhibit the lowest formation enthalpy compared to oxygen interstitials (i.e. ΔH(VCu) = 0.7 eV compared to ΔH(Oi) = 1.3 eV) and display small defect ionization energy (i.e. VCu ionization is 0.38 eV more shallow than Oi). The resulting holes are released into the valence band.47 Similarly, in the CuAlO2 delafossite, Watson et al. calculated VCu and a copper defect on the trivalent metal site (mechanisms (4) and (9) above) to have lower formation energies by 2 and 3.5 eV, respectively, than oxygen interstitials and aluminum vacancies (mechanisms (5) and (7) above).45 Even though these calculations were not specifically performed on CuFeO2, its defect chemistry is expected to be highly analogous. Thus, the p-type conductivity in intrinsic CuFeO2 is likely to be due to ionized VCu defects. The crossover to n-type behavior we observe in copper deficient CuFeO2 indicates that an n-type defect begins to dominate, the most likely being oxygen vacancy formation (mechanism (6)). Our study indicates that the introduction of holes through the introduction of copper vacancies in nonstoichiometric CuFeO2 is limited due to the formation of these competing oxygen defects.
Using the same type of analysis the possible additional point defects for Mg-doped CuFeO2 are:
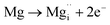 | (10) |
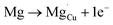 | (11) |
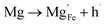 | (12) |
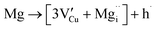 | (13) |
For low doping levels the material is p-type, but then crosses over to n-type at higher doping levels. The dominant defect chemistry in Mg-doped CuFeO2 cannot be uniquely determined from the current data. Mechanisms (10) and (11) above can be ruled out because there is no room in the Cu layer and because Mg ions do not assume stick configurations with oxygen, respectively. Mechanisms (12) and (13) above lead to p-type doping on Mg substitution. Mechanism (12) is the simple expectation, and mechanism (13) is a more complex associated defect in which a single Mg ion goes into a prismatic interstitial site in the Cu layer, but has to displace three neighboring Cu ions to make room for itself. This mechanism also leads to hole doping.
Increased p-type conductivity on introducing low quantities of Mg dopant (i.e. x = 0.0005) could be due to increased hole carriers generated by mechanisms (12) or (13). Mechanism (13) is motivated by the presence of Cu2O found as a second phase in this work, indicating thermodynamic instability of the desired CuFe1−xMgxO2 at high Mg doping levels (x ≥ 0.05), which were not tested for photoactivity, and earlier work on the same system.24 To experimentally probe the plausibility of mechanism (13), samples with stoichiometry Cu1−3xMgxFeO2 were prepared. These samples also exhibited a maximum Mg content of x = 0.02, as in CuFe1−xMgxO2 (shown in Fig. S7†). At doping concentrations above x = 0.02, Fe3O4 was observed as a second phase rather than Cu2O (Fig. S8†). Thus, at least from an empirical standpoint, Mg doping seems to lead to defects somewhere in between these two options; perhaps both defect mechanisms (12) and (13) are present. Further theoretical and experimental work is needed to clarify the defect situation. The n-type crossover at x = 0.02 in Mg-substituted CuFeO2 is attributed to the formation of oxygen vacancies, as is the case in the intrinsic or nonstoichiometric CuFeO2 host compound (mechanism (6) for undoped CuFeO2).
4 Conclusions
Photoelectrodes may provide an avenue to convert photon energy into a desirable chemical fuel. Although semiconductor oxide materials have been found to photocatalytically split water or reduce CO2, many such materials suffer from low product yields. A possible optimization method for oxide photoelectrodes is through chemical doping. In this work, we examine whether the photoresponse of CuFeO2 could be improved by changes in carrier concentration (N), experimentally modulated using two different hole formation schemes. We observed that the material with the lowest p-type carrier concentration (about 1016 cm−3) and highest mobility (about 100 cm2 V−1 s−1) gave the best photoresponse. Further, both doping studies showed that the p-type carrier concentration in CuFeO2 could not be tuned to high values due to the dominance of a n-type defect, which we believe is an oxygen vacancy, at high dopant levels. This reflects the complex defect chemistry of delafossites. Our studies provide a basis for further optimization of CuFeO2 photoelectrodes. Similar studies of p-type oxides with other defect chemistries may be of interest for future photoelectrode optimization.Acknowledgements
The authors acknowledge support of this research from the Office of Basic Energy Sciences, Department of Energy. The solid-state synthesis and physical characterization of materials were carried out under the direction of R. J. C. under Grant DE-FG02-98ER45706. Photoelectrochemical experiments and analysis were carried out under the direction of A. B. B. under Grant DE-SC0002133. A. W. acknowledges the Princeton University Andlinger Center and the Princeton Environmental Institute for research funds.References
- T. G. Deutsch, C. A. Koval and J. A. Turner, J. Phys. Chem. B, 2006, 110, 25297–25307 CrossRef CAS PubMed.
- M. Szklarczyk and J. O. M. Bockris, J. Phys. Chem., 1984, 88, 5241–5245 CrossRef CAS.
- T. O. M. Singh, in Engineered Ceramics, Wiley-American Ceramic Society, 2015, pp. 457–495 Search PubMed.
- X. Chang, T. Wang and J. Gong, Energy Environ. Sci., 2016, 9, 2177–2196 CAS.
- K. Sivula and R. van de Krol, Nature Reviews Materials, 2016, 1, 15010 CrossRef.
- K. Rajeshwar, J. Phys. Chem. Lett., 2011, 2, 1301–1309 CrossRef CAS PubMed.
- N. Serpone and A. V. Emeline, J. Phys. Chem. Lett., 2012, 3, 673–677 CrossRef CAS PubMed.
- M. P. Woodhouse and B. A. Parkinson, Chem. Soc. Rev., 2009, 38, 197–210 RSC.
- C. S. Enache, D. Lloyd, M. R. Damen, J. Schoonman and R. van de Krol, J. Phys. Chem. C, 2009, 113, 19351–19360 CAS.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- J. C. Hill and K.-S. Choi, J. Phys. Chem. C, 2012, 116, 7612–7620 CAS.
- J. R. Bolton, S. J. Strickler and J. S. Connolly, Nature, 1985, 316, 495–500 CrossRef CAS.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271 CrossRef CAS PubMed.
- A. Kwang-Soon, Y. Yanfa and A.-J. Mowafak, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2007, 25, L23–L26 CrossRef.
- D. Paluselli, B. Marsen, E. L. Miller and R. E. Rocheleau, Electrochem. Solid-State Lett., 2005, 8, G301–G303 CrossRef CAS.
- M. P. D.-E. G. Bin-Daar, J. B. Goodenough and A. Hamnett, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 1199–1213 RSC.
- W. Luo, Z. Yang, Z. Li, J. Zhang, J. Liu, Z. Zhao, Z. Wang, S. Yan, T. Yu and Z. Zou, Energy Environ. Sci., 2011, 4, 4046–4051 CAS.
- R. Shinar and J. H. Kennedy, Sol. Energy Mater., 1982, 6, 323–335 CrossRef CAS.
- C. Jorand Sartoretti, B. D. Alexander, R. Solarska, I. A. Rutkowska, J. Augustynski and R. Cerny, J. Phys. Chem. B, 2005, 109, 13685–13692 CrossRef PubMed.
- M. S. Prevot, N. Guijarro and K. Sivula, ChemSusChem, 2015, 8, 1359–1367 CrossRef CAS PubMed.
- M. Li, L. Zhao and L. Guo, Int. J. Hydrogen Energy, 2010, 35, 7127–7133 CrossRef CAS.
- W. W. Gartner, Phys. Rev., 1959, 116, 84–87 CrossRef CAS.
- M. A. Butler, J. Appl. Phys., 1977, 48, 1914–1920 CrossRef CAS.
- F. A. Benko and F. P. Koffyberg, J. Phys. Chem. Solids, 1987, 48, 431–434 CrossRef CAS.
- Y. Jin and G. Chumanov, RSC Adv., 2016, 6, 26392–26397 RSC.
- C. G. Read, Y. Park and K.-S. Choi, J. Phys. Chem. Lett., 2012, 3, 1872–1876 CrossRef CAS PubMed.
- J. Gu, A. Wuttig, J. W. Krizan, Y. Hu, Z. M. Detweiler, R. J. Cava and A. B. Bocarsly, J. Phys. Chem. C, 2013, 117, 12415–12422 CAS.
- S. Omeiri, Y. Gabès, A. Bouguelia and M. Trari, J. Electroanal. Chem., 2008, 614, 31–40 CrossRef CAS.
- A. Omeiri, B. Bellal, A. Bouguelia, Y. Bessekhouad and M. Trari, J. Solid State Electrochem., 2009, 13, 1395–1401 CrossRef.
- R. D. Shannon, C. T. Prewitt and D. B. Rogers, Inorg. Chem., 1971, 10, 719–723 CrossRef CAS.
- R. D. Shannon, D. B. Rogers, C. T. Prewitt and J. L. Gillson, Inorg. Chem., 1971, 10, 723–727 CrossRef CAS.
- F. A. Benko and F. P. Koffyberg, J. Phys. Chem. Solids, 1987, 48, 431–434 CrossRef CAS.
- R. Nagarajan, A. D. Draeseke, A. W. Sleight and J. Tate, J. Appl. Phys., 2001, 89, 8022–8025 CrossRef CAS.
- Z. Deng, X. Fang, S. Wu, Y. Zhao, W. Dong, J. Shao and S. Wang, J. Alloys Compd., 2013, 577, 658–662 CrossRef CAS.
- Y. J. Jang, Y. B. Park, H. E. Kim, Y. H. Choi, S. H. Choi and J. S. Lee, Chem. Mater., 2016, 28, 6054–6061 CrossRef CAS.
- U. Kang, S. K. Choi, D. J. Ham, S. M. Ji, W. Choi, D. S. Han, A. Abdel-Wahab and H. Park, Energy Environ. Sci., 2015, 8, 2638–2643 CAS.
- E. Mugnier, A. Barnabé and P. Tailhades, Solid State Ionics, 2006, 177, 607–612 CrossRef CAS.
- R. D. Shannon, D. B. Rogers and C. T. Prewitt, Inorg. Chem., 1971, 10, 713–718 CrossRef CAS.
- V. R. Galakhov, A. I. Poteryaev, E. Z. Kurmaev, V. I. Anisimov, S. Bartkowski, M. Neumann and T.-R. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 4584–4591 CrossRef CAS.
- S. Kimura, K. Watanabe, T. Fujita, M. Hagiwara, H. Yamaguchi, T. Kashiwagi and N. Terada, J. Phys.: Conf. Ser., 2012, 400, 032039 CrossRef.
- M. Salavati-Niasari, F. Davar, M. Mazaheri and M. Shaterian, J. Magn. Magn. Mater., 2008, 320, 575–578 CrossRef CAS.
- A. d. A. Jesus, Nature, 2011, 479, 317 CrossRef PubMed.
- B. J. Ingram, G. B. Gonzalez, T. O. Mason, D. Y. Shahriari, A. Barnabe, D. Ko and K. R. Poeppelmeier, Chem. Mater., 2004, 16, 5616–5622 CrossRef CAS.
- S. Hamwi, T. Riedl and W. Kowalsky, Appl. Phys. Lett., 2011, 99, 053301 CrossRef.
- D. O. Scanlon and G. W. Watson, J. Mater. Chem., 2011, 21, 3655–3663 RSC.
- D. O. Scanlon and G. W. Watson, J. Phys. Chem. Lett., 2010, 1, 3195–3199 CrossRef CAS.
- H. Raebiger, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045209 CrossRef.
- H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, Nature, 1997, 389, 939–942 CrossRef CAS.
- H. Yanagi, K. Ueda, S. Ibuki, T. Hase, H. Hosono and H. Kawazoe, Mater. Res. Soc. Symp. Proc., 2000, 623 CrossRef CAS.
- J. A. Thornton, Annu. Rev. Mater. Sci., 1977, 239–260 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: SEM, XPS, EDX, and UV-Vis-NIR measurements of as-synthesized CuFe1−xMgxO2 pellets. Mott–Schottky plots of CuFe1−xMgxO2. SEM and EDX analyses of CuFe1−xMgxO2 after use as a photoelectrode. XRD of CuFe1−xMgxO2 and Cu1−3xMgxFeO2. See DOI: 10.1039/c6ta06504j |
| This journal is © The Royal Society of Chemistry 2017 |