Intrinsic quantum efficiency enhancement in well-known Ir(III) complexes by virtue of a simple and controllable deuteriation strategy†
Yu
Wang
 ,
Fu-Quan
Bai
,
Fu-Quan
Bai
 * and
Hong-Xing
Zhang
* and
Hong-Xing
Zhang
 *
*
International Joint Research Laboratory of Nano-Micro Architecture Chemistry, Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130023, People's Republic of China. E-mail: baifq@jlu.edu.cn; zhanghx@jlu.edu.cn
First published on 25th April 2018
Abstract
A series of well-known iridium(III) complex molecular materials are selected for a comprehensive theoretical investigation into their complete or partial ligand deuteriation products. These compounds, respectively, are two homoleptic compounds fac-Ir(ppy)3 [ppy = 2-phenylpyridinate] (1) and fac-Ir(dfppy)3 [dfppy = 2-(2′,4′-difluorophenyl)pyridyl] (2), and two heteroleptic compounds Ir(ppy)2acac [acac = acetylacetonate] (3) and Ir(dfpypy)2pic [dfpypy = 2′,4′-difluoro-2,3′-bipyridinato-N,C4′, pic = picolinate] (4). Unlike traditional strategies for enhancing the radiative decay process or reducing the non-radiative decay process through cumbersome ligand decorations, our simple and controllable deuteriation strategy, which is insensitive to the radiative decay process, enables us to suppress the non-radiative decay process by almost 50%. It is consistent with previous experimental findings, under our theoretical evaluation, that deuterium has a significant influence on non-radiative deactivation processes due to the reduction in the amplitude and frequency of vibrational modes caused by the increased deuterium mass. The systematic computational approach for the evaluation of the non-radiative decay processes provides us with alterations of every single vibrational mode, from the primitive complexes to the completely or partially deuterated ligand complexes, in detail. The two-averaged modes assessment informs us that deuteriation exerts its main influence on the high-frequency modes, rather than the low-frequency modes. Additionally, partial ligand deuteriation has a correlation with the nature of the electronically excited state decay pathways.
1 Introduction
Phosphorescent organic light-emitting diodes (phOLEDs), as second generation OLEDs, have been attractive in recent years, owing to their ability to attain nearly 100% internal electroluminescence quantum efficiencies.1 Among the numerous phosphorescent materials, cyclometalated iridium(III) complexes have advantages over other heavy metal materials, due to their chemical stability and full-color emission tunability.2–5 Watts and co-workers reported the well-known green emitting complex fac-Ir(ppy)3 in 1991,6 and efficient fac-Ir(ppy)3 OLED devices have since been fabricated.7 In order to improve the synthesis approaches for tris-cyclometalated homoleptic iridium compounds, heteroleptic compounds with ancillary ligands have become prevalent,8 such as the representative Ir(ppy)2acac, which displays high quantum efficiency.9 The synthesis of blue-emitting Ir(III) complexes with considerable phosphorescence efficiency is still a genuine challenge because of a significant increase in the non-radiative deactivation processes.10,11 Through introducing fluorine atoms onto the ppy ligand, a blue-shifted emission could be triggered, and hence, homoleptic fac-Ir(dfppy)3, with dfppy representing 2-(4,6-difluorophenyl)pyridyl, was prepared for blue-emitting phosphors in 2003.12 In searching for a suitable host for phOLED applications, heteroleptic complexes with appropriate ancillary ligands were then prepared to address energy limitation problems.13–15 One of the typical heteroleptic blue-emitting Ir(III) compounds is Ir(dfpypy)2pic, which has a considerable phosphorescence efficiency of 90% in solution.16Nevertheless, phosphorescence emitting Ir(III) complexes still have potential in quantum efficiency enhancement. Combined with the thriving theoretical foundations and computational industries, molecular photophysical processes have been explored and assessed gradually from qualitative to quantitative levels.17 To obtain efficient phosphorescence emitting Ir(III) complexes, raising kr and reducing knr are of great concern, and in both the radiative and non-radiative processes for phosphorescent complexes, the “heavy-atom effect”, which gives rise to large spin–orbit coupling (SOC),18 contributes to the electronic transition channels between the singlet and triplet states.19 The decoration of ligands for larger SOC integrals has been implemented to increase kr, including enlarging the π-extension or adding substitute groups.20,21 However, an increased SOC constant can also facilitate non-radiative deactivation processes.22
As for the non-radiative deactivation process, factors involving structural distortions between the electronic transition states play a significant role in the determination of knr through its expressions.23 The improvement of structural rigidity is an efficient approach to suppress knr.24 Moreover, strongly σ-donating ligands enable the lifting of the detrimental d–d excited state, thereby contributing to the inhibition of knr to a significant extent.25 Notably, deuteriation is a succinct method to suppress knr and maintain kr at the same time.
The deuterium isotope effect on the photophysical properties of inorganic and organic systems is of significance due to the improvement it causes in the quantum efficiency, which was recognized as early as 1960.26 The applications of deuteriation were first investigated by Kropp and Windsor,27,28 who primarily focused on the fluorescence of rare earth ions. Nowadays, the deuterium isotope effect is still attractive, especially in the pursuit of photoelectric materials with high efficiency, and in the pursuit of mechanistic interpretations. For example, the working mechanism of aggregation-induced emission can be understood from the deuterated isotope effect in depth.29 The photophysical exploration of the deuterated Ir(III) complex IrCl2(bpy-d8)2+ (bpy = 2,2′-bipyridine) was first reported by Watts et al.30 It was found that the emission lifetime was prolonged due to the deuterium effects on the ligands. The complete deuterium effect on the well-known Ir(ppy)3 (ppy = 2-phenylpyridine) complex was also evaluated in different solvents.31 The quantum yield of the fully deuterated Ir(ppy)3 was slightly higher than that of the primitive complex, independent of the solvents. Experimental results showed that the ligand deuterium isotope effect mainly acted upon the non-radiative decay process. Additionally, observations of such a deuterium isotope effect are often noted as a weak coupling mechanism for non-radiative decay occurrences,32 which means that the temperature-dependent non-radiative decay process that is prominent in strongly coupled ground and excited states cannot exert a significant influence.
Although numerous experimental studies have discussed the influence exerted by complete or partial deuteriation on certain molecules,33,34 the mechanism of such a deuterium isotope effect on heavy-metal complexes has not been interpreted in depth from a theoretical perspective. Herein, to verify the pervasiveness of such a deuterium isotope effect, a series of well-known Ir(III) complexes, as mentioned above, are selected for a deuterium isotope effect investigation at a molecular electronic-structure level, as shown in Fig. 1. As widespread materials in phOLED applications, these four representative complexes are cogent and valuable for achieving higher quantum efficiency through such an intelligible approach. With the development of theoretical systems and the computational industry, simulations of the photophysical processes of heavy metal complexes on the basis of progressive theory can be conducted precisely and extensively.35–37 Under the integrated theoretical scheme, these four complexes, as well as their completely and partially deuterated equivalents, are comprehensively evaluated through kr and knr calculations. The computational results show that the completely deuterated complexes have smaller knr values compared with the primitive complexes, and decomposed vibrational modes that correspond to large reorganization energies are picked out for further deuterium effect research. For partially deuterated complexes, in each ligand of the complexes, only the complexes with a deuterated ligand that is involved in excited electronic transitions can result in a smaller knr. Variations in the molecular normal modes caused by partial deuteriation are also probed by resolving the typical vibrational modes into internal coordinations.
2 Theoretical background and computational details
The radiative decay rate is evaluated under the Einstein coefficient of spontaneous emission:38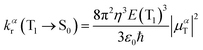 | (1) |
With consideration of the zero-field splitting (ZFS), the energy difference between the sublevels of the triplet state is taken into account for the averaged radiative decay rate, which can be expressed as:
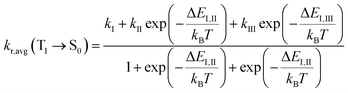 | (2) |
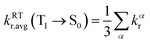 | (3) |
The temperature-independent non-radiative decay rate knr is decided by the SOC integral and the energy gap, as well as by the degree of structural distortion between the T1 and S0 states, and can be calculated under the adoption of Fermi's Golden Rule with the Condon approximation. A detailed formula can be expressed as:39
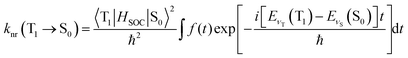 | (4) |
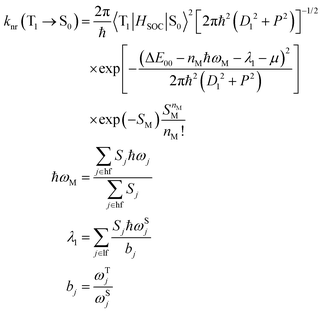 | (5) |
For geometry optimization, the hybrid functional PBE042,43 is employed throughout this work, and a basis set combined with Stuttgart Dresden ECP (SDD)44 is chosen for the heavy atom Ir(III), whilst a 6-311G* basis set is adopted for light atoms. The ground state (S0) geometry optimization is obtained with restricted density functional theory (RDFT), and the T1 state is obtained with unrestricted density functional theory (UDFT). Moreover, vibrational frequency calculations at the same level of theory are conducted to affirm the nature of the stationary points of the geometry. The properties of the electronic transitions are simulated with the B3LYP45,46 method, which has been applied to various Ir(III) complexes47,48 by means of time-dependent DFT (TDDFT). The geometry optimization and electronic transition properties are obtained with the Gaussian 09 program,49 along with a consideration of the solvent effect of dichloromethane (CH2Cl2) using the polarized continuum model (PCM).50
The T1 → S0 transition dipole moment, which serves as a crucial factor in kr, and the SOC integral between them, which is indispensable for both kr and knr, are obtained using the Amsterdam Density Functional (ADF) 2016 program.51,52 For these property calculations, the B3LYP functional with a Slater type all-electron triple-ζ basis with polarizations (TZP)53,54 is employed based on the optimized geometries. With consideration of the computational cost and accuracy, one-component zeroth order regular approximation (ZORA)55,56 TDDFT calculations are performed on the 10 lowest scalar relativistic singlet and triplet excitations, with perturbation involvement of the SOC.57,58 Also, the solvent effect of CH2Cl2 is simulated by the conductor-like screening model (COSMO).59 The reorganization energy and Huang–Rhys factors, which contain information about structural distortions, are calculated via a normal mode analysis approach using the DUSHIN program.60
3 Results and discussion
3.1 Electronic structure properties
All four iridium complexes are optimized with the PBE0 method. The deuterated complexes share the same electron configurations as their corresponding protonated complexes, and the main geometry parameters both at their S0 and T1 states are listed in Table S1 (ESI†). For homoleptic 1 and 2, the ground state geometries are constrained in C3 symmetry.61 The calculated bond lengths of Ir–N and Ir–C for complex 1 are 2.155 and 2.018 Å, respectively, which are close to the experimental values of 2.130 and 2.016 Å.61 Moreover, the mean error of the calculated geometry parameters for complex 4 is less than 1% when compared with the available experimental data. The precision of the calculated geometries confirms the credibility and reliability of our chosen method. To clarify the major transition characteristics, natural transition orbital (NTO) analysis is employed, as depicted in Fig. 2. Combining the geometry parameters with the NTO representations, the ligand involved in the charge transfer transition for both holes and electrons is the one that shortens the distance of the metal ion from the S0 and T1 states for each complex. The holes and electrons are mainly centered on the metal ion and its cyclometalating ligands for complexes 1–3, while for complex 4, the holes and electrons are mainly centered on the ancillary pic ligand, besides the metal ion.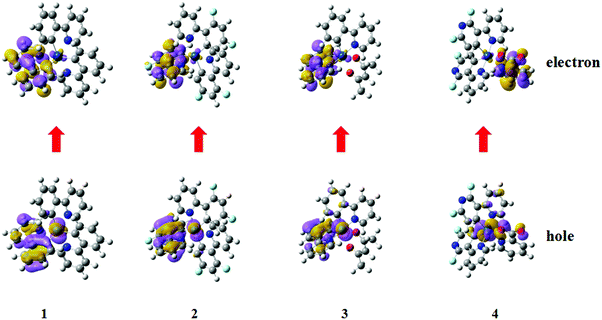 | ||
| Fig. 2 The hole and electron pairs of complexes 1–4 obtained by natural transition orbital analysis at their optimized excited state geometries. | ||
The uniform electronic structures of the deuterated and protonated complexes are also suitable for the evaluation of kr. Herein, the Einstein coefficient of spontaneous emission is applied in the assessment of the radiative decay process, as shown in eqn (1). The formula of kr employed in this study, which expresses primarily the electronic behaviour, is insensitive to deuteriation, in that the results for the deuterated and primitive complexes are the same. The calculated and experimental results are listed in Table 1. It can be seen that the computational results are fairly identical to the experimental findings, indicating the accuracy of this theoretical scheme, and the kr values for all four complexes have the same order of magnitude.
3.2 Non-radiative decay
The increase in the atomic mass via deuteriation undoubtedly enables the trigger of vibrational frequency alterations in both the ground and excited states, and such a variation can be remarkably reflected in the calculation of the non-radiative decay rate constants. As has been proven in several previous studies, spectra of heavy metal complexes can be concisely and specifically simulated by mode averaging approaches.36,37,62 Therefore, a two-averaged modes simulation method is employed in this theoretical evaluation. Computational results show that the deuteriation of these iridium complexes is bound to exert some influence on the non-radiative decay rate, and changes can be expected according to the nature of the electronically excited states. By virtue of further comparative analysis on the relationship of normal mode frequencies and reorganization energies, the alterations of the vibrational modes through deuteriation are evaluated.| ΔE00 | 〈T1|HSOC|S0〉 | λ 1 | μ | ħ 2 D 1 2 | ħ 2 P 2 | λ M | S M | k nr(theo.) | k nr(exp.) | |
|---|---|---|---|---|---|---|---|---|---|---|
| a From ref. 31. b From ref. 12. c From ref. 9. d From ref. 16. | ||||||||||
| 1 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 088 088 |
347 | 489 | 1489 | 3.04 | 1.30 | 1823 | 1.34 | 0.24 | 0.80a |
| Dall | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 142 |
582 | 1520 | 3.89 | 1.14 | 1733 | 1.25 | 0.11 | 0.50a | |
| DppyCT | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
612 | 1538 | 4.22 | 1.11 | 1713 | 1.22 | 0.08 | ||
| Dppy1 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086 |
490 | 1486 | 3.08 | 0.90 | 1832 | 1.34 | 0.26 | ||
| Dppy2 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
488 | 1482 | 3.04 | 0.98 | 1831 | 1.34 | 0.26 | ||
| 2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 548 548 |
329 | 455 | 1651 | 3.15 | 1.75 | 2210 | 1.57 | 0.90 | 3.60b |
| Dall | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 542 |
555 | 1680 | 4.06 | 1.56 | 2109 | 1.47 | 0.53 | ||
| DdfppyCT | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579 579 |
560 | 1722 | 4.18 | 1.73 | 2109 | 1.47 | 0.52 | ||
| Ddfppy1 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 539 539 |
458 | 1608 | 3.22 | 1.18 | 2208 | 1.57 | 0.86 | ||
| Ddfppy2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 537 |
458 | 1601 | 3.21 | 1.18 | 2208 | 1.57 | 0.86 | ||
| 3 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 490 |
505 | 487 | 1389 | 2.92 | 1.17 | 1485 | 1.07 | 0.34 | 4.13c |
| Dall | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534 534 |
570 | 1495 | 3.68 | 1.13 | 1406 | 0.99 | 0.18 | ||
| DppyCT | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 544 |
566 | 1510 | 3.63 | 1.08 | 1409 | 1.00 | 0.19 | ||
| Dppy1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478 478 |
489 | 1464 | 2.93 | 1.07 | 1483 | 1.07 | 0.36 | ||
| Dacac | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 488 |
492 | 1493 | 2.97 | 1.22 | 1484 | 1.07 | 0.36 | ||
| 4 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711 711 |
155 | 2396 | 1250 | 14.11 | 0.85 | 3099 | 2.22 | 1.26 | 0.40d |
| Dall | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746 746 |
2685 | 1438 | 20.66 | 6.27 | 3004 | 2.13 | 0.59 | ||
| DpicCT | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 751 751 |
2671 | 1447 | 20.27 | 5.94 | 3007 | 2.13 | 0.60 | ||
| Ddfpypy1 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
2487 | 1405 | 16.96 | 6.14 | 3099 | 2.22 | 1.04 | ||
| Ddfpypy2 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746 746 |
2466 | 1428 | 16.39 | 6.71 | 3096 | 2.22 | 1.04 | ||
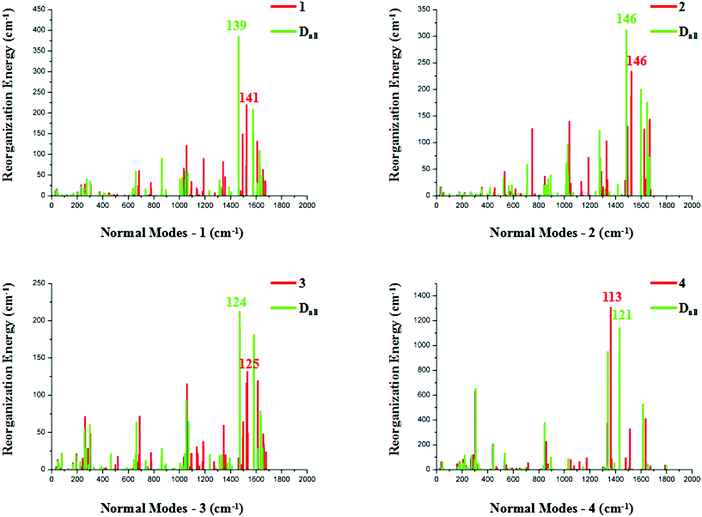
The relationships between the vibrational modes and reorganization energies of these complexes and their corresponding deuterated equivalents are depicted in Fig. 3. The LF part of complex 1 has generally the same reorganization energy distributions as its deuterated equivalent (Dall-1). There is a comparative suppression in the reorganization energy in the LF region of complex Dall-2, especially in the normal mode range of 700–800 cm−1. As for complexes 3 and 4, there are merely minor discrepancies between the reorganization energies in the LF regions for their primitive and deuterated complexes, suggesting a negligible effect of complete deuteriation on the LF promoting modes.
As for the HF regions, relatively large distinctions exist between the primitive and completely deuterated compounds. In the primitive complex 1, vibrational mode 141 corresponds to the largest reorganization energy contribution, and C–H-involved vibrations form up to 52.24% of this normal mode, as discovered through statistical analysis by decomposing the modes into internal coordinations. The vibrational composition of C–D in Dall-1 is subdued to 34.67% in mode 139, which corresponds to the largest reorganization energy contribution. Although the largest reorganization energy in Dall-1 is greater than that in its primitive complex, the overall reorganization energy in the high-frequency part is smaller, indicating fewer structure distortions in the process of electronic transition. Moreover, mode 139 of Dall-1 is mainly composed of C–C ring-breathing vibrations, as shown in Fig. S1 (ESI†), while mode 141 of the primitive complex 1 is mainly made up of C–H rocking vibrations. Vibrational mode 146 points to the largest reorganization energy contribution in both complexes 2 and Dall-2, and the 42.27% C–H vibrational ratio in primitive 2 is suppressed to a 24.75% C–D vibrational ratio in Dall-2. The heteroleptic complex 3 also has a decreased C–D-involved vibration constituent (decreased from 46.12% to 34.81%) when completely deuterated, on account of the resolved normal modes contributing the most to the reorganization energy. There is a special case in complex 4, in which the nature of the electronically exited state is centered on the pic ligand, and the C–H vibrations are not obviously inhibited in Dall-4. However, the overall reorganization energy in the HF region has been inhibited visibly.
In short, complete deuteriation of these four iridium complexes is in favor of retarding their non-radiative decay processes, thereby enhancing the probability of higher quantum efficiency.
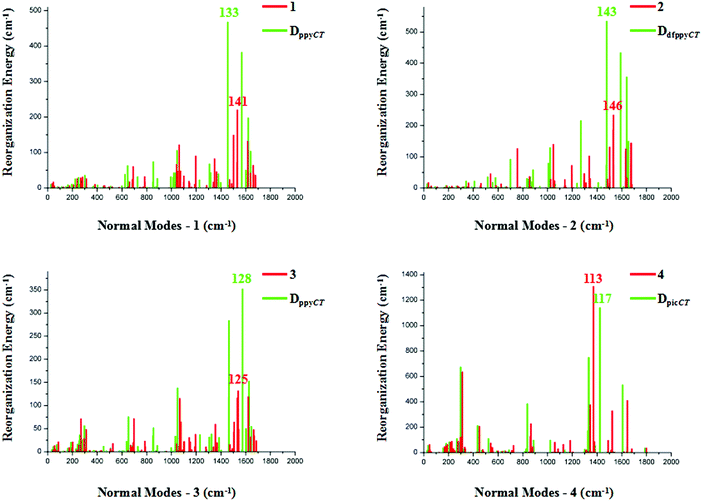
The relationships between the normal modes and reorganization energies of three partially deuterated ligand complexes of each bidentate ligand, with the addition of the primitive complexes, are presented in Fig. 4. Obviously, the partially deuterated complex of the ligand involved in the excited charge transfer (ligandCT) has a most distinctive relationship. The other two partially deuterated complexes exert no influence on the vibrational modes, in comparison with the primitive complexes. Similar to the completely deuterated complexes, the partially deuterated complex containing the ligandCT has a comparative suppression effect on the reorganization energy in the HF region, namely a smaller λM, as shown in Fig. 5.
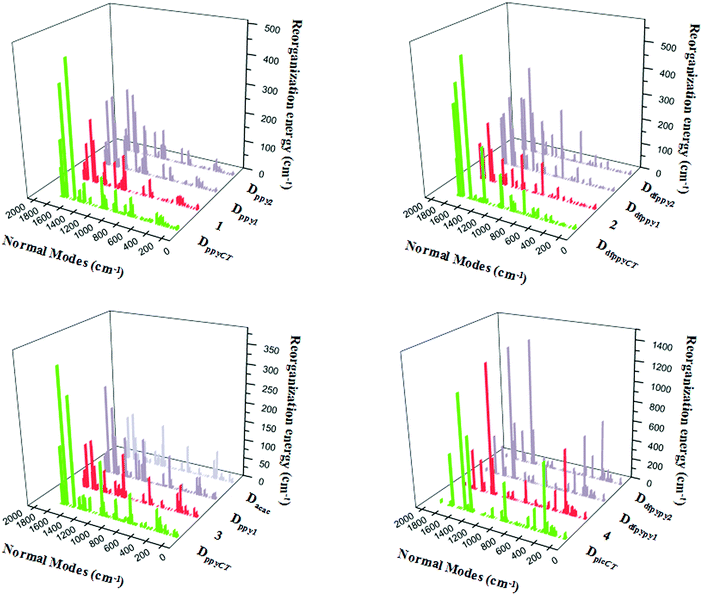 | ||
| Fig. 4 Calculated reorganization energies versus the normal mode frequencies for compounds 1–4, along with their partially deuterated ligand equivalents. | ||
Vibrational mode 133 corresponds to the largest reorganization energy contribution of partially deuterated complex 1 on ppyCT (DppyCT-1). The decomposition of this mode into internal coordinates reveals that the proportion of C–D-involved vibrations is 29.31%, which is even smaller than that in Dall-1 (34.67%). By further resolving mode 142, which corresponds to the second largest reorganization energy, it is revealed that the proportion of C–D-involved vibrations is 28.84%. It can be concluded that the partial deuteriation of the ligandCT may result in a more remarkable effect on the reduction of knr. As for DdfppyCT-2, mode 143, for which the reorganization energy is 535 cm−1, is picked out. The proportion of its C–D-involved vibrations is 33.66%, whilst the second largest reorganization energy contribution is from mode 148, and the proportion of its C–D-involved vibrations is 29.03%. Both of these are smaller than the C–H-involved vibration contributions in primitive complex 2.
Heteroleptic iridium complex 3 has a little discrepancy in the relationship between its normal modes and reorganization energies. When deuterating its acac ligand, there is no obvious variation in the reorganization energies when compared with primitive 3, but it is undoubtable that measurable differences appear for partially deuterated 3 on its ppyCT ligand. A smaller C–D-involved vibrational proportion of 31.78% is calculated for the largest reorganization energy contribution from mode 128 in DppyCT-3. However, the reorganization energies also show an increase in the HF region when deuterating the other ppy ligand, as can be seen in Fig. 4. Nonetheless, the vibrational mode corresponding to the largest reorganization energy has a relatively large ratio of C–D-involved vibrations (42.20%). The nature of the excited electronic transition in complex 4 is centered on the ancillary pic ligand, which results in a distinct suppression of the reorganization energies when deuterating the pic ligand. The vibrational compositions are similar to those of the completely deuterated complex.
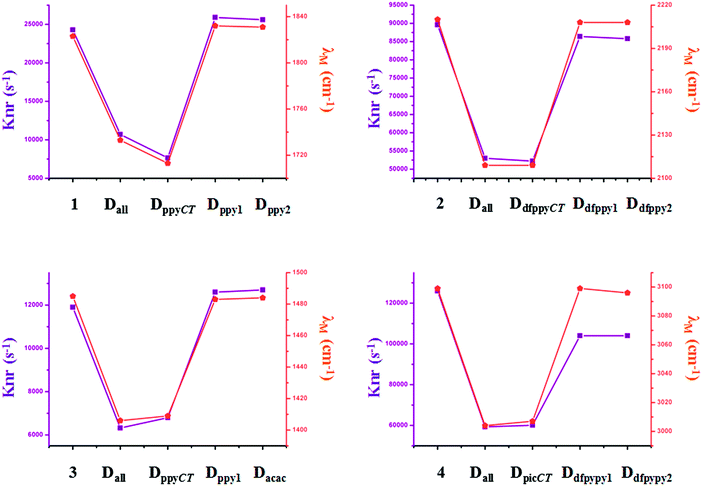
Traditional perspectives have interpreted that a decreased knr can be explained by the increased energy gap between two charge-transfer related states, as formulated by the energy gap law (EGL).63 However, the variations in knr for completely and partially deuterated complexes do not abide by the EGL absolutely. It is evident in Fig. 6 that the relationship between knr and ΔE00 does not always conform to a negative correlation. For example, the knr values are largely decreased from complex 2 to Dall-2, while the ΔE00 values show the same trends, which violates the rule of the EGL. Additionally, as shown in Fig. 6, complexes Ddfpypy1-4 and Ddfpypy2-4 have nearly the same knr values, but the ΔE00 values of these two complexes have a large discrepancy. Hence, it is inadequate to determine the value of knr under the consideration of the EGL. Alternatively, the convolution method, which takes strong coupling limits as well as more temperature-dependent factors into consideration, could serve as an improvement to the EGL approach. As shown in Fig. 7, the trend in knr has an absolute positive correlation with λM, which represents the reorganization energy in the high-frequency region. Consequently, the calculation of knr employed in this study, which serves as an improvement to the EGL approach, enables the production of more valuable results, in that the deuterium isotope effect mainly gives rise to HF accepting modes.
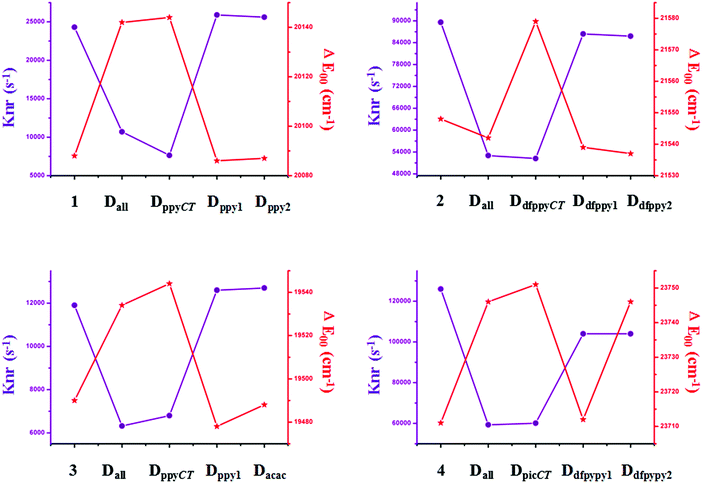 | ||
| Fig. 6 Plots of the calculated knr and ΔE00 values for the primitive and deuterated complexes of 1–4. | ||
4 Conclusions
On the basis of an in-depth theoretical evaluation, deuterium isotope effects on several well-known Ir(III) complexes are explored. Traditional perspectives on the reduction of knr in deuterated complexes, namely the traditional EGL, cannot serve as the fundamental standard. With respect to radiative deactivation processes, the calculated kr values for the protonated complexes conform to experimental results. With such credible kr calculations, neither complete deuteriation or partial ligand deuteriation compounds are altered when compared with corresponding primitive complexes. Subsequently, a two-averaged modes theoretical approximation is employed to evaluate knr. The computational decreased knr (decreased almost by half) of the completely deuterated complexes is consistent with experimental results, and the suppression of knr primarily results from reduced C–D vibrations in the high-frequency mode. Partial deuteriation enables us to distinguish the ligand involved in the excited charge transfer, due to the fact that the C–D vibrations exert the same influence as the completely deuterated complex, while other ligand deuteriations cannot make any changes to the non-radiative decay processes. Therefore, through our comprehensive theoretical approach, the impact of the deuterium isotope effects on the non-radiative deactivation processes, as well as the nature of the excited state decay processes, can be precisely evaluated. Notably, the crucial deuteriation location for smaller values of knr can also be expected from our theoretical investigation. Moreover, such a convincing theoretical evaluation system provides more possibilities to improve the quantum efficiency of Ir(III) complexes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the State Key Development Program for Basic Research of China (Grant No. 2013CB834801), the Natural Science Foundation of China (Grant No. 21573088), the Young Scholar Training Program of Jilin University, and the Open Project Funding of Beijing National Laboratory for Molecular Sciences (BNLMS).References
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051 CrossRef CAS.
- A. Tsuboyama, H. Iwawaki, M. Furugori, T. Mukaide, J. Kamatani, S. Igawa, T. Moriyama, S. Miura, T. Takiguchi, S. Okada, M. Hoshino and K. Ueno, J. Am. Chem. Soc., 2003, 125, 12971–12979 CrossRef CAS PubMed.
- T.-Y. Li, Y.-M. Jing, X. Liu, Y. Zhao, L. Shi, Z. Tang, Y.-X. Zheng and J.-L. Zuo, Sci. Rep., 2015, 5, 14912 CrossRef CAS PubMed.
- J. Wang, F.-Q. Bai, B.-H. Xia and H.-X. Zhang, J. Phys. Chem. A, 2011, 115, 11689–11695 CrossRef CAS PubMed.
- M.-X. Song, G.-F. Wang, J. Wang, Y.-H. Wang, F.-Q. Bai and Z.-K. Qin, Spectrochim. Acta, Part A, 2015, 134, 406–412 CrossRef CAS PubMed.
- K. Dedeian, P. I. Djurovich, F. O. Garces, G. Carlson and R. J. Watts, Inorg. Chem., 1991, 30, 1685–1687 CrossRef CAS.
- R. C. Kwong, S. Lamansky and M. E. Thompson, Adv. Mater., 2000, 12, 1134–1138 CrossRef CAS.
- Y. You and S. Y. Park, J. Am. Chem. Soc., 2005, 127, 12438–12439 CrossRef CAS PubMed.
- S. Lamansky, P. Djurovich, D. Murphy, F. Abdel-Razzaq, H.-E. Lee, C. Adachi, P. E. Burrows, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2001, 123, 4304–4312 CrossRef CAS PubMed.
- Y. You and S. Y. Park, Dalton Trans., 2009, 1267–1282 RSC.
- C.-L. Ho and W.-Y. Wong, New J. Chem., 2013, 37, 1665–1683 RSC.
- A. B. Tamayo, B. D. Alleyne, P. I. Djurovich, S. Lamansky, I. Tsyba, N. N. Ho, R. Bau and M. E. Thompson, J. Am. Chem. Soc., 2003, 125, 7377–7387 CrossRef CAS PubMed.
- T. Sajoto, P. I. Djurovich, A. B. Tamayo, J. Oxgaard, W. A. Goddard and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9813–9822 CrossRef CAS PubMed.
- C.-H. Lin, Y.-Y. Chang, J.-Y. Hung, C.-Y. Lin, Y. Chi, M.-W. Chung, C.-L. Lin, P.-T. Chou, G.-H. Lee, C.-H. Chang and W.-C. Lin, Angew. Chem., Int. Ed., 2011, 123, 3240–3244 CrossRef.
- C.-H. Chang, C.-L. Ho, Y.-S. Chang, I.-C. Lien, C.-H. Lin, Y.-W. Yang, J.-L. Liao and Y. Chi, J. Mater. Chem. C, 2013, 1, 2639–2647 RSC.
- Y. Kang, Y.-L. Chang, J.-S. Lu, S.-B. Ko, Y. Rao, M. Varlan, Z.-H. Lu and S. Wang, J. Mater. Chem. C, 2013, 1, 441–450 RSC.
- B. Minaev, G. Baryshnikov and H. Agren, Phys. Chem. Chem. Phys., 2014, 16, 1719–1758 RSC.
- W. Pauli, Zur quantenmechanik des magnetischen elektrons, Springer, 1988, pp. 282–305 Search PubMed.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS PubMed.
- A. Bossi, A. F. Rausch, M. J. Leitl, R. Czerwieniec, M. T. Whited, P. I. Djurovich, H. Yersin and M. E. Thompson, Inorg. Chem., 2013, 52, 12403–12415 CrossRef CAS PubMed.
- L.-M. Xie, F.-Q. Bai, W. Li, Z.-X. Zhang and H.-X. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 10014–10021 RSC.
- T. Hofbeck and H. Yersin, Inorg. Chem., 2010, 49, 9290–9299 CrossRef CAS PubMed.
- G.-M. Tong and C.-M. Che, Chem. – Eur. J., 2009, 15, 7225–7237 CrossRef CAS PubMed.
- A. F. Henwood and E. Zysman-Colman, Chem. Commun., 2017, 53, 807–826 RSC.
- I. Omae, Coord. Chem. Rev., 2016, 310, 154–169 CrossRef CAS.
- M. R. Wright, R. P. Frosch and G. W. Robinson, J. Chem. Phys., 1960, 33, 934–935 CrossRef CAS.
- J. L. Kropp and M. W. Windsor, J. Chem. Phys., 1963, 39, 2769–2770 CrossRef CAS.
- J. L. Kropp and M. W. Windsor, J. Chem. Phys., 1965, 42, 1599–1608 CrossRef CAS.
- T. Zhang, Q. Peng, C. Quan, H. Nie, Y. Niu, Y. Xie, Z. Zhao, B. Z. Tang and Z. Shuai, Chem. Sci., 2016, 7, 5573–5580 RSC.
- R. J. Watts, S. Efrima and H. Metiu, J. Am. Chem. Soc., 1979, 101, 2742–2743 CrossRef CAS.
- T. Abe, A. Miyazawa, H. Konno and Y. Kawanishi, Chem. Phys. Lett., 2010, 491, 199–202 CrossRef CAS.
- P. S. Wagenknecht and P. C. Ford, Coord. Chem. Rev., 2011, 255, 591–616 CrossRef CAS.
- S. Fanni, T. E. Keyes, C. M. O'Connor, H. Hughes, R. Wang and J. G. Vos, Coord. Chem. Rev., 2000, 208, 77–86 CrossRef CAS.
- M. Kovacs, K. L. Ronayne, W. R. Browne, W. Henry, J. G. Vos, J. J. McGarvey and A. Horvath, Photochem. Photobiol. Sci., 2007, 6, 444–453 CAS.
- M. Kleinschmidt, C. van Wüllen and C. M. Marian, J. Chem. Phys., 2015, 142, 094301 CrossRef PubMed.
- K. P. S. Zanoni, B. K. Kariyazaki, A. Ito, M. K. Brennaman, T. J. Meyer and N. Y. Murakami Iha, Inorg. Chem., 2014, 53, 4089–4099 CrossRef CAS PubMed.
- A. Ito, N. Kobayashi and Y. Teki, Inorg. Chem., 2017, 56, 3794–3808 CrossRef CAS PubMed.
- G. S. M. Tong, P. K. Chow, W.-P. To, W.-M. Kwok and C.-M. Che, Chem. – Eur. J., 2014, 20, 6433–6443 CrossRef CAS PubMed.
- K. F. Freed and J. Jortner, J. Chem. Phys., 1970, 52, 6272–6291 CrossRef CAS.
- K. F. Freed, J. Phys. Chem. B, 2003, 107, 10341–10343 CrossRef CAS.
- B. S. Brunschwig and N. Sutin, Comments Inorg. Chem., 1987, 6, 209–235 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723 CAS.
- Q. Peng, Q. Shi, Y. Niu, Y. Yi, S. Sun, W. Li and Z. Shuai, J. Mater. Chem. C, 2016, 4, 6829–6838 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. E. Gomperts, O. Stratmann, A. J. Yazyev, R. Austin, C. Cammi, J. W. Pomelli, R. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- D. P. Chong, Mol. Phys., 2005, 103, 749–761 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- K. Mori, T. P. M. Goumans, E. van Lenthe and F. Wang, Phys. Chem. Chem. Phys., 2014, 16, 14523–14530 RSC.
- A. R. G. Smith, P. L. Burn and B. J. Powell, ChemPhysChem, 2011, 12, 2429–2438 CrossRef CAS PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109 CrossRef CAS.
- R. J. F. Berger, H.-G. Stammler, B. Neumann and N. W. Mitzel, Eur. J. Inorg. Chem., 2010, 1613–1617 CrossRef CAS.
- A. Ito and T. J. Meyer, Phys. Chem. Chem. Phys., 2012, 14, 13731–13745 RSC.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Köhler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed description of kr and knr, the geometry optimization results, and detailed calculations of the displacement vectors of the typical vibrational modes for all complexes. See DOI: 10.1039/c8qm00061a |
| This journal is © the Partner Organisations 2018 |