Open Access Article
Open Access ArticleRevealing unusual rigid diamond net analogues in superhard titanium carbides†
Chunhong Xu,
Kuo Bao*,
Shuailing Ma,
Da Li ,
Defang Duan,
Hongyu Yu,
Xilian Jin
,
Defang Duan,
Hongyu Yu,
Xilian Jin ,
Fubo Tian,
Bingbing Liu
,
Fubo Tian,
Bingbing Liu and
Tian Cui
and
Tian Cui *
*
State Key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun 130012, China. E-mail: cuitian@jlu.edu.cn; baokuo@jlu.edu.cn; Fax: +86-431-85168825; Tel: +86-431-85168825
First published on 18th April 2018
Abstract
Transition metal carbides (TMCs) are considered to be potential superhard materials and have attracted much attention. With respect to titanium and carbon atoms, we confirm the pressure-composition phase diagram of the Ti–C system using structure searches and first-principles calculations. We firstly discovered stable TiC4 which was expected to be synthesized at high pressure, as well as metastable TiC2 and TiC3. These layered titanium carbides are diamond net analogues due to the unusual C-layers in the form of puckered graphene-like, diamond-like and double diamond-like C-layers. The existence of diamond-like C-layers might help to understand the formation of diamond. All the studied titanium carbides could be recoverable at ambient pressure and exhibited great mechanical properties (strong ability to resist volume and shear deformations, small anisotropy, and high hardness). Moreover, we crystallized the structure of TiC4 in other transition metal carbides and obtained five superhard TMC4s (TM = V, Zr, Nb, Hf and Ta). Interactions between layers were revealed to be the source of the great mechanical properties and high hardness through combining detailed analyses of electronic structure and chemical bonding, namely, weak ionic interactions of neighboring Ti- and C-layers and the strong covalent interactions of C- and C-layers.
Introduction
Strong covalent solids can be formed by combining the light elements B, C, N and O,1–4 which contain rigid bonding networks that can resist elastic and plastic deformation, such as diamond and cubic boron nitride.5 However, their synthesis conditions and sample choice are so strict that it hinders their industrial application.6 Subsequently, the combination of covalent and short light elements (LEs) with high valence electron density transition metals (TMs) is another way to design hard or superhard materials. Moreover, they have many excellent properties including good wear and corrosion resistance, high hardness, good superconductivity, excellent electrical and thermal conductivity, and so on.7,8 Accordingly, numerous scientists have been trying to find novel hard or superhard materials from TM–LE compounds that can replace diamond and cubic boron nitride.9–15Titanium is an abundant and less expensive transition metal with a regular bulk modulus, compared with most transition metals like tungsten, rhenium and platinum. The electron configuration of titanium atom is adopted as 3p63d34s1. It is likely to produce sp3 hybridization in the reaction of titanium and carbon (2s22p2) atoms, which would be beneficial to mechanical properties of titanium carbides. The hardness of titanium carbide compounds is closely related to chemical bonding. There are three bonding behaviors present in principle, viz., metallic Ti–Ti bonds, strong covalent C–C bonds and partial ionic Ti–C bonds. Short and covalent C–C bonds are the most important factor contributing to high hardness. Second are partially ionic Ti–C bonds. Metallic Ti–Ti bonds can introduce dislocation mobility; this is harmful for hardness. Thus the improvement of hardness can strengthen C–C and Ti–C interactions, and eliminate direct Ti–Ti interactions. Most hard TiCn (n < 1) compounds have been synthesized and studied widely.16–29 Their high hardness only derives from partially ionic Ti–C bonds. In this work, we take full advantage of this strong Ti–C interaction, and simultaneously introduce a C–C interaction to obtain novel titanium carbides. As is known to all, high pressure can cause profound changes in the electronic orbitals and bonding behaviors, which brings about many unusual hard multifunctional materials,30–32 and may become an important technique to realize our idea.
Here, based on USPEX simulations, the phase diagram of titanium carbides has been established at the pressure range of 0–100 GPa. New high pressure phases of diamond net analogue titanium carbides (TiC2, TiC3 and TiC4) are proposed and can stabilize dynamically at ambient pressure. Their structural stability and mechanical properties are discussed and correlated with electronic structures and chemical bonding. The results show that interlayer interactions are responsible for great mechanical properties and high hardness in all of the studied titanium carbides.
Computational details
We used the universal structure predictor USPEX,33–35 interfaced with the VASP code, to explore the new titanium carbides. These simulations, for all considered stoichiometries (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 8
7, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 6
5, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 5
5, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 5
4, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 4
3, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 3
3, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 1
3, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4), were performed at pressures of 0–100 GPa. The total energy calculations and local structural relaxations were carried out within the generalized gradient approximation and the exchange-correlation functional of Perdew, Burke and Ernzerhof.36 We described the interactions between the ions and the electrons by using the pseudo-potential plane-wave method. The electronic configurations of titanium, zirconium, hafnium, vanadium, niobium, tantalum and carbon are Ti: 3p63d34s1, V: 3p63d44s1, Zr: 4s24p65s24d2, Nb: 4p65s14d4, Hf: 5p66s25d2, Ta: 5p66s25d3, and C: 2s22p2. The tested cutoff energy of 850 eV and the Monkhorst–Pack k-point meshes with a grid of 2π × 0.03 Å−1 were chosen to achieve a total energy convergence of less than 1 meV per atom. To verify the mechanical and dynamical stabilities of the predicted structures, we calculated elastic constants and the phonon using the strain–stress method and a supercell approach37 implemented in the PHONOPY code,38 respectively. The mechanically stable structures should satisfy the generalized elastic stability criteria.39 The bulk modulus B, shear modulus G, Young’s modulus Y, B/G and Poisson’s ratio ν were estimated via the Voigt–Reuss–Hill (VRH) approximations.40 The theoretical Vickers hardness was estimated by using Gao’s model.41 The Mulliken bond population was calculated via the supercell method with the CASTEP code.42,43 The ultra-soft Vanderbilt pseudo-potential (USPP)44 with PBE-GGA was chosen. The cutoff energy and k-mesh were same as the setting in VASP calculations. The Reflex Tools of Materials Studio code was used to simulate the X-ray diffraction data.45 The Ti–C bonding information is analyzed by calculating the crystal orbital Hamilton population (COHP). The calculation is based on the PW method, and is performed by re-extracting atom-resolved information from the delocalized PW basis sets, which is named “projected COHP” (pCOHP).46,47
4), were performed at pressures of 0–100 GPa. The total energy calculations and local structural relaxations were carried out within the generalized gradient approximation and the exchange-correlation functional of Perdew, Burke and Ernzerhof.36 We described the interactions between the ions and the electrons by using the pseudo-potential plane-wave method. The electronic configurations of titanium, zirconium, hafnium, vanadium, niobium, tantalum and carbon are Ti: 3p63d34s1, V: 3p63d44s1, Zr: 4s24p65s24d2, Nb: 4p65s14d4, Hf: 5p66s25d2, Ta: 5p66s25d3, and C: 2s22p2. The tested cutoff energy of 850 eV and the Monkhorst–Pack k-point meshes with a grid of 2π × 0.03 Å−1 were chosen to achieve a total energy convergence of less than 1 meV per atom. To verify the mechanical and dynamical stabilities of the predicted structures, we calculated elastic constants and the phonon using the strain–stress method and a supercell approach37 implemented in the PHONOPY code,38 respectively. The mechanically stable structures should satisfy the generalized elastic stability criteria.39 The bulk modulus B, shear modulus G, Young’s modulus Y, B/G and Poisson’s ratio ν were estimated via the Voigt–Reuss–Hill (VRH) approximations.40 The theoretical Vickers hardness was estimated by using Gao’s model.41 The Mulliken bond population was calculated via the supercell method with the CASTEP code.42,43 The ultra-soft Vanderbilt pseudo-potential (USPP)44 with PBE-GGA was chosen. The cutoff energy and k-mesh were same as the setting in VASP calculations. The Reflex Tools of Materials Studio code was used to simulate the X-ray diffraction data.45 The Ti–C bonding information is analyzed by calculating the crystal orbital Hamilton population (COHP). The calculation is based on the PW method, and is performed by re-extracting atom-resolved information from the delocalized PW basis sets, which is named “projected COHP” (pCOHP).46,47
Results and discussion
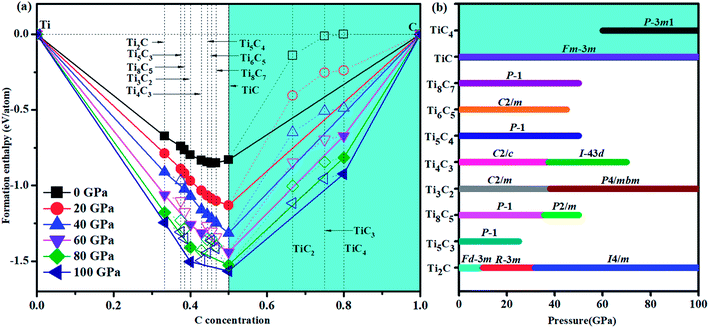
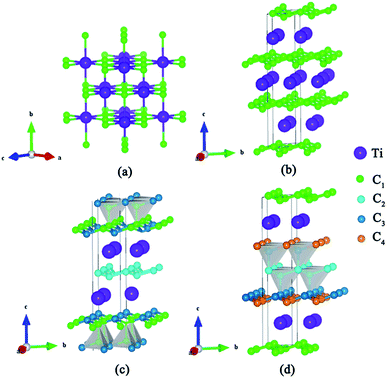
We have used the ab initio evolutionary algorithm USPEX to explore the Ti–C system. In this paper, we only discuss TiCn (n ≥ 1) compounds; other TiCn (n < 1) phases will be discussed in other papers. By evaluating the formation enthalpy ΔH for each composition at 0 K and different pressures, the convex hull at different pressures is obtained (Fig. 1). Hexagonal titanium metal (α-Ti)48 and graphite were used as reference structures. In Fig. 1a, TiC has a stable composition for all considered pressures. However, metastable phases of TiC2 and TiC3 are energetically favorable above 60 GPa and deserve to be studied. Fortunately, we found a stable high-pressure phase of TiC4 located on the convex hull in the pressure range of 60–100 GPa (Fig. 1b) for the first time. The ground state configurations of Ti2C, Ti3C2, Ti6C5 and TiC are in good agreement with pre-existing theoretical25,27,49 and experimental results.21,50 Furthermore, the simulated X-ray diffraction of cubic structures of Ti2C51 and TiC52 is in accordance with experimental results (Fig. S1†). These results suggest our methodology is credible. The crystallographic parameters of Ti2C, Ti3C2, Ti6C5, and TiC–TiC4 are listed in Table S1.† Fig. 2 shows the crystal structures of TiC–TiC4. In the predicted structures, the rock-salt-type TiC (SG: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) consists of Ti–C bonds (Fig. 2a). The Ti–C bond length of 2.168 Å is in good agreement with the experimental value of 2.164 Å. Interestingly, three unusual diamond net analogues with various C-layers were plainly observed in TiCn (n > 1) compounds. In the trigonal TiC2 (SG: R
m) consists of Ti–C bonds (Fig. 2a). The Ti–C bond length of 2.168 Å is in good agreement with the experimental value of 2.164 Å. Interestingly, three unusual diamond net analogues with various C-layers were plainly observed in TiCn (n > 1) compounds. In the trigonal TiC2 (SG: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure, the puckered graphene-like C-layers are separated by Ti-layers (Fig. 2b). The C–C bond length is 1.600 Å, which is smaller than that of RhN2–OsC2 (1.242 Å).53 What is more, the introduction of the puckered graphene-like C-layers can cause the quasi-3D effect, which usually emerges in transition metal borides,54 but has for the first time been obtained in transition metal carbides. The TiC3 structure (SG: R
m) structure, the puckered graphene-like C-layers are separated by Ti-layers (Fig. 2b). The C–C bond length is 1.600 Å, which is smaller than that of RhN2–OsC2 (1.242 Å).53 What is more, the introduction of the puckered graphene-like C-layers can cause the quasi-3D effect, which usually emerges in transition metal borides,54 but has for the first time been obtained in transition metal carbides. The TiC3 structure (SG: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) has one type of Ti atom and three types of C atom. Its lattice parameter c (30.670 Å) is so long that we have only presented its partial structure. In Fig. 2c, each C1 atom is coordinated with four C atoms, including three C3 atoms stabilized in a plane and one C1 atom, forming diamond-like C-layers along the c-axis. The puckered graphene-like C-layers between two Ti-layers consist of shared C1 atoms and C3 atoms, and bridge the diamond-like C-layers. The bond lengths of C1–C1, C1–C3 and C2–C2 are 1.586 Å, 1.584 Å and 1.567 Å, respectively. These C–C lengths are similar to those of RuC2 (ref. 55) and OsC2.53,55,56 The shortest C–C bond length is comparable to that in diamond (1.544 Å). With an additional C atom in the lattice, there is one type of Ti atom and four types of C atom in the structure of TiC4 (SG: P
m) has one type of Ti atom and three types of C atom. Its lattice parameter c (30.670 Å) is so long that we have only presented its partial structure. In Fig. 2c, each C1 atom is coordinated with four C atoms, including three C3 atoms stabilized in a plane and one C1 atom, forming diamond-like C-layers along the c-axis. The puckered graphene-like C-layers between two Ti-layers consist of shared C1 atoms and C3 atoms, and bridge the diamond-like C-layers. The bond lengths of C1–C1, C1–C3 and C2–C2 are 1.586 Å, 1.584 Å and 1.567 Å, respectively. These C–C lengths are similar to those of RuC2 (ref. 55) and OsC2.53,55,56 The shortest C–C bond length is comparable to that in diamond (1.544 Å). With an additional C atom in the lattice, there is one type of Ti atom and four types of C atom in the structure of TiC4 (SG: P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1). The bonding environment within TiC4 is similar to that of TiC3, namely, C1 atoms construct the puckered graphene-like C-layers, and C2, C3 and C4 atoms construct the double diamond-like C-layers, and bridge the puckered graphene-like C-layers. These C-layers sandwich two Ti-layers (see Fig. 2d). In comparison to TiC3, the different C–C bond lengths in TiC4 (C1–C1 = 1.559 Å, C2–C2 = 1.576 Å, C2–C3 = 1.560 Å and C3–C4 = 1.581 Å) are closer to those of diamond. Diamond-like C-layers have been reported in Ru–C and Os–C systems;53,55,56 here for the first time they appear in the thermodynamically stable phases of TiC3 and TiC4. Thus, these new titanium carbides can be considered as diamond net analogues due to the unusual C-layers along the c-axis. These titanium carbides may exhibit the characteristics of diamond, that is to say, they may possess excellent mechanical properties and high hardness. With unusual C-layers in TiCn (n > 1) compounds, when n = 2, the puckered graphene-like C-layers appear in titanium carbides; when n ≥ 3, titanium carbides begin to exhibit single and double diamond-like C-layers; when n ∼ ∞, there is a reasonable assumption of obtaining pure diamonds, where transition metal Ti atoms are the catalyst components, similar to the powerful elemental catalysts Co, Fe, Mn, Nr and Cr which are used to synthesize diamond under high pressure.57 This can widen the understanding and production of diamond. In Fig. S2,† there are no imaginary frequencies in the whole Brillouin zone of all new phases for titanium carbides at 0 and 100 GPa, indicating that all the studied high pressure phases in titanium carbides could be quenchable under ambient conditions.
m1). The bonding environment within TiC4 is similar to that of TiC3, namely, C1 atoms construct the puckered graphene-like C-layers, and C2, C3 and C4 atoms construct the double diamond-like C-layers, and bridge the puckered graphene-like C-layers. These C-layers sandwich two Ti-layers (see Fig. 2d). In comparison to TiC3, the different C–C bond lengths in TiC4 (C1–C1 = 1.559 Å, C2–C2 = 1.576 Å, C2–C3 = 1.560 Å and C3–C4 = 1.581 Å) are closer to those of diamond. Diamond-like C-layers have been reported in Ru–C and Os–C systems;53,55,56 here for the first time they appear in the thermodynamically stable phases of TiC3 and TiC4. Thus, these new titanium carbides can be considered as diamond net analogues due to the unusual C-layers along the c-axis. These titanium carbides may exhibit the characteristics of diamond, that is to say, they may possess excellent mechanical properties and high hardness. With unusual C-layers in TiCn (n > 1) compounds, when n = 2, the puckered graphene-like C-layers appear in titanium carbides; when n ≥ 3, titanium carbides begin to exhibit single and double diamond-like C-layers; when n ∼ ∞, there is a reasonable assumption of obtaining pure diamonds, where transition metal Ti atoms are the catalyst components, similar to the powerful elemental catalysts Co, Fe, Mn, Nr and Cr which are used to synthesize diamond under high pressure.57 This can widen the understanding and production of diamond. In Fig. S2,† there are no imaginary frequencies in the whole Brillouin zone of all new phases for titanium carbides at 0 and 100 GPa, indicating that all the studied high pressure phases in titanium carbides could be quenchable under ambient conditions.
For materials, the useful information of mechanical properties and hardness can be obtained from accurate elastic constants. To test the mechanical stability of the studied titanium carbides, we calculated their elastic constants using the strain–stress method. These results are listed in Table 1. Based on the elastic constants, the obtained bulk modulus B, shear modulus G, Young’s modulus Y, B/G, and Poisson’s ratio ν are tabulated in Table 1. For comparison, the elastic properties of diamond have been calculated. According to our calculated results, all elastic constants meet the mechanical stability criteria,39 which indicates their elastic stability. The calculated elastic constants of TiC and diamond are in excellent agreement with the experiment values,58,59 suggesting the credibility of our calculations. Among these titanium carbides, TiC4 has the highest C11 value of 844 GPa due to the shortest C1–C1 bond (1.559 Å) in the puckered graphene-like C-layers, similar to that of OsC4 (866 GPa)53 and larger than that of RuC4 (610 GPa),55 indicating a strong ability to resist elastic deformation in TiC4 along the a-axis. From TiC to TiC4, the increasingly large values of C33 indicate that they are difficult to compress along the c-axis. Moreover, the C11 and C33 values of TiC3 are larger by 17.7% and 9.8% than those of TiC2, respectively. This shows the evident influence of the puckered graphene-like C-layer and diamond-like C-layer. The shear constants of C44 range from 255 GPa to 302 GPa in TiCn (n > 1) compounds, which are larger than those of RuC2–RuC4 (below 200 GPa),55 suggesting these TiCn (n > 1) compounds may possess strong shear strength and high hardness.
| Phase | C11 | C33 | C44 | C66 | C12 | C13 | B | G | B/G | Y | ν | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TiC | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
515 | 167 | 120 | 252 | 178 | 1.41 | 433 | 0.21 | |||
| Exp | 513 (ref. 58) | 178 (ref. 58) | 106 (ref. 58) | 240 (ref. 58) | ||||||||
| TiC2 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
667 | 559 | 255 | 262 | 144 | 131 | 299 | 252 | 1.19 | 590 | 0.17 |
| TiC3 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
785 | 602 | 280 | 326 | 133 | 110 | 317 | 297 | 1.07 | 679 | 0.14 |
| TiC4 | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
844 | 664 | 302 | 362 | 120 | 105 | 332 | 326 | 1.02 | 738 | 0.13 |
| Diamond | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1054 | 562 | 125 | 435 | 520 | 0.84 | 1116 | 0.07 | |||
| Exp | 1081 (ref. 59) | 579 (ref. 59) | 125 (ref. 59) | 442 (ref. 59) |
The bulk modulus and shear modulus quantify the ability to resist volume, shear and tension changes. The values of bulk moduli for TiC3 (317 GPa) and TiC4 (332 GPa) are greater than 300 GPa, indicating their better ability to resist volume deformation. It is widely believed that hardness has a closer relation to shear modulus than bulk modulus. TiC3 and TiC4 possess relatively larger shear moduli of 297 GPa and 326 GPa, which are larger than those of RuC4 (ref. 55) and OsC4.53,55,56 Furthermore, Poisson’s ratio can describe the degree of directionality of covalent bonding. Low Poisson’s ratio (∼0.2) materials often have strong covalence. Specifically, TiC3 and TiC4 possess the lowest Poisson’s ratio (0.14 and 0.13) for known transition metal carbides.53,55,56 A B/G ratio value higher (lower) than 1.75 indicates the material is ductile (brittle). All these titanium carbides have B/G values smaller than 1.75, suggesting their brittle nature. It is not hard to see that high elastic constants and moduli, and small Poisson’s ratios and B/G values, imply great mechanical properties and the potential possibility of titanium carbides becoming hard or superhard materials. The elastic anisotropy is highly related with the microcracks in materials.60 So we quantitatively calculated anisotropic properties using the ElAM (Elastic Anisotropy Measures) code.61 As an example, the result of TiC2 is shown in Fig. 3, and the others are included in Fig. S3–S5.† For a real material, the three-dimensional directional dependence exhibits a perfect spherical shape. The deviation degree from the spherical shape reflects the amount of anisotropy. According to our simulated results, they all exhibit small elastic anisotropy, which is favorable to their mechanical properties and hardness.
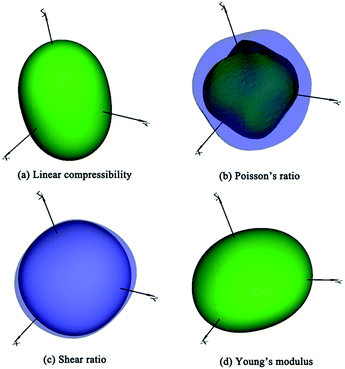 | ||
| Fig. 3 The calculated three-dimensional representations of (a) linear compressibility, (b) Poisson’s ratio, (c) shear ratio, and (d) Young’s modulus for the TiC2 structure. | ||
Hardness
In order to verify our hypothesis of the intrinsic hardness, we calculated the hardness of these titanium carbides by using Gao’s model41 which includes the role of the metallic bond to evaluate intrinsic hardness. The expressions and detailed parametric descriptions of the complex transition metal compounds have been previously reported in ref. 62. Using this formula, the related bond parameters and hardness values of diamond and the titanium carbides are listed in Table 2. Our calculated Vickers hardness values of diamond and TiC agree well with experimental data,63,64 demonstrating the reliability of the hardness model we have used. The obtained hardness values of TiC, TiC2, TiC3 and TiC4 are 32.7, 32.4, 40.8 and 49.1 GPa, respectively. TiC and TiC2 could be classified as potential hard materials, while TiC3 and TiC4 are potential superhard materials. Based on the predicted stable TiC4, we constructed five TMC4 (TM = V, Zr, Nb, Hf and Ta) structures, and also calculated their mechanical properties and hardness. These structures are reasonable in terms of their thermodynamical, mechanical and dynamical stabilities, which are shown in Tables S2, S3 and Fig. S6.† Their optimized lattice parameters and atomic coordinates at ambient pressure are listed in Table S4.† The related bond parameters of these TMC4 structures are listed in Table S5.† Using the same hardness model, the obtained Vickers hardness of VC4, ZrC4, NbC4, HfC4, and TaC4 are 50.3 GPa, 41.9 GPa, 43.9 GPa, 49.3 GPa, and 59.2 GPa, respectively. Therefore, these new TMC4 compounds are potential superhard materials and have great mechanical properties, which could broaden the range of promising superhard materials.| Crystals | Bond type | dμ (Å) | vbμ (Å3) | P | fm (×10−4) | Hv Gao (GPa) | Hv Exp (GPa) |
|---|---|---|---|---|---|---|---|
| TiC | Ti–C | 2.168 | 3.396 | 0.37 | 6.240 | 32.7 | 24.7 (ref. 63) |
| 30 ± 2 (ref. 64) | |||||||
| TiC2 | C–C | 1.600 | 1.124 | 0.85 | 0 | 32.4 | |
| Ti–C | 2.331 | 3.475 | 0.1 | 8.121 | |||
| TiC3 | C–C | 1.567 | 1.193 | 0.88 | 0 | 40.8 | |
| C–C | 1.584 | 1.232 | 0.89 | 0 | |||
| C–C | 1.586 | 1.236 | 0.75 | 0 | |||
| Ti–C | 2.327 | 3.905 | 0.09 | 7.995 | |||
| Ti–C | 2.357 | 4.058 | 0.08 | 7.995 | |||
| TiC4 | C–C | 1.559 | 1.299 | 0.89 | 0 | 49.1 | |
| C–C | 1.560 | 1.302 | 0.79 | 0 | |||
| C–C | 1.576 | 1.342 | 0.86 | 0 | |||
| C–C | 1.581 | 1.355 | 0.88 | 0 | |||
| Ti–C | 2.328 | 4.327 | 0.08 | 6.143 | |||
| Ti–C | 2.350 | 4.451 | 0.08 | 6.143 | |||
| Diamond | C–C | 1.544 | 2.836 | 0.82 | 0 | 100.9 | 96 (ref. 63) |
| 96 ± 5 (ref. 64) |
Electronic structures and chemical bonding
The desire to explore the mechanism of the great mechanical properties and high hardness from the perspective of interlayer interactions motivates us to analyze the electronic structure and chemical bonding of titanium carbides, viz., the total and partial density of states (DOS), the crystal orbital Hamilton population (COHP), Bader charge,65 and the electron localization function (ELF).66 All four structures are metals due to their finite DOS at the Fermi level, which mainly originates from the high electron occupations in the Ti 3d orbitals as seen in Fig. 4. There are pronounced pseudogaps (a sharp valley around the Fermi level to divide the bonding and antibonding states) in their DOSs. The small electronegativity difference between Ti (1.5) and C (2.5) atoms suggest hybridization effects, leading to the formation of pseudogaps,67 which will surely increase the stability of the compounds.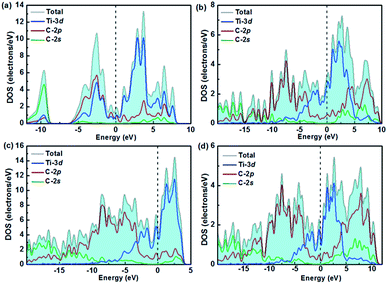 | ||
| Fig. 4 Calculated total and partial densities of states for (a) TiC, (b) TiC2, (c) TiC3, and (d) TiC4. | ||
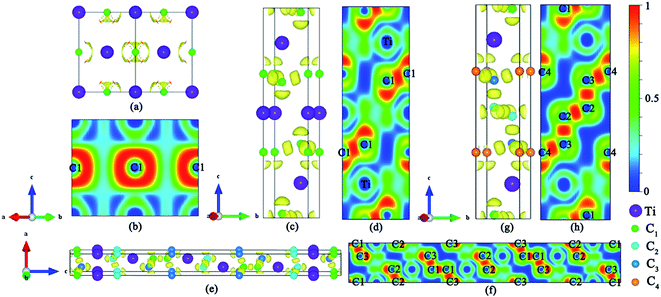
The DOS profiles in the energy range below −10 eV show nearly pure-carbon regions which correspond to strong C–C interactions. Crystal orbital Hamilton population (COHP) can be used to understand the bonding/antibonding states of metals and nonmetals from the point of view of bonding energy. Fig. 5 shows the results of –pCOHP as a function of energy for different Ti–C bonds (corresponding to those in Table S6†) for TiC–TiC4. The negative contributions to the right represent bonding energy regions and positive to the left represent antibonding energy regions. According to Fig. 5, the (nearly) full-filling of the Ti–C bonding and antibonding states suggest the formation of strong Ti–C bonding. The integrated crystal orbital Hamilton population (ICOHP) values of different Ti–C and C–C bonds, which is a quantitative evaluation of bonding strength, were calculated and are listed in Table S6.† From the –ICOHP values it can be concluded that the strongest Ti–C interaction occurs in TiC. TiC has the shortest bond length of 2.168 Å and the largest –ICOHP value of 2.99 eV. For other titanium carbide compounds, most –ICOHP values decrease with a more extended bond length of Ti–C, suggesting weaker bond strength. To further determine the nature of Ti–C and C–C bonding of the titanium carbides, the ELFs in the specific plane (110) have been calculated and are shown in Fig. 6. There being hardly any electron localization and moderate charge transfer between Ti and C atoms reflects the partially ionic Ti–C bonding. Hence, one can see that the interactions of the neighboring Ti- and C-layers are still partially ionic, which inevitably induces slippage on the layers and harms the hardness. However, charge transfer for TiC2, TiC3 and TiC4 gradually diminishes (Table S7†), demonstrating the gradually decreasing ionicity of Ti- and and C-layers. This is in agreement with the changes in –COHP values between Ti and C atoms. According to Fig. 6d, f and h, it is clearly seen that the electron density is mainly located at the center of C–C bonds, mirroring strong covalent bonding. Especially for TiC3 and TiC4, electronic channels are formed by C atoms along the [110] direction. These results may explain the high values of shear moduli and incompressibility. In one puckered graphene-like C-layer, each C atom has one electron lone pair and three C–C bonds resembling a diamond unit, without delocalized π bonds (Fig. 6c). There is obviously sp3 hybridization of C atoms. The C1 atoms in TiC3 and the C2 and C3 atoms in TiC4 all formed tetrahedral C–C bonds (Fig. 6e and g), which is characterized by typical sp3 hybridization, leading to the formation of a diamond-like C-layer. The calculated large –ICOHP values between C–C atoms also support strong covalent bonding between C atoms. These strong covalent C- and C-layers contribute towards titanium carbides becoming diamond net analogues. In a word, the weak ionic interactions of neighboring Ti- and C-layers and the strong covalent interactions of C- and C-layers may be firstly used to explain the great mechanical properties and high hardness of these layered titanium carbides.
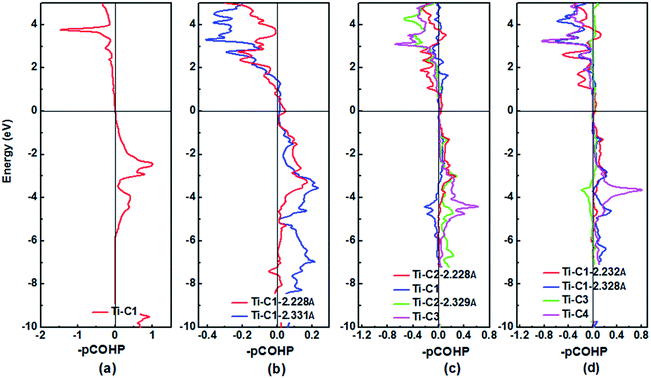 | ||
| Fig. 5 Plots of the Crystal Orbital Hamilton Population (COHP) for (a) TiC, (b) TiC2, (c) TiC3 and (d) TiC4 using the pCOHP method. The horizontal line at zero is the Fermi level. | ||
Conclusions
In summary, we first proposed layered titanium carbides and obtained a phase diagram under high pressure using structure searches and first-principles calculations, for metastable TiC2 and TiC3, and stable TiC4. The novel TiC4 was located on the convex hull and would be easy to synthesize in experiment. These predicted titanium carbides are diamond net analogues due to different C-layers. The appearance of diamond-like C-layers enhances the formation and understanding of diamond. These titanium carbides all have great mechanical properties. The estimated values of hardness indicate that TiC and TiC2 are potential hard materials, and that TiC3 and TiC4 are potential superhard materials. By replacing the Ti atom in the structure of TiC4, we obtained five potential superhard TMC4 (TM = V, Zr, Nb, Hf and Ta) compounds and extended the opportunities of finding novel superhard materials. The calculated results of electronic structures and chemical bonding were analyzed to determine the nature of the interlayer interactions. Furthermore, the weak ionic interactions of neighboring Ti- and C-layers, and the strong covalent interactions of C- and C-layers are firstly used to explain the great mechanical properties and high hardness of these layered titanium carbides. We hope our results will provide guidance for further confirmatory research under high pressure, which is very useful to further explore new hard or superhard materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51632002, 51572108, 11634004, 11104103, 11774121), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT_15R23), the 111 Project (No. B12011), and the National Fund for Fostering Talents of Basic Science (No. J1103202). Parts of the calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.References
- F. B. Tian, J. H. Wang, Z. He, Y. M. Ma, L. C. Wang, T. Cui, C. B. Chen, B. B. Liu and G. T. Zou, Superhard Semiconducting C3N2 Compounds Predicted Via First-Principles Calculations, Phys. Rev. B: Condens. Matter, 2008, 78, 235431 CrossRef.
- D. D. Liu, M. G. Yao, Q. J. Li, W. Cui, B. Zou, T. Cui, B. B. Liu, B. Sundqvist and T. Wågberg, High Pressure and High Temperature Induced Polymerization of C60 Nanotubes, CrystEngComm, 2011, 13, 3600–3605 RSC.
- D. Li, K. Bao, F. B. Tian, Z. W. Zeng, Z. He, B. B. Liu and T. Cui, Lowest Enthalpy Polymorph of Cold-Compressed Graphite Phase, Phys. Chem. Chem. Phys., 2012, 14, 4347–4350 RSC.
- X. L. Wang, F. B. Tian, L. C. Wang, T. Cui, B. B. Liu and G. T. Zou, Structural Stability of Polymeric Nitrogen: A First-Principles Investigation, J. Chem. Phys., 2010, 132, 024502 CrossRef PubMed.
- F. M. Gao, J. L. He, E. D. Wu, S. M. Liu, D. L. Yu, D. C. Li, S. Y. Zhang and Y. J. Tian, Hardness of Covalent Crystals, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed.
- L. J. Zhang, Y. C. Wang, J. Lv and Y. M. Ma, Materials Discovery at High Pressures, Nature Reviews Materials, 2017, 2, 17005 CrossRef CAS.
- R. Freer, The Physics and Chemistry of Carbides, Nitrides and Borides, 1990 Search PubMed.
- H. O. Pierson, Handbook of Refractory Carbides and Nitrides, 1996 Search PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Synthesis and Characterization of the Nitrides of Platinum and Iridium, Science, 2006, 311, 1275–1278 CrossRef CAS PubMed.
- U. Shah, S. Chackalamannil, A. K. Ganguly, M. Chelliah, S. Kolotuchin, A. Buevich and A. Mcphail, Synthesis of Novel Transition Metal Nitrides IrN2 and OsN2, Phys. Rev. Lett., 2006, 96, 155501 CrossRef PubMed.
- J. Q. Qin, D. W. He, J. H. Wang, L. M. Fang, L. Lei, Y. J. Li, J. Hu, Z. L. Kou and Y. Bi, Is Rhenium Diboride a Superhard Material?, Adv. Mater., 2008, 20, 4780–4783 CrossRef CAS.
- M. Xie, R. Mohammadi, Z. Mao, M. M. Armentrout, A. Kavner, R. B. Kaner and S. H. Tolbert, Exploring the High-Pressure Behavior of Superhard Tungsten Tetraboride, Phys. Rev. B: Condens. Matter, 2012, 85, 341–344 Search PubMed.
- Q. F. Gu, G. Krauss and W. Steurer, Transition Metal Borides: Superhard Versus Ultra-Incompressible, Adv. Mater., 2008, 20, 3620–3626 CrossRef CAS.
- X. Y. Cheng, W. Zhang, X. Q. Chen, H. Y. Niu, P. T. Liu, K. Du, G. Liu, D. Z. Li, H. M. Cheng and H. Q. Ye, Interstitial-Boron Solution Strengthened WB3+X, Appl. Phys. Lett., 2013, 103, 171903 CrossRef.
- M. Wang, Y. W. Li, T. Cui, Y. M. Ma and G. T. Zou, Origin of Hardness in WB4 and Its Implications for ReB4, TaB4, MoB4, TcB4, and OsB4, Appl. Phys. Lett., 2008, 93, 101905 CrossRef.
- J. J. Gilman, R. W. Cumberland and R. B. Kaner, Design of Hard Crystals, Int. J. Refract. Met. Hard Mater., 2006, 24, 1–5 CrossRef CAS.
- P. Wanjara, R. A. L. Drew, J. Root and S. Yue, Evidence for Stable Stoichiometric Ti2C at the Interface in TiC Particulate Reinforced Ti Alloy Composites, Acta Mater., 2000, 48, 1443–1450 CrossRef CAS.
- C. H. De Novion and J. P. Landesman, Order and Disorder in Transition Metal Carbides and Nitrides: Experimental and Theoretical Aspects, Pure Appl. Chem., 2009, 57, 1391–1402 CrossRef.
- V. N. Lipatnikov, L. V. Zueva, A. I. Gusev and A. Kottar, Disorder-Order Phase Transformations and Electrical Resistivity of Nonstoichiometric Titanium Carbide, Phys. Solid State, 1998, 40, 1211–1218 CrossRef.
- L. V. Zueva and A. I. Gusev, Effect of Nonstoichiometry and Ordering on the Period of the Basis Structure of Cubic Titanium Carbide, Phys. Solid State, 1999, 41, 1032–1038 CrossRef CAS.
- G. Amirthan, K. Nakao, M. Balasubramanian, H. Tsuda and S. Mori, Influence of N and Fe on α-Ti Precipitation in the in Situ TiC–Titanium Alloy Composites, J. Mater. Sci., 2011, 46, 1103–1109 CrossRef CAS.
- M. B. Ivanov, S. S. Manokhin, D. A. Nechaenko and Y. R. Kolobov, Features of the Crystal Structure of Disperse Carbides in Alpha Titanium, Russ. Phys. J., 2011, 54, 749–755 CrossRef CAS.
- Y. F. Yang, H. Y. Wang, J. G. Wang and Q. C. Jiang, Lattice Parameter and Stoichiometry of TiCx Produced in Alloyed Ti–C Systems by Self-Propagating High-Temperature Synthesis, J. Am. Ceram. Soc., 2008, 91, 3813–3816 CrossRef CAS.
- D. A. Aksyonov, A. G. Lipnitskii and Y. R. Kolobov, Ab Initio Study of Ti–C Precipitates in Hcp Titanium: Formation Energies, Elastic Moduli and Theoretical Diffraction Patterns, Comput. Mater. Sci., 2012, 65, 434–441 CrossRef CAS.
- C. Jiang and W. S. Jiang, Pressure–Composition Phase Diagram of Ti–C from First Principles, Phys. Status Solidi B, 2014, 251, 533–536 CrossRef CAS.
- A. I. Gusev, Phase Equilibria, Phases and Compounds in the TiC System, Russ. Chem. Rev., 2002, 71, 439–463 CrossRef CAS.
- P. A. Korzhavyi, L. V. Pourovskii, H. W. Hugosson, A. V. Ruban and B. Johansson, Ab Initio Study of Phase Equilibria in TiC(x), Phys. Rev. Lett., 2001, 88, 015505 CrossRef PubMed.
- X. X. Yu, C. R. Weinberger and G. B. Thompson, Ab Initio Investigations of the Phase Stability in Group IVB and VB Transition Metal Carbides, Comput. Mater. Sci., 2016, 112, 318–326 CrossRef CAS.
- E. M. Fryt, Defect Mobility in TiC1−X at High Temperatures, Solid State Ionics, 1997, 101–103, 437–443 CAS.
- D. W. Zhou, X. L. Jin, X. Meng, G. Bao, Y. M. Ma, B. B. Liu and T. Cui, Ab Initio Study Revealing a Layered Structure in Hydrogen-Rich KH6 under High Pressure, Phys. Rev. B: Condens. Matter, 2012, 86, 6335 Search PubMed.
- Y. M. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medv-edev, A. O. Lyakhov, M. Valle and V. Prakapenka, Transparent Dense Sodium, Nature, 2009, 458, 182–185 CrossRef CAS PubMed.
- D. F. Duan, Y. X. Liu, F. B. Tian, D. Li, X. L. Huang, Z. L. Zhao, H. Y. Yu, B. B. Liu, W. J. Tian and T. Cui, Pressure-Induced Metallization of Dense (H2S)2H2 with High-Tc Superconductivity, Sci. Rep., 2014, 4, 06968 CrossRef CAS PubMed.
- A. R. Oganov and C. W. Glass, Crystal Structure Prediction Using Ab Initio Evolutionary Techniques: Principles and Applications, J. Chem. Phys., 2009, 124, 201–419 Search PubMed.
- A. R. Oganov, A. O. Lyakhov and M. Valle, How Evolutionary Crystal Structure Prediction Works—and Why, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, New Developments in Evolutionary Structure Prediction Algorithm Uspex, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, First-Principles Determination of the Soft Mode in Cubic ZrO2, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, First-Principles Calculations of the Ferroelastic Transition between Rutile-Type and CaCl2-Type SiO2 at High Pressures, Phys. Rev. B: Condens. Matter, 2008, 78, 134106 CrossRef.
- Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Publisher’s Note: Crystal Structures and Elastic Properties of Superhard IrN2 and IrN3 from First Principles, Phys. Rev. B: Condens. Matter, 2007, 76, 054115 CrossRef.
- R. Hill, The Elastic Behaviour of a Crystalline Aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. J. Tian, Hardness of Covalent Crystals, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed.
- M. D. Segall, R. Shah, C. J. Pickard and M. C. Payne, Population Analysis of Plane-Wave Electronic Structure Calculations of Bulk Materials, Phys. Rev. B: Condens. Matter, 1996, 54, 16317 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-Principles Simulation: Ideas, Illustrations and the Castepcode, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- D. Vanderbilt, Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism, Phys. Rev. B: Condens. Matter, 1990, 41, 7892–7895 CrossRef.
- F. P. Miller, A. F. Vandome and J. Mcbrewster, Materials Studio, 2010 Search PubMed.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Crystal Orbital Hamilton Population (Cohp) Analysisas Projected from Plane-Wave Basis Sets, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic Projection from Plane-Wave and Paw Wavefunctions and Application to Chemical-Bonding Analysis in Solids, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- M. I. Mcmahon and R. J. Nelmes, High-Pressure Structures and Phase Transformations in Elemental Metals, Chem. Soc. Rev., 2006, 35, 943–963 RSC.
- D. A. Andersson, P. A. Korzhavyi and B. Johansson, First-Principles Based Calculation of Binary and Multicomponent Phase Diagrams for Titanium Carbonitride, Calphad, 2008, 32, 543–565 CrossRef CAS.
- H. J. Seifert, H. L. Lukas and G. Petzow, Thermodynamic Optimization of the Ti-C System, J. Phase Equilib., 1996, 17, 24–35 CrossRef CAS.
- H. Goretzki, Neutron Diffraction Studies on Titanium-Carbon and Zirconium-Carbon Alloys, Phys. Status Solidi B, 1967, 20, 141–143 CrossRef.
- A. N. Christensen, R. Hämäläinen, U. Turpeinen, A. F. Andresen, O. Smidsrød, C. O. Pontchour, P. Phavanantha, S. Pramatus, B. N. Cyvin and S. J. Cyvin, The Temperature Factor Parameters of Some Transition Metal Carbides and Nitrides by Single Crystal X-Ray and Neutron Diffraction, Acta Chem. Scand., 1978, 32, 89–90 CrossRef.
- L. P. Ding, P. Shao, F. H. Zhang, X. F. Huang and T. L. Yuan, Structure, Relative Stabilities, Physical Properties, and Hardness of Osmium Carbides with Various Stoichiometries: First-Principle Investigations, J. Phys. Chem. C, 2015, 119, 21639–21648 CAS.
- Q. Tao, X. P. Zhao, Y. L. Chen, J. Li, Q. Li, Y. M. Ma, J. J. Li, T. Cui, P. W. Zhu and X. Wang, Enhanced Vickers Hardness by Quasi-3d Boron Network in MoB2, RSC Adv., 2013, 3, 18317–18322 RSC.
- S. P. Zhao, Y. L. Yang, J. Lu, W. Wu, S. Sun, X. Li, X. L. Zhao, S. X. Cao, J. C. Zhang and W. Ren, Carbon-Rich Superhard Ruthenium Carbides from First-Principles, Mater. Des., 2017, 117, 353–362 CrossRef CAS.
- Y. W. Li, J. Hao and Y. Xu, Predicting Hard Metallic Osmium–Carbon Compounds under High Pressure, Phys. Lett. A, 2012, 376, 3535–3539 CrossRef CAS.
- C. M. Sung and M. F. Tai, Reactivities of Transition Metals with Carbon: Implications to the Mechanism of Diamond Synthesis under High Pressure, Int. J. Refract. Met. Hard Mater., 1997, 15, 237–256 CrossRef CAS.
- R. Chang and L. J. Graham, Low-Temperature Elastic Properties of ZrC and TiC, J. Appl. Phys., 1966, 37, 3778–3783 CrossRef CAS.
- R. C. Weast, M. J. Astle and W. H. Beyer, Handbook of Chemistry and Physics, CRC Press, Inc, 1996 Search PubMed.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, Density Functional Theory for Calculation of Elastic Properties of Orthorhombic Crystals: Application to TiSi2, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS.
- A. Marmier, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Elam: A Computer Program for the Analysis and Representation of Anisotropic Elastic Properties, Comput. Phys. Commun., 2010, 181, 2102–2115 CrossRef CAS.
- M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao, L. P. Ding and X. F. Huang, Phase Stability, Physical Properties, and Hardness of Transition-Metal Diborides MB2 (M = Tc, W, Re, and Os): First-Principles Investigations, J. Phys. Chem. C, 2013, 117, 10643–10652 CAS.
- A. Simunek and J. Vackar, Hardness of Covalent and Ionic Crystals: First-Principle Calculations, Phys. Rev. Lett., 2006, 96, 085501 CrossRef PubMed.
- R. A. Andrievski, Superhard Materials Based on Nanostructured High-Melting Point Compounds: Achievements and Perspectives, Int. J. Refract. Met. Hard Mater., 2001, 19, 447–452 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- A. D. Becke and K. E. Edgecombe, A Simple Measure of Electron Localization in Atomic and Molecular Systems, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Modeling Hardness of Polycrystalline Materials and Bulk Metallic Glasses, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra00400e |
| This journal is © The Royal Society of Chemistry 2018 |