A systematic study of the co-solvent effect for an all-organic redox flow battery

Abstract

Benzophenone and 1,4-di-tert-butyl-2,5-dimethoxybenzene are used as the anode and cathode active species respectively in an all-organic redox-flow battery. A number of organics as the co-solvents are applied in the electrolyte to improve the electrochemical performance of it. For all kinds of the mixed solvents, a lower content of acetonitrile leads to a higher solubility to 1,4-di-tert-butyl-2,5-dimethoxybenzene and a lower conductivity. The results of cyclic voltammetry tests demonstrate that the electrode reactions are controlled by diffusion. With the decrease of the content of acetonitrile, the dynamic viscosity of the electrolyte increases, which generally leads to the decrease of the diffusion coefficients of the active species.

---

1. Introduction

Renewable resources, such as wind and solar, now supply a significant amount of electrical energy in commercialized countries. However, the integration of the electricity generated into the existing grid poses a great challenge due to the variable and intermittent nature of the resources. A redox flow battery (RFB) is a cost-effective electrical energy storage technology feasible for grid-scale applications.^1,2 The early RFBs were based on redox couples in aqueous solutions and many aqueous RFBs such as all-vanadium, bromine–polysulfide and zinc–bromine systems have been demonstrated at the megawatt-scale.^3–5

Water has a narrow electrochemical window of 1.23 V under standard conditions, which restricts the voltage and hence the energy density of the RFBs with aqueous electrolytes.^6–8 In contrast, the utilization of non-aqueous electrolytes provides new dimensions to increase the cell voltage, broaden the selection of a vast number of redox couples which were impossible in aqueous solution, and enlarge the space for optimizing energy densities and electrode kinetics.^9–11 In the early years, metal complexes were examined as the active species of non-aqueous RFBs (NARFBs).^12–15 Recently, organic molecules have been also recognized as promising redox active species in NARFBs for their abundance sources and low costs compared to noble metals.^6,16,17 The cyclic voltammetry (CV) of benzophenone (BP) was measured by Tsierkezos,¹⁸ and the first NARFB using BP as the anode species to provide a low anode potential was realized by Xing et al.¹⁹ A number of redox active species based on the general structure of dimethoxy-di-tert-butylbenzene as the cathode active molecule for NARFBs were reported by Huang et al.^20,21 With a similar structure, 1,4-di-tert-butyl-2,5-dimethoxybenzene (DBB) was proposed as a stable redox shuttle with a high cathode potential.^22,23 However, it has not been used in NARFBs due to its low solubility in polar electrolyte solutions.

The effects of solvents and supporting electrolytes in electrochemical reactions have been investigated extensively. Non-aqueous electrolytes are often flammable, volatile and moisture-sensitive. Furthermore, the cost and ionic conductivities are far less competitive compared to their aqueous counterparts. Creager²⁴ postulated that for the electrolytes of batteries, polar solvents are beneficial to achieve a reasonable ionic conductivity. In addition to the polarity, the solubilities of active species and supporting electrolytes, which influence the kinetics of the electrode reactions and the energy density of the battery, are also crucial for the selection of solvents. Shinkle et al.²⁵ presented an approach to promote the cell efficiency through monitoring the property of the organic solvent. They found that the solubility of the active species vanadium acetylacetonate (V(acac)₃) and the ionic conductivity of the electrolyte increase with the rise of the polarity, Hildebrand solubility and molar volume of the solvent. Herr et al.^26,27 found that in a non-aqueous vanadium RFB, the vibrational bond energy of the solvent would be changed by the addition of a co-solvent, resulting in the variation of the solubility of the active species. Bamgbopa et al.²⁸ reported that the solvents affected the physical and electrochemical properties of the electrolytes and hence influenced the reaction kinetics of the non-aqueous vanadium RFB.

In this work, BP and DBB are used as the anode and cathode active species, respectively. Acetonitrile (AN) is employed as the main solvent. Five common organics are used as co-solvents. The effects of the co-solvents on the properties of the electrolyte and the electrode reactions are investigated.

2. Experimental

2.1. Materials preparation

The co-solvents, dimethyl carbonate (DMC, 99%, MACKLIN, China), diethyl carbonate (DEC, 99%, MACKLIN, China), gamma-butyrolactone (GBL, 99%, MACKLIN, China), dimethyl formamide (DMF, 99%, Guangfu, China) and 1,3-dioxolane (DOL, 99.5%, Energy, China) were dried with 4A molecular sieve (Guangfu, China) for 48 h before used. The solvent AN (99%, MACKLIN, China) was distilled with the presence of calcium hydride under nitrogen. The active species DBB (98%, Bide, China) and BP (98%, Guangfu, China) were used without any pretreatment.

The supporting electrolyte tetraethylammonium hexafluorophosphate (TEAPF₆) was synthesized with a two-step procedure.²⁹ Tetraethylammonium bromide (TEABr) was firstly prepared with the reaction of pure triethylamine and ethyl bromide at 55 °C for 24 h. After being washed with THF and filtered, the solid TEABr was dried in vacuum at 80 °C for 48 h. Then the TEABr and potassium hexafluorophosphate were dissolved in deionized water and stirred at 50 °C for 20 h to get the TEAPF₆ crystallites. The product was rinsed with deionized water and dried in vacuum at 60 °C for 24 h.

2.2. Characterization

The solubilities of BP and DBB in different solvents were measured by weighing solute and gradually dissolving in the quantitative solvent or solvent mixture (0.5 or 1.0 mL) with vigorous shaking. At overnight intervals, more solute (in 0.0005 or 0.0010 g increments) was added until precipitation occurred. With this method, a precision of 1 g L⁻¹ can be reached.³⁰ The conductivities of the mixed solvents with 0.01 M TEAPF₆ were measured with a DDS-307A conductivity meter (REX, China) with a DJS-1C platinum black electrode (REX, China) at 25 °C. The measurements were repeated for three times to get the average value.

2.3. Cyclic voltammetry tests

CV measurements were carried out with an electrochemical workstation (VersaSTAT 3, Ametek) at 25 °C. A three-electrode electrochemical cell was assembled. A glassy-carbon disk with a diameter of 6 mm (Aidahengsheng, China) was used as the working electrode. The reference electrode was Ag/Ag⁺ electrode (0.5 M AgNO₃ in AN, Aidahengsheng, China). A graphite plate with a geometry surface area of 5.24 cm² (Aidahengsheng, China) was adopted as the counter electrode. Prior to the measurement, the glassy-carbon electrode was polished with chamois leather and alumina powder (0.05 μm, Aidahengsheng, China). After being polished, the electrode was ultrasonically cleaned with deionized water and dried at 80 °C for 24 h. The electrolyte, which contained 0.01 M BP, 0.01 M DBB and 0.1 M TEAPF₆, was deoxygenated with nitrogen (99.999% pure, Liufang, China) for 10 min prior to all the measurements. The CV curves were recorded in the potential range from −2.6 to 1.2 V (vs. Ag/Ag⁺) at various scanning rates between 0.07 and 0.6 V s⁻¹. The diffusion coefficients of the redox species in the electrolytes were estimated based on the Randles–Sevcik equation without IR drop compensation.³¹ For a reversible electron transfer reaction:

i_p = 2.69 × 10⁵n^3/2AcD^1/2ν^1/2 (1)

For an irreversible electron transfer reaction:

i_p = 2.99 × 10⁵n^3/2α^1/2AcD^1/2ν^1/2 (2)

where i_p is the peak current (A), n the number of electrons transferred in the redox reaction process (n = 1), α the transfer coefficient (α = 0.5), A the electrode area (0.28 cm²), c the primary redox species concentration (M), ν the scanning rate (V s⁻¹) and D the diffusion coefficient (cm² s⁻¹). Generally, every CV curve need more than 5 circles to avoid error points.

3. Results and discussion

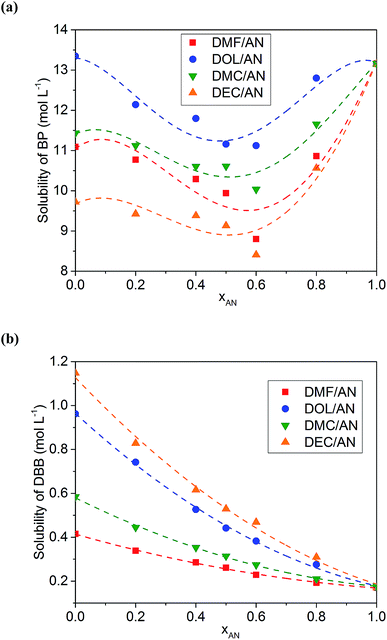
The solubilities of BP and DBB in various solvents are listed in Table 1. Table 1 also presents the physical and chemical properties of the solvents obtained from ref. 32. The solubilities of BP in all of the solvents are higher than those of DBB. AN possesses a low solubility to DBB of about 0.17 mol L⁻¹, while most of the co-solvents used in this work show a higher solubility to DBB except GBL. Generally, the solvent with a lower dielectric constant exhibits a weaker polarity, resulting in a stronger ability to dissolve low-polar molecules such as DBB. However, DMF is an exception with a high dielectric constant and a high solubility to DBB compared with those of AN. Meanwhile, AN possesses the lowest dynamic viscosity in all of the solvents.

Table 1 Physical properties of the organic solvents used in this work

Pure solvent	Dielectric constant^a	Dynamic viscosity^a (mPa s)	Solubility of BP (mol L^−1)	Solubility of DBB (mol L^−1)
a Obtained from ref. 32.
AN	35.95	0.34	13.16	0.17
DMC	3.11	0.58	11.40	0.58
DEC	2.82	0.75	9.72	1.15
DMF	36.71	0.80	11.10	0.41
DOL	6.98	0.59	13.30	0.96
GBL	39.10	1.73	11.80	0.15

---

The solubilities of BP in the binary mixed solvents with the same volume content of AN (x_AN) show an order of DOL/AN > DMC/AN > DMF/AN > DEC/AN (Fig. 1a), which is consistent with the order of the solubilities of BP in the corresponding pure co-solvents. For all of the mixed solvents, the lowest solubility of BP is obtained when x_AN is 0.6. The relationship between the solubility of BP and x_AN fits the Jouyban–Acree model, which was firstly used to calculate the viscosity of binary solvents.³³ This model has also been applied to describe the solubility of V(acac)₃ in binary solvents.²⁸ In this work, the model is expressed as:

ln S = A₀ + A₁x_AN + A₂x_AN² + A₃x_AN³ + A₄x_AN⁴ (3)

where S is the solubility of BP (mol L⁻¹). A₀, A₁, A₂, A₃ and A₄ are regression constants (ln (mol L⁻¹)), which are listed in Table 2. Fig. 1b shows the solubilities of DBB in the mixed solvents, which show an order of DEC/AN > DOL/AN > DMC/AN > DMF/AN, in accordance with the order of the solubilities of DBB in the pure co-solvents. The solubilities of BP in the mixed solvents are much higher than those of DBB. Therefore, the energy capacity of the NARFBs is mainly determined by the solubility of DBB in the solvent. With the decrease of x_AN, the solubility of DBB in all of the solvents increases, which would improve the energy capacity of the corresponding battery.

Fig. 1 Solubilities of (a) BP and (b) DBB in the mixed solvents.

Table 2 The regression constants (ln (mol L⁻¹)) in the Jouyban–Acree model to fit the solubility of BP in the mixed solvents

Mixed solvents	A0	A1	A2	A3	A4
DMF/AN	2.41	2.59	2.27	2.44	2.41
DOL/AN	2.38	2.50	2.24	2.41	2.38
DMC/AN	2.30	2.41	2.21	2.36	2.30
DEC/AN	2.33	2.47	2.24	2.36	2.33

---

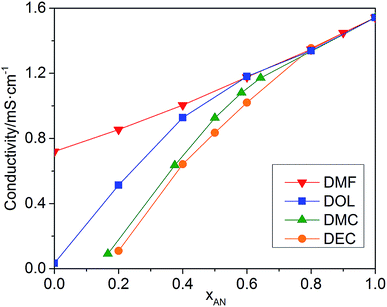
The conductivities of the mixed solvents with 0.01 M TEAPF₆ and various x_AN are plotted in Fig. 2. Pure AN presents the highest conductivity. For all of the mixed solvents, the conductivity decreases with the decrease of x_AN. When x_AN is 0.8, the conductivities of the mixed solvents are almost the same. When x_AN is lower than 0.5, the conductivities of the mixtures show an order of DMF/AN > DOL/AN > DMC/AN > DEC/AN. The electrochemical stability windows (ESWs) of the mixed solvents with 0.1 M TEAPF₆ are shown in Fig. 3. The ESW of pure AN is −3.25 to 1.64 V (vs. Ag/Ag⁺). The addition of DMC and DMF narrows the ESW of AN, while DOL/AN exhibit a comparable ESW to AN, which widens with the increase of x_AN. DEC/AN shows the widest ESW of over 5.0 V when x_AN is lower than 0.5.

Fig. 2 Conductivities of the mixed solvents with various x_AN and 0.01 M TEAPF₆.

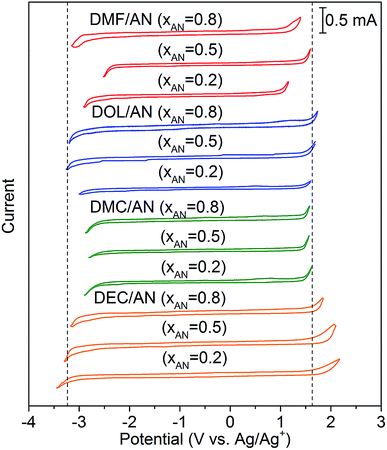Fig. 3 Cyclic voltammograms of the mixed solvents with 0.1 M TEAPF₆ at the scanning rate of 0.5 V s⁻¹. The ESW of pure AN measured in the same condition is shown as the dotted lines.

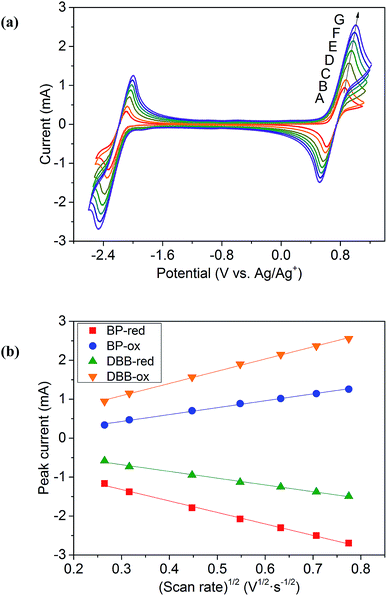
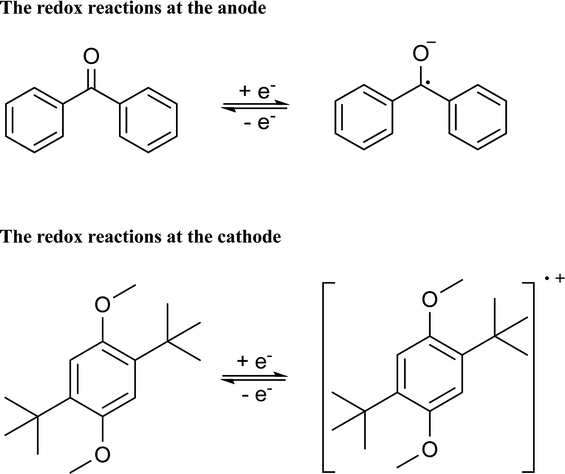
CV results of BP and DBB with a concentration of 0.01 M in the DOL/AN (x_AN = 0.5) mixture with various scanning rates are presented in Fig. 4a. The redox reactions of the active species are illustrated in Scheme 1. Only the peaks corresponding to BP⁻/BP and DBB/DBB⁺ redox couples are observed in the potential range from −2.6 to 1.2 V (vs. Ag/Ag⁺) within the ESW of the mixed solvent. When the scanning rate is 0.07 V s⁻¹, the oxidation and reduction peaks of BP appear at −2.09 and −2.33 V (vs. Ag/Ag⁺), while those of DBB are at 0.86 and 0.62 V (vs. Ag/Ag⁺), respectively. With the increase of the scanning rate, the oxidation peaks move to a higher potential, while the reduction peaks shift to a lower potential. At the scanning rate of 0.5 V s⁻¹, the peak separation between the oxidation and reduction processes of BP and DBB are 0.44 and 0.46 V, respectively, and the half-wave potentials are −2.23 and 0.76 V (vs. Ag/Ag⁺) respectively, yielding a wide theoretical cell potential of 2.99 V. For both BP and DBB, the values of the peak current ratios (i_p.a/i_p.c) are close to 1, which indicates a quasi-reversible behavior for both BP⁻/BP and DBB/DBB⁺ couples. The linear relationship between the peak currents of the electrode reactions and the square root of the scanning rate (Fig. 4b) indicates that all the reactions are controlled by diffusion.³¹ The diffusion coefficients are calculated based on eqn (1) and (2), which are in the ranges of 1.53–1.98 × 10⁻⁵ and 1.75–2.53 × 10⁻⁵ cm² s⁻¹ for BP and DBB, respectively.

Fig. 4 (a) Cyclic voltammograms of BP and DBB in DOL/AN (x_AN = 0.5) with various scanning rates: (A) 0.07 V s⁻¹, (B) 0.1 V s⁻¹, (C) 0.2 V s⁻¹, (D) 0.3 V s⁻¹, (E) 0.4 V s⁻¹, (F) 0.5 V s⁻¹ and (G) 0.6 V s⁻¹. (b) The relationship between the peak currents of the electrode reactions and the scanning rate.

Scheme 1 The redox reactions of BP and DBB at the anode and cathode sides.

The diffusion coefficients of the electrode reactions calculated by eqn (1), in which the reactions are considered as reversible reactions, are presented in Fig. 5. For DEC/AN and DMC/AN, CV curves are not obtained when x_AN is lower than 0.5 due to the low conductivity of the solvent. In all of the solvents, the diffusion coefficients of the cathode reduction and anode oxidation reactions are higher than those of the anode reduction and cathode oxidation reactions. The diffusion coefficients of the reactions generally increase with the increase of x_AN with a few exceptions. Meanwhile, the viscosities of the mixed solvents, which are calculated based on the viscosity data of the pure solvents listed in Table 1 and the Jouyban–Acree model,³³ are also shown in Fig. 5. As AN has the lowest dynamic viscosity, the dynamic viscosity of the mixed solvents rises with the reduced concentration of x_AN. Since all of the electrode reactions are diffusion controlled, the increase of the viscosity of the electrolyte with the decrease of x_AN, which is the probable reason for the decrease of the diffusion coefficients of the reactions, would lead to slower electrode kinetics. However, further investigation is still needed to explain the exceptions to this tendency as observed when DOL/AN (x_AN = 0.5) and DMC/AN (x_AN = 0.8) are used as the solvents.

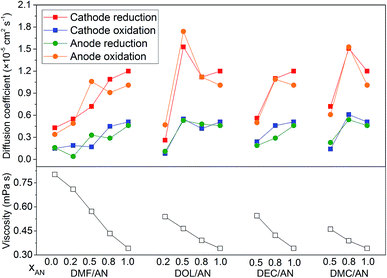Fig. 5 The viscosities of the mixed solvents with different contents and the diffusion coefficients of the electrode reactions in various solvents.

4. Conclusions

In this work, we have presented a systematic approach to screen and optimize organic solvent mixtures to improve the electrochemical performance of all-organic RFBs. DMC, DEC, DMF, DOL and GBL are investigated as the co-solvents in an all-organic redox flow battery with AN as the solvent and BP and DBB as the active species. The solubilities of BP in the mixed solvents are much higher than those of DBB. With the decrease of x_AN in the electrolyte, the solubility of DBB increases, while the conductivity of the electrolyte decreases. The potentials of BP⁻/BP and DBB/DBB⁺ redox couples are within the ESWs of the mixed solvents. The electrode reactions are controlled by diffusion. The diffusion coefficients of the reactions tend to increase with the decrease of x_AN in the electrolyte, which is probably due to the increase of the viscosity of the solvent.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The financial support of NSF of China under contract numbers 21636007 and 51402210 and the support of Tianjin Municipal Science and Technology Commission under contract numbers 15JCQNJC06500 are gratefully acknowledged. The work has been also supported by the Program of Introducing Talents to the University Disciplines under file number B06006, and the Program for Changjiang Scholars and Innovative Research Teams in Universities under file number IRT 0641.

References

1. L. H. Thaller, Presented in part at the Proc. 9th Intersoc. Energy Conv. Eng. Conf., San Francisco, CA, 26–30, August, 1974.
2. A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164.
3. G. L. Soloveichik, Chem. Rev., 2015, 115, 11533–11558.
4. S. Hameer and J. L. van Niekerk, Int. J. Energy Res., 2015, 39, 1179–1195.
5. B. R. Chalamala, T. Soundappan, G. R. Fisher, M. R. Anstey, V. V. Viswanathan and M. L. Perry, Proc. IEEE, 2014, 102, 976–999.
6. P. Leung, A. A. Shah, L. Sanz, C. Flox, J. R. Morante, Q. Xu, M. R. Mohamed, C. Ponce de León and F. C. Walsh, J. Power Sources, 2017, 360, 243–283.
7. M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55.
8. J. Noack, N. Roznyatovskaya, T. Herr and P. Fischer, Angew. Chem., Int. Ed. Engl., 2015, 54, 9776–9809.
9. X. Wei, W. Xu, J. Huang, L. Zhang, E. Walter, C. Lawrence, M. Vijayakumar, W. A. Henderson, T. Liu, L. Cosimbescu, B. Li, V. Sprenkle and W. Wang, Angew. Chem., Int. Ed. Engl., 2015, 54, 8684–8687.
10. W. Wang and V. Sprenkle, Nat. Chem., 2016, 8, 204–206.
11. M. L. Perry and A. Z. Weber, J. Electrochem. Soc., 2015, 163, A5064–A5067.
12. J. A. Suttil, J. F. Kucharyson, I. L. Escalante-Garcia, P. J. Cabrera, B. R. James, R. F. Savinell, M. S. Sanford and L. T. Thompson, J. Mater. Chem. A, 2015, 3, 7929–7938.
13. X. Xing, Y. Zhao and Y. Li, J. Power Sources, 2015, 293, 778–783.
14. X. Xing, D. Zhang and Y. Li, J. Power Sources, 2015, 279, 205–209.
15. D. Zhang, Q. Liu, X. Shi and Y. Li, J. Power Sources, 2012, 203, 201–205.
16. J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed. Engl., 2017, 56, 686–711.
17. J. A. Kowalski, L. Su, J. D. Milshtein and F. R. Brushett, Curr. Opin. Chem. Eng., 2016, 13, 45–52.
18. N. G. Tsierkezos, J. Solution Chem., 2007, 36, 1301–1310.
19. X. Q. Xing, Y. J. Huo, X. Wang, Y. C. Zhao and Y. D. Li, Int. J. Hydrogen Energy, 2017, 42, 17488–17494.
20. J. Huang, L. Cheng, R. S. Assary, P. Wang, Z. Xue, A. K. Burrell, L. A. Curtiss and L. Zhang, Adv. Energy Mater., 2015, 5, 1401782.
21. J. Huang, L. Su, J. A. Kowalski, J. L. Barton, M. Ferrandon, A. K. Burrell, F. R. Brushett and L. Zhang, J. Mater. Chem. A, 2015, 3, 14971–14976.
22. J. Chen, C. Buhrmester and J. R. Dahn, Electrochem. Solid-State Lett., 2005, 8, A59–A62.
23. F. R. Brushett, J. T. Vaughey and A. N. Jansen, Adv. Energy Mater., 2012, 2, 1390–1396.
24. S. Creager, in Handbook of Electrochemistry, Elsevier, Amsterdam, 2007, ch. 3, pp. 57–72.
25. A. A. Shinkle, T. J. Pomaville, A. E. S. Sleightholme, L. T. Thompson and C. W. Monroe, J. Power Sources, 2014, 248, 1299–1305.
26. T. Herr, J. Noack, P. Fischer and J. Tübke, Electrochim. Acta, 2013, 113, 127–133.
27. T. Herr, P. Fischer, J. Tübke, K. Pinkwart and P. Elsner, J. Power Sources, 2014, 265, 317–324.
28. M. O. Bamgbopa, N. Pour, Y. Shao-Horn and S. Almheiri, Electrochim. Acta, 2017, 223, 115–123.
29. S. V. Dzyuba and R. A. Bartsch, J. Heterocycl. Chem., 2001, 38, 265–268.
30. K. Wedege, E. Drazevic, D. Konya and A. Bentien, Sci. Rep., 2016, 6, 39101.
31. A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, Wiley, New York, 2001.
32. J. Catalan, in Handbook of Solvents, ChemTec Publishing, 2nd edn, 2014, ch. 2, pp. 581–622.
33. A. Jouyban, S. H. Maljaei, S. Soltanpour and M. A. A. Fakhree, J. Mol. Liq., 2011, 162, 50–68.

---