Open Access Article
Open Access ArticleTheoretical design of porphyrin sensitizers with different acceptors for application in dye-sensitized solar cells†
Xingyi Jin*a,
Dongyuan Lia,
Libo Suna,
Cheng-Long Wangb and
Fu-Quan Bai *b
*b
a1st Department of Neurosurgery, China-Japan Union Hospital, Jilin University, Xiantai Street No. 126, Changchun 130033, People's Republic of China. E-mail: xyjin_cjuh@163.com
bLaboratory of Theoretical and Computational Chemistry, International Joint Research Laboratory of Nano-Micro Architecture Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130023, People's Republic of China. E-mail: baifq@jlu.edu.cn
First published on 30th May 2018
Abstract
Using density functional theory (DFT) and time-dependent density functional theory (TDDFT) methods, three porphyrin dyes with different acceptors, such as carboxylic acid, cyanoacrylic acid, and 2-cyano-N-hydroxyacrylamide, have been designed. Compared to the best sensitizer (YD2-o-C8) so far, these designed dyes have small highest occupied orbital to lowest unoccupied orbital (HOMO–LUMO) band gaps, and wide absorptions with large oscillator strength at porphyrin Q bands. And the designed Dye1 is similar to YD2-o-C8 in electronic coupling with TiO2, while improved Dye2 and Dye3 are better than YD2-o-C8, thus, Dye2 and Dye3 will be much faster for electron injection in dye-sensitized solar cell systems based on their long-term stable and efficient anchor groups. All these features show that our designed dyes, especially Dye2 and Dye3, have better absorption performance and faster electron injection. In addition, our results point out that 2-cyano-N-hydroxyacrylamide is a new promising acceptor. This study is expected to assist the molecular design of new efficient dyes for the advancement of dye-sensitized solar cells.
Introduction
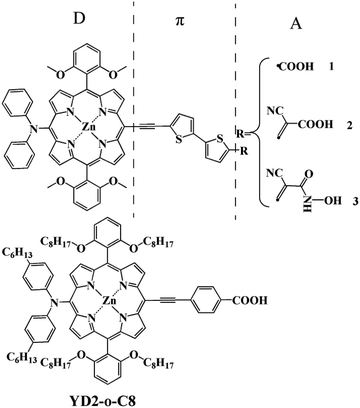
Owing to the growing renewable energy demand, dye-sensitized solar cells (DSSCs), put forward by O'Regan and Grätzel in 1991,1 have received much attention as an alternative to traditional silicon based solar cells. Ru complexes have maintained a clear lead when employed in DSSCs, with a power conversion efficiency up to 11%.2,3 The advantages of such Ru complexes include broad absorption and appropriate excited-state oxidation potentials for electron injection into the conduction band of the semiconductor.2,3 However, the expensive cost and environmental issues of Ru complexes limit their wide applications in industrial and commercial fields. In order to find cleaner materials for DSSCs, much effort has been focused on the development of new organic dyes because of their low cost and high molar absorption coefficients, as well as the facile modification of their molecular structures.4,5Among new organic dyes, porphyrins have attracted significant interest as DSSCs sensitizers. They have rigid macrocyclic structures with strong absorption in the visible region and indistinguishable electron transfer kinetics from those of the efficient Ru complexes.6 Furthermore, their optical, electrochemical, and photophysical properties can be easily modulated the peripheral substitutions due to multiple reaction sites, including four meso and eight β-positions.7,8 Thus, more and more porphyrins have been synthesized and used as sensitizers divided into a class of its own for DSSCs.7–11 The most well-known example is YD2 firstly reported by Yeh and Diau,9 which attained a power conversion efficiency (PCE) of 6.8%. The device performance of YD2 was further improved by Grätzel and co-workers,12 giving an efficiency of 10.9%, which lasted as a highest record for DSSC at that time. In 2011, based on YD2, Grätzel and co-workers synthesized YD2-o-C8 and achieved an optimized performance of 12.3%.10 Whereafter, few potential porphyrin dyes with the prototypical structure of D–π–A were proposed and reported creatively to leading high PCE beyond 13% at full sun illumination.13,14 However, from the spectroscopic point of view, these efficient sensitizers show relatively less absorption intensity in the region of 600 to 800 nm.10,15,16 In order to enhance the absorption intensity in that region, three new porphyrin-based sensitizers with different acceptor groups (as shown in Fig. 1) such as carboxylic acid, cyanoacrylic acid, and 2-cyano-N-hydroxyacrylamide are designed and studied by using the density functional theory (DFT) and time dependent density functional theory (TDDFT) methods. The carboxylic acid and cyanoacrylic acid are two traditional anchors of dyes for dye-sensitized solar cells, and many dyes with them show decent performance.15–22 2-Cyano-N-hydroxyacrylamide is a ramification of hydroxamate.23,24 Among these, hydroxamic acid stands out for its long-term stability and efficient electron injection. It has already been proven to be a potential anchor, and it is also confirmed theoretically the hydroxamate is expected to provide valuable hints into the design of efficient anchor group for DSSC application.25 Hence it can be inferred that 2-cyano-N-hydroxyacrylamide is also a potential anchor. In summary, our anchor modification from the carboxylic acid, cyanoacrylic acid and 2-cyano-N-hydroxyacrylamide groups is rational means.
The geometry structures, electronic structures, and optical properties, the interfacial electron transfer (IET) of these dyes are explored aiming to understand the relationship between structures and properties for the new dyes as well as reference dye of classical YD2-o-C8. The results reveal that the designed dyes should have better performance than the existing efficient dyes due to their improved optical properties meet our request well.
Computational details
For these porphyrin dyes, we have tried already to use several DFT functional alone with 6-31G* basis set for C, H, O, N, S atoms, and Stuttgart RLC ECP basis set for Zn atom to optimize the ground state geometries under default convergence criteria threshold (10−8).26 The calculated results showed that there is little difference in the geometric parameters optimized with different functionals. While the B3LYP functional functional has been widely used so far,27–32 so we just listed important geometric parameters obtained by B3LYP functional in Table S1† and used the corresponding geometries (shown in Fig. S1†) to further calculations.32 Frequency calculations were performed at the same level as geometry optimization to ensure that the ground-state geometries correspond to a minimum point on the potential energy surfaces. In order to choose a relatively reliable functional to simulate the absorption spectra of the porphyrin sensitizers here, we performed benchmark calculations for the reference dye (YD2-o-C8), which have recently been studied experimentally and considered to be an efficient dye.10 For the purpose of saving the computational cost, the C6H13 and C8H17 in ancillary ligands were replaced by hydrogen and methyl groups, respectively. Here different TDDFT methods were used, including B3LYP,27 PBE0,33 BHandH,34 and CAM-B3LYP,35 with a mixed basis set (6-31G* basis set for C, H, O, N, S atoms and Stuttgart RLC ECP basis set for Zn atom). The solvent effects of tetrahydrofuran (THF, the solvent used to record the experimental spectra) on the benchmark calculations, was considered in the framework of the self-consistent reaction field polarizable continuum model (PCM).36 The calculated lowest absorption energies by different TDDFT methods along with experimental value of YD2-o-C8 are summarized in Table 1. Compared the absorption energy values at B and Q bands with available experimental values, it shows that the TD-B3LYP in the THF medium provides better agreement with the experimental results.10,32 Hence, the TD-B3LYP in THF environment was chosen for further calculations. The absorption spectra with the 30 lowest-energy electronic transitions were afterwards simulated by using Gaussian function with the full-width at half-maximum (FWHM) of 0.33 eV. All the above calculations were performed with Gaussian 09 (Revision D.01) program package.37| B3LYP | PBE0 | BHandHLYP | CAM-B3LYP | Exp.10 | |
|---|---|---|---|---|---|
| Q Band | 637 | 617 | 570 | 596 | 645 |
| B Band | 436 | 424 | 391 | 396 | 448 |
The dye adsorbed on the TiO2 (101) systems were obtained by geometry optimization at the DFT level, using the Vienna Ab Initio Simulation Package (VASP).38,39 In order to understand the dye@TiO2 interaction, a large TiO2 cluster with the majority (101) of the surface exposed was simulated by 7 × 4 unit cells with two periodic atom layers. This model is enough to neglect molecular interactions between the periodic replicas and has been applied widely in many previous investigations.29,31,32 The calculations have been performed using the generalized gradient approximation (GGA) with the Perdew-Wang91 (PW91) exchange–correlation functional. It is worth noting that the PW91 functional was chosen over B3LYP and other hybrid functionals due to its relatively small computational cost and satisfactory accuracy. The Brillouin zones were sampled with the Monkhorst–Pack k-points of 1 × 1 × 1 for bulk calculation. An energy cutoff of 400 eV was used in these calculations as well as a single gamma k-point sampling because of the large size of the supercell. A conjugated gradient algorithm with an energy criterion of 0.001 eV was used for atomic convergence, and it ensured that the forces were smaller than 0.03 eV Å−1 in all cases.
The survival probability, P(t), was defined as the probability that the photoexcited electron remains in the adsorbate molecule at the time t after excitation of the system.25,40–43 P(t) allows the IET time scales and was computed as the projection of the time-evolved electronic wave function onto the atomic orbitals (AOs) of the molecular adsorbate. The time-evolved wave function is expressed as a linear combination of AOs,
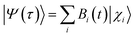 | (1) |
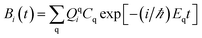 | (2) |
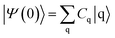 | (3) |
The eigenvectors and eigenvalues Qq and Eq were obtained by solving the generalized EH eigenvalue problem,
| HQq = EqSQq | (4) |
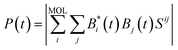 | (5) |
Results and discussion
Orbital energy level
As we know, suitable energy levels of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) orbitals of the sensitizer molecule are required to match the conduction band (CB) of the TiO2 semiconductor and the redox potential of I−/I3− electrolyte, respectively.44 The calculated data for HOMO, LUMO, and HOMO–LUMO gap for all dyes 1–3 and YD2-o-C8 are depicted in Fig. 2. To ensure efficient electron injection from the excited dye into the conduction of TiO2, the LUMO must be higher than the TiO2 conduction band edge (−4.00 eV vs. vacuum).2 Although the LUMO of Dye2 is the lowest, it is still above the CB of TiO2. Therefore, the four dyes are capable of injecting electrons into the CB of TiO2. In order to lead fast dye regeneration, the HOMO must be lower than redox I−/I3− potential (−4.6 eV vs. vacuum).45 For the designed dyes, as well as reference dye (YD2-o-C8), the HOMOs which are much lower than I−/I3− redox potential ensure a fast and efficient regeneration of the dye cation radical. From Fig. 2, it can be found that the energy gaps of all the designed dyes are smaller than the reference dye YD2-o-C8. The calculated HOMO–LUMO gaps are sorted in the order: Dye2 (1.93 eV) ≈ Dye3 (1.93) < Dye1 (2.2 eV) < YD2-o-C8 (2.32 eV). According to the previous studies that the sensitizers that have smaller energy gap values show higher harvesting efficiency in the DSSCs,46,47 hence our designed dyes will likely show better light harvesting efficiency than the reference dye.Molecular orbitals distribution
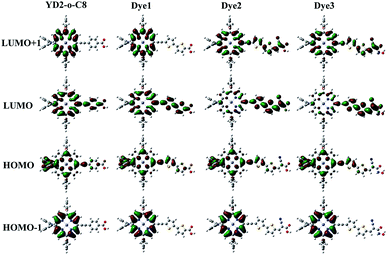
The molecular orbitals play a significant role in the charge-separated states concerned to the solar cell efficiency. For creating an efficient charge-separated state, the HOMO must be localized on the donor subunit and the LUMO must be localized on the acceptor subunit. Fig. 3 depicts the electron density distributions of the frontier molecular orbitals from HOMO−1 to LUMO+1 for all the porphyrin sensitizers that were obtained under B3LYP level. Fig. 3 shows that the electron densities of HOMO for all sensitizers are delocalized predominantly on porphyrin macrocycle and diphenylamino units, while the LUMOs are spread from porphyrin to acceptor units. The calculations indicate that distributions of electron between HOMO and LUMO are separate, thus the transition from HOMO to LUMO of these porphyrin sensitizers should be considered as good charge separated states with intramolecular charge-transfer (ICT) upon excitation.32 From Fig. 3, we can observe that the HOMO orbitals of all sensitizers show similar features, so do HOMO−1 orbitals. However, the LUMO shapes are different and the LUMO+1 are also different. These differences in LUMO and LUMO+1 are due to the different strengths of electron-withdrawing acceptors.In order to obtain more information about the HOMO, LUMO, and LUMO+1 for these porphyrin dyes, the MO compositions were calculated and listed in Table 2. For all porphyrin dyes, the contributions of donor groups to the HOMO are above 75%. However, the compositions of different acceptor to the LUMO are obviously different. In case of similar molecular geometry when anchored to TiO2, the large contribution of acceptor to the LUMO will enhance the electronic coupling between the dye and the titanium 3d orbitals and favor the electron injection.48 Our results show that the contributions from the acceptors of the Dye2 and Dye3 are much larger than that in the reference dye YD2-o-C8. For reference dye, the contribution of the acceptor to the LUMO is just 3%, which is around 30% lower than the designed Dye2 and Dye3 but similar with the Dye1. What's more, the contribution from the acceptor groups of Dye2 and Dye3 to the LUMO+1 are comparatively larger than YD2-o-C8. Therefore, our designed Dye2 and Dye3 should have stronger electron coupling with TiO2 and be more favor for electron injection than reference dye YD2-o-C8.
| System | Orbital | D | π | A |
|---|---|---|---|---|
| Dye1 | HOMO | 79 | 20 | 1 |
| LUMO | 60 | 37 | 3 | |
| LUMO+1 | 100 | 0 | 0 | |
| Dye2 | HOMO | 80 | 18 | 2 |
| LUMO | 20 | 50 | 30 | |
| LUMO+1 | 66 | 20 | 14 | |
| Dye3 | HOMO | 80 | 18 | 2 |
| LUMO | 18 | 50 | 32 | |
| LUMO+1 | 68 | 18 | 14 | |
| YD2-o-C8 | HOMO | 89 | 10 | 1 |
| LUMO | 78 | 19 | 3 | |
| LUMO+1 | 100 | 0 | 0 |
UV-vis absorption spectra
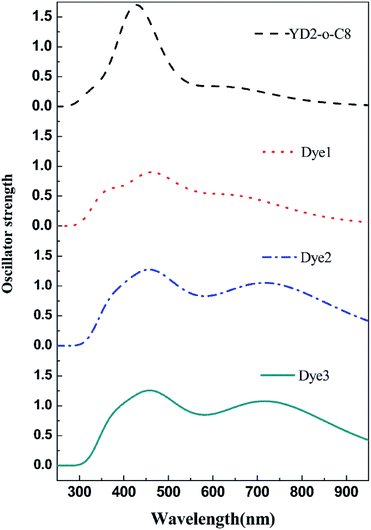
It is well known that a broad absorption covering the whole visible spectra region (400–800 nm) and even extend to the near-infrared region (∼1000 nm) is necessary to attain high light harvesting efficiency (LHE). Consequently the absorption spectra of all dyes were investigated and show in Fig. 4, and the calculated excited energies, oscillator strengths, and transition characters are listed in Table S2.† As shown in Table S2† and Fig. 4, these porphyrin sensitizers evidently exhibit two major absorption band gaps: short wavelength Soret (B) bands in the 400–500 nm region and long wavelength Q-band in the 550–750 nm region.10,32 Markedly, the B and Q bands for all designed porphyrins dyes cover broader range of absorption wavelengths than the reference dye YD2-o-C8. The Q band of YD2-o-C8 is at 637 nm, whereas the Q bands of the designed porphyrins Dye1–3 are at 665, 742, 742 nm, respectively. Moreover, the Q bands contributed from the HOMO to LUMO transitions for the designed porphyrin dyes are more intense than the reference dye YD2-o-C8. In order to compare the LHE accurately, we can get the approximate values of LHE with the following equation,49,50 LHE = 1 − 10−f, where f is the oscillator strength of the dye corresponding to λmax. So the LHE of the reference dye and Dye1–3 were calculated to be 0.686, 0.891, 0.953, and 0.956, respectively. The broadening and red shift of the absorption bands together with increased intensity of the Q bands, the designed dyes probably have improved light harvesting efficiencies.It is also noteworthy that the use of cyanoacrylic acid and 2-cyano-N-hydroxyacrylamide instead of carboxylic acid results in largely red shifts and significant broadening on the absorptions in Dye2 and Dye3 systems. From a comparison between Dye2 and Dye3, it can turn out that the 2-cyano-N-hydroxyacrylamide acceptor performs slight better in oscillator strength of Q band than the cyanoacrylic acid acceptor. Therefore, we can conclude that the 2-cyano-N-hydroxyacrylamide may be a better acceptor to capture the sunlight than the popular cyanoacrylic and carboxylic acid acceptors.
Electron injection from the sensitizer
In dye/TiO2 adsorption system, dye can form bidentate chelating, bidentate bridging, and monodentate ester-type binding with TiO2 surfaces.51 The Fourier Transform Infrared Spectroscopy (FTIR) results reported by Ma et al. show that both the bidentate chelating and bidentate bridging modes for two porphyrin derivatives with carboxylic acid acceptors.52 In the present work, we have just considered dyes bound up with TiO2 slab in one kind of forms, bidentate bridging, which was most studied in the literature and was thought to be the most stable.53 The optimized structures of dye/TiO2 complexes are shown in Fig. 5. The bond distances between O of Dye3 and 5c-Ti (O–Ti bond) of Dye3-TiO2 complex are 1.9646 and 2.0459 Å. The average O–Ti bond distance of Dye3 is slightly shorter than that of other complexes, indicating that a slightly stronger binding of Dye3 with TiO2 cluster and conceivable stronger electronic coupling. The binding energies computed as E(TiO2–dye)–E(dye)–E(TiO2) were evaluated for these systems, where E(dye), E(TiO2), and E(TiO2–dye) denote the total energy of isolated dye, TiO2 slab, and dye@TiO2 complex, respectively. A negative value of binding energy indicates stable adsorption, and the calculated results are −0.92 eV, −1.02 eV, −1.15 eV, and −1.16 eV for YD2-o-C8, and Dye1–Dye3, respectively, which are sufficiently large to allow the assumption that the dye molecules are chemisorbed on the surface of TiO2. Our computed values for the adsorption energies of Dye1–Dye3 on the surface showed that Dye3 produced a medium binding in contrast with other hydroxyacrylamide dyes.54 In most cases, the surrounding water stability of hydroxamate could compensate the adsorption energy to an impressive degree.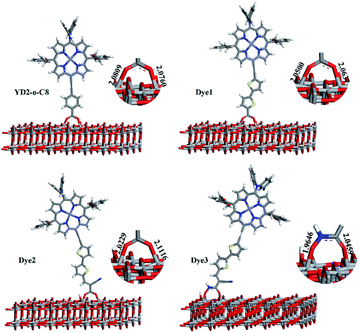 | ||
| Fig. 5 The dyes adsorbed on the TiO2 slab obtained by PW91 and the corresponding O–Ti bond lengths (Å). | ||
Fig. 6 compares the IET dynamics in every sensitizer attached to TiO2 after π → π* excitation of each sensitizer (considering electron injection from the LUMO of sensitizer molecules). It shows that the electron injection times decrease in the order: Dye3 < Dye2 ≪ YD2-o-C8 < Dye1. The huge difference in the injection rates between Dye1 and Dye2 is likely due to the presence of the cyano group. Dye3 has the fastest injection rate mostly due to its strongest interaction with TiO2 slab. The similar dyes with bithiophene and CPDT (cyclopenta[1,2-b:5,4-b′]dithiophene) as π bridge present absolute stronger quenching than biphenyl π bridge, which may be explained by the twisted molecular structure of the former with thiophene derivatives as the spacer. The strong quenching of the photoluminescence of dyes with bithiophene and CPDT as π bridge suggested that the electron transfer from the excited dyes to semiconductors is absolutely fast and efficient.32 The cyanoacrylic acid and 2-cyano-N-hydroxyacrylamide groups as anchor can help the process of electron injection further.
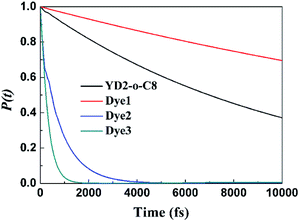 | ||
| Fig. 6 Computed electron survival probabilities P(t) with the electron injection times corresponding to photo-excited surface complexes for all mentioned dyes. | ||
Conclusions
In this work, three porphyrin sensitizers with different acceptors (carboxylic, cyanoacrylic, and 2-cyano-N-hydroxyacrylamide) for reformative DSSCs are designed and compared directly based on DFT and TDDFT calculations. The TD-B3LYP results are in agreement with experimental measurement and this functional is best for simulating the absorption spectra in our calculations. The results also show that designed dyes, especially Dye2 and Dye3, have smaller HOMO–LUMO band gaps and more broadening absorption bands together with more intensity in the Q bands than referenced YD2-o-C8. The contribution of anchoring groups of our sensitizer Dye2 and Dye3 to LUMO is 30–32%, whereas the so far known best sensitizer YD2-o-C8 contributed 2%. Clear insights into the simulation of the IET for all sensitizers were demonstrated, and our designed Dye2 and Dye3 have much faster electron injection rates into TiO2 surface than YD2-o-C8 dye is pointed out. From our calculated results, the designed dyes (especially Dye2 and Dye3) would be better candidates for DSSCs than referenced YD2-o-C8. With 2-cyano-N-hydroxyacrylamide acceptor, Dye3 performs the best in oscillator strength of Q band, implying that it is the most efficient sensitizer and 2-cyano-N-hydroxyacrylamide with elongated conjugated framework is promising acceptor. Our computed values for the adsorption energies of these dyes on the anatase surface showed that 2-cyano-N-hydroxyacrylamide produced a medium binding. Nevertheless the water stability of hydroxamate could compensate the smaller adsorption energy, rendering long-term durability to the device. Inspection of the IET process reveals that hydroxamate anchors provided efficient IET dynamics, with a timescale less than 1000 fs. The injection dynamics reflect the fact that the LUMO orbital has contributions from the anchoring groups, and stronger electronic coupling at the interface. We hope that our current work would provide new guideline to design new improved porphyrin dyes for DSSCs preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China (Grant No. 21573088 and 21203071) and the Jilin Provincial Natural Science Foundation (Grant No. 201215031) and Young Scholar Training Program of Jilin University.References
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- M. Grätzel, J. Photochem. Photobiol., A, 2004, 164, 3–14 CrossRef.
- Y. S. Yen, H. H. Chou, Y. C. Chen, C. Y. Hsu and J. T. Lin, J. Mater. Chem., 2012, 22, 8734 RSC.
- Y. Xie, Y. Tang, W. Wu, Y. Wang, J. Liu, X. Li, H. Tian and W.-H. Zhu, J. Am. Chem. Soc., 2015, 137, 14055–14058 CrossRef PubMed.
- H. Imahori, T. Umeyama and S. Ito, Acc. Chem. Res., 2009, 42, 1809–1818 CrossRef PubMed.
- C. W. Lee, H. P. Lu, C. M. Lan, Y. L. Huang, Y. R. Liang, W. N. Yen, Y. C. Liu, Y. S. Lin, E. W. G. Diau and C. Y. Yeh, Chem.–Eur. J., 2009, 15, 1403–1412 CrossRef PubMed.
- H. Song, Q. Liu and Y. Xie, Chem. Commun., 2018, 54, 1811–1824 RSC.
- C. P. Hsieh, H. P. Lu, C. L. Chiu, C. W. Lee, S. H. Chuang, C. L. Mai, W. N. Yen, S. J. Hsu, E. W. G. Diau and C. Y. Yeh, J. Mater. Chem., 2010, 20, 1127–1134 RSC.
- A. Yella, H. W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634 CrossRef PubMed.
- Y. Tang, Y. Wang, X. Li, H. Ågren, W.-H. Zhu and Y. Xie, ACS Appl. Mater. Interfaces, 2015, 7, 27976–27985 Search PubMed.
- T. Bessho, S. M. Zakeeruddin, C. Y. Yeh, E. W. Diau and M. Grätzel, Angew. Chem., Int. Ed., 2010, 49, 6646–6649 CrossRef PubMed.
- A. Yella, C.-L. Mai, S. M. Zakeeruddin, S.-N. Chang, C.-H. Hsieh, C. Y. Yeh and M. Grätzel, Angew. Chem., Int. Ed., 2014, 53, 2973–2977 CrossRef PubMed.
- S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. E. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Graätzel, Nat. Chem., 2014, 6, 242–247 CrossRef PubMed.
- S. B. Mane, J.-Y. Hu, Y.-C. Chang, L. Luo, E. W.-G. Diau and C.-H. Hung, Chem. Commun., 2013, 49, 6882–6884 RSC.
- C.-H. Wu, M.-C. Chen, P.-C. Su, H.-H. Kuo, C.-L. Wang, C.-Y. Lu, C.-H. Tsai, C.-C. Wu and C.-Y. Lin, J. Mater. Chem. A, 2014, 2, 991–999 Search PubMed.
- T. Wei, X. Sun, X. Li, H. Ågren and Y. Xie, ACS Appl. Mater. Interfaces, 2015, 7, 21956–21965 Search PubMed.
- R. B. Ambre, G. F. Chang and C. H. Hung, Chem. Commun., 2014, 50, 725–727 RSC.
- K. Kurotobi, Y. Toude, K. Kawamoto, Y. Fujimori, S. Ito, P. Chabera, V. Sundström and H. Imahori, Chem.–Eur. J., 2013, 19, 17075–17081 CrossRef PubMed.
- G. Di Carlo, A. Orbelli Biroli, M. Pizzotti, F. Tessore, V. Trifiletti, R. Ruffo, A. Abbotto, A. Amat, F. De Angelis and P. R. Mussini, Chem.–Eur. J., 2013, 19, 10723–10740 CrossRef PubMed.
- S. H. Kang, M. S. Kang, I. T. Choi, J. Y. Hong, M. J. Ju and H. K. Kim, ChemElectroChem, 2013, 1, 637–644 CrossRef.
- G. Yang, Y. Tang, X. Li, H. Ågren and Y. Xie, ACS Appl. Mater. Interfaces, 2017, 9, 36875–36885 Search PubMed.
- T. P. Brewster, S. J. Konezny, S. W. Sheehan, L. A. Martini, C. A. Schmuttenmaer, V. S. Batista and R. H. Crabtree, Inorg. Chem., 2013, 52, 6752–6764 CrossRef PubMed.
- W. R. McNamara, R. L. Milot, H.-e. Song, R. C. Snoeberger III, V. S. Batista, C. A. Schmuttenmaer, G. W. Brudvig and R. H. Crabtree, Energy Environ. Sci., 2010, 3, 917–923 Search PubMed.
- W. Li, L. G. Rego, F.-Q. Bai, C.-P. Kong and H.-X. Zhang, RSC Adv., 2014, 4, 19690–19693 RSC.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- S. Karthikeyan and J. Y. Lee, J. Phys. Chem. A, 2013, 117, 10973–10979 CrossRef PubMed.
- M. J. Zhang, Y. R. Guo, G. Z. Fang and Q. J. Pan, Comput. Theor. Chem., 2013, 1019, 94–100 CrossRef.
- K. B. Ornso, J. M. Garcia-Lastra and K. S. Thygesen, Phys. Chem. Chem. Phys., 2013, 15, 19478–19486 RSC.
- M. Xie, F.-Q. Bai, J. Wang, Y.-Q. Zheng and Z. Lin, Phys. Chem. Chem. Phys., 2018, 20, 3741–3751 RSC.
- J. Lu, B. Zhang, S. Liu, H. Li, H. Yuan, Y. Shen, J. Xu, Y. Cheng and M. Wang, Phys. Chem. Chem. Phys., 2014, 16, 24755–24762 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- L. G. C. Rego and V. S. Batista, J. Am. Chem. Soc., 2003, 125, 7989–7997 CrossRef PubMed.
- S. G. Abuabara, L. G. C. Rego and V. S. Batista, J. Am. Chem. Soc., 2005, 127, 18234–18242 CrossRef PubMed.
- S. G. Abuabara, C. W. Cady, J. B. Baxter, C. A. Schmuttenmaer, R. H. Crabtree, G. W. Brudvig and V. S. Batista, J. Phys. Chem. C, 2007, 111, 11982–11990 Search PubMed.
- W. R. McNamara, R. C. Snoeberger, G. Li, J. M. Schleicher, C. W. Cady, M. Poyatos, C. A. Schmuttenmaer, R. H. Crabtree, G. W. Brudvig and V. S. Batista, J. Am. Chem. Soc., 2008, 130, 14329–14338 CrossRef PubMed.
- P. Qin, X. Yang, R. Chen, L. Sun, T. Marinado, T. Edvinsson, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2007, 111, 1853–1860 Search PubMed.
- G. Zhang, Y. Bai, R. Li, D. Shi, S. Wenger, S. M. Zakeeruddin, M. Gratzel and P. Wang, Energy Environ. Sci., 2009, 2, 92–95 Search PubMed.
- R. Ma, P. Guo, H. Cui, X. Zhang, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. A, 2009, 113, 10119–10124 CrossRef PubMed.
- N. Santhanamoorthi, C. M. Lo and J. C. Jiang, J. Phys. Chem. Lett., 2013, 4, 524–530 CrossRef PubMed.
- D. P. Hagberg, T. Edvinsson, T. Marinado, G. Boschloo, A. Hagfeldt and L. Sun, Chem. Commun., 2006, 2245–2247 RSC.
- J. Zhang, H.-B. Li, S.-L. Sun, Y. Geng, Y. Wu and Z.-M. Su, J. Mater. Chem., 2012, 22, 568–576 RSC.
- M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Müller, P. Liska, N. Vlachopoulos and M. Grätzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef.
- M. G. K. Kalyanasundaram, Coord. Chem. Rev., 1998, 77, 347–414 CrossRef.
- T. Ma, K. Inoue, K. Yao, H. Noma, T. Shuji, E. Abe, J. Yu, X. Wang and B. Zhang, J. Electroanal. Chem., 2002, 537, 31–38 CrossRef.
- P. Persson, R. Bergström and S. Lunell, J. Phys. Chem. B, 2000, 104, 10348–10351 CrossRef.
- W. Li, L. G. C. Rego, F.-Q. Bai, J. Wang, R. Jia, L.-M. Xie and H.-X. Zhang, J. Phys. Chem. Lett., 2014, 5, 3992–3999 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional calculations, figure, detail of the calculated absorption energies (λ), oscillator strength (f), and electron transition configurations for all designed dyes and reference dye YD2-o-C8 are given. See DOI: 10.1039/c8ra02974a |
| This journal is © The Royal Society of Chemistry 2018 |