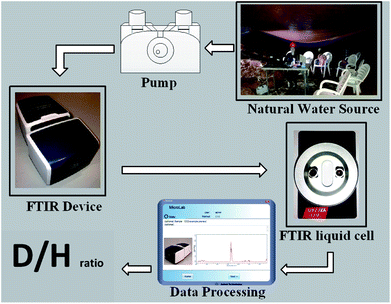
Open Access Article
Open Access ArticleOn-line in situ determination of deuterium content in water via FTIR spectroscopy
Ira Litvak *ac,
Yaakov Ankerac and
Haim Cohenb
*ac,
Yaakov Ankerac and
Haim Cohenb
aDepartment of Chemical Engineering, Ariel University, Israel. E-mail: Irachkalitvak@gmail.com
bDepartment of Chemical Sciences, Ariel University, Israel
cDepartment of Environmental Research, Eastern R&D Center, Israel
First published on 9th August 2018
Abstract
Hydrogen stable isotope ratios are critical indicators in environmental geochemical studies for characterizing runoff, determination of groundwater groups and water uptake by plants etc. (generally used in combination with 18O analysis). While the common technique for this hydrogen isotope measurement is Mass Spectrometry, FTIR (Fourier transform infra-red) spectroscopy may be an alternative method, with the advantage of direct and simple operating measurements. The FTIR spectrometer has the advantage of performing in situ measurements, which can delineate continuous geochemical processes. In situ measurements decrease errors that may be a consequence of sample delivery to the laboratory and off-site analysis procedures. In this study, we have developed a new simple procedure for in situ hydrogen stable isotope ratio measurements. We discovered that the HDO (hydrogen, deuterium, and oxygen) absorbance peak at 2504 cm−1 is the most suitable for water sample direct analysis, with the FTIR device, using a circular sample cell for liquid samples. A case study analyzing water samples from a karstic cave (Sif cave, Israel) verified the following: (a) on-line determination of water D/H ratio can be carried out with the portable FTIR spectrometer (and thus can be used for field measurements such as in the Sif cave) and (b) the D concentration sensitivity achieved was at a 0.01‰ level, with a standard deviation of 0.006‰.
Introduction
Naturally occurring stable hydrogen isotopes are very important for environmental studies since they can be used as indicators of several hydro-geochemical processes. These include identification of streamflow generation mechanisms, flow path, and water-budget model testing.1 Stable isotope analysis is also used in this perspective for quantification of stream water composition and its temporal and geographical origin,2 as well as to gain data on processes such as paleowaters and cave water cycles. In addition, it is also used to find the origin of fluid inclusions trapped within carbonate aquifer matrixes or in speleothems. In general, fluid inclusions may undergo post-depositional oxygen isotope exchange with carbonate. Thus, the oxygen isotopic content is not a reliable indicator of the original water. However, trapped water should not undergo post-depositional hydrogen isotope exchange because there is no hydrogen reservoir to enable such an exchange. Owing to that, the alternative hydrogen deuterium to hydrogen (D/H) analysis can be used as a proxy for δ18O.3Although isotopes have similar chemical properties, the mass differences induce slight changes in reaction kinetics and reaction equilibrium. Equilibrium fractionation is connected to the distribution of isotopes among various compounds in an equilibrium reaction (reversible process). When equilibrium is established, both sides of reaction rates are equal and the isotope abundances in the reactant and product remain constant. The slowest reaction rate will determine the time to equilibrium and it is temperature dependent. However, when equilibrium cannot be established meaning an irreversible process occurs, this will be kinetic isotope fractionation. Completely kinetic fractionation is only found in processes were the reaction product becomes instantly isolated from the reactant. It is often difficult to describe the processes in a quantitative manner, as the underlying physical or chemical kinetic processes are generally complicated. In nature, most processes are not kinetic, but a combination of equilibrium fractionation as well.4,5
For distinguishing between equilibrium fractionation and kinetic fractionation, it is important to understand the reason for the fractionation. Equilibrium fractionation occurs so that the total energy of the system is minimized via forming the most stable bonds possible, in other words equilibrium is related to bond stability of the isotope. Kinetic fractionation occurs because smaller molecules move faster than heavier molecules and therefore react more slowly, in other words, kinetic is related to the speed of the isotope.
In elements having low atomic numbers (Z), the isotopic variance is relatively greater, because the mass differences are large. Thus, when elements participate in chemical reactions, the various isotopes may react at slightly different rates. Or if equilibrium is established, isotopes partition themselves differently in products and reactants.6 The difference in the relative isotopic abundance of an element in different pools of the same molecular species is defined as isotopic fractionation. Isotopic fractionation results from differences in reaction rates or phase transitions, which are related to isotopes of an element.2
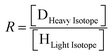
Isotope composition of stable small atomic mass elements (e.g. H, O, C) is generally not reported as an absolute number, but as delta values (δ). Delta values are commonly reported in parts per thousand, or per mill (δ × 1000‰) and are calculated by comparing the apparent isotope-abundance ratio in a sample with that of a reference material measured under precisely the same conditions, without any attempt to determine the “absolute” isotope-abundance ratios of either material.7
Delta values (δ) are calculated using the following equation:
 | (1) |
 | (2) |
The value of δ in the standard is usually defined as 0‰, but laboratories that specialize in anthropological analysis and enriched substance can present the results in percentage or ppm instead of per mill.9
This hydrogen ratio has a much higher natural variation, than for of other environmental isotopes such as 13C and 18O, because of the relatively larger mass differences between the isotopes, stemming from a more substantial fractionation process. D and 18O content are dependent on the same processes (fractionation via evaporation processes) and are usually used in conjunction for water delineation, thus these values propagate along the Global Meteoric Water Line (GMWL).10 High concentration of D is common in places where the evaporation level is high, such as tropical and sub-tropical lakes. In contrast, low concentrations of D can be found in locations with low evaporation rates such as polar ice.11
The common practice for stable isotope measurement is historically mass spectrometry (MS) and recently laser-based isotope analyzers. However since these methods analyzes a gas phase; direct measurement of liquid water is not in reach. Therefore, for example MS, water evaporation followed by vapor reduction to H2 (H2O) and HD (HDO) over a chromium catalyst maintained at 900 °C is needed.12 Furthermore, operating an instrument in high vacuum prevents MS in situ applications and might distort the D/H isotopic ratio owing to D/H exchange with water condensate on the system's metal surface inlet.13 Field fitted laser based isotope analyzers are still limited by the need to convert water to vapors, which means it will be needed to service the sample input device.14,15 Moreover, additional drawback of laser spectrophotometers is that they can produce inaccurate measurements when dissolved organic carbon (DOC).16,17 FTIR has an advantage to both methods mentioned above that is the ability to separate and differentiate between the D2O and HDO species. With this said, there are some studies that present the ability to distinguish between the species, but in the near IR with complicated laser spectrometers which is not suitable in field measurements.18
The assumptions enrolled dictate the research goal, to develop a simple and affordable method for in situ hydrogen isotope ratios measurement (D/H), directly from natural water reservoirs. For this simple, sensitive, and precise environmental task, we used a portable Fourier Transform Infra-Red spectrometer (FTIR).
Materials, methods, and instrumentation
Materials
Standard samples were prepared using Cambridge Isotope Laboratories, Inc. D2O solution, with D concentration of 999‰. All samples were prepared by using precise weight, with Ultra-Pure distilled Water (UPDI) from Dow Water & Process Solutions ion exchange system for solutions dilution. The UPDI resistance was 18.2 Mohm cm−1 at 25 °C and TOC values were lower than 5 ppb.The (International Atomic Energy Agency) (IAEA) hydrogen isotope analysis standard was VSMOW2 Vienna Standard Mean Ocean Water 2, at 25 °C. Isotope ratios of hydrogen (H/D) are usually represented relative to “Standard Mean Ocean Water” (SMOW),19 or as VSMOW “Vienna-SMOW”.20 The use of VSMOW is preferable because using these standards ensures that the measurement was calibrated to the IAEA standard, with δ values in per mill as a standard quantification unit.20
An on-line measurement test performed at a karstic cave (Sif Cave) included water samples from three locations (noted as 1–3) within the cave collected directly and measured in situ.
Methods
Standards preparation included preparation of pure D2O aliquots with an analytical balance and diluting with UPDI. The precise weighting (Table 1) was used as a reference tool, and all the samples were weighed against it. The concentrations of the samples were in the range of 0.01–0.10‰ (∓0.01‰ increments). The zero (0‰ D2O) reference UPDI D2O used as background and has natural abundance of D. The D2O concentration calibration curve relies on Beer's law| A = εlc | (3) |
| D concentration (in ‰) | Sample weight (in g) |
|---|---|
| 0.01 | 19.9660 |
| 0.02 | 19.8761 |
| 0.03 | 19.9010 |
| 0.04 | 19.8920 |
| 0.05 | 19.9854 |
| 0.06 | 19.8446 |
| 0.07 | 19.9991 |
| 0.08 | 20.0156 |
| 0.09 | 19.9783 |
The measurement method is the same for the calibration curve standard and in situ sample (triplicates) measurements. The liquid cell Circular Aperture Cell Mount 6500S from Spectra Tech Inc. was used with BaF2 windows of 32 × 3 mm diameter. For background measurements, the FTIR liquid cell was filled with the same UPDI used for preparing the samples. After measuring the background (UPDI water), the cell was filled with different calibration solutions and the IR spectrum was measured.
Measurement errors were calculated for the sample preparation and the measurement protocol and also for the instrumentation used in the study. The main causes of error were a combination of sample preparation as weighing error (0.002%), volume measurement error (0.2%), and instrumentation error (5%).22 The device error is over than order of magnitude higher than all other errors combined and a value of 5% represents the total measurement error.
In situ (on-line) measurement in the Sif cave
The portable FTIR in situ on-line D/H isotopic ratio measurement case study is a karstic cave (Sif), located in Central Israel near the town of Ariel (Fig. 1). In most karstic caves, runoff percolates through the soil and dissolves carbon dioxide, which is later released into the cave atmosphere once the water drips into the cave. In the Sif Cave, dripping water was collected via three large plastic (polyvinyl chloride – PVC) sheets from three different areas in the cave to 3 barrels denoted as 1–3. The sheet surface areas are as follows: Site 1, 17 m2; Site 2, 56 m2; and Site 3, 46 m2. The measured samples were collected from the barrels.23Water from the collection barrels1–3 was directly transferred via a syringe to the liquid cell. The volume injected into the cell was at least 50 times larger than the cell volume to assure effective washing of the previous sample measured; and all air were removed from the cell, so that the entire cell was filled with liquid (air bubbles might interfere with the instrument analysis). The measurement parameters were the same as those used for the calibration and standard measurements.
Instrumentation
Analysis of infrared spectra can determine type and concentration of molecules present in a sample. There are several types of infrared spectrophotometers, but the most common is the FTIR (Fourier Transform Infra-Red) spectrophotometer.24The absorbance A of the IR light obeys the Beer–Lambert law, as shown in eqn (3) and (4).
In Fig. 2, absorbance A (Y-axis) is displayed vs. wavenumber v cm−1 (X-axis).
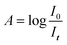 | (4) |
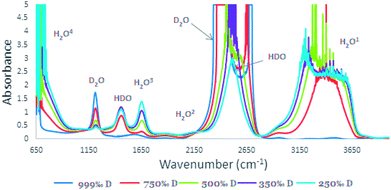 | ||
| Fig. 2 IR spectra of high concentration of D2O (250‰, 350‰, 500‰, 750‰, and 999‰) in the range of 650–4000 cm−1. | ||
Most of the infrared spectra measurements are in the Mid-IR range (400 to 4000 cm−1).24 The Fourier transform superposed mathematical functions as sine and cosine waves. By passing the light through the interferometer, the infrared beam spectrum is optically transformed into an interference pattern (the interferogram). The infrared detector measures this interference pattern, and the Fourier transform turns it back into a spectrum.24
The FTIR used in this research was Agilent's Cary 630 with a transmission accessory unit with a KBr beam splitter and deuterated triglycine sulfate (DTGS) detector. The measurement parameters of the FTIR spectrometer were as follows: resolution: 2 cm−1; wavenumber range: 400–4000 cm−1 and number of scans: 100.21 The size of the bench space of the Cary 630 FTIR is 20 × 20 cm, with a total weight of 3.6 kg, making it suitable for the purpose of in situ measurements.
Results
Determination of the source of the 2504 cm−1 absorbance band in water
The reported IR spectrum of water contains three main components: H2O, D2O, and HDO. While most of the H2O, D2O, and HDO absorbance peaks are well established (Fig. 2), the FTIR data report25,26 for the 2504 cm−1 absorbance peak source is not clear. In some publications, it is attributed to the D2O27,28 and in others to the HDO29 species. It is important to note that most of the literature is in agreement that vibrations of the D–O bond are the source of the 2504 cm−1 absorbance.25,30In order to determine the origin of the 2504 cm−1 absorbance peak25–28 and, in particular, which species was causing it, H2O/D2O mixtures with the following D2O concentrations were prepared: 999‰, 750‰, 500‰, 350‰ and 250‰ D content. The IR background spectra was measured in the range of 650–4000 cm−1 (Fig. 2) with the cell. This procedure is essential since there cannot be a zero percent solution that will fit both the H2O and the D2O as a reference. In the pure D2O solution (999‰), two absorbance bands are observed: at 2220–2800 cm−1 a multi-centered band and at 1200 cm−1 a single-center band. The high concentration of the D2O makes it impossible to distinguish the maximum value of the absorption band at 2200–2800 cm−1. Lowering the D2O concentration reduces peak intensities. With this reduction, there is an increase in the O–H absorbance at the 3000–3800 range and two additional peaks at 1450 cm−1. There is also a shift to a single centered peak at 2504 cm−1, thus emphasizing that the 2504 cm−1 band origin is HDO rather than D2O. In addition, with D2O concentration reduction, the absorbance band at 1200 cm−1 is also reduced, while the HDO peaks at absorbance bands of 1450 cm−1 and 2504 cm−1 are increasing.
FTIR measurements for calibration curves
The IR Spectra (650–4000 cm−1) for the different D2O concentrations are given in Fig. 3. In the O–H stretching region, in the ranges of 2900–3700, 1500–1700, and 650–1000 cm−1 strong H2O absorbance is observed (absorbance > 1.0). Consequently, calibration was carried out using the HDO peak at 2504 cm−1 where there was no masking of the peak (Fig. 4).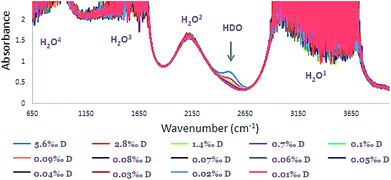 | ||
| Fig. 3 FTIR spectra of HDO calibration solutions: concentration range of 0.010–5.6‰ with 0.10 mm space (the four H2O absorbances denoted 1–4). | ||
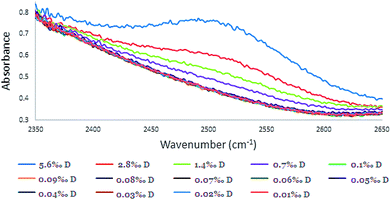 | ||
| Fig. 4 The absorbance peak of HDO in different calibration solutions at the absorbance peak of 2504 cm−1 (concentration range of 0.010–5.6‰ with 0.10 mm spacer). | ||
Although the concentration range of D in samples that were examined was 0.010–0.1‰, for intensifying and pointing out the 2504 cm−1 peak, higher concentrations of D in the range of 0.70–5.6‰ were included (Fig. 3 and 4). Although, distinguishing low concentrations in the spectra was slightly difficult, the FTIR device software was able to quantify it.
Absorbance calibration data results in Fig. 5 present values obtained with spacers 0.050 mm, 0.025 mm, and 0.10 mm. As a function of the D2O concentration for the three spacers, R2 (coefficient of determination) of the absorbance intensity is presented as well in Fig. 5: 0.996 (for 0.10 mm spacer), 0.993 (for 0.050 mm spacer), and 0.984 (for 0.025 mm spacer).
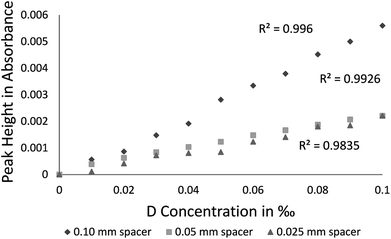 | ||
| Fig. 5 Calibration curves for D2O using optical paths 0.10, 0.025, and 0.050 in mm (reference sample: natural water). | ||
The lowest HDO concentration measured in the calibration curve was of 0.010‰, whereas the HDO peak that provided the best results is located at 2504 cm−1 (Fig. 3). Different spacers (0.025 [R2 = 0.984], 0.05 [R2 = 0.993] and 0.10 [R2 = 0.996] mm) were checked and since the best R2 was for the larger 0.10 mm spacer, it was used throughout the study. The R2 linearity fit is mostly influenced by sample measurement errors of 5% (wavenumber accuracy) of the specific instrumental precision.
The sample solutions for the calibration curve were prepared by prices analytical weight as presented in Table 1. Validation of the method was carried out by preparation of unknown samples via mixing 99.9% (999‰) D2O with UPDI water (0.01157% D) and the results of the determination was accurate within 6‰ of the prepared solutions.
In order to examine low D2O concentration reproducibility, five samples containing 0.070‰ D2O were prepared (concentration was appropriated for hydrogen isotope measurement in water). Each sample was measured three times with an optical path of 0.10 mm. The results of the measurements were in the range of 0.00416–0.00619 absorbance unit and the total average absorbance was 0.051‰ with a standard deviation of 0.0006.
Average D2O concentration from ten VSMOW2 water solution standard samples was measured with a 0.10 mm spacer. The predicted concentrations range was between 0.0102 to 0.0184‰. The standard predicted values were calculated by the 0.10 mm spacer (optical path) calibration curve equation (Fig. 5). The average concentration of the standard was 0.0143‰ (=Rstandard).
In situ measurements at Sif cave
A field experiment was performed (05.04.2017) at the Sif cave to evaluate the system's performance and the in situ measurement method applicability. The measurement results are presented in Table 2 for the three drip water collection areas, denoted 1–3. The values presented in Table 2 are the average of the measurements of the samples and vary between (−164.58) – (+16.78)‰ for delta and 0.0119–0.0146‰ for D concentration (which was calculated from the calibration curve and denoted as predicted concentration).| Sample name | D2O concentration predicted in ‰ | δD in ‰ |
|---|---|---|
| Sif 1 | 0.0119 | −164.58 |
| Sif 2 | 0.0146 | 16.78 |
| Sif 3 | 0.0136 | −53.01 |
Discussion
The field and laboratory operations performed in this study aimed to develop a method for determining δD in accuracy suitable for environmental research. The equipment consists of simple and portable FTIR spectrophotometer with liquid sample cells appropriate for the FTIR transmission unit and the results confirmed that the 2504 peak is affiliated to HDO species and not to D2O and that the D concentrations measured are lower than those reported in other studies on natural water.31,32Since direct hydrogen isotope measurement of aqueous solutions is not possible with a Mass Spectrometer or with Laser based spectrometer (as the sample has to be converted to gaseous phase); FTIR spectrophotometer with a suitable liquid cell, is capable of performing such measurement using.31
The method for D/H ratio measurement relied on D and H typical absorbance bands, but since most absorption bands are non-unique and related to other vibrations such as H2O2 at 2200 cm−1 and HDO at 1400 cm−1 (Fig. 2), the source of the absorption peak at 2504 cm−1 was somewhat unclear. Most recent studies regarded it as absorbance in liquid water, which stems from D2O.27,28,33 Other sources did not report to which species this peak is related, but rather stated that it is the consequence of a O–D vibration.34 The early literature connects this peak to a O–D vibration without stating the species origin.25 In order to resolve the dilemma, we measured the D 2504 cm−1 peak for variable HDO and D2O concentration mixtures, which revealed that it relates to the HDO vibration. The O–H absorbance is responsible to spectra shape variance as presented in Fig. 2, owing to lower H2O concentration. As shown in Fig. 2, once D2O concentration decreases the peak shape is changed from a doublet peak to a single peak, indicating that the peaks at 1450 cm−1 and 2504 cm−1 represent HDO species and that the absorption peak at 1200 cm−1 is the absorbance band of D2O.
The results emphasize that the best absorbance band that can serve as a measurement indicator to D concentration is the 2504 cm−1 band, which is not masked by H2O or D2O vibrations (like the less intense absorbance band at 1450 cm−1). The HDO signal at 2504 cm−1 is more effectively separated from the H2O signal once compared to the HDO signal at 1450 cm−1, which is totally masked by the H2O signal. Consequently, calibration was carried out using the HDO peak at 2504 cm−1 (Fig. 4).
Only two variables affect vibration peak position in reference to chemical bonds: force constant and reduced mass. These two molecular properties determine the wavenumber at which a molecule will absorb IR radiation. D has the same force constant as H, although with higher atomic mass. By practically doubling the mass of the hydrogen atom, the oxygen–hydrogen stretching vibration is reduced and shifts (Fig. 2).35 In addition, the width of the bands relates to the intermolecular interaction strength (such as hydrogen bonding). The number and strength of intermolecular interactions varies greatly within the sample, the O–H bond or O–D bond causing shifts in absorbance band location and shape as demonstrated for the 2504 cm−1 peak.36
The thermodynamic equilibrium constant of the reaction between D2O and H2O is approximately 3.9.30 Therefore, the concentration of the different species (D2O, H2O, and HDO) in a water sample containing 1‰ D at equilibrium is 99.8001% for H2O, 0.1998% for HDO, and 0.0001% for D2O.31 In these parameters, the main deuterated species in the solution is HDO and not D2O. Moreover, at low D2O concentration the HDO concentration is much higher than that of D2O and thus one cannot accurately analyze the absorption D2O peak, but rather that of the HDO, which is far more intense. Although the system's temperature range might influence the intensity of the peak, the shape for any specific temperature is the same (except for a small shift toward higher frequencies).37 Thus, the temperature variation will not affect the identification of the relevant peak. The temperature that was tested in the laboratory conditions (25 °C) and the field did not effect the results. Moreover, geological systems such as the karstic cave sampled during this study are considered closed systems with a steady state temperature (approximately 18 °C).38
The δD values calculated for the 0.10 mm spacer had shown the best consistency with Beer's law (Fig. 5). Hence, longer optical pathways contribute to the measurement consistency. Nonetheless, there is a tradeoff between optical length and energy gradient. Owing to the energy ramp, in the Cary 630 the option of using a 0.20 mm optical pathway cannot be carried out in the liquid cell but must rather use a Thumbler-IR unit [the specific FTIR that was used (Cary 630 by Agilent) has 8 different accessories which can be purchased for specific needs such as the Thumbler IR FTIR transmission, which is used for measurements of liquids, without the inconvenience of cumbersome IR transmission cells—no spacers, windows, or syringes are needed. For the purpose of our laboratory needs we have purchased the transmission accessory as it can be used in all three phases (gas, liquid and solid)]. Since measurements with a larger spacer increase measurement sensitivity and improve calculation, using the Thumbler-IR unit will probably also improve the R2 linearity fit.
In the reproducibility test, the instrument showed a standard deviation of ∓0.006‰, which is sufficient for measuring δD isotopes.39 The advantage of D determination directly from the calibration curve makes the process of data handling quicker, easier, and with smaller margin of error when compared to the complex data processing demanded of MS measurements.
When comparing this study, it can be seen that the method presented in this paper has demonstrated the feasibility of attaining greater sensitivity than the 0.1‰, using the 8400S Shimadzu FTIR with 100 μm optical path, which was reported in an IAEA publication in 2011.31 In this research, 0.01‰ sensitivity in D analysis was achieved, which is on a scale of one order of magnitude improvement. In addition when comparing to Higgins (2014), who used an Agilent 4500 Series FTIR which is capable of 0.012‰ measurement sensitivity (a special and far more expensive FTIR unit).32
In situ measurements conducted in the Sif cave demonstrated highly depleted δD values (Table 2). These low values are probably a consequence of the cave's extremely humid and closed atmosphere with low evaporation rates, which can induce variations of up to 250‰ of delta in the cave hydrological cycle.11
Conclusions
A new procedure for in situ measurement was developed and validated through measurements within a karstic cave. The 2504 cm−1 absorption peak stems from the HDO absorption band and was found most suitable for the measurements. We demonstrated that a small and portable FTIR spectrophotometer can be used for high sensitivity (D/H) isotope ratio analysis of in situ and direct HDO measurements of water solution. The measurement sensitivity increased with optical path length, while the high sensitivity achieved of 0.01‰ was obtained with the Cary 630 0.01 mm, which is the largest spacer option for its liquid cell. The FTIR instrument reproducibility was achieved with standard deviation of ∓0.006‰, sufficient for δD analysis. In our procedure, the same method can be applied for laboratory and direct field measurements as well as for all types of liquid water sources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly funded by the Yovalim Water Cooperation LTD and the Israel Water Commission.References
- R. H. Michener and K. Lajtha, Stable isotopes in ecology and environmental science. Ecological methods and concepts series, 2007, vol. xxvi, p. 566 Search PubMed.
- M. McGuire, Stable Isotope Tracers in Watershed Hydrology, Stable Isotopes in Ecology and Environmental Science, 2nd edn, 2004, ch. 11, pp. 334–365 Search PubMed.
- A. Matthews, A. Ayalon and M. Bar-Matthews, D/H ratios of fluid inclusions of Soreq cave (Israel) speleothems as a guide to the Eastern Mediterranean Meteoric Line relationships in the last 120 ky, Chem. Geol., 2000, 166(3–4), 183–191 CrossRef.
- R. V. Trigt, Laser spectrometry for stable isotope analysis of water: biomedical and paleoclimatological applications, Groningen, 2002, p. 192 Search PubMed.
- Agency IAE, and United Nations Educational S and CO, Abundance and Fractionation of stable isotopes, Environmental Isotopes in the Hydrological Cycle Principles and Applications, 2000, available from: http://www-naweb.iaea.org/napc/ih/IHS_resources_publication_hydroCycle_en.html Search PubMed.
- E. Schauble, Applying stable isotope fractionation theory to new systems, Rev. Mineral. Geochem., 2004, 55(1), 65 CrossRef , available from: https:\\papers://dee23da0-e34b-4588-b624-f878b46d7b3d/Paper/p132.
- J. R. de Laeter, J. K. Böhlke, P. De Bièvre, H. Hidaka, H. S. Peiser and K. J. R. Rosman, et al., Atomic weights of the elements. Review 2000 (IUPAC Technical Report), Pure Appl. Chem, 2003, 75(6), 785 Search PubMed , available from: http://www.degruyter.com/view/j/pac.2003.75.issue-6/pac200375060683/pac200375060683.xml.
- Harold C Urey Papers, A Hydrogen Isotope of mass 2 and its concentration, Special Collections Research Center, University of Chicago Library, 1932 Search PubMed.
- T. B. Coplen, Guidelines and recommended terms for expression of stable-isotope-ratio and gas-ratio measurement results, Rapid Commun. Mass Spectrom., 2011, 25(17), 2538–2560 CrossRef PubMed.
- H. Craig, Isotopic Variations in Meteortic Waters, Science, 1961, 133(no. 3465), 1702–1703 CrossRef PubMed.
- W. G. Mook, Natural abundance of the stable isotopes of C, O and H, Environmental isotopes in the hydrological cycle, 2000, vol. 91, 104, ch. 7, pp. 117–121 Search PubMed.
- T. Donnelly, S. Waldron, A. Tait, J. Dougans and S. Bearhop, Hydrogen isotope analysis of natural abundance and deuterium-enriched waters by reduction over chromium on-line to a dynamic dual inlet isotope-ratio mass, Rapid Commun. Mass Spectrom., 2001, 1297–1303 CrossRef PubMed.
- J. Throck Watson and O. David Sparkman, Introduction to Mass Spectrometry: Instrumentation, Applications, and Strategies for Data Interpretation, Wiley, 4th edn, 2009 Search PubMed.
- G. Koehler and L. I. Wassenaar, Realtime stable isotope monitoring of natural waters by parallel-flow laser spectroscopy, Anal. Chem., 2011, 83(3), 913–919 CrossRef PubMed.
- G. Lis, L. I. Wassenaar and M. J. Hendry, High-precision laser spectroscopy D/H and 18O measurements of microliter natural water samples, Anal. Chem., 2008, 80(1), 287–293 CrossRef PubMed , available from: https://pubs.acs.org/doi/abs/10.1021/ac701716q.
- B. Herbstritt, B. Gralher and M. Weiler, Continuous in situ measurements of stable isotopes in liquid water, Water Resour. Res., 2012, 48, 1–6 CrossRef.
- P. Gupta, D. Noone, J. Galewsky, C. Sweeney and B. H. Vaughn, Demonstration of high-precision continuous measurements of water vapor isotopologues in laboratory and remote field deployments using wavelength-scanned cavity ring-down spectroscopy (WS-CRDS) technology, Rapid Commun. Mass Spectrom., 2009, 23, 2534–2542 CrossRef PubMed.
- O. V. Naumenko, F. Mazzotti, O. M. Leshchishina, J. Tennyson and A. Campargue, Intracavity laser absorption spectroscopy of D2O between 11
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 and 11
400 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1, J. Mol. Spectrosc., 2007, 242(1), 1–9 CrossRef.
900 cm−1, J. Mol. Spectrosc., 2007, 242(1), 1–9 CrossRef. - C. G. Ruaux, P. C. Carney, J. S. Suchodolski and J. M. Steiner, New IUPAC guidelines for the reporting of stable hydrogen, carbon, and oxygen isotope-ratio data, J. Res. Natl. Inst. Stand. Technol., 1995, 100(3), 285 CrossRef PubMed , available from: https://www.ncbi.nlm.nih.gov/pubmed/22235000.
- H. Craig and L. Gordon, Deuterium and oxygen 18 variations in the ocean and the marine atmosphere, Stable Isotopes in Oceanographic Studies and Paleotemperatures, 1965, pp. 9–130, available from: http://yncenter.sites.yale.edu/sites/default/files/shen_jing_jan_2013.pdf Search PubMed.
- International Atomic Energy Agency, Reference Sheet for International Measurement Standards, IAEA, 2009, May 5, available from: https://curem.iaea.org/catalogue/SI/pdf/VSMOW2_SLAP2.pdf Search PubMed.
- ©Agilent Technologies, Specifications FTIR CARY 630, ©Agilent Technologies, Inc., 2011, Published in USA, p. 1–2 Search PubMed.
- N. A. Sheffer, M. Cohen, E. Morin, T. Grodek, A. Gimburg and E. Magal, et al., Integrated cave drip monitoring for epikarst recharge estimation in a dry Mediterranean area, Sif Cave, Israel, Hydrol. Processes, 2011, 25(18), 2837–2845 CrossRef.
- B. C. Smith, How an FTIR Works, Fundamentals of Fourier Transform Infrared Spectroscopy, 2011, ch. 2 Search PubMed.
- C. A. Swenson, Absolute infrared intensities of HDO in aqueous solution, Spectrochim. Acta, 1964, 21, 987–993 CrossRef.
- P. Rodríguez-Escales, A. Folch, G. Vidal-Gavilan and B. M. van Breukelen, Modeling biogeochemical processes and isotope fractionation of enhanced in situ biodenitrification in a fractured aquifer, Chem. Geol., 2016, 425, 52–64 CrossRef.
- S. Y. Choi, J. Choo, H. Chung, W. Sohn and K. Kim, Feasibility of Fourier Transform (FT) infrared spectroscopy for monitoring heavy water concentration in pressurized heavy water reactor, Vib. Spectrosc., 2003, 31(2), 251–256 CrossRef.
- V. SYu and F. G. Prendergast, Water (H2O and D2O) molar absorptivity in the 1000–4000 cm−1 range and quantitative infrared spectroscopy of aqueous solutions, Anal. Biochem., 1997, 248(2), 234–245 CrossRef , available from: https://www.sciencedirect.com/science/article/pii/S0003269797921369.
- T. A. F. Michael Falk, Infrared Spectrum and Structure of Liquid Water, Can. J. Chem., 1966, 44(14), 1699–1707 CrossRef.
- J. J. Max and C. Chapados, Isotope effects in liquid water by infrared spectroscopy. IV. No free OH groups in liquid water, J. Chem. Phys., 2010, 133(16), 4626–4642 CrossRef PubMed.
- IAEA, Introduction to Body Composition Assessment Using the Deuterium Dilution Technique with Analysis of Urine Samples by Isotope Ratio Mass Spectrometry, IAEA Hum. Heal. Ser. no. 13, 2011, vol. 12, p. 84, available from: http://www-pub.iaea.org/books/iaeabooks/8370/Introduction-to-Body-Composition-Assessment-Using-the-Deuterium-Dilution-Technique-with-Analysis-of-Urine-Samples-by-Isotope-Ratio-Mass-Spectrometry Search PubMed.
- A. Rein and F. Higgins, Application of the Agilent 4500 Series FTIR to the Stable Isotope Technique for Assessing Intake of Human Milk in Breastfed Infants, 2014 Search PubMed.
- IAEA, Human health series to Assess Intake of Human Milk in Breastfed Infants, IAEA Hum. Heal. Ser. no. 7, 2010, vol. 7, p. 81, available from: http://www.iaea.org/books Search PubMed.
- S. Heinze, B. Vuillemin and P. Giroux, Application of ATR-FTIR spectroscopy in quantitative analysis of deuterium in basic solutions, Analusis, 1999, 27(6), 549–551 CrossRef , available from: http://analusis.edpsciences.org/10.1051/analusis:1999133.
- B. H. Stuart, Infrared Spectroscopy: Fundamentals and Applications, Methods, 2004, p. 224, available from: http://doi.wiley.com/10.1002/0470011149 Search PubMed.
- B. C. Smith, Infrared Spectral Interpretation, CRC Press, 1999 Search PubMed.
- Y. Maréchal, Infrared spectra of water. I. Effect of temperature and of H/D isotopic dilution, J. Chem. Phys., 1991, 95(8), 5565–5573 CrossRef.
- G. Badino, Cave temperatures and global climatic change, Int J Speleol, 2004, 33, 103–113 CrossRef.
- K. J. R. Rosman and P. D. P. Taylor, Isotopic Compositions of Elements, 1998, pp. 1593–1607 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |