 Open Access Article
Open Access ArticleFactorial design analysis of parameters for the sorption-enhanced steam reforming of ethanol in a circulating fluidized bed riser using CFD†
Kiattikhoon Phuakpunka,
Benjapon Chalermsinsuwan *bcd,
Sompong Putivisutisakde and
Suttichai Assabumrungrat
*bcd,
Sompong Putivisutisakde and
Suttichai Assabumrungrat ad
ad
aCenter of Excellence in Catalysis and Catalytic Reaction Engineering, Department of Chemical Engineering, Faculty of Engineering, Chulalongkorn University, Bangkok, Thailand 10330
bFuels Research Center, Department of Chemical Technology, Faculty of Science, Chulalongkorn University, Bangkok, Thailand 10330. E-mail: Benjapon.C@chula.ac.th
cCenter of Excellence on Petrochemical and Materials Technology, Chulalongkorn University, Bangkok, Thailand 10330
dAdvanced Computational Fluid Dynamics Research Unit, Chulalongkorn University, Bangkok, Thailand 10330
eDepartment of Mechanical Engineering, Faculty of Engineering, Chulalongkorn University, Bangkok, Thailand 10330
First published on 5th July 2018
Abstract
The sorption-enhanced steam reforming of ethanol (SESRE) has recently been reported as a novel process for hydrogen (H2) production. SESRE can operate well on a Ni-based catalyst with dolomite as a sorbent in packed-bed reactors. In this study, the circulating fluidized bed (CFB) concept was proposed to obtain higher productivity and continuous operation of SESRE. Particular focus was directed to the design and selection of suitable operating conditions of the CFB riser. Two-dimensional transient models using the Euler–Euler approach and the kinetic theory of granular flows were applied to investigate the H2 production performance from a pilot-scale riser. The 2k full factorial design method was utilized to examine the significances of five specific parameters, namely, the riser diameter, inlet temperature, catalyst-to-sorbent ratio, solid flux, and inlet gas velocity on two response variables, namely, H2 purity and H2 flux. From the ANOVA results, either the main effect or the interactions of each parameter were shown to be significant on both the H2 purity and the H2 flux, particularly the riser diameter and the solid flux. For optimizing the operation and reaction parameters, the best case was the system with riser diameter of 0.2 m, inlet temperature of 600 °C, catalyst-to-sorbent ratio of 2.54 kg kg−1, solid flux of 200 kg m−2 s−1, and gas velocity of 3 m s−1, obtaining H2 purity of 91.30% on a dry basis with a significantly high H2 flux of 0.147 kg m−2 s−1. The hydrodynamics showed that SESRE reached breakthrough within the bottom dense zone. However, incomplete conversion occurred in the core of the riser because of the very dilute bed.
1. Introduction
Nowadays, global fossil-fuel reservoirs are drastically depleting, while the world's energy-consumption tendency is constantly increasing. Hydrogen fuel is a promising alternative source and has drawn widespread attention because it is a clean energy source and can be derived from renewable energy sources. At the end use, when hydrogen (H2) is combusted in internal engines or fed into fuel cells, only water is the end product without the emission of carbon dioxide (CO2), a major cause of global warming.1 However, hydrogen cannot yet be claimed to be totally renewable or green because its large-scale sources and production currently come from petroleum industries.Hydrogen is the third most abundant element on Earth. Most natural hydrogen does not exist in the form of H2 gas, but is found in organic compounds. There are many organic compounds that can be converted into H2 via many processes, e.g., dehydrogenation, gasification, and steam reforming. Steam reforming is the most effective process to produce H2 on a large scale. Conventional industrial-level hydrogen production typically uses methane (CH4), in natural gas or in tail gas from the refinery process, as a raw material via the steam methane reforming (SMR) process.
Ethanol (EtOH) is another excellent feedstock for hydrogen production via the steam reforming process. Ethanol is a renewable organic compound that can be derived from the fermentation of biomasses. Thus, ethanol can potentially replace methane from petroleum industries for H2 production. The pathways for the steam reforming of ethanol (SRE) are dependent on the types of catalyst (e.g., Ni-, Pt-, Pd-, or Co-based catalysts) and their operation conditions.2–8 Through the pathway of ethanol reforming using the Ni-based catalyst, EtOH is first converted to acetaldehyde (CH3CHO) through an ethanol dehydrogenation (ETD) reaction, as expressed in reaction (1). Then, CH3CHO is converted to CH4 through an acetaldehyde decomposition (ACD) reaction, as expressed in reaction (2).9–13
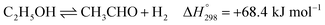 | (1) |
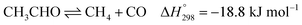 | (2) |
In practice, CH3CHO is an unstable intermediate and almost totally converted to CH4. Thus, ethanol reforming with excess steam obtains an EtOH conversion of about 100%.8,12–14 In addition, the ETD and ACD reactions can be combined in the ethanol decomposition (EDC) reaction, in which EtOH is directly converted to CH4, CO, and H2, as shown in reaction (3).15,16
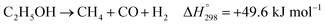 | (3) |
Furthermore, steam can react directly with EtOH in another pathway to obtain CH4, similar to the EDC reaction. This reaction is called ethanol decomposition with steam (EDC/S), as expressed in reaction (4).17
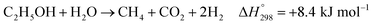 | (4) |
After ethanol is nearly completely converted to methane, methane could be further reformed with steam, similar to the conventional SMR process, via three reversible reactions: two involving steam methane reforming reactions (eqn (5) and (6)) and a water-gas shift (WGS) reaction (eqn (7)).
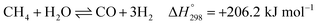 | (5) |
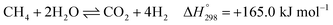 | (6) |
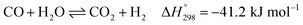 | (7) |
Overall, EtOH is converted to mainly CO2 and H2 (with minor amounts of CO and unreacted CH4) in the pathway involving the Ni-based catalyst. Notably, the main reactions of SRE can be summarized as the “overall reaction of SRE,” as shown in reaction (8).
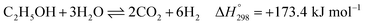 | (8) |
The overall reforming reactions of both ethanol and methane are strongly endothermic. Hence, the reactor system must be operated at high temperature. By considering thermodynamic equilibrium at 750 °C, 1 atm, and a steam/ethanol molar ratio (S/E) of 6, the maximum H2 production can approximately be only 70% H2 on a dry basis at 100% conversion of EtOH. The other produced gases consist of 19% CO2, 8% CO, and 3% CH4.18 To further purify H2, the effluent gas must pass through additional separation units, such as a pressure swing adsorption (PSA) unit or amine scrubbing unit.19,20
On integrating sorbents in the reformers, the produced CO2 from reforming can be adsorbed, shifting forward the equilibrium of the reforming reactions, as shown in reactions (5)–(7). The first advantage of this sorption enhancement is an increase in conversion of CH4 (completely converting both EtOH and CH4) and the production of more H2. Second, capturing CO2 from the effluent gas can afford high purity H2, reaching 99% on a dry basis.14,19,21–23 Thus, the separation units are unnecessary in SESRE processes. Other advantages are the use of lower operation temperature and lower energy consumption for exothermic adsorption and shifting of the reforming reactions. The reforming of EtOH with CO2 sorption is called the sorption-enhanced steam reforming of ethanol (SESRE). However, a limitation of SESRE is the discontinuous performance when the sorbent is almost full of captured CO2. The sorbent then has to release CO2 before it can be used in reprocessing in SESRE.
Several types of sorbent have been used and developed for CO2 capture, e.g., natural or pure metal oxides (e.g., CaO), synthesis metal oxides (e.g., CaxAlyOz and CaO nanoparticles), alkali mixed metal oxides (e.g., Li4SiO4), hydrotalcite-like materials (HTCls), and modified sorbents (e.g., Ni–CaO–Al2O3 multifunctional catalyst/sorbent). The CO2 capacity, rate of CO2 caption, and stability of these sorbents are important properties to increase the performance of SESRE.3,9,11,13,19,24–27 The advantages of natural CaO sorbents, such as dolomite and limestone, are that they are inexpensive, easy to find, and have higher CO2 capacity than other sorbents. However, CaO sorbents have lower thermal cyclic stability than the other sorbents. The reversible reaction involving CO2 capture by CaO (carbonation) and the reverse reaction (decarbonation) is shown in reaction (9).
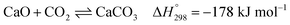 | (9) |
Limestone consists mostly of CaO, while dolomite contains mainly CaO and MgO. MgO reduces the sintering of CaO and endows dolomite higher stability for CO2 capture, although decreasing the amount of CaO reduces the CO2 capacity of dolomite more than that of limestone.18,28 Thus, dolomite is chosen for the SESRE processes, which require a regeneration step to remove captured CO2. Even though SESRE requires energy for sorbent regeneration, it has higher thermal efficiency (ratio of hydrogen energy to the summation of energy input plus ethanol energy) (about 0.45–0.82) than that of SRE (about 0.33–0.61).11,29 Wu et al.10 reported the energy consumption per H2 mole of SESRE of about 169 kJ molH2−1 and thermal efficiency equal to 0.57 in a process without energy recovery operated at 500 °C and at an S/E of 8.
In SESMR/SESRE experiments, bubbling bed reactors as well as the fixed bed reactors could produce high purity H2.30–35 However, the bubbling bed reactor had lower pressure drop and better reaction distribution throughout the bed than the fixed bed. However, SESRE operating in the bubbling bed reactor still needs to stop the process to perform a regeneration step when the SESRE reaches breakthrough by reaching the CO2 capture limit in the sorbent.
Recently, a circulating fluidized bed reactor (CFBR) was developed and expected to be useful as a reactor for large-scale hydrogen production because of its capability to be used with higher gas velocity and to simultaneously enable regeneration inside the reactor.36 Furthermore, CFBR could provide higher H2 productivity and lower pressure drop than the bubbling bed reactor.37 A general CFBR system consists of four main parts38 as follows:
(1) Riser: gas and solids come enter at the riser bottom. Solid particles are blown upward and removed off with the gas at the riser top.
(2) Cyclone: solid particles are separated from the gas and fall out at the cyclone bottom.
(3) Downer: solid particles from the cyclone fall and move out at the downer bottom. This unit could act as another reactor.
(4) Solid return system: solid particles return to the riser bottom.
Because SESRE is a very fast reaction, an increase in the feed (i.e., operating with a higher velocity of gas) can enable greater H2 production. The reformer is able to operate in the riser section, whereas the regenerator needs sufficient residence time to complete decarbornation and remove the undesired CO2. Thus, the downer section should act as a bubbling bed reactor for sorbent regeneration. The performance of H2 production in this CFBR system depends on the operation in the riser that performs the SESRE. However, the riser consists of a dilute zone and dense zone, which might lead to an incomplete SESRE. The CFBR efficiency for SESRE still has not been unveiled; thus, the riser design for SESRE will be further studied.39–41
As the CFBR system must be experimented at least on a pilot scale with appropriate design and operation, each trial of the experiments can waste expensive resources, particularly expensive materials such as the Ni-based catalyst. Consequently, computational fluid dynamics (CFD) have been utilized for the initial design of an optimal system before testing in real operations. The CFD simulations with appropriate models can give high accuracy and detailed results and can reduce the time and resources needed for the experiments. The hydrodynamics model combined with the kinetic models of SESRE can be simulated either in a 2D or 3D system. Even though the results from a 3D model are more accurate than those from a 2D model, the 3D model has much more computational demand and takes more time than the 2D model, particularly for transient simulations. In addition, in many cases, particularly with a cylindrical geometry, such as the riser, the 2D model provides results with sufficient accuracy.9,10,42–45
The main purpose of this study was to investigate the feasibility of SESRE for hydrogen production in a pilot-scale CFBR system using computations to reduce the costs from further experiments. In this study, the 2D geometry of the riser was utilized to design a suitable pilot-scale riser for hydrogen production via SESRE by studying the expected design and reaction parameters, including the riser diameter (id), inlet temperature (Tin), catalyst-to-sorbent ratio (Cat/Sb), solid flux (Gs), and gas velocity (U). All the simulations were solved by a commercial CFD program, ANSYS® Fluent® 15.0.7. The H2 flux and H2 purity of the effluent gas from the simulations were used as response variables in a 2k full factorial design analysis. The optimum case would then be predicted and chosen to analyze the hydrodynamics in that system.
2 Methodology
2.1 Computational fluid dynamics
Computational fluid dynamics (CFD) is a modern branch of hydrodynamics using algorithms and numerical methods, such as discretization methods, to solve complex fluid problems. CFD is an art of considering models of conservation combined with correlation equations (constitutive equations) and other models, such as chemical kinetic models.Fluidization is a gas–solid contacting phenomenon. There are two main approaches for fluid-particle multiphase flow modeling: the Euler–Euler approach and the Euler–Lagrange approach.46,47 The Euler–Euler model is also called the granular flow model (GFM) in a gas–solid flow. The Eulerian framework is considered for all phases and treats solid particles like a fluid. The kinetic theory of granular flow (KTGF) that represents kinetic energy oscillation must be applied for any solid particle phase.48 This Euler–Euler model with KTGF is suitable and widely used for fluidization systems that have a large amount of solid particles.30,31,38,40,42,43,49–55
There are many research studies that used the Euler–Euler approach with KTGF for the simulations of fluidization either without a reaction (cold flow)50,56–58 or with a reaction (hot flow).30,31,40,42,43,49,51–54,59–61 The cold flow validations were presented in some studies to prove the suitability of the models using the Euler–Euler approach with KTGF and were used as a base case for further hot flow simulations. All of the cold flow validations showed good agreement with the experiments.56–58
The SMR kinetics developed by Xu and Froment62 and the carbonation kinetics developed by Sun et al.64 were validated in hot flow fluidization with good results.57 Then, these were continuously applied in almost all publications from the NTNU research group.30,31,40,42,49,51–54,59 In addition, this SMR kinetics approach was also validated in other studies with very good results. Such as showing that the percentage of H2 in effluent gas had a deviation of less than 0.5%, as reported by Johnsen et al.33 and a deviation of about 3.5% for SMR and 1% for SESMR, as reported by Chen et al.61 This might prove that both kinetic models were suitable for the future studies of fluidization with SESMR using a Ni-based catalyst and dolomite. Several kinetic models of SRE on a Ni-based catalyst were applied by some researchers,9–12,15,17 but unfortunately there was no application with fluidization. The only kinetics approach for SRE applied on a typical Ni-based catalyst, such as Ni–Al2O3,15,17 is described next. The concerning conservation equations and the constitutive equations of the Euler–Euler model with KTGF chosen in this study are summarized in Tables S1 and S2,† respectively.
Model A. De-Souza et al.15 studied simulations of SRE using the favorable kinetic models of the SMR reactions (reactions (11)–(13)) together with the kinetic model of the EDC reaction (reaction (10)). Thus, this SRE approach included four reactions as follows.
| EDC: C2H5OH → CH4 + CO + H2 | (10) |
| bSMR: CH4 + H2O ⇌ CO + 3H2 | (11) |
| gSMR: CH4 + 2H2O ⇌ CO2 + 4H2 | (12) |
| WGS: CO + H2O ⇌ CO2 + H2 | (13) |
The power law kinetic rate of EDC is an irreversible first order rate derived by Sun et al.16 as follows.
| rEDC = kEDCpEtOH | (14) |
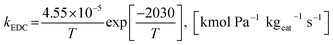 | (15) |
The kinetic models of the SMR reactions widely applied in many research studies were developed by Xu and Froment.62 These reaction rates are reversible and non-linear as follows:
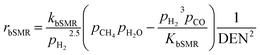 | (16) |
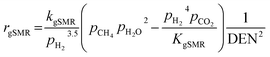 | (17) |
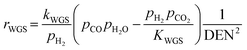 | (18) |
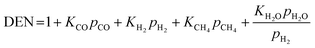 | (19) |
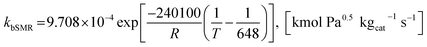 | (20) |
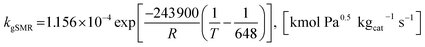 | (21) |
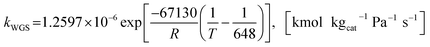 | (22) |
Also, the adsorption equilibrium constants of species k are expressed as follows.
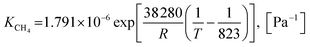 | (23) |
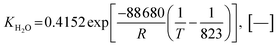 | (24) |
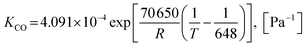 | (25) |
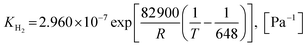 | (26) |
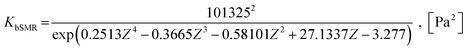 | (27) |
| KgSMR = KbSMRKWGS, [Pa2] | (28) |
| KWGS = exp(−0.29353Z3 + 0.63508Z2 + 4.1778Z + 0.31688), [—] | (29) |
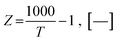 | (30) |
Although this SRE kinetics model is a combination of different experiments, both were investigated on Ni-based catalysts and the results in the study of De-Souza et al.15 satisfied these models.
Model B. This alternative model was developed by Mas et al.17, who studied the kinetics of SRE and derived their own kinetic model. Their model involved four reactions, as follows.
| EDC: C2H5OH → CH4 + CO + H2 | (31) |
| EDC/S: C2H5OH + H2O → CH4 + CO2 + 2H2 | (32) |
| bSMR: CH4 + H2O ⇌ CO + 3H2 | (33) |
| gSMR: CH4 + 2H2O ⇌ CO2 + 4H2 | (34) |
The reaction rates of these SRE reactions are expressed as follows.
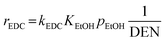 | (35) |
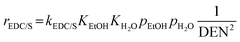 | (36) |
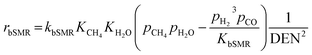 | (37) |
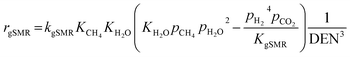 | (38) |
| DEN = 1 + KEtOHpEtOH + KH2OpH2O + KCH4pCH4 | (39) |
The rate constants of reaction i are defined as follows.
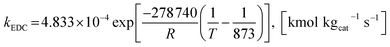 | (40) |
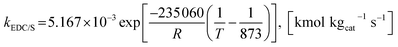 | (41) |
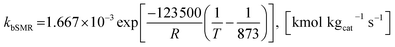 | (42) |
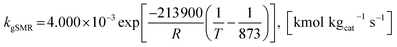 | (43) |
Also, the adsorption equilibrium constants of species k are expressed as follows.
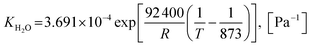 | (44) |
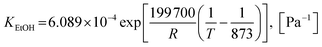 | (45) |
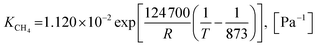 | (46) |
Lastly, the equilibrium constants of reactions, KbSMR and KgSMR could be determined according to eqn (27) and (28), respectively.
| rcarb = kcarb(pCO2 − pCO2,eq)nS0(1 − XCaO) | (47) |
(1) For T > 1173.15 K (Abanades et al.65)
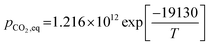 | (48) |
(2) For T ≤ 1173.15 K (Johnsen et al.32)
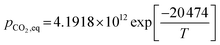 | (49) |
The rate constant of carbonation (kcarb) and the degree of partial pressure (n) depend on the amounts of CO2 as follows.
(1) For (pCO2 − pCO2,eq) > 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa
000 Pa
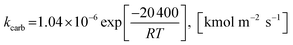 | (50) |
(2) For 0 < (pCO2 − pCO2,eq) ≤ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa
000 Pa
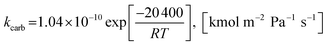 | (51) |
If (pCO2 − pCO2,eq) ≤ 0 Pa, CO2 is released via decarbonation.
2.2 System and properties
Fig. 1 shows a typical design of the riser according to Kunii and Levenspiel.36 The riser had an inlet of feed gas at the bottom section, a 0.05 m diameter channel for the inlet solid at the right, and an outlet for the mixture at the top. The channel of the inlet solid was 0.075 m above the bottom. The feed gas included EtOH and steam, while the inlet solid included two individual phases, namely, catalyst phase and sorbent phase. The SRE was performed with the catalyst phase, while the carbonation was performed with the sorbent phase. For the catalyst phase, the Ni-based catalyst properties were set and assumed to have uniform size and density. For the sorbent phase, the feed sorbent was fresh dolomite, whose properties were set and assumed to be uniform. The fresh dolomite was assumed to contain 60% CaO and 40% of MgO by weight. The properties for each solid phase are presented in Table S3.†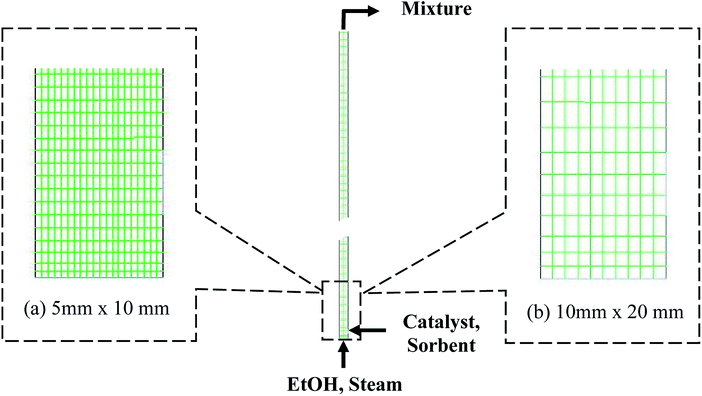 | ||
| Fig. 1 The system of the riser and the meshes with different cell sizes of the domain: (a) the smallest size and (b) the largest size. | ||
SESRE would benefit from operating in this CFBR system if the results from the chosen system satisfied these constraints/goals: (1) no solid accumulation in the riser; (2) the effluent gas should contain high H2 purity (about 94–96%) on a dry basis as a packed-bed reactor and achieve equilibrium,18 while the H2 flux should be as high as possible; and (3) CaO conversion (XCaO) at the solid outlet should be lower than 28%, which is the stable maximum capacity of dolomite after steady re-cycling.32
2.3 Simulation method and analysis
The 2D geometry of the riser and its different computational domains, as shown in Fig. 1, was drawn by ANSYS® DesignModeler™. The domains were meshed uniformly by ANSYS® Meshing™ with four different cell sizes for mesh refinement. Then, the models were calculated in the domains via ANSYS® Fluent®. The kinetic rates of SRE and carbonation were derived to be compatible in Fluent® by writing in C-language user define functions (UDFs). These rates were compiled and returned values as volumetric rates. The calculations were transient for 20 s of operation with a time step of 1 × 10−3 s. Initially, there was only inert N2 in the domain. All the gas and solid feeds entered through their inlet boundaries in the normal direction and were input in the form of velocities and volume fractions of each phase but with the same temperature. The wall surface was set as no-slip and under adiabatic conditions. The effluent gas was discharged to the atmosphere. The other phase and system properties were set as shown in Table S3.†Because there were many parameters that could mutually affect the system performance of H2 production, a statistical method, such as 2k full factorial design, was applied to analyze the significance of each single parameter (main effect) and their interactions were studied via analysis of variance (ANOVA). The five concerning parameters were sufficiently chosen for analyses with 32 runs of simulation. The studied parameters included design parameters (the gas inlet velocity, the solid flux, and the diameter of riser) and reaction parameters (the catalyst-to-sorbent ratio and the temperatures of the inlets). Two levels of these parameters and other system properties are shown in Table S4.† The H2 flux and the H2 purity, which represented the performance of H2 production, were chosen as the response variables in ANOVA. The regression models from ANOVAs can help optimizing the values of the parameters that give the best performance of SESRE in this CFBR system.
3. Results and discussion
3.1 Model validations
There were two sections of validations performed in this study: cold flow validation and hot flow validation. The cold flow validation was performed to test all the chosen hydrodynamic models listed in Tables S1 and S2.† In hot flow validation, the UDFs of the kinetic rates were compiled into simulations to test the chosen kinetic models.| Bed height [m] | |||
|---|---|---|---|
| Lin et al. | Sánchez et al. | This study | |
| U = 0.320 m s−1 | 0.12 | 0.145 | 0.130 |
| U = 0.458 m s−1 | 0.15 | 0.160 | 0.155 |
| U = 0.641 m s−1 | 0.21 | 0.185 | 0.182 |
| U = 0.892 m s−1 | 0.23 | 0.225 | 0.234 |
In the SMR/SESMR validations, the SMR kinetic model of Xu and Froment62 was used to validate the experimental results reported by Johnsen et al.33, as shown in Table 2. At first, only the SMR kinetics was compiled for SMR validation. Then, additional carbonation kinetics was employed for SESMR. A comparison of the effluent gas compositions between simulations and the experiments showed that most of them had very good agreement, with only a slight deviation in CO and CO2 in SMR. It should be noted that although both the kinetic study by Xu and Froment62 and the experiment conducted by Johnsen et al.33 were investigated on Ni-based catalysts, but the catalysts were differently synthesized. Differences in the Ni content, structure, and other physicochemical properties could have caused the deviation of the CO and CO2 compositions.
| H2 [% dry] | CH4 [% dry] | CO [% dry] | CO2 [% dry] | ||
|---|---|---|---|---|---|
| SMR | Johnsen et al. | 73.4% | 6.0% | 8.0% | 12.0% |
| This work | 74.3% | 6.4% | 2.7% | 16.6% | |
| SESMR | Johnsen et al. | 98.0% | 1.0% | 0.5% | 0.5% |
| This work | 97.7% | 1.6% | 0.4% | 0.3% |
Table 3 shows SRE/SESRE validations compared with the experimental results and equilibrium, as reported by Olivas et al.18 Two different kinetic models were used for SRE: model A, which combined the kinetics model developed by Sun et al.16 and that developed by Xu and Froment,62 and model B, which used the kinetics model developed by Mas et al.17 Next, for SESRE, the carbonation kinetic model was compiled mutually with each SRE model. The results indicated that validations using model A had satisfactory agreement with both the experiments and equilibriums of both SRE and SESRE with only a minor deviation in CO composition, which might be because of the same reason described in the previous paragraph. However, when using model B, the SRE validation showed significant differences in both CO and CO2 compositions. In addition, SESRE simulation using model B showed gas compositions exactly the same as the compositions from the SRE simulation and minor carbonation occurred at this operating condition. The drastic deviations in CO and CO2 compositions and CO2 capture when using model B was because the SRE kinetics developed by Mas et al.17 did not involve the WGS reaction, which would have further converted CO to CO2. Thus, model A was used for investigating the SRE kinetics in this study.
| H2 [% dry] | CH4 [% dry] | CO [% dry] | CO2 [% dry] | EtOH [% dry] | ||
|---|---|---|---|---|---|---|
| SRE | Olivas et al. | 64.7% | 0.7% | 4.6% | 30.0% | 0.0% |
| Equilibrium | 69.6% | 3.3% | 8.3% | 18.7% | 0.0% | |
| Sim. using model A | 69.2% | 2.2% | 14.4% | 14.2% | 0.0% | |
| Sim. using model B | 62.5% | 4.2% | 33.3% | 0.1% | 0.0% | |
| SESRE | Olivas et al. | 96.2% | 0.0% | 3.8% | 0.0% | 0.0% |
| Equilibrium | 94.1% | 1.8% | 1.6% | 2.5% | 0.0% | |
| Sim. using model A | 98.5% | 0.5% | 0.6% | 0.4% | 0.0% | |
| Sim. using model B | 62.5% | 4.2% | 33.3% | 0.1% | 0.0% |
3.2 Time averaging and mesh refinement
Because flows and movements in fluidized bed reactors have some fluctuation, time-dependent simulations have to be performed to ensure that the system reaches the quasi-steady state condition. Time-averaged results should be considered from time ranges after the full development. Fig. 2 shows the case of the fluctuation in time dependence from the simulation of run 20 as an example, for which the riser diameter was 0.2 m, inlet temperature was 600 °C, catalyst-to-sorbent ratio was 2.54 kg kg−1, gas velocity was 4 m s−1, and the solid flux was 200 kg m−2 s−1. In this case, the H2 flux and area-averaged H2 purity at the exit of the riser were plotted every 0.1 s. And became stable after approximately 3 s. In other runs of this study, the fluctuation stabilized after 3–5 s. Thus, a time-averaged range of 10–20 s is used with the further simulation results in this study.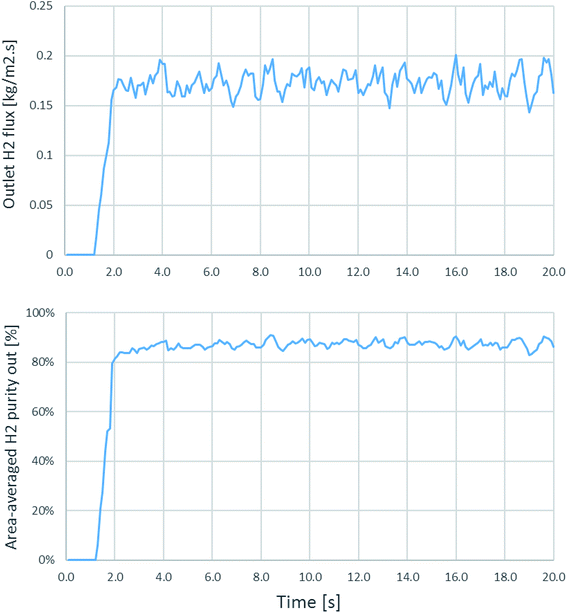 | ||
| Fig. 2 The outlet H2 flux and the area-averaged H2 purity at the outlet as a function of time in an example case of id = 0.2 m, Tin = 600 °C, Cat/Sb = 2.54, U = 4 m s−1, and Gs = 200 kg m−2 s−1. | ||
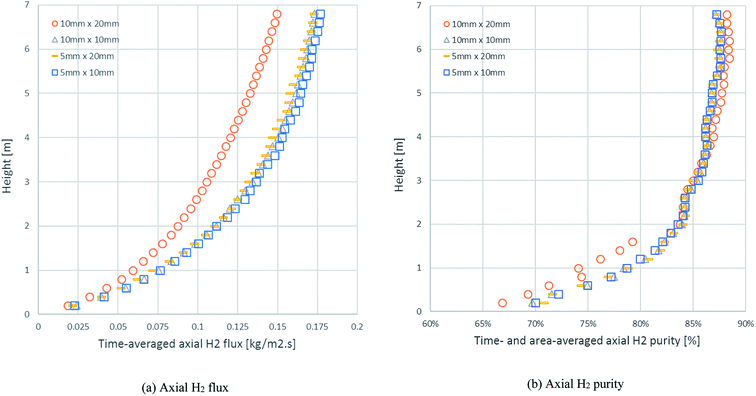
In the same example case (run 20), the mesh refinement was investigated through the axial profiles of the time-averaged H2 flux and time- and area-averaged H2 purity with different sizes of cell (ΔxΔy), as displayed in Fig. 3. The results of both the H2 flux and the H2 purity showed that the 10 mm × 20 mm cell size differed from the others and was not precise. In the case of the area-averaged H2 purity, as shown in Fig. 3b, the 10 mm × 20 mm cell size fluctuated significantly more than the other sizes with an SD of 1.74–10.09% for H2 purity (1.38–8.25% for the 5 mm × 10 mm cell size, 1.31–8.23% for the 10 mm × 10 mm cell size, and 1.34–8.18% for the 5 mm × 20 mm cell size). Although the other cell sizes showed good agreement with each other, the 5 mm × 10 mm size was not chosen because the higher number of cells required additional calculating time. Lastly, the 5 mm × 20 mm and the 10 mm × 10 mm cell sizes had the same number of cells, but the 5 mm × 20 mm size was chosen for further simulations because the radial profiles in the riser clearly had more variances than the axial profiles.
3.3 Parametric analysis with the 25 factorial design
Table S5† shows the area-averaged values of the H2 flux, H2 purity, and CaO conversion near the outlet with a time-average of 10–20 s in all 32 runs. According to the discussion by Johnsen et al.32, dolomite has decreased CaO capacity every cycle, until it steadies to 28% CaO conversion. In this study, there was no run in which CaO conversion reached 28%. Thus, dolomite could be circulated in this CFBR system for SESRE in these ranges of the parameters. Considering the H2 flux and the H2 purity as response variables, the lowest H2 flux (0.0691 kg m−2 s−1) and the lowest H2 purity (56.47% on a dry basis) occurred in the same run, i.e., run no. 14. On the contrary, the highest H2 flux was 0.174 kg m−2 s−1 when operated in run 20, but the H2 purity was only 87.57% in this case, whereas the highest H2 purity was 94.07% in run 27, but the H2 flux dropped to 0.134 kg m−2 s−1. Hence, statistical analysis, such as ANOVA, was used for investigating the best case and for sensitivity analyses. In the ANOVA of the H2 flux and the H2 purity, the riser diameter (id), the inlet temperature (Tin), the catalyst-to-sorbent ratio (Cat/Sb), the solid flux (Gs), the gas velocity (U), the H2 flux, and the H2 purity were coded as A, B, C, D, E, R1, and R2, respectively. Significantly, the main effects and interactions, which had a P-value less than 0.05,67 of both the H2 flux and the H2 purity were descending as sorted by the F-values or P-values, as shown in Tables S6 and S7.†As shown in Table S6,† all the main effects had significance to the H2 flux. The catalyst-to-sorbent ratio (C), the solid flux (D), the riser diameter (A), the inlet temperature (B), and the gas velocity (E) were very highly significant, with P-values < 0.0001, in descending order. Furthermore, the most significant interactions were AD, DE, and AE, with AD being the most significant. As shown in Table S7,† almost all the main effects had significance on the H2 purity, except for the inlet temperature (B). However, the interactions of the inlet temperature (AB, AD, BD, and ABD) also had a significant effect on the H2 purity. Moreover, the solid flux (D), the riser diameter (A), the gas velocity (E), and the catalyst-to-sorbent ratio (C), in descending order, were highly significant, with P-values < 0.0001. These results indicated that the riser diameter (A) and the solid flux (D), both of which are design parameters, were the key parameters for H2 purity in these ranges of the system.
From the ANOVAs, regression models for predicting the H2 flux and the H2 purity were determined using eqn (52) and (53), respectively.
| H2 flux = 0.126700 + 0.0095A − 0.0083B + 0.0134C + 0.0100D + 0.0041E − 0.00468AD + 0.00353AE + 0.00362DE | (52) |
| H2 purity = 83.40 + 3.88A + 2.97C + 4.03D − 3.33E + 1.96AB − 2.58AD + 2.04BD − 1.92ABD | (53) |
In additions, the sensitivity analyses were performed. The main effects and interactions on the H2 flux and the H2 purity were plotted, as shown in Fig. S1 and S2,† respectively. The slopes indicate either positive or negative effects on the response variable, while the steepness of each slope as well as the coefficients in the regression models indicate the significant order.
In the case where the H2 flux is the response variable, as shown in Fig. S1a,† all of the main effects showed a positive trend, except for the inlet temperature (B), according to their coefficients in the regression model. To obtain the most suitable and optimum condition, the catalyst-to-sorbent ratio (C) should be preferably high (2.54 kg kg−1), but the inlet temperature (B) should be preferably low (600 °C). Even though SESRE had been found to perform well at around 600–700 °C,18,28 SESRE had a breakthrough of sorption enhancement and performed similar to SRE at about 750 °C.28 At 700 °C, the sorbent would lose its CO2 capture ability and instead would more closely turn into a decarbonation condition. Hence, the carbonation of CaO, which is an exothermic reaction, prefers operation at a much lower temperature under the breakthrough temperature. The positive direction of the solid flux (D) indicates that the low flux (100 kg m−2 s−1) gave insufficient contact between the feed gas and the catalyst/sorbent particles. Considering the riser diameter (A), the larger diameter leads to a greater H2 flux because the large area of the gas inlet allows for an increased feed, even though the dilute region of the solid might be wider. Finally, an increase in the gas velocity (E) also increased the feed, despite the lower residence time. However, as SESRE has very fast kinetics, it had sufficient time to approach system equilibrium.
Considering the main effects on the H2 purity, as shown in Fig. S2a,† the solid flux (D), the riser diameter (A), and the catalyst-to-sorbent ratio (C) had positive effects on the H2 purity as well as on the H2 flux. This indicated that at the high levels of these parameters (id = 0.2 m, Gs = 200 kg m−2 s−1, and Cat/Sb = 2.54 kg kg−1), the gas-catalyst/sorbent contact was better than at the low levels. Such was the case for the H2 flux, as shown in Fig. S1a,† which confirmed that a solid flux of 100 kg m−2 s−1 gave lesser amount of catalyst/sorbent to contact with the feed when compared with a solid flux of 200 kg m−2 s−1. Also, the catalyst-to-sorbent ratio of 0.58 kg kg−1 had insufficient catalyst to produce more H2, although the reforming was enhanced by CO2 capture. Only the gas velocity (E) had a negative effect on the H2 purity, which was opposed to the H2 flux. This is because higher gas velocity (4 m s−1) might increase the feed, but the residence time is reduced, leaving it far from SESRE equilibrium.
Fig. S1b and S2b† show similar interactions between the solid flux and the riser diameter (AD) and their influence on the H2 flux and the H2 purity, respectively. When the solid flux (D) was considered constant, the lines for the high riser diameter (A+) gave higher values for both the H2 flux and the H2 purity than the lines for the low riser diameter (A−). This was because their main effects (A and D) were positive. Thus, at their high levels, they mutually enhanced both the H2 flux and the H2 purity. The slopes of all the lines for the riser diameter (A+ and A−) still had the same positive direction as the main effect (D), but with slight changes in the steepness. This indicated that the interaction (AD) was less effective than the main effects (D), according to their P-values listed in Tables S6 and S7† and their regression coefficients in eqn (52) and (53). However in case of high levels of the solid flux (D+), the more positive effect of the high riser diameter (A+) over the low riser diameter (A−) was less than that for the low levels of the solid flux (D−). In other words, when the diameter of riser was larger, the increase in the solid flux was less effective (or less significant) than with the smaller diameter riser. This was in accordance with the small negative regression coefficients of their interaction (AD) in eqn (52) and (53), which decrease the values of both the H2 flux and the H2 purity when both the solid flux and the riser diameter are positive.
Considering the interactions of the gas velocity (E) on the H2 flux, as shown in Fig. S1b and S1c,† because all of the main effects (A, D, and E) were positive, their interactions (AE and DE) were more positive on the H2 flux. When the solid flux (D) and the riser diameter (A) were at the preferably high, as previously discussed in Fig. S1a,† and were enhanced with higher gas velocity (D+E+ and A+E+), the H2 flux becomes much higher because the increase in the gas velocity increases the feed as well. However, when the riser diameter (A) was the smallest, the interactions with the gas velocity (A−E− and A−E+) were very close, i.e., it barely affected the H2 flux. This indicated that although the higher gas velocity increases the feed, the residence time would be insufficient if the riser diameter was too small. These very small deviations also indicated that the interactions (AE and DE) were less effective than the main effects (A and D), corresponding to their high P-values in Table S6† and their very small regression coefficients in eqn (52).
Lastly, considering the interaction of the inlet temperature (B) on the H2 purity, as shown in Fig. S2b and S2c,† the line for the high inlet temperature (B+) crosses the line for the low inlet temperature (B−) when both interact with the solid flux (D) and the riser diameter (A). This indicates that in this range of inlet temperature (600–700 °C), there was no clear favorite temperature for obtaining higher H2 purity. Moreover, the minor deviations in the steepness of the interactions (AD, BD, and AB) indicated that these interactions were less effective than the main effects (A and D), consistent with their P-values in Table S7† and their regression coefficients in eqn (53).
Table 4 shows optimization of the H2 flux from the regression models in eqn (52) prior to optimizing the H2 purity from eqn (53). The maximum H2 purity was predicted to be only 86.53% on a dry basis, while the H2 flux reached 0.174 kg m−2 s−1 in the riser with 0.2 m diameter, inlet temperature of 600 °C, catalyst-to-sorbent ratio of 2.54 kg kg−1, solid flux of 200 kg m−2 s−1, and gas velocity of 4 m s−1. These results from the prediction conformed very well to the results from the simulation with these values of parameters, i.e., run 20, where the H2 purity and the H2 flux were 87.57% on a dry basis and 0.174 kg m−2 s−1, respectively.
| Factor1 | A | B | C | D | E | R1 | R2 |
|---|---|---|---|---|---|---|---|
| id [m] | Tin [°C] | Cat/Sb [kg kg−1] | Gs [kg m−2 s−1] | U [m s−1] | H2 flux [kg m−2 s−1] | H2 purity [% dry] | |
| Optimizing R1 prior to R2 | 0.200 | 600.00 | 2.539 | 199.86 | 3.96 | 0.173570 | 86.53 |
| Run 20 | 0.200 | 600.00 | 2.540 | 200.00 | 4.00 | 0.173570 | 87.57 |
In the case of optimizing the H2 purity prior to optimizing the H2 flux, as shown in Table 5, the maximum H2 purity was predicted to be up to 94.07% on a dry basis, while the H2 flux dropped to 0.147 kg m−2 s−1 in the riser with diameter of 0.2 m, inlet temperature of 627 °C, catalyst-to-sorbent ratio of 2.54 kg kg−1, solid flux of 200 kg m−2 s−1, and gas velocity of 3 m s−1. To confirm the results from the prediction, another case with those values of parameters was simulated in run 33. However, the predicted H2 purity (94.07% on a dry basis) did not conform to the H2 purity from the simulation of run 33 (only 88.62% on a dry basis). Thus, the case of run 33 could not be the optimum case for the H2 purity. In this case, the inlet temperature was predicted to be 627 °C, while the other parameters (the riser diameter, the catalyst-to-sorbent ratio, the solid flux, and the gas velocity) were predicted at their limit. According to the previous discussion about unclear preferred inlet temperature, as shown in Fig. S2b and S2c,† additional prediction cases were determined for the best case instead of run 33 by changing the inlet temperature to its limits at 600 °C and 700 °C; both cases match the simulations of run 19 and run 27, respectively, as shown in Table 6.
| Factor | A | B | C | D | E | R1 | R2 |
|---|---|---|---|---|---|---|---|
| id [m] | Tin [°C] | Cat/Sb [kg kg−1] | Gs [kg m−2 s−1] | U [m s−1] | H2 flux [kg m−2 s−1] | H2 purity [% dry] | |
| Optimizing R2 prior to R1 | 0.200 | 627.11 | 2.540 | 199.94 | 3.00 | 0.147427 | 94.07 |
| Simulation (run 33) | 0.200 | 627.00 | 2.540 | 200.00 | 3.00 | 0.145503 | 88.62 |
| Factor | A | B | C | D | E | R1 | R2 |
|---|---|---|---|---|---|---|---|
| id [m] | Tin [°C] | Cat/Sb [kg kg−1] | Gs [kg m−2 s−1] | U [m s−1] | H2 flux [kg m−2 s−1] | H2 purity [% dry] | |
| Run 27: prediction | 0.200 | 700.00 | 2.540 | 200.00 | 3.00 | 0.135370 | 97.11 |
| Run 27: simulation | 0.200 | 700.00 | 2.540 | 200.00 | 3.00 | 0.133745 | 94.07 |
| Run 19: prediction | 0.200 | 600.00 | 2.540 | 200.00 | 3.00 | 0.151970 | 92.95 |
| Run 19: simulation | 0.200 | 600.00 | 2.540 | 200.00 | 3.00 | 0.146765 | 91.30 |
According to the results shown in Table 6, there was a deviation in the H2 purity in run 27, which was predicted to be 97.11%, but simulated as 94.07% on a dry basis. However, as per the previous point in Table S5,† where run 27 obtained the highest H2 purity among all 32 runs of the simulation, the simulation of run 27 also obtained H2 purity higher than that simulated in run 33 (88.62% on a dry basis), while the H2 flux (0.134 kg m−2 s−1) was less than that in run 33 (0.146 kg m−2 s−1). However, in the case of run 19, both the predicted H2 flux and the predicted H2 purity well-conformed to the results from the simulation. Furthermore, in case of the simulation of run 19, both the H2 purity and H2 flux (91.30% on a dry basis and 0.147 kg m−2 s−1, respectively) were higher than those simulated in run 33 (88.62% on a dry basis and 0.146 kg m−2 s−1, respectively). Thus, run 19 might be another candidate for the optimum case in this system.
In an additional consideration, the composition of the effluent gas in the simulations of run 27 and run 19 are shown in Table 7. Here, even the H2 purity of run 27 (which was the highest among all the runs) seemed to reach equilibrium, while EtOH still had not been converted completely compared with the experimental result and the validated result in Table 3, from which the EtOH content should be approximately 0.0% on a dry basis. This indicated that SESRE could not be performed perfectly in this CFBR system with these ranges of parameters. Moreover, the CH4 content was still high in run 27, while the CO was still high in run 19. These findings indicated that the reforming reactions of CH4 (SMRs) had not yet reached equilibrium in run 27, while the shift reaction of CO (WGS) had not yet reached equilibrium in run 19. This was because run 19 achieved both a H2 flux and H2 purity higher than run 33. Moreover, an additional shift reactor would likely be preferable than applying other effluent gas separation units to purify H2 due to the higher production of H2 in the same time. Thus, run 19 was chosen to be the best case for SESRE operated in this system with these ranges of the parameters.
| H2 [% dry] | CH4 [% dry] | CO [% dry] | CO2 [% dry] | EtOH [% dry] | |
|---|---|---|---|---|---|
| Run 27 | 94.07% | 3.87% | 1.21% | 0.36% | 0.49% |
| Run 19 | 91.30% | 0.37% | 7.42% | 0.61% | 0.31% |
3.4 Hydrodynamics in the riser
With regards to the imperfect performance of SESRE in all cases of the system, considering the hydrodynamics of the best case (run 19) compared with the worst case (run 14) could explain the causes of imperfection more clearly than considering the hydrodynamics of only the best case.Fig. 4 displays the instantaneous contour plots of the volume fraction of each solid phase (catalyst and sorbent) and gas phase at 10, 15, and 20 s in run 14 and run 19. The gradient shades of colors from blue to red represent the low volume fraction to high volume fraction of each phase. The contour plots show that both the catalyst and the sorbent particles were in dense clusters in the lower zone (below 2.5 m height in run 19 and 0.5 m height in run 14, approximately) of the riser. In the rest of the upper zone of the riser, the solid particles were dense only near the wall and were dilute in the center line (core) of riser in run 19, whereas the solid particles were very dilute in run 14. The contours of the volume fraction of the solids could explain how in the lower zone of both runs, the bed seemed to be in a turbulent fluidization regime. In contrast, in the upper zone, the bed appeared to be in fast fluidization in run 19 and dilute transportation in run 14. However, the visual similarity of the volume fraction of the catalyst phase and the sorbent phase indicated good mixing of the catalyst and the sorbent in both runs.
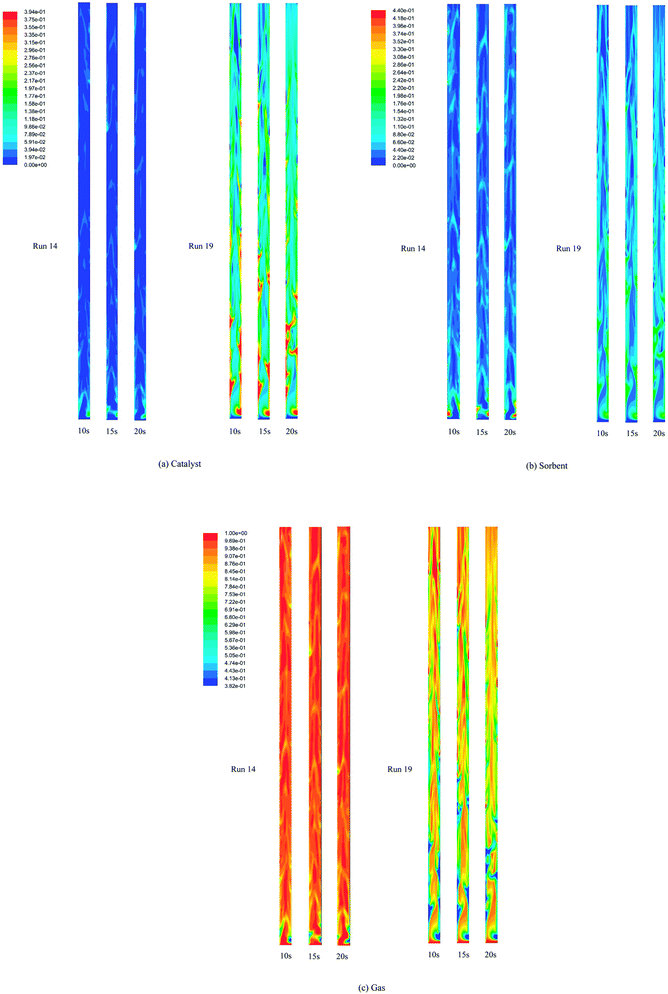 | ||
| Fig. 4 The instantaneous volume fraction of each phase at 10, 15, and 20 s in the best performance case (run 19) and the worst performance case (run 14). | ||
Fig. 5 displays the instantaneous contour plots of the mole fraction of H2, EtOH, and CO2 in the gas phase at 10, 15, and 20 s in both run 14 and run 19. The contour plots in run 19 show that the mole fraction of each component in the gas phase seemed to approach full development from a 2.0 m height of the riser, which was still located in the dense zone of the bed. However, above this zone to the exit, H2 did not reach equilibrium in the core of the riser. Also, EtOH and CO2 were not completely converted and adsorbed in the core. These contours confirmed that SESRE could not be performed perfectly even in the best case of this system. Next, considering the contour plots in run 14, the immediate increase in H2 and CO2 composition and the immediate decrease in EtOH composition nearly exactly matched with those observed for dense solids, as shown in Fig. 4, within the lower zone (below 0.5 m height). Above this zone, H2 and CO2 compositions gradually increased, while EtOH composition gradually decreased up to the outlet. The case of CO2 was notable in run 19, where CO2 immediately rose to the highest in the bottom core, and then rapidly reduced and remained steady in the upper core. In run 14, CO2 immediately rose and gathered at the both sides of the wall, but this did not occur in the core within the lower zone. These core-annulus patterns of CO2 in the bottom half of the riser, which also appeared in the cases of the produced H2, might due to the solid cluster appearance inside the system, as shown in Fig. 4a and b. However, comparing the CO2 fraction along the axial direction in the overview, it can be seen that the CO2 fraction in run 14 increased gradually throughout the riser. On the contrary, the CO2 fraction in run 19 decreased in the bottom zone and then seemed steady in the upper zone. Furthermore, the CO2 fraction in run 14 was higher than that in run 19. The CO2 fraction in run 14 indicated that the continuous increase in CO2 composition in this upper zone could indicate that SRE, which produced CO2, took place rather than the capturing of CO2. In other words, the insufficient amount of sorbent all along the axial direction might have made the CO2 composition increase gradually. Unlike in run 19, the CO2 fraction occurred higher in the bottom zone because carbonation was a slower reaction than SRE, such that more CO2 was adsorbed until it became steady in the rest of the upper zone. In conclusion, besides the incomplete conversion of EtOH, which was found in both runs but higher in run 14, the lack of sorption enhancement might be another cause for the worst performance of run 14.
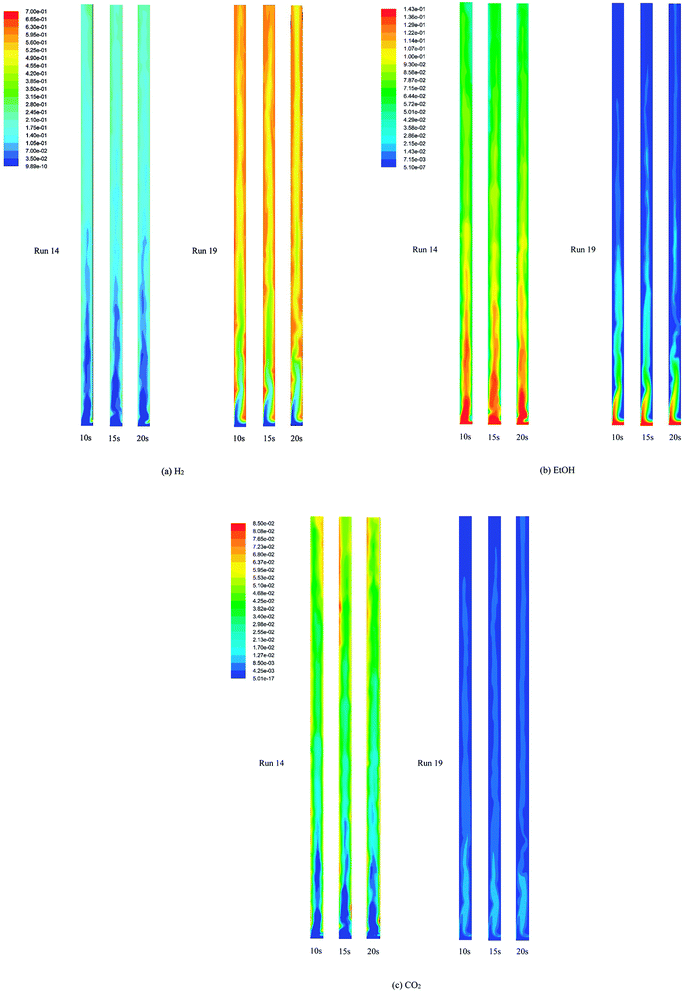 | ||
| Fig. 5 The instantaneous mole fraction (wet basis) of (a) H2 (b) EtOH and (c) CO2 in the gas phase at 10, 15, and 20 s in the best performance case (run 19) and the worst performance case (run 14). | ||
Next, the catalyst and sorbent distributions along the axial and radial directions were expected to be key hydrodynamics parameters to explain the performance of SESRE in this riser system. Inside the riser of both runs, the volume fraction of both the catalyst and sorbent phase and the volumetric catalyst-to-sorbent ratio were compared for the H2 flux and the H2 purity as follows.
As shown in Fig. 6, the time-averaged H2 flux and the time- and area-averaged H2 purity in the axial direction are plotted from 0.1 m height, which was the exact height above the solid inlet channel. The H2 flux of run 19 accumulated rapidly in the lower zone and approached its maximum at the outlet, while the H2 flux of run 14 increased gradually all along the axial direction. The H2 purity of run 19 increased suddenly to about 70% on a dry basis from the height above the solid inlet, but the H2 purity of run 14 started at about 30% on a dry basis. Then, the H2 purity of run 19 increased more within the lower zone and slightly increased in the upper zone, while the H2 purity of run 14 increased gradually. These increasing profiles of the H2 flux and the H2 purity were in accordance with the contour of the H2 fraction, as shown in Fig. 5a.
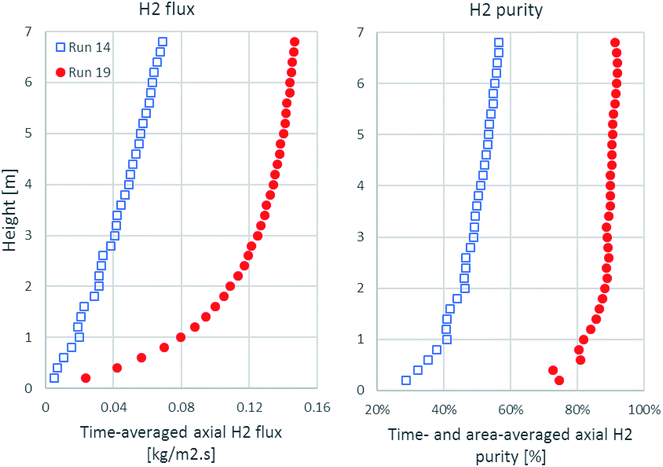 | ||
| Fig. 6 The axial profiles of time-averaged H2 flux and time- and area-averaged H2 purity in the best performance case (run 19) and the worst performance case (run 14). | ||
Fig. 7 shows the time- and area-averaged radial profiles of the H2 flux at the outlet of the riser. The radial distance at 0.0 m was the position of the left wall and that at 0.2 m was the position of the right wall. In both runs, the H2 flux near both wall sides tended to be almost zero, while the H2 flux was the highest in the core of the riser. Both the H2 flux profiles were almost symmetric and also similar to a typical developed velocity profile of a viscous fluid in an internal pipe.
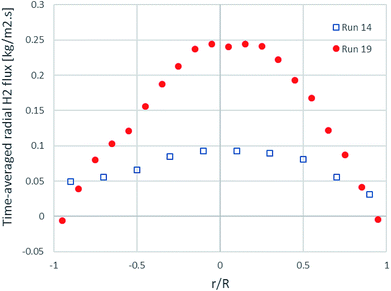 | ||
| Fig. 7 The time-averaged radial profiles of H2 flux at the outlet in the best performance case (run 19) and the worst performance case (run 14). | ||
Fig. 8 shows the time-averaged radial distributions of H2 purity at different heights with the solid inlet on the right side at 0.05–0.10 m height. Each H2 purity profile in run 14 looked similar to the H2 purity profile in run 19 at the same height but had less purity. At exactly above the solid inlet (0.1 m height) in both runs, the H2 purity reached its maximum immediately at the solid inlet on the right wall. Further, the H2 purity decreased along the left direction far from the solid inlet, and then increased near the left wall. At 1.0 m height and above, the profiles in both runs were almost symmetric to the radial H2 flux profiles in Fig. 7. Considering the development of the H2 purity profile at every height, particularly in the core of the riser, the H2 purity in run 14 was gradually higher, while the H2 purity in run 19 rapidly increased above 1.0 m height. This increase in the H2 purity in both runs conformed to the axial H2 purity profiles, as shown in Fig. 6. The H2 purity profiles between 6.0 m and 6.9 m heights of both runs were almost similar. Near the exit (6.9 m height) in both runs, the H2 purity still dropped slightly in the core, conforming to the contour of the H2 fraction in Fig. 5a.
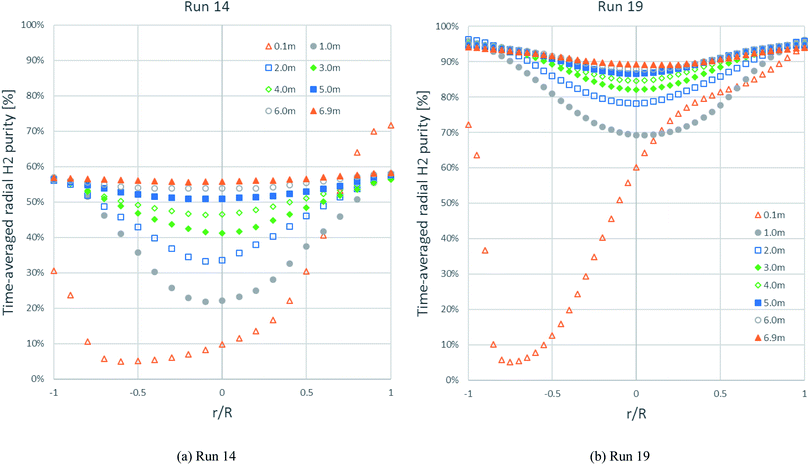 | ||
| Fig. 8 The time-averaged radial profiles of H2 purity at different heights in: (b) the best performance case (run 19) and (a) the worst performance case (run 14). | ||
As shown in Fig. 6–8, both the H2 flux and the H2 purity could be further developed to obtain slightly higher results on using a riser with height over 7 m. However, in additional simulations with a 10 m high riser, there were some cases where the solids accumulated in the riser and then caused errors in those simulations. Thus, the extent height of the riser over 7 m did not lead to better advantage for operating SESRE in this system.
Because SESRE is a very rapid reaction, solid distribution and mixing of the catalyst and the sorbent might be the cause for SESRE not performing perfectly as per the previous discussion. Fig. 9 shows the time- and area-averaged axial profiles of the volume fraction of the solid phases in both runs. First, in run 19, the amount of catalyst, sorbent, and total solids were dense in the lower zone (the volume fraction of total solids was about 0.25–0.30). In the upper zone, all the volume fractions of each solid continuously decreased up to the exit and the volume fraction of total solids was 0.06–0.20, which was the range for the fast fluidization regime.68 Considering the lower zone, this zone could also be divided into an initial acceleration region (0.5–1.5 m height) and a dense phase region (1.5–2.5 m height). In the upper zone, the decrease in the total solid volume fraction was in a transition region (not yet down into the dilute transport region).37,69 This fluidization could also be called a high-density circulation fluidized bed (HDCFB) system.70 Lastly, because the bed was dense in the lower zone (the initial acceleration region and the dense phase region), the axial profile of H2 flux of run 19, as shown in Fig. 6, increased greatly in this lower zone, whereas in run 14, the total solid was dilute and decreased (volume fraction about 0.10 or less to 0.06) in the lower zone, which was not over 1.0 m height. Then, all along the upper zone, fraction of each solid hardly decreased and the total solid volume fraction was less than 0.06, which is known as the flow in the dilute transport regime.68 The dilute fraction of each solid could cause the gradual increase in the H2 flux in run 14, as discussed in Fig. 6.
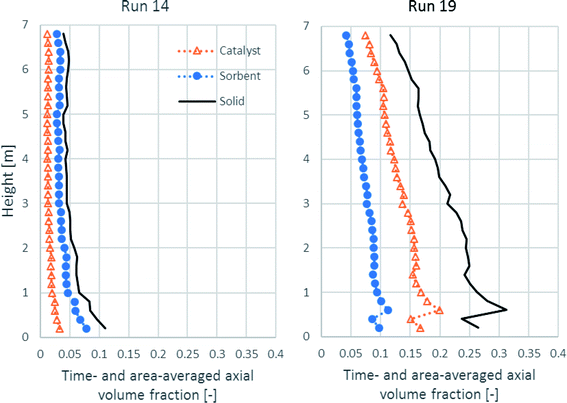 | ||
| Fig. 9 The time- and area-averaged axial profiles of volume fraction of the solid phases in the best performance case (run 19) and the worst performance case (run 14). | ||
As shown in Fig. 10, the time- and area-averaged axial profile of the volumetric catalyst-to-sorbent ratio of each run is plotted for comparing with the ratio with which the solid entered (1.778 v/v in run 19 and 0.4085 v/v in run 14). The results showed that after a sufficient height, the ratios in each run nearly equaled each inlet ratio. These results indicated the good mixing between the catalyst and the sorbent, which made the sorption enhancement uniform in the upper zone. Above the entrance of the solid up to 3.0 m height in run 14, the ratio was slightly higher because the catalyst had higher density (2200 kg m−3) than the sorbent (approximately 1540 kg m−3), so the lighter sorbent was lifted easier than the catalyst. In run 19, the ratio was nearly the same as the inlet ratio almost along the axial direction. However, the lower ratio near the solid entrance might have been affected by the turbulence.
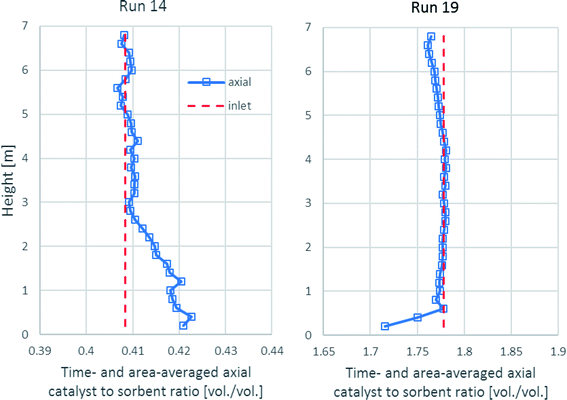 | ||
| Fig. 10 The time- and area-averaged axial profiles of the volumetric catalyst-to-sorbent ratio in the best performance case (run 19) and the worst performance case (run 14). | ||
Fig. 11 shows the time-averaged radial profiles of the volume fraction of each solid phase at different heights. At a height over the solid entrance (0.1 m height), the total solids of both runs were similarly dense near the solid entrance on the right, but dilute at a distance near the left wall, whereas there was a difference between each run at upper heights. In run 19 at 1.0 m height, the volume fraction of solids at the right wall rapidly decreased to balance with that at the left wall. At 1.0–4.0 m height, these profiles showed a core-annular flow of fast fluidization. However, the denser bed near both wall sides would be less dense when the bed was blown higher. Up to a height over 6.0 m, the radial distribution was quite uniform. Considering the situation at the core of each height, the bed was very dilute (the total solid volume fraction was about 0.15 and likely to be less) beyond the 1.0 m height. This was the major cause of the incomplete conversion of EtOH and other intermediates, confirming the results in Table 7 and the contours of run 19 in Fig. 5. In the case of run 14, the volume fraction profiles of each solid tended to develop to flat profiles (quite uniform) beyond 1.0 m height, but occurred faster than in run 19 and also, they were very dilute from this height in accordance with the axial profile in Fig. 9. These flat and very dilute profiles confirmed that the flow pattern in run 14 was in dilute transportation and could be a cause for the lowest H2 flux and the lowest H2 purity. Hence, from both runs, the concentration of each solid was the key hydrodynamic for performing SESRE in the CFBR riser.
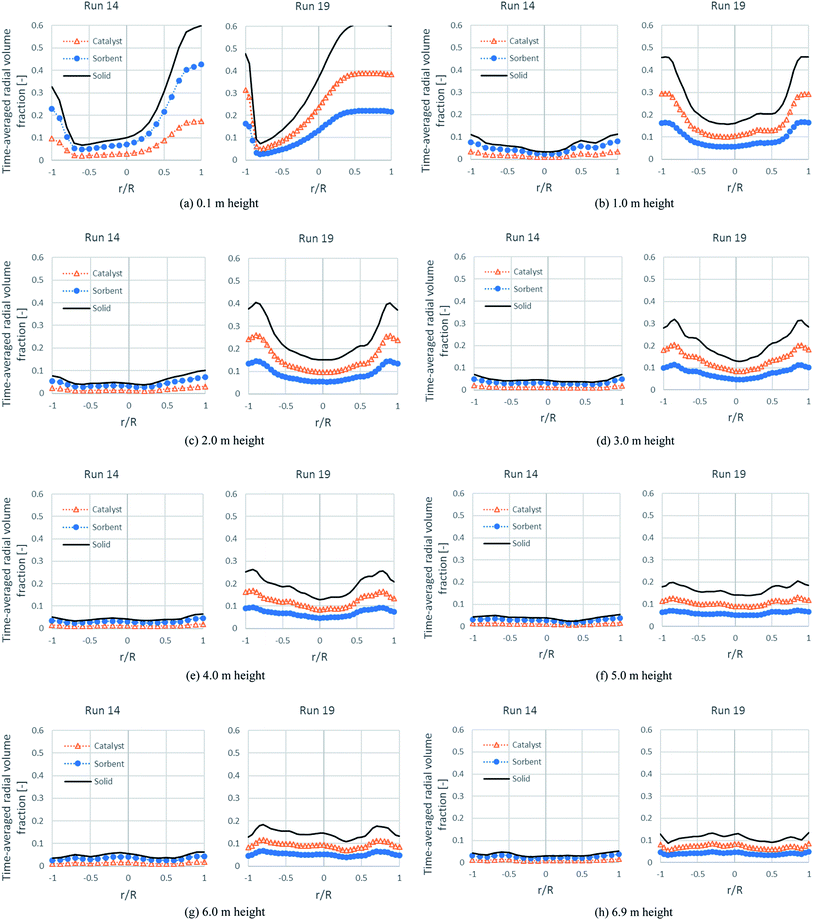 | ||
| Fig. 11 The time-averaged radial profiles of the volume fraction of the solid phases at different heights in the best performance case (run 19) and the worst performance case (run 14). | ||
As shown in Fig. 12, the time-averaged radial profiles of the volumetric catalyst-to-sorbent ratio at different heights in both runs are plotted for comparing with the ratio with which the solid entered (1.778 v/v in run 19 and 0.4085 v/v in run 14). The profile of the 0.1 m height in run 19 and the profiles of the 0.1–2.0 m height in run 14 near the left wall showed slightly higher ratio than the inlet ratio. This is because the solids entered from the channel on the right wall with normal direction to the wall, so more of the heavier catalyst could flow directly to the left wall than the sorbent, while more of the lighter sorbent would be lifted up at the right zone than the catalyst. However, the radial-averaged ratio of each height was nearly equal that with which the solids entered. Thus, the segregation between the catalyst and the sorbent in the radial direction did not severely affect SESRE, consistent with the axial profile of the volumetric catalyst-to-sorbent ratio discussed previously in Fig. 9, the segregation between the catalyst and the sorbent did not cause the incomplete performance of SESRE in this system.
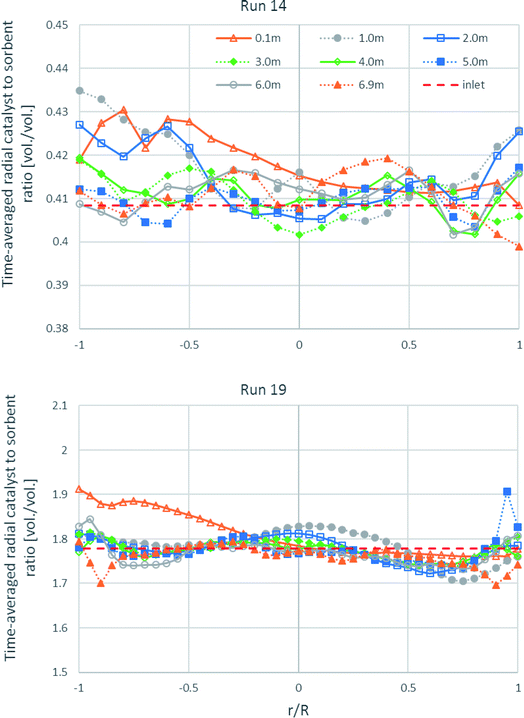 | ||
| Fig. 12 The time-averaged radial profiles of the volumetric catalyst-to-sorbent ratio at different heights in the best performance case (run 19) and the worst performance case (run 14). | ||
Overall, the major cause of the incomplete operations of SESRE in the CFBR system with these ranges of parameters was the dilute region in the core of the riser, which led to an insufficient gas-solids contact before the gas left the riser. Even though the CFBR system with the best case still did not achieve the perfect SESRE performance, the H2 purity could be raised highly up to 91.30% on a dry basis by sorption enhancement. Compared to the packed-bed reactor, in which the gas and solids have sufficient contact time, SESRE could be performed perfectly with H2 purity 96.2% on a dry basis in the experiment of Olivas et al.18 and 98.5% in the validating simulation, as shown in Table 3. Thus, the CFB riser with better modifications of design and/or operation might enable a better gas–solid contact for perfect SESRE performance. However, verifying experiments are suggested to confirm this system design.
4. Conclusion
In the present study, 2D transient models for gas–solid flows using a Euler–Euler approach accompanied with the KTGF theory and kinetic models of SRE on a Ni-based catalyst and carbonation on the dolomite sorbent were applied for simulating SESRE in a CFB riser. The pilot-scale riser design and operation were determined for the best performance of H2 production by studying the five most effective parameters involving the design parameters (the riser diameter, the gas velocity, and the solid flux) and the reaction parameters (the inlet temperature and the catalyst-to-sorbent ratio). The 25 full factorial design method was utilized to investigate the effects of each parameter on the H2 flux and the H2 purity, and to predict the optimum case of both the H2 flux and the H2 purity. Many cases of the 32 runs indicated that SESRE could perform well in the system, even though neither of them achieved the extreme level as determined in theoretical equilibrium or in the packed-bed rector. The CaO conversion was not over 28% of the circulating limitation in every case. Thus, SESRE could possibly be operated in the CFBR system.According to the results of the ANOVAs, either the main effect or its interaction with each parameter occurred and was significant with the H2 flux or the H2 purity. In descending order, the catalyst-to-sorbent ratio, the solid flux, the riser diameter, the inlet temperature, and the gas velocity had highly significant effects on the H2 flux. Moreover, the solid flux, the riser diameter, the gas velocity, and the catalyst-to-sorbent ratio had highly significant effects on the H2 purity. Remarkably, the main effects of the riser diameter and the solid flux and their interactions were significant to both the H2 flux and the H2 purity. Therefore, the riser diameter and the solid flux, which are both design parameters, were the key parameters for H2 production performance in this system. Moreover, most of the main effects and interactions positively affected both the H2 flux and the H2 purity; whereas the inlet temperature had a negative effect on the H2 flux and the gas velocity was negative to the H2 purity.
From predictions using regression models, the best case of SESRE in this CFB riser was simulated with riser diameter of 0.2 m, inlet temperature of 600 °C, catalyst-to-sorbent ratio of 2.54 kg kg−1, solid flux of 200 kg m−2 s−1, and gas velocity of 3 m s−1 to possibly achieve the highest H2 purity of 91.30% on a dry basis with a maximum H2 flux of 0.147 kg m−2 s−1.
Considering the hydrodynamics inside the riser for the best case, first of all, the solid flow was a core-annular pattern of fast fluidization, in which the bed was denser in the lower zone, as might be called a high-dense circulation fluidized bed (HDCFB). Thus, the performance of SESRE reached breakthrough in this dense zone. Next, the good mixing of the catalyst and the sorbent all along both the axial and radial directions indicated that the segregation between the catalyst and the sorbent was not the cause of the incomplete performance. The bed in the core of the riser was very dilute almost along the entire axial direction, and this was the actual cause for the incompletion of SESRE in this system, even in the best case.
Conflicts of interest
There are no conflicts to declare.Nomenclature
Acknowledgements
The authors would like to acknowledge the support from the Ratchadapisek Sompoch Endowment Fund (2016), Chulalongkorn University (CU-59-003-IC). B. Chalermsinsuwan also would like to thank the support from the Thailand Research Fund (RSA5980052). S. Assabumrungrat and S. Putivisutisak also acknowledge the NSTDA Chair Professor Grant (No. 5) funded by the Crown Property Bureau of Thailand and National Science and Technology Development Agency.References
- F. Joensen and J. R. Rostrup-Nielsen, Conversion of hydrocarbons and alcohols for fuel cells, J. Power Sources, 2002, 105, 195–201 CrossRef
.
- J. L. Contreras, J. Salmones, J. A. Colín-Luna, L. Nuño, B. Quintana, I. Córdova, B. Zeifert, C. Tapia and G. A. Fuentes, Catalysts for H2 production using the ethanol steam reforming (a review), Int. J. Hydrogen Energy, 2014, 39, 18835–18853 CrossRef
.
- G. Wu, C. Zhang, S. Li, Z. Huang, S. Yan, S. Wang, X. Ma and J. Gong, Sorption enhanced steam reforming of ethanol on Ni–CaO–Al2O3 multifunctional catalysts derived from hydrotalcite-like compounds, Energy Environ. Sci., 2012, 5, 8942–8949 RSC
.
- M. A. Ebiad, D. R. Abd El-Hafiz, R. A. Elsalamony and L. S. Mohamed, Ni supported high surface area CeO2–ZrO2 catalysts for hydrogen production from ethanol steam reforming, RSC Adv., 2012, 2, 8145–8156 RSC
.
- A. Rautio, P. K. Seelam, P. Maki-Arvela, O. Pitkanen, M. Huuhtanen, R. L. Keiski and K. Kordasa, Carbon supported catalysts in low temperature steam reforming of ethanol: study of catalyst performance, RSC Adv., 2015, 5, 49487–49492 RSC
.
- F. Liu, Y. Qu, Y. Yue, G. Liu and Y. Liu, Nano bimetallic alloy of Ni–Co obtained from LaCoxNi1−xO3 and its catalytic performance for steam reforming of ethanol, RSC Adv., 2015, 5, 16837–16846 RSC
.
- Z. Zhao, P. Ren and W. Li, Supported Ni catalyst on a natural halloysite derived silica-alumina composite oxide with unexpected coke-resistant stability for steam-CO2 dual reforming of methane, RSC Adv., 2016, 6, 49487–49496 RSC
.
- P. Vaidya and A. E. Rodrigues, Insight into steam reforming of ethanol to produce hydrogen for fuel cells: a review, Chem. Eng. J., 2006, 117, 39–49 CrossRef
.
- Y. J. Wu, P. Li, J. G. Yu, A. F. Cunha and A. E. Rodrigues, Sorption-enhanced steam reforming of ethanol on NiMgAl multifunctional materials: Experimental and numerical investigation, Chem. Eng. J., 2013, 231, 36–48 CrossRef
.
- Y. J. Wu, P. Li, J. G. Yu, A. F. Cunha and A. E. Rodrigues, Sorption-enhanced steam reforming of ethanol for continuous high-purity hydrogen production: 2D adsorptive reactor dynamics and process design, Chem. Eng. Sci., 2014, 118, 83–93 CrossRef
.
- Y. J. Wu, P. Li, J. G. Yu, A. F. Cunha and A. E. Rodrigues, High-purity hydrogen production by sorption-enhanced steam reforming of ethanol: a cyclic operation simulation study, Ind. Eng. Chem. Res., 2014, 53, 8515–8527 CrossRef
.
- Y. J. Wu, J. C. Santos, P. Li, J. G. Yu, A. F. Cunha and A. E. Rodrigues, Simplified kinetic model for steam reforming of ethanol on a Ni/Al2O3 catalyst, Can. J. Chem. Eng., 2014, 92, 116–130 CrossRef
.
- A. F. Cunha, Y. J. Wu, F. A. Diaz Alvarado, J. C. Santos, P. D. Vaidya and A. E. Rodrigues, Steam reforming of ethanol on a Ni/Al2O3 catalyst coupled with a hydrotalcite-like sorbent in a multilayer pattern for CO2 uptake, Can. J. Chem. Eng., 2012, 90, 1514–1526 CrossRef
.
- A. Haryanto, S. Fernando, N. Murali and S. Adhikari, Current status of hydrogen production techniques by steam reforming of ethanol: A review, Energy Fuels, 2005, 19, 2098–2106 CrossRef
.
- M. De-Souza, G. M. Zanin and F. F. Moraes, Parametric study of hydrogen production from ethanol steam reforming in a membrane microreactor, Braz. J. Chem. Eng., 2013, 30, 355–367 CrossRef
.
- J. Sun, X. Qiu, F. Wu and W. Zhu, H2 from steam reforming of ethanol at low temperature over Ni–Y2O3, Ni–La2O3 and Ni–Al2O3 catalysts for fuel-cell application, Int. J. Hydrogen Energy, 2005, 30, 437–445 CrossRef
.
- V. Mas, M. L. Bergamini, G. Baronetti, N. Amadeo and M. Laborde, A kinetic study of ethanol steam reforming using a nickel based catalyst, Top. Catal., 2008, 51, 39–48 CrossRef
.
- D. Y. Aceves Olivas, M. R. Baray Guerrero, M. A. Escobedo Bretado, M. Marques da Silva Paula, J. Salinas Gutiérrez, V. Guzmán Velderrain, A. López Ortiz and V. Collins-Martínez, Enhanced ethanol steam reforming by CO2 absorption using CaO, CaO*MgO or Na2ZrO3, Int. J. Hydrogen Energy, 2014, 39, 16595–16607 CrossRef
.
- L. Barelli, G. Bidini, F. Gallorini and S. Servili, Hydrogen production through sorption-enhanced steam methane reforming and membrane technology: a review, Energy, 2008, 33, 554–570 CrossRef
.
- S. D. Kenarsari, D. Yang, G. Jiang, S. Zhang, J. Wang, A. G. Russell, Q. Wei and M. Fan, Review of recent advances in carbon dioxide separation and capture, RSC Adv., 2013, 3, 22739–22773 RSC
.
- D. P. Harrison, Sorption-enhanced hydrogen production: a review, Ind. Eng. Chem. Res., 2008, 47, 6486–6501 CrossRef
.
- A. Cotton, K. Patchigolla and J. E. Oakey, Overview of, and experimental methodology for sorption enhanced hydrogen production, Energy Procedia, 2013, 37, 2232–2244 CrossRef
.
- A. E. Rodrigues, Y. J. Wu, R. Faria and L. M. Madeira, Sorption Enhanced Reaction Processes, World Scientific Publishing, USA, 2017 Search PubMed
.
- R. Singh, M. K. Ram Reddy, S. Wilson, K. Joshi, J. C. Diniz da Costa and P. Webley, High temperature materials for CO2 capture, Energy Procedia, 2009, 1, 623–630 CrossRef
.
- M. Sayyah, B. R. Ito, M. Rostam-Abadi, Y. Lu and K. S. Suslick, CaO-based sorbents for CO2 capture prepared by ultrasonic spray pyrolysis, RSC Adv., 2013, 3, 19872–19875 RSC
.
- A. Islam, S. H. Teo, E. S. Chan and Y. H. Taufiq-Yap, Enhancing the sorption performance of surfactant-assisted CaO nanoparticles, RSC Adv., 2014, 4, 65127–65136 RSC
.
- H. Ping and S. Wu, Preparation of cage-like nano-CaCO3 hollow spheres for enhanced CO2 sorption, RSC Adv., 2015, 5, 65052–65057 RSC
.
- J. Comas, M. Laborde and N. Amadeo, Thermodynamic analysis of hydrogen production from ethanol using CaO as a CO2 sorbent, J. Power Sources, 2004, 138, 61–67 CrossRef
.
- A. L. da Silva and I. L. Muller, Hydrogen production by sorption enhanced steam reforming of oxygenated hydrocarbons (ethanol, glycerol, n-butanol and methanol): thermodynamic modelling, Int. J. Hydrogen Energy, 2011, 36, 2057–2075 CrossRef
.
- Z. Chao, Y. Wang, J. P. Jakobsen, M. Fernandino and H. A. Jakobsen, Numerical investigation of the sorption enhanced steam methane reforming in a fluidized bed reactor, Energy Procedia, 2012, 26, 15–21 CrossRef
.
- Y. Wang, Z. Chao and H. A. Jakobsen, 3D Simulation of bubbling fluidized bed reactors for sorption enhanced steam methane reforming processes, J. Nat. Gas Sci. Eng., 2010, 2, 105–113 CrossRef
.
- K. Johnsen, J. R. Grace, S. S. E. H. Elnashaie, L. Kolbeinsen and D. Eriksen, Modeling of sorption-enhanced steam reforming in a dual fluidized bubbling bed reactor, Ind. Eng. Chem. Res., 2006, 45, 4133–4144 CrossRef
.
- K. Johnsen, H. J. Ryu, J. R. Grace and C. J. Lim, Sorption-enhanced steam reforming of methane in a fluidized bed reactor with dolomite as CO2-acceptor, Chem. Eng. Sci., 2006, 61, 1195–1202 CrossRef
.
- A. G. Gayubo, J. Vicente, J. Erena, C. Montero, M. Olazar and J. Bilbao, Comparison of Ni and Co
catalysts for ethanol steam reforming in a fluidized bed reactor, Catal. Lett., 2014, 144, 1134–1143 CrossRef
.
- J. Vicente, C. Montero, J. Erena, M. J. Azkoiti, J. Bilbao and A. G. Gayubo, Coke deactivation of Ni and Co catalysts in ethanol steam reforming at mild temperatures in a fluidized bed reactor, Int. J. Hydrogen Energy, 2014, 39, 21586–21596 Search PubMed
.
- D. Kunii and O. Levenspiel, Fluidization engineering, Butterworth-Heinemann, USA, 1991 Search PubMed
.
- M. B. M. Mousa, S. E. K. Fateen and E. A. Ibrahim, Hydrodynamics of a novel design circulating fluidized bed steam reformer operating in the dense suspension upflow regime, ISRN Chem. Eng., 2014, 2014, 1–13 CrossRef
.
- Y. Prajongkan, Three-dimensional simulation of hydrodynamics in riser of circulating fluidized bed reactor, Thesis of the degree of Master of Science, Chulalongkorn University, 2011
.
- B. Arstad, J. Prostak and R. Blom, Continuous hydrogen production by sorption enhanced steam methane reforming (SE-SMR) in a circulating fluidized bed reactor: Sorbent to catalyst ratio dependencies, Chem. Eng. J., 2012, 189–190, 413–421 CrossRef
.
- Y. Wang, Z. Chao, D. Chen and H. A. Jakobsen, SE-SMR process performance in CFB reactors: Simulation of the CO2 adsorption/desorption processes with CaO based sorbents, Int. J. Greenhouse Gas Control, 2011, 5, 489–497 CrossRef
.
- N. Rodríguez, M. Alonso and J. C. Abanades, Experimental investigation of a circulating fluidized-bed reactor to capture CO2 with CaO, AIChE J., 2011, 57, 1356–1366 CrossRef
.
- J. Wang, Y. Wang and H. A. Jakobsen, The modeling of circulating fluidized bed reactors for SE-SMR process and sorbent regeneration, Chem. Eng. Sci., 2014, 108, 57–65 CrossRef
.
- A. Di Carlo, E. Bocci, F. Zuccari and A. Dell'Era, Numerical investigation of sorption enhanced steam methane reforming process using computational fluid dynamics Eulerian-Eulerian code, Ind. Eng. Chem. Res., 2010, 49, 1561–1576 CrossRef
.
- T. Samruamphianskun, P. Piumsomboon and B. Chalermsinsuwan, Effect of ring baffle configurations in a circulating fluidized bed riser using CFD simulation and experimental design analysis, Chem. Eng. J., 2012, 210, 237–251 CrossRef
.
- B. Chalermsinsuwan, T. Samruamphianskun and P. Piumsomboon, Effect of operating parameters inside circulating fluidized bed reactor riser with ring baffles using CFD simulation and experimental design analysis, Chem. Eng. Res. Des., 2014, 92, 2479–2492 CrossRef
.
- V. V. Ranade, Computational flow modeling for chemical reactor engineering, Academic Press, UK, 2002 Search PubMed
.
- G. H. Yeoh and J. Tu, Computational techniques for multi-phase flows, Elsevier Ltd, UK, 2010 Search PubMed
.
- D. Gidaspow, Multiphase Flow and Fluidization: Continuum and Kinetic Theory Description, Academic Press, UK, 1994 Search PubMed
.
- R. A. Sánchez, Z. Chao, J. Solsvik and H. A. Jakobsen, One dimensional two-fluid model simulations of the SE-SMR process operated in a circulating fluidized bed reactor, Procedia Eng., 2012, 42, 1282–1291 CrossRef
.
- R. A. Sánchez, J. Solsvik and H. A. Jakobsen, Modeling and simulation of cold flow fluidized bed reactors, Energy Procedia, 2012, 26, 22–30 CrossRef
.
- R. A. Sánchez, Z. Chao, J. Solsvik and H. A. Jakobsen, An investigation of the heat integration between the two riser units constituting a circulating fluidized bed reactor for the SE-SMR process, Energy Procedia, 2013, 37, 1218–1227 CrossRef
.
- J. Solsvik, Z. Chao and H. A. Jakobsen, A one-dimensional two-fluid gas–solid model applied to fluidized bed reactors: The SMR and SE-SMR processes, Procedia Eng., 2012, 42, 283–294 CrossRef
.
- J. Solsvik, Z. Chao, R. A. Sánchez and H. A. Jakobsen, Numerical investigation of steam methane reforming with CO2-capture in bubbling fluidized bed reactors, Fuel Process. Technol., 2014, 125, 290–300 CrossRef
.
- Y. Wang, Z. Chao and H. A. Jakobsen, CFD modelling of CO2 capture in the SE-SMR process in the fluidized bed reactors, Chem. Eng. Trans., 2010, 21, 601–606 Search PubMed
.
- S. Song, Z. Hao, L. Dong, J. Li and Y. Fang, A bubble-based EMMS model for pressurized fluidization and its validation with data from a jetting fluidized bed, RSC Adv., 2016, 6, 111041–111051 RSC
.
- Z. Chao, Y. Wang, J. P. Jakobsen, M. Fernandino and H. A. Jakobsen, Derivation and validation of a binary multi-fluid Eulerian model for fluidized beds, Chem. Eng. Sci., 2011, 66, 3605–3616 CrossRef
.
- H. Lindborg, M. Lysberg and H. A. Jakobsen, Practical validation of the two-fluid model applied to dense gas–solid flows in fluidized beds, Chem. Eng. Sci., 2007, 62, 5854–5869 CrossRef
.
- M. J. Hodapp, J. J. Ramirez-Behainne, M. Mori and L. Goldstein Jr, Numerical studies of the gas–solid hydrodynamics at high temperature in the riser of a bench-scale circulating fluidized bed, Int. J. Chem. Eng., 2012, 2012, 786982 Search PubMed
.
- R. A. Sánchez and H. A. Jakobsen, Simulation of sorption enhanced steam methane reforming and chemical looping reforming in a circulating fluidized bed reactor, Ninth International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia, 2012, pp. 1–6 Search PubMed
.
- J. Solsvik, R. A. Sánchez, Z. Chao and H. A. Jakobsen, Simulations of steam methane reforming/sorption-enhanced steam methane reforming bubbling fluidized bed reactors by a dynamic one-dimensional two-fluid model: Implementation issues and model validation, Ind. Eng. Chem. Res., 2013, 52, 4202–4220 CrossRef
.
- Y. Chen, Y. Zhao, C. Zheng and J. Zhang, Numerical study of hydrogen production via sorption-enhanced steam methane reforming in a fluidized bed reactor at relatively low temperature, Chem. Eng. Sci., 2013, 92, 67–80 CrossRef
.
- J. Xu and G. F. Froment, Methane steam reforming, methanation and water-gas shift: I.Intrinsic kinetics, AIChE J., 1989, 35, 88–96 CrossRef
.
- G. Xiu, P. Li and A. E. Rodrigues, Sorption-enhanced reaction process with reactive regeneration, Chem. Eng. Sci., 2002, 57, 3893–3908 CrossRef
.
- P. Sun, J. R. Grace, C. J. Lim and E. J. Anthony, Determination of intrinsic rate constants of the CaO–CO2 reaction, Chem. Eng. Sci., 2008, 63, 47–56 CrossRef
.
- J. C. Abanades, E. J. Anthony, D. Y. Lu, C. Salvador and D. Alvarez, Capture of CO2 from combustion gases in a fluidized bed of CaO, AIChE J., 2004, 50, 1614–1622 CrossRef
.
- J. S. Lin, M. M. Chen and B. T. Chao, A novel radioactive particle tracking facility for measurement of solids motion in gas fluidized beds, AIChE J., 1985, 31, 465–473 CrossRef
.
- D. C. Montgomery, Design and Analysis of Experiments, John Wiley and Sons, USA, 2012 Search PubMed
.
- D. Kunii and O. Levenspiel, Circulating fluidized-bed reactors, Chem. Eng. Sci., 1997, 52, 2471–2482 CrossRef
.
- S. Mahmoudi, C. W. Chan, A. Brems, J. Seville and J. Baeyens, Solids flow diagram of a CFB riser using Geldart B-type powders, Particuology, 2012, 10, 51–61 CrossRef
.
- J. Zhu, Circulating turbulent fluidization-A new fluidization regime or just a transitional phenomenon, Particuology, 2010, 8, 640–644 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra03901a |
| This journal is © The Royal Society of Chemistry 2018 |

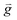
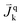
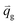
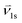
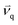
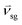
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)