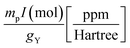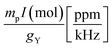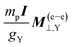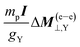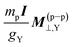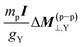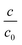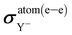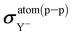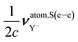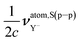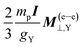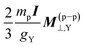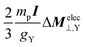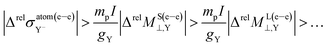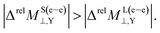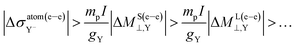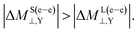Open Access Article
Open Access ArticleInfluence of the nuclear charge distribution and electron correlation effects on magnetic shieldings and spin-rotation tensors of linear molecules†
I. Agustín Aucar *,
Carlos A. Giménez and
Gustavo A. Aucar
*,
Carlos A. Giménez and
Gustavo A. Aucar
Instituto de Modelado e Innovación Tecnológica, CONICET, Departamento de Física – Facultad de Ciencias Exactas y Naturales, UNNE, Av. Libertad 5460, W3404AAS, Corrientes, Argentina. E-mail: agustin.aucar@conicet.gov.ar
First published on 4th June 2018
Abstract
The nuclear charge distribution effects (NChDE) on two response properties, the NMR magnetic shielding (σ) and the nuclear spin-rotation (SR) constants (M), are analyzed. We do it employing point-like and Gaussian-like models for describing the nuclear charge density of three linear molecules: HBr, HI and HAt. According to our results, both properties are sensitive to the NChDE. We show that the NChDE are almost completely relativistic, i.e., they nearly vanish in the non-relativistic limit of both properties. We calculated the NChDE on σ and M, and analyzed the differences between them in terms of a relativistic relation between these two properties. Using that relation we found that the electronic core mechanisms are the main ones for the NChDE on the shielding of nuclei of both, molecules and free atoms. The NChDE are smaller on SR constants than on shieldings. Nevertheless, within the relativistic polarization propagator formalism at the RPA level of approach they are very important for SR constants of nuclei in heavy-atom-containing compounds. Astatine in HAt has the largest influence: MAt = −9.95 kHz for a point-like model and −50.10 kHz for a Gaussian-like model. Correlation effects must be included and we do it using different DFT schemes. The PBE0 functional gives results that are closest to experiments for Br and I, though the LDA gives the closest for hydrogen. The value of the SR constant of At is reduced among 350 kHz and 500 kHz from its RPA value, when different and usual functionals are applied. Given that the NChDE on M and σ are mostly relativistic in their origin, these effects are also dependent on electron correlation. They have also a nonvanishing dependence with the Gaunt electron–electron interactions.
1 Introduction
Accurate representation of the electronic structure of atoms and molecules, together with its properties, requires to consider the nuclear model as a finite one. This is specially the case for studies performed within a relativistic framework.1 Besides, phenomenologically modeled distributions of the nuclear charge and the dipolar nuclear magnetization are, till present, enough to get precise theoretical results. At the moment one does not need to resort to nuclear structure calculations.Different types of both distributions can broadly be divided in two: point-like or finite-like. For the last one the first and usual option for electronic structure calculations is the spherically symmetric Gaussian-like nuclear model, due to its easy computational implementation. The electronic wave function is usually expanded in terms of Gaussian-type functions, and therefore the electron-nucleus attraction integrals appearing in the molecular calculations are easier to evaluate by employing the same efficient primitive integral routines used to evaluate the electron–electron repulsion integrals. In addition, this model depends on only one parameter, and the calculations are only sensitive to the rms charge radius.1–3
In 1993 Shabaev proposed few finite nuclear size corrections to the energy levels of multicharged ions4 and then, Visscher and Dyall were among the first to include the nuclear charge distribution effects, NChDE, in the calculation of the atomic ground state electronic energy.2,3 They considered different nuclear models and found that significant differences only appears when employing point-like or finite-like nuclear models. Their calculations gave close results for any of the following three different finite-size nuclear models: the homogeneously charged sphere, the two-parameter Fermi distribution and the Gaussian charge distribution. Few years later the NChDE were also included in electronic structure calculations of atoms and molecules by Andrae.5 He proposed an scheme to detect different values of physical properties when they are calculated using different finite nuclear models in standard quantum chemical electronic structure codes; specially in the total energy shifts and also in the energy differences in hydrogen-like atoms. One of the main conclusions of all these studies was that, to calculate the energy spectra, it is only relevant the switching from a point-like nuclear model to any of the finite-like nuclear charge distributions.
During the 90's, only the influence of the finite nuclear size models on calculations of wave functions and energies were carefully studied. More recently, considering that the hyperfine operator acts very close to the nucleus, the NChDE have become of particular interest for heavy-element-containing systems. Several works have been devoted to include such nuclear models in the expression of hyperfine operators. We can mention the work of Fukuda et al. about NMR chemical shifts at Douglas–Kroll–Hess (DKH) level of approach employing a finite-nuclear model,6 and the work of Hamaya et al. whom included the NChDE on NMR shieldings (σ) of halogen halides.7 In line with this, E. Malkin and co-workers have studied the effect of a finite nuclear model on the hyperfine structure at DKH-2/DFT level of theory8 and later at Dirac–Kohn–Sham (DKS) level of theory.9
Concerning the NChDE on NMR spectroscopic parameters, Autschbach has employed a Gaussian-type nuclear charge distribution model to calculate its influence on J-couplings.10,11 In this case the relativistic zeroth-order regular approach (ZORA), combined with both non-hybrid and hybrid density functionals were applied, and both, spin-free and two-component spin–orbit terms were calculated. It was shown that the NChDE on the hyperfine integrals are quite pronounced, and therefore, they noticeably alter J-coupling constants when heavy atoms are involved. Few years later some of us found that relativistic effects largely enhance the NChDE on those parameters and also that J-couplings are more sensitive than shieldings in both, relativistic and non-relativistic (NR) regimes. The highest effect, which is larger than 10% of variation was found for J-couplings among lead and iodine in PbIH3.12
Kita and Tachikawa13 have also found that the nuclear size effects on σ, and also on the molecular magnetic susceptibility, may be important for heavy-element-containing systems. Furthermore, Arcisauskaite et al. used a Gaussian-type model to include the NChDE on shielding constants in HgX2 (X = Cl, Br, I, CH3).14 They found that the NChDE are larger when four-component calculations are performed, as compared with ZORA results.
In the case of the relativistic spin-rotation constants, its first calculations (presented at the 10th REHE International Conference in 2012) were performed with a finite nuclear charge distribution model. It is also worth to highlight the fact that a Gaussian-type nuclear charge distribution model was employed in the first two published articles with calculations of M, performed at the relativistic four-component Dirac–Kohn–Sham15 and Dirac–Hartree–Fock levels of theory.16 In any case, until now no detailed studies of NChDE on this property were made.
Given that the relativistic nuclear spin-rotation (SR) tensor (M)17–19 is closely related to the NMR shielding tensor, or turning this statement around, the relativistic extension of Flygare's relationship20,21 shows that the NMR shielding tensor is related with the SR tensor, the shielding constant of free atoms and a new term (see below) named vS, one may expect that the NChDE should be important for M. On the other hand, given that electron correlation and relativistic effects are not independent each other for the NMR spectroscopic parameters,22 there may be a relationship among electron correlation and NChDE if these last effects are enhanced by relativistic effects, as seems to be the case. The main goals of this work are related with the answers to these two inquiries. We shall analyze the NChDE on the SR constants by the first time, and consider also its relativistic relationship with the shielding constants in some details, to shed some light on the electronic origin of the NChDE in both properties. Besides the previously mentioned aims of this work, another one is the analysis of the electron correlation as related with the total NChDE. Furthermore, we analyzed the electron correlation effects treated at the relativistic DFT level of theory, on both properties and also on its NChDE. We shall also show how important could be the consideration of the two-electron (SS|SS) integrals at the Dirac–Fock level on the NChDE, and also the electron–electron Gaunt interactions.
This article has the following structure: in Section 2 we briefly introduce a description of the nuclear charge distribution models we use. We also present in that Section a summary of the backgrounds of the relation between M and σ within a relativistic framework. In Section 3 we describe in some detail how our calculations were performed and then, an analysis of the NChDE on SR and σ is presented in Section 4, where a systematic study of the origin of these effects is exposed. It includes the analysis of the Gaunt interactions. The main conclusions are given in Section 5.
2 Theory and models
2.1 Nuclear charge distribution models
The use of finite nuclear models in electronic structure calculations modifies the electrostatic Coulomb electron–nucleus potential. Its most important consequence is associated with the change from a point-like nucleus (with a singularity at the nuclear position), to some spherically symmetric one.1There are some nuclear models available in the bibliography. In this work, we focus on one-dimensional spherically symmetric models for the nuclear charge density distributions, because the tridimensional models are not yet implemented in the computational codes commonly used to calculate the properties of our interest. There are four basic types of one-dimensional nuclear charge distributions (NChD): the point-like nuclear model and three finite-size distributions. Between the latter, we can recognize the uniform, the Gaussian-type and the Fermi-type distributions. In our case we focus our attention to only two of those models: the point-type one and the Gaussian-type one.
It is known that the differences between potential energy functions obtained from the three different finite-size nuclear distributions are always moderate.5
The nuclear charge density distribution of both, point-type and spherically symmetric Gaussian-type of a nucleus of atomic number Z (ρP(r) and ρG(r), respectively), can be written as
ρP(r) = Zδ(r); ρG(r) = ρG,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−λr2, e−λr2,
| (1) |
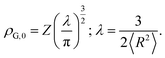 | (2) |
Atomic units were used in the last expressions and will be adopted throughout all this work.
The nuclear charge density distributions ρP(r) and ρG(r) give rise to spherically symmetric potentials, given as
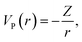 | (3) |
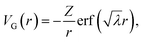 | (4) |
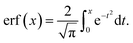 | (5) |
The main parameter used to describe the Gaussian-type distribution is the rms nuclear radius 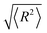 , which can be approximately related to the cubic root of the mass number A of the given nucleus via the empirical relation23
, which can be approximately related to the cubic root of the mass number A of the given nucleus via the empirical relation23 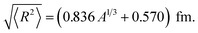
2.2 NMR shieldings and spin-rotation constants
We now turn to the relationship among the shielding and SR constants. Since the first decades of the NMR spectroscopy, a close relationship between the NMR shielding tensor of a nucleus Y, σY, and its nuclear spin-rotation tensor MY was broadly used to determine absolute scales of shieldings. It was first proposed by Ramsey24 and then improved by Flygare,25,26 being very useful until our days. Such a relationship was derived within a NR framework, and is expressed (in atomic units) as
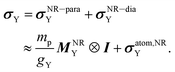 | (6) |
This relation was recently found to be not any longer valid within the relativistic framework. In eqn (6), mp is the proton mass, gY is the nuclear g-value of nucleus Y, and I is the molecular moment tensor of inertia in the equilibrium geometry, with respect to its center of mass. Besides Flygare have shown that eqn (6) is more accurate for the isotropic values than for each individual tensor element.26–28
The Ramsey–Flygare relation of eqn (6) was recently generalized to the relativistic framework.20,21 The new model can be used to obtain absolute shieldings.
The spin-rotation tensor of a nucleus Y in a molecule in its equilibrium position (for which the electric field at each nucleus is zero) can be expressed as a sum of two terms (MY = MnucY + MelecY). One of them depends only on nuclear variables (MnucY) whereas the second one includes the electronic dependence (MelecY).17,26
Working within the four-component polarization propagator, the tensor MelecY can be splitted into two terms that arises by considering separately the electronic excitations from occupied positive-energy orbitals to unoccupied positive-energy orbitals (e–e contributions) and to negative-energy ones (p–p contributions).29,30 The tensor MelecY can be expressed as
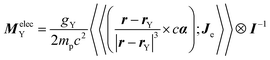 | (7) |
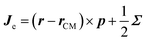 , is the sum of the corresponding orbital and spin angular momenta. The orbital angular momentum is considered with respect to the molecular center of mass, and Σ is the four-component extension of the Pauli matrices. It must be highlighted that eqn (7) does not include the effects of the Breit electron–nucleus interactions. They are not treated at all in the present work. The very small influence of these effects was analyzed in a previous work.31
, is the sum of the corresponding orbital and spin angular momenta. The orbital angular momentum is considered with respect to the molecular center of mass, and Σ is the four-component extension of the Pauli matrices. It must be highlighted that eqn (7) does not include the effects of the Breit electron–nucleus interactions. They are not treated at all in the present work. The very small influence of these effects was analyzed in a previous work.31
On the other hand, the tensor σY is written in the polarization propagator formalism as
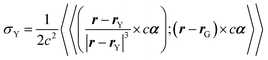 | (8) |
In order to extend the NR Ramsey–Flygare relation to the relativistic domain we started from the recognition of common electronic mechanisms in both σY and MY tensors, first applying the linear response within the elimination of the small components (LRESC) model, and then generalizing it to the four-component case.17,20,21,32 Few other research groups also published recently other developments about the relativistic extension of Ramsey–Flygare's relationship.15,19
Assuming that the LRESC model is reliable in reproducing the leading order (in a 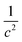 expansion) relativistic effects of SR and shielding constants for both, its (e–e) and (p–p) contributions, we proposed few models that link both properties within a relativistic framework.20,21 The most precise of them, the model M–V, relates σY and MY as follows:
expansion) relativistic effects of SR and shielding constants for both, its (e–e) and (p–p) contributions, we proposed few models that link both properties within a relativistic framework.20,21 The most precise of them, the model M–V, relates σY and MY as follows:
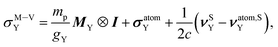 | (9) |
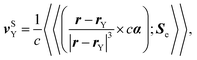 | (10) |
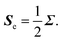
In the special case of linear molecules, the tensor σY can be written as a diagonal matrix, whose elements are σ⊥,Y (simply degenerate) and σ‖,Y. This last term is the shielding of the nucleus Y when the applied magnetic field is aligned parallel to the molecular bond axis, whereas σ⊥,Y is the shielding experienced by the nucleus when the magnetic field is aligned perpendicular to the bond axis.
The model M–V, applied to a linear molecule gives
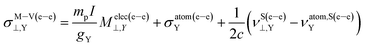 | (11) |
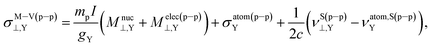 | (12) |
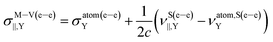 | (13) |
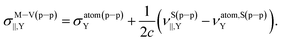 | (14) |
Therefore, the isotropic shielding constant for linear molecules 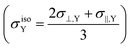 can be expressed, according to the model M–V, as
can be expressed, according to the model M–V, as
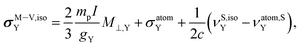 | (15) |
3 Computational details
Four-component relativistic calculations of shielding and SR tensor elements for three linear molecules were performed using a locally modified developer version of the DIRAC16 (ref. 33) program package.The previous nomenclature that pointed out any nucleus as Y shall now be enlarged to introduce a distinction between the heavy nucleus and the hydrogen. The HX (X = 79Br, 127I, 210At) molecules are our model systems. They were displayed along the z axis. For symmetry reasons, as we deal with linear molecules, only diagonal components of shielding and SR tensors are no null. In the case of the M tensor, in both relativistic and NR domains only its perpendicular components are non-zero and equal each other. These tensor elements are known as the spin-rotation constant M. On the other side, within the relativistic domain the shielding tensor has nonzero parallel (σ‖ = σzz) and perpendicular (σ⊥ = σxx = σyy) elements. However, in the NR case σNR‖ = σNRzz = 0.
Unless otherwise stated, four-component calculations are based on the Dirac–Coulomb Hamiltonian, employing the default Hamiltonian of the DIRAC code. It uses an energy correction to avoid the explicit calculation of (SS|SS) integrals, i.e., two-electron integrals containing only small component basis functions.34 In addition, in some appropriately indicated calculations the (SS|SS) integrals were also included in order to analyze the importance of this contribution. Furthermore, the most precise calculation of this work are based on the Dirac–Coulomb–Gaunt Hamiltonian (where, due to implementation reasons, the Breit electron–electron interaction is replaced by the Gaunt interaction, i.e. neglecting the retardation terms), including explicitly the calculation of (SS|SS) integrals. We assume that the Gaunt interaction provides a useful approximation to the Breit interaction; it is considered to be an order of magnitude larger than the retardation term.35,36
Most of the response calculations were performed within the Dirac–Hartree–Fock–Coulomb relativistic polarization propagator approach at the random phase level of approach (RPA). Nevertheless, some of the RPA calculations were performed taking into account the Gaunt electron–electron interaction included in the unperturbed Hamiltonian. They are explicitly indicated as such. In addition, to analyze the influence of electron correlation effects within the Dirac–Hartree–Fock–Coulomb (–Gaunt) framework, some calculations employing the pure zeroth-order approximation (PZOA) were performed.37
Non-relativistic values of σ and M (reported from here as σNR–para, σNR–dia and MNR–elec) were obtained taking a speed of light of c = 30c0. The value of the speed of light in vacuum used throughout all four-component calculations was c0 = 137.0359998 a.u.
The gauge origin of the external magnetic potential was placed at the molecular center of mass in the NMR shielding calculations. With this choice, a direct comparison with the SR results can be safely made. Furthermore, in order to calculate shieldings of nuclei in closed shell free atoms using the DIRAC code (this feature is not implemented for open shell systems), an electron was added to the halogen free atoms.
The following values of nuclear g-factors were taken from ref. 38 for the calculations of SR constants: 5.585694 for 1H, 1.404267 for 79Br and 1.125309 for 127I. As experimental data does not exist for 210At, a g-factor of 1.0 was chosen for this nucleus.
Experimental bond distances were extracted from ref. 39 for HBr and HI. For HAt, an optimized distance was used and calculated at the RPA level of approach. They are: 1.4145 Å (HBr), 1.6090 Å (HI) and 1.7117 Å (HAt).
In all calculations, the NR Dunning's augmented correlation-consistent aug-cc-pCV5Z basis set was used for the hydrogen atom.40 For Br, I and At the Dyall's relativistic acv4z basis sets (dyall.acv4z) were employed.41 In all cases, the uncontracted Gaussian basis sets were used with the common gauge-origin (CGO) approach. The small component basis sets for relativistic calculations were generated by applying the unrestricted kinetic balance prescription (UKB).
Point and finite nuclear models-modeled by Gaussian charge distributions-(PNM and GNM, respectively) were employed in all calculations, as implemented in the DIRAC code.
In order to study correlation effects, we performed PZOA, RPA and Kohn–Sham-DFT calculations employing the DIRAC code. The DFT calculations are based on the four-component Dirac–Coulomb Hamiltonian, and have been done using a variety of NR exchange-correlation functionals in several categories: (i) The local density approximation (LDA) functional,42,43 (ii) the generalized gradient approximation (GGAs) functionals: PBE,44 KT2,45 KT3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 and BP86,47,48 and (iii) the hybrid functional PBE0.49 Furthermore, calculations based on the Dirac–Coulomb–Gaunt Hamiltonian were performed employing the PBE0 functional, scaling the Gaunt integrals (with the GAUNTSCALE keyword of the DIRAC program) with the same factor as for Hartree–Fock exchange. It means that this hybrid functional include fractional Hartree–Fock Gaunt interaction.
46 and BP86,47,48 and (iii) the hybrid functional PBE0.49 Furthermore, calculations based on the Dirac–Coulomb–Gaunt Hamiltonian were performed employing the PBE0 functional, scaling the Gaunt integrals (with the GAUNTSCALE keyword of the DIRAC program) with the same factor as for Hartree–Fock exchange. It means that this hybrid functional include fractional Hartree–Fock Gaunt interaction.
For the property calculations at DFT level of theory, experimental internuclear distances were used for HBr and HI. The optimized bond distances of the HAt molecule were again obtained from each of the above mentioned functionals and basis sets. Their values are (in Å) 1.7393 (LDA), 1.7237 (KT2), 1.7209 (KT3), 1.7473 (PBE), 1.7272 (PBE0) and 1.7486 (BP86). Doing this we are as much coherent as possible with the scheme of calculations adopted.
In addition, Table 1 gives the conversion factors 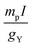 used to transform the SR constants from atomic units (Hartree) to ppm (3rd column of the table), to be used in the application of eqn (6) and (9). In the fourth column the conversion factors of SR constants from kHz to ppm are given. They are obtained by taking into account the relation between Hartrees and kHz (1 Hartree = 6.579683920711 × 1012 kHz).50
used to transform the SR constants from atomic units (Hartree) to ppm (3rd column of the table), to be used in the application of eqn (6) and (9). In the fourth column the conversion factors of SR constants from kHz to ppm are given. They are obtained by taking into account the relation between Hartrees and kHz (1 Hartree = 6.579683920711 × 1012 kHz).50
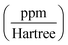 , whereas those of the fourth column are given in
, whereas those of the fourth column are given in 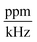
4 Results and discussion
In this Section, the influence of the NChDE on the (e–e) and (p–p) contributions to σY and MY are analyzed separately in order to understand the origin of these effects. In line with this, the NChDE are studied on the shielding of both, nuclei in free atoms and nuclei in molecules. In addition, their NR limit are also analyzed. Furthermore, the model M–V is employed to study the underlying physics of the NChDE in σY. Finally, an analysis of how much the electronic correlation affects the NChDE is presented.4.1 Four-component RPA calculations
In order to study the NChDE on σY and MY, the relativistic RPA values of σ(e–e)⊥,Y,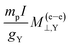 , and the NR limit of both, σNR–para⊥,Y, calculated with PNM and GNM are shown in Table 2.
, and the NR limit of both, σNR–para⊥,Y, calculated with PNM and GNM are shown in Table 2.
| Molec | Y | σNR–para⊥,Y | σ(e–e)⊥,Y | NChDE | |||||
|---|---|---|---|---|---|---|---|---|---|
| L | S | Δσ(e–e)⊥,Y | |||||||
| L | S | ||||||||
| HBr | Br | PNM | −742.0222 | −933.3812 | 199.2331 | −187.3019 | −2.3174 | 0.6091 | −0.8015 |
| GNM | −742.0164 | −932.7721 | 198.4316 | −189.6193 | |||||
| H | PNM | 16.6034 | 25.6238 | −0.2920 | 25.0586 | −0.0002 | −0.0003 | 0.0000 | |
| GNM | 16.6034 | 25.6235 | −0.2920 | 25.0584 | |||||
| HI | I | PNM | −1454.4561 | −2114.7400 | 754.8454 | 650.5588 | −22.9512 | 5.6493 | −8.0874 |
| GNM | −1454.4296 | −2109.0907 | 746.7580 | 627.6076 | |||||
| H | PNM | 17.8542 | 49.0594 | −2.0569 | 44.9705 | −0.0032 | −0.0037 | 0.0002 | |
| GNM | 17.8542 | 49.0557 | −2.0567 | 44.9673 | |||||
| HAt | At | PNM | −2661.1988 | −4445.6835 | 4383.2938 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293.7041 293.7041 |
−794.5878 | 24.8291 | −239.2336 |
| GNM | −2661.0624 | −4420.8544 | 4144.0602 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 499.1163 499.1163 |
|||||
| H | PNM | 18.4044 | 147.3452 | −22.0295 | 103.3245 | −0.1183 | −0.1989 | 0.0404 | |
| GNM | 18.4044 | 147.1463 | −21.9891 | 103.2062 | |||||
In addition, in Table 3 we show the values of σ(p–p)⊥,Y, 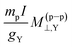 and σNR–dia⊥,Y also calculated employing both, GNM and PNM.
and σNR–dia⊥,Y also calculated employing both, GNM and PNM.
| Molec | Y | σNR–dia⊥,Y | σ(p–p)⊥,Y | NChDE | |||||
|---|---|---|---|---|---|---|---|---|---|
| L | S | Δσ(p–p)⊥,Y | |||||||
| L | S | ||||||||
| HBr | Br | PNM | 3128.2970 | 55.7286 | −55.6017 | 2916.0124 | 0.3968 | 0.0258 | −0.0257 |
| GNM | 3128.2769 | 55.7544 | −55.6274 | 2916.4092 | |||||
| H | PNM | 4.8032 | 0.0007 | −0.0005 | 4.8423 | −0.0001 | 0.0000 | 0.0000 | |
| GNM | 4.8031 | 0.0007 | −0.0005 | 4.8422 | |||||
| HI | I | PNM | 5507.2979 | 144.2528 | −143.8763 | 4889.9425 | 2.8728 | 0.4270 | −0.4262 |
| GNM | 5507.2060 | 144.6798 | −144.3025 | 4892.8153 | |||||
| H | PNM | 3.2126 | 0.0014 | −0.0005 | 3.3116 | −0.0004 | 0.0000 | 0.0000 | |
| GNM | 3.2125 | 0.0014 | −0.0005 | 3.3112 | |||||
| HAt | At | PNM | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561.1286 561.1286 |
282.9505 | −281.8745 | 8598.5672 | 40.8135 | 16.4999 | −16.4524 |
| GNM | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560.6251 560.6251 |
299.4504 | −298.3269 | 8639.3807 | |||||
| H | PNM | 1.5937 | 0.0021 | −0.0003 | 2.6640 | −0.0080 | 0.0000 | 0.0000 | |
| GNM | 1.5932 | 0.0021 | −0.0003 | 2.6560 | |||||
The SR constants are multiplied by the factor 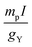 , which is the quotient between σNR–para⊥,Y and MNR–elec⊥,Y (the NR limits of σ(e–e)⊥,Y and M(e–e)⊥,Y, respectively) as proposed by the Flygare's NR relation:25
, which is the quotient between σNR–para⊥,Y and MNR–elec⊥,Y (the NR limits of σ(e–e)⊥,Y and M(e–e)⊥,Y, respectively) as proposed by the Flygare's NR relation:25
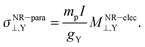 | (16) |
Given that Melec⊥,Y can be expressed as the sum of two terms (Melec⊥,Y = ML⊥,Y + MS⊥,Y; see in eqn (7) that Je = Le + Se), its values are splitted up into ML⊥,Y and MS⊥,Y. In addition, the NChDE values for each property are displayed in Tables 2 and 3.
The NChDE on σY and MY are obtained as the differences between the values of each property employing Gaussian-type and point-type nuclear charge distribution models. Throughout this work, unless otherwise stated, the symbol Δ will be exclusively employed to refer to these differences (for example, ΔσY = σGNMY − σPNMY).
One important finding is that in all cases ΔML⊥,Y and ΔMS⊥,Y have opposite signs, as shown in the last two columns of Tables 2 and 3. For the heavy nucleus X, ΔMS(e–e)⊥,X grows faster than ΔML(e–e)⊥,X as the atomic number of the X atom increases (X = Br, I, At). The opposite behavior is found for the hydrogen nucleus.
The relative value of the NChDE in both properties needs a special mention. Its importance with respect to the relativistic effects on M(e–e)⊥,Y and σ(e–e)⊥,Y (i.e. 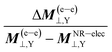 and
and 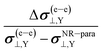 ) increases from −2.5% (SR) and −0.4% (shielding) for Br, up to −9.0% (SR) and −6.0% (shielding) for At (see Table 2). This means that the NChDE grows faster than the relativistic effects, specially for shieldings.
) increases from −2.5% (SR) and −0.4% (shielding) for Br, up to −9.0% (SR) and −6.0% (shielding) for At (see Table 2). This means that the NChDE grows faster than the relativistic effects, specially for shieldings.
It is also worth to highlight the fact that Δσ(e–e)⊥,Y represents 1.2% of σ(e–e)⊥,Y for Y = Br, and it grows up to 7.6% for Y = At. On the other hand, ΔM(e–e)⊥,Y represents 0.03% of M(e–e)⊥,Y when Y = Br and increases up to 77.5% for Y = At!
According to our results, we can state that the choice of the nuclear model used on relativistic calculations of shieldings and SR constants is increasingly more important as heavier nuclei are involved. It can still be crucial for calculations of SR constants of nuclei belonging to the 6th row of the periodic table.
As observed in Table 3, there are two important points to be highlighted for Δσ(p–p)⊥,Y and ΔM(p–p)⊥,Y. The first one is that ΔM(p–p)⊥,Y is close to zero for all nuclei. This behavior can be understood by considering the LRESC model, from which the NR limit and the leading order in a 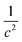 expansion of M(p–p)⊥,Y are found to be zero.17 The nucleus of At has the largest value, where
expansion of M(p–p)⊥,Y are found to be zero.17 The nucleus of At has the largest value, where 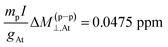 , and
, and 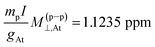 .
.
The second point is that Δσ(p–p)⊥,Y is less than 0.5% of σ(p–p)⊥,Y for all Y nuclei. Therefore, the NChDE have an influence that is greater on the (e–e) than on the (p–p) contributions for both properties.
4.2 The NR limit
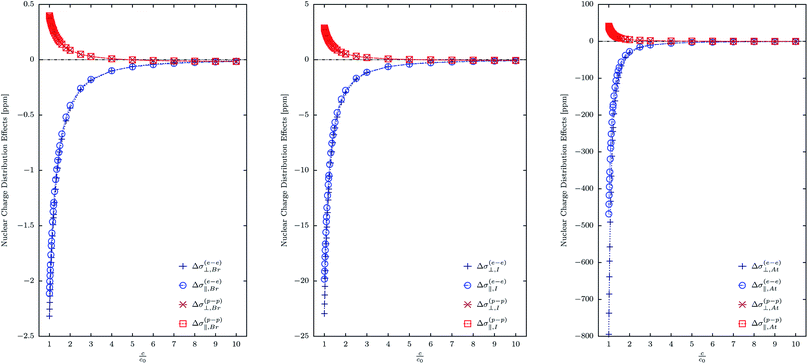
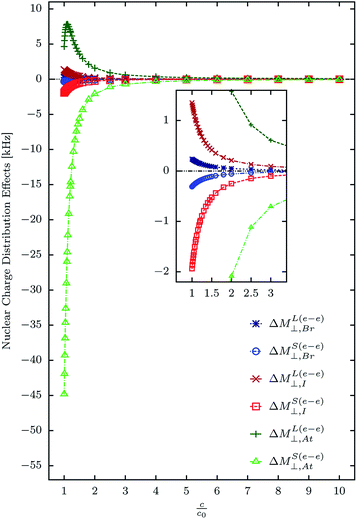
By applying the relativistic polarization propagator formalism the NR limit of ΔMY and ΔσY can be straightforwardly obtained. According to this theory the NR limit is reached when the speed of light is scaled to infinity. This is the reason why a set of calculations of the tensor elements of MY and σY was performed considering the two nuclear models, and systematically increasing the velocity of light; we employed 32 values of c between c0 and 10c0. An smooth convergence of ΔMY and ΔσY to values that are close to zero was found in all cases.In Fig. 1 and 2 one can observe the dependence of the (e–e) and (p–p) contributions to ΔσX and ΔMX with the velocity of light, respectively. It is shown that all of them become vanishingly small as c scales to infinity.
In Fig. 1 we observe that there is a higher rate of change of the (e–e) contributions as compared with the (p–p) contributions. This indicates a higher sensitivity of Δσ(e–e)X to the relativistic effects compared with Δσ(p–p)X. Furthermore, Δσ(e–e)⊥,X is more sensitive to the relativistic effects than Δσ(e–e)‖,X; this is not the behavior of the (p–p) contributions.
On the other hand, in Fig. 2 we show how ΔML(e–e)⊥,X and ΔMS(e–e)⊥,X go to zero as c scales to infinity. A higher slope of ΔMS(e–e)⊥,X than that of ΔML(e–e)⊥,X is also observed. It means that ΔMS(e–e)⊥,X is most sensitive than ΔML(e–e)⊥,X to the relativistic effects.
It is worth to mention that for At, 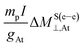 changes from −239.23 ppm to −5.95 ppm (about +233 ppm of variation) when the speed of light is scaled from c0 to 2.5c0. For the same values of c,
changes from −239.23 ppm to −5.95 ppm (about +233 ppm of variation) when the speed of light is scaled from c0 to 2.5c0. For the same values of c, 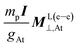 changes only −20 ppm (from 24.83 ppm to 4.88 ppm).
changes only −20 ppm (from 24.83 ppm to 4.88 ppm).
We should emphasize here that the values of σ(e–e)‖,Y, MS(e–e)⊥,Y, ML(p–p)⊥,Y and MS(p–p)⊥,Y are exactly zero in the NR limit, and therefore, their NChDE vanish in such a limit. Comparing eqn (7) with eqn (10) it can be seen that
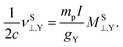 | (17) |
Then, it indicates that νS(e–e)⊥,Y and νS(p–p)⊥,Y and their NChDE are also exactly zero in the NR limit. Following the same argument, the NChDE on σatom(e–e)Y and 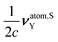 are zero in such limit.
are zero in such limit.
Therefore, we can state that Δσ(e–e)‖,Y, ΔMS(e–e)⊥,Y, ΔM(p–p)⊥,Y, Δσatom(e–e)Y, ΔνS(e–e)⊥,Y, ΔνS(p–p)⊥,Y and 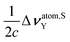 can have values that are different from zero only within the relativistic framework. All this means that only Δσ(e–e)⊥,Y, ΔML(e–e)⊥,Y, Δσ(p–p)Y and Δσatom(p–p)Y may have values that are very small in the NR limit, but not exactly zero.
can have values that are different from zero only within the relativistic framework. All this means that only Δσ(e–e)⊥,Y, ΔML(e–e)⊥,Y, Δσ(p–p)Y and Δσatom(p–p)Y may have values that are very small in the NR limit, but not exactly zero.
Still, according to eqn (11)–(14), the following NR limits are fulfilled:
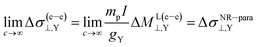 | (18) |
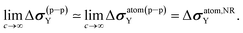 | (19) |
As shown in Fig. 1 and 2, they are vanishingly small.
4.3 Relation between the σY and MY tensors
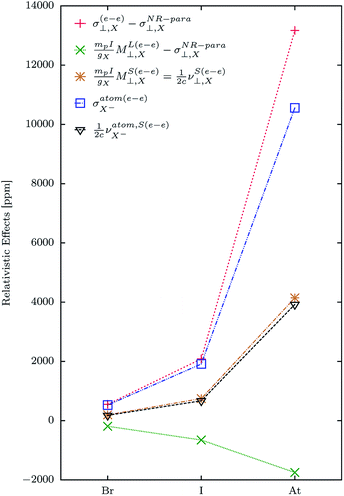
In this Section we want to shed some light on the influence of the NChDE on each of the four terms of the M–V model given in eqn (9). We shall see that the first two terms of eqn (9) contain almost the whole of the NChDE of σ in a relativistic framework because each one of the last two are close each other. Therefore we will focus our analysis on these terms.In Fig. 3 the relativistic effects (i.e., the differences between four-component and NR calculations using a GNM) on σ(e–e)⊥,X, ML(e–e)⊥,X and MS(e–e)⊥,X for the heavy nuclei X are shown. The values of σatom(e–e)X, that has only relativistic contributions, are also given.
It can easily be seen in Fig. 3 that the main relativistic contribution to σ(e–e)⊥,X comes from the shielding of the free atom X, followed far away by that of the SR constant (which is given by 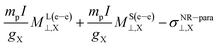 ). Besides, the relativistic effects on ML⊥,X and MS⊥,X have opposite signs, which reduces the total relativistic effect of this property.
). Besides, the relativistic effects on ML⊥,X and MS⊥,X have opposite signs, which reduces the total relativistic effect of this property.
The value of the relativistic effect on 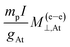 is 2384.27 ppm, whereas for
is 2384.27 ppm, whereas for 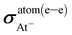 it is 10
it is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557.13 ppm (remember that it has no NR counterpart). The addition of both values gives 12
557.13 ppm (remember that it has no NR counterpart). The addition of both values gives 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941.40 ppm, which is close to the total relativistic effect of σ(e–e)⊥,At: 13
941.40 ppm, which is close to the total relativistic effect of σ(e–e)⊥,At: 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160.18 ppm. According to the M–V model (see eqn (11)) the remaining difference between those values arises from
160.18 ppm. According to the M–V model (see eqn (11)) the remaining difference between those values arises from 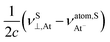 , which is equal to 219.49 ppm. It must be emphasized that νS⊥,Y and νatom,SY are zero in the NR limit.
, which is equal to 219.49 ppm. It must be emphasized that νS⊥,Y and νatom,SY are zero in the NR limit.
Another interesting finding is the fact that 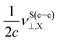 and
and 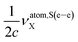 are close each other (for X = Br, I, At) and so, given that they contribute with different sign, its total contribution becomes small.
are close each other (for X = Br, I, At) and so, given that they contribute with different sign, its total contribution becomes small.
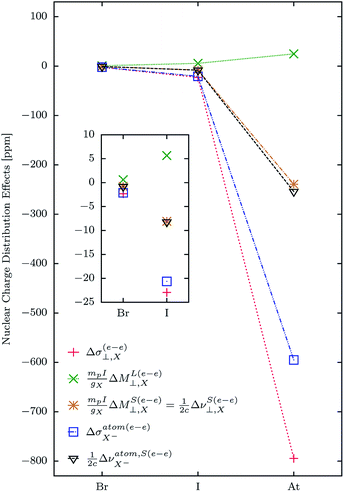
The NChDE on SR and shielding tensors have an almost complete relativistic origin, which explain the behavior of different contributions to the NChDE shown in Fig. 4. The main contribution to Δσ(e–e)⊥,X in the HX systems comes from the NChDE on the free-atom shielding, followed by 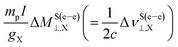 . In addition, ΔML(e–e)⊥,X is almost zero in all cases.
. In addition, ΔML(e–e)⊥,X is almost zero in all cases.
According to eqn (11), 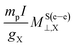 must be included two times in σM–V⊥,X. It can be seen in Fig. 4 that its NChDE is almost equal to
must be included two times in σM–V⊥,X. It can be seen in Fig. 4 that its NChDE is almost equal to 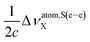 . Given that νS⊥,X and νatom,SX have opposite signs in eqn (11), the sum of their NChDE is almost zero.
. Given that νS⊥,X and νatom,SX have opposite signs in eqn (11), the sum of their NChDE is almost zero.
Finally, in Table 4 we display the values of the calculations of 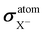 and
and 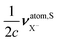 , used to obtain σM–V⊥,Y and σM–V‖,Y according to eqn (9)–(15).
, used to obtain σM–V⊥,Y and σM–V‖,Y according to eqn (9)–(15).
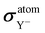 and
and 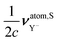 at the RPA level of approach using PNM and GNM. All values are in ppm
at the RPA level of approach using PNM and GNM. All values are in ppm
4.4 Isotropic SR and shielding constants
We turn now to the analysis of how important are the NChDE in measurable quantities, such as the total SR constants and the chemical shifts.In Table 5 it is observed that the NChDE on σisoY of all heavy elements are more important for (e–e) than for (p–p) contributions, although they have opposite signs and so partially cancel each other. As the nucleus becomes heavier, also the difference increases in such a way that for At Δσiso(e–e)At ≅ −686 ppm, while Δσiso(p–p)At ≅ +41 ppm. It means that almost all the NChDE on σisoAt arises from its (e–e) contribution, which is known to be related to the (e–e) part of the SR constant.
| Mol | Y | σ(e–e)Y | σ(p–p)Y | NChDE | |||||
|---|---|---|---|---|---|---|---|---|---|
| L | S | ΔσY | |||||||
| HBr | Br | PNM | 35.6973 | 2914.9512 | −622.2541 | 132.8221 | 0.0846 | −1.8526 | −0.1282 |
| (35.8770) | (2914.8036) | (−1.8510) | |||||||
| GNM | 33.4479 | 2915.3479 | −621.8481 | 132.2877 | 0.0846 | ||||
| (33.6276) | (2915.2020) | ||||||||
| H | PNM | 16.5881 | 19.3448 | 17.0825 | −0.1947 | 0.0001 | −0.0002 | −0.0002 | |
| (16.5798) | (19.4010) | (−0.0003) | |||||||
| GNM | 16.5879 | 19.3448 | 17.0824 | −0.1947 | 0.0001 | ||||
| (16.5796) | (19.4009) | ||||||||
| HI | I | PNM | 996.8285 | 4888.6446 | −1409.8267 | 503.2302 | 0.2510 | −19.0394 | −1.6249 |
| (997.0165) | (4889.1715) | (−19.0659) | |||||||
| GNM | 974.9165 | 4891.5173 | −1406.0605 | 497.8387 | 0.2515 | ||||
| (975.1000) | (4892.0221) | ||||||||
| H | PNM | 28.7990 | 19.2680 | 32.7063 | −1.3713 | 0.0006 | −0.0023 | −0.0023 | |
| (28.7550) | (19.0097) | (−0.0024) | |||||||
| GNM | 28.7971 | 19.2677 | 32.7038 | −1.3711 | 0.0006 | ||||
| (28.7530) | (19.0093) | ||||||||
| HAt | At | PNM | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222.0816 222.0816 |
8596.8899 | −2963.7890 | 2922.1959 | 0.7173 | −644.9436 | −142.9047 |
(10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222.6242) 222.6242) |
(8596.8895) | (−644.5038) | |||||||
| GNM | 9536.3418 | 8637.6861 | −2947.2362 | 2762.7068 | 0.7490 | ||||
| (9536.9043) | (8638.1056) | ||||||||
| H | PNM | 55.3711 | 19.5859 | 98.2302 | −14.6863 | 0.0012 | −0.0588 | −0.1057 | |
| (55.3218) | (19.1304) | (−0.0588) | |||||||
| GNM | 55.3180 | 19.5802 | 98.0975 | −14.6594 | 0.0012 | ||||
| (55.2687) | (19.1247) | ||||||||
For hydrogen in HX, ΔσisoY has also a greater (e–e) contribution than its (p–p) counterpart, but the sum of both represent only a small contribution to the total shielding. The NChDE is completely negligible for the shielding of hydrogen in this series of compounds. For H in HAt, ΔσisoH = −0.06 ppm, and the total isotropic shielding is σisoH = 74.90 ppm.
The analysis of the isotropic SR constant is unnecessary, as it would be completely analogous to that of the perpendicular contribution to the SR tensor performed above. This occurs because the parallel component of MY is always exactly zero for linear molecules. Nevertheless, as its isotropic value is related to the isotropic shielding constant, some remarks must be done. The contributions ΔMS(e–e)Y are more important than ΔML(e–e)Y, as it was shown in Section 4.1. In the special case of At, the NChDE must be included in the 4-component RPA calculations. When a PNM is used, a value of 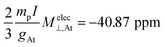 is obtained, whereas it becomes −183.78 ppm when a GNM is employed.
is obtained, whereas it becomes −183.78 ppm when a GNM is employed.
Although the NChDE has an important contribution to σisoAt in the HAt molecule (ΔσisoAt ≅ −645 ppm, whereas σisoAt ≅ 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174 ppm), the SR constant of this nucleus cannot be calculated with a PNM, at least at the RPA level of approach (ΔM⊥,At ≅ −40.15 kHz, whereas M⊥,At ≅ −50.10 kHz).
174 ppm), the SR constant of this nucleus cannot be calculated with a PNM, at least at the RPA level of approach (ΔM⊥,At ≅ −40.15 kHz, whereas M⊥,At ≅ −50.10 kHz).
Finally it can be seen in Table 5 that 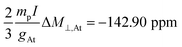 , whereas ΔσisoAt = −644.94 ppm. If we consider the relation between isotropic SR and shielding constants of eqn (15), the difference of almost −502 ppm must be originated in the NChDE on
, whereas ΔσisoAt = −644.94 ppm. If we consider the relation between isotropic SR and shielding constants of eqn (15), the difference of almost −502 ppm must be originated in the NChDE on 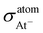 ,
, 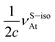 and
and 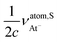 . Those contributions are −554.33 ppm, −218.30 ppm and −270.55 ppm, respectively (see Table 4). As expected, applying the model M–V we found that
. Those contributions are −554.33 ppm, −218.30 ppm and −270.55 ppm, respectively (see Table 4). As expected, applying the model M–V we found that 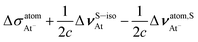 gives −502 ppm.
gives −502 ppm.
4.5 Electron correlation effects
It is already known that the influence of electron correlation on both properties, M and σ, is not vanishingly small.16,51–55 For this reason we want now to have an estimation of how large is the effect of electron correlation when it is included on top of the NChDE.On the other hand, it was also proposed that one should consider a likely relation among the electron correlation and relativistic effects.51,56–60 This relation was recently shown to be not independent one to the other.22,54 So, it may be the case that the electron correlation and the NChDE are also dependent each other.
We have calculated both properties employing the set of the DFT functionals just mentioned. Their results are then compared with those of the formalism of relativistic polarization propagator at the PZOA and RPA levels of approach.
It is worth to mention that the effect of using different optimized geometries for the HAt molecule (see Table 6) is analyzed in Section 4.7.
| Y | PZOA (30c0) | RPA (30c0) | PZOA | RPA | LDA | KT2 | KT3 | PBE | PBE0 | BP86 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimized internuclear distance of HAt, d [Å] | |||||||||||
| 1.7117 | 1.7117 | 1.7117 | 1.7117 | 1.7393 | 1.7237 | 1.7209 | 1.7473 | 1.7272 | 1.7486 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| Nuclear spin-rotation constant, M⊥,Y [kHz] | |||||||||||
| At | PNM | −195.6698 | −498.9680 | −210.0323 | −9.9507 | −508.9112 | −460.7026 | −464.0808 | −502.2031 | −380.5749 | −522.0404 |
| [−210.0691] | [−11.1909] | [−509.0746] | [−461.1092] | [−464.5591] | [−502.4821] | [−381.1630] | [−522.2780] | ||||
| (−209.3955) | (−13.9944) | (−380.6544) | |||||||||
| GNM | −195.6567 | −498.9254 | −212.7869 | −50.1043 | −521.3197 | −476.8684 | −482.5742 | −518.0560 | −401.0481 | −537.3335 | |
| [−212.8095] | [−51.2080] | [−521.4142] | [−477.1821] | [−482.9482] | [−518.2485] | [−401.5337] | [−537.4886] | ||||
| (−212.1064) | (−53.5440) | (−400.8014) | |||||||||
| NChDE | 0.0131 | 0.0426 | −2.7546 | −40.1536 | −12.4086 | −16.1658 | −18.4935 | −15.8529 | −20.4732 | −15.2932 | |
| [−2.7404] | [−40.0171] | [−12.3396] | [−16.0729] | [−18.3891] | [−15.7663] | [−20.3707] | [−15.2106] | ||||
| (−2.7108) | (−39.5496) | (−20.1470) | |||||||||
| H | PNM | 15.0352 | 22.6770 | 30.0948 | 134.6123 | 87.4231 | 108.7527 | 113.8844 | 98.9048 | 100.5139 | 98.7846 |
| [30.0720] | [134.3519] | [87.2819] | [108.5540] | [113.6760] | [98.7390] | [100.3412] | [98.6215] | ||||
| (30.0148) | (133.4457) | (99.8442) | |||||||||
| GNM | 15.0350 | 22.6770 | 30.0776 | 134.4412 | 87.3694 | 108.6787 | 113.8095 | 98.8470 | 100.4410 | 98.7280 | |
| [30.0549] | [134.1820] | [87.2286] | [108.4806] | [113.6017] | [98.6817] | [100.2688] | [98.5654] | ||||
| (29.9979) | (133.2782) | (99.7724) | |||||||||
| NChDE | −0.0002 | 0.0000 | −0.0172 | −0.1710 | −0.0537 | −0.0740 | −0.0749 | −0.0577 | −0.0729 | −0.0566 | |
| [−0.0171] | [−0.1699] | [−0.0532] | [−0.0734] | [−0.0743] | [−0.0572] | [−0.0724] | [−0.0561] | ||||
| (−0.0169) | (−0.1675) | (−0.0718) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| Isotropic shielding, σisoY [ppm] | |||||||||||
| At | PNM | 9868.2250 | 8788.9069 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 367.0409 367.0409 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818.9715 818.9715 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174.0916 174.0916 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.4577 485.4577 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465.1341 465.1341 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 193.3143 193.3143 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670.9702 670.9702 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102.6616 102.6616 |
[18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353.8247] 353.8247] |
[18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813.1328] 813.1328] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.3952] 156.3952] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 466.8488] 466.8488] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446.2788] 446.2788] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175.2538] 175.2538] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 655.5501] 655.5501] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 084.8228] 084.8228] |
||||
(18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311.2648) 311.2648) |
(18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790.1375) 790.1375) |
(17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640.2978) 640.2978) |
|||||||||
| GNM | 9867.6753 | 8788.4615 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836.8715 836.8715 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174.0279 174.0279 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609.5902 609.5902 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893.5203 893.5203 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868.1533 868.1533 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614.4299 614.4299 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078.4087 078.4087 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525.8056 525.8056 |
|
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824.455] 824.455] |
[18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168.5988] 168.5988] |
[16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 593.2425] 593.2425] |
[16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876.3551] 876.3551] |
[16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850.7811] 850.7811] |
[16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597.7836] 597.7836] |
[17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064.1743] 064.1743] |
[16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509.3639] 509.3639] |
||||
(17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784.0321) 784.0321) |
(18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147.0935) 147.0935) |
(17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 049.9388) 049.9388) |
|||||||||
| NChDE | −0.5497 | −0.4454 | −530.1694 | −644.9436 | −564.5014 | −591.9374 | −596.9808 | −578.8844 | −592.5615 | −576.8560 | |
| [−529.3697] | [−644.5340] | [−563.1527] | [−590.4937] | [−595.4977] | [−577.4702] | [−591.3758] | [−575.4589] | ||||
| (−527.2327) | (−643.0440) | (−590.3590) | |||||||||
| H | PNM | 26.7409 | 31.6572 | 34.0931 | 74.9570 | 59.3366 | 68.4100 | 70.3058 | 64.4792 | 64.2976 | 64.5248 |
| [34.0878] | [74.9061] | [59.3063] | [68.3672] | [70.2631] | [64.4466] | [64.2621] | [64.4932] | ||||
| (34.0932) | (74.7724) | (64.1956) | |||||||||
| GNM | 26.7406 | 31.6567 | 34.0831 | 74.8982 | 59.3150 | 68.3824 | 70.2789 | 64.4577 | 64.2702 | 64.5040 | |
| [34.0777] | [74.8475] | [59.2847] | [68.3397] | [70.2364] | [64.4252] | [64.2349] | [64.4725] | ||||
| (34.0833) | (74.7144) | (64.1685) | |||||||||
| NChDE | −0.0003 | −0.0005 | −0.0100 | −0.0588 | −0.0216 | −0.0276 | −0.0269 | −0.0215 | −0.0274 | −0.0208 | |
| [−0.0101] | [−0.0586] | [−0.0216] | [−0.0275] | [−0.0267] | [−0.0214] | [−0.0272] | [−0.0207] | ||||
| (−0.0099) | (−0.0580) | (−0.0271) | |||||||||
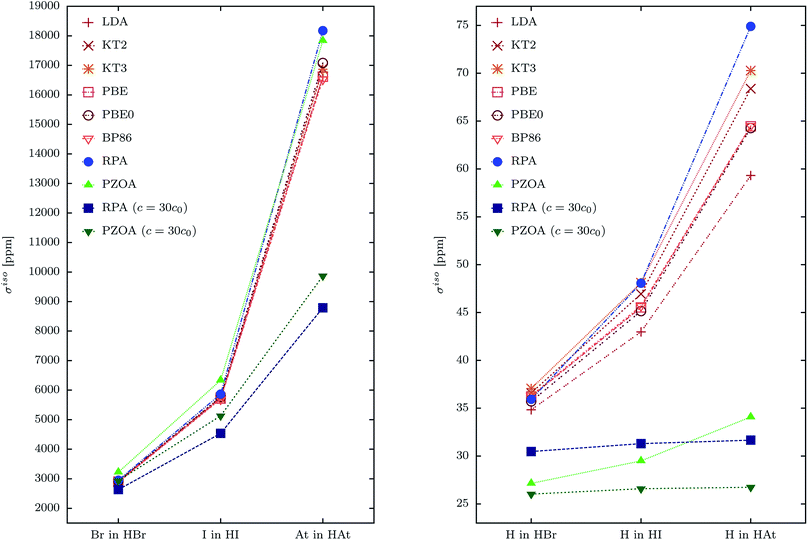
In Fig. 5 and 6 we observe the size of relativistic and electron correlation effects on SR constants and isotropic shieldings. All values in both figures were obtained employing GNM. It is also observed that, in all cases (but not for H in HBr), the DFT values are always smaller than the RPA ones. In addition, it is clearly shown that the relativistic effects at RPA level (given by the difference between the relativistic RPA values and their equivalent NR RPA which were obtained for c = 30c0) are positive and directly proportional to ZX. This behavior is similar for both properties, M⊥,Y and σisoY.
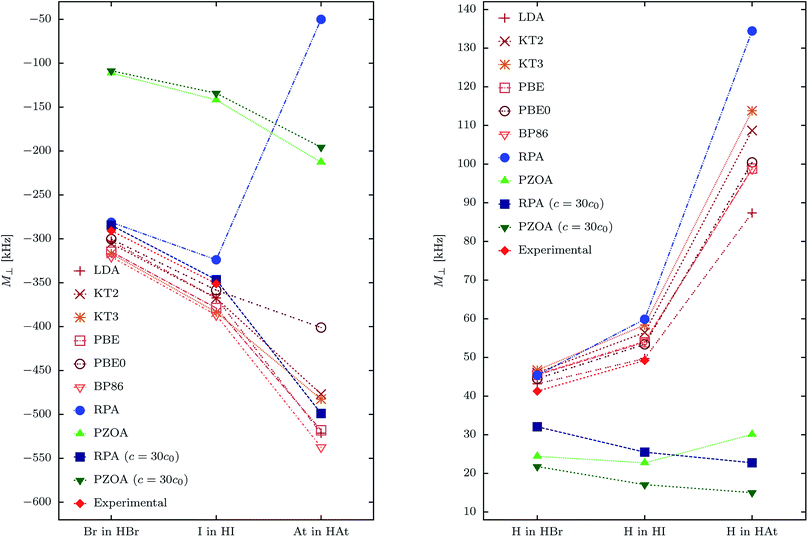 | ||
| Fig. 5 Relativistic spin-rotation values of both nuclei in HX molecules (X = Br, I, At). Results at PZOA and RPA levels of approach and also employing different DFT functionals are shown. In addition, PZOA and RPA results with c = 30c0 are displayed in order to show the behavior of M⊥ in the NR limit. All calculations were performed using the GNM, and the results are given in kHz. Experimental values (in kHz) are: 41.27(31) (H in HBr),61 −290.83(8) (Br in HBr),61 49.22(22) (H in HI)62 and −351.1(3) (I in HI).62 | ||
In the special case of M⊥,At, the relativistic RPA value is −50.10 kHz (employing GNM), and all DFT values are between −540 kHz and −400 kHz (see Table 6). This is in agreement with previous results of Komorovsky and co-authors.53 For σisoAt, the RPA calculation (with GNM) gives a result of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174.03 ppm, whereas the DFT values (also with GNM) are between 16
174.03 ppm, whereas the DFT values (also with GNM) are between 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 ppm and 17
525 ppm and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 ppm. It means that correlation effects are much more important for M⊥,At than for σisoAt.
078 ppm. It means that correlation effects are much more important for M⊥,At than for σisoAt.
The analysis of electron correlation effects within the polarization propagator theory may start considering the zeroth-order or PZOA level of approach and the consistent first order or RPA.37 The second-order level of approach or SOPPA is not included here because it is not available in the DIRAC code.
In Fig. 5 we show the behavior of M⊥,X and M⊥,H in the whole set of HX molecules. In the case of M⊥,X the PZOA approach gives similar values in both regimes, but the relativistic RPA does give a value for X = At that is far away from its NR counterpart and all DFT functionals. On the other hand, for hydrogen, the pattern of both, the NR PZOA and NR RPA is opposite to that of the relativistic PZOA and RPA. A similar pattern is found for σisoH though this time the pattern of the relativistic PZOA and RPA for values of σisoX is quite similar to the corresponding DFT values (see Fig. 6). The difference between the patterns of M⊥,X and σisoX for X = At is due to the contribution of the second term of eqn (15), the atomic contribution, which makes that the RPA value of σisoAt follows the same tendency as its equivalent DFT values.
On the other hand, the fact that the RPA value of ML(e–e)At is much smaller than its equivalent in DFT makes that the RPA value of M⊥,At is also much smaller, in absolute value, than the DFT ones (see ESI†). This explains what is shown in Fig. 5.
As can be seen in Table 6 the electron correlation on the NChDE of both, M⊥,At and σisoAt follows the same trend from PZOA to RPA as from PZOA to any DFT. The main difference is that the RPA values are little exaggerated. The same behavior is shown in the ESI† for HBr and HI.
In the case of the NChDE on M⊥ we observe that the RPA value of ΔM⊥,At is −40.15 kHz, and DFT results are between −12 kHz and −21 kHz, depending on the employed functional. These results indicate that a proper analysis of the NChDE of the M⊥,At in heavy-element-containing molecules must include correlation effects. ΔM⊥,At is of the order of 5% for the PBE0 level of theory.
On the other hand, the RPA value of ΔσisoAt is −645 ppm, but its values for different functionals are between −597 ppm and −564 ppm. These results indicate that the NChDE in σisoAt are, in relative terms, less influenced by correlation effects than the NChDE in M⊥,At. This behavior is explained by the fact that the NChDE on shieldings is mostly given by ΔσatomY (as it was shown in Section 4.3) and the fact that the shielding of free atoms is almost not influenced by correlation effects. In this case ΔσisoAt at PBE0 level is about 3%.
The correlation effect that influence the total NChDE does reduce it in both properties. For At, employing the PBE0 functional, Δσiso is reduced in 8.12% but in ΔM⊥ its reduction is of 49.01%. In other words, both, the NChDE and the correlation effects are not independent each other, as one may expect from our finding that the NChDE is almost purely relativistic, together with some previously published results where it was shown that correlation effects are not independent of relativistic effects.22
In the ESI† we give a table similar to Table 6, where results of calculations of M⊥ and σiso for the HBr and HI molecules at RPA and DFT levels of approach are given. In that cases, a similar behavior is found though much reduced in both, absolute and percentage values.
4.6 Contributions of (SS|SS) integrals and Gaunt interactions
Given that the NChDE are relatively small for M⊥,At and σisoAt, we want to go one step further and analyze how large are the contributions of the two-electron (SS|SS) integrals and the electron–electron Gaunt interactions in both properties.For M⊥,At and using GNM we observe in Table 6 that the largest contribution appears at RPA level of approach, which is of the order of 7%. At PBE0 its contribution is less than 0.1%. Furthermore the addition of both contributions, i.e. the (SS|SS) integrals and the Gaunt interactions, to the NChDE gives a total variation of the order of 1.5% at both levels of theory, RPA and PBE0.
In the case of the isotropic shielding of At, the contribution of both (SS|SS) integrals and Gaunt interactions at both, RPA and PBE0 levels of theory, is close to −0.15%. In this case its contribution to the NChDE is ≃0.3% at RPA and ≃0.37% at PBE0.
We should stress here that the contribution of Gaunt interactions are a little bit larger than the contributions of (SS|SS) integrals.
4.7 Internuclear distance
As it was expressed in Sections 3 and 4.5, all the calculations that involve the HAt molecule were performed employing different optimized geometries according to different levels of theory (RPA or the chosen DFT functionals). An analysis of the effects of the variation of distances in the calculations of shieldings and SR for the HAt molecule must therefore be given.In Table 7 we display the values of SR and isotropic shieldings of H and At, employing the smallest and largest internuclear distances optimized within the DFT level of approach: 1.7209 Å (KT3) and 1.7486 Å (BP86) (see Table 6).
| d(Å) | LDA | KT2 | KT3 | PBE | PBE0 | BP86 | |
|---|---|---|---|---|---|---|---|
| M⊥,At [kHz] | |||||||
| PNM | 1.7209 | −496.6202 | −459.2587 | −464.0807 | −486.2404 | −378.4707 | −504.2249 |
| GNM | −508.8192 | −475.3626 | −482.5742 | −501.5918 | −398.7274 | −519.0410 | |
| NChDE | −12.1990 | −16.1038 | −18.4934 | −15.3513 | −20.2567 | −14.8161 | |
| PNM | 1.7486 | −515.1978 | −473.6118 | −477.4298 | −503.0270 | −387.7653 | −522.0403 |
| GNM | −527.7124 | −490.3322 | −496.7065 | −518.9058 | −408.9899 | −537.3335 | |
| NChDE | −12.5146 | −16.7204 | −19.2766 | −15.8787 | −21.2245 | −15.2931 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| M⊥,H [kHz] | |||||||
| PNM | 1.7209 | 86.7008 | 108.5049 | 113.8844 | 97.3378 | 100.0081 | 97.2126 |
| GNM | 86.6470 | 108.4310 | 113.8095 | 97.2796 | 99.9353 | 97.1555 | |
| NChDE | −0.0538 | −0.0739 | −0.0749 | −0.0582 | −0.0727 | −0.0571 | |
| PNM | 1.7486 | 87.8273 | 111.1163 | 116.8943 | 98.9913 | 102.3894 | 98.7845 |
| GNM | 87.7737 | 111.0420 | 116.8193 | 98.9336 | 102.3158 | 98.7279 | |
| NChDE | −0.0536 | −0.0743 | −0.0749 | −0.0577 | −0.0735 | −0.0565 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| σisoAt [ppm] | |||||||
| PNM | 1.7209 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275.7605 275.7605 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 499.2449 499.2449 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465.1341 465.1341 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334.9283 334.9283 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696.7445 696.7445 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.2627 258.2627 |
| GNM | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712.2401 712.2401 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907.5696 907.5696 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868.1533 868.1533 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758.3969 758.3969 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105.0952 105.0952 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683.6181 683.6181 |
|
| NChDE | −563.5204 | −591.6753 | −596.9808 | −576.5314 | −591.6493 | −574.6446 | |
| PNM | 1.7486 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121.2399 121.2399 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360.2991 360.2991 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328.5135 328.5135 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185.8907 185.8907 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581.0419 581.0419 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102.6616 102.6616 |
| GNM | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556.2251 556.2251 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765.9612 765.9612 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727.985 727.985 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 606.8817 606.8817 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985.2613 985.2613 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525.8056 525.8056 |
|
| NChDE | −565.0148 | −594.3379 | −600.5285 | −579.009 | −595.7806 | −576.856 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| σisoH [ppm] | |||||||
| PNM | 1.7209 | 58.6675 | 68.244 | 70.3058 | 63.3212 | 63.9706 | 63.3368 |
| GNMss | 58.6459 | 68.2163 | 70.2789 | 63.2993 | 63.9433 | 63.3155 | |
| NChDE | −0.0216 | −0.0277 | −0.0269 | −0.0219 | −0.0273 | −0.0213 | |
| PNM | 1.7486 | 59.6896 | 69.9431 | 72.1216 | 64.5404 | 65.4644 | 64.5248 |
| GNM | 59.668 | 69.9155 | 72.0952 | 64.5189 | 65.437 | 64.504 | |
| NChDE | −0.0216 | −0.0276 | −0.0264 | −0.0215 | −0.0274 | −0.0208 | |
As can be seen, the influence of the variation of d(H–At) on the NChDE of both properties and also on the properties themselves is very small. It means that the main results of Section 4.5 are still valid considering this effect.
Whereas it should be interesting to analyze in more detail the importance of the effect of varying the internuclear distance on SR and shieldings (it could give insights about vibrational effects) it is out of the scope of the present work.
5 Concluding remarks
This work was focused on getting new insights about the electronic origin and the size of the NChDE on spin-rotation constants (for the first time), and also on nuclear magnetic shieldings. We also investigated the effect of electron correlation and electron–electron Gaunt interactions on both response properties, and whether such effects are related each other.We have applied several recent theoretical tools that make easier the analysis. One of them is the possibility to separate the four-component expression of response properties, within the relativistic polarization propagator formalism, into two terms: the (e–e), which is paramagnetic-like due to it goes exactly to the paramagnetic contribution when c → ∞, and the (p–p), which is diamagnetic-like because it goes to the diamagnetic contribution when c → ∞. We also applied the recent generalization of the Flygare's relationship to the relativistic framework. This relationship is such that the nuclear magnetic shielding of a nucleus in a given molecular system can be expressed as the sum of three terms: its spin-rotation constant, the shielding of the nucleus in the free atom, and the last term that have two new contributions: one that can be related, for linear molecules, with the electronic spin part of the spin-rotation constant, and the second one which is a response property for the nucleus in the free atom.
Our main results are the following:
(1) The (e–e) terms of both properties are more dependent of the NChDE than the (p–p) ones.
(2) The NChDE on both properties are almost completely relativistic in its origin.
(3) Given that, in the NR limit only ML(e–e)⊥,Y and σatom(p–p)Y are nonzero, ΔML(e–e)⊥,Y and Δσatom(p–p)Y are very small and 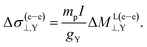
(4) The following are the terms which mainly contribute to the relativistic effects on
In the same manner, the following are the main contributions to the NChDE on
(5) Results of calculations performed at relativistic DFT/PBE0 level of theory are the closest to the experimental values of spin-rotation constants of Br and I. In the case of H the best reproduction of experimental values is given by the DFT/LDA functional.
(6) Electron correlation effects are very important for spin-rotation tensors. Values at DFT/PBE0 level of theory are eight times the values at relativistic RPA level of theory for At in HAt.
(7) When both effects, electron correlation and the NChDE are included altogether, the NChDE on M⊥,At is 5% of its total correlated value at relativistic DFT/PBE0 level of theory. In the case of relativistic RPA calculations, the NChDE is 80%.
(8) From the fact that the NChDE mostly is a relativistic effect, we can expect, and actually observe, that this effect is not independent of the electron correlation.
(9) The introduction of (SS|SS) type integrals and electron–electron Gaunt interaction modifies a few percent of the NChDE of both properties, and less than 0.3% of σisoAt.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge partial support from the Argentinian National Scientific and Technical Research Council (CONICET, Grant PIP 112-20130100361).References
- D. Andrae, in Nuclear Charge Density and Magnetization Distributions, ed. W. Liu, Springer Berlin Heidelberg, Berlin, Heidelberg, 2016, pp. 1–31 Search PubMed.
- L. Visscher and K. G. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef.
- L. Visscher, T. Saue and J. Oddershede, Chem. Phys. Lett., 1997, 274, 181–188 CrossRef.
- V. M. Shabaev, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 1103–1108 CrossRef.
- D. Andrae, Phys. Rep., 2000, 336, 413–525 CrossRef.
- R. Fukuda, M. Hada and H. Nakatsuji, J. Chem. Phys., 2003, 118, 1027–1035 CrossRef.
- S. Hamaya, H. Maeda, M. Funaki and H. Fukui, J. Chem. Phys., 2008, 129, 224103 CrossRef PubMed.
- E. Malkin, I. Malkin, O. L. Malkina, V. G. Malkin and M. Kaupp, Phys. Chem. Chem. Phys., 2006, 8, 4079–4085 RSC.
- E. Malkin, M. Repiský, S. Komorovský, P. Mach, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2011, 134, 044111 CrossRef PubMed.
- J. Autschbach, ChemPhysChem, 2009, 10, 2274–2283 CrossRef PubMed.
- S. Moncho and J. Autschbach, J. Chem. Theory Comput., 2010, 6, 223–234 CrossRef PubMed.
- A. F. Maldonado, C. A. Giménez and G. A. Aucar, J. Chem. Phys., 2012, 136, 224110 CrossRef PubMed.
- Y. Kita and M. Tachikawa, Comput. Theor. Chem., 2011, 975, 9–12 CrossRef.
- V. Arcisauskaite, J. I. Melo, L. Hemmingsen and S. P. A. Sauer, J. Chem. Phys., 2011, 135, 044306 CrossRef PubMed.
- E. Malkin, S. Komorovsky, M. Repisky, T. B. Demissie and K. Ruud, J. Phys. Chem. Lett., 2013, 4, 459–463 CrossRef PubMed.
- I. A. Aucar, S. S. Gomez, J. I. Melo, C. G. Giribet and M. C. Ruiz de Azúa, J. Chem. Phys., 2013, 138, 134107 CrossRef PubMed.
- I. A. Aucar, S. S. Gomez, M. C. Ruiz de Azúa and C. G. Giribet, J. Chem. Phys., 2012, 136, 204119 CrossRef PubMed.
- Y. Xiao and W. Liu, J. Chem. Phys., 2013, 138, 134104 CrossRef PubMed.
- Y. Xiao, Y. Zhang and W. Liu, J. Chem. Theory Comput., 2014, 10, 600–608 CrossRef PubMed.
- I. A. Aucar, S. S. Gomez, C. G. Giribet and G. A. Aucar, Phys. Chem. Chem. Phys., 2016, 18, 23572–23586 RSC.
- I. A. Aucar, S. S. Gomez, C. G. Giribet and G. A. Aucar, J. Phys. Chem. Lett., 2016, 7, 5188–5192 CrossRef PubMed.
- C. A. Giménez, A. F. Maldonado and G. A. Aucar, Theor. Chem. Acc., 2016, 135, 201–212 CrossRef.
- W. R. Johnson and G. Soff, At. Data Nucl. Data Tables, 1985, 33, 405–446 CrossRef.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef.
- W. H. Flygare, J. Chem. Phys., 1964, 41, 793–800 CrossRef.
- W. H. Flygare, Chem. Rev., 1974, 74, 653–687 CrossRef.
- W. H. Flygare and J. Goodisman, J. Chem. Phys., 1968, 49, 3122–3125 CrossRef.
- T. D. Gierke and W. H. Flygare, J. Am. Chem. Soc., 1972, 94, 7277–7283 CrossRef.
- G. A. Aucar and J. Oddershede, Int. J. Quantum Chem., 1993, 47, 425–435 CrossRef.
- G. A. Aucar, T. Saue, L. Visscher and H. J. A. Jensen, J. Chem. Phys., 1999, 110, 6208–6218 CrossRef.
- I. A. Aucar, S. S. Gomez, C. G. Giribet and M. C. Ruiz de Azúa, J. Chem. Phys., 2013, 139, 094112 CrossRef PubMed.
- G. A. Aucar, J. I. Melo, I. A. Aucar and A. F. Maldonado, Int. J. Quantum Chem., 2018, 118, e25487 CrossRef.
- DIRAC, a Relativistic Ab Initio Electronic Structure Program, Release DIRAC16 (2016), written by H. J. Aa. Jensen, R. Bast, T. Saue, and L. Visscher, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther, and S. Yamamoto (see http://www.diracprogram.org).
- L. Visscher, Theor. Chem. Acc., 1997, 98, 68–70 CrossRef.
- N. N. Dutta and S. Majumder, Phys. Rev. A, 2012, 85, 032512 CrossRef.
- K. Kozioł, C. A. Giménez and G. A. Aucar, J. Chem. Phys., 2018, 148, 044113 CrossRef PubMed.
- G. A. Aucar, R. H. Romero and A. F. Maldonado, Int. Rev. Phys. Chem., 2010, 29, 1–64 CrossRef.
- P. Raghavan, At. Data Nucl. Data Tables, 1989, 42, 189–291 CrossRef.
- W. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 97th edn, 2016 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, B864–B871 CrossRef.
- S. J. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- T. W. Keal and D. J. Tozer, J. Chem. Phys., 2003, 119, 3015–3024 CrossRef.
- T. W. Keal and D. J. Tozer, J. Chem. Phys., 2004, 121, 5654–5660 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B, 1986, 33, 8800–8802 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- P. J. Mohr, D. B. Newell and B. N. Taylor, Rev. Mod. Phys., 2016, 88, 035009 CrossRef.
- J. Autschbach and T. Ziegler, Relativistic Computation of NMR Shieldings and Spin–Spin Coupling Constants, in Advances in NMR, John Wiley and Sons, 2002, vol. 9, pp. 306–323 Search PubMed.
- A. Antušek and M. Jaszuński, Phys. Rev., 2006, 104, 1463–1474 Search PubMed.
- S. Komorovsky, M. Repisky, E. Malkin, T. B. Demissie and K. Ruud, J. Chem. Theory Comput., 2015, 11, 3729–3739 CrossRef PubMed.
- A. F. Maldonado and G. A. Aucar, J. Phys. Chem. A, 2014, 118, 7863–7875 CrossRef PubMed.
- I. L. Rusakova and L. B. Krivdin, Mendeleev Commun., 2018, 28, 1–13 CrossRef.
- E. Engel, S. Keller and R. M. Dreizler, Phys. Rev. A, 1996, 53, 1367–1374 CrossRef.
- R. Schmid, E. Engel, R. Dreizler, P. Blaha and K. Schwarz, Density Functional Theory, Academic Press, 1998, vol. 33, pp. 209–223 Search PubMed.
- T. Helgaker, M. Jaszuński and M. Pecul, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 53, 249–268 CrossRef.
- B. Jeziorski, Mol. Phys., 2010, 108, 3043–3054 CrossRef.
- I. L. Rusakova, Y. Y. Rusakov and L. B. Krivdin, Russ. Chem. Rev., 2016, 85, 356–426 CrossRef.
- F. P. Van Dijk and A. Dymanus, Chem. Phys. Lett., 1969, 4, 170–172 CrossRef.
- F. P. Van Dijk and A. Dymanus, Chem. Phys. Lett., 1968, 2, 235–236 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: It contains tables of total isotropic shieldings and nuclear spin-rotation constants for HBr and HI molecules. It also contains a more detailed description of the information given about HAt. See DOI: 10.1039/c8ra03948h |
| This journal is © The Royal Society of Chemistry 2018 |