Open Access Article
Open Access ArticleEu3+/2+ co-doping system induced by adjusting Al/Y ratio in Eu doped CaYAlO4: preparation, bond energy, site preference and 5D0–7F4 transition intensity†
Yu Pana,
Wenjun Wanga,
Yuhan Zhua,
Haibing Xua,
Liqun Zhoua,
Hyeon Mi Nohb,
Jung Hyun Jeong *b,
Xiaoguang Liu*a and
Ling Li
*b,
Xiaoguang Liu*a and
Ling Li *a
*a
aHubei Collaborative Innovation Center for Advanced Organochemical Materials, Ministry-of-Education Key Laboratory for the Synthesis and Applications of Organic Functional Molecules, Hubei University, Wuhan 430062, China. E-mail: liling402431@hotmail.com; Liuxiaoguang402@hotmail.com
bDepartment of Physics, Pukyong National University, Busan 608-737, Korea. E-mail: jhejong@pknu.ac.kr
First published on 2nd July 2018
Abstract
CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) phosphors have been synthesized via a solid-state reaction process. XRD patterns indicate that they are pure phase. The photoluminescence properties of the CaY1−xAl1+xO4:2%Eu phosphors exhibit both the blue emission of Eu2+ (4f65d1–4f7) and red-orange emission of Eu3+ (5D0–7F1,2,3,4) under UV light excitation, which showed that the Eu3+/2+ co-doping system was obtained by adjusting the Al/Y ratio. Eu3+ ions can be reduced to Eu2+ ions when the Al/Y ratio was changed. In this work, the bond energy method was used to determine and explain the mechanism of the site occupation of Eu ions entering the host matrix. Also, the emission spectrum showed an unusual comparable intensity 5D0–7F4 transition peak. The relative intensity of 5D0–7F2 and 5D0–7F4 can be stabilized by changing the relative proportions of Al3+ and Y3+. Furthermore, this was explained by the J–O theory.
1. Introduction
Rare-earth ions, as widely used activators, have been playing an irreplaceable role in lighting-emitting diodes (LEDs),1 due to their abundant emission colors based on the 4f–4f or 5d–4f transitions.2,3 The luminescence properties of different rare earth ions deliver an explicit comprehension on the internal correlations between them, which is generally determined by electronic configuration of the dopant and dynamic coupling between the dopant and the host lattices.4,5 The local structure around the rare earth in the crystal lattice also plays an important role in controlling its luminescence performance especially the 4f–5d transitions.6,7Eu ions, including Eu3+ and Eu2+, are the most commonly used activators in phosphor materials among the rare-earth ions.8–10 Eu2+ ions emit a tunable color ranging from ultraviolet to red due to its 5d–4f transition.11,12 The 5d orbit of Eu2+ is strongly affected by the environment of the crystal, thus the emission of Eu2+ is strongly influenced by the crystal field.13 Eu3+ is one of the most frequently used red-emitting activators, which mainly shows characteristic emissions resulting from the transitions of 5D0–7FJ (J = 0, 1, 2, 3, 4).14,15 However, the partly-forbidden f–f transitions of Eu3+ have low oscillator strength, resulting in low absorption efficiency and a low color rendering index (CRI). Therefore, it is a promising method to overcome the limitations of Eu3+ activated phosphors via the coexistence of Eu3+ and Eu2+ in single phase phosphors.16
The Eu3+/2+ co-doped phosphors can be prepared through a reduction annealing process in a reducing atmosphere such as H2, H2/N2 mixture or CO.16 After that, the Eu3+/Eu2+ co-doped phosphor can be obtained when Eu3+ was reduced to Eu2+ partially not completely. However, it is very difficult to obtain the Eu3+/Eu2+ co-doped CaYAlO4 even through conventional high temperature solid-state reaction under a reducing atmosphere. Another extreme example is Eu ion doped CaAl2O4, in which an abnormal reduction of Eu3+ → Eu2+ was observed in monoclinic phase of CaAl2O4: Eu that calcined in air atmosphere at high temperature.17,18 Comparing the formula of CaYAlO4 and CaAl2O4, the only change is their Al/Y ratio. Herein, we investigated the CaY1−xAl1+xO4:2%Eu system by adjusting the Al/Y ratio. In our work, the phenomenon of the reduction of Eu3+ to Eu2+ in CaY1−xAl1+xO4 systems was observed, and the bond energy method is adopted to theoretically explain the site preferential occupancy of Eu2+/Eu3+ in the CaY1−xAl1+xO4 systems.
The deviation of its bond energy in different lattice can be compared to determine which site the activators will occupy according to the similar property of chemical bonds and the similar value of their bond energy.19 The smaller deviation of the bond energy between the host and activators ions, the more easily the lattice site can be replaced by the ion. Therefore, we use this method to solve the site occupancy problem of doping rare earth ions in the matrix. In the previous research, the site preferential occupancy for Eu in Sr2V2O7, Sr9Gd(VO4)7 and Sr2V2O7/Sr9Gd(VO4)7 phosphors20 as well as the site occupancy preference of Bi2+ in β-Ca2P2O7 (ref. 21) crystal have been confirmed though the bond energy method.19 In addition, the bond energy method can connect the relationship between bond energy and preferential occupancy in Eu3+ doped in CaAl2Si2O8 crystal.22 Our calculated results are in good agreement with the experimental data and the photoluminescence spectra.
In addition, Eu3+-doped inorganic phosphors can be used as efficient orange to red emitting phosphors due to the 5D0–7FJ (J = 0, 1, 2, 3 and 4) transitions. Most of the phosphors show the dominant emission either 5D0 → 7F1 (∼593 nm) or 5D0 → 7F2 (∼610 nm) transition of Eu3+ ions. The dominated 5D0 → 7F4 (∼703 nm) transition emission is infrequent. Only some numerable phosphors show that they have stronger intensity of 5D0–7F4 than 5D0–7F1, such as Sr0.99[La(1−x)Eux]1.01Zn0.99O3.495,23 LaBO3:Eu3+,24 Na9[EuW10O36]·14H2O,25 Na2CaSiO4:Eu3+,26 Ca2Ga2SiO7:Eu3+,27 YAsO4:Eu.28 Similarly, this phenomenon has been found in CaYAlO4 with Eu doped. But, the stronger emission of 5D0–7F4 disappeared when Eu3+ and Tb3+ were co-doped into CaYAlO4.29 However, in our work, the relative intensity of 5D0–7F4 and 5D0–7F2 can be modified by changing the Al3+ and Y3+ ions ratios in CaY1−xAl1+xO4 and the Judd–Ofelt theory30 was applied to calculate the radiative properties of the prepared materials.
2. Experimental section
2.1 Materials and synthesis
A series of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2, 0.3, 0.4) phosphors was prepared by a traditional high temperature solid-state reaction route using stoichiometric amounts of CaCO3 (A.R.), Y2O3 (99.99%), Al2O3 (99.99%), Eu2O3 (99.99%) as raw materials, after the reactants were mixed and well-ground in an agate mortar, they were preheated at 1400 °C for 4 hours. Then the mixtures were reground and calcined at 1500 °C for 4 hours. All of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2, 0.3, 0.4) phosphors prepared under a reducing atmosphere of H2 (5%) and N2 (95%). The final power products were obtained after cooling to room temperature and grinding to powder sample.2.2 Characterization
The phase purity of the products was examined by X-ray diffraction (XRD) using a BRUKER D8 ADVANCE powder diffractometer with Cu Kα radiation (0.15405 nm) at room temperature, the diffraction data were collected in 2θ range from 5 to 90°. The UV-vis diffuse reflectance spectra were collected through a Cary 5000 UV-vis-NIR spectrophotometer equipped with a double out-of-plane Littrow monochromator using BaSO4 as a standard reference. All excitation, emission, decay spectra and quantum efficiency were measured on an Edinburgh FLS980 combined fluorescence lifetime, a 450 W xenon lamp was used as the excitation source of emission spectra, while a 60 W μF flash lamp with a pulse width of 1.5–3.0 μs was for the measurements of decay curves.3. Result and discussion
3.1 Phase characterization
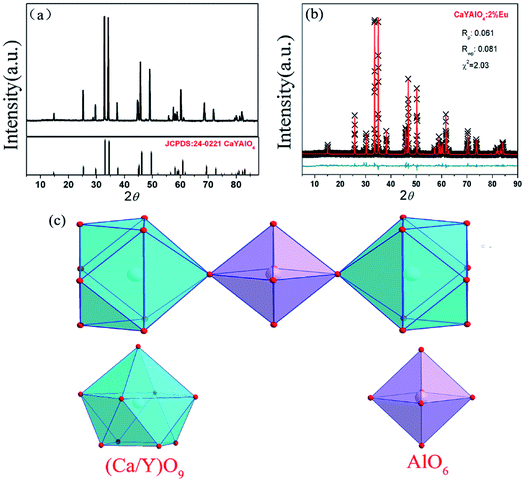
For comparison, the CaYAlO4:2%Eu was prepared firstly under a reducing atmosphere of H2 (5%) and N2 (95%). The XRD patterns of the CaYAlO4:2%Eu together with the Joint Committee on Powder Diffraction Standards (JCPDS) card no. 24-0221 are shown in Fig. 1(a). The XRD patterns of CaYAlO4:2%Eu shows that the diffraction peaks of all single samples are matched well with the standard card of CaYAlO4 (JCPDS: 24-0221), which indicates that the samples are purity phase and doping Eu ions do not cause significant changes to the crystal structure.In order to get further confirmation and knowledge regarding crystal structure information and sites of CaYAlO4:2%Eu, the XRD Rietveld refinement of CaYAlO4:2%Eu were performed by the General Structure Analysis System (GASA) program with the single crystallographic data of CaYAlO4 as the initial model. Fig. 1(b) presents red lines and black lines stand for experimental and calculated patterns, respectively, which matched well with each other. The obtained converged weighted-profiles of Rp = 8.4% and Rwp = 6.1%, which reveals a good quality of fit. As the crystallographic data of CaYAlO4:2%Eu shown in Table 1. And Fig. S1† shows the XRD refinements of CaY0.9Al1.1O4:2%Eu and CaY0.8Al1.2O4:2%Eu. This aluminate compound has a tetragonal crystal system with space group I4/mmm, a = b = 3.664 Å, c = 11.889 Å, V = 159.61 Å3. However, the lattice constants of CaYAlO4:2%Eu are a = b = 3.648 Å, c = 11.885 Å, which indicates that its crystal constants increase with increasing the concentration of Eu3+.
| Atom | Site | x | y | z | Occupancy |
|---|---|---|---|---|---|
| Ca1 | 4e | 0.0000 | 0.0000 | 0.3604 | 0.500 |
| Y1 | 4e | 0.0000 | 0.0000 | 0.3603 | 0.490 |
| Eu1 | 4e | 0.0000 | 0.0000 | 0.5000 | 0.010 |
| Al1 | 2a | 0.5000 | 0.5000 | 0.5000 | 1.000 |
| O1 | 4e | 0.5000 | 0.0000 | 0.5000 | 1.000 |
| O2 | 4e | 0.0000 | 0.0000 | 0.1686 | 1.000 |
CaYAlO4 has a tetragonal K2NiF4 structure and belongs to a family of compounds with the general formula ABCO4, where A is an alkaline earth cation, B is Y, Sc, or a trivalent rare earth element and C is Al, Ga or a transition metal ion. In the unit cell, as shown in Fig. 1(c), the Ca and Y cations are distributed almost statistically in the nine coordinated sites and Al3+ ions are coordinated with six oxygen atoms and form the AlO6 octahedron.
Notably, the (Ca/Y)O9 polyhedron is closely surrounded by AlO6 octahedrons to form a cage structure (Fig. S2†). Thus, it can be concluded that the local environment of Ca/Y sites is highly compressed due to the rigid structure of CaYAlO4, which gives rise to the difficulty of reduction of Eu3+ activators. The Lin et al. has been reported an effective approach-crystal-site engineering to control Eu3+ reduced to Eu2+.16 So, a similar way has been used to change the reduction of Eu3+ doped in CaYAlO4.
Compared with Eu3+, the smaller ions will replace the Al3+ site (such B3+ and Si4+), therefore, an artificial defect substitution will be used for Al3+ doping to CaYAlO4. Fig. 2 showed the XRD patterns of CaY1−xAl1+xO4:2%Eu (x = 0–0.4). Compared with standard card of CaYAlO4, When x > 0.2, the XRD pattern diffraction peak appeared a weak miscellaneous peak around 31°, which indicates that a new phase appeared at this time, the diffraction peak at about 31 degrees is described to Ca3Y2O6, the strongest exact diffraction peak of CaAl2O4 is at 30 degrees (see Fig. S3†), so the impurity cannot be ascribed to CaAl2O4. In addition, the properties of luminescence for Eu ions doped in Ca3Y2O6 crystals aren't detected in research works at present, which indicates that the Eu2+ or Eu3+ in Ca3Y2O6 has not any emission at room temperature. When x ≤ 0.2, the diffraction peak of the sample is consistent with the standard card diffraction peak, which means that the Al3+ actually occupy the Y3+ within a certain range. Thus, we restricted the x value to a maximum of 0.20. Table 2 summarizes the lattice parameters and reliability factors of CaY1−xAl1+xO4:2%Eu. In addition, because the Al3+ ion radius is smaller than that of Y3+, the volume of the unit cell will decrease when Al3+ occupies the Y3+ site.
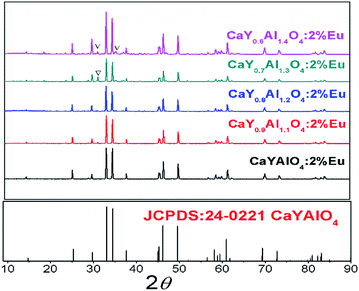 | ||
| Fig. 2 The powder X-ray diffraction patterns of CaY1−xAl1+xO4:2%Eu (x = 0–0.4) and the standard cards of CaYAlO4 (JCPDS: 24-0221). | ||
| Sample | CaYAlO4 | CaY0.9Al1.1O4 | CaY0.8Al1.2O4 |
| Rwp | 0.081 | 0.092 | 0.101 |
| Rp | 0.061 | 0.071 | 0.082 |
| χ2 | 2.410 | 2.030 | 3.890 |
| a = b (Å) | 3.664 | 3.642 | 3.610 |
| c (Å) | 11.889 | 11.882 | 11.859 |
| V (Å3) | 159.61 | 157.60 | 154.55 |
3.2 Photoluminescence properties
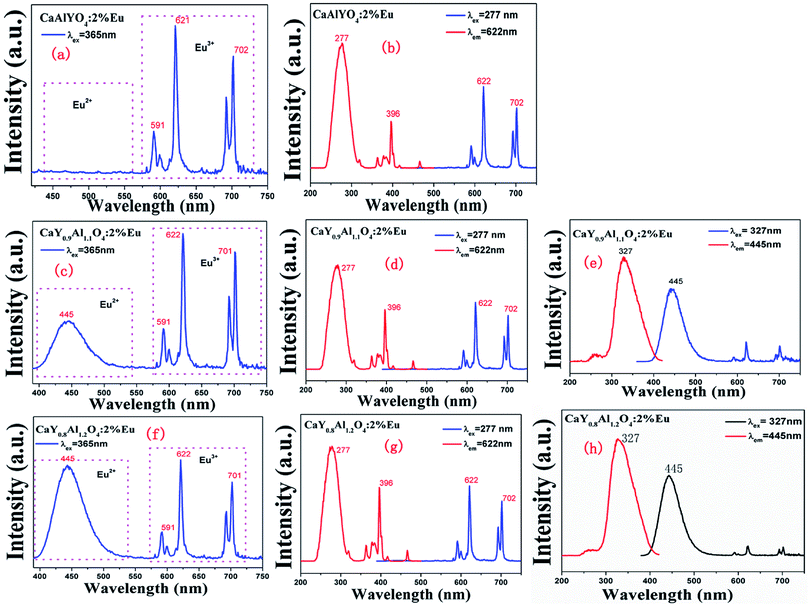
For Eu doped samples, one can clearly distinguish the different emission bands from the photoluminescence (PL) properties of the two valence states of Eu, i.e., the broad ones are attributed to the parity-allowed 4f–5d transitions of Eu2+ and the sharp ones are ascribed to the parity–forbidden transitions of Eu3+ (5D0 → 7FJ, J = 0–4). Fig. 3(a), (c) and (f) illustrate the emission spectra of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) samples under the NUV excitation of 365 nm. When x = 0, as shown in Fig. 3(b), the photoluminescence excitation (PLE) spectrum monitored at 622 nm reveals a broad band with the peak at 277 nm in the range of 200–350 nm due to the charge transfer band (CTB) from O to the Eu ions, along with some sharp peaks in the range of 350–500 nm related to the 4f–4f transitions of Eu3+ ions. Under the excitation of 277 or 365 nm, only the sharp f–f transitions can be found. The sharp emission lines of CaYAlO4:Eu can be assigned to f–f transition of Eu3+, which indicates that Eu3+ could not be directly reduced to Eu2+ in CaYAlO4:Eu system under a reducing atmosphere. All the emissions spectra are intense. The most intense emission at around 622 nm is attributed to the hypersensitive transition 5D0 → 7F2, indicating that the Eu3+ ions mainly occupy the sites without inversion symmetry. The more intense emission at 702 nm is rarely reported. This peak comes from the 5D0 → 7F4 transition of Eu3+. As shown in Fig. S2,† the excitation peaks are similar under the different monitoring wavelength (λem = 592, 621, 702 nm), which indicates that the emission peaks of Eu3+ at 592, 621, 702 nm comes from the same site of Eu3+.Fig. 3(b and f) show the emission spectra of CaY0.9Al1.1O4:Eu and CaY0.8Al1.2O4:Eu under the excitation of 365 nm, respectively. It is surprising to find an appearance of a broad band with the peak at 445 nm except for some sharp peaks in the range of 350–500 nm related to the 4f–4f transitions of Eu3+ ions. Fig. 3(e and h) show the PL spectra of CaY0.9Al1.1O4:Eu and CaY0.8Al1.2O4:Eu under the monitoring wavelength at 445 and the PLE spectra under the excitation wavelength at 327. These correspond to the 4f65d1–4f7 transition of Eu2+. This indicates that Eu3+ had been directly reduced to Eu2+ in CaY0.9Al1.1O4:Eu and CaY0.8Al1.2O4:Eu system under a reducing atmosphere. The luminescence intensity of Eu2+ increases with increasing x in CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) system (Fig. S4†), which can be attributed to the increase of x value. These results suggest that Eu3+ is partially transformed to Eu2+ in CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2).
The corresponding CIE chromaticity diagram for CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) has been shown in Fig. 4. The points A, B and C stand for the CIE coordinate position when x = 0, 0.1 and 0.2, respectively. With increasing of the Al/Y ratio in CaY1−xAl1+xO4:2%Eu, the emission color changed from A (0.583, 0.322) red to C (0.213, 0.083) blue.
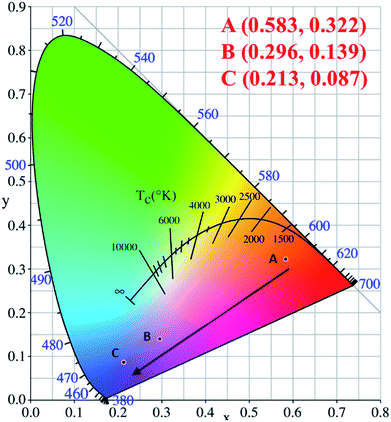 | ||
| Fig. 4 The corresponding CIE chromaticity diagram for CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) under the 365 nm excitation. (A) x = 0; (B) x = 0.1; (C) x = 0.2. | ||
The diffuse reflectance in the UV-vis region was used to calculate the experimental band-gap value of CaY1−xAl1+xO4:Eu3+(x = 0, 0.1, 0.2). Fig. 5 illustrates the diffuse reflectance of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2). The results show that the samples begin to exhibit low reflectance below 330 nm due to the high radiation absorption. This behavior is assigned to the edge absorption, corresponding to the electronic transition from the valence band to the conduction band of CaYAlO4. The matrix of yttrium aluminate and calcium shows optical transparency in the visible region between 330 and 750 nm, making it a candidate for applications in photonic devices.
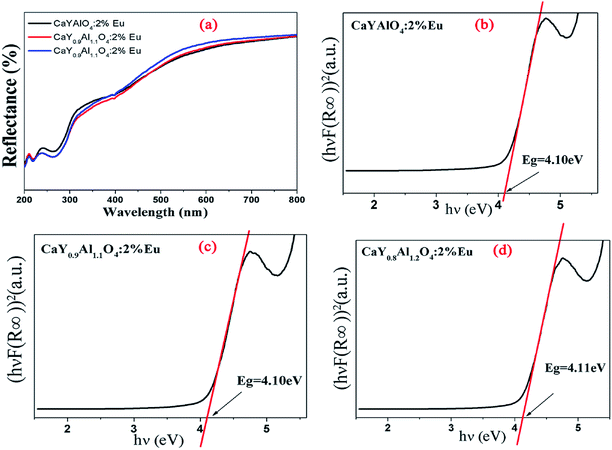 | ||
| Fig. 5 (a) Diffuse reflectance of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2). (b), (c) and (d): The (hνF(R∞))2 was plotted against the (hν) using the Kubelka–Munk function. | ||
In Fig. 5b–d, the (hνF(R∞))2 of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) was plotted against the (hν) using the Kubelka–Munk function.31 The following relational expression proposed by Tauc, Davis, and Mott is used:32,33
| [αhv]n = A(hv − Eg) | (1) |
The acquired diffuse reflectance spectra of CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) in Fig. 5 are converted to Kubella–Munk equation:32,34
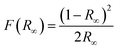 | (2) |
| (hvF(R∞))2 = C(hv − Eg) | (3) |
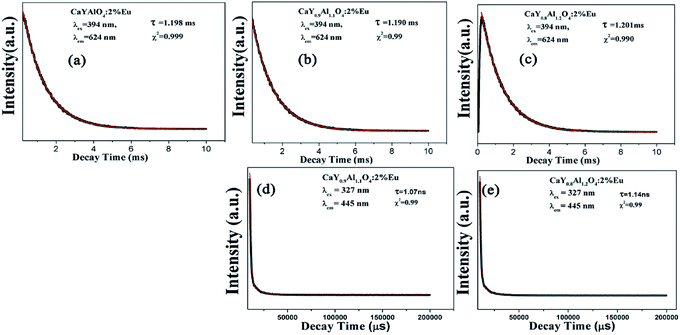
The decay curves of Eu3+ shown in Fig. 6a–c are accurately fitted using the following single-exponential equation:
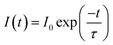 | (4) |
The decay curves of Eu2+ in Fig. 6d and e are accurately fitted well to a second-order exponential decay model based on the following formula:
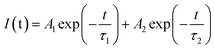 | (5) |
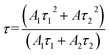 | (6) |
According to the equation, the lifetimes of Eu2+ in CaY0.9Al1.1O4:Eu and CaY0.8Al1.2O4:Eu are calculated to be 1.07 ns and 1.14 ns, respectively.
3.3 Bond energy method and preferential occupancy of Eu ions
The dopant occupancy in the matrix can be determined by comparing the deviation of its bond energy in different lattice location. The similar value of the deviation for its bond energy, the more stable the dopants in matrix are. Thus, to determine which site Eu3+ and Eu2+ will occupy, the bond-energy method has been used to study to the local structure Eu3+/Eu2+ in CaYAlO4 crystals. The bond energy of different dopants in CaYAlO4 crystallographic frame can be estimated through the following equation:19,21,22
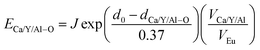 | (7) |
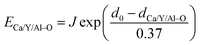 | (8) |
It is assumed that the Eu3+–O2− bonds have the similar bond lengths as Ca/Y/Al–O bonds when the dopant substitutes Ca/Y/Al cations. In this regard, the value of various un-doped and doped CaYAlO4 crystals can be evaluated. The displacement of dopants leads to a large variation of the crystal composition and bond energy, which may affect not only the crystal properties but also the crystal stability. In such a case, it is convenient to measure the variation of bond energy by the following expression when the Eu locates at Ca/Y/Al sites. Based on chemical viewpoint, the dopants preferentially occupy the sites with smaller alterations of bond energy, the sites with smaller absolute values can be expressed as below,19,21,22
| ΔECa/Y/AlEu = |ECa/Y/Al–O − EEu–O| | (9) |
Here ΔECa/Y/AlEu is the variation of bond energy when the Eu locates at Ca/Y/Al sites. Based on chemical viewpoint, the dopants preferentially occupy the sites with smaller deviation of bond energy (ECa/Y/Al–O), the sites with smaller absolute values of ΔECa/Y/AlEu.
According to the bond energy method, the values of bond energy of CaY1−xAl1+xO4:2%Eu (x = 0.1, 0.2) have been shown in Table 3. The order of variation of bond energy under the assumption that Ca2+/Y3+/Al3+ ions are substituted by Eu3+ is 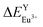 (3.236 kcal mol−1) <
(3.236 kcal mol−1) < 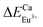 (6.533 kcal mol−1) ≪
(6.533 kcal mol−1) ≪ 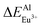 (118.789 kcal mol−1), which means that Eu3+ will preferentially replaces Y3+. The calculation result is consistent with the experiment. In addition, the order of variation of bond energy Eu2+ substituted Y3+, Ca2+ and Al3+ is
(118.789 kcal mol−1), which means that Eu3+ will preferentially replaces Y3+. The calculation result is consistent with the experiment. In addition, the order of variation of bond energy Eu2+ substituted Y3+, Ca2+ and Al3+ is 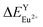 (12.386 kcal mol−1) ≈
(12.386 kcal mol−1) ≈ 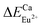 (12.633 kcal mol−1) ≪
(12.633 kcal mol−1) ≪ 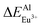 (67.149 kcal mol−1), which means that the site of Ca2+ and Y3+ could be replaced by Eu2+ equally. Considering the valence of Eu2+, we can determine that the Eu2+ is preferentially occupied the site of Ca2+.
(67.149 kcal mol−1), which means that the site of Ca2+ and Y3+ could be replaced by Eu2+ equally. Considering the valence of Eu2+, we can determine that the Eu2+ is preferentially occupied the site of Ca2+.
| Central atom | Coordination atom | Count | d (Å) | EM–O | EEu3+ | EEu2+ | ||
|---|---|---|---|---|---|---|---|---|
| Ca1 | O2 | 1× | 2.3013 | 51.291 | 39.457 | 28.407 | 6.533 | 12.633 |
| O1 | 4× | 2.5152 | 28.772 | 22.133 | 15.935 | |||
| O2 | 4× | 2.6125 | 22.119 | 17.015 | 12.250 | |||
| Al1 | O1 | 4× | 1.8375 | 73.757 | 207.306 | 149.253 | 118.784 | 67.149 |
| O2 | 2× | 1.9866 | 49.294 | 138.549 | 99.750 | |||
| Y1 | O2 | 1× | 2.3013 | 65.045 | 59.186 | 42.611 | 3.236 | 12.385 |
| O1 | 4× | 2.5152 | 36.488 | 33.200 | 23.903 | |||
| O2 | 4× | 2.6125 | 28.050 | 25.523 | 18.376 |
3.4 The 5D0–7F4 emission for CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2)
The emission spectrum showed an unusual comparable intensity 5D0–7F4 transition peak. The relative intensity of 5D0–7F2 and 5D0–7F4 can be stable by changing the relative proportions of Al3+ and Y3+. To gain some insight into the nature of the luminescence behavior of Al3+ ions in crystal CaYAlO4:2%Eu powders, the Judd–Ofelt model was applied to the determination of spontaneous emission coefficients. The intensity parameters Ω2 and Ω4 were determined from luminescence spectra using the method proposed by Kodaira et al.28,35The emission intensity, I = ℏωAN, is expressed in terms of the surface under the emission curve, where ℏω is the transition energy, N is the population of the emitting level (5D0) and the Einstein's coefficient of spontaneous emission can be given by25
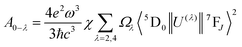 | (10) |
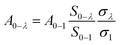 | (11) |
The lifetime (τ), non-radiative (Anrad) and radiative (Arad) rates are related through the following equation:35
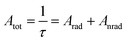 | (12) |
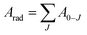 | (13) |
The emission quantum efficiency of the emitting 5D0 level is given by:35
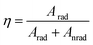 | (14) |
The values of the Ω2 and Ω4 parameters as well as other quantities derived from analysis of the luminescence spectra of Al3+ replace the Y3+ in CaYAlO4 are given in Table 4.
| Samples | Arad | Anrad | Atot | τ | Ω2 | Ω4 | η | ηa |
|---|---|---|---|---|---|---|---|---|
| CaYAlO4 | 409 | 427 | 836 | 1.198 | 4.12 | 2.97 | 0.489 | 47.69% |
| CaY0.9Al1.1O4 | 406 | 434 | 840 | 1.190 | 3.99 | 3.09 | 0.483 | 50.42% |
| CaY0.8Al1.2O4 | 403 | 429 | 832 | 1.201 | 3.91 | 3.10 | 0.484 | 55.43% |
Table 4 shows intensity parameters Ω2 and Ω4. Ωλ is the emission intensity parameters; Ω2 is the emission intensity parameter of 5D0–7F2. Ω4 means the emission intensity parameter of 5D0–7F4. Here, the Ω2 intensity parament values are higher than Ω4 for CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2). The Ω2 parameter depends rather on the lower rank components of crystal field and dynamic coupling interactions, while the Ω4 parament depend rather on the corresponding higher components. It suggests that site symmetry occupied by Eu3+ ions does not have a character of centrosymmetric chemistry environment considering that the 5D0–7F2 transitions is formally forbidden due to the electric dipole selection rule. Meanwhile, it has been commented in literature that the luminescence spectra of compounds with D4d (see Fig. 1(c)) symmetry are often dominated by the 5D0–7F4 transition of Eu3+ because of the absence of central symmetry. An undistorted square anti-prism has D4d symmetry, so a site with symmetry lowed than D4d but the coordination polyhedron close to a square anti-prism, is expected to have an intense 5D0–7F4 transition, In CaY1−xAl1+xO4:2%Eu, Eu3+ is nine-fold coordinated, this coordination polyhedron can be regarded as close to mono-capped square-anti-prism. As a result, in this compound the 5D0–7F4 transition is less intense than the 5D0–7F2 transition but much more intense than 5D0–7F1 magnetic dipole transition. The same remarks have also been for LaBO3:Eu3+, [Eu(DOTA)(H2O)]− and Sr0.99La1.01Zn0.99O3.495:Eu3+. In addition, the values of Ω4/Ω2 is 0.72, 0.77, 0.79 for CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) respectively, which indicated the 5D0–7F4 emission can be enhanced by properly adjusting the Al/Y ratio, at the same time it does not change the quantum efficiency (η). The quantum efficiency (ηa) measured by the integrating sphere is nearly the result by calculation.
4. Conclusions
A series of CaY1−xAl1+xO4:2%Eu3+ (x = 0, 0.1, 0.2, 0.3) phosphors have been identified. The powder XRD patterns and Rietveld refinement reveal that CaY1−xAl1+xO4:2%Eu3+ have a tetragonal crystal structure with the space group I4/mmm (No. 139). The photoluminescence property of the CaY1−xAl1+xO4:2%Eu (x = 0, 0.1, 0.2) phosphors exhibit both blue emission of Eu2+ (4f65d1–4f7) and red-orange emission of Eu3+ (5D0–7F1,2,3,4) under UV light excitation, which showed that Eu3+/2+ co-doping system was obtained by adjusting Al/Y ratio. Eu3+ ions can be reduced to Eu2+ ions when Al/Y ratio was changed. Calculated by the bond-energy theory found that Eu3+ takes priority over the Y3+ site, in addition, the site of Ca2+ and Y3+ all can be occupied by Eu2+. Considering the valence of Eu2+, it can determine that the Eu2+ is preferentially occupied the site of Ca2+. The Judd–Ofelt model was applied to the determination of spontaneous emission coefficients. The intensity parameters Ω2 and Ω4 were determined from luminescence spectra.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the National Natural Science Foundations of China (Grant no. 21301053 and 21571165) and Hubei Natural Science Foundations from Science and Technology Department of Hubei Province (2018CFB517). This research was supported by the Basic Science Research Program though the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (No. 2018R1A2B6005179). “Eu3+/2+ co-doping system induced by adjusting Al/Y ratio in CaY1−xAl1+xO4:2%Eu: preparation, bond energy, site preferential and 5D0–7F4 transition intensity” is supplied by the Functional Phosphor Bank at Pukyong National University.Notes and references
- S. Liu, G. Zhao, H. Ying, J. Wang and G. Han, Opt. Mater., 2008, 31, 47–50 CrossRef
.
- T. Selvalakshmi, S. Sellaiyan, A. Uedono and A. Chandra Bose, Mater. Chem. Phys., 2015, 166, 73–81 CrossRef
.
- K. Biswas, A. D. Sontakke, R. Sen and K. Annapurna, J. Fluoresc., 2012, 22, 745–752 CrossRef PubMed
.
- L. Yang, Y. Wan, Y. Huang, X. Wang, H. Cheng and H. J. Seo, Mater. Lett., 2016, 172, 23–26 CrossRef
.
- B. Wiendlocha, S. P. Kim, Y. Lee, B. He, G. Lehr, M. G. Kanatzidis, D. T. Morelli and J. P. Heremans, Phys. Chem. Chem. Phys., 2017, 19, 9606–9616 RSC
.
- P. L. Roeder, D. MacArthur, X. P. Ma, G. R. Palmer and A. N. Mariano, Am. Mineral., 1987, 72, 801–811 Search PubMed
.
- Y. Su, L. Li and G. Li, Chem. Mater., 2008, 20, 6060–6067 CrossRef
.
- H. You and C. Shi, Chin. Sci. Bull., 1996, 41, 123–126 Search PubMed
.
- J.-G. Kang, J.-S. Jung, J.-P. Hong, S.-J. Won, Y. Sohn and C. K. Rhee, J. Phys.: Condens. Matter, 2001, 13, 2835–2843 CrossRef
.
- Z. Pei, Q. Zeng and Q. Su, J. Phys. Chem. Solids, 1999, 61, 9–12 CrossRef
.
- J. S. Zhong, H. B. Gao, Y. J. Yuan, L. F. Chen, D. Q. Chen and Z. G. Ji, J. Alloys Compd., 2018, 735, 2303–2310 CrossRef
.
- Z. Jiang, X. Yu, J. Gou, L. Duan, X. Su, G. Fan and Y. Duan, J. Mater. Sci.: Mater. Electron., 2017, 28, 3630–3636 CrossRef
.
- H. Chen, X. Huang and W. Huang, Chin. J. Phys., 2016, 54, 931–939 CrossRef
.
- K. Li, H. Lian, M. Shang and J. Lin, Dalton Trans., 2015, 44, 20542–20550 RSC
.
- Y. Wang, J. Ding, Y. Li, L. Yang, X. Ding and Y. Wang, RSC Adv., 2016, 6, 42618–42626 RSC
.
- Y. Zhang, X. Li, K. Li, H. Lian, M. Shang and J. Lin, ACS Appl. Mater. Interfaces, 2015, 7, 2715–2725 CrossRef PubMed
.
- K. Kumar, A. K. Singh and S. B. Rai, Spectrochim. Acta, Part A, 2013, 102, 212–218 CrossRef PubMed
.
- Y. Zhang, J. Chen, C. Xu, Y. Li and H. J. Seo, Phys. B, 2015, 472, 6–10 CrossRef
.
- Y. He and D. Xue, J. Phys. Chem. C, 2007, 111, 13238–13243 CrossRef
.
- L. Li, W. Wang, Y. Pan, Y. Zhu, X. Liu, H. M. Noh, B. K. Moon, B. C. Choi and J. H. Jeong, RSC Adv., 2018, 8, 1191–1202 RSC
.
- L. Li, J. Cao, B. Viana, S. Xu and M. Peng, Inorg. Chem., 2017, 56, 6499–6506 CrossRef PubMed
.
- L. Li, Y. Pan, W. Wang, Y. Zhu, W. Zhang, H. Xu, L. Zhou and X. Liu, J. Alloys Compd., 2018, 731, 496–503 CrossRef
.
- R. Shi, B. Li, C. Liu and H. Liang, J. Phys. Chem. C, 2016, 120, 19365–19374 CrossRef
.
- Z. Babakhanova, M. Aripova and E. Bernardo, Glass Ceram., 2016, 73, 124–127 CrossRef
.
- R. A. Sa Ferreira, S. S. Nobre, C. M. Granadeiro, H. I. S. Nogueira, L. D. Carlos and O. L. Malta, J. Lumin., 2006, 121, 561–567 CrossRef
.
- M. Xie, Y. Li and R. Li, J. Lumin., 2013, 136, 303–306 CrossRef
.
- G. K. Behrh, R. Gautier, C. Latouche, S. Jobic and H. Serier-Brault, Inorg. Chem., 2016, 55, 9144–9146 CrossRef PubMed
.
- A. Strzep, A. Watras, K. Zawisza, P. Boutinaud and R. J. Wiglusz, Inorg. Chem., 2017, 56, 10914–10925 CrossRef PubMed
.
- D. Geng, G. Li, M. Shang, C. Peng, Y. Zhang, Z. Cheng and J. Lin, Dalton Trans., 2012, 41, 3078–3086 RSC
.
- S. Lv, Y. Wang, Z. Zhu, Z. You, J. Li, S. Gao, H. Wang and C. Tu, Appl. Phys. B: Lasers Opt., 2014, 116, 83–89 CrossRef
.
- J. Chen, W. Zhao, J. Wang and N. Wang, J. Mater. Sci.: Mater. Electron., 2016, 27, 237–244 CrossRef
.
- Y. Su, L. Peng, C. Du and X. Wang, J. Phys. Chem. C, 2012, 116, 15–21 CrossRef
.
- Y. Su, L. Peng, J. Guo, S. Huang, L. Lv and X. Wang, J. Phys. Chem. C, 2014, 118, 10728–10739 CrossRef
.
- R. V. Perrella, C. S. Nascimento Jr, M. S. Goes, E. Pecoraro, M. A. Schiavon, C. O. Paiva-Santos, H. Lima, M. A. Couto dos Santos, S. J. L. Ribeiro and J. L. Ferrari, Opt. Mater., 2016, 57, 45–55 CrossRef
.
- C. A. Kodaira, H. F. Brito, O. L. Malta and O. A. Serra, J. Lumin., 2003, 101, 11–21 CrossRef
.
- R. D. L. Gaspar, E. M. Rodrigues, I. O. Mazali and F. A. Sigoli, RSC Adv., 2013, 3, 2794 RSC
.
- Q. Zhang, X. Wang, X. Ding and Y. Wang, Inorg. Chem., 2017, 56, 6990–6998 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04432e |
| This journal is © The Royal Society of Chemistry 2018 |