Open Access Article
Open Access ArticleDFT exploration of [3 + 2] cycloaddition reaction of 1H-phosphorinium-3-olate and 1-methylphosphorinium-3-olate with methyl methacrylate†
Dhanashree Hallooman a,
Mar Ríos-Gutiérrez
a,
Mar Ríos-Gutiérrez b,
Lydia Rhyman
b,
Lydia Rhyman ac,
Ibrahim A. Alswaidand,
Luis R. Domingo
ac,
Ibrahim A. Alswaidand,
Luis R. Domingo *b and
Ponnadurai Ramasami
*b and
Ponnadurai Ramasami *ac
*ac
aComputational Chemistry Group, Department of Chemistry, Faculty of Science, University of Mauritius, Réduit 80837, Mauritius. E-mail: p.ramasami@uom.ac.mu
bDepartment of Organic Chemistry, University of Valencia, Dr. Moliner 50, E-46100 Burjassot, Valencia, Spain. E-mail: domingo@utopia.uv.es
cDepartment of Applied Chemistry, University of Johannesburg, Doornfontein, Johannesburg 2028, South Africa
dDepartment of Pharmaceutical Chemistry, College of Pharmacy, King Saud University, Riyadh 11451, Saudi Arabia
First published on 1st August 2018
Abstract
A Molecular Electron Density Theory (MEDT) study of the regio- and stereoselectivity of the [3 + 2] cycloaddition (32CA) reaction of 1H-phosphorinium-3-olate and 1-methylphosphorinium-3-olate with methyl methacrylate was carried out using the B3LYP/6-31G(d) method. In order to test the method dependence for the most favorable reaction path leading to the 1H-substituted 6-exo cycloadduct (CA) various functionals using higher basis sets were taken into consideration in the gas phase. An analysis of the energetic parameters indicates that the reaction path leading to 6-exo CA are kinetically as well as thermodynamically favored in the gas phase, THF and ethanol. The calculated energetic parameters of the 32CA reaction of these phosphorus derivatives were compared with those of methyl acrylate and their nitrogen analogues. Investigation of the global electron density transfer at the TSs indicates that these 32CA reactions have non-polar character, while electron localisation function topological analysis of the C–C bond formation along the most favorable reaction path indicates that these 32CA reactions take place through a non-concerted two-stage one-step mechanism, via highly asynchronous TSs.
1. Introduction
Cycloaddition reactions serve as an important strategy for the synthesis of various heterocyclic analogs.1,2 [3 + 2] cycloaddition (32CA) reaction is one of the widely used approaches in the formation of five-membered ring compounds from a Three-Atom-Component (TAC) and an ethylene or acetylene derivative.1,2 This reaction offers an efficient reaction path for the synthesis of natural products and bioactive molecules2,3 owing to the regio-, chemo- and stereoselectivity.4 To date, theoretical studies have been carried out to understand the mechanistic of the 32CA reaction.5,6In 1970's Katritzky's group carried out experimental studies on 32CA reaction of pyridinium-3-olates with various ethylene derivatives.7–9 Theoretical studies10,11 were carried out to have more understanding of the experimental results. In 2010, Rhyman et al. studied the 32CA reaction of substituted pyridinium-3-olates with methyl acrylate (MA) at the B3LYP/6-31G(d) computational level. It was observed that both the theoretical and experimental regio- and stereochemical reaction paths were in good agreement.10 In continuation, the regio- and stereoselectivity of the 32CA reaction of pyridinium-3-olates with hindered ethylene namely methyl methacrylate (MMA) was explored. The 32CA reaction of pyridinium-3-olates with MMA was compared to that of pyridinium-3-olates with MA and in both reactions, the most preferred reaction path is the one leading to the 6-exo cycloadduct (CA).11
Phosphorus containing heterocycles are important as they are widely used as catalysts,12–14 potential drugs,15,16 dye-sensitised solar cells17 and also as polymers.18 There are limited six-membered heterocycles consisting of phosphorus used as precursors.19–21 The Diels–Alder (DA) reaction of nucleophilic dienes with phosphaalkene was applied by Trauner et al. to synthesise phosphinine derivatives.19 In 2004, substituted λ3-phosphabenzene with alkyne was investigated by means of semi-empirical PM3 calculations to find out the effect of the nature, position and steric hindrance of the substituents on the DA reaction.20 Recently, we studied the regio- and stereoisomeric reaction paths of the 32CA reaction of 1H-phosphorinium-3-olate and 1-methylphosphorinium-3-olate with MA using the B3LYP/6-31G(d) computational level.21 It is observed that the formation of the CAs obtained from 32CA reactions of phosphorinium-3-olates is kinetically and thermodynamically more favorable than that of pyridinium-3-olates.21
In view of our previous study,21 herein we present a Molecular Electron Density Theory22 (MEDT) study of 32CA reaction of 1H-phosphorinium-3-olate, 1a, and 1-methylphosphorinium-3-olate, 1b, with MMA as shown in Scheme 1. The methyl group at α carbon of the C–C double bond of MMA acts as steric hindrance in the reaction. These 32CA reactions can yield four isomeric CAs, the endo and exo stereoisomers from the two regioisomeric reaction paths (Scheme 1). The results of the 32CA reaction of phosphorinium-3-olates with MMA obtained were analysed and compared with their nitrogen analogous11 and those of the 32CA reaction of phosphorinium-3-olates with MA.21
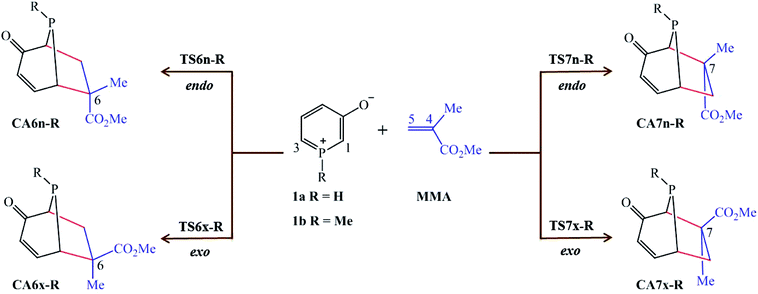 | ||
| Scheme 1 Reaction paths for the 32CA reactions of 1-substituted phosphorinium-3-olates 1a and 1b with MMA. | ||
2. Computational methods
Density functional theory (DFT) method was used to carry out all the quantum chemical computations within Gaussian 09 software suite23 running on Gridchem,24–26 whereas the processing of input and output files were done with ExcelAutomat.27 Geometry optimisation of the reactants, TSs and CAs, was performed using the B3LYP functional28,29 together with the 6-31G(d) basis set.30 in the gas phase, tetrahydrofuran (THF) and ethanol (EtOH) as solvents. The B3LYP/6-31G(d) level is known to underestimate reaction energies with a margin of error of 5 kcal mol−1.31,32 We also performed computations with B3LYP,28,29 M06-2X,33 and MPWB1K34 functionals in conjugation with 6-31G(d), 6-311G(d,p)30 and 6-311++G(d,p)35 basis sets, respectively for the reaction path leading to the 1H-substituted 6-exo CA in the gas phase. In addition, single point energy calculations at the stationary points involved in the 1H-substituted 6-exo reaction path were also carried out in the gas phase with B3LYP-D3/6-31G(d), B3LYP-D3/6-311G(d,p) and B3LYP-D3/6-311++G(d,p) methods using the geometries fully optimized by the B3LYP/6-31G(d), B3LYP/6-311G(d,p) and B3LYP/6-311++G(d,p) methods, respectively to include the effect of Grimme's D3 dispersion correction.36,37 The energetic results from the different methods are in agreement with those calculated using B3LYP/6-31G(d) method as summarised in Table S1 in the ESI.† It is also observed that calculations at low level functionals provide better explanation in some of the studies of organic reactions.38–40 Thus, only the results obtained at the B3LYP/6-31G(d) computational level are herein reported.Solvent effect was considered based on the polarisable continuum model (PCM).41,42 The stationary points were characterised by frequency computations in order to verify whether the TSs have only one imaginary frequency. The relative energies were corrected based on the zero-point energies (ZPE) whereas the thermodynamic computations were scaled by a factor of 0.96.43 Intrinsic reaction coordinate (IRC)44,45 computations were performed to determine if the TSs connect the reactants and CAs. The electronic structures of stationary points were analysed by the natural bond orbital (NBO).46,47 The global electrophilicity index, ω, which measures the stabilisation energy of a molecule when it receives an amount of electron-density, is given by, ω = (μ2/2η) in terms of the electronic chemical potential μ and the chemical hardness η.48 Both quantities may be approached in terms of the one-electron energies of the HOMO and LUMO molecular orbitals, εH and εL, as μ = (εH + εL)/2 and η = (εL − εH), respectively.49 The global nucleophilicity index, N, based on the HOMO energies obtained within the Kohn–Sham scheme,50 is specified as N = EHOMO(NU) − EHOMO(TCE), where tetracyanoethylene (TCE) is used as the reference because it renders the lowest HOMO energy in a large series of molecules already investigated in the context of polar cycloaddition reactions.51 This choice allows us to handle conveniently a nucleophilicity scale of positive values. Nucleophilic Pk− and electrophilic Pk+ Parr functions52 were obtained through the analysis of the Mulliken atomic spin density.
Topological analysis of the electron localisation function (ELF)53 was performed with the TopMod54 package, using the corresponding monodeterminantal wavefunctions and considering a cubical grid of step size of 0.1 Bohr, while non-covalent interactions (NCIs)55 studies were performed with the NCIplot56 program by evaluating the SCF density. The molecular geometries and ELF basin attractor positions were visualised using the GaussView program,57 while the representation of the ELF basin isosurfaces and NCI gradient isosurfaces was done by using the UCSF Chimera program,58 at isovalues of 0.7–0.8 a.u., and the VMD program,59 at an isovalue of 0.5 a.u., respectively.
3. Results and discussion
3.1 Energetics
The analysis of the stationary points involved in the 32CA reactions of 1H-phosphorinium-3-olate, 1a, and 1-methylphosphorinium-3-olate, 1b, with MMA indicates that these reactions follow a one-step mechanism. As a result, the reactants, 1a, 1b and MMA, followed by the four TSs represented by TS6n-R, TS6x-R, TS7n-R and TS7x-R and their corresponding CAs, CA6n-R, CA6x-R, CA7n-R and CA7x-R, where R is the substituent on the phosphorus atom, namely H or Me, were located and characterised. The relative electronic energies in the gas phase, THF and EtOH of the TSs and their corresponding CAs are gathered in Table 1 whereas the total electronic energies (E, in a.u.) are provided in Table S2.†| Gas phase | THF | EtOH | |
|---|---|---|---|
| a Relative to 1a + MMA or 1b + MMA. | |||
| 1a + MMA | |||
| TS6n-H | 12.0 | 14.5 | 14.9 |
| TS6x-H | 8.4 | 12.4 | 13.3 |
| TS7n-H | 14.3 | 17.4 | 17.9 |
| TS7x-H | 10.6 | 14.2 | 14.9 |
| CA6n-H | −42.5 | −37.4 | −36.4 |
| CA6x-H | −42.6 | −37.4 | −36.3 |
| CA7n-H | −41.9 | −36.6 | −35.6 |
| CA7x-H | −42.3 | −36.9 | −35.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 1b + MMA | |||
| TS6n-Me | 16.0 | 19.6 | 19.2 |
| TS6x-Me | 11.6 | 17.9 | 16.9 |
| TS7n-Me | 18.9 | 23.2 | 22.7 |
| TS7x-Me | 14.7 | 20.0 | 19.3 |
| CA6n-Me | −34.2 | −27.4 | −28.4 |
| CA6x-Me | −35.7 | −28.3 | −29.5 |
| CA7n-Me | −33.8 | −27.0 | −28.0 |
| CA7x-Me | −35.6 | −28.1 | −29.2 |
The gas-phase activation energies for these 32CA reactions are 12.0 (TS6n-H), 8.4 (TS6x-H), 14.3 (TS7n-H) and 10.6 (TS7x-H) kcal mol−1 for the reaction of 1a + MMA, and 16.0 (TS6n-Me), 11.6 (TS6x-Me), 18.9 (TS7n-Me) and 14.7 (TS7x-Me) kcal mol−1 for the reaction of 1b + MMA. In the gas phase, the exo reaction paths are more favored than the endo ones, forming the 6-substituted and 7-substituted TSs, respectively, by 3.6 and 3.7 kcal mol−1 for the reaction of 1a with MMA, whereas 4.4 and 4.2 kcal mol−1 for the reaction of 1b with MMA. The activation energy differences for the reactions of 1a + MMA and 1b + MMA between the 6-exo and 7-exo isomeric reaction paths are 2.2 and 3.1 kcal mol−1 whereas that for the 6-endo and 7-endo ones are 2.3 and 2.9 kcal mol−1, respectively.
Thus, on comparison it is found that both the exo and endo stereoisomers of 1H-phosphorinium-3-olates 1a are kinetically more stable than that of 1-methylphosphorinium-3-olates 1b. The 32CA reactions are exothermic ranging from −33.8 to −42.6 kcal mol−1. The kinetic and thermodynamic parameters indicate that the most preferred reaction path leads to the formation of CA6x independent of the P-substituent. These findings are consistent with the previous theoretical results for the reaction of phosphorinium-3-olates with MA.21 The 32CA reactions of both 1H-phosphorinium-3-olate, 1a, and 1-methylphosphorinium-3-olate, 1b, with MMA would tend to produce the 6-exo CA as the major product followed by a mixture of 6-endo, 7-exo and 7-endo CAs as their energies are comparable. The gas-phase activation and reaction energies for the reaction of phosphorinium-3-olates 1a and 1b with MMA and 1-substituted pyridinium-3-olates with MMA11 were compared, resulting that phosphorinium-3-olates are kinetically and thermodynamically more favorable than pyridinium-3-olates.
In the solvent medium, the reactants are more solvated than TSs and CAs. As a consequence, the activation energies associated with these 32CA reactions in polar solvents increase when compared with those in the gas-phase.60 It can be concluded that the solvent effects produce less influence on the selectivity than that in the gas-phase as the trends of the relative energies are the same. It is also observed that the 6-exo reaction path is kinetically and thermodynamically preferred for the reaction of phosphorinium-3-olate with MMA similar to that of pyridinium-3-olate with MMA.11 The 32CA reaction of 1b + MMA illustrates that the formation of the 6-esters CAs would be the major products, followed by the 7-esters CAs in a moderate regioselective manner but presenting very low stereoselectivity in the solvent medium.
The thermodynamic parameters for the 32CA reactions of 1a and 1b with MMA at 298.15 K and 1 atm in THF and EtOH are tabulated in Table 2. The activation enthalpies for the reaction 1a + MMA range from 12.1 to 16.9 kcal mol−1 in THF and 12.9 to 17.3 kcal mol−1 in EtOH, whereas those for the reaction 1b + MMA range from 16.3 to 22.2 kcal mol−1 in THF and 17.3 to 22.7 kcal mol−1 in EtOH. The activation enthalpies for the exo approach modes are lower compared to the endo ones of 1a + MMA whereas for 1b + MMA the activation enthalpies for the reaction paths leading to 6-esters CAs are comparable in THF and EtOH. The inclusion of entropies to enthalpies increases the activation Gibbs free energies by between 25.3 to 36.7 and 26.1 to 37.3 kcal mol−1 in THF and EtOH, respectively, because of the negative activation entropies associated with these bimolecular processes. The activation Gibbs free energies follow the same trend as the activation energies as in Table 1. Thus, based on the energetic parameters, it is observed that these 32CA reactions are exergonic processes. The reaction path leading to CA6x-H for the reaction 1a + MMA, is preferred kinetically as well as thermodynamically in a moderate regio- and stereoselective fashion, while that for 1b + MMA the 6-esters will be the major products, followed by the 7-esters due to the slight change in the stereoselective. In comparison with phosphorinium-3-olate with MA, it was observed that the reaction path leading to CA6x is preferred for both reactions.21 Hence, it can be concluded that the trend of the CAs varies on addition of a methyl group at the phosphorus atom rendering CA6n-Me being moderately preferred over CA6x-Me.
| THF | EtOH | |||||
|---|---|---|---|---|---|---|
| ΔH | ΔG | ΔS | ΔH | ΔG | ΔS | |
| 1a + MMA | ||||||
| TS6n-H | 14.1 | 27.6 | −45.3 | 14.5 | 28.1 | −45.6 |
| TS6x-H | 12.1 | 25.3 | −44.3 | 12.9 | 26.1 | −44.2 |
| TS7n-H | 16.9 | 31.3 | −48.3 | 17.3 | 31.7 | −48.1 |
| TS7x-H | 13.8 | 27.8 | −47.2 | 14.4 | 28.5 | −47.1 |
| CA6n-H | −38.6 | −23.1 | −51.9 | −37.6 | −22.1 | −51.8 |
| CA6x-H | −38.5 | −23.1 | −51.6 | −37.4 | −22.0 | −51.5 |
| CA7n-H | −37.8 | −22.3 | −52.0 | −36.8 | −21.3 | −52.0 |
| CA7x-H | −38.0 | −22.7 | −51.5 | −36.9 | −21.5 | −51.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| 1b + MMA | ||||||
| TS6n-Me | 18.8 | 33.2 | −48.3 | 19.2 | 33.6 | −48.6 |
| TS6x-Me | 16.3 | 30.8 | −48.4 | 17.3 | 31.8 | −48.7 |
| TS7n-Me | 22.2 | 36.7 | −48.6 | 22.7 | 37.3 | −49.0 |
| TS7x-Me | 18.7 | 33.7 | −50.4 | 19.4 | 34.4 | −50.3 |
| CA6n-Me | −29.7 | −13.1 | −55.5 | −28.6 | −12.1 | −55.5 |
| CA6x-Me | −30.7 | −14.2 | −55.4 | −29.5 | −13.0 | −55.5 |
| CA7n-Me | −29.2 | −12.8 | −55.1 | −28.2 | −11.7 | −55.4 |
| CA7x-Me | −30.5 | −14.0 | −55.3 | −29.3 | −12.8 | −55.4 |
3.2 Geometrical parameters
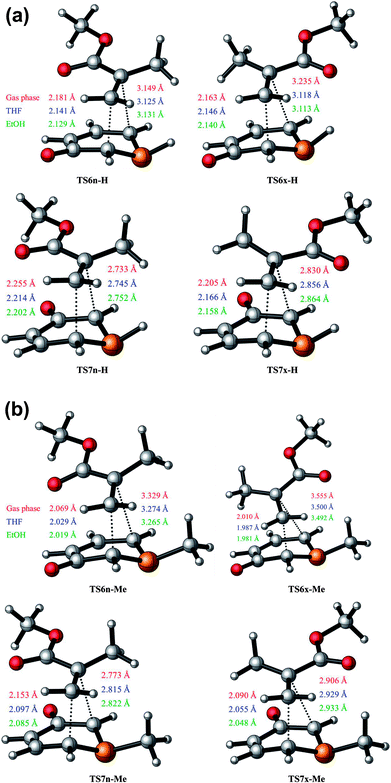
The optimised geometries of the TSs corresponding to the 32CA reactions between 1a + MMA and 1b + MMA are shown in Fig. 1(a) and (b). It is observed that the lengths of the C3–C4 and C1–C4 forming bonds are longer than the C1–C5 and C3–C5 ones, respectively, which concludes that these 32CA reactions take place via asynchronous TSs. Thus, it can be stated that the bond formation at the C5 position of MMA is more advanced than that at the C4 position, which tends to express the most electrophilic centre at the C5 carbon atom of the ethylene derivative (refer to Section 3.7).In the gas phase, the distance between the acidic P2-H hydrogen atom of 1a and the carbonyl oxygen atom of MMA at the most favorable TS6x-H is 2.267 Å. This distance points to an H–O hydrogen bond (HB) interaction which stabilises TS6x-H with respect to TS6n-H. The increase in the dielectric constant of both THF and EtOH leads to a decrease in the stabilisation energy from gas phase to solvent. Accordingly in solvent it is observed that the forming bond distances at the C5 carbon atom of MMA are shortened whereas that at C4 carbon of MMA are shorter for 6-esters in comparison to 7-esters. Thus, the TSs are slightly more advanced and asynchronous in the presence of solvent.
The degree of asynchronicity, Δd, are calculated by considering the difference between the lengths of the two forming bonds for the TSs such that Δd6 = [d(C4–C3) − d(C5–C1)] 6-ester reaction paths and Δd7 = [d(C4–C1) − d(C5–C3)] for 7-ester reaction paths (Table 3).
| Gas phase | THF | EtOH | |
|---|---|---|---|
| Δd6 | |||
| TS6n-H | 0.97 | 0.98 | 1.00 |
| TS6x-H | 1.07 | 0.97 | 0.97 |
| TS6n-Me | 1.26 | 1.25 | 1.25 |
| TS6x-Me | 1.55 | 1.51 | 1.51 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Δd7 | |||
| TS7n-H | 0.48 | 0.53 | 0.55 |
| TS7x-H | 0.62 | 0.69 | 0.71 |
| TS7n-Me | 0.62 | 0.72 | 0.74 |
| TS7x-Me | 0.82 | 0.87 | 0.88 |
In both gas phase and solvents the more favorable exo TSs are more asynchronous than the endo TSs leading to 6-esters and 7-esters, respectively, with an exception of the 6-esters in solvent for the reaction 1a + MMA where the endo TS is more asynchronous than the exo TS. The Δd values for the reaction of 1b with MMA are larger compared to the reaction of 1a with MMA. Thus, it can be noted that the presence of methyl group leads to more asynchronous TSs. The exo TSs for 1b + MMA have higher Δd than the exo TSs for 1a + MMA. On comparing the geometrical parameters for the TSs of the reaction of phosphorinium-3-olate with MA,21 it is observed that the C1–C5 and C3–C5 forming bonds are shorter whereas the C3–C4 and C1–C4 bonds are longer for the reaction of phosphorinium-3-olate with MMA, respectively. Thus, it is also observed that the Δd values increase due to the additional methyl group on the TAC. However, for the nitrogen analogues11 the bond lengths of the C–C forming bonds are shorter whereas the synchronicities for the 6-esters are lower and that for 7-esters are greater than those of the phosphorus TSs.
3.3 Wiberg bond order, dipole moment and global electron density transfer
The Wiberg bond order61 (BO) was obtained using the NBO analysis46,47 as shown in Table 4. An analysis of the Wiberg BO at the TSs corresponding to these 32CA reactions shows the asynchronicity of the bond formation processes.| Gas phase | THF | EtOH | ||||
|---|---|---|---|---|---|---|
| C3–C4 | C1–C5 | C3–C4 | C1–C5 | C3–C4 | C1–C5 | |
| TS6n-H | 0.11 | 0.36 | 0.11 | 0.39 | 0.11 | 0.40 |
| TS6x-H | 0.10 | 0.37 | 0.11 | 0.38 | 0.11 | 0.39 |
| TS6n-Me | 0.11 | 0.44 | 0.11 | 0.47 | 0.11 | 0.48 |
| TS6x-Me | 0.09 | 0.48 | 0.09 | 0.50 | 0.09 | 0.50 |
| Gas phase | THF | EtOH | ||||
|---|---|---|---|---|---|---|
| C1–C4 | C3–C5 | C1–C4 | C3–C5 | C1–C4 | C3–C5 | |
| TS7n-H | 0.19 | 0.34 | 0.19 | 0.36 | 0.19 | 0.37 |
| TS7x-H | 0.16 | 0.37 | 0.16 | 0.38 | 0.15 | 0.39 |
| TS7n-Me | 0.20 | 0.41 | 0.18 | 0.44 | 0.18 | 0.44 |
| TS7x-Me | 0.16 | 0.44 | 0.15 | 0.46 | 0.15 | 0.46 |
The relative extent of forming bonds at the TSs can be evaluated by the analysis of the quotient of the Wiberg BO of the forming bonds at the TSs and that at the CAs. The Wiberg BO values of C3–C4 and C1–C5 are 0.10 and 0.37 for TS6x-H and 1.57 and 1.56 for CA6x-H whereas for C1–C4 and C3–C5 are 0.20 and 0.41 for TS7n-Me and 1.58 and 1.56 for CA7n-Me, respectively. The relative extent of forming bonds for C3–C4 and C1–C5 bonds for TS6x-H are 0.06 and 0.24 whereas that for C1–C4 and C3–C5 bonds for TS7n-Me are 0.13 and 0.26, respectively. Thus, these values show the slight change in the extent of asynchronicity between the TSs. On comparing the Wiberg BO of these 32CA reactions, it can be seen that the BO of C3–C4 is shorter whereas that of C1–C5 is longer for phosphorinium-3-olates with MMA than that of phosphorinium-3-olates with MA (see Table S3†). Thus, it can be understood that the TSs of the 32CA reactions of phosphorinium-3-olates with MMA are slightly more asynchronous than those of phosphorinium-3-olates with MA.
Many MEDT22 studies have shown a very good correlation between the polar character and the feasibility of cycloaddition reactions. Accordingly, the polar nature of these 32CA reactions was evaluated by computing the global electron density transfer62 (GEDT) at the corresponding TSs. Reactions with GEDT values of 0.0e correspond to non-polar processes, while values higher than 0.2e correspond to polar processes. The GEDT values computed at the TSs are summarised in Table 5. The GEDT of the gas phase is almost the same as in solvents. The GEDT values are in the range 0.01e to 0.06e indicating that these 32CA reactions have a very low polar character in nature. In fact, the GEDT at TS6x-H is zero, indicating the non-polar nature of this 32CA reaction. The GEDT is slightly higher for the exo TSs compared to the endo ones in both the gas phase and in solvent.
| Gas phase | THF | EtOH | ||||
|---|---|---|---|---|---|---|
| GEDT (e) | Dipole moment (debye) | GEDT (e) | Dipole moment (debye) | GEDT (e) | Dipole moment (debye) | |
| TS6n-H | 0.01 | 5.891 | 0.01 | 8.025 | 0.01 | 8.519 |
| TS6x-H | 0.00 | 4.560 | 0.00 | 5.901 | 0.00 | 6.165 |
| TS6n-Me | 0.05 | 6.500 | 0.05 | 8.916 | 0.06 | 9.474 |
| TS6x-Me | 0.02 | 4.334 | 0.02 | 5.603 | 0.02 | 5.860 |
| TS7n-H | 0.01 | 4.824 | 0.01 | 6.991 | 0.01 | 7.519 |
| TS7x-H | 0.02 | 3.637 | 0.02 | 5.140 | 0.01 | 5.509 |
| TS7n-Me | 0.02 | 5.584 | 0.02 | 7.948 | 0.04 | 8.514 |
| TS7x-Me | 0.06 | 4.249 | 0.06 | 5.992 | 0.06 | 6.420 |
The dipole moments of the TSs are also included in Table 5. On the inclusion of solvent, the dipole moment of the TSs increases, while the GEDT values are comparable. It is observed that the total dipole moment of the endo TSs is greater than the exo TSs which explains the higher solvation of the endo TSs than the other one. The comparison of the 32CA reaction of phosphorinium-3-olates 1a and 1b with MMA to that of phosphorinium-3-olates with MA, shows that the dipole moments are slightly higher whereas the GEDT values are lower, respectively (see Table S4†).
3.4 Analysis of the global and local reactivity indices at the ground state of the reagents involved in the 32CA reactions of 1a and 1b with MMA
The analysis of the reactivity indices defined within the conceptual DFT63,64 is a powerful tool to understand the reactivity in polar processes. The reactivity indices, namely, electronic chemical potential, μ, chemical hardness, η, global electrophilicity, ω, and global nucleophilicity, N, of 1a, 1b and MMA are given in Table 6.| μ | η | ω | N | |
|---|---|---|---|---|
| MMA | −4.16 | 6.24 | 1.39 | 1.84 |
| 1a | −3.62 | 3.70 | 1.78 | 3.65 |
| 1b | −3.36 | 3.68 | 1.53 | 3.92 |
The electronic chemical potentials of 1a, μ = −3.62 eV, and 1b, μ = −3.36 eV, are higher than that of MMA, μ = −4.16 eV. Thus, along a polar process, the GEDT will take place from 1a and 1b to MMA.
The electrophilicity ω indices of 1a and 1b are 1.78 and 1.53 eV whereas the nucleophilicity N indices are 3.65 eV and 3.92 eV, respectively. These values allow classifying these phosphorinium-3-olates as strong electrophiles and the strong nucleophiles within the electrophilicity65 and the nucleophilicity66 scales. As expected, the addition of an electron-releasing methyl group in 1b decreases its electrophilicity and increases its nucleophilicity with respect to 1a.
The electrophilicity ω and nucleophilicity N indices of MMA are 1.39 and 1.84 eV, respectively. Thus, MMA is classified as a strong electrophile and a moderate nucleophile, respectively.
In spite of the high nucleophilic character of 1a and 1b, the electrophilicity of MMA is not sufficiently high to promote a polar 32CA reaction, justifying the non-polar nature of these 32CA reactions. Note that MA and MMA are one of the poorest electrophiles within the group of strong electrophiles.65
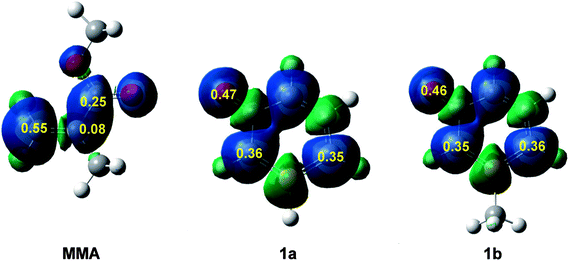
Recently, the electrophilic Pk+ and nucleophilic Pk− Parr functions have been proposed to analyse the local reactivity in polar processes involving reactions between a nucleophile/electrophile pair.52 Accordingly, the electrophilic Pk+ Parr functions for MMA and the nucleophilic Pk− Parr functions for 1a and 1b are analysed (see Fig. 2).
Analysis of the electrophilic Pk+ Parr functions of MMA indicates that the β-conjugated carbon is the most electrophilic centre of this molecule, Pk+ = 0.55. Note that this position is twice as electrophilically activated than the carbonyl carbon, Pk+ = 0.25. The very low electrophilic activation of the α-carbon, Pk+ = 0.08, accounts for the high asynchronicity found in the formation of the C–C single bond at these 32CA reactions.
On the other hand, analysis of the nucleophilic Pk− Parr functions of 1a and 1b indicates that the ortho and para carbons with respect to the phosphorus atom present a similar nucleophilic activation. The presence of the methyl group in 1b slightly favors the para carbon but only the two ortho carbons can participate in these 32CA reactions. Note that the oxygen of these species is the most nucleophilic centre, but due to the para carbon of the phosphorinium system, the oxygen cannot participate in these 32CA reactions.
In 2004, in a DFT study devoted to the regioselectivity in 32CA reactions, Domingo et al. proposed that in both non-polar and polar 32CA reactions, the most electrophilic reagents control the asynchronicity of the process by a larger bond-formation process at the most electrophilic site of the molecule.67 Analysis of the geometry of the eight TSs involved in the two 32CA reactions of 1a and 1b with MA indicates that they correspond to asynchronous bond formation processes in which the formation of the first C–C single bond begins at the β-conjugated position of MMA, which corresponds to the most electrophilic centre of this molecule. Note that although these 32CA reactions have a non-polar character, the analysis of the electrophilic Pk+ Parr functions makes it possible to explain the asynchronicity in these cycloaddition reactions.
3.5 ELF topological analysis of the C–C bond formation along the most favorable 6-exo reaction path associated with the 32CA reaction of 1H-phosphorinium-3-olate 1a with MMA
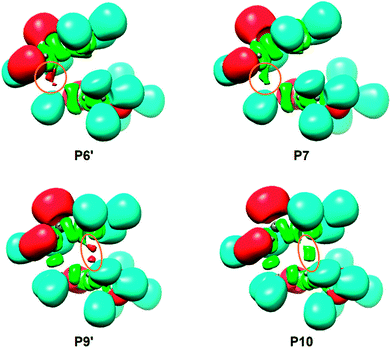
ELF has become a powerful quantum chemical tool to analyse the electronic structure of the molecules.68 After an analysis of the electron density, ELF divides the molecular electron density into basins, i.e. domains in which the probability of finding an electron pair is maximal. Basins are classified as core basins and valence basins. The latter are characterised by the synaptic order, i.e. the number of atomic valence shells in which they participate.69 Thus, there are monosynaptic, disynaptic, trisynaptic basins and so on. Monosynaptic basins, labelled V(A), correspond to non-bonding regions, while disynaptic basins, labelled V(A,B), connect the core of two nuclei, namely A and B, and, thus, correspond to a bonding region between A and B. The total population of the V(C,C) disynaptic basin in a C–C bonding region can be correlate with the Lewis's BO concept. This description recovers the Lewis bonding model, providing a very suggestive graphical representation of the molecular system.In order to characterise the C–C bond formation along the most favorable 6-exo reaction path associated with the non-polar 32CA reaction of 1H-phosphorinium-3-olate 1a with MMA, a topological analysis of the ELF of the points of the IRC directly involved in the formation of the new C1[3]–C5[4] single bonds was performed. These points were selected by applying the bonding evolution theory (BET),70 i.e. the points where the C–C single bonds are formed and the previous ones (denoted by prima). The population of the most relevant ELF valence basins, C1[3]–C5[4] forming bond distances and relative energies, of the reagents, stationary points and the selected points of the IRC involved in the formation of the new C1[3]–C5[4] single bonds are gathered in Table 7, together with the corresponding ELF-based Lewis structures. The representations of the ELF localization domains of the selected points of the IRC involved in the formation of the new C1[3]–C5[4] single bonds are displayed in Fig. 3.
| Points | 1a | MMA | MC6x-H | TS6x-H | P6′ | P7 | P9′ | P10 | CA6x-H |
|---|---|---|---|---|---|---|---|---|---|
| Phases | IV | VII | VIII | X | XI | ||||
| a Relative to the separate reagents, 1a and MMA. | |||||||||
| d(C1–C5) | 4.086 | 2.163 | 1.987 | 1.975 | 1.560 | 1.559 | 1.556 | ||
| d(C3–C4) | 6.712 | 3.235 | 3.182 | 3.179 | 2.072 | 2.060 | 1.571 | ||
| ΔE | −5.3 | 7.0 | 5.8 | 5.6 | −24.6 | −25.0 | −47.9 | ||
| V(C1,P2) | 1.80 | 1.87 | 2.59 | 2.14 | 2.12 | 1.85 | 1.85 | 1.81 | |
| V′(C1,P2) | 1.89 | 1.85 | |||||||
| V(P2) | 1.88 | 1.98 | 1.98 | 2.32 | 2.31 | 2.36 | |||
| V(P2,C3) | 1.56 | 1.63 | 2.55 | 2.54 | 2.53 | 1.99 | 1.98 | 1.82 | |
| V′(P2,C3) | 1.66 | 1.61 | |||||||
| V(C4,C5) | 1.67 | 1.73 | 3.22 | 2.80 | 2.76 | 2.00 | 2.00 | 1.90 | |
| V′(C4,C5) | 1.81 | 1.73 | |||||||
| V(C1) | 0.51 | ||||||||
| V(C5) | 0.36 | ||||||||
| V(C3) | 0.77 | ||||||||
| V(C4) | 0.58 | ||||||||
| V(C1,C5) | 0.90 | 1.77 | 1.77 | 1.81 | |||||
| V(C3,C4) | 1.37 | 1.83 | |||||||
The topological analysis of the ELF of MC6x-H, d(C1–C5) = 4.086 Å and d(C3–C4) = 6.712 Å, shows a very similar bonding pattern to that of the separated reagents. Three pairs of disynaptic basins, integrating total populations of 3.72e, 3.24e and 3.46e, are observed in the C1–P2, P2–C3 and C4–C5 bonding regions, respectively. According to the Lewis's bonding model, these electron populations suggest the presence of three double bonds and a more depopulated P2–C3 region (see the Lewis structure of MC6x-H in Table 7), possibly due to the electron-withdrawing character of the carbonyl group of 1a.
At TS6x-H, d(C1–C5) = 2.163 Å and d(C3–C4) = 3.235 Å, the three double bond regions have been depopulated in such a manner that they are now characterised by the presence of only one V(C1,P2), V(P2,C3) or V(C4,C5) disynaptic basin integrating 2.59e, 2.55e and 3.22e, respectively. As a consequence, of the depopulation of both V(C1,P2) and V(P2,C3) disynaptic basins, a new V(P2) monosynaptic basin associated with the P2 phosphorus non-bonding electron density, is observed with a population of 1.88e. Note that, although the electron density is quite delocalized in both frameworks, neither monosynaptic nor disynaptic basins between both structures are yet observed (see the Lewis structure of TS in Table 7), thus precluding any cyclic conjugation at the TS.71
At P6′, d(C1–C5) = 1.987 Å and d(C3–C4) = 3.182 Å, while the two V(C1,P2) and V(C4,C5) disynaptic basins have been depopulated to 2.14e and 2.80e, two new V(C1) and V(C5) monosynaptic basins, integrating 0.51e and 0.36e, are observed at the C1 and C5 carbons (see Fig. 3). According to the C–C single bond formation model involving multiple bond systems,62 these monosynaptic basins, which are associated with two C1 and C5 carbon pseudoradical centers (see the Lewis structure of P6′ in Table 7),62 are demanded for the subsequent formation of the V(C1,C5) disynaptic basin associated with the new C1–C5 single bond.
At P7, d(C1–C5) = 1.975 Å and d(C3–C4) = 3.179 Å, the two V(C1) and V(C5) monosynaptic basins merge into a new V(C1,C5) disynaptic basin with an initial population of 0.90e (see Fig. 3). This relevant topological change indicates that formation of the first C1–C5 single bond begins at a C–C distance of ca. 1.98 Å through the C–to–C coupling of two C1 and C5 pseudoradical centers.62 Of special note is the very low population of the recently formed C1–C5 single bond, less than 1e, which emphasizes that BO values cannot represent the extent of bond formation.72
At P9′, d(C1–C5) = 1.560 Å and d(C3–C4) = 2.072 Å, similarly to P6′, together with the further depopulation of the V(P2,C3) and V(C4,C5) disynaptic basins to 1.99e and 2.00e, two new V(C3) and V(C4) monosynaptic basins, integrating 0.77e and 0.58e, are observed at the C3 and C4 carbons (see Fig. 3). Along the same line, the population of the V(P2) monosynaptic basin increases to 2.32e as a consequence of the depopulation of the V(C1,P2) disynaptic basin to 1.85e. Note that at P9′, while all the multiple bond regions have clearly become single bonds (see the Lewis structure of P9′ in Table 7), the V(C1,C5) disynaptic basin has already reached a population of 1.77e.
At P10, d(C1–C5) = 1.559 Å and d(C3–C4) = 2.060 Å, similarly to P7, the two V(C3) and V(C4) monosynaptic basins present at P9′ merge into a new V(C3,C4) disynaptic basin integrating an initial population of 1.37e (see Fig. 3). This significant topological change indicates that formation of the second C3–C4 single bond begins at a C–C distance of 2.06 Å through the C-to-C coupling of two C3 and C4 carbon pseudoradical centers (see the Lewis structures of P9′ and P10 in Table 7).62 It is worth mentioning that the creation of the V(C3,C4) disynaptic basin takes place when the V(C1,C5) disynaptic one has reached ca. 94% of its final population at CA6x-H.
Finally, at CA6x-H, d(C1–C5) = 1.556 Å and d(C3–C4) = 1.571 Å, the two V(C1,C5) and V(C3,C4) disynaptic basins associated with the new C1–C5 and C3–C4 single bonds, as well as the two V(C1,P2) and V(P2,C3) disynaptic basins, end up integrating ca. 1.8e, while the V(P2) monosynaptic basin related to the phosphorus P2 non-bonding electron density and the V(C4,C5) disynaptic basin associated with the C4–C5 single bond integrate 2.36e and 1.90e, respectively.
Some appealing conclusions can be drawn from this ELF topological analysis: (i) formation of the two new C1–C5 and C3–C4 single bonds takes place at C–C distances of 1.98 and 2.06 Å, respectively, through the C-to-C coupling of the two corresponding C1[3] and C5[4] pseudoradical centers;62 (ii) these pseudoradical centers are formed along the reaction path after the rupture of the corresponding double bonds.62 Note that the C5 pseudoradical center created at the most electrophilic center of MMA (see Section 3.6) appears first (not shown in Table 7), regardless of the non-polar character of the reaction; (iii) formation of the second C3–C4 single bond begins when the first C1–C5 one is almost completely formed by up to 94%. Consequently, the 32CA reaction between 1a and MMA follows a two-stage one-step mechanism;73 and finally, (iv) the bonding changes observed at TS suggest that the rupture of the three C1–P2, P2–C3 and C4–C5 double bonds have only a moderate energy cost, 7.0 kcal mol−1.
3.6 Topological analysis of the NCIs at the TSs involved in the 32CA reactions between 1a and MMA
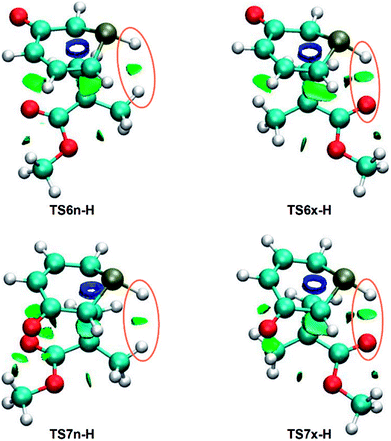
As has been aforementioned, the analysis of the geometries of the most favorable exo stereoisomeric TS6x-H and TS7x-H suggests the presence of a HB between the PH hydrogen of 1a and the carboxyl O oxygen of MMA, while this HB is not expected for the endo TSs. As the strength and nature of NCIs may be responsible for the stereoselectivity of the non-polar 32CA reaction between 1a and MMA, a topological analysis of the NCIs taking place in the four regio- and stereoisomeric TSs was carried out.Depending on their electrostatic nature, NCIs can be either attractive or repulsive. While the former are generally associated with HBs and favorable van der Waals (vdW) interactions, being quantum-chemically characterised by negative values of sign (λ2)ρ,55 the latter are commonly related to steric hindrance and unfavorable vdW interactions, being identified by positive values of sign (λ2)ρ.55 A preliminary analysis of both types of NCIs separately showed that the gradient isosurfaces as well as the strength associated with the repulsive interactions are similar in the four TSs, thus not having a significant relevance in the stereoselectivity. Consequently, only the attractive NCIs are analysed herein.
NCI topological analysis of the attractive interactions of the four TSs shows that the most notable topological change between both pairs of endo/exo stereoisomeric TSs is the presence of a surface in the PH–H or PH–O regions, respectively (see Fig. 4).
These surfaces, which have sign (λ2)ρ values of −0.010 (PH–H) and −0.020 (PH–O) a.u., can be associated with a weak PH–H interaction and a slightly stronger PH–O HB,55 in agreement with the previous geometrical analysis. Consequently, similarly to the 32CA reaction between 1H-pyridinium-3-olate and MA,21 the PH–O HB present in the exo TSs might account for the total exo stereoselectivity of the 32CA between 1a and MMA.
4. Conclusions
The B3LYP/6-31G(d) computational level was used to study the 32CA reaction of 1H-phosphorinium-3-olate, 1a, and 1-methylphosphorinium-3-olate, 1b, with MMA. The kinetic, thermodynamic and geometrical parameters associated with the formation of the endo/exo stereoisomers and the 6-ester/7-ester regioisomers were analysed in the gas phase, THF and EtOH. These 32CA reactions are exothermic process taking place through asynchronous TSs associated with a one-step mechanism. The global and local reactivity indices at the ground state of the reagents were analysed to understand the reactivity in the polar processes. Whereas the poor electrophilic character of MMA is responsible for the low polar character of these 32CA reactions, analysis of the Parr functions accounts for the asynchronicity found at the TSs. On comparing the energetic results for the 32CA reactions of phosphorinium-3-olate with MA and MMA, it is observed that the reaction path leading to CA6x is preferred for both reactions, whereas that for phosphorinium-3-olates with MMA and pyridinium-3-olates with MMA resulted the former reactions being kinetically and thermodynamically more favorable. The findings from this research work should be helpful towards the synthesis of phosphorus heterocycles. ELF topological analysis of the C–C bond formation along the most favorable 6-exo reaction path indicates that these 32CA reactions take place through a non-concerted two-stage one-step mechanism, via highly asynchronous TSs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Facilities provided by the University of Mauritius are acknowledged. This work was supported by funding provided by the Tertiary Education Commission (TEC) of Mauritius. The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for the research group Project No. RGP VPP-207. This work has also been supported by the Ministerio de Economía y Competitividad of the Spanish Government; project CTQ2013-45646-P. M. R.-G. thanks the Ministerio de Economía y Competitividad for a post-doctoral contract co-financed by the European Social Fund (BES-2014-068258).References
- J. Clayden, N. Greeves and S. Warren, Organic chemistry, University Press, Oxford, 2012 Search PubMed.
- W. Carruthers, Cycloaddition reaction in organic synthesis, Pergamon, Oxford, 1990 Search PubMed.
- A. Padwa, Synthetic applications of 1,3-dipolar cycloaddition chemistry towards heterocycles and natural products, John Wiley and Sons, Inc., New York, 2002 Search PubMed.
- S. M. Rajesh, B. D. Bala and S. Perumal, Tetrahedron Lett., 2012, 53, 5367–5371 CrossRef.
- D. H. Ess and K. N. Houk, J. Phys. Chem. A, 2005, 109, 9542–9553 CrossRef PubMed.
- D. H. Ess, G. O. Jones and K. N. Houk, Adv. Synth. Catal., 2006, 348, 2337–2361 CrossRef.
- A. R. Katritzky and Y. Takeuchi, J. Am. Chem. Soc., 1970, 92, 4134–4136 CrossRef.
- A. R. Katritzky and Y. Takeuchi, J. Chem. Soc. C, 1971, 874–877 RSC.
- N. Dennis, A. R. Katritzky and Y. Takeuchi, Angew. Chem., Int. Ed. Engl., 1976, 15, 1–9 CrossRef PubMed.
- L. Rhyman, H. H. Abdallah, S. Jhaumeer-Laulloo, L. R. Domingo, J. A. Joule and P. Ramasami, Tetrahedron, 2010, 66, 9187–9193 CrossRef.
- L. Rhyman, H. H. Abdallah, S. Jhaumeer-Laulloo, L. R. Domingo, J. A. Joule and P. Ramasami, Curr. Org. Chem., 2012, 16, 1711–1722 CrossRef.
- B. Tan, N. R. Candeias and C. F. Barbas III, J. Am. Chem. Soc., 2011, 133, 4672–4675 CrossRef PubMed.
- J. M. Bayne and D. W. Stephan, Chem. Soc. Rev., 2016, 45, 765–774 RSC.
- A. A. Zagidullin, I. A. Bezkishko, V. A. Miluykov and O. G. Sinyashin, Mendeleev Commun., 2013, 23, 117–130 CrossRef.
- M. Yamada, M. Yamashita, T. Suyama, J. Yamashita, K. Asai, T. Niimi, N. Ozaki, M. Fujie, K. Maddali, S. Nakamura and K. Ohnishi, Bioorg. Med. Chem. Lett., 2010, 20, 5946 Search PubMed.
- D. Wang and H. Wang, Acta Pharm. Sin. B, 2012, 2, 107–117 CrossRef PubMed.
- A. Kira, Y. Shibano, S. Kang, H. Hayashi, T. Umeyama, Y. Matano and H. Imahori, Chem. Lett., 2010, 39, 448–450 CrossRef.
- Y. Zhang, Y. P. Ni, M. X. He, X. L. Wang, L. Chen and Y. Z. Wang, Polymer, 2015, 60, 50–61 CrossRef.
- H. Trauner, E. Cuesta, A. Marinetti and F. Mathey, Bull. Soc. Chim. Fr., 1995, 132, 384–393 Search PubMed.
- L. Pacureanu, M. Mracec and Z. Simon, Cent. Eur. J. Chem., 2004, 2, 34–51 Search PubMed.
- D. Hallooman, M. Ríos-Gutiérrez, L. Rhyman, I. A. Alswaidan, H.-K. Fun, L. R. Domingo and P. Ramasami, Comput. Theor. Chem., 2016, 1087, 36–47 CrossRef.
- L. R. Domingo, Molecules, 2016, 21, 1319 CrossRef PubMed.
- M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- R. Dooley, K. Milfeld, C. Guiang, S. Pamidighantam and G. Allen, J. Grid Comput., 2006, 4, 195–208 CrossRef.
- K. Milfeld, C. Guiang, S. Pamidighantam and J. Giuliani, Proceedings of the 2005 linux clusters: the HPC revolution, NCSA University of Illinois, CHPC University of New Mexico and IBM, 2005 Search PubMed.
- R. Dooley, G. Allen and S. Pamidighantam, Proceedings of the 13th Annual Mardi Gras Conference, CCT, Louisiana State University, Baton Rouge, LA, 2005, vol. 83 Search PubMed.
- J. Z. A. Laloo, N. Laloo, L. Rhyman and P. Ramasami, J. Comput.-Aided Mol. Des., 2017, 31, 667–673 CrossRef PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab initio molecular orbital theory, Wiley, New York, 1986 Search PubMed.
- E. Goldstein, B. Beno and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 6036–6043 CrossRef.
- L. R. Domingo, M. Amó and J. Andrés, J. Am. Chem. Soc., 1998, 120, 1617–1618 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811–4815 CrossRef.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. F. Schaefer III, J. Phys. Chem., 1985, 89, 5336–5343 CrossRef.
- L. Simón and J. M.Goodman, Org. Biomol. Chem., 2011, 9, 689–700 RSC.
- F. O. Sanches-Neto, N. D. Coutinho and V. H. Carvalho-Silva, Phys. Chem. Chem. Phys., 2017, 19, 24467–24477 RSC.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef.
- B. Y. Simkin and I. Sheikhet, Quantum Chemical and Statistical Theory of Solutions-A Computational Approach, Ellis Horwood, London, 1995 Search PubMed.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef.
- H. P. Hratchian and H. B. Schlegel, Theory and applications of computational chemistry, the first 40 years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. Scuseria, Elsevier, Amsterdam, 2005, vol. 195 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef.
- R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- L. R. Domingo, E. Chamorro and P. Pérez, J. Phys. Chem. A, 2008, 73, 4615–4624 Search PubMed.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef.
- S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597–604 CrossRef.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- R. Dennington, T. Keth and J. Millam, GaussView, version 3, Shawnee Mission: Kansas, KS, USA, 2009 Search PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef PubMed.
- W. Benchouk, S. M. Mekelleche, B. Silvi, M. J. Aurell and L. R. Domingo, J. Phys. Org. Chem., 2011, 24, 611–618 CrossRef.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef.
- L. R. Domingo, RSC Adv., 2014, 4, 32415–32428 RSC.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef PubMed.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748 CrossRef PubMed.
- L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423 CrossRef.
- P. Jaramillo, L. R. Domingo, E. Chamorro and P. Pérez, J. Mol. Struct.: THEOCHEM, 2008, 865, 68–72 CrossRef.
- M. J. Aurell, L. R. Domingo, P. Pérez and R. Contreras, Tetrahedron, 2004, 60, 11503–11509 CrossRef.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef.
- B. Silvi, J. Mol. Struct., 2002, 614, 3–10 CrossRef.
- X. Krokidis, S. Noury and B. Silvi, J. Phys. Chem. A, 1997, 101, 7277–7282 CrossRef.
- L. R. Domingo, M. Ríos-Gutierrez, E. Chamorro and P. Pérez, ChemistrySelect, 2016, 1, 6026–6039 CrossRef.
- M. Ríos-Gutiérrez, P. Pérez and L. R. Domingo, RSC Adv., 2015, 5, 58464–58477 RSC.
- L. R. Domingo, J. A. Saéz, R. J. Zaragozá and M. Arnó, J. Org. Chem., 2008, 73, 8791–8799 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04703k |
| This journal is © The Royal Society of Chemistry 2018 |