Open Access Article
Open Access ArticleTheoretical research on excited-state intramolecular proton coupled charge transfer modulated by molecular structure
Dapeng Yang *ac,
Guang Yangb,
Min Jiaa,
Xiaoyan Songa,
Qiaoli Zhanga,
Tianjie Zhanga and
Haiyan Gaoa
*ac,
Guang Yangb,
Min Jiaa,
Xiaoyan Songa,
Qiaoli Zhanga,
Tianjie Zhanga and
Haiyan Gaoa
aSchool of Mathematics and Statics, North China University of Water Resources and Electric Power, Zhengzhou 450046, China. E-mail: dpyang_ncwu@163.com
bBasic Teaching Department, Jiaozuo University, Jiaozuo 454000, China
cState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China
First published on 21st August 2018
Abstract
At the TD-B3LYP/TZVP/IEFPCM theory level, we have theoretically studied the excited-state intramolecular proton coupled charge transfer (ESIPCCT) process for both 4′-N,N-diethylamino-3-hydroxyflavone (3HFN) and 2-{[2-(2-hydroxyphenyl)benzo[d]oxazol-6-yl]methylene}malononitrile (diCN-HBO) molecules. Our calculated hydrogen bond lengths and angles sufficiently confirm that the intramolecular hydrogen bonds O1–H1⋯O2 and O1–H1⋯N1 formed at the S0 states of 3HFN and diCN-HBO should be significantly strengthened in the S1 state, which is further supported by the results obtained based on the analyses of infrared spectra shifts, molecular orbitals and charge density differences maps. The significant strengthening of intramolecular hydrogen bonds O1–H1⋯O2 and O1–H1⋯N1 upon photoexcitation should facilitate the ESIPCCT process of the two title molecules. The scanned potential energy curves and confirmed excited-state transition states for both 3HFN and diCN-HBO show that the proton can be easily transferred from O1 to O2 (N1 for diCN-HBO) through the strengthened intramolecular hydrogen bonds upon photoexcitation to the S1 state.
1. Introduction
Proton transfer (PT), as one of the most fundamental processes involved in chemical and biochemical reactions, deserves the attention of vast numbers of scientists and leads to thousands of publications and numerous books on related topics.1–24 From the molecular point of view, proton transfer can be generally categorized into intermolecular9–17 and intramolecular18–24 ones. The former, which are frequently encountered in biological systems, involve transfer of protons from the donor molecule to the acceptor molecule and commonly require uniquely arranged proton relay systems. While the latter cases involve proton transfer within the same molecular framework. Systems invoking excited state intramolecular proton transfer (ESIPT) are the focus of this research work.ESIPT and the subsequent reverse proton transfer in the ground state achieve a fully reversible reaction cycle. Such cycles have been ubiquitously observed in aromatic molecules possessing proton donor and acceptor groups bridged with an intramolecular hydrogen bond. Hydroxyl or amino groups generally serve as the proton donors, and carbonyl oxygen or azo nitrogen serve as the proton acceptors. Upon electronic excitation, the redistribution of electronic charge makes the proton donor more acidic and the acceptor more basic. Thermodynamically, the enhancement in the basicity/acidity factor, which is several orders of magnitude, makes ESIPT energetically favorable and provides the strong driving force for its occurrence, which explains why the same reaction does not occur in the ground state.
The redistribution of electron density does not only provide the driving force of ESIPT. The charge relocation can be reinforced by the integration of weak intermolecular interactions (such as solute/solvent dipole–dipole interactions), which dramatically influence both reaction kinetics and thermodynamics. Electronically excited to the Franck–Condon state, a molecule with an enhanced distribution of electronic charge and thus a large change of dipole moment strongly polarizes the surrounding medium. This leads to a dielectrically stabilized charge-transfer (CT*) excited state. The reaction leading to this state can be referred to as the excited state intramolecular charge transfer (ESICT) state. Such stabilization can also occur from the product side of ESIPT if the reaction generates a substantial charge transfer character. In a word, upon electronic excitation, the redistribution of electronic charge from electronic charge donor to accepter obviously enhances the dipole moment of the molecule, which makes the proton donor more acidic and the acceptor more basic and finally facilitates the excited-state proton transfer.
The prerequisite of ESIPT lies in the formation of an intramolecular hydrogen bond. Recent advances have shown that hydrogen bonds play an important role in the excited-state behavior of molecular dyes. For instance, several theoretical approaches have explored the site-specific intermolecular excited state hydrogen bonding (H-bonding) property and found interesting correlations for fluorescence quenching, the dynamics of intermolecular charge transfer, and the spectral shifts versus the intermolecular H-bonding strength in the excited state.7,25–28 Thus, one would expect that the H-bonding properties, such as strength, distance and orientation, should affect ESIPT, ESICT, and consequently the ESIPT–ESICT coupled reaction.
The proton is a positively charged particle and its transfer leads to a new redistribution of electron density in the molecule in solution. When the ESIPT reaction is observed in condensed dielectric media, the dielectric polarization of the environment can have a substantial impact on photophysical events, stabilizing the charge-separated states. Therefore, the ESIPT process can be coupled with ESICT reaction both kinetically and energetically.29–31 This coupling depends strongly on the molecular structure. There are systems in which the interplay between ESICT and ESIPT is apparent, rendering drastically different photophysical phenomena such as dual emissions simultaneously associated with both ESIPT and ESICT. For example, as in the case of 3HFN22,24 (shown in Scheme 1), when ESICT takes place upon Franck–Condon excitation, i.e., N–N* (N: normal ground populated state, N*: electronically excited state), N* may thus have large charge separation. The subsequent N*–T* ESIPT (T* stands for excited tautomer), leading to strong redistribution of the electronic density, may be subject to drastic change of the dipole moment. For the other possibility, as in the case of diCN-HBO23,24 (shown in Scheme 1), the ESICT state is not formed upon excitation, whereas ESIPT is accompanied by significant charge separation. Thus, the (T*) form attains the property of the ESICT state and then relaxes to the (N) state via the (T) state, closing a reaction cycle.
The 3HFN molecule is strategically designed so that it undergoes ESICT prior to the ESIPT reaction.22,24 As depicted in Scheme 1, the electron donor (De, the dialkyamino group) and proton donor (Dp, O1–H1) occupy different positions but the same group serves as both proton acceptor and electron acceptor (Ae,p, O2). Upon photoexcitation, ultrafast ESICT takes place, generating the CT* state on time scale (a few hundred femtoseconds). Subsequently, the solvent relaxation process from CT* to 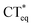 (subscript eq: equilibrium) and ESIPT occur competitively. After reaching the solvent equilibrium, proton transfer reaction from
(subscript eq: equilibrium) and ESIPT occur competitively. After reaching the solvent equilibrium, proton transfer reaction from 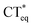 to PCT* takes place. The diCN-HBO molecule is strategically designed so that it undergoes ESIPT prior to the ESICT reaction.23,24 As depicted in Scheme 1, the proton acceptor (Ap, N1) and electron acceptor (Ae, the di-cyano group) are at different positions but the proton donor and electron donor are the same (De,p, O1–H1). The De,p group of diCN-HBO molecule is not a strong electron donating group in the excited state until it forms an anion via transferring a proton (H+) to the proton acceptor Ap. Once the proton is transferred, the resulting oxide anion –O1− becomes a powerful electron donating group. Since De,p is π-conjugated with the electron acceptor Ae, a strong coupling matrix between De− and Ae is then expected, which should execute charge transfer toward the electron accepting cyano-group via π-conjugation. However, the overall perspective mechanism of the ESIPCCT process for the two molecules are not fully understood, especially in the computational way. Therefore, in this work, we are motivated to elucidate the overall perspective mechanism of the ESIPCCT process for the two molecules 3HFN and diCN-HBO in a computational way by optimizing geometrical structures, analyzing molecular orbitals and charge density difference maps as well as the infrared vibrational spectra, especially the potential energy curves.
to PCT* takes place. The diCN-HBO molecule is strategically designed so that it undergoes ESIPT prior to the ESICT reaction.23,24 As depicted in Scheme 1, the proton acceptor (Ap, N1) and electron acceptor (Ae, the di-cyano group) are at different positions but the proton donor and electron donor are the same (De,p, O1–H1). The De,p group of diCN-HBO molecule is not a strong electron donating group in the excited state until it forms an anion via transferring a proton (H+) to the proton acceptor Ap. Once the proton is transferred, the resulting oxide anion –O1− becomes a powerful electron donating group. Since De,p is π-conjugated with the electron acceptor Ae, a strong coupling matrix between De− and Ae is then expected, which should execute charge transfer toward the electron accepting cyano-group via π-conjugation. However, the overall perspective mechanism of the ESIPCCT process for the two molecules are not fully understood, especially in the computational way. Therefore, in this work, we are motivated to elucidate the overall perspective mechanism of the ESIPCCT process for the two molecules 3HFN and diCN-HBO in a computational way by optimizing geometrical structures, analyzing molecular orbitals and charge density difference maps as well as the infrared vibrational spectra, especially the potential energy curves.
In this work, we aim to present a detailed and overall perspective of the ESIPCCT process for both 3HFN and diCN-HBO molecules at the TD-B3LYP/TZVP/IEFPCM theory level since time dependent density functional theory (TDDFT) method has been demonstrated to be a reliable tool to investigate the excited state dynamics7,25–28,32–36 and provide a clear mechanism for previous experiment. The work is organized as follows: Section 2 introduces the computational methods adopted in this work; Section 3 presents the results and discussions, including functional test, optimized geometrical structures, molecular orbitals and charge density difference maps, infrared vibrational spectra analyses as well as potential energy curves and transfer mechanism; Section 4 gives the conclusion of this research work.
2. Computational methods
Using density functional theory (DFT) and time dependent density functional theory (TDDFT) methods with Becke's three-parameter hybrid exchange function with the Lee–Yang–Parr gradient-corrected correlation functional (B3LYP)37–42 as well as the TZVP basis set, we have theoretically studied the excited-state overall perspective of proton coupled charge transfer process modulated by molecular structure within 3HFN and diCN-HBO systems by Gaussian 09 program.43 Since previous experimental works were carried out in dichloromethane and chloroform solvents for 3HFN and diCN-HBO respectively,22–24 we took these two solvents into consideration in all calculations via Polarizable Continuum Model (PCM) using the integral equation formalism variant (IEF-PCM)44–46 to be consistent with former experiments.22–24 For the ground-state part, all the corresponding structures (see Fig. 1 and 2) have been optimized without constraint using DFT methodology with vibrational frequencies analyses to ensure that all these configurations correspond to the local minima on the S0 potential energy surface (PES). The calculations about vertical excitation process were carried out from the S0-state optimized structures using TDDFT method with six low-lying absorbing transitions.Furthermore, all the S1-state calculations were also based on the S0-state optimized structures with vibrational frequencies analyses. Even though the process for scanning potential energy curves of proton transfer is very time-consuming, especially for the excited state, we have theoretically scanned the S0- and S1-state potential energy curves to provide the corresponding dynamical overall perspectives of proton coupled charge transfer qualitatively and quantitatively. All the stationary points along the proton transfer coordinate were scanned by constraining optimizations and frequency analyses (no imaginary frequency) to obtain the thermodynamic corrections in the corresponding electronic state. The excited-state transition state was confirmed based on the stationary point with the highest potential energy in the excited-state potential energy curve. The transition state should have only one imaginary frequency whose vibrational mode points to the proton transfer product. The optimization and frequency analysis of the transition state are carried out with the Gaussian 16 program.47
3. Results and discussions
3.1 Functional test
Based on experimental absorption spectra of 3HFN in dichloromethane and diCN-HBO in chloroform, we have carried out the functional test with TZVP basis set on the TD/TZVP/IEFPCM theory level and the calculated results are listed in Table 1. From Table 1 we can find that the Becke's three-parameter hybrid exchange function with the Lee–Yang–Parr gradient-corrected correlation functional B3LYP should be more suitable for describing the photoexcitation of both 3HFN in dichloromethane and diCN-HBO in chloroform. Therefore, all the calculations of the paper are at the (TD)B3LYP/TZVP/IEFPCM theory level.| B3LYP | CAM-B3LYP | WB97XD | Exp. | |
|---|---|---|---|---|
| 3HFN | 428 (0.806) | 366 (1.05) | 358 (1.07) | 410 |
| H → L (99.1%) | H → L (91.1%) | H → L (87.1%) | ||
| diCN-HBO | 417 (0.777) | 354 (1.48) | 348 (1.52) | 380 |
| H → L (98.7%) | H → L (82.8%) | H → L (78.9%) |
3.2 Optimized geometrical structures
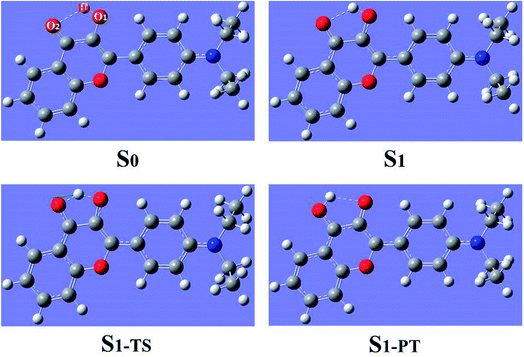
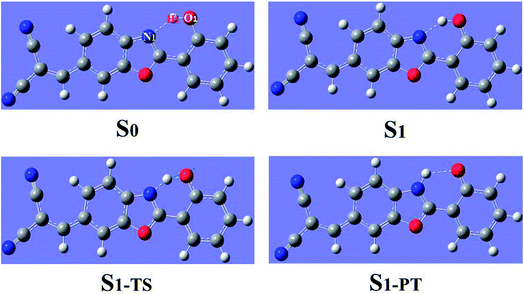
The geometrical structures of both 3HFN in dichloromethane and diCN-HBO in chloroform have been optimized at the (TD)B3LYP/TZVP/IEFPCM theory level. For convenience, we named the intramolecular hydrogen bonds within 3HFN and diCN-HBO as O1–H1⋯O2 and O1–H1⋯N1 respectively. The optimized ground-state (S0) and first singlet excited-state (S1) geometrical structures of 3HFN in dichloromethane and diCN-HBO in chloroform are provided in Fig. 1 and 2 respectively and the important hydrogen bond parameters are listed in Table 2. From Table 2, it can be found that the bond lengths of intramolecular hydrogen bonds O1–H1⋯O2 in 3HFN and O1–H1⋯N1 in diCN-HBO are both decreased from ground state S0 to first singlet excited state S1. At the same time, the bond angles of the two intramolecular hydrogen bonds are both increased from ground state S0 to first singlet excited state S1.| 3HFN | diCN-HBO | |||||
|---|---|---|---|---|---|---|
| O1–H1 | H1⋯O2 | δ (O1–H1⋯O2) | O1–H1 | H1⋯N1 | δ (O1–H1⋯N1) | |
| S0 | 0.98 | 2.00 | 119.19 | 0.99 | 1.80 | 145.22 |
| S1 | 0.99 | 1.85 | 124.71 | 1.02 | 1.65 | 147.85 |
| S1-TS | 1.24 | 1.25 | 139.42 | 1.18 | 1.32 | 150.91 |
| S1-PT | 1.97 | 0.98 | 119.42 | 1.94 | 1.02 | 124.97 |
For 3HFN in dichloromethane, the hydrogen bond length is decreased from 2.00 Å in ground state S0 to 1.85 Å in first singlet excited state S1 and the hydrogen bond angle is increased from 119.19° in ground state S0 to 124.71° in first singlet excited state S1. For diCN-HBO in chloroform, the hydrogen bond length is decreased from 1.80 Å in ground state S0 to 1.65 Å in first singlet excited state S1 and the hydrogen bond angle is increased from 145.22° in ground state S0 to 147.85° in first singlet excited state S1. Both the decreases of the hydrogen bond lengths and the increases of the hydrogen bond angles indicate that the intramolecular hydrogen bonds formed in the ground state S0 of both 3HFN and diCN-HBO systems should be significantly strengthened upon photoexcitation to the first singlet excited state S1, which should result in the excited-state proton transfer from atom O1 to atom O2 (N1) for 3HFN (diCN-HBO).
3.3 Molecular orbitals and charge density difference maps
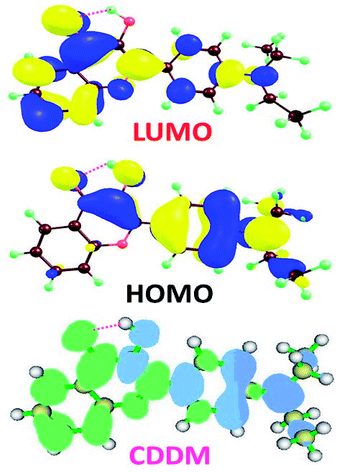
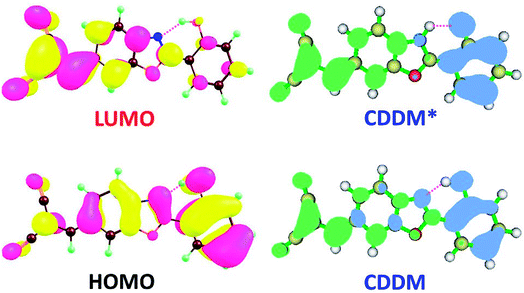
To visually illustrate the changes of charge distribution upon photoexcitation, the molecular orbitals responsible for the electronic transition of S0–S1 of 3HFN and diCN-HBO, namely the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) as shown in Table 1, are provided in Fig. 3 and 4 respectively. From Fig. 3, it can be found that the charge density localized on atom O1 in HOMO of 3HFN is totally disappeared in LUMO whereas that localized on atom O2 of 3HFN is greatly increased from HOMO to LUMO. The charge density difference map (CCDM) of 3HFN shows the same results as that of the molecular orbitals from HOMO to LUMO. The results obtained from molecular orbitals and charge density difference map analyses indicate that due to the intramolecular charge transfer from O1 and the dialkyamino group to O2, the intramolecular hydrogen bond O1–H1⋯O2 formed in the ground state S0 of 3HFN should be significantly strengthened upon photoexcitation to the first singlet excited state S1, which should result in the excited-state intramolecular proton transfer from atom O1 to atom O2 of 3HFN.For diCN-HBO, we can find from Fig. 4 that the charge densities formerly localized on both atoms O1 and N1 are almost completely disappeared from HOMO to LUMO. And the charge density difference map (CCDM) of diCN-HBO shows the same results. The charge density difference map of S1-PT-state diCN-HBO (CCDM*) shows that after excited-state proton transfer of H1 from O1 to N1, the charge density formerly localized on O1 is greatly decreased and intramolecular charge transfer takes place from O1 to the di-cyano group. That is to say, the excited-state intramolecular proton transfer of H1 from O1 to N1 in diCN-HBO results in the intramolecular charge transfer from O1 to the di-cyano group.
3.4 Infrared vibrational spectra analyses
We all know that detecting the infrared (IR) vibrational spectral shift is an effective way to explore the changes of hydrogen bonds upon photoexcitation and it has been demonstrated that the changes of hydrogen bonding can be monitored by the infrared spectra of some characteristic vibrational modes involved in the hydrogen bond formation.7,25–27 Therefore, the vibrational spectra involved in intramolecular hydrogen bonding moiety of 3HFN and diCN-HBO in the conjunct vibrational O–H stretching modes have been displayed in Fig. 5 and 6, respectively. From Fig. 5, it should be noticed that our calculated O1–H1 stretching vibrational frequency of 3HFN is redshifted from 3565.4 cm−1 in S0 state to 3309.0 cm−1 in S1 state. That is to say, the 256.4 cm−1 redshift is arisen from the photoexcitation. Similarly, the O1–H1 stretching vibrational frequency of diCN-HBO is redshifted from 3350.4 cm−1 in S0 state to 2733.4 cm−1 in S1 state and the 617 cm−1 redshift is also arisen from the photoexcitation. Han et al. have concluded that redshift of the infrared vibrational spectra of O–H upon photoexcitation should be resulted from the strengthening of hydrogen bond with O–H as hydrogen donor.7,25–27 Thus, we once again confirmed that the intramolecular hydrogen bonds formed in the ground state S0 of both 3HFN and diCN-HBO systems should be significantly strengthened upon photoexcitation to the first singlet excited state S1, which are consistent with the results obtained by both geometrical structure analyses and molecular orbital as well as charge density difference analyses.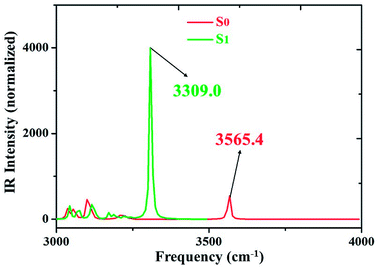 | ||
| Fig. 5 IR spectra of 3HFN in dichloromethane at the spectral region of O1–H1 stretching band in both S0 and S1 states at (TD)B3LYP/TZVP/IEFPCM theory level. | ||
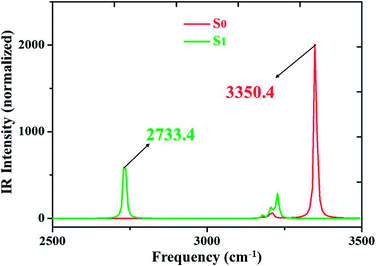 | ||
| Fig. 6 IR spectra of diCN-HBO in chloroform at the spectral region of O1–H1 stretching band in both S0 and S1 states at (TD)B3LYP/TZVP/IEFPCM theory level. | ||
3.5 Potential energy curves and transfer mechanism
To further reveal the detailed ESIPCCT mechanism, we have constructed the potential energy curves in both S0 and S1 states with fixing H1–O2 of 3HFN (H1–N1 for diCN-HBO) bond lengths at a series of certain values in step of −0.05 Å. For 3HFN system, the H1–O2 bond lengths have been fixed from 2.002 Å to 1.002 Å in step of −0.05 Å to scan the ground state potential energy curve, as shown in Fig. 7(a). From Fig. 7(a), we can find that the potential energy is gradually increased as the distance between atoms H1 and O2 decreases from 2.002 Å to 1.152 Å, with a high energy barrier 12.93 kcal mol−1. Therefore, the proton transfer cannot happen in the ground state of 3HFN due to the rather high potential energy barrier. Furthermore, to scan the S1-state potential energy curve, the H1–O2 bond lengths have been fixed from 1.851 Å to 0.951 Å in step of −0.05 Å. Quite different from the situation in ground state, there only exist a rather small potential barrier (around 5.05 kcal mol−1) separating the S1-state 3HFN and the S1-PT-state 3HFN (shown in Fig. 1, S1-PT) configurations, as shown in Fig. 7(b). Furthermore, the transition-state geometrical structure (shown in Fig. 1, S1-TS) corresponding to the point with the highest potential energy in Fig. 7(b) has been confirmed to only have one imaginary frequency that points to the direction of proton transfer. More important, the energy of the S1-PT-state 3HFN configuration is lower than that of the S1-state 3HFN by 2.15 kcal mol−1. Thus, the intramolecular proton transfer from atom O1 to atom O2 of 3HFN can be easily realized in the first singlet excited state. After the formation of S1-PT-state 3HFN, the radiation fluorescent process occurs with emission peak 585.59 nm (experimental value located at about 570 nm (ref. 22)) back to ground state, which is redshifted by more than 100 nm from that (482.34 nm) of the S1-state 3HFN (experimental value located at about 495 nm (ref. 22)).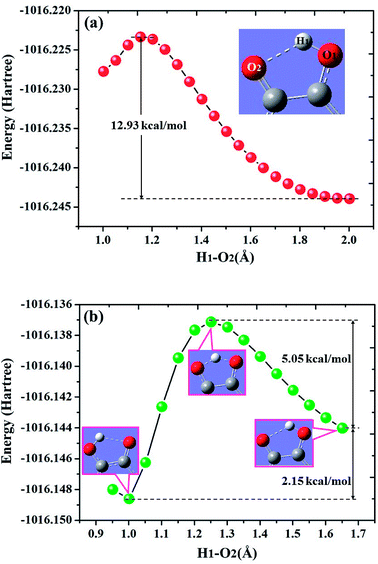 | ||
| Fig. 7 Calculated potential energy curves of both S0 (a) and S1 (b) states for 3HFN in dichloromethane along with the H1–O2 bond distance at (TD)B3LYP/TZVP/IEFPCM theory level. | ||
For diCN-HBO system, the H1–N1 bond lengths have been fixed from 1.797 Å to 0.947 Å in step of −0.05 Å to scan the ground state potential energy curve, as shown in Fig. 8(a). From Fig. 8(a), we can find that the potential energy is gradually increased as the distance between atoms H1 and N1 decreases from 1.797 Å to 1.097 Å, with a high energy barrier 11.46 kcal mol−1. Therefore, the proton transfer cannot happen in the ground state of diCN-HBO due to the rather high potential energy barrier. Furthermore, to scan the S1-state potential energy curve, the H1–N1 bond lengths have been fixed from 1.653 Å to 0.903 Å in step of −0.05 Å. Quite different from the situation in ground state, there only exist a rather small potential barrier (around 1.26 kcal mol−1) separating the S1-state diCN-HBO and the S1-PT-state diCN-HBO (shown in Fig. 2, S1-PT) configurations, as shown in Fig. 8(b). Furthermore, the transition-state geometrical structure (shown in Fig. 2, S1-TS) corresponding to the point with the highest potential energy in Fig. 7(b) has been confirmed to only have one imaginary frequency that points to the direction of proton transfer. More important, the energy of the S1-PT-state diCN-HBO configuration is rather lower than that of the S1-state diCN-HBO by 6.44 kcal mol−1. Thus, the intramolecular proton transfer from atom O1 to atom N1 of diCN-HBO can be easily realized in the first singlet excited state. After the formation of S1-PT-state diCN-HBO, the radiation fluorescent process occurs with emission peak 729.85 nm (experimental value located at about 650 nm (ref. 23)) back to ground state, which is significantly redshifted by about 250 nm from that (480.7 nm) of the S1-state diCN-HBO (experimental value located at about 435 nm (ref. 23)).
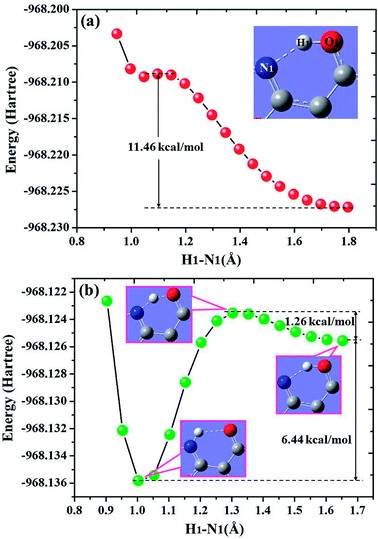 | ||
| Fig. 8 Calculated potential energy curves of both S0 (a) and S1 (b) states for diCN-HBO in chloroform along with the H1–N1 bond distance at (TD)B3LYP/TZVP/IEFPCM theory level. | ||
4. Conclusion
In summary, we have theoretically studied the ESIPCCT process for both 3HFN and diCN-HBO molecules. By carrying out the functional test and comparing with previous experimental data, we confirm that the theoretical level (TDDFT/B3LYP/TZVP/IEFPCM) is more suitable for studying these two molecules. Our calculated results sufficiently confirm that intramolecular hydrogen bonds O1–H1⋯O2 and O1–H1⋯N1 are formed in the S0 state of 3HFN and diCN-HBO molecules. Analyses of hydrogen bond lengths and bond angles indicate that the intramolecular hydrogen bonds formed within 3HFN and diCN-HBO molecules in ground state should be strengthened in the S1 state, which is consistent with the results obtained based on infrared spectra shifts, molecular orbitals and charge density differences maps. The significant strengthening of intramolecular hydrogen bonds O1–H1⋯O2 and O1–H1⋯N1 upon photoexcitation should facilitate the ESIPCCT process of the two title molecules. To obtain the detailed excited-state proton transfer mechanism, we have scanned the potential energy curves at S0 and S1 states for both 3HFN and diCN-HBO, which show the overall perspective of the ESIPCCT dynamics and provides a clear mechanism for previous experiment.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Key Scientific Research Project of Colleges and Universities of Henan Province of China (grant no. 18A140023 and 6B140002), the Aid Project for the Mainstay Young Teachers in Henan Provincial Institutions of Higher Education of China (2014GGJS-283) and Science and Technology Research Project of Henan Province (172102210391).References
- T. Elsasser and H. J. Bakker, Ultrafast hydrogen bonding dynamics and proton transfer processes in the condensed phase, Kluwer Academic Publishers, Dordrecht, Boston, 2002 Search PubMed.
- M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004 CrossRef PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2009, 42, 1881 CrossRef PubMed.
- C. J. Gagliardi, B. C. Westlake, C. A. Kent, J. J. Paul, J. M. Papanikolas and T. J. Meyer, Coord. Chem. Rev., 2010, 254, 2459 CrossRef.
- S. Hammes-Schiffer, Chem. Rev., 2010, 110, 6937 CrossRef PubMed.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939 CrossRef PubMed.
- G. J. Zhao and K. L. Han, Acc. Chem. Res., 2012, 45, 404 CrossRef PubMed.
- J. Zhao, S. Ji, Y. Chen, H. Guo and P. Yang, Phys. Chem. Chem. Phys., 2012, 14, 8803 RSC.
- P. T. Chou, M. L. Martinez, W. C. Cooper, D. Mcmorrow, S. T. Collins and M. Kasha, J. Phys. Chem., 1992, 96, 5203 CrossRef.
- P. T. Chou, C. Y. Wei, C. P. Chang and M. S. Kuo, J. Phys. Chem., 1995, 99, 11994 CrossRef.
- P. T. Chou, W. S. Yu, Y. C. Chen, C. Y. Wei and S. S. Martinez, J. Am. Chem. Soc., 1998, 120, 12927 CrossRef.
- P. T. Chou, G. R. Wu, C. Y. Wei, M. Y. Shiao and Y. I. Liu, J. Phys. Chem. A, 2000, 104, 8863 CrossRef.
- P. T. Chou, J. H. Liao, C. Y. Wei, C. Y. Yang, W. S. Yu and Y. H. Chou, J. Am. Chem. Soc., 2000, 122, 986 CrossRef.
- P. T. Chou, W. S. Yu, C. Y. Wei, Y. M. Cheng and C. Y. Yang, J. Am. Chem. Soc., 2001, 123, 3599 CrossRef PubMed.
- D. P. Yang, M. Jia, J. Y. Wu and X. Y. Song, Sci. Rep., 2017, 7, 11728 CrossRef PubMed.
- J. F. Zhao, J. S. Chen, Y. L. Cui, J. Wang, L. X. Xia, Y. M. Dai, P. Song and F. C. Ma, Phys. Chem. Chem. Phys., 2015, 17, 1142 RSC.
- D. P. Yang, M. Jia, J. Y. Wu and X. Y. Song, J. Mol. Liq., 2017, 244, 141 CrossRef.
- J. F. Zhao, H. B. Yao, J. Y. Liu and M. R. Hoffmann, J. Phys. Chem. A, 2015, 119, 681 CrossRef PubMed.
- D. P. Yang, J. F. Zhao, G. Yang, N. H. Song, R. Zheng and Y. S. Wang, Org. Chem. Front., 2017, 4, 1935 RSC.
- J. F. Zhao, J. S. Chen, J. Y. Liu and M. R. Hoffmann, Phys. Chem. Chem. Phys., 2015, 17, 11990 RSC.
- D. P. Yang, J. F. Zhao, G. Yang, N. H. Song, R. Zheng and Y. S. Wang, J. Mol. Liq., 2017, 241, 1003 CrossRef.
- P. T. Chou, S. C. Pu, Y. M. Cheng, W. S. Yu, Y. C. Yu, F. T. Hung and W. P. Hu, J. Phys. Chem. A, 2005, 109, 3777 CrossRef PubMed.
- C. C. Hsieh, Y. M. Cheng, C. J. Hsu, K. Y. Chen and P. T. Chou, J. Phys. Chem. A, 2008, 112, 8323 CrossRef PubMed.
- A. P. Demchenko, K. C. Tang and P. T. Chou, Chem. Soc. Rev., 2013, 42, 1379 RSC.
- G. J. Zhao and K. L. Han, ChemPhysChem, 2008, 9, 1842 CrossRef PubMed.
- G. J. Zhao and K. L. Han, J. Phys. Chem. A, 2009, 113, 14329 CrossRef PubMed.
- G. J. Zhao, B. H. Northrop, K. L. Han and P. J. Stang, J. Phys. Chem. A, 2010, 114, 9007 CrossRef PubMed.
- P. W. Zhou and K. L. Han, Acc. Chem. Res., 2018, 51, 1681 CrossRef PubMed.
- N. Qiao, N. N. Wei, J. N. Zhang and C. Hao, New J. Chem., 2018, 42, 11804 RSC.
- S. P. Roche, R. Cencic, J. Pelletier and J. A. Porco Jr., Angew. Chem., 2010, 122, 6683 CrossRef.
- M. Jadhao, O. R. Meitei, R. Joshi, H. Kumar, C. Das and S. K. Ghosh, J. Photochem. Photobiol., A, 2016, 326, 41 CrossRef.
- H. Yin, H. Li, G. M Xia, C. Y. Ruan, Y. Shi, H. M. Wang, M. X. Jin and D. J. Ding, Sci. Rep., 2016, 6, 19774 CrossRef PubMed.
- P. Majumdar and J. Z. Zhao, J. Phys. Chem. B, 2015, 119, 2384 CrossRef PubMed.
- C. Ma, Y. G. Yang, C. Z. Li and Y. F. Liu, J. Phys. Chem. A, 2015, 119, 12686 CrossRef PubMed.
- Y. H. Liu, S. C. Lan, C. Y. Zhu and S. H. Lin, J. Phys. Chem. A, 2015, 119, 6269 CrossRef PubMed.
- D. Wu, W. W. Guo, X. Y. Liu and G. L. Cui, ChemPhysChem, 2016, 17, 2340 CrossRef PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200 CrossRef.
- W. Kolth, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- B. Mennucci, E. Cances and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506 CrossRef.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032 CrossRef.
- R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 1449 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |