Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Allotropes of tellurium from first-principles crystal structure prediction calculations under pressure
Yuan Liu†
 ab,
Shunbo Hu†
ab,
Shunbo Hu† a,
Riccarda Caputo
a,
Riccarda Caputo c,
Kaitong Sunab,
Yongchang Liab,
Guodong Zhao
c,
Kaitong Sunab,
Yongchang Liab,
Guodong Zhao ab and
Wei Ren
ab and
Wei Ren *ab
*ab
aMaterials Genome Institute, International Centre for Quantum and Molecular Structures, and Department of Physics, Shanghai University, Shanghai 200444, China. E-mail: renwei@shu.edu.cn
bShanghai Key Laboratory of High Temperature Superconductors, Shanghai University, Shanghai 200444, China
cInternational Centre for Quantum and Molecular Structures, Shanghai University, Shanghai 200444, China
First published on 27th November 2018
Abstract
We investigated the allotropes of tellurium under hydrostatic pressure based on density functional theory calculations and crystal structure prediction methodology. Our calculated enthalpy-pressure and energy-volume curves unveil the transition sequence from the trigonal semiconducting phase, represented by the space group P3121 in the range of 0–6 GPa, to the body centered cubic structure, space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, stable at 28 GPa. In between, the calculations suggest a monoclinic structure, represented by the space group C2/m and stable at 6 GPa, and the β-Po type structure, space group R
m, stable at 28 GPa. In between, the calculations suggest a monoclinic structure, represented by the space group C2/m and stable at 6 GPa, and the β-Po type structure, space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, stable at 10 GPa. The face-centered structure is found at pressure as high as 200 GPa. As the pressure is increased, the transition from the semiconducting phase to metallic phases is observed.
m, stable at 10 GPa. The face-centered structure is found at pressure as high as 200 GPa. As the pressure is increased, the transition from the semiconducting phase to metallic phases is observed.
Introduction
Tellurium is a semiconductor with a high thermoelectric figure of merit comparable to GeSi,1 BiSb2 or other well-known materials.3–5 The chiral tellurium has been investigated for its anisotropic lattice thermal conductivity and p-type transport properties from anisotropic hole pockets of the Fermi surface.6,7 In addition, very recently, structures with few-layers of tellurium were studied as two-dimensional topological materials.8,9 In fact, it presents topological properties for electronic transport, benefitting from the nonsymmorphic screw symmetry, the lone-pair electrons and the strong spin–orbit interaction.10–12 For the ground-state chiral tellurium, the band splitting and band inversion were found upon the application of shear strain or pressure13–15 together with the existence of topological Weyl nodes near the Fermi level.13,14Regarding the crystal structure, tellurium undergoes several phase transitions under pressure. Though there is a lack of consensus of the exact phase transitions, the sequence reported in the literature suggests the transition from the ground state, represented in the trigonal space group P3121 to a puckered layer phase at 4 GPa,16 and then to the monoclinic space group P21 and to an orthorhombic structure in the pressure range of 6.6–10 GPa.16,17 Powder X-ray diffraction (XRD) measurements at 5.3 GPa and 11.5 GPa led to the conclusion that the structure at 11.5 GPa is of the β-Po type (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).18 Therefore, the overall phase transitions are from the trigonal, space group P3121 (Te-I) to the monoclinic, space group P21 (Te-II) at about 4 GPa;16 from Te-II to the orthorhombic phase (Te-III) at about 7 GPa; from Te-III to the rhombohedral phase in the trigonal space group R
m).18 Therefore, the overall phase transitions are from the trigonal, space group P3121 (Te-I) to the monoclinic, space group P21 (Te-II) at about 4 GPa;16 from Te-II to the orthorhombic phase (Te-III) at about 7 GPa; from Te-III to the rhombohedral phase in the trigonal space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Te-IV) at about 10.5 GPa; from Te-IV to the body-centered cubic phase (Te-) at 27 GPa.18,19 To the best of our knowledge, the symmetry representation of the orthorhombic phase is not reported in the literature. In contrast to that, the X-ray structural analysis20 ruled out the second-order phase transition from the monoclinic P21 to the orthorhombic phase and then to the trigonal R
m (Te-IV) at about 10.5 GPa; from Te-IV to the body-centered cubic phase (Te-) at 27 GPa.18,19 To the best of our knowledge, the symmetry representation of the orthorhombic phase is not reported in the literature. In contrast to that, the X-ray structural analysis20 ruled out the second-order phase transition from the monoclinic P21 to the orthorhombic phase and then to the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and suggested that the monoclinic should be represented instead in the C2/m space group.20 Therein the authors20 suggested the phase transitions as increasing the pressure as follows: trigonal → puckered monoclinic → monoclinic → rhombohedral → body-centered cubic (bcc). Hejny and McMahon21,22 further showed that Te-II was a triclinic structure and Te-III was an incommensurate monoclinic structure. Accordingly, the phase transition sequence they proposed is from the trigonal phase, consisting of helical spiral chains, to the commensurate triclinic structure, comprising puckered layers that contain zig-zag chains with alternating long and short bonds (such values are similar to Se-III C2/m),21 to the incommensurate monoclinic structure with a superspace group I′2/m(0q0)s0 (with a = 3.288 Å, b = 4.010 Å, c = 2.589 Å, β = 112.98°),22 and finally to a bcc phase. Therefore, the phase transition sequence investigated by Hejny et al. is as follows: trigonal → triclinic → monoclinic (→ β-Po rhombohedral under high pressure and high temperature) → bcc.21,22 In the last decade, via synchrotron radiation experiments, it was found that the cubic structure (bcc) transforms to a higher-pressure phase with face-centered cubic (fcc) superlattice structure at 100 GPa, which further transforms into the fcc phase at 255 GPa.23 Clearly, there are still controversies and ambiguities in the question of the crystal structures of tellurium under pressure from the experiments.16,18–22
m, and suggested that the monoclinic should be represented instead in the C2/m space group.20 Therein the authors20 suggested the phase transitions as increasing the pressure as follows: trigonal → puckered monoclinic → monoclinic → rhombohedral → body-centered cubic (bcc). Hejny and McMahon21,22 further showed that Te-II was a triclinic structure and Te-III was an incommensurate monoclinic structure. Accordingly, the phase transition sequence they proposed is from the trigonal phase, consisting of helical spiral chains, to the commensurate triclinic structure, comprising puckered layers that contain zig-zag chains with alternating long and short bonds (such values are similar to Se-III C2/m),21 to the incommensurate monoclinic structure with a superspace group I′2/m(0q0)s0 (with a = 3.288 Å, b = 4.010 Å, c = 2.589 Å, β = 112.98°),22 and finally to a bcc phase. Therefore, the phase transition sequence investigated by Hejny et al. is as follows: trigonal → triclinic → monoclinic (→ β-Po rhombohedral under high pressure and high temperature) → bcc.21,22 In the last decade, via synchrotron radiation experiments, it was found that the cubic structure (bcc) transforms to a higher-pressure phase with face-centered cubic (fcc) superlattice structure at 100 GPa, which further transforms into the fcc phase at 255 GPa.23 Clearly, there are still controversies and ambiguities in the question of the crystal structures of tellurium under pressure from the experiments.16,18–22
Therefore, it is highly advisable a theoretical and systematic study of the crystal structures of Te by using the state-of-the-art methodologies in crystal structure prediction combined with total energy calculations.24–27 In the present work, we employed first-principles crystal structure calculations, by using the particle swarm optimization (PSO) method, as implemented in CALYPSO28 code to generate the structures at different pressures and the Vienna Ab initio Simulation Package (VASP)29,30 for the total energy optimizations. The structural stability was checked via phonon calculations.31 A comparison with the experimentally reported structures was possible via X-ray diffraction patterns calculations.
Computational methodology
The crystal structure analysis based on the particle swarm optimization (as implemented in the CALYPSO package)28 was employed to search for possible low-energy structures of tellurium. The entire ensemble of structures were generated by using an initial cell containing 3, 4, 6 atoms and 12 atoms with 30 generations. Each generation contains 20 structures, 60% of these structures are generated from lowest-enthalpy structure provided by the previous generation, and evolved using particle swarm optimization, while the remaining 40% will be generated randomly. The pressure scan was run by steps of 2 GPa in the range of 0–32 GPa, and by steps of 50 GPa in the range of 100–250 GPa. The energy calculations and the geometry optimizations were conducted using VASP29,30 with the projector augmented wave (PAW) method.32,33 The reliability of the pseudopotential approach has also been confirmed by the full-potential linearized augmented plane waves approach. The generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional for the exchange correlation was employed.34 A plane-wave basis with a cutoff energy of 550 eV was used to expand the wave functions. The Monkhorst–Pack k-points mesh was chosen to be no larger than 0.04 Å−1. Here, we also adopted the screened hybrid functional HSE06 (ref. 35 and 36) to calculate the band gap the P3121 phase, using a fixed HF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GGA mixing ratio of 25
GGA mixing ratio of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 and a screening parameter of 0.2 Å−1. We checked the structure stability via phonon calculations, which are performed using 2 × 2 × 2 supercells, as implemented in the Phonopy package.31 X-ray powder diffraction (XRD) patterns were simulated by using the Reflex tool implemented in the Materials Studio (MS) package software. The diffraction patterns were calculated over a 2θ-range from 5° to 45° with an incremental step size of 0.05° and for the diffractometer, the silver (Kα = 0.5594075 Å) radiation source, in order to compared our results with the experimental data reported in the literature.20
75 and a screening parameter of 0.2 Å−1. We checked the structure stability via phonon calculations, which are performed using 2 × 2 × 2 supercells, as implemented in the Phonopy package.31 X-ray powder diffraction (XRD) patterns were simulated by using the Reflex tool implemented in the Materials Studio (MS) package software. The diffraction patterns were calculated over a 2θ-range from 5° to 45° with an incremental step size of 0.05° and for the diffractometer, the silver (Kα = 0.5594075 Å) radiation source, in order to compared our results with the experimental data reported in the literature.20
Results and discussion
Our first-principles crystal structure prediction results confirmed that the ground state is the trigonal P3121 phase and that it is stable in the range of 0–6 GPa. In the range 6–10 GPa we found a monoclinic C2/m structure, which transformed into the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at pressure higher than 10 GPa. As increasing further the pressure this trigonal structure in the rhombohedral representation transformed into a body center cubic structure Im
m at pressure higher than 10 GPa. As increasing further the pressure this trigonal structure in the rhombohedral representation transformed into a body center cubic structure Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, stable at 28 GPa. At very high pressures, from 100 GPa the bcc structure transformed into the face centered cubic Fm
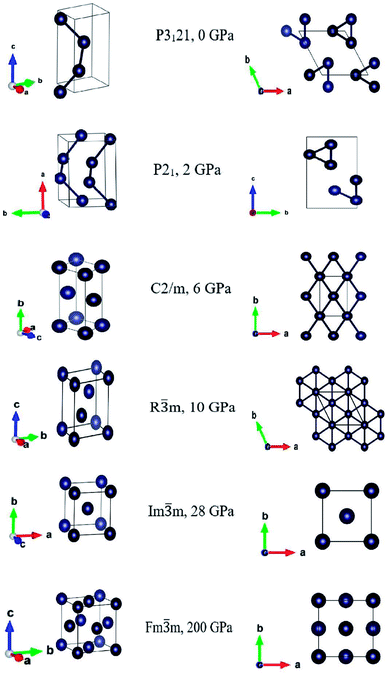
m, stable at 28 GPa. At very high pressures, from 100 GPa the bcc structure transformed into the face centered cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase, stable at 200 GPa. The three-dimensional and top views of the corresponding conventional unit cells are displayed in Fig. 1, and the structural and thermodynamic data are reported in Table 1.
m phase, stable at 200 GPa. The three-dimensional and top views of the corresponding conventional unit cells are displayed in Fig. 1, and the structural and thermodynamic data are reported in Table 1.
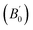 are obtained by interpolation of the energy-volume curves (at P = 0) reported in Fig. 3 and by using the eqn (1). The lattice angle β of the monoclinic C2/m is 89.245°
are obtained by interpolation of the energy-volume curves (at P = 0) reported in Fig. 3 and by using the eqn (1). The lattice angle β of the monoclinic C2/m is 89.245°
| Space group | Pressure (GPa) | a (Å) | b (Å) | c (Å) | E–E (trig) (eV) | V/atom (Å/atom) | B0 (GPa) | Site | x | y | z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The lattice parameters of the trigonal P3121 phase from experiments37 are a = 4.527 Å, c = 5.929 Åb The lattice parameters of the monoclinic C2/m phase from experiments20 are a = 8.4682(14) Å, b = 4.7424(8) Å, c = 3.9595(7) Å, β = 88.112(11)°. In the standard representation, β = 91.888° and the atoms are on the positions (2a) in (0, 0, 0) and (4i) in (0.324, 0, 0.325). | ||||||||||||
| P3121a | 0 | 4.514 | 4.514 | 5.955 | 0 | 34.833 | 50.883 | 4.664 | 3a | 0.2691 | 0 | 1/3 |
| C2/mb | 6 | 8.138 | 4.701 | 3.692 | 0.042 | 32.782 | 51.863 | 4.306 | 2a | 0 | 0 | 0 |
| 4i | 0.324 | 0 | 0.325 | |||||||||
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
10 | 4.764 | 4.764 | 3.992 | 0.111 | 29.419 | 61.243 | 5.655 | 3a | 0 | 0 | 0 |
Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
28 | 3.515 | 3.515 | 3.515 | 0.352 | 21.714 | 49.124 | 4.352 | 2a | 1/2 | 1/2 | 1/2 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
200 | 3.819 | 3.819 | 3.819 | 0.485 | 27.664 | 51.863 | 4.306 | 4b | 0 | 0 | 0 |
The P3121 phase has a trigonal crystal structure with helical chains parallel to the crystallographic c-direction. As reported,16,38 we also obtained the monoclinic P21 phase in our crystal structure calculations at 2 GPa, but it transformed back into the trigonal structure P3121 after full geometry optimization. We find an excellent consistency between the crystal structures from our CALYPSO search28 and the previous experiments.20 The lattice parameters of the trigonal P3121 structures are in good agreement with the experimental values.37
The enthalpy as a function of the pressure, reported in Fig. 2, can help to identify the phase transitions. This confirms that the P3121 phase is the most stable structure up to 4 GPa. As the pressure increases up to 5 GPa, the C2/m phase has lower enthalpy than that of P3121 phase and becomes stable at 6 GPa. At pressure less than 15 GPa, the monoclinic C2/m phase transforms into the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. Experimentally, this transition was suggested in the pressure range of 10.6–27 GPa.18,20 Furthermore, the transformation from the trigonal R
m phase. Experimentally, this transition was suggested in the pressure range of 10.6–27 GPa.18,20 Furthermore, the transformation from the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to the cubic Im
m to the cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m occurs at about 30 GPa. The X-ray-diffraction experiments20 report the transition from the rhombohedral structure to the body-centered-cubic structure at 27 ± 3 GPa. The cubic Im
m occurs at about 30 GPa. The X-ray-diffraction experiments20 report the transition from the rhombohedral structure to the body-centered-cubic structure at 27 ± 3 GPa. The cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure then transform into the fcc Fm
m structure then transform into the fcc Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at pressure larger than 100 GPa.
m structure at pressure larger than 100 GPa.
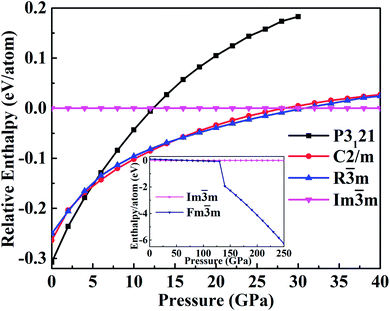 | ||
Fig. 2 The calculated enthalpies relative to the high-pressure Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase as a function of the pressure. m phase as a function of the pressure. | ||
We calculated the bulk modulus and its first derivative with respect the volume by fitting, for each phase, the total energy as a function of the volume with a third-order Birch–Murnaghan equation:39
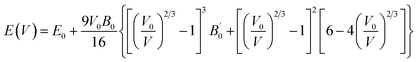 | (1) |
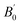 is the first derivative of the bulk modulus with respect to the pressure. The values of B0 and
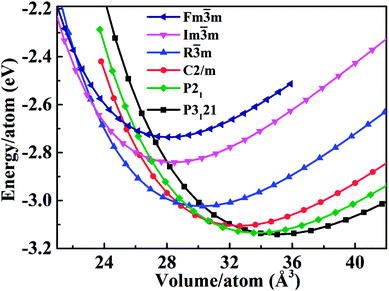
is the first derivative of the bulk modulus with respect to the pressure. The values of B0 and 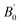 are listed in Table 1. Our energy-volume curves, shown in Fig. 3, are in good agreement with computational works reported in the literature.40 From the energy-volume curves we can confirm that the monoclinic structure C2/m represents a phase stable at intermediate pressure between the ground-state, trigonal P3121, and the high pressure trigonal R
are listed in Table 1. Our energy-volume curves, shown in Fig. 3, are in good agreement with computational works reported in the literature.40 From the energy-volume curves we can confirm that the monoclinic structure C2/m represents a phase stable at intermediate pressure between the ground-state, trigonal P3121, and the high pressure trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure.
m structure.
Actually, the structural complexity of tellurium under pressure remains elusive even experimentally.20,21,23 The very early X-ray diffraction study reported a monoclinic to orthorhombic phase transition at 6.6 GPa.16 However, such orthorhombic state might be attributed to a different representation of the monoclinic P21 structure, which we found having the lattice angle β very close to 90°, in good agreement with the experimentally reported phase transitions.29 Our enthalpy-pressure curves show that the transition sequence is: trigonal P3121 to monoclinic C2/m (at 6 GPa) to trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (at 10 GPa) to cubic Im
m (at 10 GPa) to cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (at 28 GPa) and then to the cubic Fm
m (at 28 GPa) and then to the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at pressure as large as 200 GPa.
m at pressure as large as 200 GPa.
Our calculated XRD patterns of the P3121, C2/m, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Im
m, Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures are shown in Fig. 4 for a comparison with experiments.20 We have found excellent consistency between the calculated and the experimental XRD patterns of P3121 phase.20 As the pressure increases, the small peak below 10° completely disappears in the C2/m and R
m structures are shown in Fig. 4 for a comparison with experiments.20 We have found excellent consistency between the calculated and the experimental XRD patterns of P3121 phase.20 As the pressure increases, the small peak below 10° completely disappears in the C2/m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases. Very interestingly, if we combine our simulated XRD of R
m phases. Very interestingly, if we combine our simulated XRD of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Im
m and Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures at 28 GPa, we could perfectly reproduce the phase coexistence, Te-IV + Te-V, reported at 32 GPa experimentally.20
m structures at 28 GPa, we could perfectly reproduce the phase coexistence, Te-IV + Te-V, reported at 32 GPa experimentally.20
 | ||
| Fig. 4 Simulated XRD patterns of the optimized structures at different pressures (left panel) compared with experiment work (right panel).20 | ||
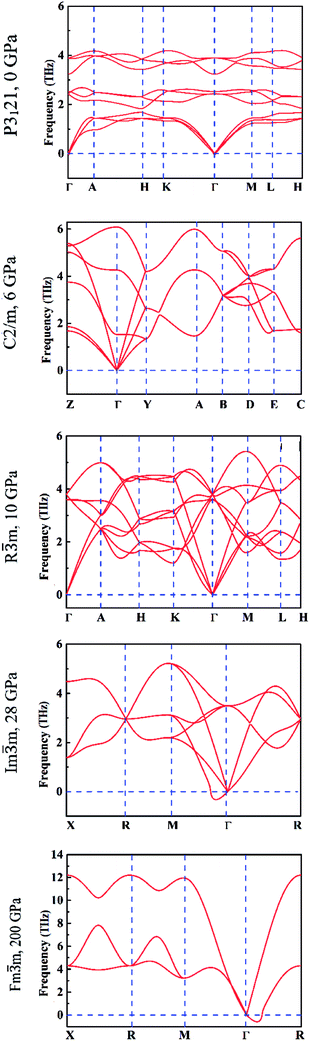
It is well known that the soft phonon modes with negative frequencies are indicative of the dynamical instability of a crystal. To get a better understanding of the dynamical and mechanical stability of these phases, we calculated the phonon dispersions and elastic constants based on the first principles and direct force-constant approaches by using the Phonopy package.31 The calculated phonon spectra of different tellurium phases are displayed in Fig. 5. We observe that the interplay between the strong covalent intra-chain and weak inter-chain interactions in trigonal P3121 tellurium41,42 gives rise to the phonon band gap between the lower and higher optical phonon branches. This is consistent with the DFT calculation results6 and also the experimental dispersion curves reported in the literature.43
The absence of negative phonon frequencies or any soft phonon mode, confirms the lattice stability of the five structures. In particular, the monoclinic C2/m structure is stable at 6 GPa, the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at 10 GPa. The two cubic structures are stable at pressure larger than 28 GPa and 200 GPa, respectively, at which the corresponding transitions occur. The dynamical instabilities of the two cubic structures visible in the corresponding phonon dispersion curves in Fig. 5 are attributable to translational modes at the respective phase transitions.
m structure at 10 GPa. The two cubic structures are stable at pressure larger than 28 GPa and 200 GPa, respectively, at which the corresponding transitions occur. The dynamical instabilities of the two cubic structures visible in the corresponding phonon dispersion curves in Fig. 5 are attributable to translational modes at the respective phase transitions.
In addition, we calculated the phonon spectra of the monoclinic P21 phase at 2 GPa and found that it is similar to the trigonal P3121 structure, confirming that it is not a distinct phase.
In Fig. 6 we report the calculated electronic band structures and the electronic density of states (DOS) for P3121 at 0 GPa, C2/m at 6 GPa, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 10 GPa, Im
m at 10 GPa, Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 28 GPa and Fm
m at 28 GPa and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 200 GPa. We found that the P3121 phase has a direct band gap of 0.15 eV by using PBE functional and 0.55 eV by using a hybrid functional. This is in good agreement with the previous ab initio calculations,40 and the experimental value of a direct gap of 0.33 eV.44 The pressure induces the phase transition from semiconductor to metal, as all phases at pressure above zero are metallic.16,18,38
m at 200 GPa. We found that the P3121 phase has a direct band gap of 0.15 eV by using PBE functional and 0.55 eV by using a hybrid functional. This is in good agreement with the previous ab initio calculations,40 and the experimental value of a direct gap of 0.33 eV.44 The pressure induces the phase transition from semiconductor to metal, as all phases at pressure above zero are metallic.16,18,38
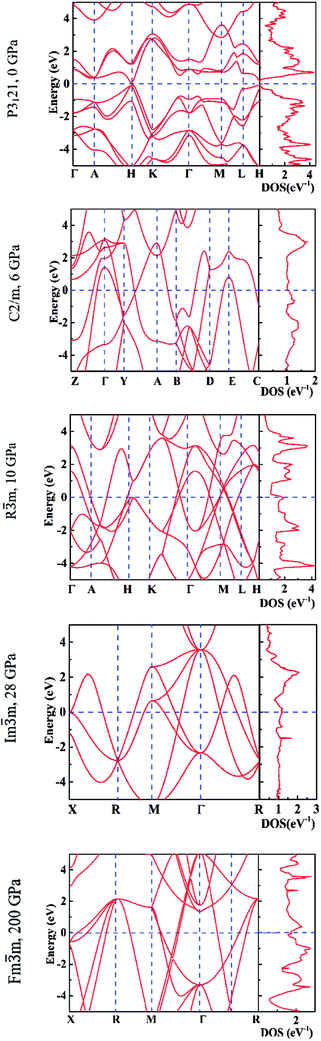 | ||
| Fig. 6 The calculated electronic band structures (left panels) and density of states (right panels). | ||
Conclusions
We investigated the allotropes of tellurium crystal under pressure by combining first-principles total energy calculations (VASP) and crystal structure prediction methodology (CALYPSO). The calculated enthalpy–volume curves indicate that tellurium transforms from the ground state, trigonal P3121 phase, to the α-Po type structure, trigonal space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, via the monoclinic C2/m phase in the range of 0–10 GPa. As increasing the pressure, the rhombohedral structure of the R
m, via the monoclinic C2/m phase in the range of 0–10 GPa. As increasing the pressure, the rhombohedral structure of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase transforms into a stable body centered cubic structure (bcc), space group Im
m phase transforms into a stable body centered cubic structure (bcc), space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, at 28 GPa. At higher pressure, larger than 100 GPa, the bcc structure transforms into a face centered cubic structure, space group Fm
m, at 28 GPa. At higher pressure, larger than 100 GPa, the bcc structure transforms into a face centered cubic structure, space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, whose lattice turns stable at 200 GPa. The comparison of the calculated and experimental XRD patterns indicates a good agreement of the sequence of the phases upon the applied pressure.20 We calculated the phonon spectra of all phases and found that the monoclinic C2/m is stable at 6 GPa, the trigonal R
m, whose lattice turns stable at 200 GPa. The comparison of the calculated and experimental XRD patterns indicates a good agreement of the sequence of the phases upon the applied pressure.20 We calculated the phonon spectra of all phases and found that the monoclinic C2/m is stable at 6 GPa, the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 10 GPa, the cubic Im
m at 10 GPa, the cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 28 GPa and the cubic Fm
m at 28 GPa and the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 200 GPa. In addition, the band structures confirmed the pressure-induced transition from the ground state semiconductor phase to the metallic phases at pressure larger than 2 GPa.
m at 200 GPa. In addition, the band structures confirmed the pressure-induced transition from the ground state semiconductor phase to the metallic phases at pressure larger than 2 GPa.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Basic Research Program of China (Grant No. 2015CB921600), the National Natural Science Foundation of China (Grants No. 51672171 and 51861145315), the fund of the State Key Laboratory of Solidification Processing in NWPU (SKLSP201703), and the supercomputing services from AM-HPC.References
- J. P. Dismukes, L. Ekstrom, E. F. Steigmeier, I. Kudman and D. S. Beers, Thermal and Electrical Properties of Heavily Doped Ge-Si Alloys up to 1300°K, J. Appl. Phys., 1964, 35(10), 2899–2907 CrossRef CAS.
- W. M. Yim and A. Amith, Bi-Sb alloys for magneto-thermoelectric and thermomagnetic cooling, Solid-State Electron., 1972, 15, 1141–1161 CrossRef CAS.
- S. Lin, W. Li, Z. Chen, J. Shen, B. Ge and Y. Pei, Tellurium as a high-performance elemental thermoelectric, Nat. Commun., 2016, 7, 10287 CrossRef CAS PubMed.
- W. Li, Y. X. Wu, S. Q. Lin, Z. W. Chen, J. Li, X. Y. Zhang, L. L. Zheng and Y. Z. Pei, Advances in Environment-Friendly SnTe Thermoelectrics, ACS Energy Lett., 2017, 2(10), 2349–2355 CrossRef CAS.
- M. Wiesner, A. Trzaskowska, B. Mroz, S. Charpentier, S. Wang, Y. Song, F. Lombardi, P. Lucignano, G. Benedek, D. Campi, M. Bernasconi, F. Guinea and A. Tagliacozzo, The electron-phonon interaction at deep Bi2Te3-semiconductor interfaces from Brillouin light scattering, Sci. Rep., 2017, 7, 16449 CrossRef CAS PubMed.
- H. Peng, N. Kioussis and D. A. Stewart, Anisotropic lattice thermal conductivity in chiral tellurium from first principles, Appl. Phys. Lett., 2015, 107(25), 251904 CrossRef.
- H. Peng, N. Kioussis and G. J. Snyder, Elemental tellurium as a chiral p-type thermoelectric material, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(19), 195206 CrossRef.
- L. Xian, A. Perez Paz, E. Bianco, P. M. Ajayan and A. Rubio, Square selenene and tellurene: novel group VI elemental 2D materials with nontrivial topological properties, 2D Mater., 2017, 4(4), 041003 CrossRef.
- Y. Liu, W. Wu and W. A. III Goddard, Tellurium: Fast Electrical and Atomic Transport along the Weak Interaction Direction, J. Am. Chem. Soc., 2018, 140(2), 550–553 CrossRef CAS PubMed.
- X.-X. Xue, Y.-X. Feng, L. Liao, Q.-J. Chen, D. Wang, L.-M. Tang and K. Chen, Strain tuning of electronic properties of various dimension elemental tellurium with broken screw symmetry, J. Phys.: Condens. Matter, 2018, 30(12), 125001 CrossRef PubMed.
- S. Gao, Y. Wang, R. Wang and W. Wu, Piezotronic effect in 1D van der Waals solid of elemental tellurium nanobelt for smart adaptive electronics, Semicond. Sci. Technol., 2017, 32(10), 104004 CrossRef.
- X. Huang, J. Guan, Z. Lin, B. Liu, S. Xing, W. Wang and J. Guo, Epitaxial Growth and Band Structure of Te Film on Graphene, Nano Lett., 2017, 17(8), 4619–4623 CrossRef CAS PubMed.
- K. Nakayama, M. Kuno, K. Yamauchi, S. Souma, K. Sugawara, T. Oguchi, T. Sato and T. Takahashi, Band splitting and Weyl nodes in trigonal tellurium studied by angle-resolved photoemission spectroscopy and density functional theory, Phys. Rev. B, 2017, 95(12), 125204 CrossRef.
- M. Hirayama, R. Okugawa, S. Ishibashi, S. Murakami and T. Miyake, Weyl Node and Spin Texture in Trigonal Tellurium and Selenium, Phys. Rev. Lett., 2015, 114(20), 206401 CrossRef PubMed.
- L. A. Agapito, N. Kioussis, W. A. 3rd Goddard and N. P. Ong, Novel family of chiral-based topological insulators: elemental tellurium under strain, Phys. Rev. Lett., 2013, 110(17), 176401 CrossRef PubMed.
- K. Aoki, O. Shimomura and S. Minomura, Crystal Structure of the High-pressure Phase of Tellurium, J. Phys. Soc. Jpn., 1980, 48(No.2), 551–556 CrossRef CAS.
- F. P. Bundy and K. J. Dunn, Electrical behavior of Se and Te to pressures of about 500 kbar, J. Chem. Phys., 1979, 71(4), 1550–1558 CrossRef CAS.
- G. Parthasarathy and W. B. Holzapfel, High-pressure structural phase transitions in tellurium, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(14), 8499–8501 CrossRef CAS.
- Y. Akahama, M. Kobayashi and H. Kawamura, Pressure-induced superconductivity and phase transition in selenium and tellurium, Solid State Commun., 1992, 84, 803–806 CrossRef CAS.
- M. Takumi, T. Masamitsu and K. Nagata, X-ray structural analysis of the high-pressure phase III of tellurium, J. Phys.: Condens. Matter, 2002, 14(44), 10609–10613 CrossRef CAS.
- C. Hejny and M. I. McMahon, Complex crystal structures of Te-II and Se-III at high pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(18), 184109 CrossRef.
- C. Hejny and M. I. McMahon, Large structural modulations in incommensurate Te-III and Se-IV, Phys. Rev. Lett., 2003, 91(21), 215502 CrossRef CAS PubMed.
- T. Sugimoto; Y. Akahama; T. Ichikawa; H. Fujihisa; N. Hirao and Y. Ohishi, Bcc-fcc structure transition of Te. in 18th Aps-Sccm and 24th Airapt, Pts 1-19, ed. W.Buttler, M.Furlanetto and W.Evans. 2014; vol. 500 Search PubMed.
- C. Lu and C. Chen, High-Pressure Evolution of Crystal Bonding Structures and Properties of FeOOH, J. Phys. Chem. Lett., 2018, 9(9), 2181–2185 CrossRef CAS PubMed.
- C. Lu, Q. Li, Y. Ma and C. Chen, Extraordinary Indentation Strain Stiffening Produces Superhard Tungsten Nitrides, Phys. Rev. Lett., 2017, 119(11), 115503 CrossRef PubMed.
- C. Lu, M. Amsler and C. Chen, Unraveling the structure and bonding evolution of the newly discovered iron oxide FeO2, Phys. Rev. B, 2018, 98(5), 054102 CrossRef.
- C. Zhang, X. Kuang, Y. Jin, C. Lu, D. Zhou, P. Li, G. Bao and A. Hermann, Prediction of Stable Ruthenium Silicides from First-Principles Calculations: Stoichiometries, Crystal Structures, and Physical Properties, ACS Appl. Mater. Interfaces, 2015, 7(48), 26776–26782 CrossRef CAS PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma*, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, First-Principles Determination of the Soft Mode in Cubic ZrO2, Phys. Rev. Lett., 1997, 78(21), 4063–4066 CrossRef CAS.
- G. Kresse and J. Furthmiiller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 18 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215 CrossRef CAS.
- S. United and H. E. Swanson, Standard X-ray diffraction powder patterns. U. S. Dept. of Commerce, National Bureau of Standards, Washington, 1953,p volumes Search PubMed.
- J. C. Jamieson and D. B. Mcwhan, Crystal Structure of Tellurium at High Pressures, J. Chem. Phys., 1965, 43(4), 1149–1152 CrossRef CAS.
- J.-P. Poirier and A. Tarantola, A logarithmic equation of state, Phys. Earth Planet. Inter., 1998, 109(1–2), 1–8 CrossRef.
- J. Li, A. Ciani, J. Gayles, D. A. Papaconstantopoulos, N. Kioussis, C. Grein and F. Aqariden, Non-orthogonal tight-binding model for tellurium and selenium, Philos. Mag., 2013, 93(23), 3216–3230 CrossRef CAS.
- R. M. Martin, G. Lucovsky and K. Helliwell, Intermolecular bonding and lattice dynamics of Se and Te, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(4), 1383–1395 CrossRef CAS.
- F. Mauri, O. Zakharov, S. d. Gironcoli, S. G. Louie and M. L. Cohen, Phonon Softening and Superconductivity in Tellurium under Pressure, Phys. Rev. Lett., 1996, 77(6), 1151–1154 CrossRef CAS PubMed.
- B. M. Powell and . Marte, The lattice dynamics of tellurium, J. Phys. Chem. Solids, 1975, 36, 1287–1298 CrossRef CAS.
- V. B. Anzin, M. I. Eremets, Y. V. Kosichkin, A. I. Nadezhdinskii and A. M. Shirokov, Energy Gap in Tellurium under Pressure, Phys. Status Solidi, 1977, 42, 385–390 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |