Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the charge transport properties of redox active metal–organic conjugated wires†
Donglei
Bu
 a,
Yingqi
Xiong
a,
Ying Ning
Tan
a,
Miao
Meng
a,
Paul J.
Low
a,
Yingqi
Xiong
a,
Ying Ning
Tan
a,
Miao
Meng
a,
Paul J.
Low
 b,
Dai-Bin
Kuang
b,
Dai-Bin
Kuang
 c and
Chun Y.
Liu
c and
Chun Y.
Liu
 *a
*a
aDepartment of Chemistry, Jinan University, 601 Huang-Pu Avenue West, Guangzhou 510632, China. E-mail: tcyliu@jnu.edu.cn
bSchool of Molecular Sciences, University of Western Australia, 35 Stirling Highway, Crawley, 6009, WA, Australia
cSchool of Chemistry, SunYat-sen University, Guangzhou 510275, P. R. China
First published on 19th February 2018
Abstract
Layer-by-layer assembly of the dirhodium complex [Rh2(O2CCH3)4] (Rh2) with linear N,N′-bidentate ligands pyrazine (LS) or 1,2-bis(4-pyridyl)ethene (LL) on a gold substrate has developed two series of redox active molecular wires, (Rh2LS)n@Au and (Rh2LL)n@Au (n = 1–6). By controlling the number of assembling cycles, the molecular wires in the two series vary systematically in length, as characterized by UV-vis spectroscopy, cyclic voltammetry and atomic force microscopy. The current–voltage characteristics recorded by conductive probe atomic force microscopy indicate a mechanistic transition for charge transport from voltage-driven to electrical field-driven in wires with n = 4, irrespective of the nature and length of the wires. Whilst weak length dependence of electrical resistance is observed for both series, (Rh2LL)n@Au wires exhibit smaller distance attenuation factors (β) in both the tunneling (β = 0.044 Å−1) and hopping (β = 0.003 Å−1) regimes, although in (Rh2LS)n@Au the electronic coupling between the adjacent Rh2 centers is stronger. DFT calculations reveal that these wires have a π-conjugated molecular backbone established through π(Rh2)–π(L) orbital interactions, and (Rh2LL)n@Au has a smaller energy gap between the filled π*(Rh2) and the empty π*(L) orbitals. Thus, for (Rh2LL)n@Au, electron hopping across the bridge is facilitated by the decreased metal to ligand charge transfer gap, while in (Rh2LS)n@Au the hopping pathway is disfavored likely due to the increased Coulomb repulsion. On this basis, we propose that the super-exchange tunneling and the underlying incoherent hopping are the dominant charge transport mechanisms for shorter (n ≤ 4) and longer (n > 4) wires, respectively, and the Rh2L subunits in mixed-valence states alternately arranged along the wire serve as the hopping sites.
Introduction
Molecular electronics has attracted great attention due to the potential applications of preprogrammed molecules as components in nanoscale circuits.1,2 Whilst molecular junctions that offer electronic function equivalent to traditional components such as rectifiers,3 switches1,4–6 and transistors7 receive growing attention, the synthesis of linear molecules that can be embedded between two electrodes and function as molecular wires continues to be of primary importance for the development of science underpinning the operation of molecular electronic devices.8–11 Generally speaking, the conductive performance of a molecular wire in a molecular junction is determined by a convolution of factors including the environment,12–14 the nature of the molecule–electrode contacts15,16 and the electronic configuration of the molecule.17,18 Detailed knowledge concerning these various structure–functionality relationships within molecular junctions is therefore much in demand before any practical usage of such devices can be realized.1,3,8,12,17,19–21 Aiming at this goal, significant efforts have been made to create molecular junctions with various backbones and controlled lengths, which are tested using an increasingly diverse array of electrode–molecule–electrode junction techniques.19,22–24 Organic compounds with π-conjugated backbones have served as models through which to explore charge transport mechanisms and the influence of (un)saturation in the molecular backbone on electrical properties.17,20,25–27 Increasingly, chemical functionality is being introduced into prototypical wire-like structures. Redox active molecular wires, linear molecules with one or more periodically inserted redox centers, show weak length-dependence of redox conduction,27–30 which can be reversibly tuned with a gate electrode.19 These features lead to growing interest in the study of molecular wires with integrated metal centers.31–33In both single molecular junctions19,34 and self-assembled monolayers (SAMs),17,20,25–27 two principal conductance mechanisms, charge tunneling for shorter wires and charge hopping for longer wires, have been identified. With increasing wire lengths, a switch in the predominant mechanism from tunneling to hopping is observed for wires of 4–6 nm.17,20,34,35 These two mechanisms are in accordance with the fundamental studies of electron transfer in donor(D)–bridge(B)–acceptor(A) compounds in solution. It is found that D–A electron transfer across a short bridge proceeds by the super-exchange mechanism, whereas long-distance electron transfer is achieved by sequential hopping.36 It is worthwhile to note that in the latter case, the individual hopping steps are interpreted through an underlying super-exchange formalism as well.36 Moreover, as is well known, D–A electron transfer kinetics is governed by donor–acceptor electronic coupling, which is tuned by the bridge structure as well as the donor–bridge energy gap.37,38 Therefore, the through-bond electron transfer in D–B–A systems is intrinsically a resonant behavior of the transferring electron, which necessitates a compatibility of the molecular orbitals in energy and symmetry.36 From the similarities in the electron transfer mechanism between D–B–A systems and electrode–molecule–electrode junctions, it would be interesting to validate the understandings on electron transfer in solution and at molecular junctions. Furthermore, to fully understand the hopping mechanism, the chemical nature of the hopping sites for a given molecular system need to be clarified.19,27 For example, for oligophenyleneimine (OPI) wires, it has been proposed that the charge-hopping site consists of three repeating conjugated subunits.17 Unfortunately, for most of the wire systems studied, the hopping sites are not clearly defined, which prevents a deeper understanding of the microscopic process of charge transport.
Investigation of the electron transport characteristics in the two mechanistic regimes and the transition from one to another relies on the development of a series of structurally related wires with precisely controlled lengths, which can be realized conveniently via layer-by-layer methods with SAM templates.17,20,25,26,39 Coordination chemistry has emerged as a particularly useful tool in this regard.28,39–41 In integrating metal complex units into a π-conjugated backbone, covalently bonded dimetal units (M2) can be desirable candidates.40 With appropriately designed and synthesized M2 building blocks and bridging ligands, both axial and equatorial linkages can be realized to construct metal–organic hybrid wires.8,40 From an equatorial linkage, metal–ligand orbital interactions would generate a d(δ)–p(π) conjugated wire,42,43 while an axial binding mode gives a wire with π(M2)–π(bridge) conjugation.8,44,45 Such well-defined electronic structures should be highly beneficial to the rational design of wire-like compounds and mechanistic study of charge transport.
In the present work, two series of metal–organic hybrid wire-like structures with similar backbones were prepared by the fabrication of the SAMs on gold surfaces through axial coordination of the dirhodium building block [Rh2(O2CCH3)4] (Rh2) with the conjugated N,N′-bidentate bridging ligands (L), pyrazine (LS) and 1,2-bis(4-pyridyl)ethene (LL), and denoted as (Rh2LS)n@Au and (Rh2LL)n@Au, respectively. By taking a stepwise fabrication approach, the number of Rh2L repeating units (n = 1–6) was precisely controlled, giving the wire-like structures lengths up to ∼9 nm. These two wire series have similar molecular backbones, but different lengths for the wires with the same number of building blocks, which permit detailed studies of the impact of Rh2L building blocks on charge transport properties in the tunneling and hopping regimes. The electron transport characteristics of the resulting SAMs were measured using conductive probe atomic force microscopy (CP-AFM). For both systems, a change of length dependence from an exponential to a linear relationship for the current–voltage (I–V) characteristics was observed at n = 4, which signals a transition in the charge transport mechanism. Notably, smaller β values were found for the system having the longer bridging ligand for both short (n = 1–4) (βT = 0.044 ± 0.002 Å−1, verses 0.101 ± 0.012 Å−1 for (Rh2LS)n@Au) and long (n = 4–6) (βH = 0.003 ± 0.001 Å−1 verses 0.035 ± 0.003 Å−1 for (Rh2LS)n@Au) junctions, although the electronic coupling within the LS bridged series is significantly stronger. DFT calculations on the Rh2L fragments coupled with estimates from spectral data reveal that the 1,2-bis(4-pyridyl)ethene-based (Rh2LL)n wires offer smaller HOMO (Rh2 dπ)–LUMO (bridge π*) gaps than the shorter pyrazine-based (Rh2LS)n systems, thus, accounting for the improved charge hopping of this system. These experimental and theoretical results suggest that in these (Rh2L)n wire systems the Rh2L complex units serve as the hopping sites for charge hopping over a long distance.
Results and discussion
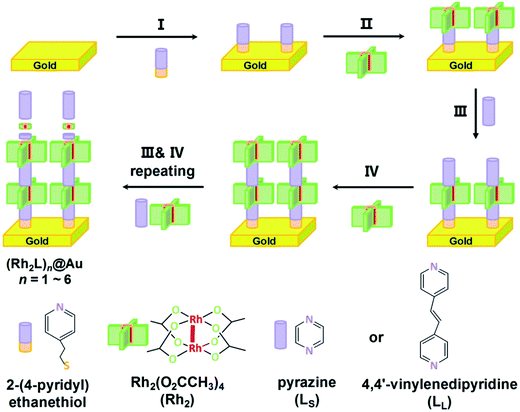
Fabrication of the (Rh2L)n@Au
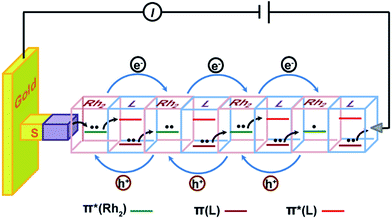
The fabrication process of the Rh2-ligand SAMs is schematically described in Fig. 1. As is well known, the dirhodium complex [Rh2(O2CCH3)4] is a strong Lewis acid with respect to its axial coordination capability and readily forms [Rh2(μ-O2CCH3)4L2] adducts with Lewis bases, L, and is stable under aerobic conditions. These features allow the facile assembly of Rh2 and linear N,N′-bidentate bridging ligands L (L = LS for pyrazine or LL for 1,2-bis(4-pyridyl)ethene), yielding a linear structure with the Rh–Rh bonds aligned with the long molecular axis. To immobilize the SAMs onto the gold substrate, 2-(4-pyridyl) ethanethiol was utilized as a molecular anchor that is bonded to the Au surface with the S atom, preparing a pyridyl group for the complexation of the incoming Rh2 building block. Similar processes involving [Rh2(phen)2(μ-O2CCH3)2(NCMe)2], pyrazine (LS) and 4-thiopyridine as a surface anchor,46 and systems consisting of bis(Rh2) dimers, 1,2-bis(4-pyridyl)ethene (LL) and 2-(4-pyridyl) ethanethiol as anchors40 have been reported by other groups.Here, the assembly process started with the immersion of the gold substrate in an ethanol solution of 2-(4-pyridyl) ethanethiol (0.01 mM) for one hour (Step I). This pyridyl-functionalized Au substrate was then soaked in an ethanol solution of [Rh2(O2CCH3)4] (0.2 mM), in which the Rh2 complex exists as EtOH solvated molecules [Rh2(O2CCH3)4(EtOH)2], at −15 °C for 1 hour. This process allows the first Rh2 unit to be immobilized onto the gold surface through metal–ligand complexation (Fig. 1, Step II), forming Rh2@Au.40 It was found that reactions at room temperature did not afford surface structures of high quality for the subsequent wire growth. In the following step, the functionalized Rh2@Au substrate was immersed in an ether solution of the ligand (L = LS or LL) for 10 minutes to generate (Rh2L)n@Au (n = 1) (Step III). In Step IV a second Rh2 moiety was introduced by further reaction with [Rh2(O2CCH3)4(EtOH)2] (2 minutes). The following steps involve alternate repeating of Steps III and IV with a dipping time of 2 minutes for both processes, which developed the satisfactory metal–organic SAMs on the gold substrates, (Rh2LS)n@Au and (Rh2LL)n@Au (n = 1–6), as indicated by electrochemical and spectroscopic characterization (vide infra). After each step, the Au substrates were rinsed with ethanol to remove the excess adsorbates and dried with a stream of N2. The fabrication of these monolayers with six Rh2L repeating units can be completed in less than three hours, faster than the stepwise fabrication of organic SAMs.17,20 For (Rh2LS)n@Au, with increasing n from 2 to 6, the thickness (T) of the SAMs increases from 2.04 ± 0.29 to 4.74 ± 0.18 nm, as determined by an AFM based nano-shaving method,39 whereas for (Rh2LL)n@Au, T = 3.08 ± 0.64 nm (n = 2) − 8.78 ± 0.53 nm (n = 6). These data are in good agreement with the wire lengths (L) estimated from the X-ray structures of similar structural motifs (Fig. S4 and S5†).47–49
Spectroscopic characterization and properties
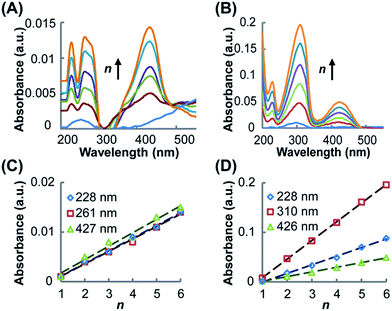
UV-vis spectroscopy was utilized to characterize the resultant SAMs and monitor the growth of the SAMs on the Au substrate. As shown in Fig. 2A for (Rh2LS)n@Au and Fig. 2B for (Rh2LL)n@Au, while the band profiles remain unchanged, the spectral absorption intensities increase linearly as the number of layers (n) increases from 1 to 6, confirming the step-by-step fabrication of (Rh2L)n (n = 1–6) on the Au substrates. The SAMs of both systems exhibit four absorption bands in the range of 200–500 nm, similar to the spectra of the oligomers (Rh2LS)n (Fig. S1A†) and (Rh2LL)n (Fig. S1B†), prepared by mixing [Rh2(OCCH3)4] with the bridging ligands. Comparison of the spectra of the molecules immobilized on the Au substrate with the spectra of the associated oligomers and free bridging ligands (Fig. S1C and D†) provides accurate spectral assignments to the electronic transitions. The low energy absorption band in the spectra (Fig. 2), ca. 427 nm (Rh2LS)n@Au and 426 nm for (Rh2LL)n@Au, is assigned to the π*(Rh–O) → σ*(Rh–O) transition within the [Rh2(O2CCR)4] core,50,51 which is insensitive to the nature of the axial ligands. The higher energy absorbances (λmax < 228 nm) are attributed to transitions occurring within the bridging ligands. In the spectra of the free bridging ligands, an intense absorption band is observed at 250 nm for pyrazine (Fig. S1C†) and at 280 nm for 1,2-bis(4-pyridyl)ethene (Fig. S1D†); for the SAMs on the Au substrate these bands are red shifted to 261 and 310 nm, respectively. These bands arise likely from the π → π* transition in the aromatic system of the ligands. It is notable that for (Rh2L)n@Au and oligomers (Rh2L)n this band is broad and asymmetrical. There is a shoulder band appearing on the low energy side of this dominant absorbance, ca. 285 nm for (Rh2LS)n@Au and 330 nm for (Rh2LL)n@Au, as shown in Fig. 2A and B, which is not present in the spectra of the free ligands (Fig. S1C and D†). Therefore, these absorption bands are ascribable to the metal (Rh2) to ligand (bridge) charge transfer (MLCT). Importantly, (Rh2LS)n@Au has a MLCT energy significantly higher than that for (Rh2LL)n@Au.Electrochemical characterization and properties
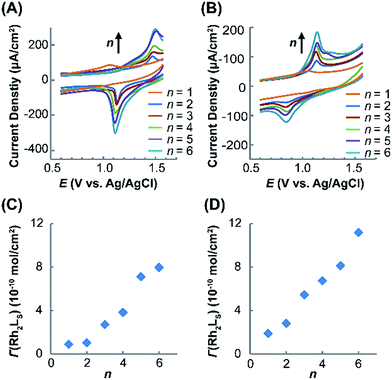
Electrochemical measurements of the immobilized SAMs were performed in CH2Cl2 with an nBu4NPF6 electrolyte (1.0 M). The cyclic voltammograms (CVs) obtained for (Rh2LS)n@Au and (Rh2LL)n@Au with n = 1–6 are shown in Fig. 3A and B, respectively. As expected, in the CVs for (Rh2L)n@Au, the current density increases with increasing the number of the Rh2 units. By variation of the scan rate from 0.10 to 0.50 V s−1 for the CV measurements (Fig. S2†), a linear correlation of the current intensity with the scan rate is observed, indicating that the Rh2 units of the linear molecules are surface bounded. The SAMs with a Rh2 monolayer (n = 1) show a weak redox wave at almost the same potentials, E1/2 = ∼1.05 V, regardless of the axial coordination of pyrazine or 1,2-bis(4-pyridyl)ethane, and the cathodic and anodic peaks appear at similar potentials (Fig. 3A and B). To validate these potentials for the Rh2 redox centers on the SAMs, two reference compounds, Rh2(O2CCH3)4(C5H5N)2 and Rh2(O2CCH3)4(C5H5NC2H2C6H6)2, analogous to the Rh2L2 complex moieties in (Rh2LS)n@Au and (Rh2LL)n@Au, respectively, were prepared and the redox properties were examined by cyclic voltammetry in CH2Cl2 solution. Quasi-reversible CVs (Fig. S3†) were observed for these Rh2 complexes, which gave the E1/2 values of 0.97 V and 0.95 V, respectively, in good agreement with the data for the SAMs of n = 1. Interestingly, after additional Rh2 layers are introduced onto the SAMs, the cathodic (Epc) and anodic (Epa) peaks are largely displaced. Then, the half wave redox potentials (E1/2), 1.30 V for (Rh2LS)n@Au (n = 2–6, Fig. 3A) and 1.03 V for (Rh2LL)n@Au (n = 2–6, Fig. 3B), are estimated from E1/2 = (Epa + Epc)/2. SAMs (Rh2LL)n@Au (n = 2–6) show an E1/2 nearly identical to that of (Rh2LL)@Au, but a large deviation from 1.05 to 1.30 V is found for the pyrazine bridged series. Therefore, these half-wave potentials (E1/2) account for the redox process Rh2II/II → Rh2II/III in the SAMs.The surface coverage (Γ) of the Rh2L unit in the SAMs with different Rh2L unit numbers (n) is determined coulometrically from the redox waves (Table 1), which increases as a function of n, as shown in Fig. 3C and D. For (Rh2LL)n@Au, the surface coverage of Rh2L increases from 1.9 × 10−10 mole cm−2 to 11.2 × 10−10 mole cm−2 as n increases from 1 to 6. Slightly smaller surface coverage values, Γ = 0.9 × 10−10 (n = 1) − 8.0 × 10−10 (n = 6) mole cm−2, are found for (Rh2LS)n@Au. The linear dependence of surface coverage on n demonstrates that the monolayers formed on the surface consist of the wires with presubscribed building blocks. These results are fully consistent with the UV-vis spectra, confirming the successful fabrication of the metal–organic wires in the expected manner.
| Monolayer | E 1/2 (V) | E pa − Epc (V) | E gap (eV) | Γ (10−10 mol cm−2) | L (nm) | T (nm) | R (106 Ω) | β |
|---|---|---|---|---|---|---|---|---|
| a E gap refers to the metal to ligand charge transfer (MLCT) energy. b Data collected only for the selected wires to show the length variation with increasing the number of the Rh2L units (n). | ||||||||
| (Rh2LS)1@Au | 1.05 | 0.02 | 4.35 | 0.9 | 1.43 | — | 10.3 ± 1.8 | 0.101 ± 0.012 |
| (Rh2LS)2@Au | 1.30 | 0.38 | 1.0 | 2.17 | 2.04 ± 0.29 | 31.9 ± 5.5 | ||
| (Rh2LS)3@Au | 2.7 | 2.91 | — | 51.9 ± 4.9 | ||||
| (Rh2LS)4@Au | 3.8 | 3.65 | 3.55 ± 0.62 | 105.7 ± 19.9 | 0.035 ± 0.003 | |||
| (Rh2LS)5@Au | 7.1 | 4.39 | — | 134.0 ± 22.1 | ||||
| (Rh2LS)6@Au | 8.0 | 5.51 | 4.74 ± 0.18 | 178.1 ± 34.5 | ||||
| (Rh2LL)1@Au | 1.05 | 0.01 | 3.76 | 1.9 | 2.05 | — | 17.9 ± 9.2 | 0.044 ± 0.002 |
| (Rh2LL)2@Au | 1.03 | 0.29 | 2.8 | 3.41 | 3.08 ± 0.64 | 28.9± 5.3 | ||
| (Rh2LL)3@Au | 5.4 | 4.77 | — | 57.4 ± 10.4 | ||||
| (Rh2LL)4@Au | 6.7 | 6.13 | 5.83 ± 0.33 | 102.7 ± 18.9 | 0.003 ± 0.001 | |||
| (Rh2LL)5@Au | 8.1 | 7.49 | — | 107.8 ± 27.3 | ||||
| (Rh2LL)6@Au | 11.2 | 8.85 | 8.78 ± 0.53 | 111.6 ± 29.4 | ||||
For the Rh2 SAMs with n = 2–6, the potential hysteresis of reduction is remarkable. These results are in contrast to the observations in most of the redox active SAMs, which have the anodic and cathodic peaks at similar potentials.39,52 The cathodic–anodic peak separations are also larger than those for SAMs with Rh2 complex building blocks (0.14 V) reported in earlier work.40 The observations that a shorter bridge gives a larger Epa − Epc splitting and a larger shift of E1/2, relative to the potentials for the SAMs with a single Rh2 complex unit and the Rh2 monomer in solution, indicate that the pronounced redox hysteresis for these two series is somehow related to the electronic coupling between neighboring Rh2 centers. Similarly, for moderately coupled mixed-valence (MV) D–B–A systems, we may observe a large Epa − Epc separation due to the two overlapped potential waves for the two redox centers. In a strong coupling case, organic SAMs constructed from redox active tetrathiafulvalene (TTF) building blocks show two separated redox waves for the two one-electron processes,20 resembling strongly coupled MV systems, for example, the Creutz–Taube complex (ΔE1/2 = 360 mV),53 [(NH3)5Ru (pyrazine)Ru(NH3)5]5+. This correlation of (Epa − Epc) with the electronic coupling between the metal centers is further supported by the Rh2 SAMs with a saturated bridging ligand (L = 1,2-dipyridylethane), which exhibit the Epa (0.92 V) and Epc (0.94 V) peaks at similar potentials.54 Therefore, we attribute the larger Epa − Epc splitting (0.38 V) for (Rh2LS)n@Au, in comparison with 0.29 V of (Rh2LL)n@Au, to the stronger bridge mediated metal–metal coupling. Similar results were obtained in other metal-containing redox conductive systems. For instance, with phenylene or multi-phenylene bridges, the bis(terpyridyl) metal complex wires showed small Epa − Epc splitting.39 However, the bis(terpyridyl) metal complex networks with a short metal–metal distance exhibit a large potential hysteresis in the electrochemical CV diagrams,55 although both systems are constructed with the same metal complex unit.
In molecular junctions, the electronic coupling between two electrodes is a sum of the coupling between the electrode and the wire, and the coupling within the molecule.56 Theoretically, the general Hamiltonian of electronic coupling can be expressed as follows:57
| H = Hmol + Helectrode + V | (1) |
Current (I)–voltage (V) characteristics
The electron transport characteristics of (Rh2LS)n@Au and (Rh2LL)n@Au were studied using CP-AFM with Pt/Ir AFM probes in contact with the termini of the wires implanted on gold surfaces. The electrical resistances of the molecular junctions formed by Au substrate-wire-AFM probe are determined by taking the reciprocal of I–V curve slopes and averaging over 30 I–V traces. Fig. 4 shows a plot of resistance (R) versus molecular length (L) for (Rh2LS)n and (Rh2LL)n (n = 1–6). As expected, R increases as a function of the wire length. However, here the length-dependence of R is best described by a correlation of R with the number (n) of the Rh2L units. As shown in Table 1, similar current resistances (R) are found for shorter wires of the two series with n ≤ 4. For the longer wires (n = 4–6), an abrupt increase of R is observed for (Rh2LS)n@Au as n increases, whereas (Rh2LL)n@Au shows a plateau of R with adding more Rh2L units, even though the wires are largely lengthened, in comparison with (Rh2LS)n@Au (Table 1). For both series, an exponential increase of R with increasing wire length is observed for systems n ≤ 4 (Fig. 4B, regime I), and a linear relationship between R and L is found for longer structures with n = 4–6 (Fig. 4B, regime II). The exponential increase of R in regime I is consistent with the characteristic R–L relationship in the charge tunneling process, described byR = R0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (βL) (βL) | (2) |
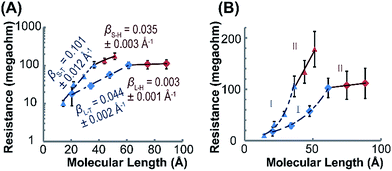 | ||
| Fig. 4 (A) Semi-log plots of resistance versus molecular length in regimes I (n = 1–4, blue) and II (n = 4–6, red) for (Rh2LS)n (triangle) and (Rh2LL)n (diamond). The wire resistances were measured with CP-AFM, in which a Pt/Ir-coated tip was brought into contact with the (Rh2L)n@Au monolayers. The I–V traces were obtained over ± 0.8 V at a load of ∼1 nN on the tip contact. Each data point is the average resistance obtained from over 30 I–V traces in the range from −0.4 to +0.4 V. The straight lines are the linear fitting of the data using eqn (2). (B) A linear plot of R versus L, demonstrating linear scaling of resistance with the length of the long wires (n = 4–6). | ||
Different length-dependences of the conductance are observed for the longer wires (n = 4–6) in region II, indicating that charge transport occurs via a different mechanism. The linear correlation of resistance with length (Fig. 4B) indicates that the hopping mechanism is in operation for charge transport in (Rh2L)4–6@Au.19,74 These results indicate a transition in the charge transport mechanism from tunneling to hopping. Tunneling to hopping transition has been observed in several π-conjugated organic systems,17,19,20,25,27 but scarcely seen in metal–organic wire series.30,31 It is important to note that for the two series, the transition occurs in wires with the same number of Rh2L units (n = 4), but with different lengths, ca. ∼3.5 nm for (Rh2LS)4@Au and ∼6 nm for (Rh2LL)6@Au. These lengths associated with the change in the conductance mechanism are compatible with other systems.17,19,20,27,28 For instance, for oligophenyleneimine (OPI) and oligo-tetrathiafulvalene-pyromellitic-diimideimine (OTPI) wires, the turning point from tunneling to hopping is at about 4–5 nm.17,20 To compare the charge transport characteristics of the wires in different regimes, the β parameters in the hopping regime (II) were also derived by exponential fitting of the data (eqn (2)), as reported in the literature.17,22βS–H = 0.035 ± 0.002 Å−1for (Rh2LS)4–6@Au and βL–H = 0.003 ± 0.001 Å−1 for (Rh2LL)4–6@Au are determined, which are substantially smaller than those for (Rh2L)n@Au with n < 4 (Fig. 4). For the wires with 1,2-bis(4-pyridyl)ethane bridges, the attenuation factor of 0.003 Å−1 is close to the smallest β values in the hopping regime reported before.22,28,64 Collectively, the wire series with larger π-conjugated bridges, (Rh2LL)n, have smaller β factors in both tunneling and hopping regimes, while these wires show generally a weak length-dependence of electrical resistance.
Fig. 5 shows the impacts of voltage (V) and electrical field (E) on current intensity (I) for the two wire series at different lengths. For both (Rh2LS)n@Au (Fig. 5A) and (Rh2LL)n@Au (Fig. 5B), symmetric I–V curves are displayed within the testing window (±0.8 V). The I–V curves for all studied wires with error bars representing the standard deviation are displayed in Fig. S6.† It is found that the current decreases as the wire length increases, consistent with the length dependence of resistance (Fig. 4). Importantly, the two series exhibit the semi-log I–V curves that can be divided into two groups considering the current variation with respect of the number of the Rh2L units (Fig. 5A and B). For short wires (n = 1–4), elongating the molecular wires yields a large decrease of the current at all potentials. However, the I–V curves for the long wires (n = 4–6) show smaller current reductions with increasing the wire length. Interestingly, for each of the two wire series, the two groups that show different conductive behaviors are separated by the wire having the same Rh2L unit number (n = 4), rather than the wire having the same lengths, in accord with the transition point observed in the length dependence of resistance (Fig. 4).
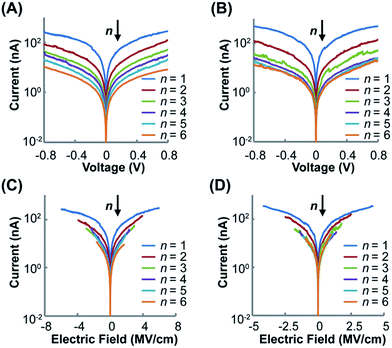 | ||
| Fig. 5 Semi-log plots of the averaged I–V curves for (Rh2LS)n@Au (n = 1–6) (A) and (Rh2LL)n@Au (n = 1–6) (B). Semi-log plots of the averaged I–E curves for (Rh2LS)n@Au (n = 1–6) (C) and (Rh2LL)n@Au (n = 1–6) (D). The deviations from the I–V and I–E curves are shown in Fig. S6 (ESI).† | ||
The large voltage-dependence of current for the short wires of both series, as shown by the semi-log I–V curves (Fig. 5A and B), corresponds to the voltage-driven characteristics for charge tunneling.17 On the other hand, in the semi-log I–E plots, (Rh2LL)n@Au (n = 4–6) (Fig. 5D) exhibits the traces that collapse nearly on the top of one another. This result reveals that for long wires (Rh2LL)n, the charge transport is field driven in nature, corresponding to the hopping mechanism.17 The I–E characteristics observed for (Rh2LL)n@Au conform well to the transition from exponential to linear relationships between the resistance (R) and the molecular length (L), confirming the conversion of the electron transport mechanism from tunneling to hopping. Furthermore, the more homogeneously spaced I–V (Fig. 5A) and I–E curves for the pyrazine derived wires (Fig. 5C) are consistent with the mild transition from regime I to II, observed for (Rh2LS)n@Au (Fig. 4). These results indicate that while charge transport in (Rh2LS)n is dominated by super-exchange tunneling in regime I, this pathway still plays a significant role in regime II where the hopping mechanism starts to operate. This is understandable from the strong coupling between the Rh2 centers and great extent of electronic delocalization for the pyrazine bridged system. The differences in I–V and I–E characteristics between (Rh2LS)n@Au and (Rh2LL)n@Au must originate from their differences in the backbone architecture.
DFT calculations
As shown above, in regime II (n ≥ 4), for wires of the two series having the same number of the bridging ligands, charge hopping behaviors are observed for the wires built by longer bridging ligand LL (1,2-bis(4-pyridyl)ethene), which shows relatively weak Rh2–Rh2 coupling, as evaluated by the electrochemical analyses. To better understand the experimental results, theoretical calculations at the density functional theory (DFT) level were carried out on the simple models that are not wired to the electrode, aiming at understanding the electronic coupling effects within the molecules. For the regime I, the calculation models are built with two Rh2L units (n = 2) and a 2-(4-pyridyl) ethanethiol group, that is, (Rh2L)2(NC5H4CH2CH2S) (L = LS or LL), as an example of the shorter wires. In the hopping regime, the models of the Rh2L moieties, Rh2(O2CCH3)4(C5H5N) (Rh2LS) and Rh2(O2CCH3)4(NC5H4CHCHC5H4N) (Rh2LL), were adopted considering that the hopping sites are relevant to the fragment orbitals but not necessarily to the MOs of the entire molecule.As shown in Fig. 6, the computational results show that one of the two Rh–Rh π anti-bonding orbitals (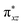 and
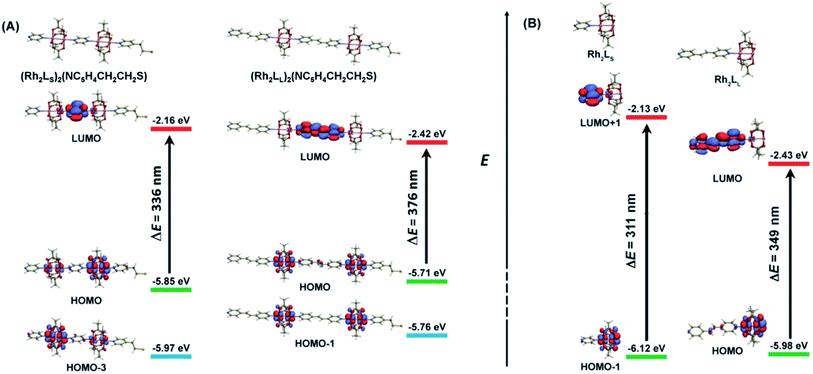
and 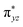 ) is symmetrically related to the π orbitals of the conjugated bridging ligand, topologically analogous to the orbital interactions between the ethynyl and phenyl groups in ethynyl benzene. Therefore, for both series, a π orbital interaction is invoked through the π*(Rh2)–π*(L) orbital interactions. In both of the Rh2 dimer and Rh2L fragment cases, the compositions of the MOs predict that the HOMOs of the molecular wires are composed of the π*(Rh2) orbitals, while the LUMOs are constructed mainly from the π*(L) orbitals. For the Rh2 dimers, calculations also show that the longer bridging ligand gives lower LUMO energy for the wire, e.g., −2.42 eV and−2.16 eV for the Rh2 dimers with longer and shorter bridges, respectively. The HOMOs result from “phase out” combination (π* − π*) of the π*(Rh2) orbitals for the pyrazine derivative, but “phase in” combination (π* + π*) for the other. The HOMO–LUMO gap for the pyrazine bridged Rh2 dimer is 3.69 eV (336 nm), larger than that for the Rh2 dimer with the longer bridge by 0.4 eV (40 nm) (Fig. 6), consistent with the experimental observation (45 nm). The calculations on the two models give similar HOMO energies, i.e., −5.85 and −5.71 eV for the molecules with shorter and longer bridges (Fig. 6A), respectively.
) is symmetrically related to the π orbitals of the conjugated bridging ligand, topologically analogous to the orbital interactions between the ethynyl and phenyl groups in ethynyl benzene. Therefore, for both series, a π orbital interaction is invoked through the π*(Rh2)–π*(L) orbital interactions. In both of the Rh2 dimer and Rh2L fragment cases, the compositions of the MOs predict that the HOMOs of the molecular wires are composed of the π*(Rh2) orbitals, while the LUMOs are constructed mainly from the π*(L) orbitals. For the Rh2 dimers, calculations also show that the longer bridging ligand gives lower LUMO energy for the wire, e.g., −2.42 eV and−2.16 eV for the Rh2 dimers with longer and shorter bridges, respectively. The HOMOs result from “phase out” combination (π* − π*) of the π*(Rh2) orbitals for the pyrazine derivative, but “phase in” combination (π* + π*) for the other. The HOMO–LUMO gap for the pyrazine bridged Rh2 dimer is 3.69 eV (336 nm), larger than that for the Rh2 dimer with the longer bridge by 0.4 eV (40 nm) (Fig. 6), consistent with the experimental observation (45 nm). The calculations on the two models give similar HOMO energies, i.e., −5.85 and −5.71 eV for the molecules with shorter and longer bridges (Fig. 6A), respectively.
It is remarkable that the computational results are in excellent agreement with the ionization energies (IE) for the corresponding Rh2 oligomers, i.e., 5.98 and 5.88 eV determined by XPS (Fig. S7†). Therefore, experimental and theoretical results indicate that in both of the two Rh2 wire systems, the HOMO is below, but very close to, the gold Fermi level (−5.31 eV).75 Given this energetic alignment of the HOMO with the electrode Fermi level, sufficiently strong electronic coupling between the molecule and the electrode is maintained, which facilitates the charge injection from the electrode to the molecule. Since the optically determined HOMO–LUMO gaps can be significantly reduced in the metallic junction,9 strong electronic coupling is ensured in the molecular junctions for both of the two wire systems, as evidenced by the large hysteresis of the reduction potential for the (Rh2L)n@Au (vide supra).
The calculations also convey important information on the electronic coupling within the molecules. For (Rh2LS)2(NC5H4CH2CH2S), the counterpart of the HOMO (π* − π*) is HOMO-3 (π* + π*), as shown in Fig. 6A. These two metal-based MOs are separated in energy by 0.12 eV. Remarkably, in XPS, two peaks at 5.98 eV and 6.18 eV were observed (Fig. S7†), corresponding to the removal of the valence electrons from these metal-based MOs. In contrast, for (Rh2LL)2(NC5H4CH2CH2S), the energy difference between the HOMO (π* + π*) and HOMO-1 (π* − π*) is only 0.05 eV and XPS exhibits a single peak at 5.88 eV, consistent with the calculated value (−5.71 eV). These MOs are non-degenerate due to the mediation of the bridging ligand, and the larger the spacing, the stronger the electronic coupling. Thus, the energy difference between the MO counterparts is a measurement of the strength of Rh2–Rh2 electronic coupling, similar to the equatorially bridged Mo2 dimers where the magnitude of the energy gap between (δ + δ) and (δ − δ) has been used to evaluate the metal–metal coupling strength.43 Therefore, evidently, the Rh2–Rh2 coupling in the pyrazine bridged wires is appreciably stronger than that in the 1,2-bis(4-pyridyl)ethene bridged system, consistent with the experimental results. For the latter, the HOMO–(HOMO−1) gap of 0.05 eV indicates that the metal–metal interaction is relatively weak,43 being in the charge localized regime.
Calculations on the fragment models show that the HOMO and LUMO are contributed mainly by the Rh2 center and bridging ligand orbitals, respectively (Fig. 6B). This π*(Rh2)–π*(L) interaction is transformed by the HOMO → LUMO electronic transition in Rh2LL. For Rh2LS, such a π*(Rh2)–π*(L) interaction is represented by the HOMO−1 → LUMO+1 transition. Therefore, these transitions correspond to the metal to ligand charge transfer (MLCT) absorptions in the electronic spectra (vide supra). As shown in Fig. 6B, the π*(Rh2) (HOMO) energy for Rh2LL is higher than that (HOMO−1) for Rh2LS, which is in agreement with its lower redox potential (Fig. 3 and Table 1). In addition to the higher π*(Rh2) orbital energy for Rh2LL, the π*(L) orbital energy is substantially low in comparison with that for Rh2LS. Therefore, the two Rh2L fragments differ in the energy gap between these Rh2-based and L-based MOs. The metal to ligand charge transfer energy for the Rh2LS and Rh2LL fragments is calculated to be 3.99 eV (311 nm) and 3.55 eV (349 nm), respectively. The calculated transition energies are in good agreement with the observed MLCT band energies in the UV-vis spectra for the SAMs on the gold substrate, 285 nm for (Rh2LS)n@Au and 330 nm for (Rh2LL)n@Au, as shown in Fig. 2.
Interpretation of charge transport behaviors
Given the experimental and theoretical results for the two wire series, the conducting behaviors and the charge transport mechanisms of the systems may be elucidated under the McConnell super-exchange formalism,58,59 which is widely accepted for the study of the intramolecular electron transfer in solution and proposed in the molecular junction.76 In a D–B–A molecular system, according to the super-exchange mechanism, reducing the energy gaps between the donor and bridge and/or the bridge and acceptor benefits directly the charge transfer from the D (A) site to the bridge or vice versa, consequently accelerating the D → A electron transfer.45,58,59 Similarly, here, better charge transport characteristics are observed for (Rh2LL)n@Au due to the smaller optical gaps. From the lower π* (LL) orbital energies for this series, as shown in Fig. 6, higher energy filled π(LL) orbitals are anticipated, which would help hole hopping via a ligand to metal transition (LMCT). Therefore, under the super-exchange formalism, charge transport between two neighboring Rh2 centers in both tunneling and hopping pathways is favored for the (Rh2LL)n wires. On the other hand, in (Rh2LS)n, the extra Coulomb repulsion caused by the short Rh2–Rh2 distance would resist the charge hopping between the adjacent Rh2 centers. Therefore, the large optical gap and strong electrostatic effects provide the pyrazine bridged wires with poorer redox conduction in the hopping regime. In the tunneling regime, however, similar charge transport characteristics are observed for (Rh2LS)n and (Rh2LL)n (Table 1). It appears that the increased coupling effects resulting from the shorter charge transfer distance and delocalization for (Rh2LS)n are offset by the larger HOMO–LUMO gap and electrostatic repulsion. Therefore, our results show that the generally defined electronic coupling within the molecule is not an impetus to drive the charge transport under the condition of bias voltage, and accordingly, the extent of electron delocalization may not be used as an effective criterion for the assessment of charge transport characteristic in molecular junctions. Of course, better electronic delocalization in (Rh2LS)n@Au should be helpful for efficient charge tunneling; this is why for this series, the attenuation factor β in the hopping regime (n > 4) is close to that for the shorter wires (n < 4), showing the tunneling characteristics. Finally, it should be addressed that when electrons traverse the molecules through bonds in a short distance, both super-exchange and resonance pathways may be involved. For example, as shown in Fig. 6, resonant tunneling may occur between the two non-degenerate metal-based HOMOs. However, it is hard to account for the contributions made by each of them. Therefore, the use of terminology super-exchange tunneling in this context does not preclude the resonant effects.As is noticed, electron delocalization does not extend throughout the entire long π conjugated wire;17 for wires with a sufficiently long length, charges are unevenly distributed along the wires. Therefore, redox exchange, for which the presence of charge localized redox centers is the perquisite, has been considered in diverse molecular junctions.77 The study of a single electron transistor reveals that several distinct redox states in the phenylenevinylene oligomer (3.2 nm in length) can be reached with small addition energies, which controls the charge transport properties.35 According to Nishihara, different redox states for the [Fe(tpy)2] sites in the wire, generated after electron injection from the gold electrode, are responsible for the intra-wire hopping between the [Fe(tpy)2] sites along the wire.28 The hypothesis of mixed-valence state exchange for redox molecular conduction junctions is also supported by recent theoretical work.78 In this study, the experimental observations and computational data lead us to propose that under a bias voltage the Rh2 redox sites in the wires are in mixed-valence states, a reduced Rh2II/II(D) and oxidized Rh2II/III(A), and redox exchange between two adjacent Rh2 centers occurs as follows:
| –(Rh2II/II–L–Rh2II/III)– → –(Rh2II/III–L–Rh2II/II)– | (3) |
A microscopic description for this hopping mechanism is schematized in Fig. 7, showing charge transport through multiple redox hopping steps under a certain bias. We assume that the mixed-valance states are in the localized regime and there is not any instant charge occupation on the bridge. As shown in Fig. 7, the wire ends with a bridging ligand which is in contact with the conducting probe. Upon application of a bias voltage, migration of the charge carriers starts with the first injection of charge (hole) from the electrodes, creating the first MV Rh2II/II–L–Rh2II/III unit close to the electrode.9,56 Within a Rh2II/II–L–Rh2II/III unit, Rh2 → Rh2 electron transfer proceeds through bridge-mediated electron and hole hopping pathways, or electron/hole super-exchange reactions, in which the bridging ligand is involved by providing a low lying empty π* orbital and high lying filled π orbital.38 By this hypothesis, the super-exchange tunneling to hopping transition is controlled by the number of Rh2–L–Rh2 units, instead of the wire length. Experimentally, we observed that for both wire series, the mechanistic transition occurs in the wire with two Rh2–L–Rh2 units (n = 4), but with different lengths. In the situation of molecular junctions, electron self-exchange is not an isolated redox event occurring in a single Rh2–L–Rh2 unit. Simultaneous and concerted actions of all the Rh2–L–Rh2 units along the wire generate the redox conductivity in the electrical circuit (Fig. 7). This mechanism conforms well to a previous theoretical study, which proposes a conduction channel dominated by electron localization at the redox centers.78
The hopping mechanism proposed here is based on the super-exchange formalism. The metal–ligand interactions, as indicated by the HOMO–LUMO energy difference (optical gap) of the Rh2L unit, govern the electron transfer across the bridge. This optical gap can be referred to as the energy barrier for electron hopping between two bridged Rh2 centers.79 Notably, this is different from organic π conjugated wires, in which the hopping barrier is determined by structural conformation factors.17 Our results show that localized systems with small optical gaps present high performance of electrical conductance. These results are parallel with the observations on π-conjugated organic wires constructed with a redox active donor (tetrathiafulvalene, TTF) and acceptor (pyromelliticdiimide, PMDI), which show an enhanced hopping transport with respect to the homogeneous wire systems.17,20 It is noted that this oligo-tetrathiafulvalene-pyromelliticdiimide-imine (OTPI) system is fully charge localized because of the large internal potential difference (redox asymmetry) between the D and A sites, but has the wire conductivity nearly two orders of magnitude higher than that of the charge delocalized oligophenyleneimine (OPI) wires.17,20 In both of the two examples of organic and metal–organic redox systems, the hopping efficiency is controlled by the HOMO–LUMO gap, as predicted by the CNS model proposed by Creutz, Newton and Sutin based on the McConnell super-exchange formalism.80 However, in the asymmetrical organic D–B–A wires, the HOMO–LUMO gap corresponds to the potential difference between the D and A sites. Differently, for the symmetrical, metal–organic redox wires under investigation, the optical gap is correlated with the differences in orbital energy between the MOs of the redox center and the bridge ligand.
Conclusion
Through axial coordination, the dirhodium complex [Rh2(O2CCH3)4] with N,N′-bidentate ligands was fabricated linearly and alternately on Au substrates, developing two series of highly ordered π conjugated wires (Rh2LS)n (Ls = pyrazine) and (Rh2LL)n (LL = 1,2-bis(4-pyridyl)ethene) (n = 1–6). With the Rh2 redox centers incorporated into the molecular backbones, these two metal–organic hybrid wire systems exhibit generally weak length dependence of electrical resistance due to the good alignment of the molecular HOMO with the gold Fermi level in energy and the π–π conjugation between the Rh2 unit and the bridging ligand. Analyses of the current (I)–voltage (V) characteristics reveal that in both series, a transition of the charge transport mechanism from super-exchange tunneling to hopping occurs in wires of n = 4, disregarding the wire lengths. Surprisingly, smaller attenuation factors (β) of electric resistance against increasing the length are found for (Rh2LL)n with longer bridging ligands in both tunneling (β = 0.044 Å−1) and hopping regimes (β = 0.003 Å−1), although in (Rh2LS)n the metal–metal interactions are much stronger. This unusual phenomenon is rationalized by two coupling effects that diminish the charge transport ability of the molecules (Rh2LS)n with small bridging ligands, that is, the relatively high MLCT gap and the charge delocalization that imposes strong electrostatic repulsion between the hopping sites. These results suggest that in these wires, the Rh2L units function as the hopping sites and the optical gap, corresponding to the HOMO–LUMO energy difference, accounts for the hopping barrier. This hypothesis is supported by DFT calculations on the Rh2L motifs, which define the π(Rh2)–π(L) orbital interaction and confirm the spectral assignments to the Rh2 → L electronic transition. On this basis, it is proposed that under a bias voltage, the redox sites in the wire are in mixed-valence states and simultaneous and consecutive electron (or hole) self-exchange across the bridging ligand generates redox conductivity in the circuit. This work indicates that localized redox active wires with small optical gaps exhibit excellent long-distance conductance. The obtained understanding opens the door for the development of highly conductive molecular wires.Materials and methods
Materials
1,2-bis(4-pyridyl)ethene, pyrazine, rhodium(II) chloride trihydrate, and tetrabutyl ammonium hexafluorophosphate (nBu4NPF6), 2-(4-pyridyl) ethanethiol, ethanol, ether and dichloride methane were obtained from commercial sources and used without further purification. The tetraacetate dirhodium(II) were synthesized according to a literature method.81Preparation of gold films
Three types of gold films were used in this study. A transparent gold film was used for UV-vis spectroscopy study, gold on quartz was used for electrochemical measurements and ultra-flat gold was used for AFM characterization.Preparation of transparent gold film and gold film on quartz
First, quartz plates (1 × 4.5 cm2, thickness 0.2 cm) were washed using piranha solution (concentrated sulfuric acid: 30% hydrogen peroxide = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) followed by water and ethanol sequentially and dried in N2. Second, a 3–5 nm thick Ti layer was deposited on the plate by magnetron sputtering. Finally, a 20 nm thick Au layer was deposited on the Ti layer by magnetron sputtering. For electrochemical measurements a 100 nm Au layer was deposited on the Ti layer by magnetron sputtering.
1) followed by water and ethanol sequentially and dried in N2. Second, a 3–5 nm thick Ti layer was deposited on the plate by magnetron sputtering. Finally, a 20 nm thick Au layer was deposited on the Ti layer by magnetron sputtering. For electrochemical measurements a 100 nm Au layer was deposited on the Ti layer by magnetron sputtering.
Preparation of the ultra-flat gold film
Freshly cleaved mica sheets (5 × 5 cm2) were placed onto a stainless steel sample holder in a high vacuum evaporator (Model TRP-450 Sky Technology Development, Shenyang, China). Gold (99.999%, Alfa Aesar, Ward Hill, MA) was evaporated at 3 Å s−1 until 150–200 nm thickness was reached at a pressure around 7 × 10−6 Torr.82,83 Then, ultra-flat gold with large global flatness is prepared on glass according to the method developed by Hegner et al.84 and Wagner et al.85 First, microscope cover slips with a diameter of 12 mm were washed using piranha solution followed by water and ethanol sequentially and dried in N2. Second, these cover slips were glued with Epotek 377 (Epoxy Technology, Billerica, MA) onto the gold thin films. After bring the cover slips in contact with the gold thin film, the samples were annealed at 150 °C for 2 hours, allowing the glue to cure. The cover slip was peeled off from the mica substrate with a gold film glued on it prior to use.Preparation of metal–organic hybrid SAMs on gold substrates
First, SAMs of 2-(4-pyridyl) ethanethiol were prepared by soaking gold films in 0.01 mM 2-(4-pyridyl) ethanethiol in ethanol for 1 hour at room temperature.40 The SAMs were rinsed with ethanol and dried by nitrogen blowing. The fabrication of the metal–organic hybrid oligomers on these SAMs involves two repeating steps. The first step was soaking the SAMs in a 0.2 mM Rh2 ethanol solution at −15 °C for 1 hour.40 Second, these samples were rinsed with ethanol and dried by nitrogen blowing, followed by soaking in a 0.1 mM solution of the bridging molecules (pyrazine or 1,2-bis(4-pyridyl)ethene) in ether at room temperature for 10 minutes. After taking out from the solutions, the samples were rinsed with ethanol and dried in a nitrogen stream followed by repeating the two steps shown above. After the first cycle, soaking times for both solutions were reduced to 2 minutes.Physical measurements
The surface coverage values of Rh2LL and Rh2LS units were estimated by the integration of the oxidation peak areas. This integration gives the number of electrons transported from the SAMs' terminal to a gold electrode (Q). Therefore, Γ can be estimated using the following equation:
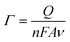 | (4) |
Wire length calculations
The wire lengths were estimated from the X-ray single crystal structures of the Rh2L units that construct the wires. An Rh2LL unit is 13.6 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 in length and an Rh2LS unit is 7.4 Å.48 The length of the molecule 2-(4-pyridyl) ethanethiol on the gold surface is 6.9 Å.49
47 in length and an Rh2LS unit is 7.4 Å.48 The length of the molecule 2-(4-pyridyl) ethanethiol on the gold surface is 6.9 Å.49
DFT calculations
All calculations were run using Gaussian 09 programs (revision A.01). For all calculation models, the geometry was optimized for the neutral states at a DFT level using the B3LYP functional and CPCM (conductor-like polarizable continuum model) solvent model (dichloromethane) in conjunction with the LANL2DZ basic set for rhodium and 6-31G for other atoms. Post-processing for visualization of the molecular orbitals generated by the DFT calculations was performed using VMD and POV-Ray programs. The calculated results are summarized in Fig. S8.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are greatly thankful to the National Natural Science Foundation of China (No. 21371074 and 90922010), Natural Science Foundation of Guangdong Province (No. 2016A030313093 and 2017A030310023), China Postdoctoral Science Foundation (No. 2016M592598), and Jinan University and the Fundamental Research Funds for the Central Universities for the financial support, and the High-performance Computing Platform of Jinan University for computational resource.References
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- R. M. Metzger, Chem. Rev., 2015, 115, 5056–5115 CrossRef CAS PubMed.
- B. Capozzi, J. Xia, O. Adak, E. J. Dell, Z.-F. Liu, J. C. Taylor, J. B. Neaton, L. M. Campos and L. Venkataraman, Nat. Nanotechnol., 2015, 10, 522–527 CrossRef CAS PubMed.
- Z. Liu, S. Ren and X. Guo, Top. Curr. Chem., 2017, 375, 56 CrossRef PubMed.
- P. A. Lewis, C. E. Inman, F. Maya, J. M. Tour, J. E. Hutchison and P. S. Weiss, J. Am. Chem. Soc., 2005, 127, 17421–17426 CrossRef CAS PubMed.
- A. M. Moore, B. A. Mantooth, Z. J. Donhauser, Y. Yao, J. M. Tour and P. S. Weiss, J. Am. Chem. Soc., 2007, 129, 10352–10353 CrossRef CAS PubMed.
- R. J. Nichols and S. J. Higgins, Acc. Chem. Res., 2016, 49, 2640–2648 CrossRef CAS PubMed.
- A. K. Mahapatro, J. Ying, T. Ren and D. B. Janes, Nano Lett., 2008, 8, 2131–2136 CrossRef CAS PubMed.
- S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J. L. Brédas, N. Stuhrhansen, P. Hedegård and T. Bjørnholm, Nature, 2003, 425, 698 CrossRef CAS PubMed.
- I. Diez-Perez, Z. Li, J. Hihath, J. Li, C. Zhang, X. Yang, L. Zang, Y. Dai, X. Feng and K. Muellen, Nat. Commun., 2010, 1, 31 Search PubMed.
- K. Wang and B. Xu, Top. Curr. Chem., 2017, 375, 17 CrossRef PubMed.
- D. C. Milan, O. A. Al-Owaedi, M.-C. Oerthel, S. Marqués-González, R. J. Brooke, M. R. Bryce, P. Cea, J. Ferrer, S. J. Higgins and C. J. Lambert, J. Phys. Chem. C, 2015, 120, 15666–15674 Search PubMed.
- B. Choi, B. Capozzi, S. Ahn, A. Turkiewicz, G. Lovat, C. Nuckolls, M. L. Steigerwald, L. Venkataraman and X. Roy, Chem. Sci., 2016, 7, 2701 RSC.
- V. Fatemi, M. Kamenetska, J. B. Neaton and L. Venkataraman, Nano Lett., 2011, 11, 1988–1992 CrossRef CAS PubMed.
- C. Jia and X. Guo, Chem. Soc. Rev., 2013, 42, 5642–5660 RSC.
- J. Hihath and N. Tao, Semicond. Sci. Technol., 2014, 29, 054007 CrossRef.
- S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486 CrossRef CAS PubMed.
- F. Schwarz, G. Kastlunger, F. Lissel, C. Egler-Lucas, S. N. Semenov, K. Venkatesan, H. Berke, R. Stadler and E. Lörtscher, Nat. Nanotechnol., 2015, 11, 170 CrossRef PubMed.
- L. Sun, Y. A. Diaz-Fernandez, T. A. Gschneidtner, F. Westerlund, S. Lara-Avila and K. Moth-Poulsen, Chem. Soc. Rev., 2014, 43, 7378–7411 RSC.
- S. H. Choi and C. D. Frisbie, J. Am. Chem. Soc., 2010, 132, 16191–16201 CrossRef CAS PubMed.
- L. A. Bumm, J. J. Arnold, M. T. Cygan, T. D. Dunbar, T. P. Burgin, L. Jones, D. L. Allara, J. M. Tour and P. S. Weiss, Science, 1996, 271, 1705–1707 CAS.
- C. Huang, A. V. Rudnev, W. Hong and T. Wandlowski, Chem. Soc. Rev., 2015, 44, 889 RSC.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- B. A. Mantooth and P. S. Weiss, Proc. IEEE, 2003, 91, 1785–1802 CrossRef CAS.
- B. Kim, J. M. Beebe, C. Olivier, S. Rigaut, D. Touchard, J. G. Kushmerick, X.-Y. Zhu and C. D. Frisbie, J. Phys. Chem. C, 2007, 111, 7521–7526 CAS.
- L. Luo, A. Benameur, P. Brignou, S. H. Choi, S. Rigaut and C. D. Frisbie, J. Phys. Chem. C, 2011, 115, 19955–19961 CAS.
- C. S. Sangeeth, A. T. Demissie, L. Yuan, T. Wang, C. D. Frisbie and C. A. Nijhuis, J. Am. Chem. Soc., 2016, 138, 7305–7314 CrossRef CAS PubMed.
- R. Sakamoto, K.-H. Wu, R. Matsuoka, H. Maeda and H. Nishihara, Chem. Soc. Rev., 2015, 44, 7698–7714 RSC.
- Q. Lu, K. Liu, H. Zhang, Z. Du, X. Wang and F. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- Q. Lu, C. Yao, X. Wang and F. Wang, J. Phys. Chem. C, 2012, 116, 17853–17861 CAS.
- Y.-Y. Sun, Z.-L. Peng, R. Hou, J.-H. Liang, J.-F. Zheng, X.-Y. Zhou, X.-S. Zhou, S. Jin, Z.-J. Niu and B.-W. Mao, Phys. Chem. Chem. Phys., 2014, 16, 2260–2267 RSC.
- C. E. Chidsey and R. W. Murray, Science, 1986, 231, 25–31 CAS.
- Y. Tanaka, M. Kiguchi and M. Akita, Chem.–Eur. J., 2017, 23, 4741–4749 CrossRef CAS PubMed.
- W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS PubMed.
- W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60 CrossRef CAS.
- V. Lloveras, J. Vidal-Gancedo, T. M. Figueira-Duarte, J.-F. Nierengarten, J. J. Novoa, F. Mota, N. Ventosa, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2011, 133, 5818–5833 CrossRef CAS PubMed.
- M. P. Eng and B. Albinsson, Angew. Chem., Int. Ed., 2006, 45, 5626–5629 CrossRef CAS PubMed.
- C. Y. Liu, X. Xiao, M. Meng, Y. Zhang and M. J. Han, J. Phys. Chem. C, 2013, 117, 19859–19865 CAS.
- R. Sakamoto, Y. Ohirabaru, R. Matsuoka, H. Maeda, S. Katagiri and H. Nishihara, Chem. Commun., 2013, 49, 7108–7110 RSC.
- C. Lin and C. R. Kagan, J. Am. Chem. Soc., 2003, 125, 336–337 CrossRef CAS PubMed.
- V. Kaliginedi, H. Ozawa, A. Kuzume, S. Maharajan, I. V. Pobelov, N. H. Kwon, M. Mohos, P. Broekmann, K. M. Fromm, M.-a. Haga and T. Wandlowski, Nanoscale, 2015, 7, 17685–17692 RSC.
- W. Fang, Q. He, Z. F. Tan, C. Y. Liu, X. Lu and C. A. Murillo, Chem.–Eur. J., 2011, 17, 10288–10296 CrossRef CAS PubMed.
- X. Xiao, C. Y. Liu, Q. He, M. J. Han, M. Meng, H. Lei and X. Lu, Inorg. Chem., 2013, 52, 12624–12633 CrossRef CAS PubMed.
- T. Ren, Organometallics, 2005, 24, 4854–4870 CrossRef CAS.
- Y. Sekine, T. Yokoyama, N. Hoshino, M. Ishizaki, K. Kanaizuka, T. Akutagawa, M.-a. Haga and H. Miyasaka, Chem. Commun., 2016, 52, 13983–13986 RSC.
- K. S. Lokesh, S. Chardon-Noblat, F. Lafolet, Y. Traoré, C. Gondran, P. Guionneau, L. Guérente, P. Labbé, A. Deronzier and J.-F. Létard, Langmuir, 2012, 28, 11779–11789 CrossRef CAS PubMed.
- M. Mikuriya, J. Yamamoto, D. Yoshioka, H. Tanaka and M. Handa, X-Ray Struct. Anal. Online, 2011, 27, 27–28 CrossRef CAS.
- S. Takamizawa, E.-i. Nakata and T. Saito, Inorg. Chem. Commun., 2003, 6, 1415–1418 CrossRef CAS.
- S. Onaka, M. Yaguchi, R. Yamauchi, T. Ozeki, M. Ito, T. Sunahara, Y. Sugiura, M. Shiotsuka, K. Nunokawa and M. Horibe, J. Organomet. Chem., 2005, 690, 57–68 CrossRef CAS.
- V. M. Miskowski, W. P. Schaefer, B. S. Sadeghi, B. D. Santarsiero and H. B. Gray, Inorg. Chem., 1984, 23, 1154–1162 CrossRef CAS.
- F. A. Cotton, E. A. Hillard and C. A. Murillo, J. Am. Chem. Soc., 2002, 124, 5658–5660 CrossRef CAS PubMed.
- R. Sakamoto, S. Katagiri, H. Maeda, Y. Nishimori, S. Miyashita and H. Nishihara, J. Am. Chem. Soc., 2015, 137, 734–741 CrossRef CAS PubMed.
- C. Creutz and H. Taube, J. Am. Chem. Soc., 1969, 91, 3988–3989 CrossRef CAS.
- Unpublished results. Wires (Rh2L)n@Au (L = 1,2-dipyridylethane, n = 1–15) show a anionic and cationic peaks at 0.92 V and 0.94 V (vs. Ag/AgCl), respectively, in the cyclic voltammgrams.
- K.-H. Wu, H. Maeda, T. Kambe, K. Hoshiko, E. J. H. Phua, R. Sakamoto and H. Nishihara, Dalton Trans., 2013, 42, 15877–15880 RSC.
- X.-Y. Zhu, Surf. Sci. Rep., 2004, 56, 1–83 CrossRef CAS.
- M. Galperin, M. A. Ratner, A. Nitzan and A. Troisi, Science, 2008, 319, 1056–1060 CrossRef CAS PubMed.
- H. M. McConnell, J. Chem. Phys., 1961, 35, 508–515 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- R. E. Holmlin, R. Haag, M. L. Chabinyc, R. F. Ismagilov, A. E. Cohen, A. Terfort, M. A. Rampi and G. M. Whitesides, J. Am. Chem. Soc., 2001, 123, 5075–5085 CrossRef CAS PubMed.
- M. Baghbanzadeh, C. M. Bowers, D. Rappoport, T. Żaba, L. Yuan, K. Kang, K. C. Liao, M. Gonidec, P. Rothemund, P. Cyganik, A. Aspuru-Guzik and G. M. Whitesides, J. Am. Chem. Soc., 2017, 139, 7624–7631 CrossRef CAS PubMed.
- J. Ponce, C. R. Arroyo, S. Tatay, R. Frisenda, P. Gaviña, D. Aravena, E. Ruiz, H. S. van der Zant and E. Coronado, J. Am. Chem. Soc., 2014, 136, 8314–8322 CrossRef CAS PubMed.
- R. Davidson, J.-H. Liang, D. Costa Milan, B.-W. Mao, R. J. Nichols, S. J. Higgins, D. S. Yufit, A. Beeby and P. J. Low, Inorg. Chem., 2015, 54, 5487–5494 CrossRef CAS PubMed.
- N. Tuccitto, V. Ferri, M. Cavazzini, S. Quici, G. Zhavnerko, A. Licciardello and M. A. Rampi, Nat. Mater., 2009, 8, 41 CrossRef CAS PubMed.
- W. Zhang, S. Gan, A. Vezzoli, R. J. Davidson, D. C. Milan, K. V. Luzyanin, S. J. Higgins, R. J. Nichols, A. Beeby and P. J. Low, ACS Nano, 2016, 10, 5212–5220 CrossRef CAS PubMed.
- H. Maeda, R. Sakamoto and H. Nishihara, J. Phys. Chem. Lett., 2015, 6, 3821–3826 CrossRef CAS PubMed.
- S. Ryota, K. Shunsuke, M. Hiroaki and N. Hiroshi, Chem. Lett., 2013, 42, 553–555 CrossRef.
- C. Musumeci, G. Zappalà, N. Martsinovich, E. Orgiu, S. Schuster, S. Quici, M. Zharnikov, A. Troisi, A. Licciardello and P. Samorì, Adv. Mater., 2014, 26, 1688–1693 CrossRef CAS PubMed.
- G. Sedghi, L. J. Esdaile, H. L. Anderson, S. Martin, D. Bethell, S. J. Higgins and R. J. Nichols, Adv. Mater., 2012, 24, 653–657 CrossRef CAS PubMed.
- G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott, N. Bennett, J. E. Macdonald and R. J. Nichols, Nat. Nanotechnol., 2011, 6, 517 CrossRef CAS PubMed.
- R. C. Bruce, R. Wang, J. Rawson, M. J. Therien and W. You, J. Am. Chem. Soc., 2016, 138, 2078–2081 CrossRef CAS PubMed.
- Z. Li, T.-H. Park, J. Rawson, M. J. Therien and E. Borguet, Nano Lett., 2012, 12, 2722–2727 CrossRef CAS PubMed.
- Q. Ferreira, A. M. Bragança, L. Alcácer and J. Morgado, J. Phys. Chem. C, 2014, 118, 7229–7234 CAS.
- E. Petrov, Y. V. Shevchenko, V. Teslenko and V. May, J. Chem. Phys., 2001, 115, 7107–7122 CrossRef CAS.
- H. B. Michaelson, J. Appl. Phys., 1977, 48, 4729–4733 CrossRef CAS.
- M. Baghbanzadeh, C. M. Bowers, D. Rappoport, T. Żaba, M. Gonidec, M. H. Al-Sayah, P. Cyganik, A. Aspuru-Guzik and G. M. Whitesides, Angew. Chem., 2015, 127, 14956–14960 CrossRef.
- R. L. McCreery, ChemPhysChem, 2009, 10, 2387–2391 CrossRef CAS PubMed.
- A. Migliore and A. Nitzan, J. Am. Chem. Soc., 2013, 135, 9420–9432 CrossRef CAS PubMed.
- C. E. B. Evans, M. L. Naklicki, A. R. Rezvani, C. A. White, V. V. Kondratiev and R. J. Crutchley, J. Am. Chem. Soc., 1998, 120, 13096–13103 CrossRef CAS.
- C. Creutz, M. D. Newton and N. Sutin, J. Photochem. Photobiol., A, 1994, 82, 47–59 CrossRef CAS.
- G. Rempel, P. Legzdins, H. Smith, G. Wilkinson and D. Ucko, Inorg. Synth., 2007, 13, 90–91 CrossRef.
- D. Bu, T. J. Mullen and G.-y. Liu, ACS Nano, 2010, 4, 6863–6873 CrossRef CAS PubMed.
- D. Bu, S. Riechers, J. Liang and G.-y. Liu, Nano Res., 2015, 8, 2102–2114 CrossRef CAS.
- M. Hegner, P. Wagner and G. Semenza, Surf. Sci., 1993, 291, 39–46 CrossRef CAS.
- P. Wagner, M. Hegner, H.-J. Guentherodt and G. Semenza, Langmuir, 1995, 11, 3867–3875 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc04727d |
| This journal is © The Royal Society of Chemistry 2018 |