Twist sense control in terminally functionalized ortho-phenylenes

Abstract

Many abiotic foldamers are based on achiral repeat units but adopt chiral geometries, especially helices. In these systems, there is no inherent preference for one handedness of the fold; however, it is well-established that the point chirality of substituents can be communicated to the helix. This capability represents a basic level of control over folding that is necessary for applications in molecular recognition and in the assembly of higher-order structures. The ortho-phenylenes are a structurally simple class of aromatic foldamers that fold into helices driven by arene–arene stacking interactions. Although their folding is now reasonably well-understood, access to o-phenylenes enriched in one twist sense has been limited to resolution, yielding conformationally dynamic samples that racemize over the course of minutes to hours. Here, we report a detailed structure–property study of chiral induction from o-phenylene termini using a combination of NMR spectroscopy, CD spectroscopy, and computational chemistry. We uncover mechanistic details of chiral induction and show that the same substituents can give effective twist sense control in opposite directions in mixtures of interconverting conformers; that is, they are “ambidextrous”. This behavior should be general and can be rationalized using a simple model based on sterics, noting that arene–arene stacking is, to a first approximation, unaffected by flipping either partner. We demonstrate control over this mechanism by showing that chiral groups can be chosen such that they both favor one orientation and provide effective chiral induction.

---

Introduction

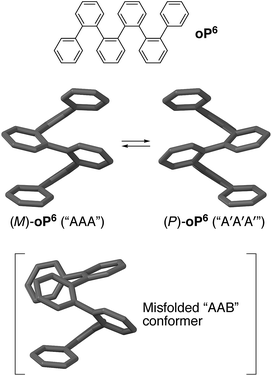
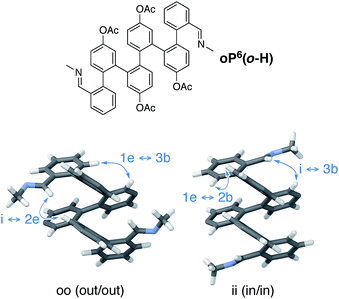
Oligomers that adopt well-defined secondary structures, or foldamers, represent a first step toward controlling macromolecular geometry by mimicking the hierarchical structure found in nature.^1–3 Unlike, for example, α-peptides in biology, many abiotic foldamers make use of achiral components, especially those based on aromatic repeat units.^4–7 While these compounds typically fold into (chiral) helices, there will be no predisposition toward a specific handedness of the fold. Controlling folding by communicating the point chirality of substituents to the helix is therefore of great significance, particularly for applications in, for example, (bio)molecular recognition^8,9 and spintronics.¹⁰ It is also critically important to efforts to combine multiple foldamer subunits into higher-order structures (i.e., analogous to 3° structures in biology),¹ since complex diastereomeric mixtures of conformers are unlikely to be useful. Accordingly, there are many examples of the use of chiral groups attached both as side chains^11–16 and to the termini^17–30 of helical aromatic foldamers to bias their twist senses.

Our work has focused on the folding behavior of the ortho-phenylenes.^31–33 As shown in Fig. 1 for hexa(o-phenylene) (oP⁶), they spontaneously fold into compact, helical conformations in solution with three phenylene units per turn. Folding in these systems is driven by (offset) arene–arene stacking interactions parallel to the helical axis, and can be tuned through the use of appropriate substituents to give systems for which the population of misfolded conformers is below the detection limit of NMR spectroscopy.³⁴o-Phenylenes offer an attractive combination of properties that complements those of other classes of aromatic foldamers based on hydrogen bonding.^4,6 They are of interest both as helical oligomers and polymers^32,35–39 and also as prototypical systems for other o-arylenes^40–44 and the broader class of sterically crowded polyphenylenes,⁴⁵ including oligo- and polynaphthalenes,^46–48 cages,⁴⁹ and other complex architectures.^50–54

Fig. 1 Folding of the parent hexa(o-phenylene) oP⁶. (Middle) M and P helices of the perfectly folded “AAA” conformer. (Bottom) The “AAB” conformer is the most populated misfolded state for a typical o-phenylene hexamer.

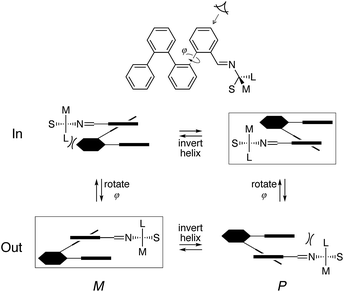
The folding state of an o-phenylene is defined by the torsional angles along its backbone. These can be described using a simple A/B nomenclature, where A represents a backbone biaryl torsional angle of (roughly) −55° and B represents a torsional angle of +135°; likewise, A′ and B′ correspond to +55° and −135°, respectively.³³ The perfectly folded hexamer, for example, is either an M (left-handed) helix that corresponds to the AAA state, or a P helix that corresponds to the A′A′A′ state (Fig. 1). Misfolding, corresponding to B states, tends to occur at the ends of o-phenylenes; thus, the (enantiomeric) AAB and A′A′B′ conformers should be the most populated misfolded states of hexa(o-phenylene) derivatives. Helix inversion at room temperature should occur on the order of seconds to minutes for short oligomers,⁵⁵ whereas interconversion between (mis)folded states will generally be much faster, albeit still slow on the NMR time scale.³³

While many examples of o-phenylenes have now been reported, access to specific backbone twist senses has been limited to resolution by chiral chromatography⁵⁵ and mechanical separation of conglomerates;³² enantioselective synthesis of conformationally static oligonaphthalenes has also been demonstrated.⁴⁷ Future applications of o-phenylenes, in particular their incorporation into more complex architectures,^56,57 require strategies to control the direction of their folding. Fortunately, they are uniquely well-suited to the analysis of structure–property effects on chiral induction, given that their folding behavior can be analyzed in detail in solution.³³ Here, we show that substitution at o-phenylene termini with chiral imine moieties allows their helical twist sense to be biased. By systematically varying the structure of the chiral group, we obtain a detailed view of the underlying conformational distributions and ultimately the mechanisms of chiral induction through a combination of NMR spectroscopy, CD spectroscopy, and computational chemistry. We show that the orientation of the chiral group with respect to the helix is critically important; in some systems, low net twist sense excess results from the cancellation of strong chiral induction in opposite directions in different conformations. This behavior can be controlled through a careful choice of the chiral group to manipulate the conformational distribution. These results provide a first step toward understanding how to control the stereochemistry of folding of o-phenylenes specifically and conformationally mobile polyphenylenes in general.

Results and discussion

We focused on o-phenylene hexamers, shown in Fig. 2, because they are long enough that the oligomer undergoes two full turns of the helix, ensure that backbone conformational changes are slow on the NMR time scale,⁵⁹ and are short enough that the NMR spectra can be fully analyzed even for complex mixtures of folded states (for this same reason we also limit ourselves to symmetrical substitution). The use of an acetoxy-functionalized backbone ensures that the oligomers are predominantly well-folded by strengthening the arene–arene stacking interactions.³⁴ Because of the relative conformational rigidity of folded o-phenylenes, the specific site of functionalization was expected to play an important role in chiral induction. Hence, both para and ortho substitution of the terminal rings was examined. We chose imines as the chiral groups because of the ready availability of enantiomerically pure amines, synthetic convenience, and the potential of eventually combining chiral induction with self-assembly through dynamic covalent chemistry.^56,57 The imines were also expected to promote folding as they are electron-withdrawing groups.⁶⁰ They were synthesized using standard methods† and were stable to hydrolysis over the course of weeks. Unfortunately, attempts to grow crystals of key compounds were unsuccessful.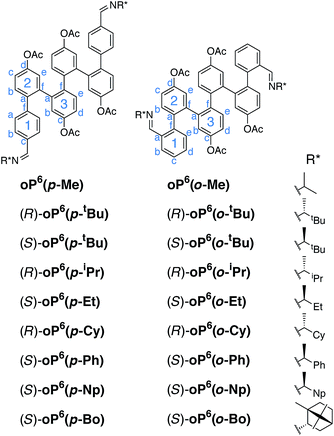

Fig. 2 o-Phenylene hexamers with terminal para and ortho imines (Cy = cyclohexyl, Np = 1-naphthyl, Bo = bornyl⁵⁸).

Twist sense induction from the para position

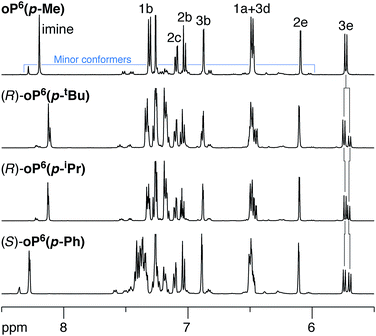
We began with the p-imine series, which was expected to be more straightforward to analyze because the two rotamers with respect to the terminal rings are equivalent. ¹H NMR spectra of the oligomers were acquired in chloroform-d at 273 K as the signals were slightly sharper below room temperature (i.e., slower chemical exchange). As shown in Fig. 3 (top), the 500 MHz ¹H NMR spectrum of “achiral”⁶¹oP⁶(p-Me) is typical of o-phenylene hexamers, with major signals corresponding to one predominant conformation coexisting with some smaller signals that correspond to misfolded states. EXSY spectroscopy confirms that these minor signals are not due to impurities, as there are clear cross peaks representing chemical exchange with the major species on the NMR time scale. The signals for the major species could be assigned using standard 2D NMR experiments (COSY, HSQC, HMBC) (see Fig. 2 for labels). The pattern of chemical shifts confirms that these signals correspond to the perfectly folded, enantiomeric AAA/A′A′A′ conformers, which place key protons (notably H_3d, H_2e, and H_1a) directly into the shielding zones of nearby aromatic rings.³³ The spectrum is directly analogous to those of other, similar o-phenylene oligomers that have been shown to fold well.³⁴

Fig. 3 Representative ¹H NMR spectra (500 MHz, CDCl₃, 273 K) of p-imine o-phenylenes (aromatic region). Protons H_3e were used to evaluate de's. Small peaks corresponds to misfolded conformers, as confirmed by EXSY spectroscopy.

Representative examples of the ¹H NMR spectra of the p-imine oligomers with chiral groups are also shown in Fig. 3. For these compounds, the signals analogous to oP⁶(p-Me) are doubled, which we attribute to separate signals for the now-diastereomeric left- and right-handed o-phenylene helices. Given the bulkiness of some of the substituents, the additional signals could also represent misfolded states. However, the pairs of signals remain close together in the spectra, with Δδ ≤ 0.15 ppm. This difference is far less than would be expected if the backbone were misfolding: protons H_3e, for example, are typically shifted by nearly 2 ppm in misfolded conformers, as any misfolding moves them out of the shielding zones of nearby aromatic rings.³⁴ We therefore conclude that substitution with these groups has a negligible effect on the overall folding propensity. The populations of the two twist senses could be easily determined by deconvolution of the NMR spectra, with helical diastereomeric excesses (de's) compiled in Table 1. The signals corresponding to H_3e were particularly useful in this regard as they were always well-resolved and well-separated from those of the other aromatic protons.

Table 1 Twist sense control in p-imine o-phenylenes

Compound	de^a	Twist sense^b
a Determined from ^1H NMR deconvolution at 273 K (CDCl3). Only the perfectly folded state was considered. b Assigned from CD spectroscopy (sign of Cotton effect at 260 nm).
(R)-oP^6(p-^tBu)	40%	M
(S)-oP^6(p-^tBu)	40%	P
(R)-oP^6(p-^iPr)	24%	M
(S)-oP^6(p-Et)	8%	P
(R)-oP^6(p-Cy)	14%	M
(S)-oP^6(p-Bo)	28%	P
(S)-oP^6(p-Ph)	8%	n.d.
(S)-oP^6(p-Np)	10%	n.d.

---

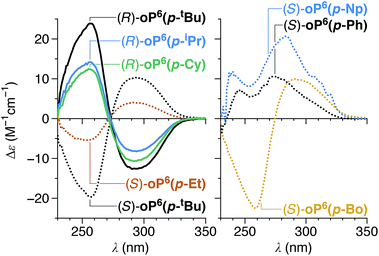
All of the chiral p-imines give significant CD bands in chloroform, as shown in Fig. 4 (see ESI† for UV-vis spectra). The compounds with non-aromatic chiral groups (oP⁶(p-^tBu), oP⁶(p-ⁱPr), oP⁶(p-Et), oP⁶(p-Cy), oP⁶(p-Bo)) were of particular interest: excitation in the examined spectral range (≥230 nm) should be centered on the o-phenylene moiety, and so the CD signals should reflect only the twist sense of the backbone. The CD spectra of these compounds have nearly identical shapes, with characteristic Cotton effects at approximately 260 and 300 nm. The intensities of these two bands roughly correlate with the de's determined by NMR spectroscopy (Table 1), confirming that the doubled sets of NMR signals correspond to diastereomers differing in the handedness of the helix. For the hexamers with arene-containing imines (oP⁶(p-Ph) and oP⁶(p-Np)), direct excitation of the chiral group should also occur in the same region of the spectrum, and the shapes of the CD spectra are markedly different.

Fig. 4 Experimental CD spectra of p-imine o-phenylenes (CHCl₃).

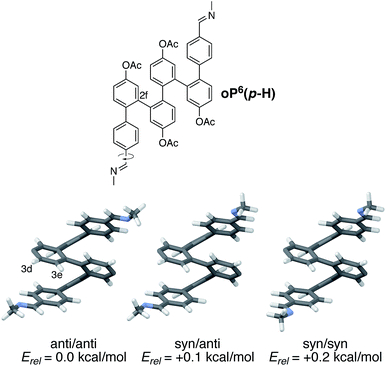
Understanding chiral induction in these systems requires, of course, detailed knowledge of the geometries of the o-phenylene backbone. Possible geometries of model compound (M)-oP⁶(p-H), which lacks the chiral groups, were therefore optimized, with full details provided in the ESI.† All three possible orientations of the imine N atoms were explicitly considered and are shown in Fig. 5; they are named according to the orientation of the imine relative to C_2f: in the syn conformer, the N atoms are directed inward, toward the center of the helix, and in the anti conformer they are directed outward.

Fig. 5 Optimized geometries and relative stabilities of folded model compound (M)-oP⁶(p-H) (PCM(CHCl₃)/B97-D/TZV(2d,2p)), differing in the orientation of the imine N atoms. Acetoxy groups were included in the optimization but are not shown (they are located at the positions with missing substituents).

The symmetrical anti/anti conformer of oP⁶(p-H) was found to be the most stable, but the relative stabilities E_rel of all three possible orientations were within 0.2 kcal mol⁻¹ and thus all should be significantly populated at room temperature (the syn/anti conformer should in fact be the most populated because of its lower symmetry). The optimized geometries show why protons H_3e are particularly sensitive reporters on the twist sense of the helix: when folded, they are directed toward the imine (in contrast to H_2e, for example, which is directed away from the chiral group and does not show a significant Δδ).

Given the amenability of the o-phenylene backbone to TD-DFT calculations,^62,63 and precedents for the prediction of CD spectra⁶⁴ for helicenes⁶⁵ and aromatic foldamers,^42,66 we investigated the use of computational models to assign the absolute configurations of the o-phenylene backbones. The method was first validated† against an o-phenylene octamer reported by Fukushima and Aida³² which is, to the best of our knowledge, the only example of an o-phenylene for which both the absolute configuration and CD spectrum are unambiguously known.

We then turned our attention to TD-DFT calculations on model structure (M)-oP⁶(p-H) using the previously optimized geometries.† The predicted UV-vis and CD spectra for (M)-oP⁶(p-H) are shown in Fig. 6, and are excellent matches to the shapes of the experimental UV-vis and CD spectra of oP⁶(p-^tBu), oP⁶(p-ⁱPr), oP⁶(p-Et), oP⁶(p-Cy), and oP⁶(p-Bo). The calculations show that the Cotton effect at 260 nm is associated with MOs localized primarily on the o-phenylene backbone and is relatively unaffected by imine orientation. Thus, it should be a better marker of the absolute twist sense, with a positive Cotton effect at 260 nm associated with an M (left-handed) twist of the helix. The absolute twist senses of the o-phenylenes were assigned on this basis and are included in Table 1.

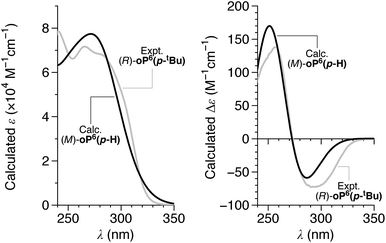Fig. 6 Calculated UV-vis (left) and CD (right) spectra for (M)-oP⁶(p-H) (black) (PCM(CHCl₃)/TD/CAM-B3LYP/6-31G(d,p)//PCM(CHCl₃)/B97-D/TZV(2d,2p)). The calculated spectra are the Boltzmann-weighted averages of those for the three conformers in Fig. 5, obtained by assuming a peak half-width at half-height of 0.333 eV. The experimental spectra of (R)-oP⁶(p-^tBu) are included for comparison (gray, a.u.).

With both de's and absolute configurations in hand, some conclusions can be drawn regarding chiral induction for the p-imine series. First, its overall efficiency is obviously modest, with maximum de's of 40%. Second, if one considers the series oP⁶(p-^tBu), oP⁶(p-ⁱPr), oP⁶(p-Et), and oP⁶(p-Cy), it is clear that the degree of chiral induction increases with increasing steric demand of the largest group on the chiral center (with Me as the medium-sized group and H as the smallest group in all cases). This trend also holds for oP⁶(p-Bo) if one considers that the contrast in size between the large and medium groups in the bornyl moiety should be less than between the t-butyl and methyl in oP⁶(p-^tBu). Chiral-induction from arene-based groups is clearly ineffective, given that (S)-oP⁶(p-Ph) and (S)-oP⁶(p-Np) give among the lowest de's. Therefore, there does not appear to be a significant effect of arene–arene interactions in chiral communication in these systems. Third, note that for all of the chiral groups used here, the R/S configurations obtained via the Cahn–Ingold–Prelog rules happen to also represent the configurations of groups around the chirality center ranked according to their steric demand; it is clear then that the oligomers with R configurations all yield M (left-handed) o-phenylene helices, and those with S configurations yield P helices.

To better understand the mechanism of chiral induction in these systems, we performed a brief computational study on model compound (R)-oP⁴(p-^tBu), shown in Fig. 7. While highly simplified, this structure should capture the essential features of the interaction of the chiral p-imine with an o-phenylene backbone. Although this model omits the acetoxy groups, note that the substitution pattern of the synthesized compounds directs them away from the imine on folding (Fig. 5) and thus, while they should affect overall differences in stability, we expect the sense of chiral induction to be unaffected. Global energy minima for both the M and P configurations of (R)-oP⁴(p-^tBu) were identified as discussed in the ESI,† and are shown in Fig. 7 along with their relative stabilities.

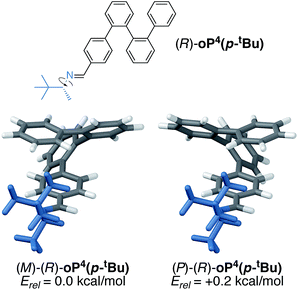Fig. 7 Optimized M and P geometries of model structure (R)-oP⁴(p-^tBu) (PCM(CHCl₃/B97-D/TZV(2d,2p))).

These DFT calculations correctly predict the sense of chiral induction for the p-imine series (i.e., the M/R combination is slightly more stable than P/R). However, the calculated energy difference between the two conformers is very small (∼0.2 kcal mol⁻¹). While this is consistent with the low observed de's, the predictive success should be interpreted cautiously. That said, some general features emerge from the models in Fig. 7 (and PES scans†). First, there is (unsurprisingly) a strong preference for the small group about the chirality center (H) to adopt a syn-periplanar orientation with respect to the imine. The most stable conformations in both cases are then those that orient the large t-butyl group closer to the backbone; in fact, for the more-stable M helix, the t-butyl group is predicted to be significantly closer to the o-phenylene backbone than in the less-favorable P helix, with a closest contact distance of 2.65 vs. 3.24 Å.

We conclude that sterics do not play a significant role in chiral induction in the p-imine series, and instead either a weak interaction between the large group and the o-phenylene or the minimization of free volume may be important. We note that when the B98 functional, which should not accurately treat dispersion interactions, is used in place of B97-D,† the predicted relative stabilities of the two twist senses is reversed, providing some support for the former explanation. Most importantly, however, substitution at the terminal para position places the substituents too far from the backbone to effectively communicate their point chirality to o-phenylene folding.

Twist sense induction from the ortho position

We reasoned that placement of the imine at the terminal ortho position would put the chirality center closer to the helix and thus increase the degree of chiral induction. However, this adjustment also complicates the system since rotation of the terminal arene no longer gives equivalent conformers. That is, the imine groups can either be oriented “inward”, along the path of the helix, or “outward”, toward the sides of the helix. There are therefore three well-folded conformers that must be considered: two that are of twofold symmetry, in–in (ii) and out–out (oo), and one that is unsymmetrical, in–out (io). Importantly, it was quickly apparent that these three conformers interconvert slowly on the NMR time scale at (or below) room temperature and are readily distinguished. This behavior contrasts with the behavior of the p-imine series discussed above (e.g., note the equivalence of protons H_1a or H_1b); however, substitution ortho to the backbone is known to slow conformational interconversion at o-phenylene termini.⁵⁵

For the o-imine series, ¹H NMR spectra were acquired at 850 MHz and 278 K in chloroform-d, which gave better resolution of the signals from different conformers than was possible at 500 MHz. As above for the p-imine series, proton H_3e serves as a very useful reporter on the folding state of the oligomer. For achiral oP⁶(o-Me), separate signals are observed for the three conformational states, as shown in Fig. 8 (top). The io conformer is readily assigned on the basis of its symmetry (i.e., two signals of equal intensity). The remaining two signals, clearly separated (by 0.35 ppm), therefore correspond to the symmetrical ii and oo conformers.

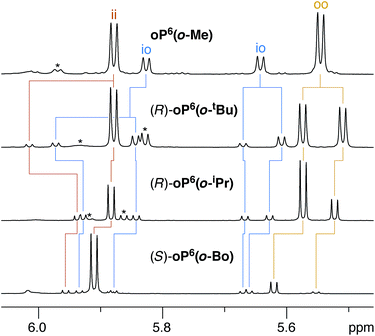Fig. 8 Representative ¹H NMR spectra (850 MHz, CDCl₃, 278 K) of o-imine o-phenylenes (H_3e region). Signals corresponding to misfolded (AAB) conformers are marked *.

The assignment of these signals is key to understanding the behavior of these systems. Computational models of the ii, oo, and io conformers of model structure (M)-oP⁶(o-H) were generated as for (M)-oP⁶(p-H). The most favorable geometries for the oo and ii conformers are shown in Fig. 9 (see ESI† for the io conformer). In general, the syn/anti orientation of the imine N atom was much better defined for the o-imine series, with the preferred orientation, anti to C_1f, more stable by at least 1.7 kcal mol⁻¹; thus, the contribution of these minor contributors was ignored.

Fig. 9 Optimized geometries of model compound oP⁶(o-H) (PCM(CHCl₃)/B97-D/TZV(2d,2p)). Acetoxy groups were included in the optimization but are not shown. Key NOESY correlations that were used to make NMR assignments are highlighted.

The geometries suggest spatial relationships between protons that could be used to distinguish the two conformers. Inspection of the NOESY spectra then revealed several key correlations, highlighted on the models in Fig. 9, that could be used to unambiguously assign the ¹H NMR signals for both conformations. As labeled in Fig. 8, for H_3e the signals corresponding to the ii conformers are downfield from those for the oo conformers. The relative populations of the ii, oo, and io conformers for oP⁶(o-Me) were determined to be 33 : 42 : 26 by integration of the ¹H NMR spectrum (CDCl₃, 278 K); that is, io is the least populated. In the absence of stabilizing effects, one would predict a 25 : 25 : 50 ratio on the basis of symmetry; with interactions that stabilize one imine orientation, the population of the io configuration would be predicted to fall between those of the two other states. The simplest explanation for this disparity is that the io conformer is more polar than the other two, and should be destabilized in (nonpolar) chloroform (calculated for (M)-oP⁶(o-H): μ = 2.3 D for io, 1.37 for ii, and 1.17 for oo). Similar effects are known to significantly affect the folding behavior of other o-phenylenes.⁶⁷

As observed for the p-imine series, the ¹H NMR signals are doubled for the o-imines with chiral groups, as shown in Fig. 8 for representative examples. Examination of the NMR spectra (especially COSY and EXSY) allowed the signals for H_3e to be assigned and distinguished from small populations of misfolded oligomers. That is, the resolution of and information contained in the NMR spectra was sufficient to extract the relative populations of the different imine orientations (ii vs. oo vs. io) and the de's within each orientation for all compounds except (S)-oP⁶(o-Np).⁶⁸ As shown in Table 2, the de's for the o-imine series are generally much larger (up to 88%) than those for the p-imine series (up to 40%). There was considerable variation in both relative conformer populations and de's depending on the structure of the chiral group.

Table 2 Twist sense control in o-imine o-phenylenes^a

Compound	Conf.	Pop.^b	de^b	Twist sense^c
a Conf. = conformer, Pop. = population. b Determined from ^1H NMR deconvolution at 278 K (CDCl3). Only the perfectly folded state was considered. c Assigned as discussed in the text.
(R)-oP^6(o-^tBu)	ii	33%	88%	P
	io	20%	42%	P
	oo	47%	0%	—
(R)-oP^6(o-^iPr)	ii	25%	68%	P
	io	20%	10%	P
	oo	55%	38%	M
(S)-oP^6(o-Et)	ii	25%	20%	M
	io	20%	16%	P
	oo	55%	58%	P
(R)-oP^6(o-Cy)	ii	24%	68%	P
	io	17%	8%	P
	oo	59%	54%	M
(S)-oP^6(o-Bo)	ii	65%	88%	M
	io	18%	14%	M
	oo	18%	52%	P
(S)-oP^6(o-Ph)	ii	28%	74%	n.d.
	io	23%	36%	n.d.
	oo	49%	16%	n.d.

---

To a first approximation, the chiral groups at the two ends of the oligomer should act independently, and thus the de's of the io conformers would be expected to lie between those of the ii and oo conformers. Indeed, the average ii/oo de is an excellent predictor of the io de, with a correlation coefficient of R = 0.95,† but only if the effect of the chiral groups in the ii and oo conformers is assumed to be mismatched. That is, it appears that the chiral groups induce opposite twist senses of the o-phenylene helix depending on whether they are directed inward or outward. For example, consider (R)-oP⁶(o-Cy): the 8% de of the io conformer is very close to the midpoint (7%) between the 68% de of the ii conformer and the 54% de of the oo conformer if they are of opposite handedness (and the de's have opposite sign). We can further speculate that the predominant twist sense of the io conformer should match that of the symmetrical species with the highest de, since the substituent is inducing a stronger bias from that position. This analysis yields a first guess of the relative helix configurations for the three conformers of each o-imine hexamer.

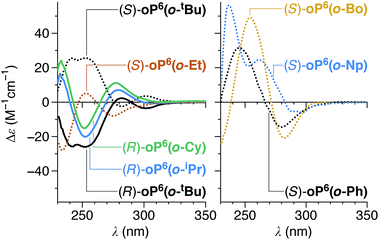
CD spectra for the o-imine series were acquired and are shown in Fig. 10 (see ESI† for UV-vis spectra). In general, while the spectra of the compounds with non-aromatic chiral groups oP⁶(o-^tBu), oP⁶(o-ⁱPr), oP⁶(o-Et), oP⁶(o-Cy), and oP⁶(o-Bo) share similar features, their shapes are much less well matched than those of the analogous p-imines. The difference presumably reflects the greater complexity of the o-imine series, as the substituents affect not only the de's but also the distribution between the ii, oo, and io conformers. It is also noteworthy that the Cotton effect at 260 nm for the o-imine series tends to have the opposite sign of that for the analogous group in the p-imine series. This band stands out for (S)-oP⁶(o-Bo), as it is at least double the intensity of those for any of the other compounds in this study (and should be uncomplicated by contributions from the chiral group itself).

Fig. 10 Experimental CD spectra of o-imine o-phenylenes (CHCl₃).

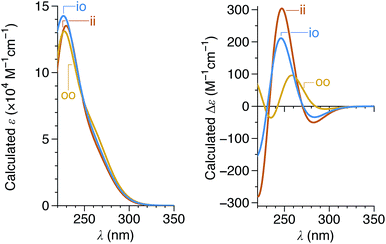
Since the CD spectra are a convolution of contributions from all three imine orientations, TD-DFT calculations of model compound (M)-oP⁶(o-H) (Fig. 9) were carried out for each possible geometry.† As shown in Fig. 11, the orientation of the imine has relatively little effect on the predicted UV-vis spectra, but substantially affects the predicted CD spectra, with the oo conformer expected to yield much weaker band intensities. As before, the calculations suggest that the M configuration of the helix is associated with a positive Cotton effect at ∼260 nm.

Fig. 11 Calculated UV-vis (left) and CD (right) spectra for the ii, oo, and io conformers of (M)-oP⁶(o-H) (PCM(CHCl₃)/TD/CAM-B3LYP/6-31G(d,p)//PCM(CHCl₃)/B97-D/TZV(2d,2p)). Spectra were simulated assuming a peak half-width at half-height of 0.333 eV.

The conformer populations and relative configurations obtained from the NMR analysis (Table 2) in combination with the predicted TD-DFT CD spectra for the three conformers of (M)-oP⁶(o-^tBu) (Fig. 11) are, in principle, sufficient to calculate the spectra for the bulk solutions of each compound and thus determine absolute configurations. Using the signs of the Cotton effect at ∼260 nm as a first guess of the predominant twist senses, CD spectra were calculated for oP⁶(o-^tBu), oP⁶(o-ⁱPr), oP⁶(o-Et), and oP⁶(o-Bo) and are shown in Fig. 12. The match to the experimental spectra is excellent in all four cases, in terms of both the structure of each individual spectrum and especially the relative intensities from compound to compound (note that while the experimental spectra have been scaled in the figure, they are all scaled identically). This result establishes the absolute configurations of the oligomers and strongly supports both the de's and the notion that the ii and oo conformers adopt opposite twist senses in each case. The assigned twist senses of the o-phenylene helices for the o-imine series are tabulated in Table 2.

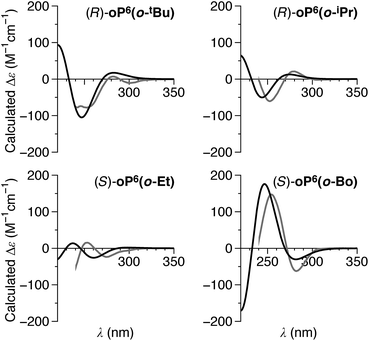Fig. 12 Predicted CD spectra of (R)-oP⁶(o-^tBu), (R)-oP⁶(o-ⁱPr), (S)-oP⁶(o-Et), and (S)-oP⁶(o-Bo) (black). Experimental spectra (gray) were scaled identically (i.e., relative intensities can be directly compared). The simulated spectra were generated by estimating the contributions of the calculated spectra for (M)-oP⁶(o-H) (Fig. 11) using the conformer populations and diastereomeric excesses determined by ¹H NMR (Table 2).

The data in Table 2 for oP⁶(o-^tBu), oP⁶(o-ⁱPr), and oP⁶(o-Et) reveals several important trends. First, chiral induction from the inward imine position is generally much stronger than that from the outward position, with oP⁶(o-Et) standing as the only exception. Second, chiral groups that have larger large groups around the chirality center give much better chiral induction from this inward position (e.g., 88% de for oP⁶(o-^tBu)vs. 20% for oP⁶(o-Et)). Third, for the oo conformers it appears that smaller large groups about the chirality centers, curiously, give more effective chiral induction (e.g., 58% de for oP⁶(o-Et)vs. 0% for oP⁶(o-^tBu)). These latter two points suggest that the details of the interaction between the chiral group and the helix is strongly dependent on their relative orientations.

Taken together, the results indicate that effective twist sense bias in these systems requires both a group capable of good chiral induction and control over its positioning with respect to the o-phenylene helix. In strict terms of achieving maximum twist sense excess, most of the compounds examined here fall short in one or both aspects. For example, although (R)-oP⁶(o-^tBu) exhibits a high de in its ii conformer (88%), this conformer accounts for only 33% of the total population. However, chiral induction and imine orientation are, in principle, independent phenomena that can be affected separately. This control is achieved with the bornyl group in (S)-oP⁶(o-Bo), which both directs the imines inward toward the ii conformer and provides effective chiral induction. This is immediately obvious in its ¹H NMR spectrum (Fig. 8, bottom), where it is clear that one species accounts for the majority of the total population. Nevertheless, there is still some room for improvement: accounting for all the minor conformers, the net M : P ratio for (S)-oP⁶(o-Bo) remains about 3 : 1.

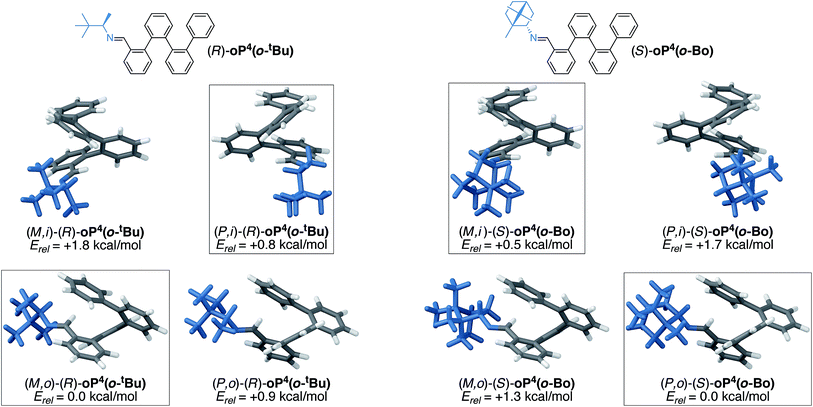
Further insight into the mechanism of chiral induction in the o-imine systems was obtained through computational modeling of simplified compounds (R)-oP⁴(o-^tBu) and (S)-oP⁴(o-Bo), which should capture the essential features of the interaction of the chiral o-imines with an o-phenylene backbone. Both twist senses with both inward- and outward-imines were optimized for these systems. In all four cases, global conformational energy minima were identified as discussed in the ESI,† with the resulting geometries shown in Fig. 13.

Fig. 13 Optimized M and P geometries and their relative stabilities of inward- (i) and outward-facing (o) conformers for (R)-oP⁴(o-^tBu) (left) and (S)-oP⁴(o-Bo) (right) (PCM(CHCl₃/B97-D/TZV(2d,2p))). Boxes indicate the favored conformers for each imine orientation.

The DFT calculations of the models are in excellent agreement with the experimental results. They successfully predict the direction of chiral induction for both the t-butyl and bornyl groups in both the inward and outward orientations; that is, they match the experimental configurations and support the idea that the sense of chiral induction changes when the chiral group is reoriented. The calculations are also consistent with the observation that the bornyl group favors the inward-imine orientation, at least in that they produce the correct trend. That the outward-facing conformer is still the overall energy minimum for oP⁴(o-Bo) may reflect, at least in part, the omission of the acetoxy groups, which ought to make the helix more sensitive to structural perturbations by strengthening the arene–arene interactions.

Inspection of the geometries in Fig. 13 provides some insight into why (S)-oP⁶(o-Bo) prefers the ii conformation. The bornyl group is significantly larger than the others considered here, especially because of the dimethyl-substituted bridge. In the conformers with inward-facing imines, this added steric bulk can be directed away from the helix and the overall surface interacting with the o-phenylene moiety is rather similar regardless of substitution. In contrast, the conformer with outward-facing imines places these groups closer to the side of the helix and forces additional steric clashes with the backbone. This increased sensitivity to sterics may also help to explain why chiral induction from the outward orientation is more effective with smaller chiral groups, as in (S)-oP⁶(o-Et).

The models in Fig. 13 show that, in all cases, the imine N atom is always anti to the helix and the small group (H) on the chirality center prefers to be syn to the imine bond (although in the less-stable conformers of (S)-oP⁴(o-Bo) it is forced away from a periplanar orientation). These results can be refined into a simple model to explain chiral induction in ortho-functionalized o-phenylenes, shown in Fig. 14. Applying the two constraints orients the chirality center relative to the o-phenylene backbone. The four principal configurations (in/out, M/P) can then be described using quasi-Newman projections. Assuming the chirality center has the R configuration, this model predicts that when the chiral group is directed inward the P configuration of the o-phenylene will be favored as there would be a steric clash between the large group and the M-helix. When the terminal ring is rotated to place the chiral group into the outward position (i.e., rotation about ϕ in Fig. 14) the large and medium groups change places relative to the o-phenylene. Consequently, the sense of chiral induction changes via the same steric mechanism.

Fig. 14 Model of chiral induction in o-imine o-phenylenes, based on the steric bulk of small (S), medium (M), and large (L) groups about the chirality center. Boxes indicate the favored conformers. The configuration of the chirality center is R assuming the Cahn–Ingold–Prelog priorities go as N > L > M > S.

Thus, the chiral groups are “ambidextrous”, in that they can induce opposite twist senses depending on their specific position. In either case, once the torsional angle of the first biaryl bond is set, its configuration should be effectively communicated throughout the rest of the o-phenylene backbone. Models of o-phenylene folding based on simple considerations of biaryl torsional behavior predict that there are no simple, stable folding defects that allow the helix to invert within a single strand;³³ that is, once the first biaryl torsion is set to (approximately) +55° or −55°, there are no stable conformers that allow an opposite dihedral angle (−55° or +55°) to coexist within the same single molecule. This model is supported by the strong length-dependence of racemization rates.⁵⁵ Thus, while not directly examined here, chiral induction from one end should persist over significant length scales.

While future examples of o-phenylenes functionalized with groups for chiral induction may not make use of imines specifically, the essential features of the mechanism above rely only on there being some consistent conformational preference for the chiral group relative to the backbone. The concept that rotation about the terminal biaryl bond should invert the twist sense by swapping the relative positions of the large and medium groups on the chirality center is a consequence of the geometry of o-phenylenes, relying on the fact that arene–arene stacking is nondirectional; that is, flipping the terminal ring by 180° yields a geometry that nominally also satisfies all of the folding requirements of the system. This structural feature of o-phenylenes is slightly unusual, in that foldamer systems designed around hydrogen bonding, torsional preferences, or the outward radiation of solvophilic groups will typically have an intrinsically preferred orientation.^2,6

Other studies probing the effect of varying the structure of a chiral group on handedness bias in nonpeptidic foldamers have made careful use of crystallography^20,29 to develop models for the mechanism of chiral induction in solution. While we would obviously have liked to supplement the results for the o-phenylenes with solid-state structures, the information available from the NMR/CD spectra and computational models for these short oligomers gives a very nuanced picture of their behavior in solution. For example, compound (R)-oP⁶(o-ⁱPr) exhibits only a net 2% excess of the M helix, but this results from a balancing of reasonably strong chiral induction in opposite directions for the ii and oo conformers. In cases where the conformers cannot be distinguished experimentally, this group could easily be classified as giving only very weak chiral induction, whereas it is in fact fairly effective but in opposite directions for different geometries. This is an important distinction for the optimization of twist sense control and ultimately for the development of more complex dynamic foldamer systems.²³

Conclusions

In summary, we have shown that a preferred twist sense for folded o-phenylenes can be induced by chiral imines attached to their termini. A detailed, conformationally resolved picture of structure–property effects in these systems has been obtained through a combination of NMR spectroscopy, CD spectroscopy, and computational chemistry. For the compounds examined here, chiral induction from the para position is modest and increases with increasing size of the chiral group, although not because of steric effects; instead, there is better contact between the group and the o-phenylene helix, likely via dispersion interactions. Richer behavior is observed for chiral groups attached at the ortho positions, as they are closer to the helix and thus able to interact with it more strongly. Separate well-folded conformations differing in the positioning of the chiral group relative to the o-phenylene backbone can be distinguished by NMR spectroscopy. The twist sense of chiral induction is highly dependent on this conformational isomerism; that is, the chiral groups are ambidextrous, inducing opposite handedness depending on their position. This behavior can be rationalized using a simple steric model, and should be general for o-phenylenes regardless of how the chiral groups are connected to the backbone. We demonstrate at least rudimentary control over this phenomenon by showing that the increased steric bulk of the bornyl group in (S)-oP⁶(o-Bo) favors the inward-facing conformer and gives good selectivity for the M o-phenylene helix.

The mechanism provides an attractive strategy toward foldamers with switchable twist sense if rotation about this bond can be actively controlled. In this sense, the results here could ultimately be used to give responsive compounds that behave similarly to systems from Feringa;⁶⁹ Clayden and Moretto;²¹ Hecht;⁷⁰ and Jeong.⁷¹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the National Science Foundation (CHE-1608213) for support of this work.

Notes and references

1. S. H. Gellman, Acc. Chem. Res., 1998, 31, 173–180.
2. D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, Chem. Rev., 2001, 101, 3893–4011.
3. G. Guichard and I. Huc, Chem. Commun., 2011, 47, 5933–5941.
4. Y. Ferrand and I. Huc, Acc. Chem. Res., 2018, 51, 970–977.
5. B. A. Ikkanda and B. L. Iverson, Chem. Commun., 2016, 52, 7752–7759.
6. D.-W. Zhang, X. Zhao, J.-L. Hou and Z.-T. Li, Chem. Rev., 2012, 112, 5271–5316.
7. K. Yamato, M. Kline and B. Gong, Chem. Commun., 2012, 48, 12142–12158.
8. M. J. Kim, Y. R. Choi, H.-G. Jeon, P. Kang, M.-G. Choi and K.-S. Jeong, Chem. Commun., 2013, 49, 11412–11414.
9. N. Chandramouli, Y. Ferrand, G. Lautrette, B. Kauffmann, C. D. Mackereth, M. Laguerre, D. Dubreuil and I. Huc, Nat. Chem., 2015, 7, 334–341.
10. P. C. Mondal, C. Fontanesi, D. H. Waldeck and R. Naaman, Acc. Chem. Res., 2016, 49, 2560–2568.
11. R. B. Prince, L. Brunsveld, E. W. Meijer and J. S. Moore, Angew. Chem., Int. Ed., 2000, 39, 228–230.
12. M. Kudo, T. Hanashima, A. Muranaka, H. Sato, M. Uchiyama, I. Azumaya, T. Hirano, H. Kagechika and A. Tanatani, J. Org. Chem., 2009, 74, 8154–8163.
13. J. Jiang, M. M. Slutsky, T. V. Jones and G. N. Tew, New J. Chem., 2010, 34, 307–312.
14. A. Tanatani, A. Yokoyama, I. Azumaya, Y. Takakura, C. Mitsui, M. Shiro, M. Uchiyama, A. Muranaka, N. Kobayashi and T. Yokozawa, J. Am. Chem. Soc., 2005, 127, 8553–8561.
15. R. W. Sinkeldam, M. H. C. J. van Houtem, K. Pieterse, J. A. J. M. Vekemans and E. W. Meijer, Chem.–Eur. J., 2006, 12, 6129–6137.
16. H. B. Jang, Y. R. Choi and K.-S. Jeong, J. Org. Chem., 2018, 83, 5123–5131.
17. V. R. Naidu, M. C. Kim, J.-m. Suk, H.-J. Kim, M. Lee, E. Sim and K.-S. Jeong, Org. Lett., 2008, 10, 5373–5376.
18. Z. Dong, J. N. Plampin III, G. P. A. Yap and J. M. Fox, Org. Lett., 2010, 12, 4002–4005.
19. L. Zheng, Y. Zhan, C. Yu, F. Huang, Y. Wang and H. Jiang, Org. Lett., 2017, 19, 1482–1485.
20. J. Kim, H.-G. Jeon, P. Kang and K.-S. Jeong, Chem. Commun., 2017, 53, 6508–6511.
21. D. Mazzier, M. Crisma, M. De Poli, G. Marafon, C. Peggion, J. Clayden and A. Moretto, J. Am. Chem. Soc., 2016, 138, 8007–8018.
22. H. Jiang, C. Dolain, J.-M. Léger, H. Gornitzka and I. Huc, J. Am. Chem. Soc., 2004, 126, 1034–1035.
23. B. A. F. Le Bailly and J. Clayden, Chem. Commun., 2016, 52, 4852–4863.
24. Z. Liu, X. Hu, A. M. Abramyan, Á. Mészáros, M. Csékei, A. Kotschy, I. Huc and V. Pophristic, Chem.–Eur. J., 2017, 23, 3605–3615.
25. H.-Y. Hu, J.-F. Xiang, Y. Yang and C.-F. Chen, Org. Lett., 2008, 10, 1275–1278.
26. J. Clayden, A. Castellanos, J. Solà and G. A. Morris, Angew. Chem., Int. Ed., 2009, 48, 5962–5965.
27. S. J. Dawson, Á. Mészáros, L. Pethő, C. Colombo, M. Csékei, A. Kotschy and I. Huc, Eur. J. Org. Chem., 2014, 4265–4275.
28. Z. Dong, R. J. Karpowicz Jr, S. Bai, G. P. A. Yap and J. M. Fox, J. Am. Chem. Soc., 2006, 128, 14242–14243.
29. C. Dolain, H. Jiang, J. Léger, P. Guionneau and I. Huc, J. Am. Chem. Soc., 2005, 127, 12943–12951.
30. A. M. Kendhale, L. Poniman, Z. Dong, K. Laxmi-Reddy, B. Kauffmann, Y. Ferrand and I. Huc, J. Org. Chem., 2010, 76, 195–200.
31. J. He, J. L. Crase, S. H. Wadumethrige, K. Thakur, L. Dai, S. Zou, R. Rathore and C. S. Hartley, J. Am. Chem. Soc., 2010, 132, 13848–13857.
32. E. Ohta, H. Sato, S. Ando, A. Kosaka, T. Fukushima, D. Hashizume, M. Yamasaki, K. Hasegawa, A. Muraoka, H. Ushiyama, K. Yamashita and T. Aida, Nat. Chem., 2011, 3, 68–73.
33. C. S. Hartley, Acc. Chem. Res., 2016, 49, 646–654.
34. S. Mathew, L. A. Crandall, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2014, 136, 16666–16675.
35. Y. Mizukoshi, K. Mikami and M. Uchiyama, J. Am. Chem. Soc., 2015, 137, 74–77.
36. M. Riello, G. Doni, S. V. Filip, M. Gold and A. De Vita, J. Phys. Chem. B, 2014, 118, 13689–13696.
37. T. Kajitani, Y. Suna, A. Kosaka, T. Osawa, S. Fujikawa, M. Takata, T. Fukushima and T. Aida, J. Am. Chem. Soc., 2013, 135, 14564–14567.
38. D. R. Lee, C. W. Lee and J. Y. Lee, J. Mater. Chem. C, 2014, 2, 7256–7263.
39. M. Rickhaus, M. Mayor and M. Jurícek, Chem. Soc. Rev., 2016, 45, 1542–1556.
40. Y. Tokoro, N. Ohtsuka, A. Kusakabe and S.-i. Fukuzawa, Eur. J. Org. Chem., 2017, 2353–2358.
41. M. J. Marsella, K. Yoon, A. Almutairi, S. K. Butt and F. S. Tham, J. Am. Chem. Soc., 2003, 125, 13928–13929.
42. T. Nakashima, K. Imamura, K. Yamamoto, Y. Kimura, S. Katao, Y. Hashimoto and T. Kawai, Chem.–Eur. J., 2014, 20, 13722–13729.
43. W. Yang and T. Nakano, Chem. Commun., 2015, 51, 17269–17272.
44. H.-H. Zhang, C. Ma, P. V. Bonnesen, J. Zhu, B. G. Sumpter, J.-M. Y. Carrillo, P. Yin, Y. Wang, A.-P. Li and K. Hong, Macromolecules, 2016, 49, 4691–4698.
45. B. A. G. Hammer and K. Müllen, Chem. Rev., 2016, 116, 2103–2140.
46. D. Lehnherr, C. Chen, Z. Pedramrazi, C. R. DeBlase, J. M. Alzola, I. Keresztes, E. B. Lobkovsky, M. F. Crommie and W. R. Dichtel, Chem. Sci., 2016, 7, 6357–6364.
47. D. Lotter, M. Neuburger, M. Rickhaus, D. Häussinger and C. Sparr, Angew. Chem., Int. Ed., 2016, 55, 2920–2923.
48. S. Ito, K. Takahashi and K. Nozaki, J. Am. Chem. Soc., 2014, 136, 7547–7550.
49. H. Sato, J. A. Bender, S. T. Roberts and M. J. Krische, J. Am. Chem. Soc., 2018, 140, 2455–2459.
50. S. J. Hein, D. Lehnherr, H. Arslan, F. J. Uribe-Romo and W. R. Dichtel, Acc. Chem. Res., 2017, 50, 2776–2788.
51. F. Chen, T. Tanaka, Y. Hong, W. Kim, D. Kim and A. Osuka, Chem.–Eur. J., 2016, 22, 10597–10606.
52. S. J. Hein, H. Arslan, I. Keresztes and W. R. Dichtel, Org. Lett., 2014, 16, 4416–4419.
53. M. Rickhaus, L. M. Bannwart, M. Neuburger, H. Gsellinger, K. Zimmermann, D. Häussinger and M. Mayor, Angew. Chem., Int. Ed., 2014, 53, 14587–14591.
54. K. Manabe and T. Kimura, Org. Lett., 2013, 15, 374–377.
55. S. Ando, E. Ohta, A. Kosaka, D. Hashizume, H. Koshino, T. Fukushima and T. Aida, J. Am. Chem. Soc., 2012, 134, 11084–11087.
56. Z. J. Kinney and C. S. Hartley, Org. Lett., 2018, 20, 3327–3331.
57. Z. J. Kinney and C. S. Hartley, J. Am. Chem. Soc., 2017, 139, 4821–4827.
58. To keep consistent with the other compounds, we name the configuration of the bornyl-substituted hexamers oP⁶(p-Bo) and oP⁶(o-Bo) as S, referring to the chirality center α to the imine. Note, however, that these compounds are synthesized from (1R,2S,4R)-(+)-bornylamine, which is commonly referred to as (R)-bornylamine..
59. S. M. Mathew and C. S. Hartley, Macromolecules, 2011, 44, 8425–8432.
60. S. M. Mathew, J. T. Engle, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2013, 135, 6714–6722.
61. Of course, even the oligomers without chirality centers are chiral in the sense that they exist as a dynamic racemate of helices..
62. P. Guiglion and M. A. Zwijnenburg, Phys. Chem. Chem. Phys., 2015, 17, 17854–17863.
63. C. S. Hartley, J. Org. Chem., 2011, 76, 9188–9191.
64. G. Pescitelli, L. Di Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603–4625.
65. F. Furche, R. Ahlrichs, C. Wachsmann, E. Weber, A. Sobanski, F. Vögtle and S. Grimme, J. Am. Chem. Soc., 2000, 122, 1717–1724.
66. S. Resa, D. Miguel, S. Guisán-Ceinos, G. Mazzeo, D. Choquesillo-Lazarte, S. Abbate, L. Crovetto, D. J. Cárdenas, M. C. Carreño, M. Ribagorda, G. Longhi, A. J. Mota, L. Álvarez de Cienfuegos and J. M. Cuerva, Chem.–Eur. J., 2018, 24, 2653–2662.
67. G. N. Vemuri, M. Chu, H. Dong, B. J. Spinello and C. S. Hartley, Org. Biomol. Chem., 2017, 15, 845–851.
68. The populations of (S)-oP⁶(o-Np) were not determined as the NMR spectra were too complex to assign with confidence..
69. D. Pijper and B. L. Feringa, Angew. Chem., Int. Ed., 2007, 46, 3693–3696.
70. R. M. Meudtner and S. Hecht, Angew. Chem., Int. Ed., 2008, 47, 4926–4930.
71. J.-m. Suk, V. R. Naidu, X. Liu, M. S. Lah and K.-S. Jeong, J. Am. Chem. Soc., 2011, 133, 13938–13941.

---

Footnote

† Electronic supplementary information (ESI) available: Supplemental figures and discussion referred to in the text, synthetic details, experimental procedures, NMR spectra, and computational data. See DOI: 10.1039/c8sc02821d

---