DOI:
10.1039/C8CE01673A
(Paper)
CrystEngComm, 2019,
21, 41-52
Structure determination of fatty acid ester biofuels via in situ cryocrystallisation and single crystal X-ray diffraction†
Received
30th September 2018
, Accepted 5th November 2018
First published on 5th November 2018
Abstract
In situ cryocrystallisation in combination with a zone-melting technique enabled the crystal structure determination of a homologous series of low-melting n-alkyl methyl esters Cn−1H2n+1CO2CH3, from methyl pentanoate (n = 5) to methyl tridecanoate (n = 13), by single crystal X-ray diffraction. Two isostructural groups were identified: the odd-numbered triclinic members (C9,11,13) and the even-numbered orthorhombic members (C8,10,12). All observed structural trends, similarities and differences in intermolecular contacts, including the odd–even effect observable in melting point behaviour and unit cell parameters, were easily visualised and described by 2D fingerprint plots generated from the calculated Hirshfeld surfaces, in combination with atom–atom Coulomb–London–Pauli (AA-CLP) lattice energy calculations.
Introduction
Current interest in biodiesel sprouts not only from environmental concerns but also from the global shortage of fossil fuels with the concomitant upsurge in the cost of crude oil.1 Biodiesel offers several advantages over diesel fuel, but its widespread use is hampered by some serious economic and technical issues related to its physical properties. Obstinate technical problems include poor cold flow performance, decreased oxidative stability and increased NOx exhaust emissions. Biodiesels are derived from biomass with a substantial triglyceride content through transesterification with methanol or ethanol in the presence of a catalyst, which leads to a mixture of glycerol and fatty acid esters (FAEs). The FAE profiles are identical to the profile of the source oil.2,3 Fuel properties, including cold flow, are directly impacted by the structure of composite FAEs, which makes simultaneous solving of technical issues problematic, since the resolution of one problem may intensify the next.4 Poor cold flow properties result from the relatively high melting points of the various FAE components and result in the fuel solidifying at cold temperatures to form crystalline precipitates which hampers the use of biodiesels in colder climates.5 Various tactics towards tackling these issues exist,6 including the use of additives,7–9 mixing/blending with mineral-derived diesel,5,10 changing the chemical structure of the FAEs by using an acyl acceptor other than methanol/ethanol or by altering the FAE composition either physically, by winterization,11,12 or by genetic modification of the seed oils.6 The ignition quality of biodiesel is indicated by the cetane number (CN)3,4 and is inversely related to the ignition delay time.4 The standards for biodiesel require a minimum CN of 47 (ASTM D6517) or 51 (EN14214).4 CN requirements therefore prevent the use particularly of fatty acid methyl esters (FAMEs) of the general formula C4H9CO2CH3–C12H25CO2CH3 (Scheme 1) shorter than C7H15CO2CH3 as biodiesel, although they have been used as surrogates in modeling13–18 studies. Little is known about the solid state structures and properties of the crystalline precipitates that form at reduced temperatures. A systematic study of the crystallisation of various pure FAMEs of biodiesel may provide structural insights into melting point suppression with subsequent control by providing a solid-state chemistry model.19 Growing single crystals of the individual FAMEs, amenable for analysis by single crystal X-ray diffraction (SCXRD), proved challenging, since these compounds are all liquid at room temperature (ca. 25 °C). The resurgence of SCXRD analysis of low-melting materials, due to advances in both in situ crystal growth techniques and equipment, is therefore timely.20 Single crystals of the liquid FAMEs were grown by in situ cryocrystallisation in combination with a zone-melting technique with the aid of an optical heating and cooling device (OHCD III), as described in detail elsewhere.21–23 Hirshfeld surface analysis24–26 and atom–atom Coulomb–London–Pauli (AA-CLP)27,28 lattice energy calculations were used to enhance the analysis of the different packing arrangements and interactions present in the 3D structures. Hirshfeld surfaces allow extraction and quantification of the contributions of different types of intermolecular contacts to the observed crystal packing. The generated 2D fingerprint plots summarise these interactions graphically, with the differences between plots giving valuable information on both non-covalent interactions and close contacts at minimal computational costs. AA-CLP27,28 was used to calculate lattice energies and interaction energies of molecular pairs. This technique enables partitioning of the total energy into electrostatic, polarization, dispersion, and repulsion components to evaluate the importance of non-covalent interactions in the crystal packing.
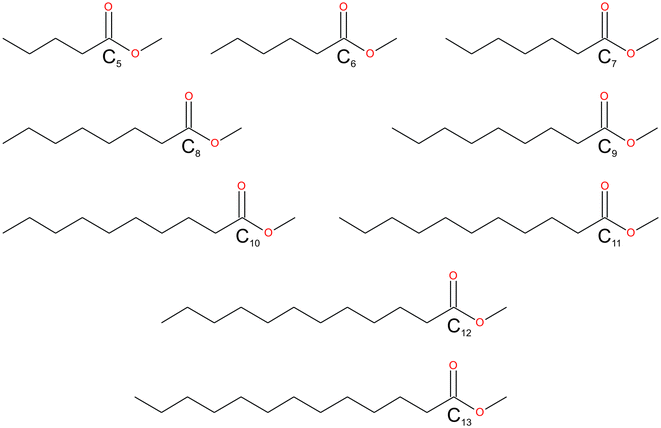 |
| | Scheme 1 The fatty acid methyl esters (FAMEs) reported in this study: C4H9CO2CH3–C12H25CO2CH3. The FAMEs were abbreviated in the text and refer to the length of the alkyl chain, C5–C13. | |
Experimental
Synthesis
In this work, a continuous range, starting from C4H9CO2CH3–C12H25CO2CH3, of FAMEs were synthesised (Fig. 1), following a standard Fischer esterification procedure,29 from the respective even- and odd-numbered neat carboxylic acid with methanol as both the acyl acceptor and solvent using the following general method: to a stirred solution of each respective carboxylic acid (0.20 g) in a large reagent excess of methanol (15 mL), a catalytic amount of H2SO4 (conc., 5.0 mol%) was added at room temperature (ca. 25 °C). The solution was heated at reflux for approximately 3 h, with the reaction progress monitored by thin layer chromatography (TLC). After completion, the reaction vessel was left to cool to room temperature, whereafter the solution was diluted with hexane (15 mL). The layers were separated and the aqueous layer extracted with hexane (3 × 20 mL). The combined organic layers were washed with NaHCO3 (sat. aq., 2 × 10 mL) and brine (2 × 20 mL), dried (NaSO4), filtered and evaporated under reduced pressure, with the bath temperature dictated by the volatility of the expected ester product, to yield the products as colourless liquids. No further purification was necessary. Yields ranged from 60% to near quantitative.
 |
| | Fig. 1 General synthesis of FAMEs. | |
Single crystal X-ray diffraction studies
Single crystals of the liquid FAMEs were grown via in situ crystallization in a 0.3 mm diameter Lindemann capillary using the OHCD. Diffraction quality crystals were grown using a zone-melting technique where a small region of the capillary was heated with a CO2 IR laser to create a molten zone (the temperature of which is sample dependent and slightly below the melting temperature of the pure sample). Melting points were recorded and the DSC traces for all compounds are given in the ESI.† The molten zone was slowly moved along the length of the capillary at about 3 cm/30 min by adjusting the position of the laser and allowing for recrystallization of the molten zone.22,23 The cycle was repeated several times until a single crystal amenable for analysis by SCXRD was obtained. The number of cycles, cycle time and laser intensity required to obtain a good quality single crystal is sample dependent, and the whole process can take several days (further details are provided in the ESI†). Since the samples are sensitive to temperature and melt easily, the whole experiment was carried out in the measurement device (the diffractometer), hence the term in situ. In general, the crystal size of C5–C13 was estimated to be 1.00 mm × 0.30 mm × 0.30 mm. Single crystal data of the liquid FAMEs were collected on a BRUKER D8 VENTURE X-ray diffractometer equipped with a Photon 100 CMOS camera using Mo-Kα (0.71073 Å) radiation. The crystal-to-detector distance was fixed at 80 mm for all the crystals to maintain uniformity over data collection. Complete data sets were collected for all the compounds by the strategies generated using the APEX3 module of the Bruker software suite. The scan width per frame was Δω = 0.5°. The cell refinement and data reduction were carried out using SAINT+30 and multi-scan absorption correction was performed using the program SADABS.31 The crystal structures were solved by SHELXTL32,33 structure solution software and were refined with full-matrix least squares on F2 included in the WinGX package suite.34 Non-hydrogen atoms were refined anisotropically and hydrogen atoms were fixed on geometrically ideal positions during the refinement. Twin laws were required in the refinements of C5, C6, C9, C11 and C13. The atomic numbering scheme and ORTEP style displacement ellipsoids for all the structures are given in the ESI.†
Hirshfeld surface calculations
Molecular Hirshfeld surface calculations were performed using the CrystalExplorer-3.1 (ref. 35) program. The bond lengths to hydrogen were automatically modified to the standard neutron values (C–H = 1.083 Å) upon using the respective cif-files as input. The 2D fingerprint plots, with de and di distance scales displayed on the respective graph axes, were generated using the standard 0.6–2.6 Å view.
AA-CLP calculations
Lattice and molecule⋯molecule interaction energies were calculated using the August 2014 version of AA-CLP.27 Atom coordinates for all calculations were taken from X-ray diffraction studies with normalization of H-bond positions as implemented in the CLP computer program package. The fully empirical atom–atom Coulomb–London–Pauli (AA-CLP) force field model was applied with default scaling parameters for coulombic, polarization, dispersion and repulsion terms for quick estimation of approximate lattice energies.
Differential scanning calorimetry (DSC)
Differential scanning calorimetry data (Table S2†) were collected using a Mettler Toledo 822e with aluminium pans under air purge. Star SW 9.20 was used for instrument control and data analysis. Exothermic events were shown as peaks. Various heating and cooling protocols were performed to determine temperatures and enthalpies of phase changes. The temperature and energy calibrations were performed using pure indium (purity 99.99%, m.p. 156.6 °C, heat of fusion 28.45 J g−1).
Results and discussion
Reported here are the crystal structures of the compounds (C4H9CO2CH3–C12H25CO2CH3) which are all liquid at room temperature and in which crystallisation was achieved by in situ cryocrystallisation. All compounds had an all-trans conformation. For simplicity, we will refer to the FAMEs as Cn, where n is the number of fatty acid carbons, e.g. C4H9CO2CH3 is abbreviated to C5. All crystallographic parameters are given in Table 1. The discussion is structured according to space group assignment, with the monoclinic C5,6,7 triad discussed in isolation, since, as also noted by Bond,36 “the early members of most homologous chemical series display substantial deviation in their crystal structures”. From C8 onwards, the unit cell dimensions resemble those of some membrane lipids,37 as well as those of the orthogonally derived unit cells of the homologous series of n-alkyl carboxylic acids (C6–15) reported by Bond.36 In this work, two isostructural groups were identified: the even-membered orthorhombic members (C8,10,12) and the odd-membered triclinic members (C9,11,13). As suggested by Bond,36 on the crystal structures of a homologous series of n-alkyl carboxylic acids, the discussion of the crystal structures can conveniently be separated into packing arrangement descriptions ‘within layers’, ‘between layers’.38–40 A representative example of this ‘layer’ description for C5 is shown in Fig. 2, showing the packing arrangement of the molecules shown in red within an individual monolayer (Fig. 2a), and the relative packing between two monolayers (red and blue coloured molecules), shown side-on (Fig. 2b). When describing the relative arrangements of adjacent molecules, we will refer to the hydrophilic ester part as the head section and the hydrophobic alkyl part as the tail section. Any weak hydrogen bonds and short contacts were identified using the default settings in MERCURY.41
Table 1 Crystallographic parameters of C5–13
| Parameter |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
C11 |
C12 |
C13 |
| Chemical formula |
C4H9CO2CH3 |
C5H11CO2CH3 |
C6H13CO2CH3 |
C7H15CO2CH3 |
C8H17CO2CH3 |
C9H19CO2CH3 |
C10H21CO2CH3 |
C11H23CO2CH3 |
C12H25CO2CH3 |
| Formula weight |
116.16 |
130.18 |
144.21 |
158.23 |
172.26 |
186.28 |
200.31 |
214.34 |
456.72 |
| Temperature (°C) |
−114 |
−100 |
−100 |
−100 |
−100 |
−100 |
−100 |
−100 |
−100 |
| Crystal system |
Monoclinic |
Monoclinic |
Monoclinic |
Orthorhombic |
Triclinic |
Orthorhombic |
Triclinic |
Orthorhombic |
Triclinic |
| Space group |
P21/c |
C2/c |
P21/n |
Pbcn
|
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Pbcn
|
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Pbcn
|
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
|
a (Å) |
7.309(11) |
38.19(2) |
9.173(3) |
50.25(3) |
5.565(3) |
58.86(2) |
5.5680(16) |
67.940(6) |
5.5474(7) |
|
b (Å) |
16.54(2) |
4.088(2) |
5.6554(17) |
7.055(4) |
7.183(4) |
7.100(3) |
7.214(2) |
7.1161(6) |
7.1923(9) |
|
c (Å) |
6.169(9) |
9.951(5) |
17.357(5) |
5.609(3) |
27.043(14) |
5.574(2) |
31.782(9) |
5.5638(5) |
36.076(5) |
|
α (°) |
90 |
90 |
90 |
90 |
90.145(7) |
90 |
89.956(6) |
90 |
89.983(3) |
|
β (°) |
108.823(15) |
90.206(10) |
104.928(3) |
90 |
91.445(7) |
90 |
85.324(4) |
90 |
89.626(4) |
|
γ (°) |
90 |
90 |
90 |
90 |
90.099(7) |
90 |
89.866(4) |
90 |
89.903(3) |
|
V (Å3) |
705.9(18) |
1553.6(14) |
870.0(4) |
1988(2) |
1080.7(10) |
2329.4(15) |
1272.4(6) |
2689.9(4) |
1439.3(3) |
|
Z
|
4 |
8 |
4 |
8 |
4 |
8 |
4 |
8 |
4 |
| Density (mg m−3) |
1.093 |
1.113 |
1.101 |
1.057 |
1.059 |
1.062 |
1.046 |
1.059 |
1.054 |
| Absorption coefficient (mm−1) |
0.080 |
0.079 |
0.077 |
0.072 |
0.071 |
0.070 |
0.069 |
0.069 |
0.068 |
|
F(000) |
256 |
576 |
320 |
704 |
384 |
832 |
448 |
960 |
512 |
|
θ range (°) |
3.192 to 25.500 |
3.201 to 25.498 |
3.775 to 25.498 |
2.916 to 25.500 |
2.932 to 25.500 |
2.890 to 25.498 |
3.102 to 25.498 |
2.998 to 25.494 |
2.888 to 25.497 |
| Reflections collected/unique |
5577/1331 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225/1431 225/1431 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012/1601 012/1601 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160/1824 160/1824 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894/3713 894/3713 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 016/2150 016/2150 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 693/4662 693/4662 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984/2419 984/2419 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217/5641 217/5641 |
|
R(int) |
0.0903 |
0.1140 |
0.0331 |
0.0693 |
0.0938 |
0.0817 |
0.0381 |
0.0737 |
0.1020 |
| Completeness (%) |
99.6 |
99.9 |
99.5 |
98.3 |
99.4 |
99.1 |
99.7 |
96.5 |
99.8 |
| Goodness-of-fit on F2 |
1.153 |
1.057 |
1.053 |
1.143 |
1.009 |
1.861 |
1.031 |
1.1090 |
1.082 |
|
R(obs)/R(all) |
0.0947/0.1521 |
0.0841/0.0937 |
0.0441/0.0546 |
0.0948/0.1042 |
0.0725/0.1693 |
0.1548/0.1867 |
0.0548/0.0791 |
0.0973/0.1383 |
0.1012/0.1574 |
| wR2(obs)/R(all) |
0.2257/0.2510 |
0.2448/0.2534 |
0.1114/0.1192 |
0.2464/0.2505 |
0.1684/0.2063 |
0.4634/0.4772 |
0.1456/0.1590 |
0.2764/0.2967 |
0.2479/0.2778 |
| Largest diff. peak and hole (e Å−3) |
0.339/−0.294 |
0.478/−0.387 |
0.186/−0.137 |
0.391/−0.376 |
0.226/−0.196 |
0.683/−0.507 |
0.179/−0.220 |
0.592/−0.353 |
0.335/−0.266 |
| CCDC no. |
1590402
|
1590404
|
1590403
|
1590405
|
1590406
|
1590407
|
1590408
|
1590409
|
1590410
|
Table 2 Hydrogen bonding geometries involved in FAMEs C5–13
| FAMEs |
D–H⋯A |
D–H (Å) |
H⋯A (Å) |
D⋯A (Å) |
D–H⋯A (°) |
Symmetry |
| C5 |
C(2)–H(2A)⋯O(1) |
0.99 |
2.69 |
3.670(7) |
169 |
−x + 1, −y + 1, −z + 1 |
| C6 |
C(2)–H(2B)⋯O(2) |
0.99 |
2.52 |
3.448(6) |
156 |
x, −y + 1, z + 1/2 |
| C(4)–H(4A)⋯O(2) |
0.99 |
2.71 |
3.587(6) |
148 |
x, −y + 1, z + 1/2 |
| C7 |
C(8)–H(8A)⋯O(2) |
0.98 |
2.62 |
3.416(2) |
138 |
x, y − 1, z |
| C(8)–H(8B)⋯O(2) |
0.98 |
2.70 |
3.573(2) |
149 |
−x + 1/2, y − 1/2, −z + 3/2 |
| C8 |
C(2)–H(2A)⋯O(2) |
0.99 |
2.63 |
3.542(5) |
154 |
x, y, z – 1 |
| C(3)–H(3A)⋯O(2) |
0.99 |
2.63 |
3.393(5) |
134 |
x, −y + 1, z − 1/2 |
| C9 |
C(2)–H(2B)⋯O(4) |
0.99 |
2.50 |
3.225(5) |
130 |
|
| C(12)–H(12B)⋯O(4) |
0.99 |
2.71 |
3.612(5) |
152 |
x + 1, y, z |
| C(20)–H(20A)⋯O(2) |
0.98 |
2.62 |
3.569(5) |
163 |
−x + 1, −y + 1, −z + 1 |
| C10 |
C(2)–H(2B)⋯O(2) |
0.99 |
2.61 |
3.527(7) |
154 |
x, y, z – 1 |
| C(3)–H(3B)⋯O(2) |
0.99 |
2.63 |
3.398(6) |
135 |
x, −y, z − 1/2 |
| C11 |
C(2)–H(2A)⋯O(4) |
0.99 |
2.53 |
3.254(3) |
130 |
|
| C(14)–H(14A)⋯O(4) |
0.99 |
2.70 |
3.606(3) |
152 |
x + 1, y, z |
| C(24)–H(24A)⋯O(2) |
0.98 |
2.63 |
3.583(3) |
166 |
−x, −y + 1, −z + 1 |
| C12 |
C(2)–H(2B)⋯O(2) |
0.99 |
2.61 |
3.529(4) |
155 |
x, y, z + 1 |
| C(3)–H(3A) ⋯O(2) |
0.99 |
2.63 |
3.408(5) |
135 |
x, −y + 1, z + 1/2 |
| C13 |
C(2)–H(2B)⋯O(4) |
0.99 |
2.54 |
3.248(7) |
129 |
|
| C(16)–H(16B)⋯O(4) |
0.99 |
2.69 |
3.600(7) |
152 |
x + 1, y, z |
| C(28)–H(28B)⋯O(2) |
0.98 |
2.61 |
3.582(7) |
170 |
−x, −y + 1, −z + 1 |
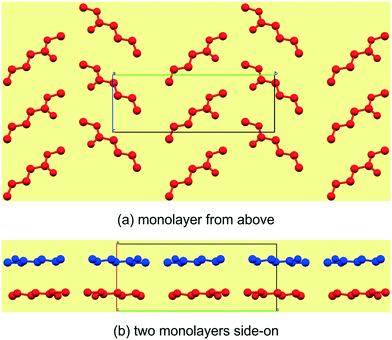 |
| | Fig. 2 The general view of an individual mono layer in C5 (a), which can be described by how the molecules arrange within the layer in two crystallographic directions. The third descriptor is then how individual mono layers arrange relative to each other (b). | |
Structural commentary on C5–7
The C5–7n-alkyl esters crystallise in monoclinic space groups, each with Z′ = 1. The C5 and C7 FAMEs crystallize in primitive space groups and C6 in C-centered. In structure C5, the monolayer in the bc-plane overall resembles a chevron arrangement, with adjacent molecules packing head-to-tail (parallel) along the c-axis and head-to-tail (anti-parallel) along the b-axis (Fig. 3a). There exists a short contact between the carbonyl O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and methyl C(6) within this monolayer (Fig. 4a and Table 3). Adjacent monolayers are stabilised by two symmetry equivalent C(2)–H(2A)⋯O(1)–C hydrogen bonds forming an R22(8) hydrogen bonded ring (Fig. 4a). In contrast, in C6, the molecules within monolayers defined by the ac-plane pack head-to-tail (parallel) in both the a-axis and c-axis (Fig. 3b). Adjacent molecules in this monolayer interact via two C(4)–H(4A)⋯O(2)
C and methyl C(6) within this monolayer (Fig. 4a and Table 3). Adjacent monolayers are stabilised by two symmetry equivalent C(2)–H(2A)⋯O(1)–C hydrogen bonds forming an R22(8) hydrogen bonded ring (Fig. 4a). In contrast, in C6, the molecules within monolayers defined by the ac-plane pack head-to-tail (parallel) in both the a-axis and c-axis (Fig. 3b). Adjacent molecules in this monolayer interact via two C(4)–H(4A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C(2)–H(2B)⋯O(2)
C and C(2)–H(2B)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds forming an R12(6) ring and a short contact exists between the methyl groups, C(7), of the head section (Fig. 4b and Table 3). This forms a lamellar arrangement. C7, being odd-membered, shows the same chevron arrangement as C5 where adjacent molecules pack head-to-head (parallel) along the b-axis but head-to-tail (anti-parallel) along the (101) direction (Fig. 3c). Adjacent monolayers interact via C(8)–H(8A)⋯O(2)
C hydrogen bonds forming an R12(6) ring and a short contact exists between the methyl groups, C(7), of the head section (Fig. 4b and Table 3). This forms a lamellar arrangement. C7, being odd-membered, shows the same chevron arrangement as C5 where adjacent molecules pack head-to-head (parallel) along the b-axis but head-to-tail (anti-parallel) along the (101) direction (Fig. 3c). Adjacent monolayers interact via C(8)–H(8A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C(8)–H(8B)⋯O(2)
C and C(8)–H(8B)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds to form repeating R23(9) rings (Fig. 4c).
C hydrogen bonds to form repeating R23(9) rings (Fig. 4c).
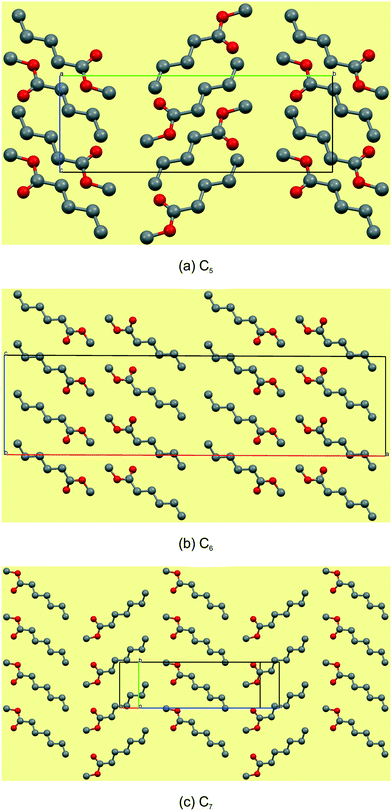 |
| | Fig. 3 Views of the monolayers of C5–7. Note that the monolayers of these early members of the series do not show any consistency, packing head-to tail in both directions in C5 (a), head-to-head and tail-to-tail in C6 (b) and head-to-head and head-to-tail in C7 (c). | |
Table 3 Relevant distances (Å) and angles (°) within layer arrangements for compounds C5–7
|
|
Head-to-head O–CH3⋯CH3–O (Å) |
Tail-to-tail C–CH3⋯H3C–C (Å) |
Head-to-tail O–CH3⋯H3C–C (Å) |
|
(i): 1/2 − x, 1/2 − y, −z; (ii): 1/2 − x, 3/2 − y, −z.
|
| C5 |
C(6)⋯O(2)i: 3.843(8) |
— |
— |
| C6 |
C(7)⋯C(7)ii: 3.377(7) |
— |
— |
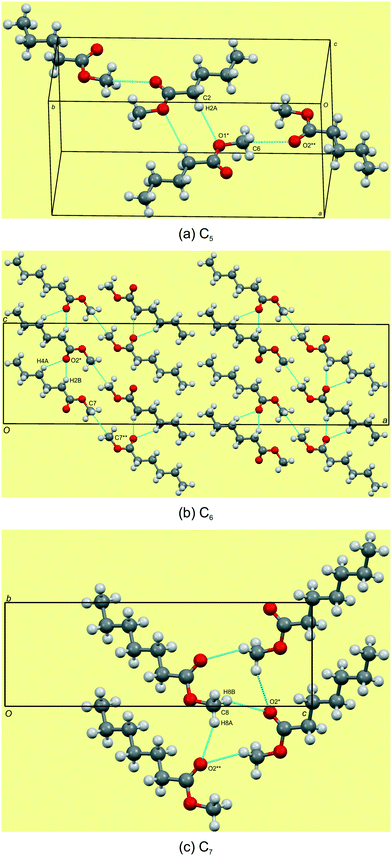 |
| | Fig. 4 Hydrogen bonding views showing the weak C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–H⋯O–C hydrogen bonds in C5–7 (a–c). Note the short contact of the head groups of C5 and C6. For detailed geometrical parameters see Tables 2 and 3. C and C–H⋯O–C hydrogen bonds in C5–7 (a–c). Note the short contact of the head groups of C5 and C6. For detailed geometrical parameters see Tables 2 and 3. | |
Packing and hydrogen bonding description for C8,10,12
The even-membered C8,10,12 all crystallise in the orthorhombic space group Pbcn with Z' = 1 and are isostructural. Again, starting to describe the arrangement of molecules within a monolayer makes for an easier comparative description. In all the structures, the monolayer is defined by the ac-plane. Adjacent molecules pack head-to-head (parallel) along the c-axis, and alternatingly head-to-head (parallel) and tail-to-tail (anti-parallel) along the a-axis (Fig. 5a). This results in an overall herringbone arrangement in C6 (Fig. 5a), unlike the chevron arrangement in C5 and C7. At the interface of the head groups, the molecules are braided together via weak C(2)–H(2A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds along the a-axis (Fig. 6a). Molecules in adjacent layers interact via a C(3)–H(3A)⋯O(2)
C hydrogen bonds along the a-axis (Fig. 6a). Molecules in adjacent layers interact via a C(3)–H(3A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds along the b-axis (Fig. 7a). The same description of the packing and hydrogen bonding for C10 and C12 holds as for C8 (shown in Fig. 5b and c).
C hydrogen bonds along the b-axis (Fig. 7a). The same description of the packing and hydrogen bonding for C10 and C12 holds as for C8 (shown in Fig. 5b and c).
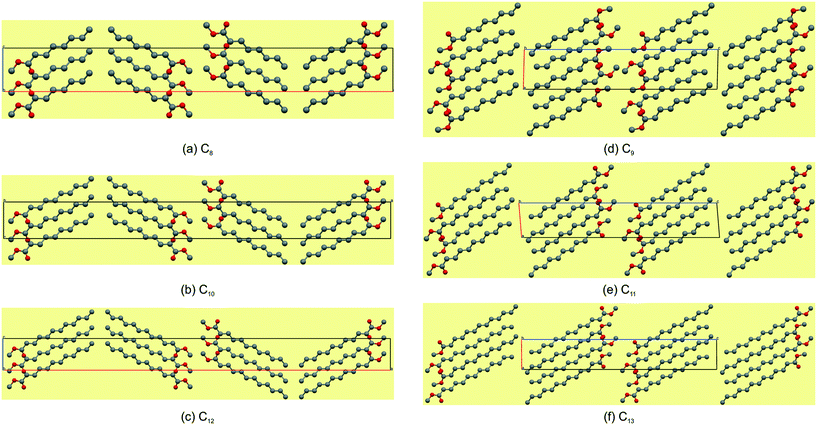 |
| | Fig. 5 The most marked difference is that the even-membered FAMEs have a herringbone arrangement (a–c) and the odd-membered have a lamellar arrangement (d–f). | |
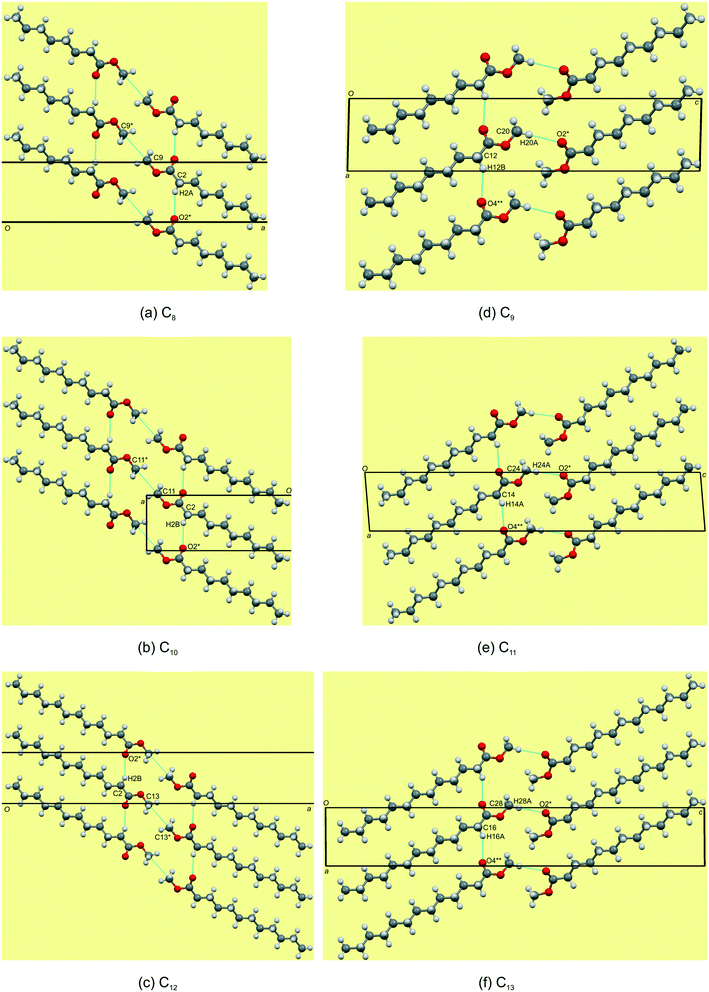 |
| | Fig. 6 Detailed views of the hydrogen bonding arrangements of C8–13 (a–f). For detailed geometrical parameters see Tables 2 and 4. | |
 |
| | Fig. 7 Representative arrangements of two mono layers for the even-membered (a) and odd-membered (b) C8–13 FAME series. For detailed geometrical parameters see Table 2. | |
The distance between aligned head methyl groups increase slightly through C8,10,12, with the dihedral angle between linearly aligned carbonyl functionalities at ca. 131–133° (Table 4). The terminal carbon atoms of the tail end methyl groups are equidistant within the respective layers, with the C⋯C distances decreasing through C8,10,12. The angle formed between flanking terminal carbon atoms increases towards 90°, through C8,10,12 (Table 4), and results in a herringbone packing arrangement at this interface (Fig. 5). Molecules in adjacent layers (between layers) are tilted relative to each other with the tilt angle increasing down the series (Table 4). The weak C(3)–H(3A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonding and dispersive interactions responsible for cohesion between layers in the b-direction (Fig. 7a) also correspond to the largest contributory term Ed (e.g. C8: −91.8 kJ mol−1) of the total calculated lattice energies, Et (e.g. C8: −96.3 kJ mol−1), as calculated using the atom–atom approach of the CLP27,42 manifold as collated in Table 5. The terminal methyl groups at the tail ends of the chains line up between adjacent layers, to form a linear interface between adjacent layer stacks.
C hydrogen bonding and dispersive interactions responsible for cohesion between layers in the b-direction (Fig. 7a) also correspond to the largest contributory term Ed (e.g. C8: −91.8 kJ mol−1) of the total calculated lattice energies, Et (e.g. C8: −96.3 kJ mol−1), as calculated using the atom–atom approach of the CLP27,42 manifold as collated in Table 5. The terminal methyl groups at the tail ends of the chains line up between adjacent layers, to form a linear interface between adjacent layer stacks.
Table 4 Relevant distances (Å) and angles (°) within layer arrangements for compounds C8–13
|
|
Head-to-head O–CH3⋯CH3–O (Å) |
Dihedral angle between carbonyl roups at ester interface (°) |
Tail-to-tail C–CH3⋯H3C–C (Å) |
|
(i): 1 − x, y, 5/2 − z; (ii): 3/2 − x, 1/2 − y, −1/2 + z; (iii): −x, y, 5/2 − z; (iv): 1/2 − x, 1/2 − y, 1/2 + z; (v): 1 − x, y, −1/2 − z; (vi): 1/2 − x, 3/2 − y, z + 1/2; (vii): −x, 1 − y, 1 − z; (viii): 3 − x, 1 − y, −z; (ix): −1 − x, 1 − y, 1 − z; (x): x, 1 + y, z.
|
| Even-chain |
| C8 |
C(9)⋯C(9)i: 3.370(7) |
132.6(3) |
C(8)⋯C(8)ii: 4.019(6) |
| C10 |
C(11)⋯C(11)iii: 3.366(9) |
131.1(4) |
C(10)⋯C(10)iv: 3.982(8) |
| C12 |
C(13)⋯C(13)v: 3.406(7) |
131.8(3) |
C(12)⋯C(12)vi: 3.971(6) |
| Odd-chain |
| C9 |
C(10)⋯C(20)vii: 3.507(6) |
57.1(4) |
C(9)⋯C(19)viii: 3.941(6) |
| C11 |
C(12)⋯C(24)ix: 3.497(4) |
57.1(2) |
C(11)⋯C(23)viii: 3.927(4) |
| C13 |
C(14)⋯C(28)ix: 3.512(8) |
56.0(5) |
C(13)⋯C(27)x: 4.00(1) |
Table 5 Results of AA-CLP calculations as partitioned lattice energy contributions (kJ mol−1)a to the total calculated lattice energies of the C5 to C13 FAMEs
|
|
E
c
|
E
p
|
E
d
|
E
r
|
E
t
|
|
Total lattice energies (Et), coulombic energies (Ec), polarization energies (Ep), dispersion energies (Ed), and repulsion (Er) terms.
|
| C5 |
−9.8 |
−27.6 |
−69 |
32.4 |
−74.1 |
| C6 |
−8.8 |
−31 |
−69.9 |
23.9 |
−85.9 |
| C7 |
−10.5 |
−33.6 |
−90 |
42.2 |
−91.9 |
| C8 |
−8.5 |
−35 |
−91.8 |
39.8 |
−96.3 |
| C9 |
−8.1 |
−38.4 |
−95.4 |
32.3 |
−109.5 |
| C10 |
−8.3 |
−41.6 |
−104.1 |
34.5 |
−119.6 |
| C11 |
−8 |
−43.3 |
−109.9 |
35 |
−126.2 |
| C12 |
−8.3 |
−45.2 |
−128.8 |
51.5 |
−130.8 |
| C13 |
−8.8 |
−47.8 |
−138.2 |
55.5 |
−139.2 |
Packing and hydrogen bonding description for C9,11,13
The odd-membered C9,11,13 all crystallise in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z' = 2 and are isostructural. The two molecules in the asymmetric unit are labelled mol1 (ester groups O(1) & O(2)) and mol2 (ester groups O(3) & O(4)). By inspecting the cell angles, all being close to 90°, a higher symmetry crystal system and space group would be expected with Z' = 1. However, the two molecules in the asymmetric unit have different hydrogen bonding interactions and show distinct fingerprint plots, which will be discussed further below. Nonetheless, in C9, the monolayer is again defined by the ac-plane, with a difference arising in the alignment along one of the axis directions. Adjacent molecules pack head-to-head (parallel, identical to the even-membered ones) along the a-axis, and alternatingly head-to-head (parallel, identical to the even-membered ones) and tail-to-tail (parallel; anti-parallel in the even-membered) along the c-axis (Fig. 5d–f). This no longer results in an overall herringbone arrangement as seen in the even-membered C8,10,12 but more akin to the lamellar arrangement seen for C6 (Fig. 3b). The hydrogen bonding between the head groups of mol1 and mol2 aligned along the c-axis consists of C(20)–H(20A)⋯O(2)
with Z' = 2 and are isostructural. The two molecules in the asymmetric unit are labelled mol1 (ester groups O(1) & O(2)) and mol2 (ester groups O(3) & O(4)). By inspecting the cell angles, all being close to 90°, a higher symmetry crystal system and space group would be expected with Z' = 1. However, the two molecules in the asymmetric unit have different hydrogen bonding interactions and show distinct fingerprint plots, which will be discussed further below. Nonetheless, in C9, the monolayer is again defined by the ac-plane, with a difference arising in the alignment along one of the axis directions. Adjacent molecules pack head-to-head (parallel, identical to the even-membered ones) along the a-axis, and alternatingly head-to-head (parallel, identical to the even-membered ones) and tail-to-tail (parallel; anti-parallel in the even-membered) along the c-axis (Fig. 5d–f). This no longer results in an overall herringbone arrangement as seen in the even-membered C8,10,12 but more akin to the lamellar arrangement seen for C6 (Fig. 3b). The hydrogen bonding between the head groups of mol1 and mol2 aligned along the c-axis consists of C(20)–H(20A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds. However, and this is the reason for the non-equivalence of mol1 and mol2, mol2 has a C(12)–H(12B)⋯O(4)
C hydrogen bonds. However, and this is the reason for the non-equivalence of mol1 and mol2, mol2 has a C(12)–H(12B)⋯O(4)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond using the carbonyl C
C hydrogen bond using the carbonyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O acceptor. In mol1, no such hydrogen bond is formed. Cohesion between layers is afforded by a weak C(2)–H(2B)⋯O(4)
O acceptor. In mol1, no such hydrogen bond is formed. Cohesion between layers is afforded by a weak C(2)–H(2B)⋯O(4)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond, as well as short C
C hydrogen bond, as well as short C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contacts and dispersive interaction between the alkyl chains (Fig. 7b). As was the case in the even C8,10,12, the molecules in adjacent layers are tilted relative to each other in the b-direction, with the angles between the relevant molecular planes larger than those observed for C8,10,12 and increasing down the series (Table 4). The methyl groups at the tail ends of the molecules, within layers, form a serrated interface between adjacent layer stacks, showing partial interdigitation of the chain ends of the molecules at the layer interface. In this case, the tail-ends of adjacent layers are arranged in a lamellar fashion (Fig. 4), with the distances between the terminal methyl groups slightly shorter than those of the even-membered members but also decreasing slightly from C9–13 (Table 4).
O contacts and dispersive interaction between the alkyl chains (Fig. 7b). As was the case in the even C8,10,12, the molecules in adjacent layers are tilted relative to each other in the b-direction, with the angles between the relevant molecular planes larger than those observed for C8,10,12 and increasing down the series (Table 4). The methyl groups at the tail ends of the molecules, within layers, form a serrated interface between adjacent layer stacks, showing partial interdigitation of the chain ends of the molecules at the layer interface. In this case, the tail-ends of adjacent layers are arranged in a lamellar fashion (Fig. 4), with the distances between the terminal methyl groups slightly shorter than those of the even-membered members but also decreasing slightly from C9–13 (Table 4).
Comparative structural commentary on C8–13
In compounds C8–13, when considering the unit cell lengths, the shortest axis at ca. 5.5 Å corresponds to the distance between laterally adjacent molecules within the respective layers. The b-axis unit cell lengths alternate between odd- and even-membered members of the series, with the even members displaying the shorter distances but increasing overall across the series from C8–13. This distance, at ca. 7.1 Å for C8,10,12 and at ca. 7.2 Å for C9,11,13, corresponds to double the distance between the defined layers. The observed oscillation in the b-axis unit cell length coincides with a decreased, alternating accordingly, relative contribution of the close O⋯H, C⋯O and O⋯O intermolecular contacts to the 2D fingerprint plots (Fig. 9), generated from the calculated Hirshfeld surface areas, with the O⋯O intermolecular contacts only present in the odd C9,11,13 members of the series (Table 6).25,26 The observed alternation in the b-axis unit cell length also reflects in the calculated AA-CLP coulombic energy (Ec) term which shows the same alternation when considering the total lattice energies calculated for each compound (the sequence from C8–13 is as follows: Ec = −8.5, −8.1, −8.3, −8.0, −8.3 and −8.8 kJ mol−1). This may result from the tilt angle between the molecular planes, with concomitant positioning of the ester functionalities and resulting weak hydrogen bonding interactions along this direction. This exact yet opposite trend was observed by Boese et al.23 upon considering a homologous series of short-chain n-alkanes and was attributed as a compensating consequence of the pronounced differences observed in the long axes. In the case of our FAMEs, the long axes increase overall across the series but alternate between the odd- and even-membered members of the series. This trend has also been rationalised by Bond36 upon his investigation of a homologous series of n-alkyl carboxylic acids. In the case of our FAMEs, however, the exact opposite is observed in that doubling of the long axes is observed in the even-membered members of the series, from C8–13. This may be due to the herringbone packing arrangement adopted by the even-membered members compared to the lamellar arrangement adopted by odd members. As is common for most terminally substituted n-alkane derivatives,36 the n-alkyl methyl esters considered in this paper also present melting point alternations34 between the odd- and even-membered compounds comprising this series. This is depicted graphically in Fig. 8 for C8–13 showing the systematically lower melting point of the odd members C9,11,13 (see Table 6).
Table 6 The melting points and relative percentage contributions (out of 100%) to the 2D fingerprint plots generated from the calculated Hirshfeld surfaces for the close H⋯H, O⋯H, C⋯H, C⋯O and O⋯O intermolecular contacts in C5–13
| FAMEa |
m.p.b (°C) |
H⋯H (%) |
H⋯O (%) |
C⋯H (%) |
C⋯O (%) |
O⋯O (%) |
|
For compounds with Z' = 2, the values were calculated for each molecule (mol1/mol2 respectively) in the asymmetric unit.
Ref. 43.
|
| C5 |
−90.7 |
71.5 |
25.4 |
3.1 |
0.0 |
0.0 |
| C6 |
−69.6 |
77.1 |
19.9 |
0.6 |
1.0 |
1.3 |
| C7 |
−55.8 |
77.2 |
20.2 |
2.5 |
0.0 |
0.2 |
| C8 |
−36.7 |
79.9 |
18.1 |
1.3 |
0.7 |
0.0 |
| C9 |
−34.4 |
83.4/80.9 |
14.0/16.5 |
1.0/1.0 |
0.9/0.9 |
0.7/0.8 |
| C10 |
−12.8 |
82.9 |
15.4 |
1.1 |
0.6 |
0.0 |
| C11 |
−11.4 |
85.7/83.3 |
12.0/14.4 |
0.9/0.9 |
0.8/0.8 |
0.6/0.7 |
| C12 |
4.9 |
85.1 |
13.4 |
0.9 |
0.6 |
0.0 |
| C13 |
5.9 |
87.4/85.4 |
10.6/12.6 |
0.7/0.7 |
0.7/0.7 |
0.6/0.6 |
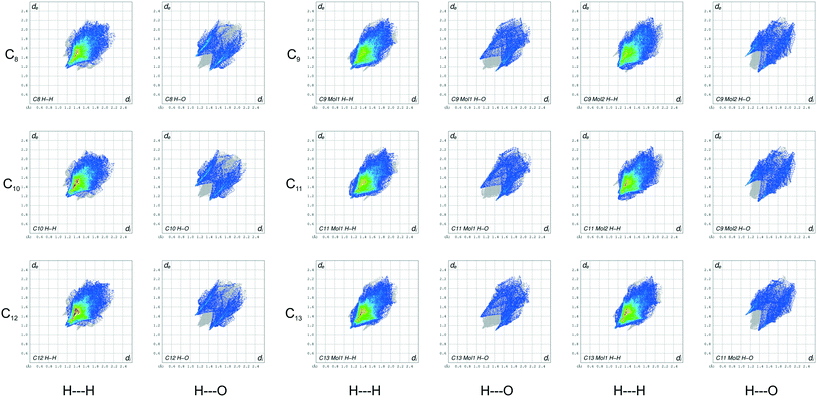 |
| | Fig. 8 Fingerprint plots for the even- (left) and odd-membered (right) FAMEs, resolved into H⋯H and H⋯O contacts, with the full fingerprint plot displayed as a grey shadow beneath each decomposed plot. Note the difference between mol1 and mol2 for the odd-membered C9,11,13 plots. | |
Hirshfeld and fingerprint plot analysis for C8–13
The 2D fingerprint plots (Fig. 9) generated from the calculated Hirshfeld surfaces give a visual depiction of the intermolecular interactions with concomitant trends, reaffirming the value of the Hirshfeld surface as a valuable tool for the speedy comparison and analysis of molecular structures.25,26 In Fig. 8, these plots are arranged into two main columns, which separates the even-numbered (left) and odd-membered (right) C8–13 FAME series. Each main column is further resolved to highlight the O⋯H and H⋯H contacts for each compound (includes reciprocal contacts). Immediately evident from these plots is the soft pointy shape of the decomposed O⋯H plots. In these O⋯H fingerprint plots, the spikes correspond to weak CH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond interactions in C8,10,12 and CH3⋯O
C hydrogen bond interactions in C8,10,12 and CH3⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and CH2⋯O
C and CH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions in C9,11,13. The top left spikes, where di < de, correspond to surface points around the –CH2/–CH3 donor surfaces, while the bottom right counter spikes (de < di) resemble the surface around the O
C interactions in C9,11,13. The top left spikes, where di < de, correspond to surface points around the –CH2/–CH3 donor surfaces, while the bottom right counter spikes (de < di) resemble the surface around the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C acceptor surfaces. The O⋯H plots of the even-membered all show additional secondary wings which portray long distance CH2⋯O
C acceptor surfaces. The O⋯H plots of the even-membered all show additional secondary wings which portray long distance CH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions, which are absent in the odd members due to the different orientation of the carbonyl groups relative to each other between molecules in the b-direction as well the lateral slippage present between odd-numbered molecules in the same direction. The analogous O⋯H plots of C9,11,13 show a substantial number of points at large de and di, which are absent in the plots of their even-numbered counterparts, and depict long range CH3⋯O–CH3 interactions caused by the lateral slippage mentioned above. The light blue stripes accentuating the O⋯H wings in the plots of the even members show that a larger fraction of points on the calculated Hirshfeld surfaces of the C8,10,12 FAMEs include O⋯H interactions as compared to the duller colour observed in the odd-numbered plots. The intensity of the light blue highlights decreases from C8 to C13, mirroring the decreasing contribution of the AA-CLP coulombic energies Ec to the total calculated lattice energies and in which the Ec contribution is systematically smaller for the odd members, as described above.
C interactions, which are absent in the odd members due to the different orientation of the carbonyl groups relative to each other between molecules in the b-direction as well the lateral slippage present between odd-numbered molecules in the same direction. The analogous O⋯H plots of C9,11,13 show a substantial number of points at large de and di, which are absent in the plots of their even-numbered counterparts, and depict long range CH3⋯O–CH3 interactions caused by the lateral slippage mentioned above. The light blue stripes accentuating the O⋯H wings in the plots of the even members show that a larger fraction of points on the calculated Hirshfeld surfaces of the C8,10,12 FAMEs include O⋯H interactions as compared to the duller colour observed in the odd-numbered plots. The intensity of the light blue highlights decreases from C8 to C13, mirroring the decreasing contribution of the AA-CLP coulombic energies Ec to the total calculated lattice energies and in which the Ec contribution is systematically smaller for the odd members, as described above.
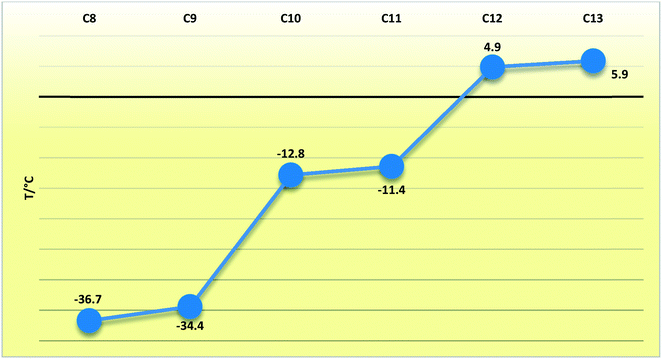 |
| | Fig. 9 Line chart depicting the melting points (T/°C) of the C8–13 FAMEs. | |
The decomposed plots depicting the reciprocal H⋯H interaction of the C8–13 FAMEs resemble the 2D fingerprint plots of the n-alkanes reported by Spackman and McKinnon.25 The red highlighted area present in the H⋯H plots of C8,10,12 indicates that a large fraction of points on the Hirshfeld surfaces involve closely aligned H⋯H contacts between the n-alkyl chains as well as at the two methyl group interfaces at the tail part of the molecules. The said dab is lighter in the plots of C9,11,13 although the colour intensifies with the increase in hydrocarbon chain length. The red dab grows in size down the series, indicating the increase in length of the alkyl chain and the concomitant increase in dispersive interactions (Ed = −91.8; −104.1, −128.8 for C8,10,12; Ed = −95.4; −109.9; and 138.2 kJ mol−1 C9,11,13).
Conclusions
The crystal structures of a continuous range of FAMEs (C4H9CO2CH3–C12H25CO2CH3) were elucidated from SCXRD data. The single crystals of these compounds, which are liquid at room temperature, were successfully grown via in situ cryocrystallisation in combination with a zone-melting technique. The early members of the series, C5–7, crystallised in monoclinic space groups, while the structures of C8–C13 arranged themselves into two isostructural groups: the odd-membered triclinic (C9,11,13) and the even-membered orthorhombic (C8,10,12). In the C5–C7n-alkyl ester triad, the molecules comprising structures C5 and C6 are woven together via weak O–CH3⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds in a head-to-head herringbone-(C5) or lamellar (C6) type arrangement. C7 shows molecules that pack in a head-to-tail herringbone-type packing arrangement. All show a parallelogram lateral packing mode (Fig. 5). In the orthorhombic members of the series (C8,10,12), when viewed within the monolayer parallel to the ac-plane, the molecules arrange into layers, braided together at the head group ends via weak hydrogen O–(CH3)⋯O–(CH3) bonds in a linear head-to-head fashion. The distance between aligned head methyl groups increases slightly from C8 to C13. The angle formed between flanking terminal carbon atoms results in a herringbone packing arrangement at this interface, while the lateral packing mode is rectangular. In the odd-membered triclinic counterparts, when viewed within layers, the molecules arrange in a head-to-head lamellar fashion via weak O–(CH3)⋯O
C hydrogen bonds in a head-to-head herringbone-(C5) or lamellar (C6) type arrangement. C7 shows molecules that pack in a head-to-tail herringbone-type packing arrangement. All show a parallelogram lateral packing mode (Fig. 5). In the orthorhombic members of the series (C8,10,12), when viewed within the monolayer parallel to the ac-plane, the molecules arrange into layers, braided together at the head group ends via weak hydrogen O–(CH3)⋯O–(CH3) bonds in a linear head-to-head fashion. The distance between aligned head methyl groups increases slightly from C8 to C13. The angle formed between flanking terminal carbon atoms results in a herringbone packing arrangement at this interface, while the lateral packing mode is rectangular. In the odd-membered triclinic counterparts, when viewed within layers, the molecules arrange in a head-to-head lamellar fashion via weak O–(CH3)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds. The tail-ends of adjacent molecules also arrange in a lamellar fashion in this triad. All observed structural trends, including the odd–even effect observable in the oscillating nature of the melting points and unit cell parameters along the series, are easily visualized and described by 2D fingerprint plots, generated from the calculated Hirshfeld surfaces, in combination with AA-CLP lattice energy calculations, performed using the CLP program package.
C hydrogen bonds. The tail-ends of adjacent molecules also arrange in a lamellar fashion in this triad. All observed structural trends, including the odd–even effect observable in the oscillating nature of the melting points and unit cell parameters along the series, are easily visualized and described by 2D fingerprint plots, generated from the calculated Hirshfeld surfaces, in combination with AA-CLP lattice energy calculations, performed using the CLP program package.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors wish to acknowledge the Claude Leon Foundation and NRF Green Economy Fund (Grant UID: 98053) for financial assistance. They would also like to acknowledge the NRF (Grant UID: 78572) for the purchase of the D8 VENTURE and OHCD device. This article is dedicated to Professor Roland Boese for his development of in situ cryocrystallography.
References
- D. Y. C. Leung, X. Wu and M. K. H. Leung, Appl. Energy, 2010, 87, 1083 CrossRef CAS.
- F. Ma and M. A. Hanna, Bioresour. Technol., 1999, 70, 1 CrossRef CAS.
- G. Knothe, Energy Fuels, 2008, 1358 CrossRef CAS.
- G. Knothe, Fuel Process. Technol., 2005, 86, 1059 CrossRef CAS.
- N. M. Ribeiro, A. C. Pinto, C. M. Quintella, G. O. da Rocha, L. S. G. Teixeira, L. L. N. Guarieiro, M. do Carmo Rangel, M. C. C. Veloso, M. J. C. Rezende, R. Serpa da Cruz, A. M. de Oliveira, E. A. Torres and J. B. de Andrade, Energy Fuels, 2007, 21, 2433 CrossRef CAS.
- P. C. Smith, Y. Ngothai, Q. Dzuy Nguyen and B. K. O'Neill, Renewable Energy, 2010, 35, 1145–1151 CrossRef CAS.
- R. D. Misra and M. S. Murthy, Renewable Sustainable Energy Rev., 2011, 15, 2413 CrossRef CAS.
- M. De Torres, G. Jiménez-Osés, J. A. Mayoral and E. Pires, Bioresour. Technol., 2011, 102, 2590 CrossRef CAS PubMed.
- H. Joshi, B. R. Moser, J. Toler, W. F. Smith and T. Walker, Biomass Bioenergy, 2011, 35, 3262 CrossRef CAS.
- A. Robles-Medina, P. A. González-Moreno, L. Esteban-Cerdán and E. Molina-Grima, Biotechnol. Adv., 2009, 27, 398–408 CrossRef CAS PubMed.
- Á. Pérez, A. Casas, C. M. Fernández, M. J. Ramos and L. Rodríguez, Bioresour. Technol., 2010, 101, 7375–7381 CrossRef PubMed.
- I. Lee, L. A. Johnson and E. G. Hammond, J. Am. Oil Chem. Soc., 1996, 73, 631–636 CrossRef CAS.
- K. C. Lin, H. Tao, F. H. Kao and C. Te Chiu, Energy Fuels, 2016, 30, 1354–1363 CAS.
- S. Som and D. E. Longman, Combustion, 2011, 1–18 Search PubMed.
- Y. Chang, M. Jia, Y. Li, M. Xie, H. Yin, H. Wang and R. D. Reitz, Energy Fuels, 2015, 29, 1076–1089 CrossRef CAS.
- S. Gail, M. J. Thomson, S. M. Sarathy, S. A. Syed, P. Dagaut, P. Diévart, A. J. Marchese and F. L. Dryer, Proc. Combust. Inst., 2007, 31, 305–311 CrossRef.
- Y. Jiao, F. Zhang and T. S. Dibble, J. Phys. Chem. A, 2015, 119, 7282 CrossRef CAS PubMed.
- W. K. Metcalfe, S. Dooley, H. J. Curran, J. M. Simmie and M. V. Navarro, Society, 2007, 111, 4001–4014 CAS.
- I. Weissbuch, R. Popovitz-Biro, M. Lahav and L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 115 CrossRef.
- A. D. Bond, Chem. Commun., 2003, 250–251 RSC.
- A. R. Choudhury, N. Winterton, A. Steiner, A. I. Cooper and K. A. Johnson, CrystEngComm, 2006, 8, 742 RSC.
- V. R. Thalladi, H.-C. Weiss, D. Blasser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702 CrossRef CAS.
- R. Boese, H.-C. Weiss and D. Blaser, Angew. Chem., Int. Ed., 1999, 38, 988 CrossRef CAS PubMed.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378 RSC.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC.
- A. Gavezzotti, New J. Chem., 2011, 35, 1360–1368 RSC.
- A. Gavezzotti, Z. Kristallogr., 2005, 220, 499–510 CAS.
- E. Fischer and A. Speier, Ber. Dtsch. Chem. Ges., 1895, 28, 3252–3258 CrossRef CAS.
-
Bruker, SAINT+, 2012, BIS (version 6.2.4/2016-09-30), Bruker, Bru, 2012 Search PubMed.
-
G. M. Sheldrick, SADABS, University of Göttingen, Germany, 1996 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849 CrossRef CAS.
-
K. Wolff, D. J. Grimwood, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystalExplorer-3.1, University of Western Australia, Perth, 2007 Search PubMed.
- A. D. Bond, New J. Chem., 2004, 28, 104–114 RSC.
- I. Pascher, M. Lundmark, P.-G. Nyholm and S. Sundell, Biochim. Biophys. Acta, 1992, 1113, 339–373 CrossRef CAS.
- D. M. Small, J. Lipid Res., 1984, 25, 1490–1500 CAS.
- C. W. Bunn, Trans. Faraday Soc., 1939, 35, 482–491 RSC.
-
A. I. Kitaigorodskii, in Molecular Crystals and Molecules, Academic Press, New York, 1973, p. 48ff Search PubMed.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453 CrossRef CAS.
- A. Gavezzotti, Mol. Phys., 2008, 206, 1473–1484 CrossRef.
- N. Adriaanse, H. Dekker and J. Coops, Recl. Trav. Chim. Pays-Bas, 1964, 83, 557 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Labelled Ortep diagrams, packing diagrams, OHCD parameters and DSC scans. CCDC 1590402–1590410. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8ce01673a |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab,
Manuel A.
Fernandes
*ab,
Manuel A.
Fernandes
 a and
Andreas
Lemmerer
a and
Andreas
Lemmerer
 *a
*a

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225/1431
225/1431![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012/1601
012/1601![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160/1824
160/1824![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894/3713
894/3713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 016/2150
016/2150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 693/4662
693/4662![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984/2419
984/2419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217/5641
217/5641![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and methyl C(6) within this monolayer (Fig. 4a and Table 3). Adjacent monolayers are stabilised by two symmetry equivalent C(2)–H(2A)⋯O(1)–C hydrogen bonds forming an R22(8) hydrogen bonded ring (Fig. 4a). In contrast, in C6, the molecules within monolayers defined by the ac-plane pack head-to-tail (parallel) in both the a-axis and c-axis (Fig. 3b). Adjacent molecules in this monolayer interact via two C(4)–H(4A)⋯O(2)
C and methyl C(6) within this monolayer (Fig. 4a and Table 3). Adjacent monolayers are stabilised by two symmetry equivalent C(2)–H(2A)⋯O(1)–C hydrogen bonds forming an R22(8) hydrogen bonded ring (Fig. 4a). In contrast, in C6, the molecules within monolayers defined by the ac-plane pack head-to-tail (parallel) in both the a-axis and c-axis (Fig. 3b). Adjacent molecules in this monolayer interact via two C(4)–H(4A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C(2)–H(2B)⋯O(2)
C and C(2)–H(2B)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds forming an R12(6) ring and a short contact exists between the methyl groups, C(7), of the head section (Fig. 4b and Table 3). This forms a lamellar arrangement. C7, being odd-membered, shows the same chevron arrangement as C5 where adjacent molecules pack head-to-head (parallel) along the b-axis but head-to-tail (anti-parallel) along the (101) direction (Fig. 3c). Adjacent monolayers interact via C(8)–H(8A)⋯O(2)
C hydrogen bonds forming an R12(6) ring and a short contact exists between the methyl groups, C(7), of the head section (Fig. 4b and Table 3). This forms a lamellar arrangement. C7, being odd-membered, shows the same chevron arrangement as C5 where adjacent molecules pack head-to-head (parallel) along the b-axis but head-to-tail (anti-parallel) along the (101) direction (Fig. 3c). Adjacent monolayers interact via C(8)–H(8A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C(8)–H(8B)⋯O(2)
C and C(8)–H(8B)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds to form repeating R23(9) rings (Fig. 4c).
C hydrogen bonds to form repeating R23(9) rings (Fig. 4c).

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–H⋯O–C hydrogen bonds in C5–7 (a–c). Note the short contact of the head groups of C5 and C6. For detailed geometrical parameters see Tables 2 and 3.
C and C–H⋯O–C hydrogen bonds in C5–7 (a–c). Note the short contact of the head groups of C5 and C6. For detailed geometrical parameters see Tables 2 and 3.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds along the a-axis (Fig. 6a). Molecules in adjacent layers interact via a C(3)–H(3A)⋯O(2)
C hydrogen bonds along the a-axis (Fig. 6a). Molecules in adjacent layers interact via a C(3)–H(3A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds along the b-axis (Fig. 7a). The same description of the packing and hydrogen bonding for C10 and C12 holds as for C8 (shown in Fig. 5b and c).
C hydrogen bonds along the b-axis (Fig. 7a). The same description of the packing and hydrogen bonding for C10 and C12 holds as for C8 (shown in Fig. 5b and c).



![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonding and dispersive interactions responsible for cohesion between layers in the b-direction (Fig. 7a) also correspond to the largest contributory term Ed (e.g. C8: −91.8 kJ mol−1) of the total calculated lattice energies, Et (e.g. C8: −96.3 kJ mol−1), as calculated using the atom–atom approach of the CLP27,42 manifold as collated in Table 5. The terminal methyl groups at the tail ends of the chains line up between adjacent layers, to form a linear interface between adjacent layer stacks.
C hydrogen bonding and dispersive interactions responsible for cohesion between layers in the b-direction (Fig. 7a) also correspond to the largest contributory term Ed (e.g. C8: −91.8 kJ mol−1) of the total calculated lattice energies, Et (e.g. C8: −96.3 kJ mol−1), as calculated using the atom–atom approach of the CLP27,42 manifold as collated in Table 5. The terminal methyl groups at the tail ends of the chains line up between adjacent layers, to form a linear interface between adjacent layer stacks.![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z' = 2 and are isostructural. The two molecules in the asymmetric unit are labelled mol1 (ester groups O(1) & O(2)) and mol2 (ester groups O(3) & O(4)). By inspecting the cell angles, all being close to 90°, a higher symmetry crystal system and space group would be expected with Z' = 1. However, the two molecules in the asymmetric unit have different hydrogen bonding interactions and show distinct fingerprint plots, which will be discussed further below. Nonetheless, in C9, the monolayer is again defined by the ac-plane, with a difference arising in the alignment along one of the axis directions. Adjacent molecules pack head-to-head (parallel, identical to the even-membered ones) along the a-axis, and alternatingly head-to-head (parallel, identical to the even-membered ones) and tail-to-tail (parallel; anti-parallel in the even-membered) along the c-axis (Fig. 5d–f). This no longer results in an overall herringbone arrangement as seen in the even-membered C8,10,12 but more akin to the lamellar arrangement seen for C6 (Fig. 3b). The hydrogen bonding between the head groups of mol1 and mol2 aligned along the c-axis consists of C(20)–H(20A)⋯O(2)
with Z' = 2 and are isostructural. The two molecules in the asymmetric unit are labelled mol1 (ester groups O(1) & O(2)) and mol2 (ester groups O(3) & O(4)). By inspecting the cell angles, all being close to 90°, a higher symmetry crystal system and space group would be expected with Z' = 1. However, the two molecules in the asymmetric unit have different hydrogen bonding interactions and show distinct fingerprint plots, which will be discussed further below. Nonetheless, in C9, the monolayer is again defined by the ac-plane, with a difference arising in the alignment along one of the axis directions. Adjacent molecules pack head-to-head (parallel, identical to the even-membered ones) along the a-axis, and alternatingly head-to-head (parallel, identical to the even-membered ones) and tail-to-tail (parallel; anti-parallel in the even-membered) along the c-axis (Fig. 5d–f). This no longer results in an overall herringbone arrangement as seen in the even-membered C8,10,12 but more akin to the lamellar arrangement seen for C6 (Fig. 3b). The hydrogen bonding between the head groups of mol1 and mol2 aligned along the c-axis consists of C(20)–H(20A)⋯O(2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds. However, and this is the reason for the non-equivalence of mol1 and mol2, mol2 has a C(12)–H(12B)⋯O(4)
C hydrogen bonds. However, and this is the reason for the non-equivalence of mol1 and mol2, mol2 has a C(12)–H(12B)⋯O(4)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond using the carbonyl C
C hydrogen bond using the carbonyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O acceptor. In mol1, no such hydrogen bond is formed. Cohesion between layers is afforded by a weak C(2)–H(2B)⋯O(4)
O acceptor. In mol1, no such hydrogen bond is formed. Cohesion between layers is afforded by a weak C(2)–H(2B)⋯O(4)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond, as well as short C
C hydrogen bond, as well as short C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contacts and dispersive interaction between the alkyl chains (Fig. 7b). As was the case in the even C8,10,12, the molecules in adjacent layers are tilted relative to each other in the b-direction, with the angles between the relevant molecular planes larger than those observed for C8,10,12 and increasing down the series (Table 4). The methyl groups at the tail ends of the molecules, within layers, form a serrated interface between adjacent layer stacks, showing partial interdigitation of the chain ends of the molecules at the layer interface. In this case, the tail-ends of adjacent layers are arranged in a lamellar fashion (Fig. 4), with the distances between the terminal methyl groups slightly shorter than those of the even-membered members but also decreasing slightly from C9–13 (Table 4).
O contacts and dispersive interaction between the alkyl chains (Fig. 7b). As was the case in the even C8,10,12, the molecules in adjacent layers are tilted relative to each other in the b-direction, with the angles between the relevant molecular planes larger than those observed for C8,10,12 and increasing down the series (Table 4). The methyl groups at the tail ends of the molecules, within layers, form a serrated interface between adjacent layer stacks, showing partial interdigitation of the chain ends of the molecules at the layer interface. In this case, the tail-ends of adjacent layers are arranged in a lamellar fashion (Fig. 4), with the distances between the terminal methyl groups slightly shorter than those of the even-membered members but also decreasing slightly from C9–13 (Table 4).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond interactions in C8,10,12 and CH3⋯O
C hydrogen bond interactions in C8,10,12 and CH3⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and CH2⋯O
C and CH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions in C9,11,13. The top left spikes, where di < de, correspond to surface points around the –CH2/–CH3 donor surfaces, while the bottom right counter spikes (de < di) resemble the surface around the O
C interactions in C9,11,13. The top left spikes, where di < de, correspond to surface points around the –CH2/–CH3 donor surfaces, while the bottom right counter spikes (de < di) resemble the surface around the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C acceptor surfaces. The O⋯H plots of the even-membered all show additional secondary wings which portray long distance CH2⋯O
C acceptor surfaces. The O⋯H plots of the even-membered all show additional secondary wings which portray long distance CH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions, which are absent in the odd members due to the different orientation of the carbonyl groups relative to each other between molecules in the b-direction as well the lateral slippage present between odd-numbered molecules in the same direction. The analogous O⋯H plots of C9,11,13 show a substantial number of points at large de and di, which are absent in the plots of their even-numbered counterparts, and depict long range CH3⋯O–CH3 interactions caused by the lateral slippage mentioned above. The light blue stripes accentuating the O⋯H wings in the plots of the even members show that a larger fraction of points on the calculated Hirshfeld surfaces of the C8,10,12 FAMEs include O⋯H interactions as compared to the duller colour observed in the odd-numbered plots. The intensity of the light blue highlights decreases from C8 to C13, mirroring the decreasing contribution of the AA-CLP coulombic energies Ec to the total calculated lattice energies and in which the Ec contribution is systematically smaller for the odd members, as described above.
C interactions, which are absent in the odd members due to the different orientation of the carbonyl groups relative to each other between molecules in the b-direction as well the lateral slippage present between odd-numbered molecules in the same direction. The analogous O⋯H plots of C9,11,13 show a substantial number of points at large de and di, which are absent in the plots of their even-numbered counterparts, and depict long range CH3⋯O–CH3 interactions caused by the lateral slippage mentioned above. The light blue stripes accentuating the O⋯H wings in the plots of the even members show that a larger fraction of points on the calculated Hirshfeld surfaces of the C8,10,12 FAMEs include O⋯H interactions as compared to the duller colour observed in the odd-numbered plots. The intensity of the light blue highlights decreases from C8 to C13, mirroring the decreasing contribution of the AA-CLP coulombic energies Ec to the total calculated lattice energies and in which the Ec contribution is systematically smaller for the odd members, as described above.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds in a head-to-head herringbone-(C5) or lamellar (C6) type arrangement. C7 shows molecules that pack in a head-to-tail herringbone-type packing arrangement. All show a parallelogram lateral packing mode (Fig. 5). In the orthorhombic members of the series (C8,10,12), when viewed within the monolayer parallel to the ac-plane, the molecules arrange into layers, braided together at the head group ends via weak hydrogen O–(CH3)⋯O–(CH3) bonds in a linear head-to-head fashion. The distance between aligned head methyl groups increases slightly from C8 to C13. The angle formed between flanking terminal carbon atoms results in a herringbone packing arrangement at this interface, while the lateral packing mode is rectangular. In the odd-membered triclinic counterparts, when viewed within layers, the molecules arrange in a head-to-head lamellar fashion via weak O–(CH3)⋯O
C hydrogen bonds in a head-to-head herringbone-(C5) or lamellar (C6) type arrangement. C7 shows molecules that pack in a head-to-tail herringbone-type packing arrangement. All show a parallelogram lateral packing mode (Fig. 5). In the orthorhombic members of the series (C8,10,12), when viewed within the monolayer parallel to the ac-plane, the molecules arrange into layers, braided together at the head group ends via weak hydrogen O–(CH3)⋯O–(CH3) bonds in a linear head-to-head fashion. The distance between aligned head methyl groups increases slightly from C8 to C13. The angle formed between flanking terminal carbon atoms results in a herringbone packing arrangement at this interface, while the lateral packing mode is rectangular. In the odd-membered triclinic counterparts, when viewed within layers, the molecules arrange in a head-to-head lamellar fashion via weak O–(CH3)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds. The tail-ends of adjacent molecules also arrange in a lamellar fashion in this triad. All observed structural trends, including the odd–even effect observable in the oscillating nature of the melting points and unit cell parameters along the series, are easily visualized and described by 2D fingerprint plots, generated from the calculated Hirshfeld surfaces, in combination with AA-CLP lattice energy calculations, performed using the CLP program package.
C hydrogen bonds. The tail-ends of adjacent molecules also arrange in a lamellar fashion in this triad. All observed structural trends, including the odd–even effect observable in the oscillating nature of the melting points and unit cell parameters along the series, are easily visualized and described by 2D fingerprint plots, generated from the calculated Hirshfeld surfaces, in combination with AA-CLP lattice energy calculations, performed using the CLP program package.