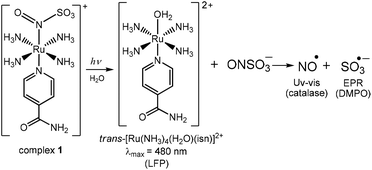
Light-activated generation of nitric oxide (NO) and sulfite anion radicals (SO3˙−) from a ruthenium(II) nitrosylsulphito complex†‡
Antonio C.
Roveda
Jr.
 *a,
Willy G.
Santos
a,
Maykon L.
Souza
a,
Charles N.
Adelson
b,
Felipe S.
Gonçalves
*a,
Willy G.
Santos
a,
Maykon L.
Souza
a,
Charles N.
Adelson
b,
Felipe S.
Gonçalves
 a,
Eduardo E.
Castellano
c,
Claudio
Garino
a,
Eduardo E.
Castellano
c,
Claudio
Garino
 d,
Douglas W.
Franco
a and
Daniel R.
Cardoso
d,
Douglas W.
Franco
a and
Daniel R.
Cardoso
 *a
*a
aSão Carlos Institute of Chemistry, University of São Paulo, CEP 13560-970, São Carlos, SP, Brazil. E-mail: acroveda@usp.br; drcardoso@usp.br
bDept. of Chemistry, Stanford University, CA, USA
cSão Carlos Institute of Physics, University of São Paulo, São Carlos, SP, Brazil
dDept. of Chemistry and NIS Interdepartmental Centre, University of Turin, Italy
First published on 25th June 2019
Abstract
This manuscript describes the preparation of a new Ru(II) nitrosylsulphito complex, trans-[Ru(NH3)4(isn)(N(O)SO3)]+ (complex 1), its spectroscopic and structural characterization, photochemistry, and thermal reactivity. Complex 1 was obtained by the reaction of sulfite ions (SO32−) with the nitrosyl complex trans-[Ru(NH3)4(isn)(NO)]3+ (complex 2) in aqueous solution resulting in the formation of the N-bonded nitrosylsulphito (N(O)SO3) ligand. To the best of our knowledge, only four nitrosylsulphito metal complexes have been described so far (J. Chem. Soc., Dalton Trans., 1983, 2465–2472), and there is no information about the photochemistry of such complexes. Complex 1 was characterized by spectroscopic means (UV-Vis, EPR, FT-IR, 1H- and 15N-NMR), elemental analysis and single-crystal X-ray diffraction. The X-ray structure of the precursor complex 2 is also discussed in the manuscript and is used as a reference for comparisons with the structure of 1. Complex 1 is water-soluble and kinetically stable at pH 7.4, with a first-order rate constant of 3.1 × 10−5 s−1 for isn labilization at 298 K (t1/2 ∼ 373 min). Under acidic conditions (1.0 M trifluoroacetic acid), 1 is stoichiometrically converted into the precursor complex 2. The reaction of hydroxide ions (OH−) with 1 and with 2 yields the Ru(II) nitro complex trans-[Ru(NH3)4(isn)(NO2)]+ with second-order rate constants of 2.1 and 10.5 M−1 s−1 (at 288 K), respectively, showing the nucleophilic attack of OH− at the nitrosyl in 2 (Ru–NO) and at the nitrosylsulphito in 1 (Ru–N(O)SO3). The pKa value of the –SO3 moiety of the N(O)SO3 ligand in 1 was determined to be 5.08 ± 0.06 (at 298 K). The unprecedented photochemistry of a nitrosylsulphito complex is investigated in detail with 1. The proposed mechanism is based on experimental (UV-Vis, EPR, NMR and Transient Absorption Laser Flash Photolysis) and theoretical data (DFT) and involves photorelease of the N(O)SO3− ligand followed by formation of nitric oxide (NO˙) and sulfite radicals (SO3˙−, sulfur trioxide anion radical).
Introduction
Although the sulfite ion (SO32−) is potentially toxic to living cells, this species is widely applied as an antioxidant and preservative in food and beverages,2 and its chemistry has received increasing attention in the last few years.2b,3 The SO32− anion influences the metabolism of thiocyanate (SCN−) and nitrite (NO2−) in the human saliva and stomach,2a and has been associated with several physiological conditions, such as the enhancement and suppression of nitrite-dependent NO˙ production in the stomach,2a skin and respiratory tract health, and anaphylactic reactions.2b SO32− is metabolized by the enzyme sulfite oxidase,3c,4 for which deficiency may be lethal to humans. Most of the SO32− toxicity is related to the production of SOX anion radicals, formed through chain propagation steps (eqn (1)–(4)):3d,5| SO32− → SO3˙− + e− | (1) |
| SO3˙− + O2 → −O3SOO˙\quadk = 1.5 × 109 M−1 s−1 | (2) |
| −O3SOO˙ + SO32– → SO4˙− + SO42−\quadk = 1.3 × 107 M−1 s−1 | (3) |
| SO4˙− + SO32− → SO42− + SO3˙−\quadk > 2 × 109 M−1 s−1 | (4) |
Oxidation of SO32− yields the sulfite anion radical (SO3˙−), eqn (1), which in the presence of O2 reacts to form the oxygen-centered radicals, peroxymonosulfate radical anion (SO5˙−) and sulfate radical anion (SO4˙−), eqn (2)–(4). Recent studies showed that SO3˙− could be produced through oxidation of SO32− by prostaglandin H synthase, myeloperoxidase, human eosinophil peroxidase and cytochrome c.3b–f SO3˙− and SO5˙− are mild oxidants (E° = 0.63 V and 1.1 V vs. NHE at pH 7, respectively),5b,6 but are precursors of the sulfate radical anion (SO4˙−) (eqn (1)–(4)), a strong oxidant (E° = 2.5–3.1 V vs. NHE)5b,7 comparable to the hydroxyl radical.8 Due to its oxidizing strength, SO4˙− has been widely studied and recently applied in advanced oxidation process technologies,9 DNA damage10 and organic synthesis.11
Analogously to SO32−, the NO2− ion is also used as an antioxidant and preservative in food and beverages,2a and the reaction between these ions is argued to produce the somewhat elusive nitrososulfonate ion (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–SO3−, described from herein as N(O)SO3−) in the human stomach.2a N(O)SO3− is considered an intermediate of several nitrogen reactive species,2a,12 such as nitric oxide (NO˙), hydroxyimidogen (NOH) and hyponitrous acid (H2N2O2). Furthermore, the N(O)SO3− ion has also been proposed as an intermediate in the Raschig synthesis of hydroxylamine.1,12,13 Nevertheless, little is known about the chemistry and physical properties of N(O)SO3−. The only compounds isolated and characterized are the N-bonded derivative species generated by the Boedeker Reaction, i.e. the nitrosylsulphito complexes [Fe(CN)5N(O)SO3]4−,13,14 [RuCl(py)4N(O)SO3] (py = pyridine) and cis-[RuX(bipy)2N(O)SO3] (X = Cl− or Br−, bipy = 2,2′-bipyridine),1 of which, only the structure of cis-[RuCl(bipy)2N(O)SO3] has been crystallographically characterized.1 The reactivity of these complexes has not yet been fully studied mainly owing to their insolubility and instability.1 Moreover, the photochemistry of the N(O)SO3− ion and the related nitrosylsulphito complexes has never been described.
N–SO3−, described from herein as N(O)SO3−) in the human stomach.2a N(O)SO3− is considered an intermediate of several nitrogen reactive species,2a,12 such as nitric oxide (NO˙), hydroxyimidogen (NOH) and hyponitrous acid (H2N2O2). Furthermore, the N(O)SO3− ion has also been proposed as an intermediate in the Raschig synthesis of hydroxylamine.1,12,13 Nevertheless, little is known about the chemistry and physical properties of N(O)SO3−. The only compounds isolated and characterized are the N-bonded derivative species generated by the Boedeker Reaction, i.e. the nitrosylsulphito complexes [Fe(CN)5N(O)SO3]4−,13,14 [RuCl(py)4N(O)SO3] (py = pyridine) and cis-[RuX(bipy)2N(O)SO3] (X = Cl− or Br−, bipy = 2,2′-bipyridine),1 of which, only the structure of cis-[RuCl(bipy)2N(O)SO3] has been crystallographically characterized.1 The reactivity of these complexes has not yet been fully studied mainly owing to their insolubility and instability.1 Moreover, the photochemistry of the N(O)SO3− ion and the related nitrosylsulphito complexes has never been described.
Herein we describe the reactivity of N(O)SO3− coordinated to a Ru(II) complex, trans-[Ru(NH3)4(isn)(N(O)SO3)]+ (complex 1, isn = isonicotinamide), Fig. 1. This complex was synthesized by the reaction of the Ru(II) nitrosyl complex trans-[Ru(NH3)4(isn)(NO)]3+ (complex 2 in Fig. 1) with SO32−, eqn (5):
| trans-[Ru(NH3)4(isn)(NO)]3+ + SO32− → trans-[Ru(NH3)4(isn)(N(O)SO3)]+ | (5) |
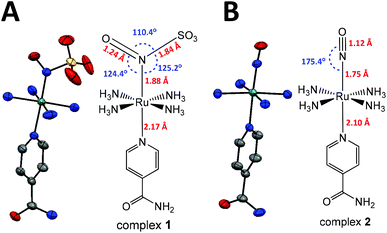 | ||
| Fig. 1 X-ray and molecular structures of complexes (A) 1 and (B) 2. The numbers in red show the bond lengths, and in blue, the angles. Ellipsoids at 50% probability; H omitted for clarity. | ||
The family of trans-[Ru(NH3)4(L)(NO)]3+ complexes is well known to be kinetically stable and water-soluble,15 supporting the choice of this type of nitrosyl as the synthetic precursor of complex 1. As expected, 1 is water-soluble and kinetically stable at pH 7.4 (at 298 K), and the N(O)SO3− ion is stabilized upon coordination to Ru(II), making studying its reactivity possible. The solubility and stability of 1 in water are higher than those of all four previously reported complexes [L5M–N(O)SO3]n (M = Fe, Ru). Our investigations on 1 also contribute to a current interesting topic in the chemistry of nitrosyl complexes and sulfur nucleophiles,16 and of S,N,O species.16c,17 Moreover, the light-triggered generation of the relevant radicals (NO˙ and SO3˙−) from 1 may find utility in many important redox and photochemical based applications.18
Results and discussion
X-ray crystallography and Infrared spectroscopy
The reaction of the nitrosyl complex trans-[Ru(NH3)4(isn)(NO)]3+ (2) with SO32− (eqn (5)) yields the new nitrosylsulphito ion complex trans-[Ru(NH3)4(isn)(N(O)SO3)]+ (1), Fig. 1, a green solid. This reaction occurs through the nucleophilic addition of the sulfite ion to the nitrogen atom of the nitrosyl moiety (Ru–NO) of complex 2. Complex 1 was characterized by elemental analysis and by several spectroscopies, and the experimental data correlated well with the DFT calculations (see the ESI‡).The crystal structures of 1 and of its synthetic precursor (2) are shown in Fig. 1. Table 1 shows the main bond lengths and angles for 1, 2 and for a previously described nitrosylsulphito complex, cis-[RuCl(bipy)2N(O)SO3] (3).1
| Ru complex | |||
|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
|
| a This work. b Ref. 1. c Average of the four Ru-NH3 bonds. | |||
| Distances (Å) | |||
Ru–![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) ( (![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (O)SO3 or (O)SO3 or ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O) O) |
1.877(3) | 1.750(3) | 1.904(14) |
| N–O | 1.244(5) | 1.119(4) | 1.208(17) |
| N–S | 1.844(4) | — | 1.820(15) |
| Ru–Nisn | 2.167(3) | 2.099(3) | — |
| Ru–NH3c | 2.12 | 2.10 | — |
| Angles (°) | |||
| Ru–N–O | 124.4(4) | 175.4(3) | 123.8(12) |
| Ru–N–S | 125.2(19) | — | 127.9(7) |
| O–N–S | 110.4(3) | — | 108.0(11) |
Nisn–Ru–![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) ( (![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (O)SO3 or (O)SO3 or ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O) O) |
178.32(14) | 177.39(12) | — |
In both complexes 1 and 2 (Fig. 1), the aromatic moiety of the isn ligand is perpendicular to the plane formed by the four nitrogens of the equatorial ammines (NH3) and bisects two opposite N–Ru–N angles of NH3. The Nisn–Ru–NN(O)SO3 bond angle in 1 is almost linear and very close to that observed for the Nisn–Ru–NNO bond angle in 2 (Table 1). Complexes 1 and 2 have slightly different Ru–NH3 bond distances (Table 1). The Ru–N(O)SO3 bond length in 1 is ∼0.24 Å shorter than the average of the four Ru–NH3 distances (Table 1), showing an increase in the bond order in Ru–N(O)SO3 relative to Ru–NH3 due to π interactions in the former. A similar behavior is observed for complex 2. However, the Ru–NO bond length in 2 is ∼0.13 Å shorter than the Ru–N(O)SO3 bond length in 1 (Fig. 1 and Table 1). This indicates a stronger back-bonding of the NO ligand in 2 than that of the N(O)SO3 ligand in 1. This result is consistent with the Ru–N–O angle, which is close to linear in 2 (175.4°) and is 124.4° in 1 (Fig. 1). The linear angle of Ru–N–O provides a greater overlap of the Ru dπ orbital with the π* orbital of NO19 in 2, and consequently, a stronger Ru–NO bond in 2 than the Ru–N(O)SO3 bond in 1.
The longer Ru–Nisn bond length in 1 than in 2 (Fig. 1 and Table 1) shows a stronger trans-influence of the N(O)SO3 ligand than that of the NO ligand, regarding isn in the trans position. Furthermore, the S–N bond length of ∼1.84 Å for the N(O)SO3 ligand in 1 is ca. 10% longer than that of other S–N compounds, e.g. nitrosopersulfide (SSNO−) and thionitrite (SNO−), 1.689 Å and 1.707 Å, respectively.16c It is also longer than S-nitrosothiols coordinated to transition metal complexes.16g,h
The Ru–N–O and Ru–N–S angles in 1 (124.4° and 125.2°, respectively) are slightly different from those reported for a closely related complex, trans-[Ru(NH4)P(OEt)3(NO2)](PF6), in which the Ru–N–O angle is 120.9° for one of the oxygen atoms of the NO2 ligand, and 121.4° for the other.20 The Ru–N–O, Ru–N–S and O–N–S angles in 1 are close to those reported for S-nitrosothiols coordinated to transition metal complexes.16g,h For the N(O)SO3 ligand in 1, the S–O bond lengths are shorter than those in sodium sulfite (Na2SO3), ∼1.40 Å and 1.53 Å, respectively. However, the O–S–O angles are larger in 1 than those in Na2SO3, 112–117° and 107.4°, respectively.21
The bond lengths and angles for the [RuN(O)SO3] moiety of complex 1 are very similar to those reported for cis-[RuCl(bipy)2(N(O)SO3)] (complex 3),1 with differences lower than 0.04 Å and 3° for the bond lengths and angles, respectively, Table 1. Therefore, despite considerable differences in the coordination spheres of 1 and 3, there were no significant discrepancies among the bond angles and bond distances of the [Ru–N(O)SO3] fragments in these complexes.
The FT-IR spectra of 1 and 2 are shown in Fig. S1 (ESI‡) and the main IR frequencies of the complexes 1, 2, [Fe(CN)5N(O)SO3]4–, [RuCl(py)4N(O)SO3] and cis-[RuX(bipy)2N(O)SO3] (X = Cl− or Br−)13,14 are shown in Table 2. The ν(NO) observed for 2 at 1933 cm−1 was shifted to 1366 cm−1 on 1 (Table 2, and Fig. S1 ESI‡). This shift is consistent with the weakening of the N–O bond in 1 (1.24 Å) in comparison with 2 (1.12 Å) (Fig. 1 and Table 1). All the IR bands observed for the nitrosylsulphito complexes showed similar frequencies for the N(O)SO3 moiety, with differences lower than 30 cm−1 (Table 2). These data revealed that the vibrational frequencies of the N(O)SO3 moiety were not strongly affected by modifications in the coordination sphere of the complexes, in agreement with the X-ray results as discussed above for 1 and 3.
| Complex | Assignmenta | |||||
|---|---|---|---|---|---|---|
| ν(N–O) | ν asym (S–O) | ν sym (S–O) | ν sim (S–O) | δ asym (O–N–S) | δ asym (O–S–O) | |
| a Ref. 1. b This work; s = strong; m = medium; w = weak; sh = shoulder. | ||||||
| trans-[Ru(NH3)4(isn)(N(O)SO3)]+ (1)b | 1366s | 1263sh | 1225s | 1040s | 778m | 623s |
| trans-[Ru(NH3)4(isn)(NO)]3+ (2)b | 1933s | — | — | — | — | — |
| cis-[RuCl(bipy)2(N(O)SO3)] (3)a | 1370s | 1267sh | 1250s | 1038s | 775 | 612 |
| cis-[RuBr(bipy)2(N(O)SO3)]a | 1372s | 1270sh | 1255s | 1040s | 775 | 605s |
| trans-[RuCl(py)4(N(O)SO3)]a | 1346s | 1273sh | 1258s | 1031s | 770 | 604 |
| Cs4[Fe(CN)5(N(O)SO3)]a | 1357s | 1252s | 1229s | 1041s | 758w | 621s |
Electronic structure, 1H- and 15N-NMR, and EPR spectroscopy
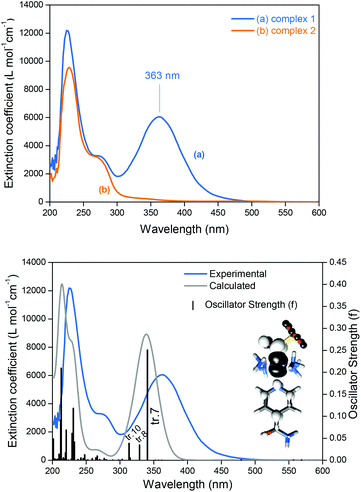
Complex 1 has two doublets in the 1H-NMR spectra with chemical shifts (δ) at δ = 8.87 and 8.13 ppm (Fig. S2, ESI‡), assigned respectively to the ortho and meta hydrogens of the isn ligand in 1. The 15N NMR spectrum of 1 only exhibits one peak at δ = 192.8 ppm (Fig. S3, ESI‡). The sharp narrow-width peaks observed in the 1H-NMR spectrum and the lack of EPR signals (EPR silent at 77 K) are consistent with a S = 0 ground state of 1, in agreement with the electronic structure description for the parent precursor nitrosyl complex 2, and for the family of trans-[Ru(NH3)4(L)(NO)]3+ complexes.15,22Nucleophilic attack at coordinated nitrosyls in ruthenium and iron complexes is well documented in the literature.16a,23 In the case of the family of trans-[Ru(NH3)4(L)(NO)]3+ complexes, nucleophilic attack of OH− or of thiols occurs on the nitrosyl ligand (Ru–NO) and leads to species with an intense and broad band in the long-wave UV and visible ranges of the spectra.16a,f,i,24 This behavior is consistent with the electronic absorption band observed for 1 at λmax = 363 nm (Fig. 2) formed after the nucleophilic addition of SO32− to the nitrosyl ligand of 2 (eqn (5)). This intense band (ε = 6.0 × 103 M−1 cm−1) was assigned by TD-DFT as a metal to ligand charge transfer (MLCT) transition, Ru → N(O)SO3 (inset of Fig. 2B; Fig. S6, S7, Table S5, ESI‡). This MLCT transition is of higher energy in comparison with that of the complexes [Fe(CN)5N(O)SO3]4–, [RuCl(py)4N(O)SO3] and cis-[RuX(bipy)2N(O)SO3] (X = Cl− or Br−),1 which are in the range of 450–475 nm.1 The theoretical spectrum of 1 is in agreement with the experimental results (Fig. 2B and S6 of the ESI‡), and the detailed assignments of all the electronic absorption bands of 1 are given in Table S5 (ESI‡).
Thermal stability of 1 at pH 7.4 and under acidic conditions
The thermal stability of 1 was investigated using electronic absorption (UV-Vis) and 1H NMR spectroscopy (Fig. S8–S11, ESI‡), and the results showed that 1 is kinetically stable at pH 7.4, with a rate constant of 3.1 × 10−5 s−1 for isn labilization at 298 K (t1/2 ∼ 373 min). The activation parameters for the isn labilization from 1 are listed in Table S6 (ESI‡). This reaction is governed by the positive values of the enthalpic (ΔH‡ ≈ 26.5 kcal mol−1) and entropic terms (ΔS‡ ≈ 9.1 cal mol−1 K−1), suggesting a dissociative (Id) rate-determining step. The product formed after isn labilization from 1 was characterized by 15N NMR (using 15N-labeled N(O)SO3 ligand in 1) as being the hydroxo nitrosyl complex25trans-[Ru(NH3)4(OH)(15NO)]2+, at δ ∼−40.3 ppm25 (Fig. S12 and S13, ESI‡). Correspondingly, the decomposition of trans-[RuCl(py)4N(O)SO3] in neutral solution also yields the hydroxo nitrosyl complex [RuOH(py)4NO]2+.1In acidic solution (1.0 M trifluoroacetic acid), complex 1 was stoichiometrically converted into the precursor nitrosyl (complex 2) by heterolytic cleavage of the S–N bond of the N(O)SO3 moiety, based on the FT-IR and 1H NMR results (Fig. S14 and S15 ESI‡). These findings are in agreement with the data reported for the complexes cis-[RuCl(bipy)2(N(O)SO3] and trans-[RuCl(py)4(N(O)SO3)] in aqueous HCl (4.0 M).1
The reaction of hydroxide ions (OH−) with the complexes 1 and 2
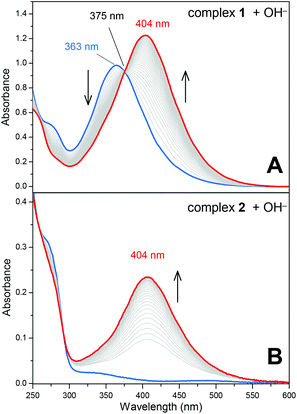
One of the main topics of interest in nitrosyl chemistry is metal nitrosyl complex electrophilicity.1,16a,23,24,26 The reaction of nitrosyl complexes with a variety of nucleophiles is well documented, and the main species studied are OH−, HS−, N3−, NH2OH and RS− (thiols). Aiming to investigate the electrophilic character of the N(O)SO3 ligand in 1, the reaction of this complex and also that of complex 2 with OH− were performed. Of note, in general, nitrosyl complexes of the type [L5M(NO)]n react with OH− yielding the respective nitro complexes [L5M(NO2)](n−2).16a,24 This reaction was already investigated for a series of trans-[Ru(NH3)4(L)(NO)]3+ nitrosyl complexes,24 but here we show unprecedented electrophilic behavior of a nitrosylsulphito complex.Both the reactions of 1 and 2 with OH− produced the respective nitro complex trans-[Ru(NH3)4(isn)(NO2)]+,15,24 with a characteristic band at λ = 404 nm (Fig. 3). During the reaction of 1 with OH−, the characteristic band of 1 at 363 nm decreases at the rate that the 404 nm band grows in (Fig. 3A), with an isosbestic point at 375 nm. Analogously, the 404 nm band appears as complex 2 reacts with OH−. These results were confirmed by 15N NMR spectroscopy, by means of comparisons of the reaction of OH− with 15N-labelled 1 and 2 (Fig. S16, ESI‡).15,24 The formation of a single peak at δ15N = 158.2 ppm in the 15N NMR (Fig. S16, ESI‡) confirmed that the reactions of 1 and 2 with OH− yielded the same product, i.e. the complex trans-[Ru(NH3)4(isn)(NO2)]+.15,24
A complete set of kinetic data for the reaction of OH− with 1 and with 2 is provided in the ESI‡ (Fig. S17, S18 and Table S7). Under pseudo-first-order conditions ([OH−] ≫ [complexes 1 or 2]) the rate constants for the formation of trans-[Ru(NH3)4(isn)(NO2)]+ are 2.1 and 10.5 M−1 s−1 (at 288 K) for 1 and 2, respectively (Table S7, ESI‡). The mechanism of the reaction of 1 with OH− was investigated by DFT calculations, and the results showed that the formation of trans-[Ru(NH3)4(isn)(NO2)]+ occurs by the nucleophilic attack of OH− on the nitrogen atom of the N(O)SO3 ligand in 1 (Fig. S19 and Table S8, ESI‡). This finding is in agreement with our experimental results (UV-Vis and 15N NMR, Fig. 3 and Fig. S16 (ESI‡), respectively) and is comparable to the mechanism reported for the reaction of OH− with the family of trans-[Ru(NH3)4(L)(NO)]3+ complexes.15,24
Therefore, the experimental and DFT data showed for the first time the susceptibility of a nitrosylsulphito ligand to nucleophilic attack by hydroxide ions, then yielding the respective Ru(II) nitro complex.
pKa of the N(O)SO3 ligand in complex 1
The pKa of the N(O)SO3 ligand was determined spectrophotometrically through titration of 1 with aqueous trifluoroacetic acid solutions (Fig. S20A, ESI‡). The titration curve is shown in Fig. S20B (ESI‡), and the pKa values obtained by two treatments (see the Experimental section; Fig. S20B and S21A, ESI‡) were 5.03 and 5.12, respectively, for the protonation shown in eqn (6):| trans-[Ru(NH3)4(isn)(N(O)SO3)]+ + H3O+ ⇌ trans-[Ru(NH3)4(isn)(N(O)SO2OH)]2+ + H2O | (6) |
Unfortunately, no previous studies on nitrosylsulphito complexes reported pKa values, thus making comparisons not possible. However, the pKa determined for 1 (eqn (6)) is within an expected range given that the sulfite ion (SO32−, non-coordinated) has a pKa value of 7.2 (ref. 4c) and that this value should diminish upon coordination to the nitrosyl precursor (eqn (5)). From these values, we can estimate that the pKa of the free N(O)SO3− ion (non-coordinated to the Ru complex) is between 5.1 < pKa < 7.2 (for the protonation of one of the oxygen atoms of the SO3 moiety).
Photochemistry
Irradiation of 1 with light of wavelengths of 355 or 410 nm produces NO˙, SO3˙− and isn in solution, and no Ru(III), as discussed in detail below. Of note, since there are no available data on the photochemistry of nitrosylsulphito complexes (to the best of our knowledge) some comparisons about the photochemistry of 1 will be performed with analogous Ru(II) nitro complexes, [L5Ru–NO2]n.The MLCT (Ru → N(O)SO3) band at 363 nm (Fig. 2A) decreases with the irradiation time of 1 (Fig. S22, ESI‡), and this behavior can be associated with labilization of the N(O)SO3− ligand. This hypothesis corroborates the results reported for the parent nitro complex trans-[Ru(NH3)4P(OEt)3(NO2)]+ (P(OEt)3 = triethyl phosphite),20 and also for other [L5Ru-NO2]n complexes,20,27 which upon irradiation the MLCT band (Ru → NO2) decreases, resulting in labilization of NO2− (eqn (7)) and no Ru(III) formation:
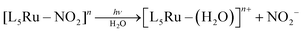 | (7) |
In some of these nitro complexes, nitric oxide (NO˙) was also detected in solution during photolysis, and this process was related to secondary photochemical reactions,20,27beqn (8):
 | (8) |
In analogy to eqn (7) and (8), the products most likely formed upon N(O)SO3− release during irradiation of 1 are the radical species NO˙ and SO3˙−. To investigate this hypothesis, catalase was used for the detection of NO˙, and DMPO (5,5-dimethyl-1-pyrroline-N-oxide) for the detection of SO3˙−. Of note, two well-documented procedures used for NO˙ detection (oxymyoglobin and PTIO)28 were not effective for distinguishing among the formation of NO˙ or SO3˙− (Fig. S23, S24, ESI‡).
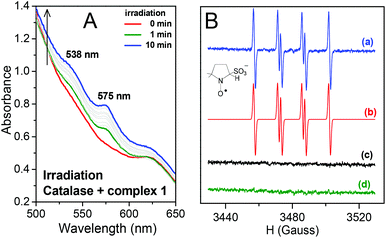
When 1 was irradiated in the presence of catalase two new bands appeared at 538 and 575 nm (Fig. 4A). This is in agreement with the spectral changes reported for the binding of NO˙ to catalase,29 thus confirming the formation of NO˙ during irradiation of 1. The EPR results for irradiation of 1 in the presence of DMPO are depicted in Fig. 4B. The simulated spectrum and the hyperfine coupling constants (shown in the caption of Fig. 4) are consistent with those reported for the DMPO/˙SO3− adduct,3d,30 thus confirming SO3˙− as a photoproduct of 1 (Fig. 4B). Therefore, the hypothesis that irradiation of 1 could result in the formation of NO˙ and SO3˙− species was confirmed.
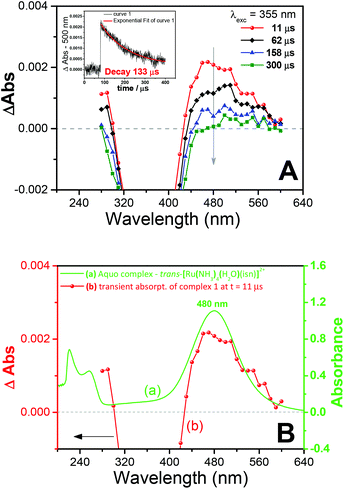
Transient absorption Laser Flash Photolysis (LFP) studies were performed to gain further insight into the photochemistry of 1. The transient spectra obtained after laser excitation of 1 are shown in Fig. 5A. The transient spectrum has a maximum at 480 nm (Fig. 5A), and as can be seen in Fig. 5B, this band matches the band of the aquo complex trans-[Ru(NH3)4(H2O)(isn)]2+ at λmax = 480 nm(ref. 31) (in this aquo complex the coordinated H2O has a pKa value of 11.731a). Therefore, the transient spectrum (Fig. 5) can be assigned to the photoproduct aquo complex trans-[Ru(NH3)4(H2O)(isn)]2+, formed upon irradiation of 1.
LFP thus supports the hypothesis that the N(O)SO3 ligand dissociates from the Ru center upon irradiation of 1, forming the aquo complex and the radical species NO˙ and SO3˙−, as summarized in Fig. 6. This mechanism is also supported by DFT calculations on the electronic excited state resulting from excitation of the MLCT Ru → N(O)SO3 of 1 (tr. 7 in Fig. 2B). The DFT analysis of the orbitals involved in this electronic transition highlights the depopulation of the bonding HOMO-2 orbital and the population of the antibonding LUMO as main components, with respect to the Ru–N(O)SO3 bond (Table S5 and Fig. S7, ESI‡). Geometry optimization shows that the resulting electronic excited state is significantly distorted along the z-axis with respect to the GS (labeled S7 in Fig. S25, ESI‡), with a long Ru–N(O)SO3 bond distance of 2.60 Å (for GS this bond length is calculated as ∼1.91 Å), thus further supporting the mechanism of photolabilization of N(O)SO3− from 1 (Fig. 6).
Additionally, in situ1H NMR of the irradiation of 1 showed that the isonicotinamide ligand (isn) is also capable of photodissociating from the Ru center (Fig. S26, ESI‡). Since the formation of the aquo complex trans-[Ru(NH3)4(H2O)(isn)]2+ was identified by LFP (Fig. 5B), the labilization of the isn ligand thus must arise from a consecutive photochemical event, occurring after the N(O)SO3− photolabilization, as it is most improbable that irradiation of 1 would cause simultaneous labilization of both N(O)SO3− and isn ligands. Analogous consecutive dual photolyses have been previously reported for other Ru(II) systems, in which two ligands were photolabilized during irradiation.32 Moreover, the band at 480 nm observed in the transient spectra (by LFP) is formed and then decays (Fig. 5A), showing that the isn labilization occurs after dissociation of N(O)SO3− from 1. This conclusion is based on the fact that the 480 nm band is a MLCT Ru → isn transition31 of the aquo complex trans-[Ru(NH3)4(H2O)(isn)]2+, and the decay of this band would be related to the labilization of the isn ligand, in agreement with the 1H NMR results of the in situ irradiation of 1.
Identical results to those shown in Fig. 5 were obtained when LFP experiments with complex 1 were performed in the presence of an excess of DMPO or of isonicotinamide. This result shows that the formation of the aquo complex trans-[Ru(NH3)4(H2O)(isn)]2+, followed by its decay (Fig. 5), is not directly influenced by the presence or absence of either the sulfite radical (SO3˙−) or the isn ligand in solution.
In addition, the quantum yield (ϕ) for the photoinduced labilization of the ligands in complex 1 was measured using electronic absorption spectroscopy by monitoring the decrease of its MLCT band (363 nm) during 355 nm irradiation (Fig. S22, ESI‡), and was calculated as ϕ = 0.12 ± 0.03. Very similar ϕ values were obtained by monitoring the photodissociation of isn by 1H NMR for the in situ irradiation of 1 (Fig. S26, ESI‡).
In summary, light irradiation of 1 leads to the labilization of N(O)SO3−, which then undergoes rapid homolysis to form NO˙ and SO3˙− (Fig. 6). Therefore, the two possible pathways for the formation of NO˙ and SO3˙− are through thermal and photochemical decomposition of the free N(O)SO3− ion: (i) by the thermal homolysis of the S–N bond of the N(O)SO3− ion, thus dissociating into NO˙ and SO3˙− radicals and (ii) by the photodecomposition of N(O)SO3− through a process similar to that observed during photolysis of S-nitrosothiols (via formation of NO˙ and thiyl radicals,33 and also analogous to the mechanism observed for the photodecomposition of the nitro ligand in Ru(II) nitro complexes,20eqn (7) and (8)).
Molecules with S–N bonds and structures similar to N(O)SO3−, such as thionitrous acid (HSNO, S–N bond length of 1.78–1.93 Å)34 and other S-nitrosothiols, are proposed to undergo light induced homolysis of the weak S–N bond.33 Therefore, the two possible pathways for N(O)SO3− decomposition, i.e. (i) thermal and (ii) photochemical S–N cleavage, are both likely to occur. The investigation of the mechanism for the formation of NO˙ and SO3˙− radicals from N(O)SO3− was performed by DFT, and the results are provided in detail in the next section.
Formation of NO˙ and SO3˙− by the S–N bond dissociation of N(O)SO3−
As discussed in the crystallographic section, the S–N bond length of the N(O)SO3− ligand in 1 is 1.84 Å, ca. 10% longer than that of other S–N compounds. Therefore, it is not surprising that the N(O)SO3− anion (formed in solution after irradiation of 1) may rapidly decompose to form NO˙ and SO3˙− (Fig. 6), and this event is likely to occur through thermal and photochemical reaction pathways.Unconstrained geometry optimizations of N(O)SO3− were performed on both the singlet and triplet surfaces. The resulting singlet structure is 10.7 kcal mol−1 more stable than the optimized triplet structure (thus showing that N(O)SO3− has a singlet ground state), and has a 1.877 Å S–N bond length. The energy profile of the thermal homolysis of the S–N bond of N(O)SO3− (singlet) is shown in Fig. 7. The transition state for homolysis has ΔG‡ = 13 kcal mol−1, a single normal mode with a low imaginary frequency of −40.85 cm−1 (due to the large reduced masses of the NO and SO3 fragments, Fig. S28, ESI‡), and a bond length of 2.451 Å. Collectively, these geometric and electronic structure parameters indicate that the transition state is late on the homolysis pathway, and proceeds after substantial S–N bond cleavage has occurred. The NO˙ and SO3˙− products collectively have ΔG = 6.4 kcal mol−1 above that of the N(O)SO3− molecule (Fig. 7), showing that S–N homolysis is slightly endergonic. According to the energy barrier predicted for the thermal homolysis of the S–N bond of N(O)SO3− (ΔG‡ = 13 kcal mol−1, Fig. 7), this reaction is nearly instantaneous at room temperature (298 K). This is in agreement with the above results (Fig. 4) which demonstrated that the radicals NO˙ and SO3˙− are formed upon irradiation of 1, thus corroborating with the mechanism proposed (Fig. 6).
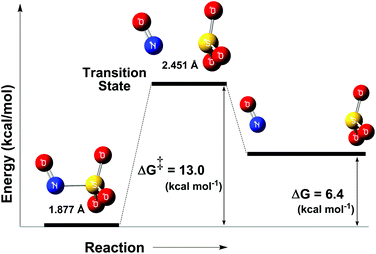 | ||
| Fig. 7 Reaction coordinate of the thermal decomposition of the S–N bond of the ion N(O)SO3− (left). Transition state (middle), and NO˙ and SO3˙− (right). | ||
The enthalpy of the reaction in eqn (9) at 298 K (ΔrH298), which is by definition35 the bond dissociation enthalpy (BDE) of the ion N(O)SO3−, was calculated according to the literature.36 The BDE of this reaction (eqn (9)) was predicted as 17.8 kcal mol−1.
| N(O)SO3− → NO˙ + SO3˙− | (9) |
The S–N BDE of N(O)SO3− is smaller than that predicted for a series of representative S-nitrosothiols (CH3SNO, CH3CH2SNO, (CH3)2CHSNO (CH3)3CSNO, CH2CHSNO, ca. 23.3–32.4 kcal mol−1),37 and this can be explained by the fact that SO3˙− is a resonance-stabilized radical. Indeed, this behavior was already observed in that series of S-nitrosothiols, in which the vinyl-substituted thiol (CH2CHSNO) had the smallest BDE of the series (23.3 kcal mol−1) because of the resonance-stabilized thiyl radical formed after the homolytic S–N dissociation (the BDE values of the other S-nitrosothiols of the series were in the range of 31.3–32.4 kcal mol−1).37
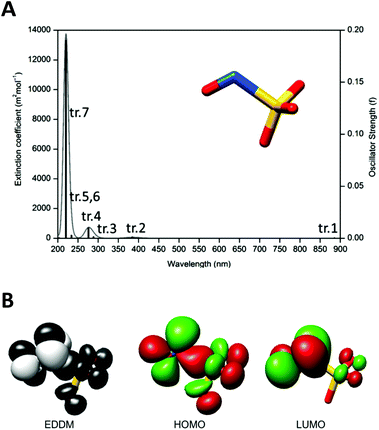
The second pathway investigated by DFT for the dissociation of the N(O)SO3− into NO˙ and SO3˙− radicals is the photochemical. The theoretical UV-Vis absorption spectrum of N(O)SO3− is characterized by a series of transitions in the UV region, plus a transition in the far red-region (Fig. 8A). Among the seven electronic transitions (tr.1–tr.7, Fig. 8A), tr.1 and tr.2 have the smallest oscillator strengths. The first six electronic transitions (tr.1–tr.6 in Fig. 8A) all involve the population of the LUMO, that is antibonding along the S–N bond (Table S9, ESI‡). In particular, the first electronic excited state (S1) has strong dissociative nature. This can be clearly seen by the related electron density difference map (Fig. 8B) that shows a loss of electron density along the S–N bond (black surface), as a consequence of the electronic transition (tr. 1). The geometry optimization of the first singlet excited state (S1) further supports its dissociative nature. The relaxed geometry displays a S–N bond length of 2.20 Å, about 0.25 Å longer with respect to the ground state (Fig. S29, ESI‡). Although S1 can be hardly populated directly by light absorption due to the extremely low value of the oscillator strength of the tr.1, Fig. 8A (which is also low for tr.2 and tr.3), it can be assumed that S1 is the arrival point of the de-excitation process from higher electronic excited states. Therefore, irradiation of N(O)SO3− with light might lead to the formation of NO˙ and SO3˙−, but this process seems to be favorable only for irradiation with UV light of higher energy (i.e. λirrad < 300 nm), in which the oscillator strengths have higher values (Fig. 8A). However, λirrad < 300 nm is out of the range used in this study.
Overall, our data support the view that the decomposition of N(O)SO3− into NO˙ and SO3˙− (eqn (9)) could occur by both thermal and photochemical pathways. Nevertheless, because of the very low oscillator strengths predicted for N(O)SO3− in the wavelength range of 300–900 nm (Fig. 8A), the thermal pathway is favored regarding the photochemical one. Moreover, based on the low energy barrier predicted for the thermal homolysis of the S–N bond (∼13 kcal mol−1, Fig. 7), the dissociation of N(O)SO3− (eqn (9)) should occur instantaneously at room temperature. Therefore, the irradiation of complex 1 with light leads to the photodissociation of N(O)SO3− (Fig. 6), which then dissociates by the thermolysis of the S–N bond (Fig. 7), yielding NO˙ and SO3˙−.
Conclusion
In summary, the stabilization of N(O)SO3− provided by its coordination in complex 1 allowed us to better understand the chemical properties of this anion. Our study on the stability of 1 at neutral and acidic pH is in accordance with previous studies of nitrosylsulphito complexes. The electrophilic behavior described here for N(O)SO3− in 1 is the first reported for nitrosylsulphito complexes, and we furthermore showed that the nucleophilic attack of OH− on 1 produces the respective Ru(II) nitro complex. Therefore, these results provide a useful insight to understand the reaction pathways of N(O)SO3− under biological conditions, where hydrolysis and attack by nucleophilic species are speculated. Also, the photochemical results presented here are the first described for the nitrosylsulphito complexes, and demonstrated the production of two important radicals, NO˙ and SO3˙−, when 1 was irradiated with light. In the context of applications, the main advantage of triggering the release of NO˙ and SO3˙− by light is the possibility of control of dosage and timing (i.e. on demand release). Hence, the results showed that complex 1 has significant potential as a photoactive source of the radical species NO˙ and SO3˙−.Based on the importance and applications of both nitric oxide and SOx˙− radicals (eqn (1)–(4)), the studies performed here with complex 1 contribute to the development of other stable and water-soluble [L5M–N(O)SO3]n complexes tuned to release NO˙ and SO3˙− over an expanded range of wavelengths, mainly for biological purposes.
Experimental
Chemicals
Unless otherwise noted, reagents and solvents were purchased from Sigma-Aldrich, Merck or JT Baker at the highest quality available and were used without further purification. Milli-Q water (18.2 MΩ) was used throughout the experiments. Ruthenium(III) chloride hydrate (Strem Chemicals) was the synthetic precursor of all the ruthenium complexes. Sodium sulfite anhydrous (Na2SO3, Merck) was used for the synthesis of the nitrosylsulphito complexes. Unless otherwise noted, all solutions were deaerated with Ar (99.999%) for at least 30 min.General
Electronic spectra (UV-Vis) were recorded on a Shimadzu UV3600 or in a Thermo Scientific Multiskan GO UV-Vis spectrophotometer, using a 1.00 cm quartz cell. Infrared spectra were recorded in a Shimadzu FTIR Spectrophotometer model IRAffinity-1 (for KBr pellets experiments), or in a Vertex 70v Bruker (for the experiments in solution). 1H- and 15N-NMR spectra were recorded on an Agilent 500 MHz NMR Spectrometer (Model 500/54 Premium Shield). 3-(Trimethylsilyl)propionic-2,2,3,3-d4 (TMSP-d4) was used as an internal reference (δ = 0 ppm) for 1H NMR experiments, and a glass capillary filled with 15NH4Cl (δ = –354 ppm vs. chemical shift of CH3NO2, δCH3NO2 = 0 ppm) was used as reference in the 15N-NMR experiments. Electron paramagnetic resonance (EPR) spectra were recorded in a Bruker EMX Plus X-band spectrometer at room or liquid nitrogen temperature (77 K). Elemental analysis was performed in a PerkinElmer 2400 Series II CHNS/O Elemental Analyzer.Synthesis
The synthetic precursor complexes15,22,38 [RuCl(NH3)5]Cl3, trans-[RuCl(NH3)4(SO2)]Cl, trans-[Ru(SO4)(NH3)4(isn)]Cl (isn = isonicotinamide), trans-[Ru(NH3)4(isn)(NO)](BF4)3, and the aquo complex31trans-[Ru(NH3)4(H2O)(isn)](PF6)2 were prepared and characterized as described elsewhere.15,22,31,38 The 15N-labeled trans-[Ru(NH3)4(isn)(15NO)](BF4)3 was synthesized using Na15NO2.28cX-ray data collection and structure determination
| pH = pKa + log [(A − AM)/(AI − A)] | (10) |
pKa was also determined by the first and second derivative of the titration curve.
Stability of complex 1 in aqueous solutions
Reaction of hydroxide ions (OH−) with complexes 1 and 2
The reaction of complexes 1 and 2 with hydroxide ions (OH−) was performed using the same methodology described for the reaction of a series of nitrosyl complexes with OH−,24 which is briefly described below. The reaction progress was followed by electronic spectroscopy (UV-Vis), under pseudo-first order conditions ([OH−] ≫ [Ru]). Aqueous solutions of the Ru complexes (CRu = 1.0 × 10−4 M) and OH− ranging from 0.01 M to 0.045 M, with ionic strength I = 1.0 M (NaCl), and in the temperature ranges T = 15 and 25 °C (for 1) and 15 °C for 2, were used. At least five experiments were performed for each concentration of OH− used. This afforded at least 25 values for the observed rate constant (kobs). Plots of kobsversus [OH−] were built for both complexes. In all cases, a linear distribution was observed. The slope was equal to the second-order rate constant. 15N-NMR spectra were also recorded for the reaction of OH− with the 15N-labeled complexes 1 and 2 in order to characterize the products formed.For the detection of the sulfite radical species (SO3˙−) by EPR spectroscopy, irradiation of 1 was performed in situ (quartz capilar), and the detection was accomplished using the spin trap 5,5-dimethyl-1-pyrroline N-oxide (DMPO). The EPR spectra were recorded at room temperature (T = 25 °C), and the spectrometer settings were as follows: modulation frequency, 100 kHz; modulation amplitude, 1.0 G; microwave power, 2 mW; microwave frequency, 9.79 GHz; field sweep, 100 G; receiver gain, 5 × 104; time constant, 20.48 ms; sweep time, 41.94 s; number of scans, 1. Computer simulations of the EPR spectra were performed using SimFonia software.
In the experiments using catalase (from bovine liver, 2000–5000 units per mg protein, Sigma) for the detection of nitric oxide (NO˙), fresh stock solutions of catalase were prepared in phosphate buffer pH 7.4, diluted to reach the desired concentration (λmax = 403 nm, ε = 4.3 × 105 M−1 cm−1)29 and the photolysis was performed in a cuvette at T = 25 °C; the spectral changes were monitored by electronic spectroscopy (UV-Vis).
Experiments using oxymyoglobin (oxyMb)28b,c and carboxy-PTIO28a for the detection of NO˙ followed previously published procedures.28a,b,c Phosphate buffer solutions (pH 7.4) containing sodium sulfite (Na2SO3) and PTIO or oxyMB were photolyzed in a 1.00 path quartz cuvette; in the case of oxyMb, the reaction course was followed by UV-Vis spectroscopy, and in the case of PTIO, by EPR spectroscopy.
In all cases, the experimental details, such as concentration and temperature used, are described in the caption of the figures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support by the Brazilian agencies FAPESP (12/23651-4, 17/01189-0) and CNPq (306491/2015-0). This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. Dr. Gustavo Metzker is acknowledged for the critical review of this manuscript and Dr. Elena Amadio for help in the realization of the cover artwork.Notes and references
- F. Bottomley, W. V. F. Brooks, D. E. Paez, P. S. White and M. Mukaida, J. Chem. Soc., Dalton Trans, 1983, 2465–2472 RSC.
- (a) U. Takahama and S. Hirota, J. Agric. Food Chem., 2012, 60, 1102–1112 CrossRef CAS PubMed; (b) H. Vally, N. L. A. Misso and V. Madan, Clin. Exp. Allergy, 2009, 39, 1643–1651 CrossRef CAS PubMed.
- (a) P. B. Woolsey, J. Altern. Complement. Med., 2008, 14, 1159–1164 CrossRef PubMed; (b) C. Mottley, R. P. Mason, C. F. Chignell, K. Sivarajah and T. E. Eling, J. Biol. Chem., 1982, 257, 5050–5055 CAS; (c) K. Ranguelova, S. Chatterjee, M. Ehrenshaft, D. C. Ramirez, F. A. Summers, M. B. Kadiiska and R. P. Mason, J. Biol. Chem., 2010, 285, 24195–24205 CrossRef CAS PubMed; (d) K. Ranguelova, A. B. Rice, A. Khajo, M. Triquigneaux, S. Garantziotis, R. S. Magliozzo and R. P. Mason, Free Radical Biol. Med., 2012, 52, 1264–1271 CrossRef CAS PubMed; (e) K. Ranguelova, A. B. Rice, O. M. Lardinois, M. Triquigneaux, N. Steinckwich, L. J. Deterding, S. Garantziotis and R. P. Mason, Free Radical Biol. Med., 2013, 60, 98–106 CrossRef CAS PubMed; (f) M. Velayutham, C. F. Hemann, A. J. Cardounel and J. L. Zweier, Biochem. Biophys. Rep., 2016, 5, 96–104 Search PubMed; (g) W. T. Lee, Brain Dev., 2011, 33, 745–752 CrossRef PubMed.
- (a) H. J. Cohen and I. Fridovich, J. Biol. Chem., 1971, 246, 359–366 CAS; (b) J. L. Johnson and K. V. Rajagopalan, J. Biol. Chem., 1977, 252, 2017–2025 CAS; (c) K. Ranguelova and R. P. Mason, Free Radical Biol. Med., 2009, 47, 128–134 CrossRef CAS PubMed.
- (a) E. Hayon, A. Treinin and J. Wilf, J. Am. Chem. Soc., 1972, 94, 47–57 CrossRef CAS; (b) P. Neta, R. E. Huie and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 1027–1284 CrossRef CAS.
- R. E. Huie and P. Neta, J. Phys. Chem., 1984, 88, 5665–5669 CrossRef CAS.
- L. Eberson, Adv. Phys. Org. Chem., 1982, 18, 79–185 CrossRef CAS.
- Y. Guo, X. Lou, C. Fang, D. Xiao, Z. Wang and J. Liu, Environ. Sci. Technol., 2013, 47, 11174–11181 CrossRef CAS PubMed.
- (a) Y. Deng and C. M. Ezyske, Water Res., 2011, 45, 6189–6194 CrossRef CAS PubMed; (b) D. N. Zhou, H. Zhang and L. Chen, J. Chem. Technol. Biotechnol., 2015, 90, 775–779 CrossRef CAS; (c) Y. Yang, J. Jiang, X. L. Lu, J. Ma and Y. Z. Liu, Environ. Sci. Technol., 2015, 49, 7330–7339 CrossRef CAS PubMed; (d) L. S. Lian, B. Yao, S. D. Hou, J. Y. Fang, S. W. Yan and W. H. Song, Environ. Sci. Technol., 2017, 51, 2954–2962 CrossRef CAS PubMed.
- M. Roginskaya, R. Mohseni, D. Ampadu-Boateng and Y. Razskazovskiy, Free Radical Res., 2016, 50, 756–766 CrossRef CAS PubMed.
- (a) C. B. Bai, N. X. Wang, X. W. Lan, Y. J. Wang, Y. L. Xing, J. L. Wen, X. W. Gao and W. Zhang, Sci. Rep., 2016, 6, 20163 CrossRef PubMed; (b) Y. F. Guo, S. Mahmood, B. H. Xu, X. Q. Yao, H. Y. He and S. J. Zhang, J. Org. Chem., 2017, 82, 1591–1599 CrossRef CAS PubMed.
- (a) S. N. Mendiara, E. Ghibaudi, L. J. Perissinotti and A. J. Colussi, J. Phys. Chem., 1992, 96, 8089–8091 CrossRef CAS; (b) S. B. Oblath, S. S. Markowitz, T. Novakov and S. G. Chang, J. Phys. Chem., 1982, 86, 4853–4857 CrossRef CAS.
- J. H. Swinehart, Coord. Chem. Rev., 1967, 2, 385–402 CrossRef CAS.
- (a) W. Moser, R. A. Chalmers and A. G. Fogg, J. Inorg. Nucl. Chem., 1965, 27, 831–840 CrossRef CAS; (b) A. G. Fogg, A. H. Norbury and W. Moser, J. Inorg. Nucl. Chem., 1966, 28, 2753–2755 CrossRef CAS.
- E. Tfouni, M. Krieger, B. R. McGarvey and D. W. Franco, Coord. Chem. Rev., 2003, 236, 57–69 CrossRef CAS.
- (a) M. L. Souza, A. C. Roveda Jr., J. C. M. Pereira and D. W. Franco, Coord. Chem. Rev., 2016, 306, 615–627 CrossRef CAS; (b) Y. Gao, A. Toubaei, X. Q. Kong and G. Wu, Chem. – Eur. J., 2015, 21, 17172–17177 CrossRef CAS PubMed; (c) M. M. Cortese-Krott, A. R. Butler, J. D. Woollins and M. Feelisch, Dalton Trans., 2016, 45, 5908–5919 RSC; (d) M. A. Rhine, B. C. Sanders, A. K. Patra and T. C. Harrop, Inorg. Chem., 2015, 54, 9351–9366 CrossRef CAS PubMed; (e) Y. Gao, B. Mossing and G. Wu, Dalton Trans., 2015, 44, 20338–20343 RSC; (f) J. C. M. Pereira, M. L. Souza and D. W. Franco, Eur. J. Inorg. Chem., 2015, 2015, 1005–1011 CrossRef CAS; (g) L. L. Perissinotti, D. A. Estrin, G. Leitus and F. Doctorovich, J. Am. Chem. Soc., 2006, 128, 2512–2513 CrossRef CAS PubMed; (h) L. L. Perissinotti, G. Leitus, L. Shimon, D. Estrin and F. Doctorovich, Inorg. Chem., 2008, 47, 4723–4733 CrossRef CAS PubMed; (i) F. Roncaroli and J. A. Olabe, Inorg. Chem., 2005, 44, 4719–4727 CrossRef CAS PubMed; (j) M. R. Filipovic, M. Eberhardt, V. Prokopovic, A. Mijuskovic, Z. Orescanin-Dusic, P. Reeh and I. Ivanovic-Burmazovic, J. Med. Chem., 2013, 56, 1499–1508 CrossRef CAS PubMed; (k) S. L. Quiroga, A. E. Almaraz, V. T. Amorebieta, L. L. Perissinotti and J. A. Olabe, Chem. – Eur. J., 2011, 17, 4145–4156 CrossRef CAS PubMed.
- T. Chivers and R. S. Laitinen, Chem. Soc. Rev., 2017, 46, 5182–5192 RSC.
- (a) W. Deng, H. L. Zhao, F. P. Pan, X. H. Feng, B. Jung, A. Abdel-Wahab, B. Batchelor and Y. Li, Environ. Sci. Technol., 2017, 51, 13372–13379 CrossRef CAS PubMed; (b) A. Fraix and S. Sortino, Photochem. Photobiol. Sci., 2018, 17, 1709–1727 RSC; (c) R. Radi, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5839–5848 CrossRef CAS PubMed; (d) S. Sortino, Chem. Soc. Rev., 2010, 39, 2903–2913 RSC; (e) L. Chen, M. Tang, C. Chen, M. Chen, K. Luo, J. Xu, D. Zhou and F. Wu, Environ. Sci. Technol., 2017, 51, 12663–12671 CrossRef CAS PubMed; (f) D. N. Zhou, L. Chen, J. J. Li and F. Wu, Chem. Eng. J., 2018, 346, 726–738 CrossRef CAS.
- D. M. P. Mingos, Nitrosyl Complexes in Inorganic Chemistry, Biochemistry and Medicine I, Springer, Heidelberg, New York, Dordrecht, London, 2014 Search PubMed.
- R. M. Carlos, D. R. Cardoso, E. E. Castellano, R. Z. Osti, A. J. Camargo, L. G. Macedo and D. W. Franco, J. Am. Chem. Soc., 2004, 126, 2546–2555 CrossRef CAS PubMed.
- A. F. Holleman and E. Wiberg, Inorganic Chemistry, Academic Press, San Diego; De Gruyter, Berlin, New York, 2001 Search PubMed.
- S. S. Borges, C. U. Davanzo, E. E. Castellano, J. Z-Schpector, S. C. Silva and D. W. Franco, Inorg. Chem., 1998, 37, 2670–2677 CrossRef CAS PubMed.
- F. Doctorovich and F. Di Salvo, Acc. Chem. Res., 2007, 40, 985–993 CrossRef CAS PubMed.
- F. Roncaroli, M. E. Ruggiero, D. W. Franco, G. L. Estiu and J. A. Olabe, Inorg. Chem., 2002, 41, 5760–5769 CrossRef CAS PubMed.
- M. A. Il'yin, V. A. Emel'anov, A. V. Belyaev, A. N. Makhinya, S. V. Tkachev and N. I. Alferova, Russ. J. Inorg. Chem., 2008, 53, 1070–1076 CrossRef.
- F. Bottomley, Acc. Chem. Res., 1978, 11, 158–163 CrossRef CAS.
- (a) C. A. Bignozzi, C. Chiorboli, Z. Murtaza, W. E. Jones and T. J. Meyer, Inorg. Chem., 1993, 32, 1036–1038 CrossRef CAS; (b) R. G. Lima, M. G. Sauaia, D. Bonaventura, A. C. Tedesco, R. F. V. Lopez, L. M. Bendhack and R. S. da Silva, Inorg. Chim. Acta, 2005, 358, 2643–2650 CrossRef.
- (a) A. C. Roveda Jr., T. B. R. Papa, E. E. Castellano and D. W. Franco, Inorg. Chim. Acta, 2014, 409 part A, 147–155 CrossRef; (b) A. C. Merkle, A. B. McQuarters and N. Lehnert, Dalton Trans., 2012, 41, 8047–8059 RSC; (c) A. C. Roveda Jr., H. D. Aguiar, K. M. Miranda, C. C. Tadini and D. W. Franco, J. Mater. Chem. B, 2014, 2, 7232–7242 RSC.
- M. Hoshino, K. Ozawa, H. Seki and P. C. Ford, J. Am. Chem. Soc., 1993, 115, 9568–9575 CrossRef CAS.
- G. R. Buettner, Free Radical Biol. Med., 1987, 3, 259–303 CrossRef CAS PubMed.
- (a) C. C. Kuehn and H. Taube, J. Am. Chem. Soc., 1976, 98, 689–702 CrossRef CAS; (b) S. S. Isied and H. Taube, Inorg. Chem., 1976, 15, 3070–3075 CrossRef CAS.
- (a) M. R. Camilo, C. R. Cardoso, R. M. Carlos and A. B. P. Lever, Inorg. Chem., 2014, 53, 3694–3708 CrossRef CAS PubMed; (b) P. C. Ford, Chem. Sci., 2016, 7, 2964–2986 RSC; (c) G. Malouf and P. C. Ford, J. Am. Chem. Soc., 1977, 99, 7213–7220 CrossRef CAS.
- (a) R. J. Singh, N. Hogg, J. Joseph and B. Kalyanaraman, J. Biol. Chem., 1996, 271, 18596–18603 CrossRef CAS PubMed; (b) M. Marazzi, A. Lopez-Delgado, M. A. Fernandez-Gonzalez, O. Castano, L. M. Frutos and M. Temprado, J. Phys. Chem. A, 2012, 116, 7039–7049 CrossRef CAS PubMed; (c) R. J. Singh, N. Hogg, J. Joseph and B. Kalyanaraman, FEBS Lett., 1995, 360, 47–51 CrossRef CAS PubMed.
- M. Nava, M. A. Martin-Drumel, C. A. Lopez, K. N. Crabtree, C. C. Womack, T. L. Nguyen, S. Thorwirth, C. C. Cummins, J. F. Stanton and M. C. McCarthy, J. Am. Chem. Soc., 2016, 138, 11441–11444 CrossRef CAS PubMed.
- (a) S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed; (b) E. R. Cohen, T. Cvitas, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry, IUPAC Green Book, 3rd edn, IUPAC & RSC Publishing, Cambridge, 2007 RSC.
- J. W. Ochterski , Thermochemistry in Gaussian, (accessed November, 2018).
- M. D. Bartberger, J. D. Mannion, S. C. Powell, J. S. Stamler, K. N. Houk and E. J. Toone, J. Am. Chem. Soc., 2001, 123, 8868–8869 CrossRef CAS PubMed.
- M. G. Gomes, C. U. Davanzo, S. C. Silva, L. G. F. Lopes, P. S. Santos and D. W. Franco, J. Chem. Soc., Dalton Trans, 1998, 601–607 RSC.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van De Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef CAS.
- G. M. Sheldrick, SHELXS97 Program for Crystal Structure Refinement, University of Gottingen, Gottingen, Germany, 1997 Search PubMed.
- G. M. Sheldrick, SHELXS97, Program for Crystal Structure Analysis, University of Gottingen, Gottingen, Germany, 1997 Search PubMed.
- A. Albert and E. P. Serjeant, The Determination of Ionization Constants: A Laboratory Manual, Chapman and Hall, New York, 1984 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- (a) M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS; (b) R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- (a) M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS; (b) S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- P. Fuentealba, H. Preuss, H. Stoll and L. Vonszentpaly, Chem. Phys. Lett., 1982, 89, 418–422 CrossRef CAS.
- A. D. Mclean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- (a) W. R. Browne, N. M. O'Boyle, J. J. McGarvey and J. G. Vos, Chem. Soc. Rev., 2005, 34, 641–663 RSC; (b) M. Head-Gordon, A. M. Grana, D. Maurice and C. A. White, J. Phys. Chem., 1995, 99, 14261–14270 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
Footnotes |
| † This paper is dedicated in memoriam of Prof. Dr Douglas Wagner Franco. |
| ‡ Electronic supplementary information (ESI) available: Complimentary characterization and reactivity data are provided. CCDC 1915847 and 1922883. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9dt01432b |
| This journal is © The Royal Society of Chemistry 2019 |