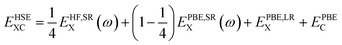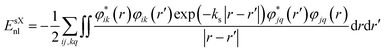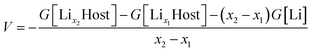Re-evaluation of experimental measurements for the validation of electronic band structure calculations for LiFePO₄ and FePO₄

Abstract

Experimental measurements used to validate previous electronic band structure calculations for olivine LiFePO₄ and its delithiated phase, FePO₄, have been re-investigated in this study. Experimental band gaps of LiFePO₄ and FePO₄ have been determined to be 6.34 eV and 3.2 eV by electron energy loss spectroscopy (EELS) and UV-Vis-NIR diffusion reflectance spectroscopy, respectively. X-ray photoemission (XPS) and Raman spectroscopy show that the surfaces of very carefully synthesized LiFePO₄ display Li-depletion, which affects optical reflectance determinations. Based on these experimental measurements, functionals for density functional theory (DFT) calculations of the electronic properties have been revisited. Overall, electronic structures of LiFePO₄ and FePO₄ calculated using sX-LDA show the best self-consistent match to combined experimentally determined parameters. Furthermore, the open-circuit voltages of the LiFePO₄ half-cell have been interpreted in terms of both Fermi levels and Gibbs free energies, which provides additional support for the electronic band structures determined by this research.

---

1. Introduction

Concerns about greenhouse gas emissions, global warming and fossil fuel depletion are driving increased vehicle electrification as well as storage of renewable energy.¹ Rechargeable Li-ion batteries (LIBs) are currently the preferred choice for hybrid electric vehicles (HEVs) and electric vehicles (EVs), due to their high energy density and relatively long cycling stability.^2,3 Since the original work of Goodenough et al.,⁴ olivine LiFePO₄ has been considered as one of the best cathode materials for commercial LIBs due to its high structural stability afforded by phosphate bonds. However, the high-rate performance of LiFePO₄ is greatly inhibited by its poor electronic conductivity (∼10⁻⁹ S cm⁻¹) and low ionic diffusivity (10⁻¹³ to 10⁻¹⁶ cm² s⁻¹).⁵

In order to improve these properties, a range of experimental and theoretical techniques have been deployed to understand the electronic band structure and conduction mechanisms of Li_xFePO₄ phases (0 ≤ x ≤ 1). To optimize the materials for LIBs, theoretical computational approaches can be applied to provide guidance for experimental developments.

Calculations within the framework of density functional theory (DFT) have been widely used to explain the electronic band structure, Li insertion voltage, Li diffusivity and phase stability for Li-ion intercalation materials.^6–8 However, for a predictive use of DFT attempting to enhance battery properties using modified compositions and structures, it is imperative to carry out a thorough experimental validation of the theoretical approaches, checking on the overall consistency of a variety of complementary pieces of experimental information. In addition, the theoretical approaches need to be truly self-consistent, that is, they cannot rely on parameters that may require adjustments for each structural modification.

The band gap is a major factor determining the electronic conductivity of a solid, and it is an important characteristic of battery materials. In the case of LiFePO₄ and FePO₄, a wide range of experimentally determined band gap values have been reported in the literature^9–13 (these are summarized and compared in detail in Discussions Section 6.1). Along with the disagreement on experimental determinations, various DFT functionals and parameters have been applied in the electronic structure calculations in previous studies with varying results.

Antiferromagnetic transitions at 52 K and at 125 K for LiFePO₄ and FePO₄, respectively, have been confirmed experimentally.^14,15 Accordingly, antiferromagnetic (AFM) configurations have been set up in some DFT calculations,¹⁶ since DFT is, in principle, a ground state theory (valid at absolute 0 K). However, in terms of the battery applications, we are more interested in properties at room temperature, where the magnetic order is paramagnetic for both LiFePO₄ and FePO₄. As a consequence, calculations with alternative ferromagnetic (FM) and non-magnetic (NM) configurations have also been reported in previous literature.^9,17–20 By using the local density approximation (LDA) with ferromagnetic configuration, Xu et al.²¹ claimed that LiFePO₄ is a half metal with spin-down Fe-3d states across the Fermi level, while the generalized gradient approximation (GGA) with antiferromagnetic configuration showed a band gap of 0.5 eV.¹⁶

It is well established that the LDA and GGA functionals generally underestimate band gaps for semiconductors, insulators and strongly correlated systems, to the point that it is usually referred to as ‘the band gap problem’.²² Because of the presence of partially filled highly localized 3d-orbitals in Fe^2+/3+ ions, LiFePO₄ and FePO₄ are grouped with the strongly correlated systems, for which the band gap would be severely underestimated using LDA and GGA.^23–25 Therefore, DFT (LDA or GGA) with Hubbard U corrections (DFT+U), as a low-cost correction method, has become the most popular functional used in the electronic structure calculation of LiFePO₄ and FePO₄. Hubbard U is a Coulomb parameter, which introduces a repulsion between the localized electrons in d or f orbitals, which can cause a split of these orbitals and thereby can open up a gap.²⁶ Therefore, the choice of Hubbard U is critical to obtain a theoretical band gap close to the experimentally determined values.

Cococcioni et al.²⁷ reported a Hubbard U of 3.71 eV for LiFePO₄ and 4.90 eV for FePO₄ with olivine structure calculated by a self-consistent method. Zhou et al.⁹ achieved good agreement with the most accepted experimental optical gap of 3.8 eV for LiFePO₄ using GGA+U with U = 4.3 eV (the average of U values obtained in the literature²⁷ for LiFePO₄ and FePO₄). More recently, the hybrid functional Heyd–Scuseria–Ernzerhof (HSE06) has also been used in the investigation of the electronic structure of LiFePO₄.^28–31 Improved accuracy on the prediction of the band gap and the character near the Fermi level was found compared with GGA+U, along with an increase in computational cost.

In this study, LiFePO₄, and its delithiated phase, FePO₄, with low residual carbon were prepared using various synthesis approaches. Their band gaps were studied experimentally by UV-Vis-NIR diffusion reflectance spectroscopy and electron energy loss spectroscopy (EELS) to provide a solid basis to validate the DFT calculations. Particle surface characteristics were also examined using X-ray photoemission spectroscopy (XPS) and Raman spectroscopy. Based on results from our use of simultaneous experimental techniques, a range of functionals for DFT calculations of the band structure of olivine LiFePO₄ and FePO₄ have been re-evaluated, including GGA, GGA+U and HSE06. The effect of magnetic configuration and Hubbard U on the estimated band gaps and band structures near the Fermi level were investigated in detail. Calculations with screened-exchange LDA (sX-LDA, CA-PZ),^32,33 which is another recommended hybrid functional for more accurate band gap calculations, not used or reported previously as extensively as HSE06, were also carried out. An interpretation of open-circuit voltage of a LiFePO₄ cell system has also been attempted from combined experimental inputs and electronic band structure calculation perspectives.

2. Experimental methods

2.1 Sample preparation

To investigate the band gap experimentally, LiFePO₄ with low residual carbon was prepared by both hydrothermal and solution-based synthesis methods. For hydrothermal synthesis, the raw material handling was conducted under Ar atmosphere inside purged glove bag. FeSO₄·7H₂O (≥99%, Sigma-Aldrich) and H₃PO₄ (85 wt%) were dissolved in 25 mL deionized water with magnetic stirring. 25 mL of LiOH·H₂O (99%, Sigma-Aldrich) solution was then slowly added to the above solution to bring the concentration of Fe²⁺ to 0.3 M and the molar ratio Li : Fe : P = 3 : 1 : 1. The resulting mixture was deoxygenated using bubbling Ar for 30 min and then transferred into a 100 mL stainless steel autoclave with Teflon lining. The sealed autoclave was placed into a muffle furnace and heated up to 170 °C for 12 h under Ar. Subsequently, the autoclave was cooled down to room temperature before opening. The precipitates were washed six times by immersing them in deionized water and ethanol and separating the precipitates via centrifuge. For solution-based synthesis, oxalic acid dihydrate (≥99%, Sigma-Aldrich) and Fe oxalate dihydrate (99%, Sigma-Aldrich) were mixed in deionized water first. 30 wt% H₂O₂ was slowly added into the mixture under magnetic stirring to dissolve Fe oxalate. The temperature was controlled below 65 °C during this process to avoid the formation of impurities. Stoichiometric amounts of Li₂CO₃ (≥99%, Sigma-Aldrich) and H₃PO₄ (85 wt%) were added into the solution. A very small amount of polyethylene glycol (PEG) was added to obtain nano particles. The resultant clear green solution was drawn into a vessel and reacted under vacuum. The resultant precursors were ring milled and calcined at 710 °C under Ar atmosphere to form the LiFePO₄ phase. A fraction of the powders was mixed with 8 wt% sucrose and calcined in an Ar atmosphere for carbon coating. FePO₄ was obtained by chemical delithiation of LiFePO₄. H₂O₂ was used as oxidant for LiFePO₄ powder dispersed in water, as the stability of LiFePO₄ in water has been reported previously.³⁴

2.2 Microstructural characterization

The structure and morphology of the samples were characterized by X-ray diffraction (XRD) and scanning electron microscopy (SEM). XRD was collected on a PANalytical X'Pert pro diffractometer with Co-Kα radiation, over a 2θ range between 15° and 90° with a 2θ step size of 0.017. The morphology and microstructure of the samples were investigated with a JEOL 7001 SEM. Carbon analyses were conducted using a LECO TruMac CNS analyser. The furnace temperature for the sample was 1300 °C. The oxidation state of Fe was investigated with X-ray photoelectron spectroscopy (XPS, Kratos AXIS Supra photoelectron spectrometer) using a focused monochromated Al K_α radiation (hν = 1486.6 eV). The spectra were calibrated using the C 1s peak at 285.0 eV. Particle surface characteristics were also examined with Raman spectroscopy with a Renishaw inVia Microscope equipped with a long working distance 50× objective lens and a 534 nm Ar⁺ laser light source. The power was controlled at 1% to avoid damaging the sample during measurement.

2.3 Band gap measurements

To validate the DFT functionals, the band gaps of LiFePO₄ and FePO₄ were investigated using various techniques. UV-Vis-NIR diffusion reflectance of the synthesized LiFePO₄ and delithiated FePO₄ were measured by a double-beam spectrophotometer Agilent Cary 5000. The wavelength range was set to 175–2800 nm. Data were collected at a scan rate of 600 nm min⁻¹ with a data interval of 1.0 nm, a signal bandwidth of 2.0 nm and signal averaging time of 0.1 s in the UV-Vis range. In the near IR range, the signal bandwidth was set at 4.0 nm. During the collection, the grating and detector were changed over at 800 nm, and the light source was changed over at 350 nm.

Electron energy loss spectroscopy (EELS) of the LiFePO₄ phase was conducted on an FEI Tecnai F20 scanning transmission electron microscope operating at 80 kV. At this operating voltage, the resolution was determined to be 0.6 eV. Lowering the acceleration voltage can minimize the beam damage and eliminate the peak caused by Cherenkov losses.³⁵ A short exposure time of 0.5 s was used during the acquisition of the low energy loss spectrum. To eliminate the overlap of plasmon peaks in the low energy loss spectra, the powders were pressed into pellets and ion milled to ∼20 nm in thickness using a precision ion polishing system (Gatan, Model 691).

3. Theoretical calculations

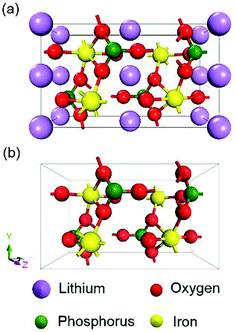
All the calculations were performed within the framework of DFT using the CASTEP module in Material Studio 2017. Approaches with GGA-PBE,³⁶ GGA+U (U = 0, 1, 2, 3, 4, 5, 6 eV), HSE06 and sX-LDA (CA-PZ) functionals were conducted. The calculated Hubbard U in the literature (U = 3.71 eV for LiFePO₄ and U = 4.90 eV for FePO₄)²⁷ were also used for comparisons. The electronic wave functions at each k-point were expanded in terms of a plane-wave basis set and an energy cut-off of 900 eV was chosen. The separation of k-points in GGA and GGA+U was set to 0.03 Å⁻¹, while that for HSE06 and sX-LDA was set to 0.07 Å⁻¹ to reduce the computational cost. Norm-conserving pseudo potentials and density mixing schemes were used in the calculations when the method allowed it, otherwise, ‘All Bands/EDFT’ was applied. The chosen parameters guaranteed that the total energy of the system could be evaluated accurately and the energy convergence is within 1.0 × 10⁻⁶ eV per atom. Schematics of the crystal structures of olivine LiFePO₄ and FePO₄ are shown in Fig. 1. The crystal structure and lattice parameters used for calculation were obtained from the PDF-4 database. The lattice parameters for LiFePO₄ at room temperature (RT) are a = 10.32525 Å, b = 6.00594 Å and c = 4.69246 Å with a space group of Pnmb (group number 62),³⁷ while those for FePO₄ are a = 9.8142 Å, b = 5.7893 Å and c = 7.4820 Å with a space group of Pnma (group number 62).³⁸ Given that both LiFePO₄ and FePO₄ are antiferromagnetic with Neel temperatures 52 K and 125 K, respectively,^14,15 ground state antiferromagnetic configurations are set up for all calculations with magnetic moment alignment based on previous literature.³⁹ Calculations are often undertaken in the Energy setup of the calculation, where lattice parameters remain constant at the chosen RT values. Since paramagnetism is expected at RT, non-magnetic (NM) configurations have also been explored.

Fig. 1 Crystal structure of olivine (a) LiFePO₄ and (b) FePO₄ obtained from the PDF-4 database.

4. Experimental results

4.1 Microstructure characterization

The XRD pattern of the synthesized LiFePO₄, together with the reference peak positions, are shown in Fig. 2a. No other peaks, except those of olivine LiFePO₄, were detected for samples synthesized with both the solution-based (LFP-S) and hydrothermal (LFP-H) methods. The crystallite size calculated from XRD using the Scherrer equation was 64 nm for LFP-S and 74 for LFP-H. SEM micrographs are displayed in Fig. 2c and d. The LFP-S samples consisted of nano particles of ∼350–400 nm in diameter and the LFP-H samples consisted of plate-like particles of ∼3–6 μm indicating that the particles were polycrystalline. The XRD pattern, together with the reference peak positions, and a SEM micrograph for the LFP-S samples after 48 h delithiation are shown in Fig. 2b and e, respectively. Pure olivine FePO₄, within the detection limits of XRD (about 2%) was obtained without obvious change of the morphology of the particles and labelled as FP-S. Therefore, this delithiated sample was used to study the band structure of FePO₄. 0.08% residual carbon was detected in both LFP-S and FP-S.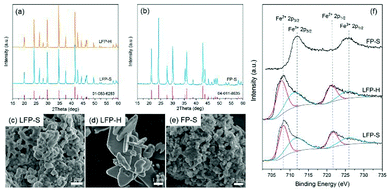

Fig. 2 (a and b) XRD patterns, (c–e) SEM micrographs and (f) XPS spectra for synthesized LiFePO₄ and FePO₄ samples respectively.

The surface oxidation states were investigated via XPS. The Fe-2p high-resolution spectra are illustrated in Fig. 2f. Around 50% of Fe ions were detected to be Fe³⁺ on the surface of both LFP-S and LFP-H particles, even though XRD indicated phase purity. In order to achieve charge neutrality, 50% Li vacancies must appear on the LiFePO₄ surface, which has been proven to be the most stable surface arrangement by energy minimization calculations and annular bright field (ABF) imaging in aberration-corrected scanning transmission electron microscopy (STEM) in the literature.⁴⁰ On the other hand, no Fe²⁺ 2p peaks were detected on the surface of delithiated samples.

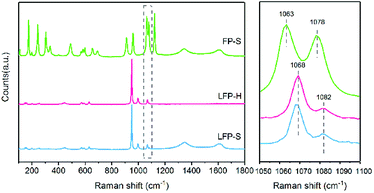
Raman spectroscopy has also been conducted to confirm the surface state of the samples. As shown in Fig. 3, the peak at 1068 cm⁻¹ appears accompanied by a tiny peak at 1082 cm⁻¹ in both LiFePO₄ samples. According to the investigation of Burba et al.,⁴¹ these peaks originate from the antisymmetric stretching mode of PO₄³⁻ anion in LiFePO₄ at ∼1072 cm⁻¹ due to deficiency of Li. These two peaks red-shift along with the extraction of Li. The 1063 cm⁻¹ and 1078 cm⁻¹ peak are assigned to the antisymmetric stretching mode of PO₄³⁻ anion in FePO₄. Therefore, the existence of Li depletion and Fe³⁺ on the surface of LiFePO₄ has been confirmed by both XPS and Raman spectroscopy.

Fig. 3 Raman spectra for the synthesized samples.

4.2 Band gap measurements

The band gaps of LiFePO₄ and FePO₄ were initially investigated via UV-Vis-NIR diffusion reflectance spectroscopy. The measured absorbance spectra and the corresponding Tauc plots⁴² obtained for LiFePO₄ and FePO₄ are shown in Fig. 4. The steps in the absorbance spectra at ∼1.55 eV (800 nm) were caused by the changeover of the detector. Unlike the results reported in previous literature,^9,11 the absorbance rose gradually in the range of 1.7–5 eV and no obvious absorbance edge in the measured energy range could be found for LFP-S. More pronounced absorption features were observed for LFP-H samples, as a peak at ∼0.3 eV and as a sharpened edge rising up at ∼2.8 eV, which may be caused by increased signal from (020) facets (as illustrated in the XRD spectra in Fig. 2a).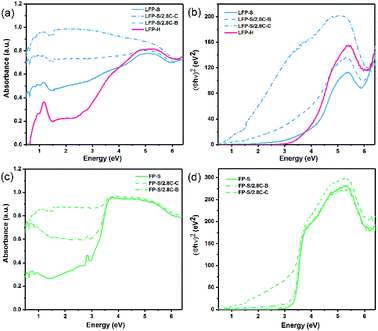

Fig. 4 UV-Vis-NIR absorbance spectra and corresponding Tauc plots for (a and b) LiFePO₄ and (c and d) FePO₄.

To further understand the role of residual or added carbon on the gradual absorbance increase or the position of the absorbance edge, 2.8 wt% carbon was coated around (labelled LFP-S/2.8C–C) or mechanically blended with (labelled LFP-S/2.8C–B) the LFP-S particles. An estimate of the average thickness of the carbon coating, assuming spherical LiFePO₄ particles of uniform 350–400 nm diameter (consistent with SEM images (see Fig. 2)), results in about 2.5–2.9 nm thickness. Thus, as demonstrated in Fig. 4a, a thin carbon coating (<3 nm thick) largely erases the hump-shaped gradual absorption of LiFePO₄ from 2.5 to 4.5 eV. Similar erasing of the absorption feature was also found in LFP-H samples, as shown in ESI Fig. S1.† It appears that there may be an absorption edge in LiFePO₄ when the energy is higher than 6 eV (undetectable in FePO₄). However, the optical spectrum beyond 6.5 eV could not be obtained due to limitations of the equipment. In contrast to the LiFePO₄, FePO₄ had a main absorption edge at 3.2 eV with a small peak at 2.7 eV, as shown in Fig. 4b. This result is consistent with the measurements of Furutsuki et al.¹³ reported recently. These two characteristics became less prominent but didn't disappear or shift position with the addition of carbon, suggesting they are inherent properties of the bulk of FePO₄.

Tauc plots of (Φhν)ⁿ vs. photon energy, are widely used to interpret the UV-Vis diffusion reflectance results, where Φ = (1 − R)²/(2R) is the Kubelka–Munk (KM) function,^43,44 R is the reflectance and n = 2 and n = 0.5 (ref. 11) have been previously used for LiFePO₄ and FePO₄, respectively. In Fig. 4b and d, n = 2 is used for both LiFePO₄ and FePO₄, which appears to produce a sharper and more linear edge compared to n = 0.5. The spectra of FePO₄ shows clear linear edges. Extrapolation the linear part of the Tauc plot to the x-axis results in a band gap of 3.24 eV, which is close to the value obtained directly from the absorbance spectra. On the other hand, the Tauc plots of LiFePO₄ samples show gradual absorption edges and more pronounced Urbach tails⁴⁵ compared with those of FePO₄ samples. Further, while the addition of carbon didn't have a significant effect on the positions of the Tauc plot edges in FePO₄, the coated carbon produced a significant shift of ∼3 eV toward lower energies in the Tauc plot absorption edge of LiFePO₄ (see Fig. 4b), indicating that a nm-scale carbon coating has a more complex interaction with the surface of LiFePO₄ particles than just producing an increased background absorption. This also opens the question as to what complex effects a nano-scale delithiated surface layer will have on the absorbance spectra of LiFePO₄. It thus appears that absorption humps and tails are not part of the inherent absorption edge for the core of the LiFePO₄ material, but a result of a combination of nm-scale surface layers of lithium depletion and carbon. The Tauc plots of LFP-H samples are displayed in ESI Fig. S1.†

EELS was utilized to obtain the energy absorption beyond 6 eV and to determine the band gap of LiFePO₄. Fig. 5 illustrates the low electron energy loss spectrum (LEELS) for LFP-S. The small downward slope before 3 eV is the tail of the zero-loss peak (ZLP). The main energy absorption starts at 6.34 eV (as shown in Fig. 5b), indicating a band gap of 6.34 eV, which is much larger than previously reported optical results.^9,11 It is worth noticing that there is a small amount of absorption before the onset of the main absorption peak, which was consistent with the slow rise in the range of 1.55–5 eV of the UV-Vis-NIR absorbance spectrum of LiFePO₄ in Fig. 4a. Although not measured in this paper, the LEELS spectrum for FePO₄ can be found in several ref. 35 and 46–48. An energy absorption peak below 5 eV can be found in all of the FePO₄ results, although because of the existence of ZLP at 0 eV (whose width is usually ∼0.2–2 eV), the onset of the absorption is usually merged with the tail of ZLP and hard to be determined. So EELS is not very suitable for the band gap determination when the value is less than 5 eV. However, those absorption features in the 3–6 eV region in the EELS of FePO₄ are clearly absent in the EELS of LiFePO₄.^35,47,48 Thus, this is not attributable to limitations of the technique, but more likely to the fact that those peaks are not representative of the bulk, core LiFePO₄ materials.

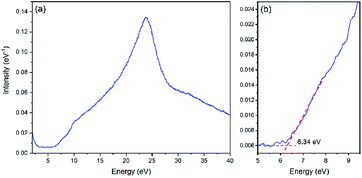Fig. 5 (a) Low electron energy loss spectrum (LEELS) for LiFePO₄. (b) Magnification of the onset of energy loss in LEELS.

5. Electronic structure calculations

Since band gaps of 3.8 eV and 1.8 eV have been generally accepted for LiFePO₄ and FePO₄, respectively, many of the validations in previous literatures of the DFT functionals for the electronic band structure calculations of LiFePO₄ and FePO₄ have been conducted based on those values. As larger band gaps, 6.34 eV for LiFePO₄ and 3.2 eV for FePO₄, have been determined in this study, the validity of the currently used DFT functionals is questionable. Therefore, the electronic band structure calculations with various different DFT functionals, such as GGA, GGA+U and HSE06, have been revisited. The validity of sX-LDA, which has not been applied to LiFePO₄ and FePO₄ to our knowledge, also has been studied.

5.1 (Semi-)local functionals

Although the band gap underestimation for GGA has been widely reported before, the calculations on LiFePO₄ and FePO₄ have been revisited in this study. As both LiFePO₄ and FePO₄ are antiferromagnetic at 0 K and paramagnetic at room temperature, GGA with antiferromagnetic (AFM) and non-magnetic (NM) configurations were established to determine the effect, if any, of magnetic order on the calculated band gaps. The resulting electronic band structures are displayed in ESI Fig. S2.† Similar electronic band structures with gaps of 0.50 eV and 0.63 eV were obtained for LiFePO₄ with NM and AFM configurations, respectively, while FePO₄ showed a metallic feature with NM configuration and a semiconductor feature with a band gap of 1.31 eV with AFM configuration. Therefore, the band structure prediction of FePO₄ is more affected by the inclusion of spin polarization.

Although the inclusion of spin polarization can open up the band gap to some extent, GGA is incapable of producing relatively accurate electronic structure calculations for both LiFePO₄ and FePO₄. The impact of the correction parameter, Hubbard U, has also been studied. Due to the necessity of spin polarization in GGA+U, AFM was set up in all of these calculations. The changing trends of estimated band gaps with respect to Hubbard U are demonstrated in Fig. 6. The estimated band gap increased almost linearly along with the increase of Hubbard U for both LiFePO₄ and FePO₄ when U was below 4 eV and increased more gradually when U was beyond 4 eV. The band gap of LiFePO₄ showed more sensitivity to Hubbard U than that of FePO₄. Even though the maximum estimation of 3.96 eV was achieved when U = 6 eV in this work, the estimated band gap for LiFePO₄ was much smaller than the experimental value of 6.34 eV. The largest gap of 2.53 eV was obtained between the VBM and unoccupied localized Fe-3d states for FePO₄, approaching the experimentally determined band gap, but still somewhat underestimated.

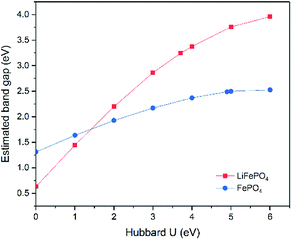Fig. 6 Changing trends of estimated band gaps with respect to chosen Hubbard U parameters. Due to the requirement of GGA+U, only AFM configuration was carried out.

In addition to the significant underestimation of the band gap, the orbital character of LiFePO₄ near the Fermi level also changed along with the increase of Hubbard U. As shown in Fig. 7a, for olivine LiFePO₄, the unoccupied d states were pushed upwards from the Fermi level to open up a wider band gap with the inclusion of a larger Hubbard U. In the meantime, the occupied O-2p states were also moved towards the Fermi level with the increase of U. When U was above 4 eV, the occupied d states started to align with the O-2p states. The VBM for LiFePO₄ changed from occupied Fe-3d states to hybridized Fe-3d–O-2p states. O-2p states even became the majority states in the VBM when the Hubbard U was 6 eV, which is physically unrepresentative for LiFePO₄,⁴⁹ as it will be discussed in detail later. Although the composition of the VBM and CBM didn't change, the proportion of Fe-3d in the VBM also decreased with the increase of Hubbard U for FePO₄ (Fig. 7b).

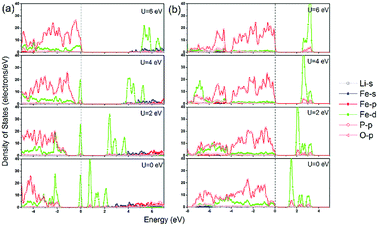Fig. 7 Partial density of stats (PDOS) calculated in GGA and GGA+U for (a) LiFePO₄ and (b) FePO₄ with AFM configuration.

5.2 Hybrid functionals

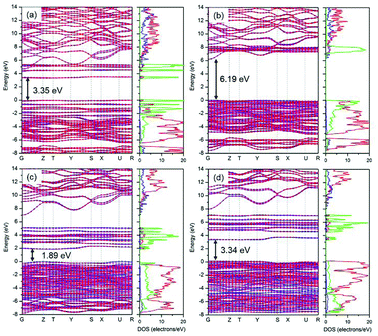
As mentioned above, HSE06 has recently been applied to LiFePO₄ and related olivine phosphates and has been proven to be superior to GGA+U.^29–31 However, as another most reliable functional for electronic structure calculations and band gap determinations,^32,50 sX-LDA does not appear to have been used as extensively for electronic band structure calculation for either LiFePO₄/FePO₄ or other olivine phosphates. In this study, sX-LDA and HSE06 with NM and AFM configurations have been conducted for comparison. The estimated band structures and DOS with NM configurations are shown in ESI Fig. S3.† Similar to GGA, FePO₄ showed metallic features with valence states crossing the Fermi level when excluding spin polarization within hybrid functionals, while band gaps of 3.55 eV and 6.19 eV between occupied and unoccupied Fe-3d states were observed for LiFePO₄ within HSE06 and sX-LDA, respectively. Fig. 8 illustrates the band structures obtained by HSE06 and sX-LDA with AFM configurations. The magnetic order did not have a significant effect on the electronic band structure for LiFePO₄ (compare Fig. 8a, b and Fig. S3a, b†). The calculated band gap of about 6.2 eV within sX-LDA showed better agreement with the experimental value of LiFePO₄ (6.34 eV) than that obtained by HSE06 (3.35 eV). Hybridized Fe-3d–O-2p states were predicted for the VBM, indicating that there was partial charge transferred from oxygen to iron during delithiation, which is consistent with a recent experimental study.⁵¹ In the meantime, the inclusion of AFM order opened up a band gap of 3.34 eV for FePO₄ within sX-LDA (Fig. 8c), which also matched well with the experimental measurement. HSE06 exhibited a relatively small band gap of 1.89 eV and a Fe-3d-dominated VBM for FePO₄, which is in conflict with the experimental fact.³⁵

Fig. 8 Estimated band structure and DOS of (a and b) LiFePO₄ and (c and b) FePO₄ within HSE06 and sX-LDA respectively. AFM configuration was applied. The blue and red lines represent the alpha and beta spin.

For further scrutiny, the calculated DOS of HSE06, sX-LDA and GGA+U have been compared to the experimental XPS valence band spectra in Fig. 9. The Hubbard U used here is taken from prior calculated values in the literature.²⁷ Both of the hybrid functionals reproduce the valence band structures of LiFePO₄ and FePO₄ better than GGA+U. The relative peak positions are better reproduced using HSE06 and sX-LDA, although the spectra are slightly compressed in the range of 0–10 eV for both compounds. The spectra using GGA+U are compressed in the whole measured energy range leading to underestimation of the binding energy.

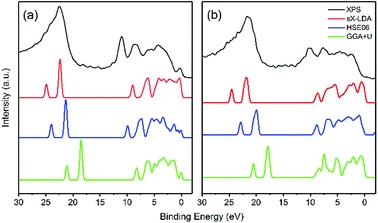Fig. 9 Comparison of experimental valence band structure of (a) LiFePO₄ and (b) FePO₄ to the DOS of DFT calculations.

6. Discussions

The following discussion first revisits the wide range of reported band gaps in Section 6.1, opening the question why such a variability exists and if there is a possible connection with some kind of undetected or uncharacterized microstructural feature. This is followed by Section 6.2, where clear evidence of delithiated surfaces in very carefully synthesized LiFePO₄ samples is discussed and connected to the possibility of significant absorption edge shifts (of several eVs) by such thin layers. These results are shown to allow for a more consistent and coherent picture of combined experimental observations, both previously reported and obtained in the present study. Section 6.3 then re-assesses the DFT calculations of band gaps for LiFePO₄ and FePO₄ phases, in light of the extensive, combined experimental evidence, that surface delithiation is a very likely source for impurity-like in-gap states.

6.1 Comparison of experimental band gaps

As summarized in Table 1, the band gaps of LiFePO₄ and FePO₄ have been measured by several techniques. Zhou et al.⁹ first studied the band gap of LiFePO₄ by UV-Vis-NIR diffusion reflectance spectroscopy, and a band gap of 3.8–4.0 eV was obtained. The results by Zhou et al. had an enhanced slope around 4 eV, which looks similar to the absorption of our LFP-H samples. Unfortunately, Zhou et al.'s spectrum was truncated below 2.1 eV, not allowing full comparison with our results. We clearly see that sharpening of the 4 eV edge is accompanied by the rise of a peak feature at about 0.6 eV (see Fig. 4 above). Zhou et al.'s result was in good agreement with the investigation of Zaghib et al.,¹¹ which also displayed a truncated spectrum (1.8–6.2 eV). A band gap of 1.88 eV for FePO₄ was also determined in Zaghib et al.'s study and became the generally accepted value in following studies. However, an absorption edge at 1.88 eV would likely result in an orange or red colour of the material, which is not consistent with the greyish colour of FePO₄ powders. Recently, the band gap of FePO₄ reported by Furutsuki et al.¹³ was ∼3.0 eV, which is close to the result in this study. They also claimed that the band gap of LiFePO₄ was 4.8 eV, but no significant absorption was found before 5.8 eV. The features labelled as the band gap appears to be equivalent to the beginning of the Urbach tails and not the linear part of the Tauc plot. So the linear absorption, corresponding to the 5.8 eV absorption, is more in line with our claim that the true band gap absorption edge is at 6.34 eV (see Fig. 5).

Table 1 Comparison of band gap measurements in previous studies the present work for LiFePO₄ and FePO₄

	Method	Band gap	Reference
LiFePO4	UV-Vis	3.8–4.0 eV	9
	UV-Vis	3.84 eV	11
	UV-Vis	4.8 eV, but no significant absorption before 5.8 eV	13
	XAS and RIXS	<0.95 eV	10
	XAS and XES	4.0 or 0.5 eV	12
	EELS	6.34 eV	This work
FePO4	UV-Vis	1.88 eV	11
	XAS and XES	1.7 eV	12
	UV-Vis	∼3.0 eV	13
	UV-Vis	3.2 eV	This work

---

XAS, combined with RIXS¹⁰ or XES,¹² were also applied to study the electronic band structure of LiFePO₄ and FePO₄. Unfortunately, no specific value of band gap was clearly reported. Augustsson et al.¹² claimed that the band gap could not be determined easily because of the uncertainty identifying the CBM from XAS spectra, due to the presence of a small bump between the VBM and the high intensity absorption peak. Thus, it appears that Augustsson et al. had issues with the relatively weak absorption nature of the pre-edge feature around 4 eV, and decided to label this value as the band gap, just because the absorption was detected, not further questioning a possible localized or impurity-like nature of the detected absorption. Similar pre-edge bumps have also been reported in soft X-ray absorption spectra of the O–K edge of LiFePO₄ nanoparticles by Liu et al.⁵² They identified them as a result from surface effects, due to the absence of this pre-edge feature in the spectra from single crystal LiFePO₄. A band gap of 6.2 eV for LiFePO₄ could be obtained if we boldly assume the main absorption peak (A4 in Fig. 2 of ref. 12) in X-ray absorption-emission spectra represents the CBM, which matches well with our band gap obtained by EELS.

As mentioned above, increase of absorbance for LiFePO₄ at ∼4 eV was also found, but not considered as the absorption edge in this work. Small amount of carbon coating or addition totally eliminate the bump in the absorption spectra of LiFePO₄, or shift the linear region of the Tauc plot to lower energies by several eVs (for the coating case), making the bump look like a surface related absorption, as discussed further below.

6.2 Surface delithiation

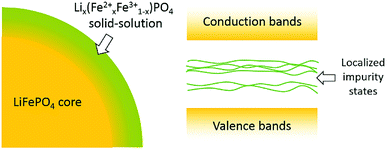
As mentioned above, the surface delithiation of the LiFePO₄ particles has been confirmed by XPS and Raman spectroscopy in both LFP-S and LFP-H. It is tempting to associate the surface delithiation to poor quality samples or to loss of Li from high temperature or initial off-stoichiometry in the raw material mix. However, hydrothermal samples are prepared in an excess of lithium hydroxide and at a temperature limited to <200 °C. Therefore, it appears that delithiated surfaces are a preferred equilibrium condition for good quality LiFePO₄ samples. Similar surface delithiation has also been observed in other investigations.^53,54

A schematic of a LiFePO₄ particle surface is illustrated in Fig. 10. As detected by XPS, nearly half of Fe ions on the surface were Fe³⁺, suggesting a solid-solution Li_x(Fe_x²⁺Fe_1−x³⁺)PO₄ outer layer around the LiFePO₄ core. Intervalence charge transfer has been confirmed experimentally and explained theoretically in the literature¹³ for Li_0.6(Fe_0.6²⁺Fe_0.4³⁺)PO₄ solid-solution, as the Fe³⁺-3d states fell in the gap between Fe²⁺-3d states. Similar situation can also be expected that the mixed oxidation states of Fe on the surface result in localized Fe-3d impurity states inside the band gap of bulk LiFePO₄ (as shown in Fig. 10), leading to the gradual increase in optical absorption spectra in the range of 1.7–4 eV. A similar effect of a solid-solution surface on the optical absorption spectra has also been found for HfO₂ with well-controlled Al and N surface diffusion.⁵⁵ Nanometer-scale diffusion profiles were responsible for substantial reductions in the onset of optical absorption edge energies and for much more gradual slopes, very closely resembling the in-gap features observed in LiFePO₄.

Fig. 10 Schematic of LiFePO₄ particle surface and resulting electronic band structure. The existence of Fe³⁺ ions on the surface introduces localized impurity states in the band gap of bulk LiFePO₄ which results in the gradual increase in optical absorbance spectra.

6.3 Comparison of DFT functionals

GGA+U, HSE06 and sX-LDA, the most practical DFT functionals for electronic band structure calculations with more reliable band gap determinations, are being compared in this section. It is worth pointing out that the dispersion of the dense VBM and CBM regions appear similar in all the calculations and that the main differences are related to the position of the localized d states and to the band energy separations that define the band gaps.

Since being developed in the 1990s,⁵⁶ DFT+U has become a well-accepted functional to deal with electron correlation in transition metal and rare earth compounds. With this functional, the delocalized states are treated by conventional LDA/GGA while the localized states are treated by inclusion of a Hubbard-like term. According to its basic features, the Hubbard model accounts for the electronic ground states through balancing two competing energies: the hopping energy and the Coulomb energy. The hopping energy includes motion of electrons with the same spin between different atoms, while the Coulomb energy represents the repulsion of electrons with opposite spin on the same site as a function of the Hubbard U parameter.⁵⁷ Therefore, the choice of Hubbard U is critical in DFT+U calculations. However, the value of Hubbard U varies with atomic species, valence states of ions, lattice structures and coordination polyhedral, limiting its ab initio applications. It is thus difficult to determine a self-consistent U value for a specific material. Despite this, DFT+U has been extensively used in electronic structure investigations of olivine phosphates. Although Hubbard U of 3.71 eV and 4.0 eV were calculated by Cococcioni for Fe²⁺ and Fe³⁺ in the olivine structure,²⁷ widely different values of Hubbard U have been chosen depending on the specific purpose (as summarized in Table S1†). In recent studies, U ≈ 4.5 eV for Fe in LiFePO₄ has become most popular because of the high accuracy based on the optical energy gap of 3.8 eV.

In this study, since the band gap of LiFePO₄ was determined to be 6.34 eV, GGA+U resulted in band gap underestimation even if Hubbard U of 6 eV was applied. Moreover, the major atomic states character at the VBM changed with respect to the increase of Hubbard U, which also leads to problems with physico-chemical interpretation. The same changes in VBM also happens for other olivine phosphates. ESI Fig. S4† shows the PDOS of LiMPO₄ (M = Fe, Mn, Co and Ni) estimated with GGA and GGA+U. The Hubbard U was taken from previous calculations by Cococcioni et al.,²⁷ which were obtained by a self-consistent linear response method. Except for LiFePO₄, the dominant states of the VBM for all other three olivine phosphates changed to O-2p states after the application of Hubbard U. For LiMnPO₄, even GGA provides dominant O-2p states at the VBM. In the scenario of battery application, the electrons leave the cathode with the extraction of Li⁺ during charging, while the reverse process occurs during discharging. Accordingly, the composition of the VBM for the cathode material determines which electrons take part in the charge transfer during charging and discharging. ESI Fig. S5† illustrates schematic energy levels for a LIB system with different types of VBMs in the cathode. The partially filled transition metal 3d states (TM-3d) represent the transition metal redox couple. If the TM-3d states locate at the top of O-2p states and dominate the VBM as shown in Fig. S5a,† it indicates the oxidation/reduction of the transition metal ions will occur along with the extraction/insertion of Li⁺ during charging and discharging. This interpretation is consistent with the LiMPO₄/MPO₄ phase transformation observed in previous studies.^4,46 If O-2p states take control of the VBM of the cathode, the oxidation of O²⁻ will lead to the release of O₂ in the process of charging, which eventually leads to the collapse of the lattice structure, contradicting experimental evidence. Similar discussions have been made in previous literature.^28,30 Therefore, it can be concluded that GGA+U may provide values that match some experimental determinations of band gaps, however, it does so at the expense of the DOS character, which is very important for physico-chemical interpretation. Therefore, as a whole, GGA+U may be inadequate as a DFT functional for electronic structure calculations for olivine phosphates LiMPO₄ (M = Fe, Mn, Co and Ni).

Improvements in band gap calculations of a wide range of semiconductors and insulators have been reported previously for HSE06 and sX-LDA.^32,50 Both functionals mix a portion of Hartree–Fock (HF) exchange with (semi-)local functionals to achieve improved results. HSE functional separates the local potential into long- and short-range with the application of 25% HF exchange.^58,59 For HSE, the exchange–correlation energy is determined as

where E^HF,SR_X is the short-range HF exchange energy, E^PBE,SR_X and E^PBE,LR_X are the short- and long-range PBE exchange energy and E^PBE,SR_C is the PBE correlation energy.^59,60 The screening parameter ω represents the separation range, which has been determined to be 0.11 bohr⁻¹ for HSE06.⁵⁰ Compared with HSE06, sX-LDA includes 100% of HF exchange, which is screened to moderate the correlation effect, into LDA. This nonlocal potential is achieved by the inclusion of a factor which decays exponentially with electron separation. Its contribution to the total energy is
where i and j label electronic bands, k and q are k points and k_s is the Thomas–Fermi screening length,³² which determines the screening range of the electron interaction and is usually evaluated from the average electron density. Thus, the screening plays a similar role to U in DFT+U, by providing self-interaction correction and repulsion (or less attraction) for electrons with opposite spin at the same point.^32,61 It is worth noting that sX-LDA can achieve the correct asymptotic limit of the free electron gas and the sX-LDA functional is closer to the Coulomb-hole and screened-exchange (COHSEX) in the first-order GW method,⁶² indicating a better performance can be expected.

Although both HSE06 and sX-LDA give relatively reasonable valence band structure compared with GGA+U, HSE06 is still not efficient enough to open up the larger band gaps of LiFePO₄ and FePO₄. It has been reported that the calculated band gaps are closer to experimental results when ω gets smaller in the range of 0.11–0.20 bohr⁻¹.⁵⁰ However, further decrease of ω makes the calculations difficult to converge, which leads to extremely increased computational cost. Therefore, we can conclude that sX-LDA is superior for the electronic band structure calculation of olivine LiFePO₄ and FePO₄. Its effectiveness on the other olivine phosphates will be further studied and reported separately.

Although hybrid functionals show overall superiority in electronic band structure calculations, their weakness is more apparent in magnetic structure identification. High spin configurations for Fe²⁺ (3d↑)⁵(3d↓)¹ and Fe³⁺ (3d↑)⁵(3d↓)⁰ have been confirmed experimentally in previous literature.^15,39,63 As the Fe PDOS illustrated in ESI Fig. S6,† low or intermediate spin configurations [(3d↑)³(3d↓)³ or (3d↑)⁴(3d↓)² for Fe²⁺, and (3d↑)³(3d↓)² or (3d↑)⁴(3d↓)¹ for Fe³⁺] have been obtained within hybrid functionals for both LiFePO₄ and FePO₄, even though the high spin configurations was set as input for calculations. This change in spin configuration may result from the usage of ‘All Bands/EDFT’ minimizer, which will ignore the atomic configurations during calculations.⁶⁴ In comparison, the pre-set high spin configurations are ‘stabilized’ during GGA+U calculations by spin orientation and allowed transitions rules imposed as part of the construction of the methodology, which leads to a good match with experimental results.

6.4 Open-circuit voltage

Since the electrons transfer between cathode and anode through an external circuit along with the Li movement through the electrolyte during charging and discharging, the open-circuit voltage (V_OC) of a Li-ion battery system can be interpreted from both the perspective of the Fermi level and Gibbs free energies.^65,66

It has been generally accepted that the average voltage for Li insertion/extraction is given after appropriate electronic band structure alignment by:

where G is the Gibbs free energy of the materials. x₁ = 0 and x₂ = 1 were typically taken in as the composition limits. Hence, the energy of LiFePO₄, FePO₄ and Li metal was calculated to determine the voltage for Li intercalation. As shown in Fig. 11, sX-LDA shows the highest accuracy on the estimation of Li intercalation voltage among the compared functionals, while GGA and HSE06 underestimate and GGA+U overestimates the Li intercalation voltage for LiFePO₄.

Fig. 11 Estimated Li intercalation voltage for LiFePO₄ with different DFT functionals.

From the Fermi level perspective, the V_OC can be related to the difference of Fermi levels between the cathode and anode in a cell system, after appropriate work functions alignment (with respect to the vacuum level), as shown in the equation in Fig. 12. Because the electrons flow from the cathode with lower Fermi level to the anode with higher Fermi level during charging, driven by the external charging potential, they flow back to the cathode during discharging.⁶⁵ In the case of the LiFePO₄ half-cell, the V_OC at the fully discharged or charged states are related to the energy difference between the Fermi level of LiFePO₄ or FePO₄ and that of Li metal, respectively. Fig. 12 shows a typical charging curve of a LiFePO₄ half-cell and the relative phase diagram. The V_OC of LiFePO₄ and FePO₄ were obtained experimentally in a previous investigation.⁶⁷ As the Fermi level (or electrochemical potential) of Li metal does not change during charging, the V_OC differences of the fully charged and discharged state refer to the Fermi level position difference of FePO₄ and LiFePO₄. The Fermi energies of LiFePO₄ and FePO₄ (E_F,LFP and E_F,FP, respectively) have been obtained with GGA theoretically, which is considered more useful for the determination of the Fermi level⁶⁸ and is in reasonably good agreement with the experimental V_OC difference (∼1.8 V in the literature⁶⁷). The work functions of LiFePO₄ and FePO₄ have also been determined by ultraviolet photoelectron spectroscopy (UPS) with He I radiation (21.21 eV) experimentally. As shown in ESI Fig. S7,† the work functions of 5.98 and 6.82 eV have been determined for LiFePO₄ and FePO₄, respectively. The result for LiFePO₄ is in a good agreement with previous measurement by Kelvin Probe Force Microscopy (KPFM).⁶⁹ Though the relative alignment of Fermi levels for LiFePO₄ and FePO₄ has been confirmed experimentally, the relatively smaller difference in experimental work functions for the two phases may be related to the morphology, atmospheric exposure during sample handling, crystal orientation, difficulties with poorly conducting materials, etc.⁷⁰ Moreover, a work function lower that the value of the band gap appears unfeasible at first sight, however, it is not uncommon for materials with large band gaps to display negative electron affinities.^71–73

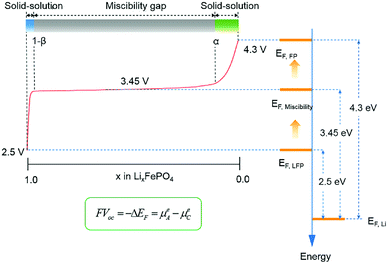Fig. 12 Typical charging curve of a LiFePO₄ half-cell with relative phase diagram and energy alignment at different charging states.

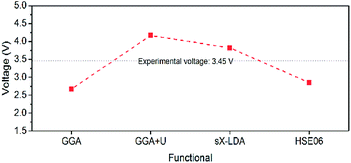
A two-phase reaction has been confirmed to be responsible for the voltage plateau at ∼3.45 eV for LiFePO₄ in a previous study.⁷⁴ From the perspective of the Fermi levels and work functions, the voltage plateau corresponds to the Fe^2+/Fe³⁺ redox couple, which sits approximately at the average Fermi levels of xLiFePO₄/(1 − x)FePO₄ (E_{F,Miscibility}), between E_F,LFP and E_F,FP, regardless of the proportion of the two phases. Furthermore, the plateau also provides a few hints about the relative position of E_F,Li and the electronic bands of LiFePO₄ and FePO₄. E_F,Li must be located in the forbidden gap of xLiFePO₄/(1 − x)FePO₄, below unoccupied d states, to achieve the flat working voltage. If the conductive bands of the cathode are located below the Fermi level of Li, a second voltage plateau with lower electrochemical potential difference would be expected to appear in the charge–discharge curve. It is also worth noticing that the V_OC in the solid-solution regions (0 < x < α, or 1 − β < x < 1) changes substantially with respect to any small change of x in Li_xFePO₄. It indicates that small changes in Li concentration at the solid-solution ends have a significant impact on the position of Fermi level for Li_xFePO₄.

7. Conclusions

In this study, electronic band gaps of 6.34 eV and 3.2 eV for LiFePO₄ and FePO₄ were experimentally determined, respectively. The continuous energy absorption for LiFePO₄ starting from ∼1.7 eV was shown to be a likely consequence of the existence of Fe²⁺/Fe³⁺ and Li deficiency on the LiFePO₄ surface. Such lithium deficiency exists at the nm or sub-nm scale and appears to be a preferred equilibrium feature, since it is present in all, including the most carefully synthesized, samples. The DFT functionals, GGA, GGA+U, HSE06 and sX-LDA, were re-examined according to the experimental band gaps. (Semi-)local functionals, GGA and GGA+U, show difficulties to achieve self-consistent prediction of the electronic structure of LiFePO₄, FePO₄ and other olivine phosphates (LiMnPO₄, LiCoPO₄ and LiNiPO₄), but succeed in stabilization of AFM configuration with high spin states. The inclusion of HF exchange within hybrid functionals can improve the valence band evaluation during electronic band structure calculation. Compared with HSE06, sX-LDA shows highest accuracy in electronic structure prediction for LiFePO₄ and FePO₄ with acceptable computational cost. However, both of the hybrid functionals compromise the atomic magnetic high spin order of the materials. The open-circuit voltage and charge–discharge curve of LiFePO₄/FePO₄ were interpreted from a Gibbs free energy and from a Fermi levels/work functions perspective. Both of them show good agreement with experimental facts, it thus gives indirect proof of the effectiveness of sX-LDA for the theoretical calculations of LiFePO₄ and FePO₄. Therefore, sX-LDA can be used as an appropriate guide in future compositional and structural modifications of LiFePO₄ to achieve improvements in properties such as higher power rate capability.

Besides optical diffuse reflectance measurements (which is limited to about 6 eV with standard light sources) and EELS mentioned in the paper, large band gaps (>6 eV) can be experimentally determined using UV ellipsometry or photo-conductivity measurements with a vacuum ultraviolet (VUV) monochromator.^75,76 Unfortunately, these suitable light sources are more specialized and not as readily available. Mirror reflectance spectra in the VUV region using synchrotron light or a deuterium lamp as an excitation source⁷⁷ can also give an energy range beyond 7 eV, but single crystal samples are needed. Further clarification on the band gap of LiFePO₄ and other olivine phosphates will be pursued, as soon as one of these alternative experimental techniques can be accessed or outsourced.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Yin Zhang would like to acknowledge CSIRO for the studentship, and the involvement of CRRC and the Rail Manufacturing Cooperative Research Centre (funded jointly by participating rail organisations and the Australian Federal Government's Cooperative Research Centres Program). The experimental data reported in this paper were obtained at the Central Analytical Research Facility operated by the Institute for Future Environments, Queensland University of Technology (QUT), Brisbane, Australia. Computational resources and services used in this work were provided by the HPC and Research Support Group, QUT. The authors would like to acknowledge Mr Llew Rintoul, QUT, for the assistance of Raman spectroscopy and Prof. Ian Mackinnon, QUT, for the critical review of the manuscript.

References

1. V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Challenges in the development of advanced Li-ion batteries: a review, Energy Environ. Sci., 2011, 4(9), 3243–3262.
2. L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, A review on the key issues for lithium-ion battery management in electric vehicles, J. Power Sources, 2013, 226, 272–288.
3. P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu and K. G. Gallagher, et al., Odyssey of Multivalent Cathode Materials: Open Questions and Future Challenges, Chem. Rev., 2017, 117(5), 4287–4341.
4. A. K. Padhi, K. Nanjundaswamy and J. B. Goodenough, Phospho-olivines as positive-electrode materials for rechargeable lithium batteries, J. Electrochem. Soc., 1997, 144(4), 1188–1194.
5. X.-C. Tang, L.-X. Li, Q.-L. Lai, X.-W. Song and L.-H. Jiang, Investigation on diffusion behavior of Li⁺ in LiFePO₄ by capacity intermittent titration technique (CITT), Electrochim. Acta, 2009, 54(8), 2329–2334.
6. M. Aydinol, A. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(3), 1354.
7. F. Zhou, M. Cococcioni, K. Kang and G. Ceder, The Li intercalation potential of LiMPO₄ and LiMSiO₄ olivines with M = Fe, Mn, Co, Ni, Electrochem. Commun., 2004, 6(11), 1144–1148.
8. Y. S. Meng and M. E. Arroyo-de Dompablo, First principles computational materials design for energy storage materials in lithium ion batteries, Energy Environ. Sci., 2009, 2(6), 589.
9. F. Zhou, K. Kang, T. Maxisch, G. Ceder and D. Morgan, The electronic structure and band gap of LiFePO₄ and LiMnPO₄, Solid State Commun., 2004, 132(3–4), 181–186.
10. A. Hunt, W. Y. Ching, Y. M. Chiang and A. Moewes, Electronic structures of LiFePO₄ and FePO₄ studied using resonant inelastic x-ray scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(20), 205120.
11. K. Zaghib, A. Mauger, J. B. Goodenough, F. Gendron and C. Julien, Electronic, optical, and magnetic properties of LiFePO₄: small magnetic polaron effects, Chem. Mater., 2007, 19(15), 3740–3747.
12. A. Augustsson, G. V. Zhuang, S. M. Butorin, J. M. Osorio-Guillen, C. L. Dong and R. Ahuja, et al., Electronic structure of phospho-olivines Li_(x)FePO₄ (x = 0, 1) from soft-x-ray-absorption and -emission spectroscopies, J. Chem. Phys., 2005, 123(18), 184717.
13. S. Furutsuki, S.-C. Chung, S.-i Nishimura, Y. Kudo, K. Yamashita and A. Yamada, Electrochromism of Li_xFePO₄ Induced by Intervalence Charge Transfer Transition, J. Phys. Chem. C, 2012, 116(29), 15259–15264.
14. A. Ait-Salah, J. Dodd, A. Mauger, R. Yazami, F. Gendron and C. Julien, Structural and magnetic properties of LiFePO₄ and lithium extraction effects, Z. Anorg. Allg. Chem., 2006, 632(8–9), 1598–1605.
15. C. M. Julien, A. Ait-Salah, A. Mauger and F. Gendron, Magnetic properties of lithium intercalation compounds, Ionics, 2006, 12(1), 21–32.
16. M. Milović, D. Jugović, N. Cvjetićanin, D. Uskoković, A. S. Milošević and Z. S. Popović, et al., Crystal structure analysis and first principle investigation of F doping in LiFePO₄, J. Power Sources, 2013, 241, 70–79.
17. Y.-N. Xu, S.-Y. Chung, J. T. Bloking, Y.-M. Chiang and W. Y. Ching, Electronic Structure and Electrical Conductivity of Undoped LiFePO₄, Electrochem. Solid-State Lett., 2004, 7(6), A131.
18. J. Jiang, C. Ouyang, H. Li, Z. Wang, X. Huang and L. Chen, First-principles study on electronic structure of LiFePO₄, Solid State Commun., 2007, 143(3), 144–148.
19. C. Ban, W.-J. Yin, H. Tang, S.-H. Wei, Y. Yan and A. C. Dillon, A Novel Codoping Approach for Enhancing the Performance of LiFePO₄ Cathodes, Adv. Energy Mater., 2012, 2(8), 1028–1032.
20. T.-F. Yi, Z.-K. Fang, Y. Xie, Y.-R. Zhu and C. Dai, Band structure analysis on olivine LiMPO₄ and delithiated MPO₄ (M = Fe, Mn) cathode materials, J. Alloys Compd., 2014, 617, 716–721.
21. Y.-N. Xu, W. Y. Ching and Y.-M. Chiang, Comparative studies of the electronic structure of LiFePO₄, FePO₄, Li₃PO₄, LiMnPO₄, LiCoPO₄, and LiNiPO₄, J. Appl. Phys., 2004, 95(11), 6583–6585.
22. F. Giustino, Materials modelling using density functional theory: properties and predictions, Oxford University Press, 2014.
23. A. Yamada and S.-C. Chung, Crystal Chemistry of the Olivine-Type Li(Mn_yFe_1−y)PO₄ and (Mn_yFe_1−y)PO₄ as Possible 4 V Cathode Materials for Lithium Batteries, J. Electrochem. Soc., 2001, 148(8), A960.
24. S. Shi, L. Liu, C. Ouyang, D.-s Wang, Z. Wang and L. Chen, et al., Enhancement of electronic conductivity of LiFePO₄ by Cr doping and its identification by first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(19), 195108.
25. P. Tang and N. A. W. Holzwarth, Electronic structure of FePO₄, LiFePO₄, and related materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(16), 165107.
26. V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943.
27. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, First-principles prediction of redox potentials in transition-metal compounds with LDA+U, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(23), 235121.
28. V. L. Chevrier, S. P. Ong, R. Armiento, M. K. Y. Chan and G. Ceder, Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(7), 075122.
29. S. P. Ong, V. L. Chevrier and G. Ceder, Comparison of small polaron migration and phase separation in olivine LiMnPO₄ and LiFePO₄ using hybrid density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(7), 075112.
30. M. D. Johannes, K. Hoang, J. L. Allen and K. Gaskell, Hole polaron formation and migration in olivine phosphate materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(11), 115106.
31. M. Nakayama, S. Yamada, R. Jalem and T. Kasuga, Density functional studies of olivine-type LiFePO₄ and NaFePO₄ as positive electrode materials for rechargeable lithium and sodium ion batteries, Solid State Ionics, 2016, 286, 40–44.
32. S. J. Clark and J. Robertson, Screened exchange density functional applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(8), 085208.
33. R. Gillen and J. Robertson, Accurate screened exchange band structures for the transition metal monoxides MnO, FeO, CoO and NiO, J. Phys.: Condens. Matter, 2013, 25(16), 165502.
34. K. Zaghib, M. Dontigny, P. Charest, J. Labrecque, A. Guerfi and M. Kopec, et al., Aging of LiFePO₄ upon exposure to H₂O, J. Power Sources, 2008, 185(2), 698–710.
35. M. K. Kinyanjui, P. Axmann, M. Wohlfahrt-Mehrens, P. Moreau, F. Boucher and U. Kaiser, Origin of valence and core excitations in LiFePO(4) and FePO(4), J. Phys.: Condens. Matter, 2010, 22(27), 275501.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
37. Y. Mishima, T. Hojo, T. Nishio, H. Sadamura, N. Oyama and C. Moriyoshi, et al., MEM Charge Density Study of Olivine LiMPO₄ and MPO₄ (M = Mn, Fe) as Cathode Materials for Lithium-Ion Batteries, J. Phys. Chem. C, 2013, 117(6), 2608–2615.
38. A. S. Andersson, B. Kalska, L. Häggström and J. O. Thomas, Lithium extraction/insertion in LiFePO₄: an X-ray diffraction and Mössbauer spectroscopy study, Solid State Ionics, 2000, 130(1), 41–52.
39. G. Rousse, J. Rodriguez-Carvajal, S. Patoux and C. Masquelier, Magnetic structures of the triphylite LiFePO₄ and of its delithiated form FePO₄, Chem. Mater., 2003, 15(21), 4082–4090.
40. S. Kobayashi, C. A. Fisher, T. Kato, Y. Ukyo, T. Hirayama and Y. Ikuhara, Atomic-Scale Observations of (010) LiFePO₄ Surfaces Before and After Chemical Delithiation, Nano Lett., 2016, 16(9), 5409–5414.
41. C. M. Burba and R. Frech, Raman and FTIR Spectroscopic Study of Li_xFePO₄ (0 ≤ x ≤ 1), J. Electrochem. Soc., 2004, 151(7), A1032–A1038.
42. J. Tauc, Optical properties and electronic structure of amorphous Ge and Si, Mater. Res. Bull., 1968, 3(1), 37–46.
43. P. Kubelka and F. Munk, An article on optics of paint layers, Z. Tech. Phys., 1931, 12, 593–601.
44. P. Kubelka, New contributions to the optics of intensely light-scattering materials. Part I, J. Opt. Soc. Am., 1948, 38(5), 448–457.
45. M. Schreiber and Y. Toyozawa, Numerical experiments on the absorption lineshape of the exciton under lattice vibrations. III. The Urbach rule, J. Phys. Soc. Jpn., 1982, 51(5), 1544–1550.
46. M. Lachal, R. Bouchet, A. Boulineau, S. Surblé, C. Rossignol and F. Alloin, et al., Remarkable impact of grains boundaries on the chemical delithiation kinetics of LiFePO₄, Solid State Ionics, 2017, 300, 187–194.
47. P. Moreau, V. Mauchamp, F. Pailloux and F. Boucher, Fast determination of phases in Li_xFePO₄ using low losses in electron energy-loss spectroscopy, Appl. Phys. Lett., 2009, 94(12), 123111.
48. W. Sigle, R. Amin, K. Weichert, P. A. van Aken and J. Maier, Delithiation Study of LiFePO₄ Crystals Using Electron Energy-Loss Spectroscopy, Electrochem. Solid-State Lett., 2009, 12(8), A151.
49. C. Julien, A. Mauger, K. Zaghib and H. Groult, Comparative Issues of Cathode Materials for Li-Ion Batteries, Inorganics, 2014, 2(1), 132.
50. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106.
51. S. Miao, M. Kocher, P. Rez, B. Fultz, R. Yazami and C. C. Ahn, Local Electronic Structure of Olivine Phases of Li_xFePO₄, J. Phys. Chem. A, 2007, 111(20), 4242–4247.
52. X. Liu, Y. J. Wang, B. Barbiellini, H. Hafiz, S. Basak and J. Liu, et al., Why LiFePO₄ is a safe battery electrode: Coulomb repulsion induced electron-state reshuffling upon lithiation, Phys. Chem. Chem. Phys., 2015, 17(39), 26369–26377.
53. L. Castro, R. Dedryvère, J.-B. Ledeuil, J. Bréger, C. Tessier and D. Gonbeau, Aging mechanisms of LiFePO₄//graphite cells studied by XPS: redox reaction and electrode/electrolyte interfaces, J. Electrochem. Soc., 2012, 159(4), A357–A363.
54. H. Shang, W. Chu, J. Cheng, F. Pan, D. Cheng and D. Xia, et al., Surface phase composition of nanosized LiFePO₄ and their enhanced electrochemical properties, J. Mater. Chem. A, 2013, 1(22), 6635–6641.
55. P. S. Lysaght, J. C. Woicik, M. A. Sahiner, J. Price, C. Weiland and P. D. Kirsch, Spectroscopic analysis of Al and N diffusion in HfO₂, J. Appl. Phys., 2012, 112(6), 064118.
56. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(8), R5467–R5470.
57. J. Stöhr and H. C. Siegmann, Magnetism: from fundamentals to nanoscale dynamics, Springer Science & Business Media, 2007.
58. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215.
59. J. Heyd and G. E. Scuseria, Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional, J. Chem. Phys., 2004, 121(3), 1187–1192.
60. J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105(22), 9982–9985.
61. B. Lee, L.-W. Wang, C. D. Spataru and S. G. Louie, Nonlocal exchange correlation in screened-exchange density functional methods, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(24), 245114.
62. H. Li, R. Gillen and J. Robertson, The screening effects of the screened exchange hybrid functional in surface systems: A case study on the CO/Pt(111) problem, AIP Adv., 2016, 6(6), 065309.
63. G. Liang, K. Park, J. Li, R. E. Benson, D. Vaknin and J. T. Markert, et al., Anisotropy in magnetic properties and electronic structure of single-crystal LiFePO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(6), 064414.
64. CASTEP Guide Materials Studio 8.0, http://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/content/pdfs/castep.htm.
65. J. Gao, S.-Q. Shi and H. Li, Brief overview of electrochemical potential in lithium ion batteries, Chin. Phys. B, 2016, 25(1), 018210.
66. A. Urban, D.-H. Seo and G. Ceder, Computational understanding of Li-ion batteries, npj Comput. Mater., 2016, 2(1), 16002.
67. G. Kobayashi, S.-i Nishimura, M.-S. Park, R. Kanno, M. Yashima and T. Ida, et al., Isolation of Solid Solution Phases in Size-Controlled Li_xFePO₄ at Room Temperature, Adv. Funct. Mater., 2009, 19(3), 395–403.
68. M. M. Kalantarian, S. Asgari and P. Mustarelli, A theoretical approach to evaluate the rate capability of Li-ion battery cathode materials, J. Mater. Chem. A, 2014, 2(1), 107–115.
69. W. Yang, Z. Wang, L. Chen, Y. Chen, L. Zhang and Y. Lin, et al., Suppression of degradation for lithium iron phosphate cylindrical batteries by nano silicon surface modification, RSC Adv., 2017, 7(53), 33680–33687.
70. A. Kahn, Fermi level, work function and vacuum level, Mater. Horiz., 2016, 3(1), 7–10.
71. D. T. Pierce, F. Meier and P. Zürcher, Negative electron affinity GaAs: A new source of spin-polarized electrons, Appl. Phys. Lett., 1975, 26(12), 670–672.
72. J. van der Weide, Z. Zhang, P. K. Baumann, M. G. Wensell, J. Bernholc and R. J. Nemanich, Negative-electron-affinity effects on the diamond (100) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(8), 5803–5806.
73. M. Powers, M. Benjamin, L. Porter, R. Nemanich, R. Davis and J. Cuomo, et al., Observation of a negative electron affinity for boron nitride, Appl. Phys. Lett., 1995, 67(26), 3912–3914.
74. M. Takahashi, S. Tobishima, K. Takei and Y. Sakurai, Characterization of LiFePO₄ as the cathode material for rechargeable lithium batteries, J. Power Sources, 2001, 97, 508–511.
75. S.-G. Lim, S. Kriventsov, T. N. Jackson, J. H. Haeni, D. G. Schlom and A. M. Balbashov, et al., Dielectric functions and optical bandgaps of high-K dielectrics for metal-oxide-semiconductor field-effect transistors by far ultraviolet spectroscopic ellipsometry, J. Appl. Phys., 2002, 91(7), 4500–4505.
76. J. Selj, T. Mongstad, B. Hauback and S. Z. Karazhanov, The dielectric functions and optical band gaps of thin films of amorphous and cubic crystalline Mg_∼2NiH_∼4, Thin Solid Films, 2012, 520(22), 6786–6792.
77. D. Spassky, N. Kozlova, V. Nagirnyi, A. Savon, Y. A. Hizhnyi and S. Nedilko, Excitation energy transfer to luminescence centers in M^IIMoO₄ (M^II = Ca, Sr, Zn, Pb) and Li₂MoO₄, J. Lumin., 2017, 186, 229–237.

---

Footnote

† Electronic supplementary information (ESI) available: Additional optical absorption spectra, band structure calculations with NM and AFM GGA and with NM hybrid functionals, PDOS of GGA and GGA+U for LIMPO₄, energy schematics of LIB systems, PDOS of Fe in LiFePO₄ and FePO₄ with various functionals, UPS spectra for LiFePO₄ and FePO₄ and brief summary on previous band gap estimation of LiFePO₄ with GGA+U. See DOI: 10.1039/c8ra09154d

---