DOI:
10.1039/C8RA09166H
(Paper)
RSC Adv., 2019,
9, 65-76
Large magnetocaloric entropy change at room temperature in soft ferromagnetic manganites
Received
5th November 2018
, Accepted 10th December 2018
First published on 20th December 2018
Abstract
In this paper, La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples were prepared by the flux method. Crystallographic study revealed that the x = 0.15 sample is characterized by the coexistence of a mixture of orthorhombic and rhombohedral structures with Pbnm and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space groups, respectively. While, the x = 0.20 sample crystallized in the rhombohedral structure with a R
c space groups, respectively. While, the x = 0.20 sample crystallized in the rhombohedral structure with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. Magnetic data, under a magnetic field of 0.05 T, indicated that our samples undergo a ferromagnetic (FM)–paramagnetic (PM) phase transition, on increasing the temperature. The magnetic field dependence of the magnetocaloric properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples, with the second phase transition, was investigated. Near room temperature, the x = 0.20 sample exhibited a large magnetic entropy change with maxima of 6.01 and 3.12 J kg−1 K−1, respectively, under applied magnetic fields of 5 and 2 T. Also, the relative cooling power (RCP) was calculated. According to hysteresis cycles, for our studied samples, at 10 K a typical soft FM behavior with a low coercive field was observed. These results make our samples promising candidates for magnetic refrigerators, magnetic recording, and memory devices.
c space group. Magnetic data, under a magnetic field of 0.05 T, indicated that our samples undergo a ferromagnetic (FM)–paramagnetic (PM) phase transition, on increasing the temperature. The magnetic field dependence of the magnetocaloric properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples, with the second phase transition, was investigated. Near room temperature, the x = 0.20 sample exhibited a large magnetic entropy change with maxima of 6.01 and 3.12 J kg−1 K−1, respectively, under applied magnetic fields of 5 and 2 T. Also, the relative cooling power (RCP) was calculated. According to hysteresis cycles, for our studied samples, at 10 K a typical soft FM behavior with a low coercive field was observed. These results make our samples promising candidates for magnetic refrigerators, magnetic recording, and memory devices.
1. Introduction
During the past few years, perovskite manganites with a general formula Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1−xMMnO3 (where Ln is a rare earth element and M is a divalent alkaline ion) have attracted particular attention from several researchers. This is thanks to their interesting interplay between magnetic and electronic features, as well as to being very promising for future technological applications.1–7 Additionally, they have many advantages such as low production cost, convenient preparation, softer vibration, longer usage time, small volume requirement and chemical stability. Moreover, these materials are environment-friendly and do not cause noise pollution. This makes them attractive to further research in relation to the widely-used refrigeration technology based on gas compression. The parent compound, LnMnO3, is an antiferromagnetic (AFM)-insulator characterized by a superexchange (SE) coupling between Mn3+ ions. When the Ln site is substituted with a divalent ion, a proportional number of Mn3+ ions with the electronic configuration (3d4, t32g↑ e1g↑, S = 2) are converted into Mn4+ ions with the electronic configuration (3d3, t32g↑ e0g, S = 3/2). This mixed Mn3+/Mn4+valence gives rise to a double exchange (DE)8 transfer of eg electrons from Mn3+ to Mn4+ ion via the O2− ion network. DE plays an important role in the properties of these materials.9 These properties are very dependent on the substitution rate x, average size of the cation, cationic disorder and the elaboration method.10 La1−xCaxMnO3 has attracted the attention of several researchers. This is thanks to the very rich phase diagram observed in this series.11,12 Pekala et al.13 investigated its magnetic field dependence of electrical resistivity in fine grains and analyzed the influence of external magnetic field on the transport processes in detail. Yi et al.14 observed that the magnetoresistance of nanosized La0.75Ca0.25MnO3 is enhanced at low temperatures due to the spin-polarized tunneling behavior. In addition, the pressure dependence of magnetic phase separation and transport behavior in La0.75Ca0.25MnO3 has also been investigated in recent paper.15 On other hand, with the substitution of Na on LaMnO3 sample, an amount 2× of Mn3+ is converted to Mn4+. Zhong et al.16 have studied the magnetocaloric properties in La1−xNaxMnO3 (0 ≤ x ≤ 0.2) and found that for x = 0.2, |–ΔSmaxM| reaches 1.96 J kg−1 K−1 upon a magnetic applied field change of 1 T. This paper investigates the effect of Na substitution on the structural, magnetic and magnetocaloric effect (MCE) of (x = 0.15 and 0.20) samples, synthesized by flux method, using sodium chloride (NaCl) as a flux. A theoretical investigation was used to predict the MCE properties for x = 0.20.
1−xMMnO3 (where Ln is a rare earth element and M is a divalent alkaline ion) have attracted particular attention from several researchers. This is thanks to their interesting interplay between magnetic and electronic features, as well as to being very promising for future technological applications.1–7 Additionally, they have many advantages such as low production cost, convenient preparation, softer vibration, longer usage time, small volume requirement and chemical stability. Moreover, these materials are environment-friendly and do not cause noise pollution. This makes them attractive to further research in relation to the widely-used refrigeration technology based on gas compression. The parent compound, LnMnO3, is an antiferromagnetic (AFM)-insulator characterized by a superexchange (SE) coupling between Mn3+ ions. When the Ln site is substituted with a divalent ion, a proportional number of Mn3+ ions with the electronic configuration (3d4, t32g↑ e1g↑, S = 2) are converted into Mn4+ ions with the electronic configuration (3d3, t32g↑ e0g, S = 3/2). This mixed Mn3+/Mn4+valence gives rise to a double exchange (DE)8 transfer of eg electrons from Mn3+ to Mn4+ ion via the O2− ion network. DE plays an important role in the properties of these materials.9 These properties are very dependent on the substitution rate x, average size of the cation, cationic disorder and the elaboration method.10 La1−xCaxMnO3 has attracted the attention of several researchers. This is thanks to the very rich phase diagram observed in this series.11,12 Pekala et al.13 investigated its magnetic field dependence of electrical resistivity in fine grains and analyzed the influence of external magnetic field on the transport processes in detail. Yi et al.14 observed that the magnetoresistance of nanosized La0.75Ca0.25MnO3 is enhanced at low temperatures due to the spin-polarized tunneling behavior. In addition, the pressure dependence of magnetic phase separation and transport behavior in La0.75Ca0.25MnO3 has also been investigated in recent paper.15 On other hand, with the substitution of Na on LaMnO3 sample, an amount 2× of Mn3+ is converted to Mn4+. Zhong et al.16 have studied the magnetocaloric properties in La1−xNaxMnO3 (0 ≤ x ≤ 0.2) and found that for x = 0.2, |–ΔSmaxM| reaches 1.96 J kg−1 K−1 upon a magnetic applied field change of 1 T. This paper investigates the effect of Na substitution on the structural, magnetic and magnetocaloric effect (MCE) of (x = 0.15 and 0.20) samples, synthesized by flux method, using sodium chloride (NaCl) as a flux. A theoretical investigation was used to predict the MCE properties for x = 0.20.
2. Experimental details
Generally, ceramic materials are highly affected by the preparation routes and heat treatments. The synthesis methods based on the conventional ceramic or solid state reaction are not suitable for advanced technological applications, as these methods produce particles of large size at high temperatures. Alternatively, to produce a very high-quality, homogenous and nano-polycrystalline powder of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds, at low temperature, we used the flux method, NaCl as a flux. The scheme of the synthetic route is to take stoichiometric amounts of high purity La2O3, MnO2 and CaCO3 in the appropriate molar ratio. The last mixture was ground, for half an hour, with an appropriate quantity of NaCl in an agate mortar. Then, the mixture was heated at 800 °C for 24 h in a recrystallized alumina crucible. After that, the melt was washed with distilled water and filtrated in order to remove easily the residual salts. The resulting powder was dried at 110 °C for 3 h and heated at 800 °C for 6 h. Finally, the powder was pressed into disks under 5 tonnes per cm2 and sintered at 800 °C. In order to characterize our samples we carried out, at room temperature, the phase purity by powder X-ray diffraction (XRD) using a Panalytical X pert Pro-diffractometer with Cu-Kα radiation (λ = 1.5406 Å). Data refinement was obtained with 2θ from 10 and 100° with a step size of 0.017 and a step time of 18 s. The microstructure was determined, at room temperature, by a scanning electron microscope (SEM) using a Philips XL30. The compositions of our samples were obtained by a semi-quantitative analysis performed at 20 kV accelerating voltage using energy dispersive X-ray analysis (EDX). The magnetic analysis was carried out using BS1 and BS2 magnetometers developed in Louis Neel Laboratory of Grenoble.
3. Results and discussion
3.1 X-Ray diffraction study
To analyze the structural properties of our samples, we carried out XRD analysis with CuKα radiation at room temperature. The data were analyzed by Rietveld method using Fullprof program.17 Fig. 1(a) and (b) exemplifies the Rietveld refinement of XRD profile, for the x = 0.15 and 0.20 samples, respectively. A good agreement between the observed and the calculated profiles was remarked. This is due to the excellent goodness of fit (χ2), confirming the high quality of refinement. From this figure, we can deduce that the x = 0.15 sample is a mixture of orthorhombic and rhombohedral structures, respectively, with Pbnm and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space groups, around 2θ = 32°. In this region, the system showed a sign of multi-phased behavior with no complete splitting into the double line of the intense peak. This result is in concordance with that observed in ref. 18. The relative amount of the orthorhombic phase was 81.68%. However, that of the rhombohedral phase was 18.32%. We can conclude that the orthorhombic phase is dominant. On the other hand, x = 0.20 sample crystallized in the rhombohedral structure with R
c space groups, around 2θ = 32°. In this region, the system showed a sign of multi-phased behavior with no complete splitting into the double line of the intense peak. This result is in concordance with that observed in ref. 18. The relative amount of the orthorhombic phase was 81.68%. However, that of the rhombohedral phase was 18.32%. We can conclude that the orthorhombic phase is dominant. On the other hand, x = 0.20 sample crystallized in the rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. Also, we can see the appearance of a small quantity of Mn3O4, as found in recent works.19,20
c space group. Also, we can see the appearance of a small quantity of Mn3O4, as found in recent works.19,20
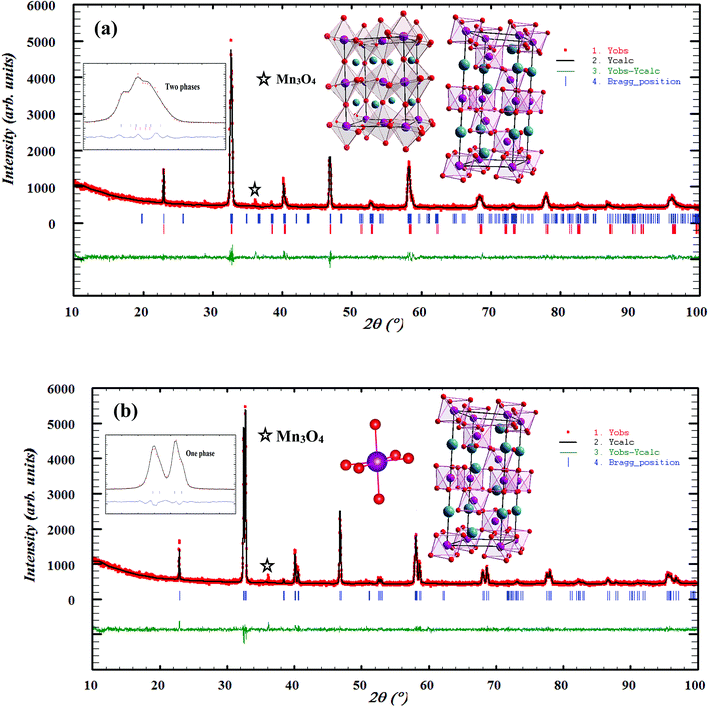 |
| | Fig. 1 Observed and calculated (solid line) of XRD patterns of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds. The vertical bars show the Bragg peak positions and the bottom of the figure shows the difference between the observed and the calculated patterns. The insets show the crystal structure of our samples. | |
The different fitting parameters of our samples are summarized in Table 1. According to Shannon,21 the ionic radius of Na+ (rNa+ = 1.24 Å) is higher than that of Ca2+ (rCa2+ = 1.18 Å). This can be explained by the slight increase of the lattice size with increasing Na content. It has been reported that the deformation of the MnO6 octahedron may be responsible for the distortion in the perovskite structures. The crystal structures and the MnO6 octahedron for the samples (x = 0.15 and 0.20) were drawn using the VESTA program (inset of Fig. 1(a) and (b)).22 To better understand the regularities governing the formation of perovskite-type systems, Goldschmidt's tolerance factor, TG, is usually introduced. It is defined by the following expression:23,24
| |
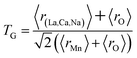 | (1) |
where
r(La,Ca,Na),
rO and
rMn are the ionic radii of the different elements. The manganese oxide compounds have a perovskite structure if 0.89 <
TG < 1.02.
25 The obtained values of
TG for our samples were listed in
Table 1. This confirmed the stability of this structure.
Table 1 Refined structural parameters for La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples determined from X-ray after the Rietveld refinement at room temperature
| |
x = 0.15 |
|
x = 0.20 |
| Space group |
Pbnm |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
| a (Å) |
5.502(5) |
5.482(4) |
5.508(6) |
| b (Å) |
5.461(5) |
5.482(4) |
5.508(6) |
| c (Å) |
7.751(8) |
13.406(3) |
13.331(9) |
| V (Å3) |
232.963 |
348.975 |
350.357 |
| La/Ca/Na |
| x |
0.498(9) |
|
0.0000 |
| y |
0.013(1) |
|
0.0000 |
| z |
0.2500 |
|
0.2500 |
| Biso (Å2) |
1.16(3) |
|
1.08(2) |
| Mn |
| Biso (Å2) |
0.66(2) |
|
0.68(4) |
| O1 |
| x |
0.226(7) |
|
0.443(8) |
| y |
0.306(5) |
|
0.0000 |
| z |
0.008(9) |
|
0.2500 |
| Biso (Å2) |
1.45(2) |
|
1.51(3) |
| O2 |
| x |
0.576(8) |
|
— |
| y |
0.494(6) |
|
— |
| z |
0.2500 |
|
— |
| Biso (Å2) |
1.41(5) |
|
— |
| Discrepancy factors |
| Rp (%) |
4.38 |
4.05 |
3.83 |
| Rwp (%) |
5.82 |
5.16 |
4.87 |
| χ2 |
1.81 |
1.40 |
1.30 |
| Bond lengths and bond angles |
| θMn–O1–Mn (°) |
161.31 |
|
— |
| θMn–O2–Mn (°) |
155.34 |
|
— |
| 〈θMn–O–Mn〉 (°) |
158.32 |
|
161.90 |
| dMn−O1 (Å) |
2.09(2) |
|
— |
| dMn−O2 (Å) |
1.98(3) |
|
— |
| 〈dMn−O〉 (Å) |
2.03(7) |
|
1.96(4) |
| Bandwidth W (10−2) (u.a.) |
8.1 |
|
9.3 |
| Tolerance factor TG |
0.9758 |
|
0.9795 |
The experimental density (Dexp) is determined from the weight and geometrical dimensions of the cylindrical pellets.26 It was found to be 5.963 and 5.958 g cm−3, respectively, for x = 0.15 and 0.20 samples.
The XRD density (DXRD) of our samples is determined from X-ray measurements.26 It was found to be 6.085 and 6.081 g cm−3 for x = 0.15 and 0.20, respectively. These values are in agreement with those obtained in other manganites.27,28 The compactness26 is thus calculated, the obtained values are 98% and 97% for x = 0.15 and 0.20 samples, respectively.
3.2 Morphological study
From the reflection of 2θ values of XRD profile, the crystallite size (D) was calculated using Scherer's equation (eqn (2)):| |
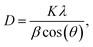 | (2) |
where K is the shape factor, which usually takes a value of about 0.9, λ = 1.5406 Å is the wavelength for CuKα radiation, θ is the diffraction angle of the most intense peak and β is the full width at half maximum of the highest peak. D values are listed in Table 2. The obtained values are comparable with those reported in the literature.26–30 Regarding the SEM micrograph, insets (a) and (b) of Fig. 2, show a homogenous microstructure and a uniform grain size distribution, for x = 0.15 as an example. The grain sizes were estimated to be mostly within 2.12 and 2.14 μm for x = 0.15 and 0.20, respectively. Obviously, the particle sizes observed by SEM were much larger than those calculated using Scherer's formula. This indicates that each grain observed by SEM consists of several crystallites.31,32
Table 2 Average crystallite size determined by Scherrer's formula and SEM
| Samples |
x = 0.15 |
x = 0.20 |
| 〈rA〉 (Å) |
1.362 |
1.365 |
| DSch (nm) |
49.38 |
50.71 |
| DSEM (μm) |
2.12 |
2.14 |
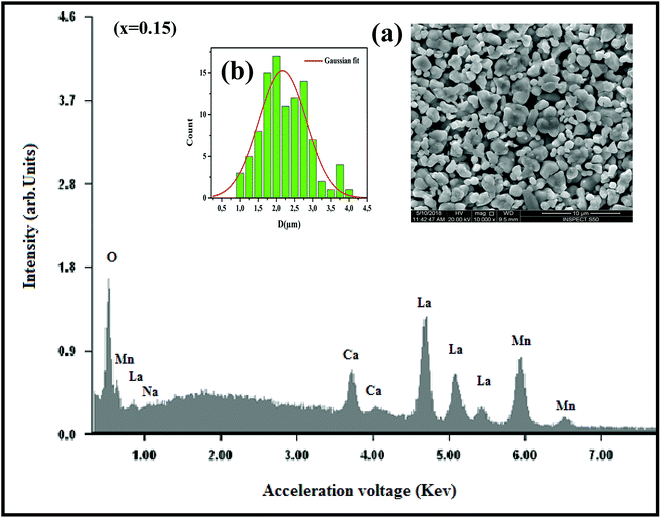 |
| | Fig. 2 The EDX analysis for x = 0.15 sample. Insets: (a) shows the typical SEM and (b) shows the histogram of the distribution of particle size. | |
In order to check the existence of all elements in La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds, EDX analysis was performed. The EDX spectrum, for x = 0.15 as an example, is shown in Fig. 2, The typical cationic compositions are listed in Table 3. It is clear that all elements (La, Ca, Na, Mn, and O) are present with no loss of any integrated elements during the sintering process.
Table 3 Results of EDX analysis
| Nominal composition |
Typical cationic composition from EDX |
| La |
Ca |
Na |
Mn |
| La0.75Ca0.10Na0.15MnO3 |
0.751 |
0.101 |
0.149 |
1.000 |
| La0.75Ca0.05Na0.20MnO3 |
0.750 |
0.049 |
0.201 |
1.001 |
3.3 Magnetic study
Following the Morphological study, we discussed the thermal variation of the magnetic properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20). Fig. 3(a) and (b) shows the zero-field-cooled (ZFC) and field-cooled (FC) magnetizations of our samples under an applied field of 0.05 T in the temperature range 5 to 400 K. We can remark a net PM–FM transition, at their TC. A small divergence between ZFC and FC plots can be observed at the irreversibility temperature T = 270 and 250 K, respectively for x = 0.15 and 0.20. This phenomenon can be attributed to the appearance of an isotropic field generated from FM clusters.32 At low temperatures, a small peak was observed around 40 K. This indicates the appearance of Mn3O4 phase.33,34 TC can be determined from d2M/dT2(T) graphs (Fig. 3(a) and (b)). From this figure, we remarked the appearance of different inflection points. For the x = 0.20 sample, a classical behavior at 300 K was observed, corresponding to its TC. While the x = 0.15 sample presented two inflection points, around room temperature, corresponding to two Curie temperatures. This can be interpreted by the presence of two different FM phases. The Curie temperatures were measured at TC1 = 273 K and TC2 = 301.5 K. Additionally, we can see a slight decrease of TC with increasing Na+ content. According to Asma Zaidi et al.35 the decrease of TC can be interpreted in terms of the increase in Mn4+ content above 40%, which produces a decrease in the DE interaction (Mn3+–O2−–Mn4+) and enhances the SE interaction (Mn4+–O2−–Mn4+). Here, we can discuss the evolution of the bandwidth using eqn (3)| |
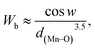 | (3) |
where w = 1/2(π − 〈Mn–O–Mn〉) and d(Mn–O) is the bond length characterized by the overlap between Mn3d and O2p orbitals.36 The calculated Wb values are tabulated in Table 1.
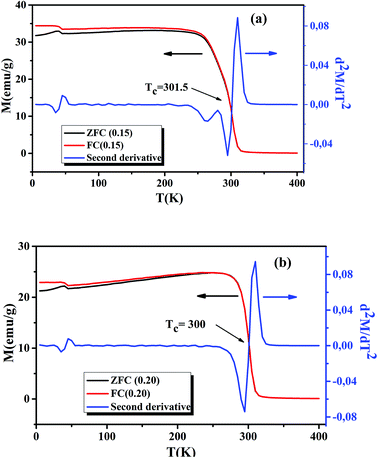 |
| | Fig. 3 Temperature dependence of the ZFC and FC magnetization and d2M/dT2 plots for La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds, under a magnetic field of 0.05 T. | |
To understand the dynamics of spin, we carried out the inverse of susceptibility as function of temperatures, as shown in Fig. 4. In PM region, χ−1 can be fitted by Curie–Weiss (CW) law.37 Fitting the linear part; we get the θp values (Table 4). It is worth to mentioning that θp values can be negative, positive or null according to AFM, FM or PM behavior, respectively. In our case, θp values are positive, confirming the FM behavior. It is clear that the θp value is higher than TC. This can be interpreted by the magnetic inhomogeneity above TC.38 The experimental effective moment (μexpeff) and the theoretical effective moment (μtheoeff) are, also, calculated. The obtained values of μexpeff and μtheoeff are listed in Table 4. We can notice that the difference between the experimental and the theoretical values is attributed to the FM correlations in PM region. These are probably due to the formation of FM cluster.39Our results are comparable with other works.40,41 In addition, it is important to mention that the percentage of Mn3+ and Mn4+ ions can be checked quantitatively by the so-called chemical titration. To verify these percentages, we carried out a chemical analysis. In fact, our obtained powder was dissolved in concentrated sulfuric acid and oxalic acid dihydrate. The obtained solution is titrated by potassium permanganate and the values of manganese ions concentration are (Mn3+ = 60.1%) and (Mn4+ = 39.9%) for x = 0.15 and (Mn3+ = 54.8%) and (Mn4+ = 45.2%) for x = 0.20. In order to get a deeper insight into the magnetic properties at low temperatures, we analysed the hysteresis cycles M(μ0H). Fig. 5(a) and (b) displays M(μ0H) at 10 K, μ0H = ±6 T. We remarked clearly that the curves are quite similar to each other with a small hysteresis loop. In the weak field region at low temperatures, magnetization increased significantly and reached saturation upon increasing field. The saturation magnetization (MS) was found to be 88.10 and 92.21 emu g−1, for x = 0.15 and x = 0.20, respectively. The insets of Fig. 5(a) and (b) show a zoom of the central portion, at low magnetic fields, of M(μ0H) curves. It is clear that M(μ0H) curves have negligible values of coercive field (μ0HC) and remnant magnetization (Mr). μ0HC values are found to be 21 × 10−4 and 16 × 10−4 T, for x = 0.15 and x = 0.20, respectively. Mr values were found to be 1.49 and 1.11 emu g−1, for x = 0.15 and x = 0.20 respectively. The small hysteresis loop with important saturation values indicates the typical soft FM behavior of materials. According to these results, our samples could be used for reading and writing process in high density recording media or information storage.42
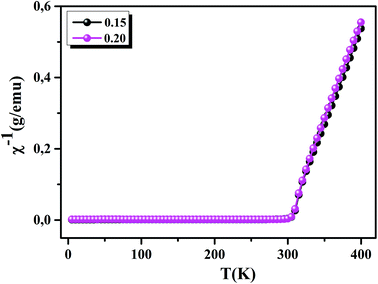 |
| | Fig. 4 Inverse of susceptibility as a function of temperatures for La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples determined in a field of 0.05 T. | |
Table 4 Some experimental values for La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds
| |
x = 0.15 |
x = 0.20 |
| TC (K) |
301.5 |
300 |
| θp (K) |
301, 66 |
301, 11 |
| μtheoeff (μB) |
4.51 |
4.46 |
| μexpeff (μB) |
5.62 |
5.33 |
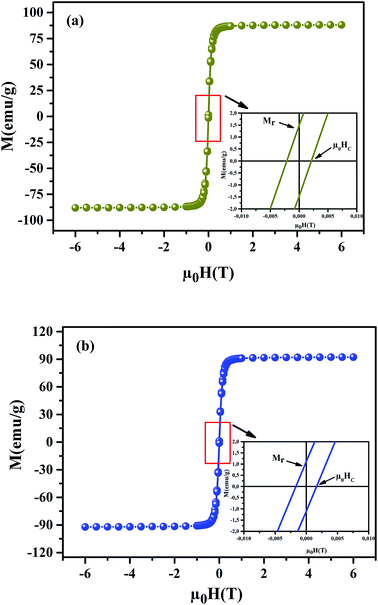 |
| | Fig. 5 Magnetic hysteresis cycles at T = 10 K of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples. The insets show a zoom of the central portion of the hysteresis at a low field. | |
Magneto-crystalline anisotropy is an intrinsic property of materials, playing an important role in coercivity.43 It is used to describe the effect of the internal energy on the direction of magnetization.
According to Stoner–Wohlfarth's theory, the anisotropy constant (Ka) can be determined from eqn (4)44
| | |
μ0HC = (0.98 × Ka)/MS,
| (4) |
where
Ka values are 188.7 J m
−3 and 161.9 J m
−3, for the
x = 0.15 and
x = 0.20 samples, respectively.
The remanence ratio (R) using (eqn (5)):
is an important parameter, used to understand the isotropic nature of our studied samples.
R values are equal to 0.0169 and 0.0120, for the
x = 0.15 and 0.20 samples, respectively. The small obtained values undergo the isotropic natures.
45 Together with
M(
μ0H) investigation; we have measured the isothermal magnetization as a function of applied magnetic fields up to 5 T at different temperatures, for our samples, around their
TC (inset of
Fig. 6(a) and (b)). We can notice that these curves reveal a rapid increase in the magnetization at a very weak magnetic field corresponding to a quick rearrangement of the magnetic domains. This is due to the complete alignment of the spins in these samples from the value of the magnetic field, 1 T. To clarify the nature of the magnetic phase transition, we derived the Arrott's plots (
M2 vs. μ0H/
M) from
M(
μ0H)). The obtained curves are shown in
Fig. 6(a) and (b), for the
x = 0.15 and 0.20 samples. According to Banerjee's criterion, a positive slope corresponds to second order magnetic transition, while a negative slope corresponds to first order transition.
46 From
Fig. 6(a) and (b), we can see a positive slope without inflection points in the high-field regions for our samples. This indicates that our samples undergo a second order nature of phase FM–PM transition.
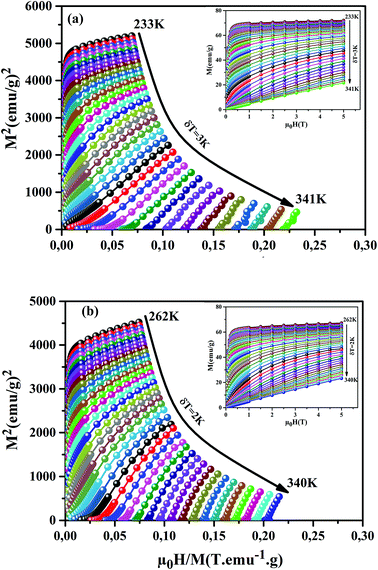 |
| | Fig. 6 M2 vs. μ0H/M plots for our samples, around TC. The insets show M(μ0H) curves at different temperatures. | |
3.4 Magnetocaloric properties
For the determination of MCE especially in magnetic materials, both the experimental and theoretical approaches are used. However, for the theoretical investigation of MCE, several approaches were used. Recently, a theoretical model proposed by Hamad47 began to receive attention. Based on this model, the dependence of magnetization on the temperatures is defined as:| |
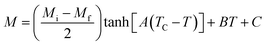 | (6) |
where Mi and Mf are the initial and the final values of magnetization at FM–PM transition, respectively. 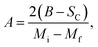 B is the magnetization sensitivity dM/dT at FM state before transition. SC is the magnetization sensitivity dM/dT at TC.
B is the magnetization sensitivity dM/dT at FM state before transition. SC is the magnetization sensitivity dM/dT at TC. 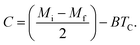
According to this model, −ΔSM under applied magnetic fields in the range of 0 to μ0Hmax is expressed by:48
| |
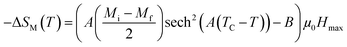 | (7) |
At T = TC, we obtained −ΔSmaxM value, defined as the following expression:49
| |
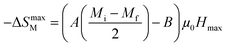 | (8) |
In magnetic refrigeration, it is important to take into account not only the −ΔSM, but also the relative cooling power (RCP) as an important parameter which represents the amount of heat exchange per kilogram between the hot and cold sinks in the ideal refrigeration cycle. It is computed by:50
| |
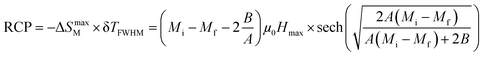 | (9) |
(δ
TFWHM) presents the full width at half maximum, defined as:
48| |
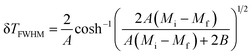 | (10) |
Another important parameter for magnetic refrigeration is the heat capacity ΔCP,μ0H associated with an applied magnetic field (1–5 T) can be determined by:
| |
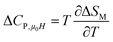 | (11) |
Δ
CP,μ0H can be rewritten as:
51| | |
ΔCP,μ0H = −TA2(Mi − Mf) × sech2[A(TC − T)]tanh[A(TC − T)]μ0Hmax
| (12) |
In the rest of our work, the MCE properties for x = 0.15 will be determined experimentally, while x = 0.20 will be determined experimentally and theoretically.
Before studying the MCE properties of our samples, Fig. 7 represents M(T) in different applied magnetic field, for x = 0.20 sample. The symbol is the experimental data, while the solid red line is the modeled data (using eqn (6)). From M(T), it is easy to determined Mi, Mf, B and SC parameters in order to investigate theoretically −ΔSM, RCP, −ΔCP,μ0H and ΔTad curves. The obtained parameters are summarized in Table 5.
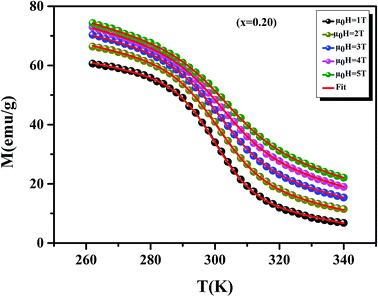 |
| | Fig. 7 Magnetization as function of temperatures under a magnetic fields, for x = 0.20 sample. The red line curves represent the modeled data and symbols are the experimental data. | |
Table 5 Model parameters for La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds in different applied magnetic fields
| μ0H (T) |
Mi (emu g−1) |
Mf (emu g−1) |
B (emu g−1 K−1) |
SC (emu g−1 K−1) |
TC (K) |
| 1 |
49.60 |
11.25 |
−0.204 |
−1.772 |
299.97 |
| 2 |
53.75 |
16.17 |
−0.233 |
−1.597 |
301 |
| 3 |
58.66 |
22.73 |
−0.247 |
−1.365 |
301.65 |
| 4 |
62.48 |
31.39 |
−0.294 |
−1.321 |
302.13 |
| 5 |
63.59 |
34.57 |
−0.303 |
−1.286 |
303.45 |
It is noteworthy that the theoretical model is in good agreement with the experimental data.
Fig. 8(a) and (b) shows the variation of −ΔSM as a function of temperature, under applied magnetic fields of 1–5 T, for the x = 0.15 and 0.20 samples, respectively. For the x = 0.20 sample, it is clear that the theoretical results (using eqn (7)) are consistent with the experimental results. This confirms the validity of this model. From Fig. 8, we can see a positive sign of −ΔSM in the entire temperature range, confirming the FM character. Around TC, the x = 0.20 sample exhibited a classical behavior of −ΔSM with a maximum peak of 6.01 J kg−1 K−1 under μ0H = 5 T field. While, for the x = 0.15 sample, we remarked the coexistence of two peaks. This corresponds to two-Curie temperatures. When studying the effect of Ag+ in the La0.7Ca0.3MnO3 sample, Kalyana et al. have shown that the x = 0.10 sample admits two magnetic transitions. This can be due to the existence of canted FM phase in the FM matrix.52 A. Krichene et al. have shown that the La0.4Gd0.1Ca0.5MnO3 and La0.4Eu0.1Ca0.5MnO3 samples admit two maxima of −ΔSM. The first one corresponds to TC. While, the second one is an anomaly, which explained as metamagnetic transition: in fact, PM and AFM transitions coexist above TC.53 Hence, in our case the presence of two peaks in −ΔSM may be attributed to the combination of orthorhombic and rhombohedral structures in this sample. This is in agreement with that observed by Kima et al.54 The obtained −ΔSmaxM are comparable with those obtained in the literature (Table 6).
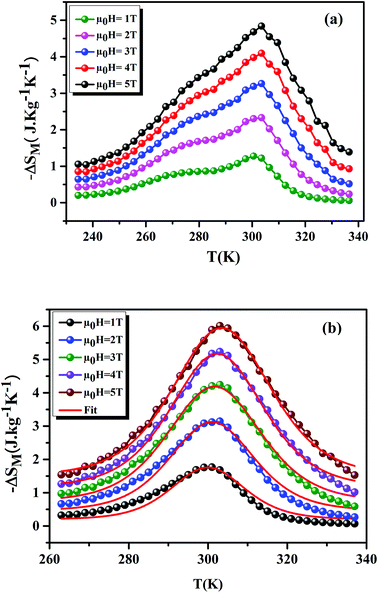 |
| | Fig. 8 −ΔSM as a function of temperature at different μ0H fields, for x = 0.15 and 0.20 compounds. The red line curves represent the modeled data and symbols are the experimental data. | |
Table 6 Summary of MC properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) compounds compared with other works
| Samples |
TC (K) |
μ0H (T) |
−ΔSmaxM (J kg−1 K−1) |
RCP (J kg−1) |
Ref. |
| La0.75Ca0.10Na0.15MnO3 |
301.5 |
5 |
4.83 |
230 |
Present work |
| La0.75Ca0.10Na0.15MnO3 |
— |
2 |
2.33 |
110 |
Present work |
| La0.75Ca0.05Na0.20MnO3 |
300 |
5 |
6.01 |
225 |
Present work |
| La0.75Ca0.05Na0.20MnO3 |
— |
2 |
3.12 |
90 |
Present work |
| La0.5Sm0.1Sr0.4Mn0.95In0.05O3 |
294 |
5 |
4.50 |
193.48 |
55 |
| La0.5Sm0.1Sr0.4Mn0.95In0.05O3 |
294 |
2 |
2.80 |
97.30 |
55 |
| La0.67Ba0.33Mn0.98Ti0.02O3 |
314 |
5 |
3.24 |
307 |
56 |
| Gd |
293 |
2 |
5 |
153 |
57 |
| Gd |
293 |
5 |
9.5 |
410 |
58 |
| La0.57Nd0.1Sr0.33Mn0.95Sn0.05O3 |
281 |
5 |
2.8 |
51 |
59 |
| La0.7Sr0.3Mn0.95Ti0.05O3 |
308 |
2 |
2.2 |
90 |
60 |
| La0.8Ba0.2MnO3 |
295 |
5 |
4.5 |
130 |
61 |
| La0.7Sr0.3Mn0.9Fe0.1O3 |
260 |
2 |
1.7 |
83 |
62 |
| La0.67Sr0.1Ca0.23MnO3 |
294 |
2 |
3.72 |
149.43 |
63 |
| La0.7Ca0.2Sr0.1MnO3 |
308 |
5 |
7.45 |
374 |
64 |
The different values of RCP for our samples are listed in Table 6. These parameters increase with increasing the external magnetic field. This is because the effect of spin coupling became less important when the applied magnetic field was increased. We can see that the proposed compounds exhibit important values. In addition, we can note that our samples can be considered as potential candidates for magnetic refrigeration thanks to their high RCP values, compared to conventional refrigerant materials (Table 6).
Using eqn (11) and (12), Fig. 9 display the experimental and the theoretical ΔCP,μ0H plots, for x = 0.20 sample as an example. The symbol represents the experimental data, while the solid red line represents the modeled data. We can see clearly that the experimental results are in a good agreement with the calculated results. Additionally, we can remark that the value of −ΔCP,μ0H suddenly changed from positive to negative around TC. Then, it decreased rapidly with decreasing temperature.65 The sum of the two parts represents the magnetic contribution to the total specific heat. The positive or negative values of ΔCP,μ0H can strongly alter the heating or cooling power of a magnetic refrigerator. The obtained maximum/minimum values of ΔCP,μ0H at 315/293 K, exhibited an increasing trend with the external magnetic field. It was found to be 63.98/−62.62 J kg−1 K−1 at a 5 T applied magnetic field. Our results are comparable with those obtained in recent works.4
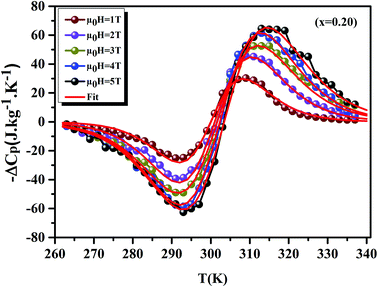 |
| | Fig. 9 Experimental and theoretical curves of ΔCP versus temperatures for x = 0.20 compounds under different magnetic fields. | |
To have a wider understanding of the MCE properties, the adiabatic temperature change (ΔTad) was calculated. It is defined as following:51
| |
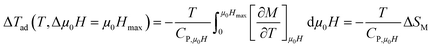 | (13) |
Taking into account the eqn (6) in eqn (13) ΔTad can be rewritten as:
| |
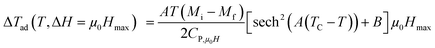 | (14) |
CP,μ0H represents the specific heat, it can be calculated from the sum of the lattice and magnetic contributions using
eqn (15)66,67where
CD is the Debye specific heat and
CM is the magnetic contribution to the specific heat capacity).
CM is given by (∂
UM/∂
T), and is determined from:
66,67| |
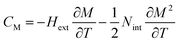 | (16) |
where
Nint presents the mean field constant. It is equal to
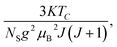 g
g is the Landé factor,
J is the total angular momentum and
NS is the number of spins per unit mass.
Using eqn (13) and (14), Fig. 10(a) and (b) shows the experimental and theoretical curves of ΔTad for our samples, respectively. The symbol represents the experimental data, while the solid red line refers to the modeled data. It is obvious that the results of calculation are in good agreement with the experimental results. Also, it is clear that ΔTad maintains practically the nature of −ΔSM. The maximum values of ΔTad range from 2.93 and 3.64 K at 5 T, for x = 0.15 and 0.20, respectively.
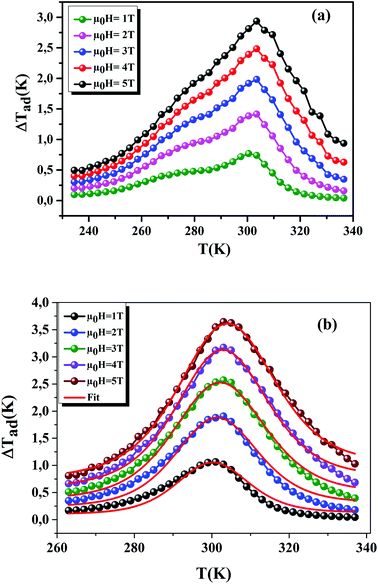 |
| | Fig. 10 ΔTad plotted as a function of temperature at different μ0H fields, for x = 0.15 and 0.20 compounds. The red line curves represent the modeled data and symbols are the experimental data. | |
A phenomenological universal curve for the field dependence of −ΔSM has been proposed, by Franco et al.68 It is based on the normalization of all −ΔSM(T, μ0H) curves using eqn 17
| | |
ΔS′ = ΔSM(T, μ0H)/ΔSmaxM.
| (17) |
After that, the temperatures' axes are differently rescaled below and above TC, defined as (eqn (18)):69
| |
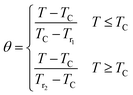 | (18) |
where,
Tr1 and
Tr2 are the temperatures of two reference points, associated to Δ
SM(
Tr1,2) = −Δ
SmaxM/2 (
Tr1 <
TC and
Tr2 >
TC).
Fig. 11 displays the
θ dependence of Δ
S′ under different magnetic fields, for the
x = 0.20 sample, as an example. It is clearly seen that all data points collapse on one single curve. Therefore, the FM–PM phase transition in our sample was confirmed to be of second order nature.
70
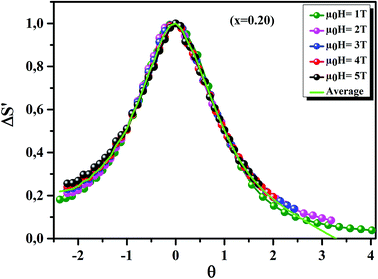 |
| | Fig. 11 The universal behavior of ΔS′(θ) plots for x = 0.20 sample, under different magnetic fields. | |
The universal curve can be well fitted by Lorentz's function using (eqn (19)):
| |
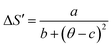 | (19) |
where
a,
b, and
c are free parameters. Taking into consideration the asymmetry of the curves (for
x = 0.20 as an example), we can use two different regions of constants such as: for
T <
TC region,
a = 1.458 ± 0.037,
b = 1.391 ± 0.026 and
c = 0.174 ± 0.021. While, for
T >
TC region,
a = 0.717 ± 0.046;
b = 0.743 ± 0.048 and
c = 0.122 ± 0.030. Our obtained parameters are comparable to those obtained in
ref. 71. According to
eqn (19), only the different parameters namely
TC, −Δ
SmaxM,
Tr1 and
Tr2 values are needed to characterize −Δ
SM. That is to say, we need only the last parameters, which are determined from the properties of these materials, to determine −Δ
SM from Δ
S′(
θ).
Generally, −ΔSM is dependent on the variation of magnetization near TC. It can be expressed by:72
| | |
ΔSM(T, μ0H) = a(T)(μ0H)n
| (20) |
where
n is an exponent which depends on the magnetic transition and defined as:
73| |
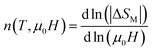 | (21) |
Fig. 12 displays the variation of n as function of temperatures, under different applied fields, for the x = 0.20 sample. We can see that the value of n approaches 1 in the FM region and admits a minimum in TC. Then, it approaches 2 in the PM state. These results are observed in different magnetic materials.74–76
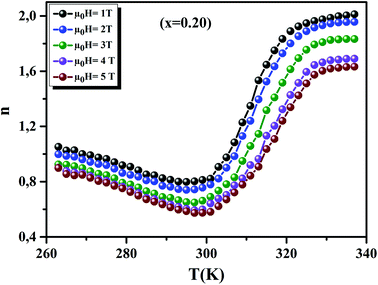 |
| | Fig. 12 Temperature dependence of the exponent n, for x = 0.20, under different magnetic fields. | |
4. Conclusion
In summary, we have investigated the structural, morphological, magnetic and MCE properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples, synthesized using the flux method. Rietveld refinement of XRD patterns shows that x = 0.20 crystallized in a rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group, at room temperature. While, the x = 0.15 sample admits both phases with different percentages. Magnetization measurements as function of temperatures in a magnetic field of 0.05 T show that our studied samples undergo a second-order PM–FM phase transition, upon decreasing temperature. Around room temperature, a large MCE is observed for our samples, under a magnetic field of 5 T. –ΔSmaxM is found to be 6.01 J kg−1 K−1 under μ0H = 5 T magnetic field for x = 0.20. For the x = 0.15 sample, −ΔSM curves show the existence of two maxima, which may be attributed to the structural inhomogeneity. The RCP is also analyzed. From, −ΔSM curves, we have investigated the dependence of temperature on the adiabatic temperature change (−ΔTad). Its maximum is found to be 2.93 K, for the x = 0.15 sample, in an applied magnetic field of 5 T. From the hysteresis cycles, at 10 K for the studied samples, we can remark a typical soft FM behavior with a small hysteresis loop and a low coercive field (μ0HC). The small values of coercive field confirm that the magnetic domains can rotate easily to the direction of the applied magnetic field. These results make our samples promising candidates for magnetic refrigeration, magnetic recording and memory devices.
c space group, at room temperature. While, the x = 0.15 sample admits both phases with different percentages. Magnetization measurements as function of temperatures in a magnetic field of 0.05 T show that our studied samples undergo a second-order PM–FM phase transition, upon decreasing temperature. Around room temperature, a large MCE is observed for our samples, under a magnetic field of 5 T. –ΔSmaxM is found to be 6.01 J kg−1 K−1 under μ0H = 5 T magnetic field for x = 0.20. For the x = 0.15 sample, −ΔSM curves show the existence of two maxima, which may be attributed to the structural inhomogeneity. The RCP is also analyzed. From, −ΔSM curves, we have investigated the dependence of temperature on the adiabatic temperature change (−ΔTad). Its maximum is found to be 2.93 K, for the x = 0.15 sample, in an applied magnetic field of 5 T. From the hysteresis cycles, at 10 K for the studied samples, we can remark a typical soft FM behavior with a small hysteresis loop and a low coercive field (μ0HC). The small values of coercive field confirm that the magnetic domains can rotate easily to the direction of the applied magnetic field. These results make our samples promising candidates for magnetic refrigeration, magnetic recording and memory devices.
Conflicts of interest
The authors declare that they have no conflict of interest.
References
- T. L. Phan, T. A. Ho, P. D. Thang, Q. T. Tran, T. D. Thanh, N. X. Phuc, M. H. Phan, B. T. Huy and S. C. Yu, J. Alloys Compd., 2014, 615, 937–945 CrossRef CAS.
- T. A. Ho, T. L. Phan, P. D. Thang and S. C. Yu, J. Electron. Mater., 2016, 45, 2328–2333 CrossRef CAS.
- M. A. Gdaiem, Ah. Dhahri, J. Dhahri and E. K. Hlil, Mater. Res. Bull., 2017, 88, 91–97 CrossRef CAS.
- A. Belkahla, K. Cherif, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2017, 715, 266–274 CrossRef CAS.
- R. Skini, A. Omri, M. Khlifi, E. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2014, 364, 5–10 CrossRef CAS.
- Y. C. Kim, K. H. Kim, D. Y. Son, D. N. Jeong, J. Y. Seo, Y. S. Choi, I. T. Han, S. Y. Lee and N. G. Park, Nature, 2017, 550, 87–91 CrossRef CAS PubMed.
- J. Khelifi, A. Tozri, F. Issaoui, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2014, 584, 617–624 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 81, 440–444 CrossRef CAS.
- J. B. Goodenough, J. Appl. Phys., 1997, 81, 5330–5335 CrossRef CAS.
- P. Levy, F. Parisi, G. Polla, D. Vega, G. Leyva and H. Lanza, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6437–6441 CrossRef CAS.
- K. H. Ahn, X. W. Wu, K. Liu and C. L. Chien, J. Appl. Phys., 1997, 81, 5505–5507 CrossRef CAS.
- M. Pissas and G. Kallias, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134414–134422 CrossRef.
- M. Pekala, V. Drozd and J. Mucha, J. Magn. Magn. Mater., 2005, 928–932 CrossRef CAS.
- T. Yi, S. Gao, X. Qi, Y. Zhu, F. Cheng, B. Ma, Y. Huang and C. Yan, J. Phys. Chem. Solids, 2000, 61, 1407–1413 CrossRef CAS.
- M. Baldini, et al., J. Phys.: Condens. Matter, 2012, 24, 045601–045605 CrossRef CAS PubMed.
- W. Zhong, W. Cheng, W. P. Ding, N. Zhang, Y. W. Du and Q. J. Yan, Solid State Commun., 1998, 106, 55–58 CrossRef CAS.
- D. B. Wiles and R. A. Young, J. Appl. Crystallogr., 1981, 14, 149–151 CrossRef CAS.
- M. Koubaa, W. Cheikhrouhou-Koubaa and A. Cheikhrouhou, J. Phys. Chem. Solids, 2009, 70, 326–333 CrossRef CAS.
- S. Choura-Maatar, R. Mnassri, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Cheikhrouhou and E. K. Hlil, J. Magn. Magn. Mater., 2017, 433, 239–247 CrossRef CAS.
- M. Khlifi, M. Bejar, O. El Sadek, E. Dhahri, M. A. Ahmed and E. K. Hlil, J. Alloys Compd., 2011, 509, 7410–7415 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- Z. Wei, A. Chak-Tong and D. Y. Wei, Chin. Phys. B, 2013, 22, 057501 CrossRef.
- P. Schiffer, A. P. Ramirez, K. N. Franklin and S.-W. Cheon, Phys. Rev. Lett., 1996, 77, 2085–2088 CrossRef CAS PubMed.
- H. L. Ju, H. C. Sohn and K. M. Krishnan, Phys. Rev. Lett., 1997, 79, 3230–3233 CrossRef CAS.
- K. Cherif, A. Belkahla, A. Dhahri and J. Dhahri, J. Supercond. Novel Magn., 2015, 28, 2241–2248, DOI:10.1007/s10948-015-3070-1.
- R. Thaljaoui, W. Boujelben, M. Pękała, K. Pękała, J. Antonowicz, J.-F. Fagnard, P. Vanderbemden, S. Dą browska and J. Mucha, J. Alloys Compd., 2014, 611, 427–432 CrossRef CAS.
- G. Lalitha and P. Venugopal Reddy, J. Magn. Magn. Mater., 2008, 320, 754–759 CrossRef CAS.
- A. Taylor, X-Ray Metallography, Wiley, New York, 1961 Search PubMed.
- N. Kallel, S. Kallel, O. Pena and M. Oumezzine, Solid State Sci., 2009, 11, 1494–1498 CrossRef CAS.
- C. V. Vazquez, M. C. Blanco, M. A. L. Quintela, R. D. Sanchez, J. Rivas and S. B. Oseroff, J. Mater. Chem., 1998, 8, 991–1000 RSC.
- J. Gutierrez, A. Pena, J. M. Barandiran, J. L. Pizarro, T. Hernandez, L. Lezama, M. Insausti and T. Rojo, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9028–9035 CrossRef CAS.
- W. Boujelben, A. Cheikh-Rouhou and J. C. Joubert, Eur. Phys. J. B, 2001, 24, 419–423 CrossRef CAS.
- L. Q. Zheng and Q. F. Fang, Phys. Status Solidi A, 2001, 185, 267–275 CrossRef CAS.
- A. Zaidi, K. Cherif, J. Dhahri, E. K. Hlil, M. Zaidi and T. Alharbi, J. Alloys Compd., 2015, 650, 210–216 CrossRef CAS.
- M. Medarde, J. Mesot, P. Lacorre, S. Rosenkranz, P. Fischer and K. Gobrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9248–9258 CrossRef CAS.
- A. H. Morrish, The Physical Principles of Magnetism, IEEE Press, New York, 2001 Search PubMed.
- S. Mnefgui, A. Dhahri, N. Dhahri, El. K. Hlil and J. Dhahri, J. Magn. Magn. Mater., 2013, 340, 91–96 CrossRef CAS.
- R. P. Borges, F. Ott, R. M. Thomas, V. Skumryev, J. M. D. Coey, J. I. Arnaudas and L. Ranno, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 12847–12851 CrossRef CAS.
- A. Belkahla, K. Cherif, J. Dhahri, K. Taibi and E. K. Hlil, RSC Adv., 2017, 7, 30707–30716 RSC.
- M. Baazaoui, N. Hamdaoui, M. R. Laouyenne, W. Cheikhrouhou-Koubaa, L. Beji and M. Oumezzine, J. Supercond. Novel Magn., 2017, 30, 2763–2770 CrossRef CAS.
- K. El Maalam, M. Ben Ali, H. El Moussaoui, O. Mounkachi, M. Hamedoun, R. Masrour, E. K. Hlil and A. Benyoussef, J. Alloys Compd., 2015, 622, 761–764 CrossRef CAS.
- S. S. Nair, M. Mathews, P. A. Joy, S. D. Kulkarni and M. R. Anantharaman, J. Magn. Magn. Mater., 2004, 283, 344–352 CrossRef CAS.
- S. J. Haralkar, R. H. Kadam, S. S. More, S. E. Shirsath, M. L. Mane, S. Patil and D. R. Mane, Phys. B, 2012, 407, 4338–4346 CrossRef CAS.
- S. Thankachan, B. P. Jacob, S. Xavier and E. M. Mohammed, Phys. Scr., 2013, 87, 1–7 CrossRef.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16–17 CrossRef.
- M. A. Hamad, Phase Transitions, 2012, 85, 106–112 CrossRef CAS.
- N. P. Kumar, G. Lalitha, E. Sagar and P. V. Reddy, Phys. B, 2015, 457, 275–279 CrossRef CAS.
- M. S. Anwar, F. Ahmed and B. H. Koo, J. Alloys Compd., 2014, 617, 893–898 CrossRef CAS.
- R. Cherif, E. K. Hlil, M. Ellouze, F. Elhalouani and S. Obbade, J. Mater. Sci., 2014, 49, 8244–8251 CrossRef CAS.
- M. A. Hamad, J. Supercond. Novel Magn., 2014, 27, 277–280 CrossRef CAS.
- Y. K. Lakshmi and P. V. Reddy, Solid State Sci., 2010, 12, 1731–1740 CrossRef.
- A. Krichene, W. Boujelben and A. Cheikhrouhou, J. Alloys Compd., 2013, 550, 75–82 CrossRef CAS.
- J. S. Kim, A. N. Ulyanov, Y. M. Kang, S. G. Min, S. C. Yu and S. I. Yoo, J. Magn. Magn. Mater., 2007, 310, 2818–2819, DOI:10.1016/j.jmmm.2006.10.964.
- M. Dhahri, A. Zaidi, K. Cherif, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2017, 691, 578–586 CrossRef CAS.
- M. Oumezzine, S. Zemni and O. Pena, J. Alloys Compd., 2010, 508, 292–296 CrossRef CAS.
- E. Brück, O. Tegus, D. T. C. Thanh and K. H. J. Buschow, J. Magn. Magn. Mater., 2007, 310, 2793–2799 CrossRef.
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479–1539 CrossRef.
- E. Tka, K. Cherif and J. Dhahri, Appl. Phys., 2014, 116, 1181–1191 CAS.
- D. I. N. H. Nam, N. V. Dai, L. V. Hong, N. X. Phuc, S. C. Yu, M. Tachibana and E. Takayama-Muromachi, J. Appl. Phys., 2008, 103, 043905–043909 CrossRef.
- S. Ghodhbane, A. Dhahri, N. Dhahri, E. K. Hlil and J. Dhahri, J. Alloys Compd., 2013, 550, 358–364 CrossRef CAS.
- S. K. Barik, C. Krishnamoorthi and R. Mahendiran, J. Magn. Magn. Mater., 2011, 323, 1015–1021 CrossRef CAS.
- Za. Mohamed, M. Abassi, E. Tka, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2015, 646, 23–31 CrossRef CAS.
- M. H. Phan, S. C. Yu and N. H. Hur, Appl. Phys. Lett., 2005, 86, 072504 CrossRef.
- A. Ben Hassine, A. Dhahri, L. Bouazizi, M. Oumezzine and E. K. Hlil, Solid State Commun., 2016, 233, 6–10 CrossRef CAS.
- A. H. Morrish, The Physical Principle of Magnetism,John Wiley & Sons, Inc., New York, 1965 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, London:Saunders College Publishing, 1976 Search PubMed.
- V. Franco, J. S. Blázquez and A. Conde, Appl. Phys. Lett., 2006, 89, 222512 CrossRef.
- V. Franco and A. Conde, Int. J. Refrig., 2010, 33, 465–473 CrossRef CAS.
- Q. Y. Dong, H. W. Zhang, J. R. Sun, B. G. Shen and V. Franco, J. Appl. Phys., 2008, 103, 116101–116103 CrossRef.
- A. Ben Jazia Kharrat, E. K. Hlil and W. Boujelben, J. Alloys Compd., 2018, 739, 101–113 CrossRef CAS.
- T. D. Shen, R. B. Schwarz, J. Y. Coulter and J. D. Thompson, J. Appl. Phys., 2002, 91, 5240–5245 CrossRef CAS.
- V. Franco, A. Conde, E. J. M. Romero and J. S. Blazquez, J. Phys.: Condens. Matter, 2008, 20, 285207–285211 CrossRef.
- C. P. Reshmi, S. Savitha Pillai, M. Vasundhara, G. R. Raji, K. G. S uresh and M. Raama Varma, J. Appl. Phys., 2013, 114, 033904–033910 CrossRef.
- V. Franco, C. F. Conde, J. S. Blazquez, A. Conde, P. Svec, D. Janičkovic and L. F. Kiss, J. Appl. Phys., 2007, 101, 093903 CrossRef.
- P. Nisha, S. Savitha Pillai, M. RaamaVarma and K. G. Suresh, Solid State Sci., 2012, 14, 40–47 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
J. Dhahria and
E. K. Hlilb
*a,
J. Dhahria and
E. K. Hlilb
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space groups, respectively. While, the x = 0.20 sample crystallized in the rhombohedral structure with a R
c space groups, respectively. While, the x = 0.20 sample crystallized in the rhombohedral structure with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. Magnetic data, under a magnetic field of 0.05 T, indicated that our samples undergo a ferromagnetic (FM)–paramagnetic (PM) phase transition, on increasing the temperature. The magnetic field dependence of the magnetocaloric properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples, with the second phase transition, was investigated. Near room temperature, the x = 0.20 sample exhibited a large magnetic entropy change with maxima of 6.01 and 3.12 J kg−1 K−1, respectively, under applied magnetic fields of 5 and 2 T. Also, the relative cooling power (RCP) was calculated. According to hysteresis cycles, for our studied samples, at 10 K a typical soft FM behavior with a low coercive field was observed. These results make our samples promising candidates for magnetic refrigerators, magnetic recording, and memory devices.
c space group. Magnetic data, under a magnetic field of 0.05 T, indicated that our samples undergo a ferromagnetic (FM)–paramagnetic (PM) phase transition, on increasing the temperature. The magnetic field dependence of the magnetocaloric properties of La0.75Ca0.25−xNaxMnO3 (x = 0.15 and 0.20) samples, with the second phase transition, was investigated. Near room temperature, the x = 0.20 sample exhibited a large magnetic entropy change with maxima of 6.01 and 3.12 J kg−1 K−1, respectively, under applied magnetic fields of 5 and 2 T. Also, the relative cooling power (RCP) was calculated. According to hysteresis cycles, for our studied samples, at 10 K a typical soft FM behavior with a low coercive field was observed. These results make our samples promising candidates for magnetic refrigerators, magnetic recording, and memory devices.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1−xMMnO3 (where Ln is a rare earth element and M is a divalent alkaline ion) have attracted particular attention from several researchers. This is thanks to their interesting interplay between magnetic and electronic features, as well as to being very promising for future technological applications.1–7 Additionally, they have many advantages such as low production cost, convenient preparation, softer vibration, longer usage time, small volume requirement and chemical stability. Moreover, these materials are environment-friendly and do not cause noise pollution. This makes them attractive to further research in relation to the widely-used refrigeration technology based on gas compression. The parent compound, LnMnO3, is an antiferromagnetic (AFM)-insulator characterized by a superexchange (SE) coupling between Mn3+ ions. When the Ln site is substituted with a divalent ion, a proportional number of Mn3+ ions with the electronic configuration (3d4, t32g↑ e1g↑, S = 2) are converted into Mn4+ ions with the electronic configuration (3d3, t32g↑ e0g, S = 3/2). This mixed Mn3+/Mn4+valence gives rise to a double exchange (DE)8 transfer of eg electrons from Mn3+ to Mn4+ ion via the O2− ion network. DE plays an important role in the properties of these materials.9 These properties are very dependent on the substitution rate x, average size of the cation, cationic disorder and the elaboration method.10 La1−xCaxMnO3 has attracted the attention of several researchers. This is thanks to the very rich phase diagram observed in this series.11,12 Pekala et al.13 investigated its magnetic field dependence of electrical resistivity in fine grains and analyzed the influence of external magnetic field on the transport processes in detail. Yi et al.14 observed that the magnetoresistance of nanosized La0.75Ca0.25MnO3 is enhanced at low temperatures due to the spin-polarized tunneling behavior. In addition, the pressure dependence of magnetic phase separation and transport behavior in La0.75Ca0.25MnO3 has also been investigated in recent paper.15 On other hand, with the substitution of Na on LaMnO3 sample, an amount 2× of Mn3+ is converted to Mn4+. Zhong et al.16 have studied the magnetocaloric properties in La1−xNaxMnO3 (0 ≤ x ≤ 0.2) and found that for x = 0.2, |–ΔSmaxM| reaches 1.96 J kg−1 K−1 upon a magnetic applied field change of 1 T. This paper investigates the effect of Na substitution on the structural, magnetic and magnetocaloric effect (MCE) of (x = 0.15 and 0.20) samples, synthesized by flux method, using sodium chloride (NaCl) as a flux. A theoretical investigation was used to predict the MCE properties for x = 0.20.
1−xMMnO3 (where Ln is a rare earth element and M is a divalent alkaline ion) have attracted particular attention from several researchers. This is thanks to their interesting interplay between magnetic and electronic features, as well as to being very promising for future technological applications.1–7 Additionally, they have many advantages such as low production cost, convenient preparation, softer vibration, longer usage time, small volume requirement and chemical stability. Moreover, these materials are environment-friendly and do not cause noise pollution. This makes them attractive to further research in relation to the widely-used refrigeration technology based on gas compression. The parent compound, LnMnO3, is an antiferromagnetic (AFM)-insulator characterized by a superexchange (SE) coupling between Mn3+ ions. When the Ln site is substituted with a divalent ion, a proportional number of Mn3+ ions with the electronic configuration (3d4, t32g↑ e1g↑, S = 2) are converted into Mn4+ ions with the electronic configuration (3d3, t32g↑ e0g, S = 3/2). This mixed Mn3+/Mn4+valence gives rise to a double exchange (DE)8 transfer of eg electrons from Mn3+ to Mn4+ ion via the O2− ion network. DE plays an important role in the properties of these materials.9 These properties are very dependent on the substitution rate x, average size of the cation, cationic disorder and the elaboration method.10 La1−xCaxMnO3 has attracted the attention of several researchers. This is thanks to the very rich phase diagram observed in this series.11,12 Pekala et al.13 investigated its magnetic field dependence of electrical resistivity in fine grains and analyzed the influence of external magnetic field on the transport processes in detail. Yi et al.14 observed that the magnetoresistance of nanosized La0.75Ca0.25MnO3 is enhanced at low temperatures due to the spin-polarized tunneling behavior. In addition, the pressure dependence of magnetic phase separation and transport behavior in La0.75Ca0.25MnO3 has also been investigated in recent paper.15 On other hand, with the substitution of Na on LaMnO3 sample, an amount 2× of Mn3+ is converted to Mn4+. Zhong et al.16 have studied the magnetocaloric properties in La1−xNaxMnO3 (0 ≤ x ≤ 0.2) and found that for x = 0.2, |–ΔSmaxM| reaches 1.96 J kg−1 K−1 upon a magnetic applied field change of 1 T. This paper investigates the effect of Na substitution on the structural, magnetic and magnetocaloric effect (MCE) of (x = 0.15 and 0.20) samples, synthesized by flux method, using sodium chloride (NaCl) as a flux. A theoretical investigation was used to predict the MCE properties for x = 0.20.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space groups, around 2θ = 32°. In this region, the system showed a sign of multi-phased behavior with no complete splitting into the double line of the intense peak. This result is in concordance with that observed in ref. 18. The relative amount of the orthorhombic phase was 81.68%. However, that of the rhombohedral phase was 18.32%. We can conclude that the orthorhombic phase is dominant. On the other hand, x = 0.20 sample crystallized in the rhombohedral structure with R
c space groups, around 2θ = 32°. In this region, the system showed a sign of multi-phased behavior with no complete splitting into the double line of the intense peak. This result is in concordance with that observed in ref. 18. The relative amount of the orthorhombic phase was 81.68%. However, that of the rhombohedral phase was 18.32%. We can conclude that the orthorhombic phase is dominant. On the other hand, x = 0.20 sample crystallized in the rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. Also, we can see the appearance of a small quantity of Mn3O4, as found in recent works.19,20
c space group. Also, we can see the appearance of a small quantity of Mn3O4, as found in recent works.19,20
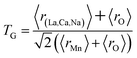
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c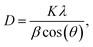

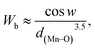




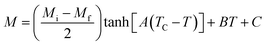
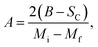 B is the magnetization sensitivity dM/dT at FM state before transition. SC is the magnetization sensitivity dM/dT at TC.
B is the magnetization sensitivity dM/dT at FM state before transition. SC is the magnetization sensitivity dM/dT at TC. 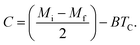
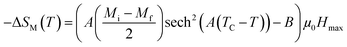
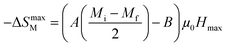
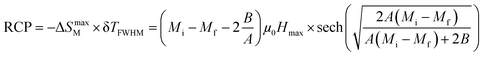
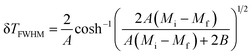
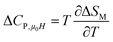



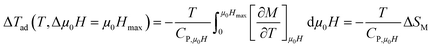
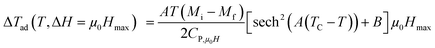
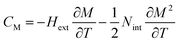
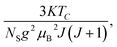 g is the Landé factor, J is the total angular momentum and NS is the number of spins per unit mass.
g is the Landé factor, J is the total angular momentum and NS is the number of spins per unit mass.

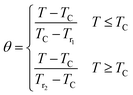

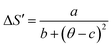
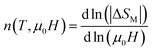
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group, at room temperature. While, the x = 0.15 sample admits both phases with different percentages. Magnetization measurements as function of temperatures in a magnetic field of 0.05 T show that our studied samples undergo a second-order PM–FM phase transition, upon decreasing temperature. Around room temperature, a large MCE is observed for our samples, under a magnetic field of 5 T. –ΔSmaxM is found to be 6.01 J kg−1 K−1 under μ0H = 5 T magnetic field for x = 0.20. For the x = 0.15 sample, −ΔSM curves show the existence of two maxima, which may be attributed to the structural inhomogeneity. The RCP is also analyzed. From, −ΔSM curves, we have investigated the dependence of temperature on the adiabatic temperature change (−ΔTad). Its maximum is found to be 2.93 K, for the x = 0.15 sample, in an applied magnetic field of 5 T. From the hysteresis cycles, at 10 K for the studied samples, we can remark a typical soft FM behavior with a small hysteresis loop and a low coercive field (μ0HC). The small values of coercive field confirm that the magnetic domains can rotate easily to the direction of the applied magnetic field. These results make our samples promising candidates for magnetic refrigeration, magnetic recording and memory devices.
c space group, at room temperature. While, the x = 0.15 sample admits both phases with different percentages. Magnetization measurements as function of temperatures in a magnetic field of 0.05 T show that our studied samples undergo a second-order PM–FM phase transition, upon decreasing temperature. Around room temperature, a large MCE is observed for our samples, under a magnetic field of 5 T. –ΔSmaxM is found to be 6.01 J kg−1 K−1 under μ0H = 5 T magnetic field for x = 0.20. For the x = 0.15 sample, −ΔSM curves show the existence of two maxima, which may be attributed to the structural inhomogeneity. The RCP is also analyzed. From, −ΔSM curves, we have investigated the dependence of temperature on the adiabatic temperature change (−ΔTad). Its maximum is found to be 2.93 K, for the x = 0.15 sample, in an applied magnetic field of 5 T. From the hysteresis cycles, at 10 K for the studied samples, we can remark a typical soft FM behavior with a small hysteresis loop and a low coercive field (μ0HC). The small values of coercive field confirm that the magnetic domains can rotate easily to the direction of the applied magnetic field. These results make our samples promising candidates for magnetic refrigeration, magnetic recording and memory devices.


