Orbital-dependent redox potential regulation of quinone derivatives for electrical energy storage

Abstract

Electrical energy storage in redox flow batteries has received increasing attention. Redox flow batteries using organic compounds, especially quinone-based molecules, as active materials are of particular interest owing to the material sustainability, tailorable redox properties, and environmental friendliness of quinones and their derivatives. In this report, various quinone derivatives were investigated to determine their suitability for applications in organic RFBs. Moreover, the redox potential could be internally regulated through the tuning of σ and π bonding contribution at the redox-active sites. Furthermore, the binding geometry of some selected quinone derivatives with metal cations was studied. These studies provide an alternative strategy to identify and design new quinone molecules with suitable redox potentials for electrical energy storage in organic RFBs.

---

Introduction

The development of renewable energy technologies that are not dependent on fossil fuels is essential for energy security, economic benefits, and climate-change mitigation. Consequently, it is of particular importance to develop the corresponding energy storage technologies addressing safety, cost, efficiency, and sustainability.^1–4 Among the well-established energy storage technologies, batteries have received considerable research interest in the past few decades. For upcoming large-scale applications, it is crucial to address the issues of material sustainability and eco-efficient processability. As one of the most promising battery technologies, redox-flow batteries (RFBs) are of particular interest for large-scale electrical energy storage owing to their unique split cell design, which stores electro-active species externally in the circulated flowing liquid electrolytes.^5,6 The split cell design offers many comparative advantages over the batteries using a solid electrode, and these include independent scaling of energy and power, modular construction, and replaceability of the defective components.^7,8 Traditional RFBs are based on transition metal ions in acidic solutions. The challenges arising from such battery chemistry include electrolyte corrosivity, poor redox kinetics, high material cost, and relatively low efficiency, which prevent their large-scale commercialization.^9,10 The development of future RFBs should address these challenges, and one of the major tasks in response to these challenges would be exploring new redox-active electrolytes that are highly efficient, safe, low-cost, and non-toxic/non-corrosive.^11–13

To this end, the notion of organic RFBs has been proposed and has received considerable research attention.^14–19 Particularly, quinones and their derivatives stand out as some of the most promising material systems for organic RFBs because of their chemical tunability and rapid redox kinetics.^20–22 Many studies focus on the redox potential tuning of quinone molecules by means of functional group substitution and binding effect from metal cations.^23–30 At present, the reduction potentials of 700 quinone couples have been experimentally compiled,³¹ which is the most detailed source of information. Despite the investigations on quinones and their derivatives, only limited fundamental studies focus on the understanding of their redox chemistry. Up to now, only a few computational studies have examined the redox properties of quinone derivatives.^{24,25,27,31–39} Bachman et al. have investigated the redox properties of various anthraquinone derivatives including the tuning of reduction or oxidation potential, the stability upon reduction in solution, the effect of functional group substitution on the solvation energies, and the influence of lithium salts and decomposition products of the salts on reduction potentials.²⁵ Er et al. identified prospective candidates for both the negative and positive sides of quinone-based aqueous RFBs; they predicted that functionalization near to ketones impacts the reduction potential and that away from the ketones improves solubility.³⁷ Kim et al. studied the Li binding thermodynamics and redox properties of seven quinone derivatives; they found that the redox potential decreased with an increase in aromaticity, while it increased by attaching electron withdrawing functional groups or by using an electrolyte with a high dielectric constant.²⁸

Compared to the investigations on the redox properties affected by extrinsic factors such as functional group substitution, studies on the intrinsic factors, especially the basic chemical bonds, which exhibit a profound impact on the origin of the redox potential, are limited. To design quinone-based materials with the desired redox properties, in this investigation, we aimed to determine the redox potential and its corresponding internal regulation mechanism of various quinone derivatives. We showed that the redox potential of quinone-based materials is highly dependent on the chemical bond structure including the energy gaps, the contribution ratio, and the overlapping degrees of σ bonds and π bonds. We also showed the substantial effect of binding metal cations on the redox potential. This is the first study that correlated the redox potential of quinone-based materials from the view of chemical bonds, which might further enhance the fundamental understanding and contribute to the design of appropriate quinone-based materials for organic RFBs.

Calculation method

NICS and ACID

NICS values were calculated using the standard GIAO (GIAO = NMR)⁴⁰ at the level of (U)B3LYP/6-31G(d,p). To obtain the best NICS aromaticity index, NICSzz values were selected.⁴¹ Anisotropy of the induced current density (ACID) plots (iso-value = 0.04) was calculated by using the method developed by Herges.⁴²

Redox potential

The thermodynamic cycle was used to predict the redox potentials of the quinone derivatives.^39,43 The redox potential (ΔE^red) with respect to an Li/Li⁺ reference electrode of an active positive electrode material in solution can be predicted by the equation ΔE^red = −ΔG^soln/nF − 1.44 V, where ΔG^soln is the difference in the Gibbs free energies in solution during the reduction, n is the number of electrons transferred, and F is the Faraday constant.²⁸ The constant 1.44 V indicates the redox potential of the Li/Li⁺ reference electrode.^43–45 The electronic properties (the HOMO and LUMO energy levels as well as the electron affinity) of the active positive electrode materials were also calculated to rationalize the predicted redox potentials.

Metal cation binding energy

All of the optimized calculations were performed by using Gaussian 09 software package⁴⁶ with 6-31+G(d,p) basis set and B3lyp level of theory.^47–51 All the calculations were conducted in vacuum except the redox potential and the solvation free energy. The molecular orbital calculations were performed using M062X functional after the structure optimization. The binding energies (BE) of the 1Li case (one Li⁺-ion per molecule) and 2Li case (two Li⁺-ions per molecule) were calculated based on DFT (B3lyp) using BE = E(Q − Li) − E(Q) −E(Li) and BE = E(Q − 2Li) − E(Q − 1Li) −E(Li), respectively, where E(Q − 2Li), E(Q − Li), E(Q), and E(Li) denote the total energies of the quinone–2Li complex, the quinone–1Li complex, pristine quinone, and Li atoms, respectively.²⁸ The SMD solvation model performed favorably in the computation of redox potentials (acetonitrile) and solvation free energy (n,n-dimethylacetamide).

Results & discussion

Ground state energy of selected quinone derivatives

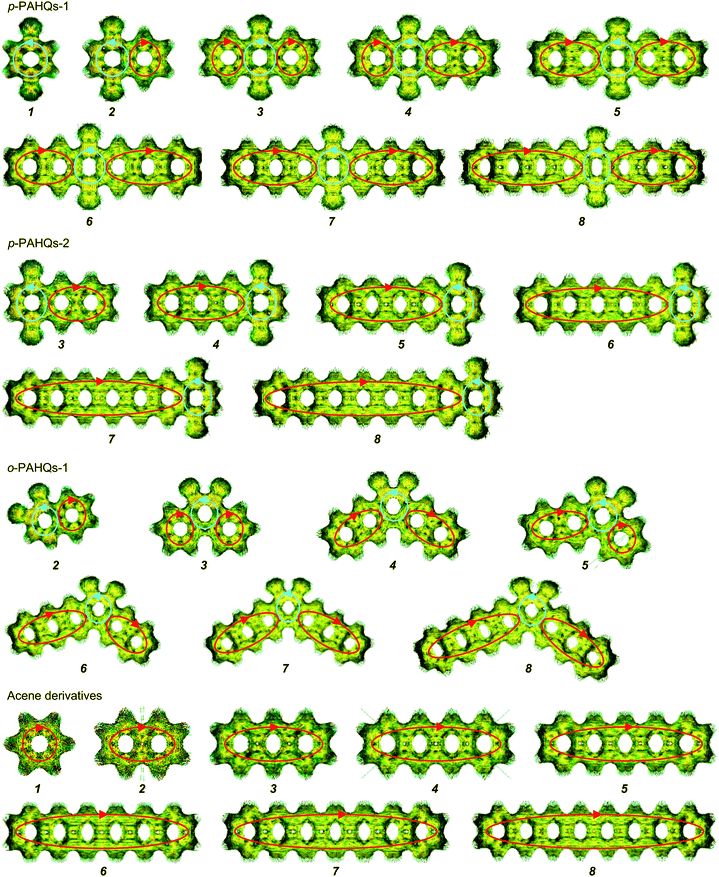
The stability of redox active materials in the electrolyte and at the electrode surfaces is one of the key properties determining the long-term stability in RFBs. For organic RFB application, it is preferable to use molecules with low ground state energy. Fig. S1 (ESI†) shows the optimized ground state energy difference of a series of quinone derivatives, in which the aromatic ring numbers range from one to four with two carbonyl functional groups occupying different sites. Para-polycyclic aromatic hydrocarbon quinones (denoted as p-PAHQs) and ortho-polycyclic aromatic hydrocarbon quinones-1 (denoted as o-PAHQs-1) showed much lower ground state energy than ortho-polycyclic aromatic hydrocarbon quinones-2 (denoted as o-PAHQs-2). With the increase in substituted phenyl groups, relatively low ground state energy structures were found in 1,4-anthraquinone derivatives with substituted phenyl groups on both sides of 1,4-anthraquinone (denoted as p-PAHQs-1, orange frames), 1,4-anthraquinone derivatives with substituted phenyl groups on either side of 1,4-anthraquinone (denoted as p-PAHQs-2, green frames), and ortho-polycyclic aromatic hydrocarbon quinones with substituted phenyl groups on both sides of the carbonyl moiety (denoted as o-PAHQs-1, blue frames). In contrast, ortho-polycyclic aromatic hydrocarbon quinones with substituted phenyl groups on either side of the carbonyl moiety (denoted as o-PAHQs-2, grey frames) showed relatively high ground state energy. The reason was that o-PAHQs-2 exhibited gradually enhanced magnetism with the increase in the number of substituted phenyl groups. The gradually enhanced magnetism of o-PAHQs-2 was due to enhanced π–σ coupling, as indicated by the calculated partial electron spin density (Fig. S2, ESI†). In order to investigate the electrochemical properties of quinone derivatives and to determine the corresponding internal regulation mechanism, four quinone derivatives, namely, p-PAHQs-1, p-PAHQs-2, o-PAHQs-1, and o-PAHQs-2 were selected as representative examples (Fig. 1). Acene derivatives were investigated as the reference because the π electrons solely dominated their electrochemical properties (Fig. S3, ESI†).

Fig. 1 Investigated molecular structures of p-PAHQs-1, p-PAHQs-2, o-PAHQs-1, o-PAHQs-2, and the referential acene derivatives.

Aromatic analysis

Aromaticity is a key factor that allows the π-electrons to delocalize within the conjugated ring, thereby contributing to the decrease in the ground state energy and increase in the stability of the molecule.^52–55 According to Hückel's rules, conjugated species with 4n + 2 π-electrons are aromatic, while those with 4n π-electrons are anti-aromatic.^56,57 The aromaticity of quinone derivatives was investigated by the NICS (nucleus-independent chemical shift) and ACID (anisotropy of the induced current density) analyses. Considering that NICS(1)zz has a better aromaticity index than the NICS(0) value when taking into account the contribution of σ-bond to the ring current,⁴¹ only the NICS(1)zz value of an individual ring was investigated. The rings containing the carbonyl group in p-PAHQs-1, p-PAHQs-2, and o-PAHQs-1 exhibited weak anti-aromaticity, while others including the referential benzene derivatives were aromatic with large negative NICS(1)zz values (<−19 ppm, Fig. S4, ESI†). The calculated NICS values were consistent with the results of ACID analysis (Fig. 2), in which counterclockwise and clockwise diatropic ring currents were clearly observed in the carbonyl group hosting rings and the rest of the rings, respectively. The counterclockwise diatropic ring current suggested that the anti-aromaticity was weak in the carbonyl group hosting rings, but the diatropic ring currents of all other rings were clockwise and formed large π-conjugate aromatic circular currents with the increase in the number of aromatic rings. For the referential acene derivatives, all the rings were aromatic and the aromaticity became stronger with the increase in the number of rings due to the conjugation enhancement. Moreover, the aromaticity of the rings decreased from centre to edge, which was due to the weakened conjugation intensity. However, for p-PAHQs-1 and p-PAHQs-2, the existence of carbonyl groups changed the hosting ring from aromatic to weakly anti-aromatic, but the other rings retained their aromaticity. It should be pointed out that the whole molecules still exhibited strong aromaticity, but the aromaticity of the rings near the carbonyl group hosted ring decreased due to the synergy effect of conjugation intensity and conjugation weakening by carbonyl groups.

Fig. 2 Calculated ACID of p-PAHQs-1, p-PAHQs-2, o-PAHQs-1, and the referential acene derivatives. The basal plane of the molecules is placed perpendicular to the magnetic field vector. The small green arrows are the computed current density vectors. The red and cyan circles labeled by arrows reflect the global clockwise or counterclockwise diatropic ring currents, respectively.

Relationship between the energy level and the redox potential

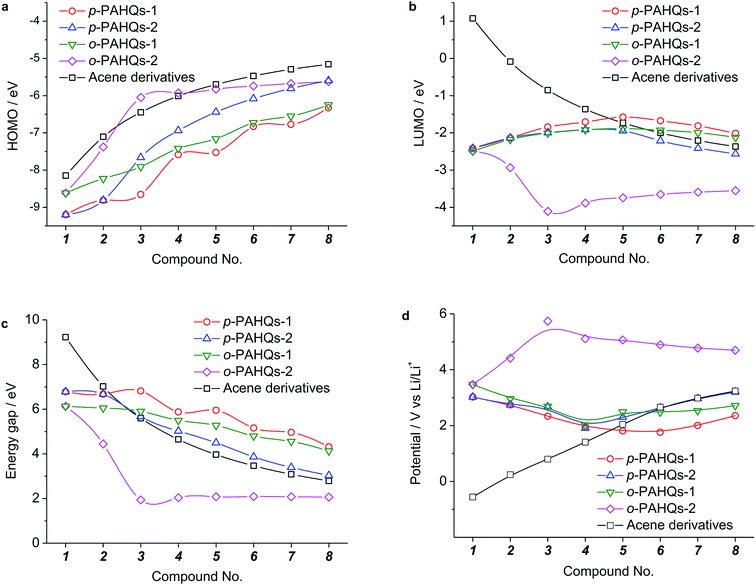
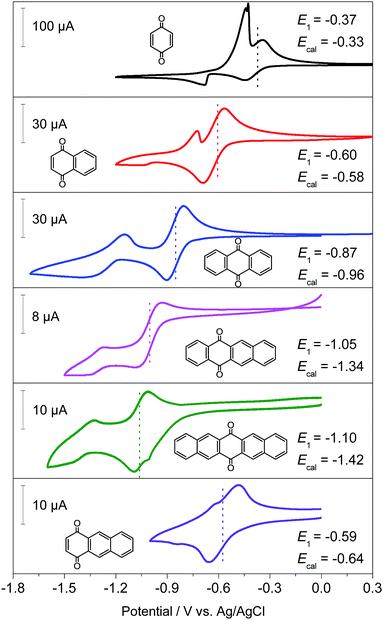
Generally, the redox potential shows strong correlation to the energy level of the molecule.^25,34,39 For a redox-active molecule, a lower LUMO energy level usually results in higher redox potential. For both the selected quinone derivatives and referential acene derivatives, the HOMO energy levels shifted towards higher energy (Fig. 3a) with the increase in the ring number. The LUMO energy level increased for ring numbers less than five, and it decreased when the ring numbers were greater than or equal to five (Fig. 3b). This phenomenon was due to the σ–π coupling effect, which is discussed in the density of state (DOS) analysis. The energy gap (LUMO–HOMO) gradually decreased with the increase in ring numbers (Fig. 3c). This was consistent with the aromatic analysis: increased aromaticity strengthened the electron delocalization and thereby narrowed the energy gap. The calculated redox potentials of p-PAHQs-1, p-PAHQs-2, and o-PAHQs-1 exhibited an opposite trend to the LUMO energy level (Fig. 3d). To this end, to achieve quinone derivatives with high redox potential, it is preferable to enhance the aromaticity by means of enhancing electron delocalization. It should be mentioned that o-PAHQs-2, especially compounds 3–5, behaved differently from other quinone derivatives because these o-PAHQs-2 compounds exhibited magnetism, which was responsible for the sudden decrease in the LUMO energy level. The frequency analysis demonstrated that compounds 3–5 in o-PAHQs-2 were unstable with one (−56.71 cm⁻¹), two (−35.38 cm⁻¹, −65.18 cm⁻¹), and three (−41.11 cm⁻¹, −50.39 cm⁻¹, −68.51 cm⁻¹) imaginary frequencies, respectively. With the increase in the ring numbers, such frequencies were eliminated, which could be attributed to the enhanced conjugating effect. To experimentally verify the predicted redox potential, compounds 1–5 in p-PAHQs-1 and compounds 1–3 in p-PAHQs-2 were subjected to CV measurements (Fig. 4). All the tested quinone derivatives underwent successive two-step one-electron redox reactions. The half-wave redox potential for the first reduction reaction was very close to the calculated values with small variations. The calculated redox potentials were also in good agreement with the experimentally obtained results in previous investigations (Fig. S5, ESI†).

Fig. 3 Calculated energy levels and the redox potentials of p-PAHQs-1, p-PAHQs-2, o-PAHQs-1, o-PAHQs-2, and the referential acene derivatives. (a) HOMO energy level. (b) LUMO energy level. (c) Energy gap. (d) Redox potential.

Fig. 4 Cyclic voltammetry profiles of p-PAHQs-1 and p-PAHQs-2 at a scan rate of 20 mV s⁻¹. A cell with three-electrode configuration is used with glassy carbon, Pt wire, and AgCl/Ag electrodes serving as the working, counter, and reference electrodes, respectively. The composition of the electrolytes was 5 mM active materials and 1 M LiPF₆ in dimethylacetamide.

Orbital component analysis

There are only two types of bonds present in organic molecules: the localized σ bond and delocalized π bond. The effects of the σ and π bonds on the redox potential were systematically analyzed using quinone derivatives and referential acene derivatives. The effect of aromatic ring numbers on the redox potential was analyzed based on 32 quinone derivatives (compound 1–8 in p-PAHQs-1, p-PAHQs-2, o-PAHQs-1, o-PAHQs-2) and 8 acene derivatives (compound 1–8 in acene derivatives). Fig. 3d summarizes the redox potentials of the 40 molecules. For p-PAHQs-1, p-PAHQs-2, and o-PAHQs-1, the redox potential distribution decreased at small ring numbers but increased at large ring numbers. The turning point was found to be 6 for p-PAHQs-1 and 4 for p-PAHQs-2 and o-PAHQs-1; however, o-PAHQs-2 showed an opposite tendency and higher redox potential than other quinone derivatives. For acene derivatives, the redox potential was in proportion to the ring numbers because of pure π-electron configuration.

To extend the regulation mechanism of the redox potential, orbital component analysis was performed to quantitatively distinguish the contribution of σ and π bonds rather than electron affinity or molecular orbital analysis commonly used in previous investigations.²⁶ The redox potential was regulated by three main factors: the σ bond contribution, the π bond contribution, and the effect of the coupling coefficient of σ–π components. As a demonstration, p-PAHQs-1 and o-PAHQs-2 were investigated as representative examples (Fig. 5). First, the π component increase obeyed a quadratic function with the molecular length, whereas the σ component decreased with the molecular length. The effect of both of these two components on redox potential seemed opposite. For quinone derivatives with smaller molecule length or less ring number, the contribution from the σ component was greater than that from the π component; however, for quinone derivatives with larger molecule length or more ring numbers, the contribution from the π component was greater than that from the σ component. Second, the coupling coefficient of σ and π in o-PAHQs-2 was higher than that of p-PAHQs-1. Finally, σ bond of p-PAHQs-1 was higher than that of o-PAHQs-2 at molecular lengths below 6 Å. However, when the molecular length reached 6 Å, the σ component of p-PAHQs-1 was lower than that of o-PAHQs-2. The strong σ and π coupling coefficient and higher σ component of o-PAHQs-2 explained the higher redox potential compared with that of p-PAHQs-1. It seems that quinones with desired redox potentials can be achieved by fine-tuning the σ/π component and the σ–π coupling coefficient.

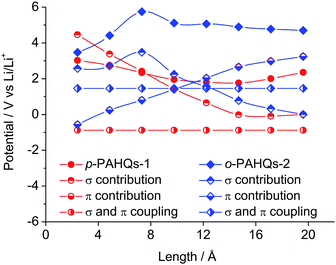Fig. 5 The contributions of σ bond, π bond, σ and π coupling coefficient to the redox potential of p-PAHQs-1 and o-PAHQs-2.

Density of state (DOS) analysis

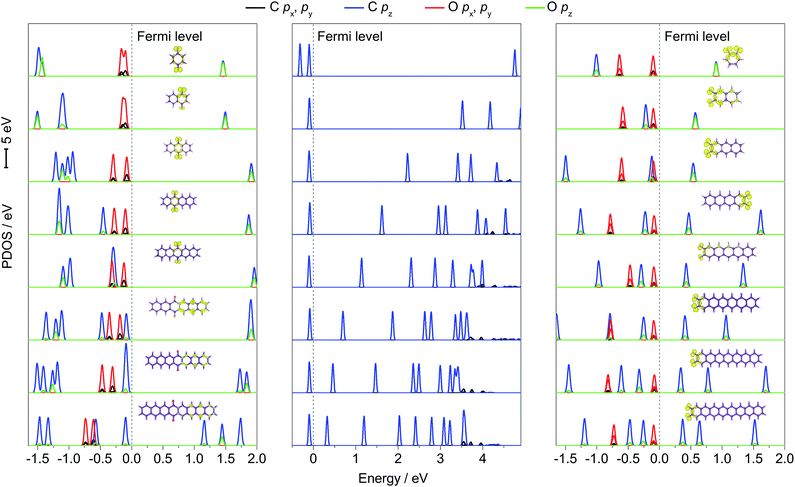
To further explain the regulation mechanism of the redox potential, the density of state (DOS) values of p-PAHQs-1, o-PAHQs-2, and referential acene derivatives were calculated. The partial density of state (PDOS) and total DOS are shown in Fig. 6 and S6 (ESI†), respectively. In the case of acene derivatives, DOS showed that the top of valence band (VB) and the bottom of conduction band (CB) were occupied solely by π bonds (middle panel of Fig. 6). The energy gap decreased rapidly with the increase in ring numbers by means of the shift of the bottom of CB towards the Fermi energy level, which was in agreement with the result of the aforementioned LUMO–HOMO energy gap analysis. However, this was more complicated in the case of p-PAHQs-1 because of the existence of σ bond. First, the π bonds (C p_z and O p_z) always occupied the bottom of CB, suggesting that the π bonds acted as an important factor in determining the energy gap. The main contribution of the π bonds originated from the p_z orbital of O atoms to p_z orbital of C atoms with the increase in ring numbers (left panel of Fig. 6). Second, the σ bonds of C and O atoms (C p_x/p_y and O p_x/p_y) occupied the top of VB for ring numbers less than five, implying that the σ bonds of the O atoms suppressed the π bonds of the C atoms. When the ring number exceeded six, the σ bonds of the O and C atoms moved away from the Fermi energy level. However, the π bonds of C atoms (C p_z) moved towards the Fermi energy level until they occupied the top of VB, in which the σ bonds of O atoms (O p_x/p_y) were substituted by the π bonds of C atoms (C p_z). Finally, the energy levels for the CB of p-PAHQs-1 with ring numbers of 3 and 4 were significantly larger than those of the corresponding acene derivatives. According to the generally accepted view that the energy level of LUMO is in linear relationship with the redox potential,²⁶ the redox potential of p-PAHQs-1 should be lower than that of the corresponding acene derivatives. However, the redox potential of p-PAHQs-1 was actually higher than that of the corresponding acene derivatives. This could be due to the contribution of σ bonds of O atoms in carbonyl groups, which played a much more important role than the π bonds in determining the redox potential.

Fig. 6 PDOS of p-PAHQs-1 (left panel), referential acene derivatives (middle panel), and o-PAHQs-2 (right panel). The corresponding molecular orbitals on the top of the VB are also provided. The π bond on the bottom of the CB and above the Fermi energy level is assigned as π*.

In the case of o-PAHQs-2, PDOS showed three distinct characteristics, as revealed in the right panel of Fig. 6. On one hand, the π bonds between C and O atoms (C p_z and O p_z) showed a stronger coupling coefficient than those observed for p-PAHQs-1 and acene derivatives. The π bonds of C and O atoms occupied the bottom of CB and shifted towards the Fermi energy level with the increase in ring numbers, thus lowering the bottom of CB energy level. On the other hand, the σ bonds of O atoms in the carbonyl groups kept occupying the top of VB in all cases; the σ bond of the O atoms (O p_x, p_y) strongly suppressed the π bond of C atoms (C p_z) and could not be overlapped. From compound 1–3 of o-PAHQs-2, the energy gaps of σ–π* and π–π* (π* refers to the π bond on the bottom of CB and above the Fermi energy level) decreased with the latter showing more significant decrease in energy gap. The redox potential of o-PAHQs-2 thus increased from compound 1–3. In contrast, the energy gap of σ–π* showed negligible variation for compounds 4–8 of o-PAHQs-2. However, the π–π* energy gap gradually increased with the increase in ring numbers. This phenomenon could be attributed to the shift of π bond from O and C atoms on the top of VB away from the Fermi energy level. The net effect resulted in the gradual decrease in redox potentials. Besides, the energy gaps of σ–π* and π–π* of o-PAHQs-2 were smaller than those of p-PAHQs-1, and the coupling strength between σ and π on the top of VB of o-PAHQs-2 was stronger than that observed for p-PAHQs-1. The two factors resulted in a higher redox potential of o-PAHQs-2 compared with that of p-PAHQs-1. Based on the above analysis, quinones with desired redox potential could be obtained through the molecular design combined with DOS analysis. High redox potential could be achieved for quinones with small π–π* and σ–π* energy gaps, for those with a higher contribution ratio of σ bonds in the top of VB, or for those with σ bond in the top of VB without overlapping with π bond.

The binding effect of Li⁺-ion

The most widely used chemistry in non-aqueous RFBs is based on Li⁺ ions.^25,28 The binding effect of Li⁺ ions plays a substantial role for the redox potential of quinones. The interaction between Li⁺ ions and the redox active sites of p-PAHQs-1, o-PAHQs-2, and referential acene derivatives was investigated as a prerequisite to justify their role as positive or negative electrode materials. Fig. S7 (ESI†) shows the possible binding sites for one Li⁺-ion (abbreviated as 1Li case) and two Li⁺-ions (abbreviated as 2Li case). In the 1Li case of referential acene derivatives (Fig. 7a), the binding energy (BE) became more negative with the increase in ring numbers, indicating a stronger interaction between the Li⁺ ions and π electrons of the molecule. In the same molecule, BE became more negative from the edge sites to the central site(s) because of stronger aromatic character of the central ring(s) compared with that of the edge rings. In the 1Li case of p-PAHQs-1 and o-PAHQs-2 (Fig. 7b and c), the most stable binding site for the Li⁺ ions should be at the carbonyl group (site 2) rather than the central site of the rings (other sites) because the electron-deficient Li⁺ ions prefer to bind with the electron pair-donating carbonyl functional group through Lewis acid–Lewis base interactions.²⁸ The calculated BE values indicated that the oxygen atoms of the carbonyl groups formed a chemical bond with the Li⁺ ions, which was consistent with the results of a previous study on the chemical reactions between Li and carbonyl oxygen.²⁸ In addition, BE of o-PAHQs-2 (site 2) remained almost constant, and BE of p-PAHQs-1 (site 2) showed less negative values with the increase in ring numbers, which was different from BE of referential acene derivatives. The reason might be that the localized σ electrons rather than delocalized π electrons served as the binding sites, and the aromaticity of the π electrons in the carbonyl groups weakened with the increase in ring numbers. Besides, the binding ability of the carbonyl groups was stronger than that of the corresponding referential acene derivatives, and the binding ability of the adjacent carbonyl groups was more than that of the groups at the para-position. Therefore, the binding ability of o-PAHQs-2 was the strongest with the most negative BE.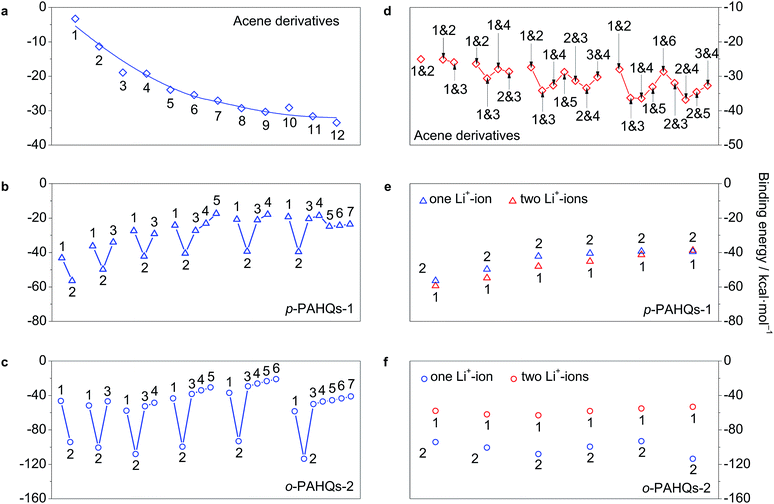

Fig. 7 The binding energy of acene derivatives, p-PAHQs-1 and o-PAHQs-2 with one Li⁺-ion (a–c) and two Li⁺-ions (d–f). The binding position of Li⁺-ion is indicated with a site number, which is in accordance with the one shown in Fig. S7.†

Similarly, in the 2Li case of referential acene derivatives (Fig. 7d), the second Li⁺ ion preferred to host in the ring close to the centre of the molecule but not in the neighbour with the central site already occupied by the first Li⁺ ion. Such a configuration would avoid both the steric effect and the coulombic repulsion between the two Li⁺ ions. In the case of p-PAHQs-1 (Fig. 7e), BE of the second Li⁺ ion was more negative than that of the first Li⁺ ion because the binding of the first Li⁺ ion with the carbonyl group facilitated the binding of the second Li⁺ ion. However, for o-PAHQs-2 (Fig. 7f), BE of the second Li⁺ ion was smaller than that of the first Li⁺ ion because the second Li⁺ ion preferred to bind to the benzene ring close to the carbonyl group (Fig. S8, ESI†) rather than to the other carbonyl group to avoid the large steric effect and coulombic repulsion between the two Li⁺ ions. The stability of o-PAHQs-2 was better than that of p-PAHQs-1 because of more negative binding energy. Nevertheless, strong binding energy could decrease the reactivity of the active centre, which may lead to worse reversibility during the redox reactions.

The effect of substituted groups on solubility

The solubility of the active materials is another important factor in the determination of the energy density of RFBs. The solubility can be estimated from the solvation free energy of the active material in selected solvents.^28,37 Among the aforementioned quinone derivatives, eight molecules (Fig. S9, ESI†) were selected as promising candidates for organic RFBs considering their stability, redox potential, and molecular weight. The calculated solvation free energies of the selected quinone derivatives in the representative organic solvents are summarized in Table S1 (ESI†). The solubility of the molecules in N,N-dimethylacetamide was better than that in acetonitrile in general. The solubility increased with the increase in the aromatic ring number, and the solubility of o-PAHQs was better than that of p-PAHQs. When functionalized with ether chains or aliphatic, hydroxyl or sulfonic acid groups, the solvation free energy further decreased (Table S2, ESI†), suggesting enhanced solubility. The molecules modified with the sulfonic acid groups and aliphatic groups exhibited better solubility than those substituted with hydroxyl groups and ether chains. Moreover, it seemed that the molecules with substituted positions close to the carbonyl moiety showed lower solvation free energy than other positions in most cases. For ortho-quinones (7 and 8 in Fig. S9, ESI†), lower solvation free energy was found at sites substituted with ether chain far from the carbonyl moiety or with aliphatic groups close to the carbonyl moiety.

Conclusions

In conclusion, we systematically studied the redox potential and its corresponding internal regulation mechanism for various quinone derivatives. The aromaticity analysis demonstrated that the total aromaticity of quinones was enhanced with the increase in ring numbers. Orbital component analysis suggested that the contribution from σ/π bond and σ–π coupling efficiently determined the redox potential of the quinone derivatives. The contribution from σ bond was more significant than that from the π bond. The DOS analysis further suggested that the high redox potential can be realized in quinones having small π–π* and σ–π* energy gaps, higher contribution ratio of the σ bonds in the top of VB, or σ bond in the top of the VB without overlapping with π bond. The binding energy calculations revealed that the Li⁺ ions preferred to bind with the O atoms of carbonyl groups, and the binding energy became less negative with the increase in ring numbers. Combined with the refined structures and established guidelines for functional group substitution in previous investigations, the results in this study would be useful in understanding the internal regulation mechanism of redox chemistry, which may lead to the design of appropriate quinone-based electrode materials for organic RFB applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 51772199 and 21805234), the Six Talent Peaks Project of Jiangsu Province (Grant No. XCL-063), the Collaborative Innovation Centre of Suzhou Nano Science & Technology, the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), the 111 Project, Joint International Research Laboratory of Carbon-Based Functional Materials and Devices. This work is also supported by the Shenzhen Fundamental Research Foundation (JCYJ20170818103918295) and President's funds from CUHK-Shenzhen.

Notes and references

1. J. B. Goodenough and Y. Kim, J. Power Sources, 2011, 196, 6688–6694.
2. B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935.
3. Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613.
4. A. Castillo and D. F. Gayme, Energy Convers. Manage., 2014, 87, 885–894.
5. Y. Zhao, Y. Ding, Y. Li, L. Peng, H. R. Byon, J. B. Goodenough and G. Yu, Chem. Soc. Rev., 2015, 44, 7968–7996.
6. C. Zhang, L. Zhang, Y. Ding, S. Peng, X. Guo, Y. Zhao, G. He and G. Yu, Energy Storage Materials, 2018, 15, 324–350.
7. A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164.
8. W. Wang, Q. Luo, B. Li, X. Wei, L. Li and Z. Yang, Adv. Funct. Mater., 2013, 23, 970–986.
9. L. Li, S. Kim, W. Wang, M. Vijayakumar, Z. Nie, B. Chen, J. Zhang, G. Xia, J. Hu, G. Graff, J. Liu and Z. Yang, Adv. Energy Mater., 2011, 1, 394–400.
10. P. Alotto, M. Guarnieri and F. Moro, Renewable Sustainable Energy Rev., 2014, 29, 325–335.
11. C. Zhang, L. Zhang, Y. Ding, X. Guo and G. Yu, ACS Energy Lett., 2018, 3, 2875–2883.
12. Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Chem. Soc. Rev., 2018, 47, 69–103.
13. Y. Ding and G. Yu, Angew. Chem., Int. Ed., 2017, 56, 8614–8616.
14. F. R. Brushett, J. T. Vaughey and A. N. Jansen, Adv. Energy Mater., 2012, 2, 1390–1396.
15. X. Wei, W. Xu, M. Vijayakumar, L. Cosimbescu, T. Liu, V. Sprenkle and W. Wang, Adv. Mater., 2014, 26, 7649–7653.
16. J. Huang, L. Cheng, R. S. Assary, P. Wang, Z. Xue, A. K. Burrell, L. A. Curtiss and L. Zhang, Adv. Energy Mater., 2015, 5, 1401782.
17. M. Park, D.-S. Shin, J. Ryu, M. Choi, N. Park, S. Y. Hong and J. Cho, Adv. Mater., 2015, 27, 5141–5146.
18. Y. Ding and G. Yu, Chem, 2017, 3, 917–919.
19. C. Zhang, Z. Niu, Y. Ding, L. Zhang, Y. Zhou, X. Guo, X. Zhang, Y. Zhao and G. Yu, Chem, 2018, 4, 2814–2825.
20. Y. Ding and G. Yu, Angew. Chem., Int. Ed., 2016, 55, 4772–4776.
21. M. R. Gerhardt, L. Tong, R. Gómez-Bombarelli, Q. Chen, M. P. Marshak, C. J. Galvin, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2017, 7, 1601488.
22. A. Shimizu, K. Takenaka, N. Handa, T. Nokami, T. Itoh and J.-I. Yoshida, Adv. Mater., 2017, 29, 1606592.
23. W. Wang, W. Xu, L. Cosimbescu, D. Choi, L. Li and Z. Yang, Chem. Commun., 2012, 48, 6669.
24. B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198.
25. J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860.
26. B. Yang, L. Hoober-Burkhardt, F. Wang, G. K. Surya Prakash and S. R. Narayanan, J. Electrochem. Soc., 2014, 161, A1371–A1380.
27. Y. Ding, Y. Li and G. Yu, Chem, 2016, 1, 790–801.
28. K. C. Kim, T. Liu, S. W. Lee and S. S. Jang, J. Am. Chem. Soc., 2016, 138, 2374–2382.
29. K. Wedege, E. Dražević, D. Konya and A. Bentien, Sci. Rep., 2016, 6, 39101.
30. Y. Liang, Y. Jing, S. Gheytani, K.-Y. Lee and P. Liu, Nat. Mater., 2017, 16, 841–848.
31. P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755.
32. M. Namazian, P. Norouzi and R. Ranjbar, J. Mol. Struct.: THEOCHEM, 2003, 625, 235–241.
33. M. Namazian, J. Mol. Struct.: THEOCHEM, 2003, 664–665, 273–278.
34. M. Namazian, H. A. Almodarresieh, M. R. Noorbala and H. R. Zare, Chem. Phys. Lett., 2004, 396, 424–428.
35. K. Alizadeh and M. Shamsipur, J. Mol. Struct.: THEOCHEM, 2008, 862, 39–43.
36. J.-H. Chen, L.-M. He and R. L. Wang, J. Electrochem. Soc., 2012, 159, A1636–A1645.
37. S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Chem. Sci., 2015, 6, 885–893.
38. L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput and K. J. Phys, Chem. Lett., 2015, 6, 283–291.
39. J. H. Park, T. Liu, K. C. Kim, S. W. Lee and S. S. Jang, ChemSusChem, 2017, 10, 1584–1591.
40. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842.
41. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Org. Lett., 2006, 8, 863–866.
42. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
43. D. G. Truhlar, C. J. Cramer, A. Lewis and J. A. Bumpus, J. Chem. Educ., 2004, 81, 596.
44. W. A. Donald, R. D. Leib, J. T. O'Brien, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 3371–3381.
45. S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680.
46. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, P. Jr, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision A.02, Gaussian, Inc., Wallingford, 2009.
47. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
48. J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923.
49. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
50. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
51. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
52. K. Hernández-Burgos, S. E. Burkhardt, G. G. Rodríguez-Calero, R. G. Hennig and H. D. Abruña, J. Phys. Chem. C, 2014, 118, 6046–6051.
53. Q. Wang, T. Y. Gopalakrishna, H. Phan, T. S. Herng, S. Dong, J. Ding and C. Chi, Angew. Chem., Int. Ed., 2017, 56, 11415–11419.
54. X. Lu, S. Lee, Y. Hong, H. Phan, T. Y. Gopalakrishna, T. S. Herng, T. Tanaka, M. E. Sandoval-Salinas, W. Zeng, J. Ding, D. Casanova, A. Osuka, D. Kim and J. Wu, J. Am. Chem. Soc., 2017, 139, 13173–13183.
55. H. Wei, Y. Liu, T. Y. Gopalakrishna, H. Phan, X. Huang, L. Bao, J. Guo, J. Zhou, S. Luo, J. Wu and Z. Zeng, J. Am. Chem. Soc., 2017, 139, 15760–15767.
56. D. Chen, T. Shen, K. An and J. Zhu, Chem. Commun., 2018, 1, 18.
57. C. Liu, M. E. Sandoval-Salinas, Y. Hong, T. Y. Gopalakrishna, H. Phan, N. Aratani, T. S. Herng, J. Ding, H. Yamada, D. Kim, D. Casanova and J. Wu, Chem, 2018, 4, 1586–1595.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09377f

‡ These authors contribute equally to this work.

---