Structural exploration of Au_xM⁻ (M = Si, Ge, Sn; x = 9–12) clusters with a revised genetic algorithm

Abstract

We used a revised genetic algorithm (GA) to explore the potential energy surface (PES) of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) clusters. The most interesting finding in the structural study of Au_xSi⁻ (x = 9–12) is the 3D (Au₉Si⁻ and Au₁₀Si⁻) → quasi-planar 2D (Au₁₁Si⁻ and Au₁₂Si⁻) structural evolution of the Si-doped clusters, which reflects the competition of Au–Au interactions (forming a 2D structure) and Au–Si interactions (forming a 3D structure). The Au_xM⁻ (x = 9–12; M = Ge, Sn) clusters have quasi-planar structures, which suggests a lower tendency of sp³ hybridization and a similarity of electronic structure for the Ge or Sn atom. Au₉Si⁻ and Au₁₀Si⁻ have a 3D structure, which can be viewed as being built from Au₈Si⁻ and Au₉Si⁻ with an extra Au atom bonded to a terminal gold atom, respectively. In contrast, the quasi-planar structures of Au_xM⁻ (x = 9–12; M = Ge, Sn) reflect the domination of the Au–Au interactions. Including the spin–orbit (SO) effects is very important to calculate the simulated spectrum (structural fingerprint information) in order to obtain quantitative agreement between theoretical and future experimental PES spectra.

---

I. Introduction

The properties of nanoclusters with several hundreds of atoms and molecules strongly depend on both their size and shape. The discovery of catalytic activities of supported gold nanoparticles has attracted intense research interest in the structures and properties of gaseous gold clusters,¹ which provides an atomic-level understanding of catalytic mechanisms of gold nanoparticles. Various techniques have been used to investigate the structures of gold nanoclusters, such as photoelectron spectroscopy (PES),² ion mobility,^3,4 infrared multiphoton dissociation spectroscopy,^5,6 and trapped ion electron diffraction.⁷ All of these techniques are quite powerful, especially when combined with ab initio calculations in obtaining structural information. Many of the unusual properties of the gold clusters derive from the strong relativistic effects that reduce the Au 5d–6s energy gap and enhance s–d hybridization.^8–10 Small-sized anion gold clusters (Au_n⁻) up to 12 atoms have been found to have 2D planar structures and are understood in terms of the s–d hybridization.^3,10,11 In the medium-sized gold clusters, Au₁₆⁻ to Au₁₈⁻ clusters have been found to possess highly stable hollow-cage structures,^7,12 and both Au₂₀⁻ and Au₂₀ clusters have tetrahedral structures.^6,13 Au₂₄⁻ possibly possesses tubular structure,^14,15 and other large gold clusters, such as Au₂₅⁻, Au₃₂⁻, Au₃₄⁻, and Au₅₅⁻ to Au₆₄⁻,^15–23 show core shell structures.

In comparison to pure gold clusters, doped gold clusters have received increasing attention because that the properties of gold clusters can be greatly influenced by the presence of impurities.^24–32 For example, both W and V atoms can change the structure of the pure Au₁₂⁻ cluster to form an endohedral structure.^33–35 The pure gold clusters doped with transition-metal atom also have been studied through experiment and theory.^36–38 However, doping an isoelectronic substitution atom, such as Ag and Cu, in a pure gold cluster has a little effect on the electronic and geometrical structure of gold cluster anions.^39–42

Few studies have been undertaken on the gold clusters doped with group-14 atoms.^26,43–62 Small Si-doped gold clusters, such as Au₄Si^−1/0, Au₄Si₂^−1/0, Au₂Si₂^−1/0, and Au₃Si₃^−1/0/+1, have been investigated by Wang et al.^26,43,44 The Au/H analogy has been found in the tetrahedral Au₄Si^−1/0 cluster. For Ge or Sn dopant, they also affect the structure of gold clusters by different ways relative to the Si dopant. For example, the theoretical calculation shows that tetrahedral structure does not exist in Au₄Ge⁻ and Au₄Sn⁻, and they have square-pyramidal structures.⁴⁶ The tetrahedral structure derives from the sp³ hybridization in the Au₄Si⁻. The results suggest that Si atom has stronger tendency to form directional bonding by sp³ hybridization than Ge and Sn. In order to obtain different isomers of atom cluster system, the genetic algorithm (GA) combined with density functional theory has been used to search the potential energy surface (PES). This method has been proven as an effective stochastic global search algorithm.^63,64 To compare with the future experimental data, we computed the density of state (DOS) spectra by including the relativistic and spin–orbit effects for several lowest-lying isomers. The simulated DOS spectra for the isomers of different systems will be compared with future experimental data, providing considerable credence for the identified isomers for these clusters.

In this paper, the revised genetic algorithm was used to explore the possible low-lying cluster structures of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems. We want to explore the structure evolution of different Si-, Ge-, and Sn-doped gold anion clusters and find out the different effect of Si, Ge, and Sn atoms on pure gold clusters (Au_x; x = 9–12).

II. Theoretical methods

A revised genetic algorithm (GA), which is a global searching method based on biological evolution theory, was used to search global minimum of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems.⁶⁴ The GA method contains several similar procedures as Deaven used: initial population, fitness function evaluation, selection, crossover, mutation and selecting new population.⁶³ A new subprocess was added after crossover by our GA. The new process was called “exchange operation”, switching Cartesian coordinates of “M” and “Au” element in cluster (M = Si, Ge, Sn). Fig. 1 shows the basic operator of mating by cut and swap. Due to the complex PES of multicomponent cluster, the swap operator is very important for multicomponent searching to effectively explore the local minimum around PES basin of a fixed cluster architecture. The initial population containing 20 individuals were generated by random process, and their coordinates were optimized by quasi-Newton L-BFGS routine.⁶⁵ The fitness was calculated by individual energy in population, and the fitness functions can be represented as below:

P = (E_i − E_min)/(E_max − E_min)

where E_max and E_min are the highest and lowest energy clusters in the current population, respectively. The selection of two parent individuals was accomplished by roulette wheel, and the low energy individual will have high probability to be selected for crossover. The crossover was achieved by a random plane passing through the center of mass of parent clusters, and the child was generated by collecting two slices atoms which lay above and below the plane of parent 1 and parent 2. The swap operation, which has been executed by exchanging coordinates between different elements based on local optimization structure, was performed for each new produced child. This operation was carried out by a fixed number of times set up by user (10 times for current research), and the lowest energy structure was selected as a new child to replace the child generated by crossover. The mutation is very important for keeping population diversity and also prevents searching trapped in local basin on PES. Ten percent of the offspring were selected for mutation, and the mutation was accomplished by the perturbation of each atomic coordinates with randomly values ranging from −1 to 1. Relaxation to local minimum was performed using L-BFGS method after each operation.⁶⁵ All processes of crossover, mutation and selection were then repeated for a specified number of generations. Fig. 2 shows the total energy of Au₁₂Ge⁻ and Au₁₂Sn⁻ clusters against genetic generation by our revised GA.

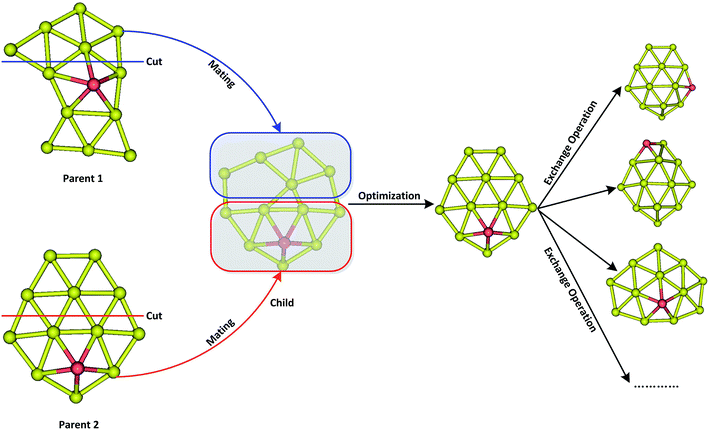Fig. 1 The schematic diagram of mating operator by cut and swap operator via exchanging two different elements after mating.

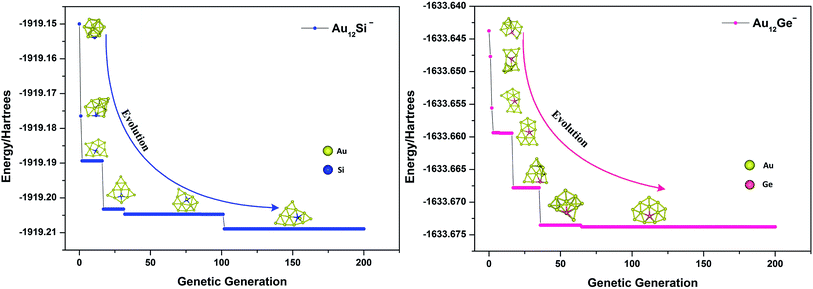Fig. 2 The total energy against genetic generation of Au₁₂Si⁻ and Au₁₂Ge⁻ clusters using revised genetic algorithm.

To search for low-lying structures of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems, we used the revised GA global optimization technique combined with DFT for geometry optimization. Generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE)⁶⁶ functional and the double-numerical polarized (DNP) basis set with effective core potentials (ECPs), implemented in the DMol³ code,⁶⁷ were chosen for structure optimization of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems. To generate enough isomers in GA searches, a medium level convergence criterion was chosen such that the optimization gradient convergence was less than 4 × 10⁻³ hartree per Å and the optimization energy convergence was 2 × 10⁻⁵ hartree in the DFT calculations. When more than 200 generations were collected, the top-5 lowest-energy structures for last generation were reoptimized using the hybrid functional PBE0 and CRBNBL basis set for all of elements (PBE0/CRBNBL) in the NWChem software package.⁶⁸ The isomers were ranked according to their relative energies. The relative energies of the top-5 isomers of the Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems were further calculated using the PBEPBE/Def2-TZVPPD functional/basis set, PBE1PBE/Def2-TZVPPD functional/basis set, B3LYP/Def2-TZVPPD functional/basis set, and MP2/Def2-TZVPPD second-order Møller–Plesset perturbation theory/basis set, implemented in Gaussian 09 software package.⁶⁹ In order to further confirm cluster structure information and compare with future experiment data, we simulated the photoelectron spectroscopy of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems. It is very important to include the spin–orbit (SO) effects in the calculation of the density of states in order to obtain quantitative agreement between theoretical and experimental PES spectra.⁵⁸ We calculated simulated spectra of all candidate isomers at the PBE0/CRBNBL(SO) level using NWChem software package.⁶⁸ Photoelectron spectra were calculated using PBE0 functional and CRBNBL basis set for Si, Ge, and Sn, CRBNBL basis set for Au with spin–orbit effects included. The first vertical detachment energies (VDEs) of the anion clusters were calculated at PBE0/CRENBL(SO) level as the energy difference between the optimization anion isomer and the neutral at the corresponding anion geometry. The binding energies of deeper orbitals were then added to the first VDE to approximate the higher binding energy detachment features. Each peak was then fitted with a 35 meV-wide Gaussian curve to simulate the DOS spectra.

III. Theoretical results and discussions

The top-5 lowest-energy structures of the Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems are depicted in Fig. S1–S4 in the ESI,† respectively, together with their simulated PES spectra and coordinates. Tables 1–4 list the relative energies of the corresponding isomers at several levels of theory (see table titles). The simulated spectra of the primary structures of the Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems are depicted in Fig. 3–6.

Table 1 Relative energies of five low-lying isomers of Au₉M⁻ (M = Si, Ge, Sn) at PBE0/CRENBL (NWChem) and PBEPBE/Def2-TZVPPD (G09), PBE1PBE/Def2-TZVPPD (G09), B3LYP/Def2-TZVPPD (G09), and MP2/Def2-TZVPPD (G09) levels of theory and basis set^a

Relative energies (eV)
Isomer		PBE0	PBEPBE	PBE1PBE	B3LYP	MP2
a Isomers are ranked according to their relative energies at the PBE0/CRENBL level of theory.
Au9Si^−	1	0.000	0.000	0.000	0.040	0.448
	2	0.182	0.174	0.265	0.315	0.972
	3	0.186	0.141	0.252	0.195	0.908
	4	0.186	0.072	0.171	0.160	0.802
	5	0.379	0.170	0.127	0.000	0.000
Au9Ge^−	1	0.000	0.034	0.122	0.150	0.422
	2	0.005	0.000	0.000	0.000	0.019
	3	0.047	0.001	0.104	0.097	0.409
	4	0.069	0.123	0.205	0.336	0.828
	5	0.104	0.069	0.074	0.069	0.000
Au9Sn^−	1	0.000	0.000	0.000	0.000	0.034
	2	0.090	0.140	0.015	0.147	0.000
	3	0.270	0.295	0.206	0.330	0.322
	4	0.271	0.232	0.129	0.229	0.112
	5	0.273	0.324	0.233	0.379	0.372

---

Table 2 Relative energies of five low-lying isomers of Au₁₀M⁻ (M = Si, Ge, Sn) at PBE0/CRENBL (NWChem) and PBEPBE/Def2-TZVPPD (G09), PBE1PBE/Def2-TZVPPD (G09), B3LYP/Def2-TZVPPD (G09), and MP2/Def2-TZVPPD (G09) levels of theory and basis set^a

Relative energies (eV)
Isomer		PBE0	PBEPBE	PBE1PBE	B3LYP	MP2
a Isomers are ranked according to their relative energies at the PBE0/CRENBL level of theory.
Au10Si^−	1	0.000	0.000	0.000	0.000	0.017
	2	0.010	0.113	0.249	0.281	0.789
	3	0.032	0.011	0.048	0.044	0.182
	4	0.069	0.075	0.084	0.152	0.185
	5	0.072	0.098	0.144	0.045	0.000
Au10Ge^−	1	0.000	0.133	0.082	0.321	0.647
	2	0.015	0.000	0.019	0.144	0.526
	3	0.066	0.099	0.069	0.196	0.388
	4	0.101	0.060	0.000	0.000	0.000
	5	0.140	0.176	0.147	0.291	0.483
Au10Sn^−	1	0.000	0.000	0.000	0.000	0.098
	2	0.078	0.103	0.060	0.063	0.000
	3	0.112	0.161	0.146	0.187	0.291
	4	0.149	0.151	0.185	0.190	0.353
	5	0.175	0.213	0.186	0.205	0.192

---

Table 3 Relative energies of five low-lying isomers of Au₁₁M⁻ (M = Si, Ge, Sn) at PBE0/CRENBL (NWChem) and PBEPBE/Def2-TZVPPD (G09), PBE1PBE/Def2-TZVPPD (G09), B3LYP/Def2-TZVPPD (G09), and MP2/Def2-TZVPPD (G09) levels of theory and basis set^a

Relative energies (eV)
Isomer		PBE0	PBEPBE	PBE1PBE	B3LYP	MP2
a Isomers are ranked according to their relative energies at the PBE0/CRENBL level of theory.
Au11Si^−	1	0.000	0.001	0.031	0.022	0.243
	2	0.082	0.000	0.000	0.000	0.000
	3	0.106	0.074	0.089	0.259	0.506
	4	0.114	0.136	0.159	0.188	0.394
	5	0.130	0.415	0.459	0.951	1.658
Au11Ge^−	1	0.000	0.009	0.065	0.186	0.470
	2	0.035	0.238	0.161	0.828	1.264
	3	0.051	0.043	0.112	0.247	0.643
	4	0.125	0.000	0.000	0.000	0.000
	5	0.134	0.047	0.116	0.122	0.210
Au11Sn^−	1	0.000	0.000	0.000	0.032	0.226
	2	0.009	0.037	0.050	0.106	0.410
	3	0.100	0.022	0.143	0.071	0.474
	4	0.144	0.075	0.088	0.000	0.000
	5	0.196	0.183	0.257	0.200	0.452

---

Table 4 Relative energies of five low-lying isomers of Au₁₂M⁻ (M = Si, Ge, Sn) at PBE0/CRENBL (NWChem) and PBEPBE/Def2-TZVPPD (G09), PBE1PBE/Def2-TZVPPD (G09), B3LYP/Def2-TZVPPD (G09), and MP2/Def2-TZVPPD (G09) levels of theory and basis set^a

Relative energies (eV)
Isomer		PBE0	PBEPBE	PBE1PBE	B3LYP	MP2
a Isomers are ranked according to their relative energies at the PBE0/CRENBL level of theory.
Au12Si^−	1	0.000	0.000	0.021	0.150	0.640
	2	0.084	0.069	0.000	0.192	0.343
	3	0.117	0.075	0.003	0.000	0.000
	4	0.131	0.268	0.249	0.942	2.037
	5	0.142	0.099	0.137	0.000	0.741
Au12Ge^−	1	0.000	0.016	0.031	0.147	0.511
	2	0.005	0.000	0.000	0.000	0.102
	3	0.135	0.175	0.127	0.124	0.000
	4	0.157	0.151	0.152	0.142	0.217
	5	0.182	0.357	0.241	0.680	0.764
Au12Sn^−	1	0.000	0.000	0.000	0.092	0.332
	2	0.089	0.111	0.062	0.138	0.167
	3	0.090	0.038	0.033	0.000	0.000
	4	0.163	0.324	0.204	0.821	1.140
	5	0.216	0.323	0.185	0.735	0.856

---

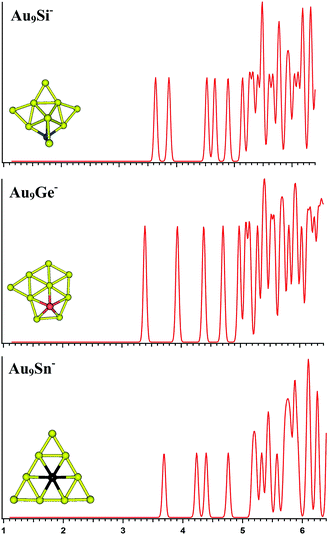Fig. 3 The simulated photoelectron spectra of Au₉M⁻ (M = Si, Ge, Sn) using PBE0/CRENBL (NWChem) level of theory and basis set including the relativistic and spin–orbit effects. The insets show the corresponding structures. The dopant atoms are shown in color (Si in blue, Ge in red, and Sn in black).

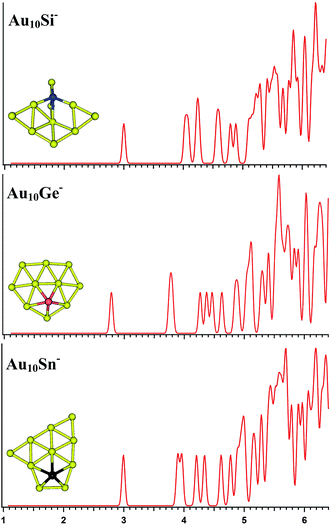Fig. 4 The simulated photoelectron spectra of Au₁₀M⁻ (M = Si, Ge, Sn) using PBE0/CRENBL (NWChem) level of theory and basis set including the relativistic and spin–orbit effects. The insets show the corresponding structures. The dopant atoms are shown in color (Si in blue, Ge in red, and Sn in black).

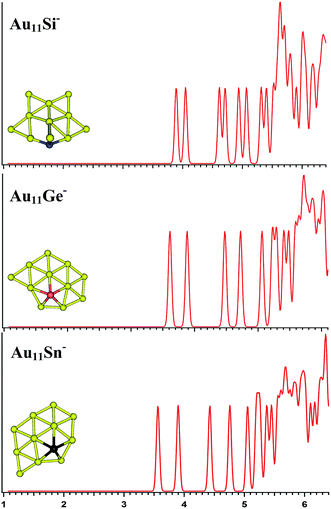Fig. 5 The simulated photoelectron spectra of Au₁₁M⁻ (M = Si, Ge, Sn) using PBE0/CRENBL (NWChem) level of theory and basis set including the relativistic and spin–orbit effects. The insets show the corresponding structures. The dopant atoms are shown in color (Si in blue, Ge in red, and Sn in black).

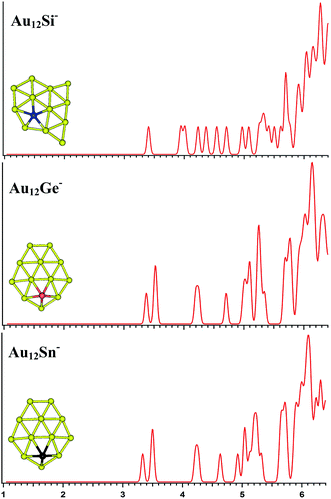Fig. 6 The simulated photoelectron spectra of Au₁₂M⁻ (M = Si, Ge, Sn) using PBE0/CRENBL (NWChem) level of theory and basis set including the relativistic and spin–orbit effects. The insets show the corresponding structures. The dopant atoms are shown in color (Si in blue, Ge in red, and Sn in black).

Au₉M⁻

For Au₉Si⁻, PBE0 (NWChem), PBEPBE, and PBE1PBE computations all predict isomer 1 as the global minimum structure (Fig. S1la in the ESI†), which can be viewed as the lowest-energy structure of Au₈Si⁻ cluster bonded by another Au atom through a terminal gold atom.⁵⁸ The B3LYP and MP2 calculations seem to prefer isomer 5 (Fig. S1le in the ESI†) as the lowest energy structure. In order to further identify the primary structure information for future PES experiment spectrum of Au₉Si⁻ cluster, the simulated spectra of the top-5 lowest-energy structures of Au₉Si⁻ cluster (Fig. S1la–e in the ESI†) have been calculated at the PBE0/CRENBL(SO) level. It is very important for theoretical spectrum simulation of Au atom to consider spin-orbital interaction by previous study.⁵⁸ For Au₉Ge⁻, PBE0 (NWChem) computation predicts isomer 1 (Fig. S1ma in the ESI†) as the global minimum structure, while the PBEPBE, PBE1PBE and B3LYP computations suggest isomer 2 (Fig. S1mb in the ESI†) as the global minimum structure. The MP2 calculations seem to prefer isomer 5 (Fig. S1me in the ESI†) as the lowest energy structure. For Au₉Sn⁻, PBE0 (NWChem), PBEPBE, PBE1PBE, and B3LYP computations all predict isomer 1 as the global minimum structure (Fig. S1ra in the ESI†), while the MP2 computation suggests isomer 2 (Fig. S1rb in the ESI†) as the global minimum structure. Due to the similar chemical properties of Ge and Sn atom, they should have similar lowest-energy structure as previous study. But the Au₉Ge⁻ and Au₉Sn⁻ have different lowest energy structures by our calculation. Fig. 3 shows the simulated spectra of the primary structures of Au₉M⁻ (M = Si, Ge, Sn) clusters. The primary structure of Au₉Si⁻ cluster was dominated by Au₈Si⁻ cluster, reflecting that the electronic structure of Au₉Si⁻ cluster should be similar with Au₈Si⁻ cluster. The result shows that the lowest-energy structure of Au₉Si⁻ cluster has a strong tendency of forming tetrahedral bonding structure by sp³ hybridization for Si atom. However, Ge- and Sn-doped gold anion cluster have a quasi-planar structure differing from Au₉Si⁻ cluster. It suggests the lower tendency of sp³ hybridization for Ge and Sn atoms. The primary structures of Au₉Ge⁻ and Au₉Sn⁻ are mainly dominated by Au–Au interactions.

Au₁₀M⁻

The PBE0 (NWChem), PBEPBE, PBE1PBE, and B3LYP calculations predict isomers 1 (Fig. S2la in the ESI†) as the global minimum structure for Au₁₀Si⁻. Isomer 1 can be viewed based on the isomer 1 (Fig. S1la in the ESI†) of Au₉Si⁻ cluster by adding an Au atom. However, the MP2 calculation reveals isomer 5 as the lowest energy structure, which has a quasi-planar structure differing from isomer 1 (Fig. S2la in the ESI†). For Au₁₀Ge⁻, The PBE0 (NWChem) computation (Table 2) indicates that isomer 1 (Fig. S2ma in the ESI†) has the global minimum, while PBEPBE calculation seems to prefer isomer 2 (Fig. S2mb in the ESI†) as the lowest energy structure, and PBE1PBE, B3LYP, and MP2 calculations reveal isomer 4 as the lowest energy structure. The isomer 1 of Au₁₀Ge⁻ is also a quasi-planar structure and can be viewed as being derived from isomer 1 of Au₉Ge⁻ by adding one Au atom. For Au₁₀Sn⁻, PBE0 (NWChem), PBE1PBE, PBEPBE and B3LYP calculations reveal that isomer 1 is the lowest-energy structure, while MP2 calculation prefers isomer 2 (Fig. S2rb in the ESI†) as the lowest energy structure. Different theory level computations produce different energy order (Table 2). The isomer 1 and isomer 2 are the primary structures of Au₁₀Sn⁻ and can be viewed as being derived from isomer 2 of Au₉Sn⁻. Fig. 4 shows the simulated spectra of the primary structures of Au₁₀M⁻ (M = Si, Ge, Sn) clusters. Au₁₀Si⁻ has a 3D structure, and shows a strong tendency of forming tetrahedral bonding structure by sp³ hybridization for Si atom. Au₁₀M⁻ (M = Ge, Sn) systems show the quasi-planar structures, reflecting that the structure is mainly dominated by Au–Au interactions.

Au₁₁M⁻

For Au₁₁Si⁻, the PBE0 (NWChem) calculation (Table 3) reveals isomer 1 (Fig. S3la in the ESI†) as the ground-state structure. Isomer 1 can be viewed as being derived from isomer 5 (Fig. S2le in the ESI†) of Au₁₀Si⁻ by attaching one Au atom to form triangle structure, and has a quasi-planar structure differing from the 3D structures of Au₉Si⁻ and Au₁₀Si⁻ because of sp³ hybridization for Si atom. Other computations suggest that isomer 2 (Fig. S3lb in the ESI†) is the lowest energy structure. The simulated spectrums of 5-top isomers of Au₁₁Si⁻ cluster can be found in ESI† (Fig. S3la–e in the ESI†). For Au₁₁Ge⁻, PBE0 (NWChem) calculation (Table 3) indicates that isomer 1 (Fig. S3ma in the ESI†) is the global minimum structure and can be viewed as being derived from isomer 3 (Fig. S2mc in the ESI†) of Au₁₀Ge⁻ by adding one Au atom to form triangle structure. Other computations suggest isomer 2 (Fig. S3mb in the ESI†) as the lowest energy structure. For Au₁₁Sn⁻, the lowest-energy structure is found to be isomer 1 (Fig. S3ra in the ESI†), which has the same structure as Au₁₁Ge⁻ (Fig. S3ma in the ESI†) for PBE0 (NWChem) calculation. B3LYP and MP2 calculations reveal that isomer 4 is the lowest-energy structure, and can be viewed as being derived from isomer 2 (Fig. S2rb in the ESI†) of Au₁₀Sn⁻ by attaching one Au atom to form triangle structure. Fig. 5 shows the simulated spectra of the primary structures of Au₁₁M⁻ (M = Si, Ge, Sn) clusters. All of the Au₁₁M⁻ (M = Si, Ge, Sn) systems show the same quasi-planar structure, reflecting that the structure is mainly dominated by Au–Au interactions.

Au₁₂M⁻

The PBE0 (NWChem) and PBEPBE calculations indicate that isomer 1 (Fig. S4la in the ESI,† a quasi-planar structure) is the lowest-energy structure for Au₁₂Si⁻ cluster, and other calculations reveal isomer 2 and isomer 3 as the ground state structure. For Au₁₂Ge⁻, PBE0 (NWChem) calculation (Table 4) reveals isomer 1 (Fig. S4ma in the ESI†) as the lowest energy structure, while PBE1PBE, PBEPBE, and B3LYP computations predict isomer 2 (Fig. S4mb in the ESI†) as the global minimum structure. Isomer 2 has very similar quasi-planar structure with isomer 1 of Au₁₂Si⁻ cluster. The MP2 calculations reveal isomer 3 has the global minimum, which can be viewed evolved from the isomer 1 of Au₁₁Ge⁻ by attaching one Au atom and subsequent structural relaxation. For Au₁₂Sn⁻, PBE0 (NWChem), PBEPBE, and PBE1PBE calculations predict isomer 1 (Fig. S4ra in the ESI†) as the global minimum, which has a similar structure with isomer 1 of Au₁₂Ge⁻ cluster. However, the B3LYP and MP2 calculation reveals isomer 3 (Fig. S4rc in the ESI†) as the lowest energy structure. Fig. 6 shows the simulated spectra of the primary structures of Au₁₂M⁻ (M = Si, Ge, Sn) clusters. The Au₁₂M⁻ (M = Si, Ge, Sn) clusters have quasi-planar structures, reflecting that their structures are dominated by Au–Au interactions.

To summarize, the structure evolutions of Au_xM⁻ (x = 9–12, M = Si, Ge, Sn) systems have been explored by revised GA method. The most intriguing finding is the structure change of 3D to quasi-planar for Au_xSi⁻ (x = 9–12). The result suggests the competition between the tendency of forming tetrahedral bonding structure by sp³ hybridization for Si atom (Au–M interaction) and the tendency of forming planar structures by Au–Au interactions for small anion gold clusters. The Si-doped gold clusters easily form local tetrahedral bonding structures because of the strong sp³ hybridization of the Si atom. But the structure changing from 3D to quasi-planar is found at x = 11 for Au_xSi⁻ (x = 9–12) systems, which reflects that their structures are dominated by Au–Au interactions when the cluster size increases for Au_xSi⁻ (x = 9–12) systems. However, the Ge- or Sn-doped gold clusters exhibit different structural images from pure gold anion clusters, which reflects its lower tendency of sp³ hybridization in the doped clusters. The structural evolutions of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) systems reflect that the Au–Au interactions become competitive in deciding the cluster structures when the cluster size increases for dopant clusters of gold. Including the spin–orbit (SO) effects are very important to calculate the density of states in order to obtain quantitative agreement between theoretical and future experimental PES spectra.

IV. Conclusion

In conclusion, a detailed investigation of the structures and isomers of Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) clusters using revised genetic algorithm combined with density functional theory were reported. The subprocess of exchange operation was added to explore local basin on PES for multicomponent systems in GA method. The Au₉Si⁻ and Au₁₀Si⁻ clusters have a tetrahedral-based 3D structure, and Au₁₁Si⁻ and Au₁₂Si⁻ clusters have a quasi-planar structure. The results show that the Si-doped gold clusters, which often form 3D direction bonding structure owing to the strong sp³ hybridization of Si atom, will be replaced by Au–Au interactions to form quasi-planar structure when the cluster size increases for dopant clusters of gold. However, the quasi-planar structures of Ge- or Sn-doped gold clusters reflect that the Ge and Sn atoms have the lower tendency of s–p hybridization in the doped clusters. For Au_xM⁻ (x = 9–12; M = Ge, Sn) systems, quasi-planar structures tend to be formed due to the domination of Au–Au interactions, suggesting that the Ge and Sn atoms have the lower tendency of s–p hybridization in the doped clusters.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The theoretical work was supported by the National Natural Science Foundation of China (Grant No. 51601189), and the foundation from Sichuan science and technology program (Grant No. 2017JY0117). Some of the computations were performed at the Supercomputing Center of the Chinese Academy of Sciences.

References

1. M. Haruta, Catal. Today, 1997, 36, 153–166.
2. K. J. Taylor, C. L. Pettiettehall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319–3329.
3. F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990.
4. P. Weis, Int. J. Mass Spectrom., 2005, 245, 1–13.
5. A. Fielicke, A. Kirilyuk, C. Ratsch, J. Behler, M. Scheffler, G. von Helden and G. Meijer, Phys. Rev. Lett., 2004, 93, 023401–023405.
6. P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676.
7. X. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B, 2006, 74, 165423.
8. P. Pyykko, Chem. Rev., 1988, 88, 563–594.
9. P. Pyykko, Inorg. Chim. Acta, 2005, 358, 4113–4130.
10. H. Hakkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89, 033401–033405.
11. H. Hakkinen, B. Yoon, U. Landman, X. Li, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2003, 107, 6168–6175.
12. S. Bulusu, X. Li, L.-S. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326–8330.
13. J. Li, X. Li, H. J. Zhai and L. S. Wang, Science, 2003, 299, 864–867.
14. B. Yoon, P. Koskinen, B. Huber, O. Kostko, B. von Issendorff, H. Hakkinen, M. Moseler and U. Landman, ChemPhysChem, 2007, 8, 157–161.
15. S. Bulusu, X. Li, L.-S. Wang and X. C. Zeng, J. Phys. Chem. C, 2007, 111, 4190–4198.
16. M. Ji, X. Gu, X. Li, X. G. Gong, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2005, 44, 7119–7123.
17. A. F. Jalbout, F. F. Contreras-Torres, L. A. Perez and I. L. Garzon, J. Phys. Chem. A, 2008, 112, 353–357.
18. A. Lechtken, D. Schooss, J. R. Stairs, M. N. Blom, F. Furche, N. Morgner, O. Kostko, B. von Issendorff and M. M. Kappes, Angew. Chem., Int. Ed., 2007, 46, 2944–2948.
19. X. Gu, S. Bulusu, X. Li, X. C. Zeng, J. Li, X. G. Gong and L.-S. Wang, J. Phys. Chem. C, 2007, 111, 8228–8232.
20. I. E. Santizo, F. Hidalgo, L. A. Perez, C. Noguez and I. L. Garzon, J. Phys. Chem. C, 2008, 112, 17533–17539.
21. I. L. Garzon, K. Michaelian, M. R. Beltran, A. Posada-Amarillas, P. Ordejon, E. Artacho, D. Sanchez-Portal and J. M. Soler, Phys. Rev. Lett., 1998, 81, 1600–1603.
22. H. Hakkinen, M. Moseler, O. Kostko, N. Morgner, M. A. Hoffmann and B. von Issendorff, Phys. Rev. Lett., 2004, 93, 093401–093405.
23. W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 897–904.
24. T. K. Ghanty, A. Banerjee and A. Chakrabarti, J. Phys. Chem. C, 2010, 114, 20–27.
25. D. Yuan, X. Gong and R. Wu, Phys. Rev. B, 2008, 78, 035441.
26. X. Li, B. Kiran, L. F. Cui and L. S. Wang, Phys. Rev. Lett., 2005, 95, 253401.
27. K. Koszinowski, D. Schroder and H. Schwarz, ChemPhysChem, 2003, 4, 1233–1237.
28. A. M. Joshi, W. N. Delgass and K. T. Thomson, J. Phys. Chem. B, 2006, 110, 23373–23387.
29. S. Pande, T. Jian, N. S. Khetrapal, L. S. Wang and X. C. Zeng, J. Phys. Chem. C, 2018, 122, 6947–6954.
30. N. S. Khetrapal, T. Jian, G. V. Lopez, S. Pande, L. S. Wang and X. C. Zeng, J. Phys. Chem. C, 2017, 121, 18234–18243.
31. N. S. Khetrapal, T. Jian, R. Pal, G. V. Lopez, S. Pande, L. S. Wang and X. C. Zeng, Nanoscale, 2016, 8, 9805–9814.
32. Y. R. Zhao, Y. Qian, M. G. Zhang and Y. F. Hu, Mol. Phys., 2015, 113, 3598–3605.
33. P. Pyykko and N. Runeberg, Angew. Chem., Int. Ed., 2002, 41, 2174–2176.
34. X. Li, B. Kiran, J. Li, H. J. Zhai and L. S. Wang, Angew. Chem., Int. Ed., 2002, 41, 4786–4789.
35. H. J. Zhai, J. Li and L. S. Wang, J. Chem. Phys., 2004, 121, 8369–8374.
36. Y. Gao, S. Bulusu and X. C. Zeng, J. Am. Chem. Soc., 2005, 127, 15680–15681.
37. Y. Gao, S. Bulusu and X. C. Zeng, ChemPhysChem, 2006, 7, 2275–2278.
38. S. Neukermans, E. Janssens, H. Tanaka, R. E. Silverans and P. Lievens, Phys. Rev. Lett., 2003, 90, 033401–033405.
39. L.-M. Wang, S. Bulusu, H.-J. Zhai, X.-C. Zeng and L.-S. Wang, Angew. Chem., Int. Ed., 2007, 46, 2915–2918.
40. L.-M. Wang, R. Pal, W. Huang, X. C. Zeng and L.-S. Wang, J. Chem. Phys., 2009, 130, 051101–051105.
41. L.-M. Wang, R. Pal, W. Huang, X. C. Zeng and L.-S. Wang, J. Chem. Phys., 2010, 132, 114306–114314.
42. R. Pal, L.-M. Wang, W. Huang, L.-S. Wang and X. C. Zeng, J. Chem. Phys., 2011, 134, 054306–054307.
43. B. Kiran, X. Li, H. J. Zhai, L. F. Cui and L. S. Wang, Angew. Chem., Int. Ed., 2004, 43, 2125–2129.
44. B. Kiran, X. Li, H.-J. Zhai and L.-S. Wang, J. Chem. Phys., 2006, 125, 133204.
45. P. Pyykko and Y. F. Zhao, Chem. Phys. Lett., 1991, 177, 103–106.
46. R. Pal, S. Bulusu and X. C. Zeng, J. Comput. Methods Sci. Eng., 2007, 7, 185–193.
47. C. Majumder, A. K. Kandalam and P. Jena, Phys. Rev. B, 2006, 74, 205437.
48. C. Majumder, Phys. Rev. B, 2007, 75, 235409.
49. M. Walter and H. Hakkinen, Phys. Chem. Chem. Phys., 2006, 8, 5407–5411.
50. Q. Sun, Q. Wang, G. Chen and P. Jena, J. Chem. Phys., 2007, 127, 214706.
51. L.-M. Wang, S. Bulusu, W. Huang, R. Pal, L.-S. Wang and X. C. Zeng, J. Am. Chem. Soc., 2007, 129, 15136.
52. M. Abe, T. Nakajima and K. Hirao, J. Chem. Phys., 2002, 117, 7960–7967.
53. R. Pal, L.-M. Wang, W. Huang, L.-S. Wang and X. C. Zeng, J. Am. Chem. Soc., 2009, 131, 3396–3404.
54. S. J. Lu, X. L. Xu, H. G. Xu and W. J. Zheng, J. Chem. Phys., 2018, 148, 244306.
55. Y. Zhao, F. Zhao and L. H. Kang, J. Mol. Model., 2018, 24, 61–68.
56. K. Joshi and S. Krishnamurty, J. Phys. Chem. C, 2017, 121, 17514–17522.
57. E. M. Dore and J. T. Lyon, J. Cluster Sci., 2016, 27, 1365–1381.
58. Y. R. Liu, T. Huang, Y. B. Gai, Y. Zhang, Y. J. Feng and W. Huang, Sci. Rep., 2015, 5, 17738–17745.
59. S. Gautam, N. Goel and K. Dharamvir, RSC Adv., 2014, 4, 13927–13933.
60. T. Quoc Tri, S.-J. Lu, L.-J. Zhao, X.-L. Xu, H.-G. Xu, T. Van Tan, J. Li and W. J. Zheng, J. Phys. Chem. A, 2018, 122, 3374–3382.
61. S.-J. Lu, X.-L. Xu, G. Feng, H.-G. Xu and W.-J. Zheng, J. Phys. Chem. C, 2016, 120, 25628–25637.
62. S. J. Lu, L. R. Hu, X. L. Xu, H. G. Xu, H. Chen and W. J. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 20321–20329.
63. D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291.
64. R. L. Johnston, Dalton Trans., 2003, 4193–4207.
65. R. H. Byrd, P. H. Lu, J. Nocedal and C. Y. Zhu, SIAM J. Sci. Comput., 1995, 16, 1190–1208.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
67. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
68. R. A. Kendall, E. Apra, D. E. Bernholdt, E. J. Bylaska, M. Dupuis, G. I. Fann, R. J. Harrison, J. L. Ju, J. A. Nichols, J. Nieplocha, T. P. Straatsma, T. L. Windus and A. T. Wong, Comput. Phys. Commun., 2000, 128, 260–283.
69. R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910.

---

Footnote

† Electronic supplementary information (ESI) available: Predicted low-energy structures of the Au_xM⁻ (x = 9–12; M = Si, Ge, Sn) clusters using the revised genetic algorithm combined with density functional theory. See DOI: 10.1039/c9ra01019j

---