Open Access Article
Open Access ArticleHydrogen evolution reaction activity related to the facet-dependent electrocatalytic performance of NiCoP from first principles†
Jie Mouab,
Yuyue Gaoab,
Jingbo Wangb,
Jianyi Ma a and
Haisheng Ren
a and
Haisheng Ren *b
*b
aInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, Sichuan 610065, China
bSchool of Chemical Engineering, Sichuan University, Chengdu, Sichuan 610065, China. E-mail: renhs@scu.edu.cn
First published on 15th April 2019
Abstract
Transition metal phosphides (TMPs) have been proven to act as highly active catalysts for the hydrogen evolution reaction (HER). Recently, single-phase ternary NiCoP electrocatalysts have been shown through experiments to display remarkable catalytic activity for the HER during water splitting. But, the inherent mechanism is not well understood. Herein, the HER activity of NiCoP with low-Miller-index facets, including (111), (100), (001)-NiP-t, and (001)-CoP-t, was systematically investigated using periodic density functional theory (DFT). The calculated Gibbs free energy of hydrogen adsorption (ΔGH) values reveal that all calculated facets have good catalytic activity for the HER. The (111) facet with the lowest surface energy in a vacuum has optimal ΔGH values close-to-zero for a range of hydrogen coverage. Ab initio thermodynamic analysis of hydrogen coverage was conducted to obtain the stabilities of surfaces, which follow the trend: (111) > (001)-CoP-t > (100) > (001)-NiP-t at 1 atm H2 and 298 K. We hope that this work can shed new light on further understanding the HER in relation to NiCoP and can give guidance for the design and synthesis of transition bimetal phosphide-based catalysts.
Introduction
As an energy carrier, hydrogen has attracted great interest due to its energy conversion potential and high gravimetric energy density.1,2 The environmentally friendly and carbon-free behavior related to hydrogen generation are a result of interconversion between water and hydrogen.3 Water splitting using light or some other renewable energy source has been widely accepted as an alternative way to generate H2. The hydrogen evolution reaction is usually involved. The HER involves protons and electrons, which convert into hydrogen molecules (2H+ + 2e− → H2) at the electrode surface. Molecular electrocatalysts with low overpotentials are indispensable for driving the HER, and are required to achieve high energy efficiency.4,5To date, platinum and its alloys have been regarded as the most efficient catalysts for the electrochemical HER in acidic media due to their small overpotentials, but the high cost and scarcity of platinum group metals limit their wide usage in practice.6 Thus, it is highly urgent to explore earth-abundant and non-noble-metal HER materials to replace platinum. Over the years, some promising HER materials have been developed, such as sulfides,7,8 borides,9 selenides,10 carbides,11,12 and nitrides,13 as substitutes for benchmark platinum materials. However, these satisfactory achievements did not meet the needs of industrial progress. Transition metal phosphides (TMPs), as a consequence, have received much interest from researchers worldwide due to their high catalytic activities for the HER compared to other non-precious electrocatalysts.14–16 For example, TMPs, including phosphides of molybdenum,17,18 iron,19,20 cobalt,21,22 and nickel,23,24 are well known as hydrogenase-like catalysts, with high catalytic activity and durability. In particular, ternary Ni2−xCoxP systems, which have been researched extensively, have been shown to be highly efficient catalysts for the HER and oxygen evolution reaction (OER).25–31 Among these systems, single-phase ternary NiCoP nanocrystals deliver near-optimal HER catalytic activity, with an overpotential as low as 59 mV and reaching a catalytic current density of 10 mA cm−2. In addition, the derived Tafel slope of the NiCoP nanocrystals is about 50 mV dec−1, approaching that of Pt/C (30 mV dec−1).32 Although there are so many exciting experimental results relating to NiCoP, insights into ternary NiCoP for systematic hydrogen absorption are lacking, which is of critical importance for further enhancing the activities and stabilities of HER electrocatalysts.
The Volmer reaction involves a proton from an acidic solution bonding to an active site on a facet to form H˙ (H+ + e− + ˙ → H˙)33 (here, ˙ represents an active site on the facet and H˙ means adsorbed H). Volmer–Heyrovsky and Volmer–Tafel processes are two types of possible pathways that have been proposed for the HER mechanism in acidic media. In the former, a solvated proton from the water layer reacts with H˙ to form H2 (H+ + e− + H˙ → H2 + ˙),34 while in the latter, two adsorbed hydrogen atoms react with each other to form a H2 molecule (H˙ + H˙ → H2 + 2˙).35 Therefore, good electrocatalysts for the HER should have the advantages of both being able to attract protons from solution and desorb H2 molecules.
The Gibbs free energy of hydrogen adsorption (ΔGH) is regarded as the most important factor for describing the HER activity of an electrocatalyst. Parsons36 first proposed that the optimal HER activity of an electrocatalyst should have a ΔGH value of around zero. Subsequently, Nørskov et al.37,38 and other groups7,8,16 combined experiment and theory to further prove this. When the value of ΔGH equals zero, the maximum HER activity is obtainable. A more negative value of ΔGH results in stronger binding between hydrogen and the facets, which will impede the desorption of H2 molecules. On the other hand, a more positive value of ΔGH will result in weaker binding between hydrogen and the facets, which will hinder the proton/electron-transfer step. Thus, efficient HER electrocatalysts can be obtained at a ΔGH value close to zero.
In order to figure out the HER mechanisms on NiCoP, the absorption structures and energetics of atomic hydrogen on four low-Miller-index facets of NiCoP have been systematically investigated using periodic DFT in this work. We use the calculated ΔGH values to predict the HER activities of the surfaces. In addition, ab initio atomistic thermodynamics was employed to determine the most stable and active facet of NiCoP at 1 atm H2 pressure and 298 K. It is expected that our results can provide useful insights and guidelines for designing transition bimetal phosphide HER electrocatalysts.
Computational methods
Spin-polarized periodic DFT calculations were performed via the plane-wave technique implemented in the Vienna ab initio simulation package (VASP).39 The ion–electron interactions were described with the projector augmented plan wave (PAW) method,40,41 and the exchange–correlation energies of interacting electrons were represented using the Perdew–Burke–Ernzerhof (PBE) functional with generalized gradient approximation (GGA).42 The Gaussian smearing method was adopted to describe the total energy, with a smearing width of 0.02 eV. A plane-wave cutoff energy was tested and set to 400 eV. Structure optimization was continued until the residual force converged to less than 0.01 eV Å−1 and the total energy converged to less than 1.0 × 10−6 eV. Slabs more than 10 Å thick in (2 × 2) supercells, with 15 Å of vacuum along the perpendicular catalyst facets, were used to build the adsorbate–facet systems for (111), (100), (001)-NiP-t and (001)-CoP-t facets. A gamma k-point of 7 × 7 × 12 and a Monkhorst–Pack k-point mesh of 3 × 3 × 1 were set to optimize bulk NiCoP and the four adsorbate-facet systems of NiCoP, respectively. The added hydrogen atoms together with the top two layers were allowed to move during the geometry optimization over the whole calculation.The surface energy was defined as
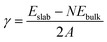 | (1) |
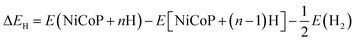 | (2) |
| ΔGH = ΔEH + ΔEZPE − TΔSH | (3) |
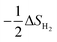 , where ΔSH2 is the entropy of an isolated H2 molecule in the gas phase under standard conditions. Thus, the value of TΔSH is close to −0.2 eV. ΔEZPE can be expressed as
, where ΔSH2 is the entropy of an isolated H2 molecule in the gas phase under standard conditions. Thus, the value of TΔSH is close to −0.2 eV. ΔEZPE can be expressed as
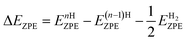 | (4) |
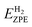 are the zero-point energies of n and (n − 1) adsorbed hydrogen atoms, as well as a gas phase hydrogen molecule, respectively. The zero-point energy can be given as
are the zero-point energies of n and (n − 1) adsorbed hydrogen atoms, as well as a gas phase hydrogen molecule, respectively. The zero-point energy can be given as
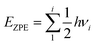 | (5) |
Ab initio atomistic thermodynamics44 was used to identify the most stable phase of each facet at 1 atm H2 and 298 K. ΔGH at a specific temperature and pressure, ΔGad(T,P), was calculated using
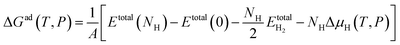 | (6) |
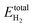 and ΔμH(T,P) indicate the total energy of NiCoP with NH hydrogen atoms adsorbed on a facet, the total energy of a clean facet, the energy of a gas phase H2 molecule, and the chemical potential of hydrogen at different temperatures and pressures, respectively. Obviously, the Gibbs free energy is a function of the hydrogen chemical potential for a particular surface at a particular H coverage. Therefore, the stability of H-covered facets can be calculated at a given hydrogen chemical potential. ΔμH(T,P) is related to specific conditions using
and ΔμH(T,P) indicate the total energy of NiCoP with NH hydrogen atoms adsorbed on a facet, the total energy of a clean facet, the energy of a gas phase H2 molecule, and the chemical potential of hydrogen at different temperatures and pressures, respectively. Obviously, the Gibbs free energy is a function of the hydrogen chemical potential for a particular surface at a particular H coverage. Therefore, the stability of H-covered facets can be calculated at a given hydrogen chemical potential. ΔμH(T,P) is related to specific conditions using
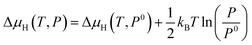 | (7) |
Results and discussion
Surface energy and electronic density of states (DOS) for different facets
The bulk NiCoP shown in Fig. 1 has a hexagonal Fe2P-type structure with the symmetry group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m. Each unit cell has three nickel atoms, three cobalt atoms and three phosphorous atoms. The equilibrium lattice parameters, together with available experimental data45 and recent calculations,32 from DFT with PBE functionals are listed in Table 1. The agreement is very good. The differences between the calculated and experimental findings do not exceed 0.03 Å.
2m. Each unit cell has three nickel atoms, three cobalt atoms and three phosphorous atoms. The equilibrium lattice parameters, together with available experimental data45 and recent calculations,32 from DFT with PBE functionals are listed in Table 1. The agreement is very good. The differences between the calculated and experimental findings do not exceed 0.03 Å.
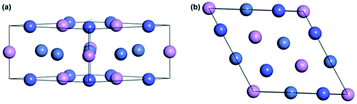 | ||
| Fig. 1 Bulk NiCoP: (a) side view and (b) top view. Note that the colors gray, blue and pink stand for Ni, Co and P atoms, respectively. | ||
Usually low Miller-index facets are considered preferentially in surface science studies due to their high durability. For hexagonal Fe2P-type NiCoP, the low Miller-index facets can be cleaved to (111), (100) and (001) examples. For the (001) facet, with respect to hollow sites with three Ni or three Co atoms, there are two different truncation surfaces called (001)-NiP-t and (001)-CoP-t. The optimized structures of these facets are shown in Fig. 2 and the corresponding surface energies are listed in Table 2.
| (111) | (100) | (001)-NiP-t | (001)-CoP-t | |
|---|---|---|---|---|
| Surface energy | 108.20 | 135.64 | 122.83 | 129.47 |
In general, more stable facets have lower surface energies and can be synthesized in experiments.46 Thus, the stability of the clean facets in a vacuum follow the order: (111) > (001)-NiP-t > (001)-CoP-t > (100), based on computing the surface energy. The most stable example is the (111) facet, which agrees with experiments in which the (111) facet of NiCoP has been synthesized.47–50 On the other hand, the surface packing density is usually used to identify the stability.22 The surface packing densities of (111), (001)-NiP-t, (001)-CoP-t and (100) facets are 20, 17, 17, and 15 atoms per nm2, respectively.
To understand the electronic structures of the four facets, electronic density of states (DOS) data have been calculated, as depicted in Fig. 3. It is found that all facets show metallic behavior with none-zero DOS data at the Fermi level, and the (111) facet has the highest DOS at the Fermi level. It is worth mentioning that the DOS curve for the (100) facet is gentle, indicating that it has small average numbers of electron-occupation states in the valence band because it has a low surface atom packing density and larger interplanar spacing.
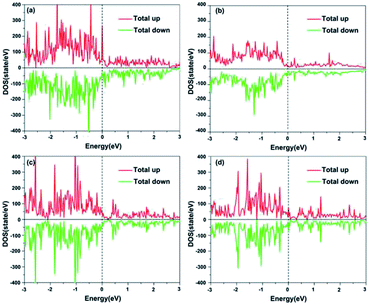 | ||
| Fig. 3 Spin-polarized total DOS for clean NiCoP facets: (a) (111); (b) (100); (c) (001)-NiP-t; and (d) (001)-CoP-t. The Fermi level is set as zero (dashed line). | ||
Hydrogen adsorption
To find the global lowest energy hydrogen adsorption sites, all possible adsorption sites on the four facets were carefully tested. Then the values of ΔGH were calculated to describe the HER activity. Finally, ab initio atomistic thermodynamics was used to evaluate the most stable phase for each facet. To systematically understand the HER activity, we will respectively investigate hydrogen adsorption on the four facets.(111) facet
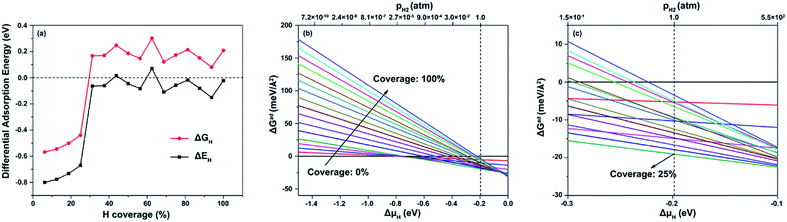
The calculated results reveal that there are only three local minimum sites for hydrogen adsorption, named H1, NC2 and P1, as shown in Fig. S1.† Table S2† lists the adsorption energies of each site. It is found that the most favorable adsorption site is H1. The adsorption energies of all sites follow the trend: H1 < NC2 < P1. Thus, the initial hydrogen atoms were placed at H1 sites. In the same way, the second lowest energy site was obtained. With an assumption that hydrogen atoms easily spread over the facet at the lowest energy sites for each type of hydrogen coverage, we found the global minimum of hydrogen adsorption for each type of hydrogen coverage on the (111) facet, as depicted in Fig. 4 for typical 25%, 50%, 75% and 100% coverage (here 100% coverage means 9H atoms per nm2). For less than 25% hydrogen coverage, hydrogen atoms strongly adsorb on H1 sites. For 25–50% hydrogen coverage, they are mainly on NC2 sites. Interestingly, hydrogen atoms on NC2 sites will shift to adjacent C2 sites when the hydrogen coverage is 56–75%. The distance between proximal hydrogen atoms is 0.875 Å, close to the bond length of 0.741 Å found for H2 by Huber et al.,43 and they are proposed to react with each other to form H2.Fig. 5a shows the calculated ΔEH and ΔGH values for H adsorption on the (111) facet for different hydrogen coverage. When the hydrogen coverage is in the range of 56–75%, ΔGH is extremely close to zero. Besides, when the hydrogen coverage is 25–50%, ΔGH is close to −0.2 eV, which is a favorable value for the HER. Therefore, it is indicated that the (111) facet can favor the HER over a large hydrogen coverage range.
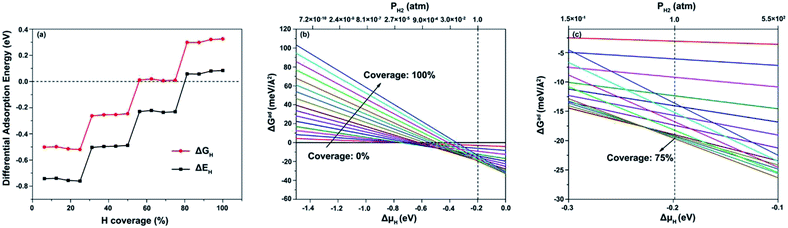 | ||
| Fig. 5 (a) ΔEH and ΔGH values at various hydrogen coverages on the (100) facet; and ΔGad at 298 K with ΔμH ranging from (b) −1.5 to 0.0 eV and (c) −0.3 to −0.1 eV. | ||
Furthermore, to calculate the most stable coverage of hydrogen on the NiCoP (111) facet at 1 atm H2 and 298 K, ab initio atomistic thermodynamics was used to determine ΔGad(T,P) along with the hydrogen chemical potential ΔμH and pressure, as plotted in Fig. 5b and c. Each line expresses a given H coverage. Clearly, the most stable phase at 1 atm H2 and 298 K is 75% hydrogen coverage, in which the active sites for the HER are C2 sites.
(100) facet
Fig. S2† shows the hydrogen adsorption sites named N1, NP1, P1 and so on. The most stable adsorption site is N1, as listed in Table S3.† Fig. S5† shows the optimized structures of the (100) facet at typical hydrogen coverages of 25%, 50%, 75% and 100% (here 100% coverage means 10H atoms per nm2). Because the adsorption sites will change with increasing hydrogen coverage, the NC1 sites can adsorb hydrogen, as mentioned below.Fig. 6a illustrates ΔEH and ΔGH values for the (100) facet along with different hydrogen coverage. For 37.5–50% hydrogen coverage, hydrogen atoms adsorb on NC1 sites with a difference in hydrogen adsorption energy of near −0.2 eV, which is because of interactions between adsorbed hydrogen atoms. Furthermore, values of ΔGH close to zero are obtained at NC1 sites for 50% hydrogen coverage, indicating that the (100) facet can also be suitable for HER activity, and adsorbed hydrogen atoms have a great influence on the HER. Fig. 6b and c show plots of ΔGad as a function of ΔμH and pressure at 298 K for the (100) facet for different hydrogen coverage. It is found that there are two stable hydrogen coverages, 37.5% and 50%, at 1H2 atm and 298 K, respectively. The main absorption sites are NC1 for such stable hydrogen coverages. Therefore, NC1 sites are the active HER sites for the NiCoP (100) facet with hydrogen coverage of 50%.
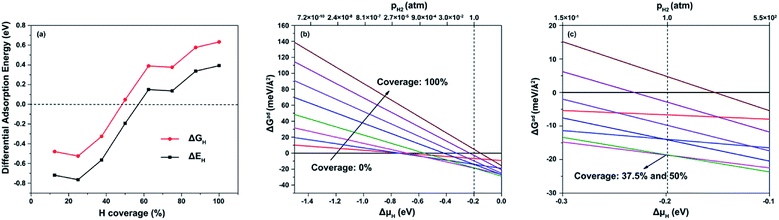 | ||
| Fig. 6 (a) ΔEH and ΔGH values at various hydrogen coverages on the (001)-NiP-t facet; ΔGad at 298 K with ΔμH ranging from: (b) −1.5 to 0.0 eV and (c) −0.3 to −0.1 eV. | ||
(001) facet
As mentioned above, the (001) facet has two different truncation surfaces called (001)-NiP-t and (001)-CoP-t. Fig. S3 and S4† show the absorption sites for these two facets. The most stable adsorption sites are H2 and H3 for (001)-NiP-t (as shown in Table S4†) and (001)-CoP-t (as shown in Table S5†), respectively. But the adsorption energy of (001)-CoP-t is much larger than that of (001)-NiP-t, which indicates that hydrogen adsorption on the (001)-CoP-t facet is too strong to desorb H2 at lower hydrogen coverage.The optimized structures under different hydrogen coverage (100% coverage represents 7H atoms per nm2 for (001)-NiP-t and 14H atoms per nm2 for (001)-CoP-t) are shown in Fig. S6† for (001)-NiP-t and in Fig. S7† for (001)-CoP-t. It can be found that most active HER sites are H2 for (001)-NiP-t and C1 for the (001)-CoP-t facet.
Fig. 7a and 8a plot ΔEH and ΔGH values at various hydrogen coverages for the (001)-NiP-t and (001)-CoP-t facets. When the hydrogen coverage of the (001)-NiP-t facet is less than 50%, the values of ΔGH are close to zero, indicating that the (001)-NiP-t facet has relatively good HER activity with no initial hydrogen coverage, in line with a recent study by Liu et al.51 Conversely, the values of ΔEH are around zero for the (001)-CoP-t facet when the hydrogen coverage is more than 31%, revealing weak bonding between hydrogen and the facet. Meanwhile, the values of ΔGH are close to zero when the hydrogen coverage is more than 31%, illustrating that the hydrogen coverage has an effect on the HER activity and that initial hydrogen coverage is required for favorable HER activity on the (001)-CoP-t facet. Fig. 7(b, c) and 8(b, c) depict ΔGad as a function of ΔμH and pressure at 298 K for the (001)-NiP-t and (001)-CoP-t facets along with different hydrogen coverage. One can see that the most stable hydrogen coverage at 1H2 atm and 298 K is 50% for (001)-NiP-t and 25% for the (001)-CoP-t facet.
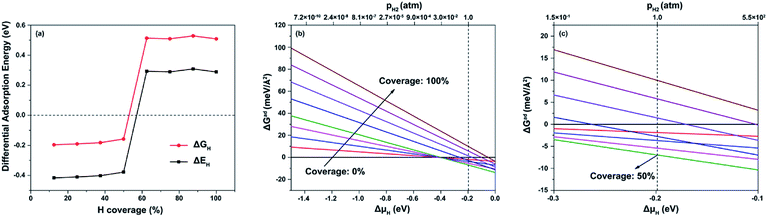 | ||
| Fig. 7 (a) ΔEH and ΔGH values at various hydrogen coverages on the (001)-CoP-t facet; ΔGad at 298 K with ΔμH ranging from: (b) −1.5 to 0.0 eV and (c) −0.3 to −0.1 eV. | ||
 | ||
| Fig. 8 (a) ΔEH and ΔGH values at various hydrogen coverages on the (001)-CoP-t facet; ΔGad at 298 K with ΔμH ranging from: (b) −1.5 to 0.0 eV and (c) −0.3 to −0.1 eV. | ||
HER activity and stability
Table 3 lists the values of ΔGad and ΔGH for the four low Miller-index facets at 1H2 atm and 298 K. We find that durability for the HER follows the trend: (111) > NiCoP(001)-CoP-t > (100) > (001)-NiP-t on the basis of ΔGad. Using a ΔGH value close to zero as the criterion, the most efficient HER facet is (111). Therefore, from a comprehensive point of view, the (111) facet is the optimal facet for the high-activity HER at 1H2 atm and 298 K.| (111) | (100) | (001)-NiP-t | (001)-CoP-t | |
|---|---|---|---|---|
| ΔGad (meV Å−2) | −19.92 | −18.78 | −7.09 | −19.18 |
| ΔGH (eV) | 0.01 | 0.05 | −0.16 | 0.44 |
Conclusions
In this work, we reported a systematic study of the HER activities of four low Miller-index facets of NiCoP using periodic DFT calculations. The energy electronic structure, Gibbs free energy of hydrogen adsorption and ab initio thermodynamics of hydrogen coverage were investigated to reveal the HER characteristics of NiCoP.From calculations involving the electronic structures of the surfaces, we found that the stability of the clean facets in a vacuum follows the order: (111) > (001)-NiP-t > (001)-CoP-t > (100), and all facets have metallic behavior with none having zero DOS at the Fermi level. The values of ΔGH illustrated that all the calculated facets have good catalytic activities for the HER. When hydrogen coverage is from 56% to 75% on the (111) facet, the distance between proximal hydrogen atoms is 0.875 Å, which is close to the bond length of 0.741 Å for H2, and they are proposed to react with each other to form H2. From ab initio atomistic thermodynamic analysis, we found that the durability for the HER follows the trend: (111) > (001)-CoP-t > (100) > (001)-NiP-t, and the NiCoP (111) facet is the optimal facet for the high-activity HER at 1H2 atm and 298 K.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China No. 91641120 and No. 91841301.References
- I. Dincer, Int. J. Energy Res., 2007, 31, 29–55 CrossRef CAS.
- X. Cheng, Z. Shi, N. Glass, L. Zhang, J. Zhang, D. Song, Z. Liu, H. Wang and J. Shen, J. Power Sources, 2007, 165, 739–756 CrossRef CAS.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536 CrossRef CAS.
- Y. Li, H. Wang, L. Xie, Y. Liang, G. Hong and H. Dai, J. Am. Chem. Soc., 2011, 133, 7296–7299 CrossRef CAS PubMed.
- M. A. Abbas and J. H. Bang, Chem. Mater., 2015, 27, 7218–7235 CrossRef CAS.
- B. Hinnemann, P. G. Moses, J. Bonde, K. P. N. Jorgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309 CrossRef CAS PubMed.
- T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- H. Vrubel and X. Hu, Angew. Chem., 2012, 51, 12703–12706 CrossRef CAS PubMed.
- D. Kong, H. Wang, Z. Lu and Y. Cui, J. Am. Chem. Soc., 2014, 136, 4897–4900 CrossRef CAS PubMed.
- W. F. Chen, J. T. Muckerman and E. Fujita, Chem. Commun., 2013, 49, 8896–8909 RSC.
- J. Wang, F. Xu, H. Jin, Y. Chen and Y. Wang, Adv. Mater., 2017, 29, 1605838 CrossRef PubMed.
- W. F. Chen, K. Sasaki, C. Ma, A. I. Frenkel, N. Marinkovic, J. T. Muckerman, Y. Zhu and R. R. Adzic, Angew. Chem., 2012, 51, 6131–6135 CrossRef CAS PubMed.
- S. T. Oyama, T. Gott, H. Zhao and Y. K. Lee, Catal. Today, 2009, 143, 94–107 CrossRef CAS.
- P. Xiao, W. Chen and X. Wang, Adv. Energy Mater., 2015, 5, 1500985 CrossRef.
- J. Kibsgaard, C. Tsai, K. Chan, J. D. Benck, J. K. Nørskov, F. Abild-Pedersen and T. F. Jaramillo, Energy Environ. Sci., 2015, 8, 3022–3029 RSC.
- Y. Zhang, H. Lei, D. Duan, E. Villota, C. Liu and R. Ruan, ACS Appl. Mater. Interfaces, 2018, 10, 20429–20439 CrossRef CAS PubMed.
- X. Chen, D. Wang, Z. Wang, P. Zhou, Z. Wu and F. Jiang, Chem. Commun., 2014, 50, 11683–11685 RSC.
- C. Y. Son, I. H. Kwak, Y. R. Lim and J. Park, Chem. Commun., 2016, 52, 2819–2822 RSC.
- P. Jiang, Q. Liu, Y. Liang, J. Tian, A. M. Asiri and X. Sun, Angew. Chem., 2014, 53, 12855–12859 CrossRef CAS PubMed.
- J. Tian, Q. Liu, A. M. Asiri and X. Sun, J. Am. Chem. Soc., 2014, 136, 7587–7590 CrossRef CAS PubMed.
- G. Hu, Q. Tang and D. E. Jiang, Phys. Chem. Chem. Phys., 2016, 18, 23864–23871 RSC.
- L. A. Stern, L. Feng, F. Song and X. Hu, Energy Environ. Sci., 2015, 8, 2347–2351 RSC.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed.
- H. Liang, A. N. Gandi, D. H. Anjum, X. Wang, U. Schwingenschlogl and H. N. Alshareef, Nano Lett., 2016, 16, 7718–7725 CrossRef CAS PubMed.
- Y. Li, J. Liu, C. Chen, X. Zhang and J. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 5982–5991 CrossRef CAS PubMed.
- Y. Feng, X. Y. Yu and U. Paik, Chem. Commun., 2016, 52, 1633–1636 RSC.
- Y. Bai, H. Zhang, L. Liu, H. Xu and Y. Wang, Chem.–Eur. J., 2016, 22, 1021–1029 CrossRef CAS PubMed.
- C. Wang, J. Jiang, T. Ding, G. Chen, W. Xu and Q. Yang, Adv. Mater. Interfaces, 2016, 3, 1500454 CrossRef.
- M. Kong, Z. Wang, W. Wang, M. Ma, D. Liu, S. Hao, R. Kong, G. Du, A. M. Asiri, Y. Yao and X. Sun, Chem.–Eur. J., 2017, 23, 4435–4441 CrossRef CAS PubMed.
- J. Li, G. Wei, Y. Zhu, Y. Xi, X. Pan, Y. Ji, I. V. Zatovsky and W. Han, J. Mater. Chem. A, 2017, 5, 14828–14837 RSC.
- J. Li, M. Yan, X. Zhou, Z. Q. Huang, Z. Xia, C.-R. Chang, Y. Ma and Y. Qu, Adv. Funct. Mater., 2016, 26, 6785–6796 CrossRef CAS.
- T. Volmer and M. Z. Erdey-Gruz, Phys. Chem. A, 1930, 150, 203–213 Search PubMed.
- J. Heyrovsky, Recl. Trav. Chim. Pays-Bas, 1927, 46, 582–585 CrossRef CAS.
- J. Z. Tafel, Phys. Chem. A, 1905, 50, 641–712 CAS.
- R. Parsons, Trans. Faraday Soc., 1958, 54, 1053–1063 RSC.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Norskov, Nat. Mater., 2005, 5, 909–913 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew and K. Burke, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg,Molecular structure and molecular spectra IV: constants of diatomic molecules, Van Nostrand-Reinhold, New York, 1979 Search PubMed.
- D. R. Stull and H. Prophet, Natl. Stand. Ref. Data Ser., 1971, 35, 5 Search PubMed.
- J. P. Sénateur, A. Rouault, P. L’Héritier, A. F. Krumbugel-Nylund, R. Fruchart, D. Fruchart, P. Convert and E. Roudaut, Mater. Res. Bull., 1973, 8, 229–238 CrossRef.
- Z. Liang, X. Zhong, T. Li, M. Chen and G. Feng, ChemElectroChem, 2019, 6, 260–267 CrossRef CAS.
- Z. Cai, A. Wu, H. Yan, Y. Xiao, C. Chen, C. Tian, L. Wang, R. Wang and H. Fu, Nanoscale, 2018, 10, 7619–7629 RSC.
- L. Su, H. Li, Y. Xiao, G. Han and M. Zhu, J. Alloys Compd., 2019, 771, 117–123 CrossRef CAS.
- T. Liu, X. Yan, P. Xi, J. Chen, D. Qin, D. Shan, S. Devaramani and X. Lu, Int. J. Hydrogen Energy, 2017, 42, 14124–14132 CrossRef CAS.
- C. Wang, J. Jiang, T. Ding, G. Chen, W. Xu and Q. Yang, Adv. Mater. Interfaces, 2016, 3, 1500454 CrossRef.
- J. Liu, Z. Wang, J. David, J. Llorca, J. Li, X. Yu, A. Shavel, J. Arbiol, M. Meyns and A. Cabot, J. Mater. Chem. A, 2018, 6, 11453–11462 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Vibrational frequencies and adsorption energies of hydrogen adsorption sites; and possible adsorption sites and optimized structures relating to hydrogen coverage. See DOI: 10.1039/c9ra01560d |
| This journal is © The Royal Society of Chemistry 2019 |