Open Access Article
Open Access ArticleSolving the enigma of weak fluorine contacts in the solid state: a periodic DFT study of fluorinated organic crystals†
Elena O. Levina af,
Ivan Y. Chernyshov
af,
Ivan Y. Chernyshov b,
Alexander P. Voronin
b,
Alexander P. Voronin c,
Leonid N. Alekseiko
c,
Leonid N. Alekseiko d,
Adam I. Stash
d,
Adam I. Stash e and
Mikhail V. Vener
e and
Mikhail V. Vener *g
*g
aMoscow Institute of Physics and Technology, Dolgoprudny, Russia
bN.D. Zelinsky Institute of Organic Chemistry, Moscow, Russia
cG.A. Krestov Institute of Solution Chemistry of RAS, Ivanovo, Russia
dFar Eastern Federal University, Vladivostok, Russia
eKarpov Institute of Physical Chemistry, Moscow, Russia
fResearch Centre of Biotechnology, Russian Academy of Sciences, Moscow, Russia
gD. Mendeleev University of Chemical Technology, Moscow, Russia. E-mail: mikhail.vener@gmail.com
First published on 23rd April 2019
Abstract
The nature and strength of weak interactions with organic fluorine in the solid state are revealed by periodic density functional theory (periodic DFT) calculations coupled with experimental data on the structure and sublimation thermodynamics of crystalline organofluorine compounds. To minimize other intermolecular interactions, several sets of crystals of perfluorinated and partially fluorinated organic molecules are considered. This allows us to establish the theoretical levels providing an adequate description of the metric and electron-density parameters of the C–F⋯F–C interactions and the sublimation enthalpy of crystalline perfluorinated compounds. A detailed comparison of the C–F⋯F–C and C–H⋯F–C interactions is performed using the relaxed molecular geometry in the studied crystals. The change in the crystalline packing of aromatic compounds during their partial fluorination points to the structure-directing role of C–H⋯F–C interactions due to the dominant electrostatic contribution to these contacts. C–H⋯F–C and C–H⋯O interactions are found to be identical in nature and comparable in energy. The factors that determine the contribution of these interactions to the crystal packing are revealed. The reliability of the results is confirmed by considering the superposition of the electrostatic potential and electron density gradient fields in the area of the investigated intermolecular interactions.
1. Introduction
Non-covalent interactions involving halogens have gained increasing interest of researchers in the last decade because of their significance in chemistry,1,2 biology,3 drug design4,5 and materials science.6–8 There is ample literature on the X-ray and theoretical studies of organic crystals with intermolecular halogen⋯halogen contacts (“halogen bonds”).9–12 The F⋯F interactions are often considered together with other C–Hal⋯Hal–C interactions, where Hal = Cl, Br and I.13,14 However, due to its low polarizability15 and tightly contracted lone pairs fluorine tends to fall out of the dependences typical of halogen bonds.16 This leads to a number of specific properties of the C–F⋯F–C interactions in comparison with C–Hal⋯Hal–C. (i) The anisotropic electronic distribution is negligible on fluorine in comparison with other halogens;17 as a result, the directionality of the C–F⋯F–C interactions is insignificant compared to the C–Hal⋯Hal–C contacts.18 (ii) The energy of the C–F⋯F–C interactions is less than that of the C–Hal⋯Hal–C interactions in molecular crystals. This follows from the experimental values of the sublimation enthalpy ΔHsub, which equals ∼16, ∼39 and ∼52 kJ mol−1 for crystalline CF4, CCl4 and CBr4, respectively.19 (iii) Halogen bonds with Cl, Br and I are widely used as building blocks in crystal engineering,20 while the C–F⋯F–C interactions do not play any structure-directing role. (iv) Fluorine tends to form C–H⋯F–C interactions rather than C–F⋯F–C contacts, whereas heavier halogens seem to prefer the formation of halogen⋯halogen interactions.21Intermolecular C–H⋯F–C interactions usually occur in the crystal structures of organofluorine compounds.22 In contrast to C–F⋯F–C, these interactions play an important role in directing supramolecular assembly in chemical and biological systems.21,23 As far as we know, there has been no detailed comparison of the intermolecular C–F⋯F–C and C–H⋯F–C interactions in crystals of organofluorine compounds. Crystallographic analyses have led to controversial conclusions on the considered problem24 due to the use of area and shape corrections for C–F⋯F–C contacts18 and the cone correction for C–H⋯F–C contacts.25 Comparison of C–F⋯F–C and C–H⋯F–C contacts obtained from the X-ray experiment is not straightforward, since normalization of the C–H bonds leads to a shortening of the contacts H⋯F by ∼0.15 Å.26 In addition, the presence of a relatively short halogen⋯halogen contact in the crystal does not mean that there is an interaction between the atoms in question.27 All this makes it necessary to refine the hydrogen positions in molecular crystals through geometry optimization by periodic DFT28 or additional neutron diffraction analysis.29 However, the number of papers devoted to the neutron diffraction analysis or periodic DFT computations of crystals of organofluorine compounds is very limited.30,31
The intermolecular C–F⋯F and C–H⋯F interactions were theoretically studied in detail in the gas phase.32–34 Complexes of fluorinated methane, HF and F2 with simple molecules (H2O, C2H4 etc.) were considered. All the computations point to dominating dispersive contributions, in particular for very weak C–H⋯F interactions with H⋯F distances larger than 2.5 Å.33 The approaches based on semi-empirical methods, such as the PIXEL scheme,35–37 gave conflicting results on C–H⋯F–C interactions in crystals. In some cases, these interactions were mainly of a dispersive nature,36 in other cases they were characterized by a substantial coulombic contribution.35 There are several reasons explaining the current situation: (i) limited applicability of non-periodic models for describing non-covalent interactions in crystals;38 (ii) using experimental geometry in PIXEL calculations of crystals of organofluorine compounds; (iii) lack of systematic theoretical studies of C–F⋯F–C and C–H⋯F–C contacts in organic crystals. Indeed, the X23,39 C60 (ref. 40) and Z20 (ref. 41) benchmark sets for noncovalent interactions in solids do not contain these contacts.
C–F⋯F–C and C–H⋯F–C contacts in molecular crystals are characterized by energies ∼2 and ∼5 kJ mol−1, respectively,35,36,42–44 i.e. they are weak intermolecular interactions. Firmer conclusions on such interactions are expected from extended studies of complexes in crystals under the conditions in which other intermolecular interactions are minimized.33 In particular the dependence of the properties of C–F⋯F–C  C–H⋯F–C interactions on the underlying donor C(sp, sp2, sp3)–H and acceptor (primary, secondary or tertiary F–C moieties) parameters36 can be elucidated from thermodynamic experiments.33
C–H⋯F–C interactions on the underlying donor C(sp, sp2, sp3)–H and acceptor (primary, secondary or tertiary F–C moieties) parameters36 can be elucidated from thermodynamic experiments.33
In the present work, an in-depth study of the intermolecular C–F⋯F–C and C–H⋯F–C interactions in crystals of organofluorine compounds has been carried out by periodic DFT calculations coupled with the experimental data on the structure and sublimation thermodynamics of the studied crystals. To minimize the other intermolecular interactions, several sets of organic crystals were considered: (1) perfluorinated compounds; (2) molecular crystals with dominant C–F⋯F–C/C–H⋯F–C contacts; (3) crystals with C–F⋯F–C, C–H⋯F–C and C–H⋯O interactions. To avoid the controversial conclusions of the previous theoretical studies and crystallographic analyses of the C–F⋯F–C/C–H⋯F–C interactions33,35,36,45–47 the following steps were taken. First, the optimal level of periodic DFT computations was established and the relaxed molecular structures obtained by this level of approximation were used in subsequent calculations. Second, different theoretical approaches for evaluation of the ΔHsub value of crystals of perfluorinated molecules were considered. Third, a Bader analysis of theoretical crystalline electron density function was performed. Finally, superpositions of the gradient fields of electrostatic potential and of electron density and deformation density maps in the area of the studied intermolecular interactions were plotted to clarify the difference in the nature of C–F⋯F–C/C–H⋯F–C contacts. To the best of our knowledge, a periodic DFT study of the interplay between intermolecular C–F⋯F–C and C–H⋯F–C interactions in organofluorine crystals has not been done yet. The methodological aspects of different DFT-based approaches (including non-periodic calculations) for studying C–F⋯F–C and C–H⋯F–C interactions in crystals of organofluorine compounds are also discussed.
The competition between C–H⋯O and C–H⋯F–C has been the subject of heated discussions.21,47–52 To clarify this problem, we combined the Cambridge Structural Database (CSD) screening53 with the results of periodic DFT computations of the crystals of partly fluorinated molecules with C–H⋯O interactions.
The aim of this work is threefold. (1) To find a functional/basis set combination for periodic DFT calculations, which gives best results for the intermolecular C–F⋯F–C contacts in crystals and to establish a theoretical approach, which gives the reasonable ΔHsub values for crystals of perfluorinated molecules. (2) To determine the specific features of intermolecular C–H⋯F–C/C–F⋯F–C interactions in crystals of organofluorine compounds. (3) To clarify the role of the C–H⋯F–C contacts in crystal packing with/without C–H⋯O contacts. We start by introducing crystal structures containing organic fluorine as well as the used computational methods in Section 2. Section 3.1 describes the search for the level of DFT calculations which gives the best results for the metric and electron density parameters of the C–F⋯F–C contacts. Estimation of the lattice energy of crystals of perfluorinated molecules by different theoretical approaches is discussed in Section 3.2. The role of the C–H⋯F–C contacts in crystal packing is described in Section 3.3. The competition of the C–H⋯F–C interactions with nonconventional C–H⋯O bonds is discussed in Section 3.4. The applicability of Bader's theory to describing the intermolecular interactions and differences between C–H⋯F–C interactions and conventional hydrogen bonds is discussed in Section 4. Finally, we draw conclusions in Section 5.
2. Methods
2.1. Crystals under study
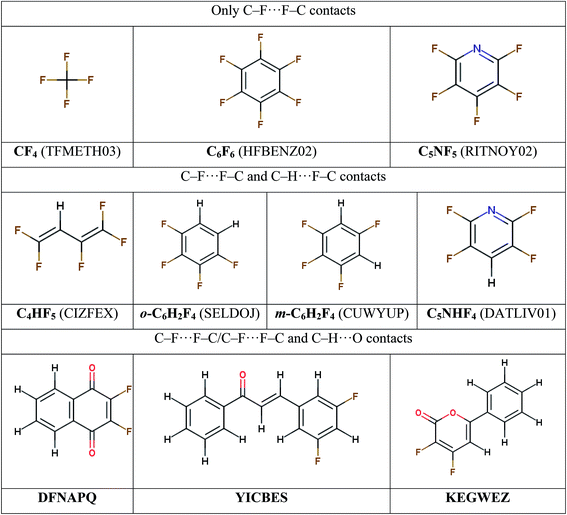
To study the nature of fluorine-based intermolecular interactions and interplay of interactions of particular types, several sets of molecular crystals are considered with the intention to minimize the possible contribution of other intermolecular contacts (Scheme 1). (i) Perfluorinated compounds with only C–F⋯F–C contacts: tetrafluoromethane (CF4),54 hexafluorobenzene (C6F6)55 and pentafluoropyridine (C5NF5).56 (Fluorine and nitrogen atoms are considered to be isolobal with respect to the supramolecular architecture in the crystalline phase57). (ii) Molecular crystals with prevalent C–F⋯F–C/C–H⋯F–C contacts: 1,1,2,4,4-pentafluorobuta-1,3-diene (C4HF5),58 1,2,3,5-tetrafluorobenzene (m-C6H2F4),23 1,2,3,4-tetrafluorobenzene (o-C6H2F4)59 and 2,3,5,6-tetrafluoropyridine (C5NHF4).56 (iii) Crystals where a competition occurs between intermolecular C–F⋯F–C, C–H⋯F–C and C–H⋯O contacts: 2,3-difluoro-1,4-naphthoquinone (DFNAPQ),60 3-(3,5-difluorophenyl)-1-phenylprop-2-en-1-one (YICBES)61 and 3,4-difluoro-6-phenyl-2H-pyran-2-one (KEGWEZ)62. The designations of the crystals given in bold; they will be used below.At the level of theory validation stage we additionally choose a smaller training set of crystals, where the lattice energies calculated by different approaches are compared against experimental ΔHsub values. For this purpose we select from ref. 19 the fluorine-containing crystals for which both X-ray diffraction data and ΔHsub are available, namely, CF4, C6F6, and pentafluorobenzoic acid (C6F5COOH).63
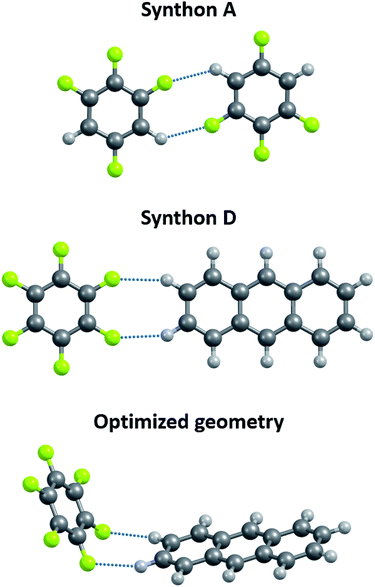
In order to reveal the applicability of non-periodic models to the crystals of partially fluorinated molecules, the DFT computations of non-periodic systems were carried out. For that purpose the dimers which form C–H⋯F–C synthons of types A and D23 are considered. DFT computations of isolated dimers were performed using Gaussian 09 package.64
2.2. Periodic DFT calculations
Two different approaches are widely used for the atomic simulation of molecular crystals within periodic DFT calculations: the first approach exploits a linear combination of plane-wave functions as a basis set28 and the second one adopts a linear combination of local atomic orbitals usually represented as Gaussian-type orbitals.65 The pros and cons of each approach are discussed elsewhere.66Two codes with plane wave basis sets were tested for computations of molecular crystals with perfluorinated compounds. The pseudopotential method is implemented in Quantum Expresso,67 while ELK is based on the full-potential linearized augmented-plane-wave method.68 Due to the difficulties associated with geometry optimization of the crystals with C–F⋯F–C contacts in Quantum Expresso and bad self-consistent field (SCF) convergence in some cases in ELK, the plane wave basis sets were not used below (for more information see ESI†).
In the CRYSTAL17 (ref. 69) calculations, the B3LYP and PBE functionals were employed with all-electron Gaussian-type localized orbital basis sets 6-31G**, pob-TZVP, and 6-31(F+)G**. In the latter diffuse functions with exponent factor equal to 0.1076 were added to the fluorine atoms. It is greater than the critical value 0.06 (ref. 70) below which problems in the SCF procedure arise.
London dispersion interactions were taken into account by using the semi-empirical D3 scheme.71 Tolerances on energies which control the self-consistent field convergence for geometry optimizations and frequency computations were set to 1 × 10−8 and 1 × 10−10 hartree, respectively. The shrinking factor of the reciprocal space net was set to 4. The space groups and the unit cell parameters of the considered crystals obtained in the experimental studies54–56,58–63 were fixed for the calculations. This is a common approximation for calculating molecular crystals with Hal⋯Hal contacts27,72,73 as the change in the volume of a cell of molecular crystals appears to be insignificant after full optimization.40,74
Periodic DFT computations of molecular crystals sometimes lead to the appearance of imaginary frequencies.75,76 This problem is usually solved by reducing the space symmetry to a minimum (P1 space group).74 In the present study, such procedure was applied to the CF4 crystal (C2/c space symmetry group54).
2.3. Estimation of the lattice energy
The approaches to lattice energy Elatt evaluation can be divided into two groups. The methods of the first group consider the as difference between the total electronic energy of a relaxed bulk crystal (Ebulk) and an isolated molecule (Ei) in its relaxed geometry:| Elatt = Ebulk/Z − Ei | (1) |
In order to obtain physically relevant results, the basis set superposition error needs to be taken into account in the Ei calculation either by Boys–Bernardi counterpoise correction77 (MOLEBSSE keyword in CRYSTAL17 (ref. 70)) or geometric counterpoise (gCP) scheme recently proposed by Grimme et al.39 It should be noted that the basis set superposition error evaluation is not straightforward for conformationally flexible molecules and crystals with more than one molecule in the asymmetric unit.78 According to our computations, the geometry is virtually unchanged, and conformation energies of studied compounds are rather small (∼1–3 kJ mol−1). Therefore, Elatt values evaluated using eqn (1) can be compared with the experimental sublimation enthalpy of the considered crystals.
The second group of methods considers the lattice energy as sum of energies of all pair intermolecular interactions within the asymmetric unit:
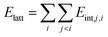 | (2) |
To ensure the consistence of obtained results with already existing data on fluoroorganic compounds,35–37 default calculation parameters were used for AA-CLP, PIXEL and CE-B3LYP. In AA-CLP and PIXEL, C–H/F–H/OH distances (if any) were normalized to standard values prior lattice energy estimation using the built-in function.
2.4. Evaluation of energy of intermolecular interactions in crystals using QTAIMC
In QTAIMC,82 the particular intermolecular interaction is associated with the existence of a bond critical point (BCP) between the pair of atoms. The energy of each specific interaction is considered totally independent of the others. The effects of the crystal environment, long-range electrostatic forces, etc. are taken into account implicitly, via the crystalline electronic wave function, and are coded in the BCP features.The energy of the particular intermolecular interaction Eint was evaluated according:83
| Eint = kGb (in atomic units) | (3) |
2.5. Superposition of gradient fields of electrostatic potential and electron density; deformation density maps
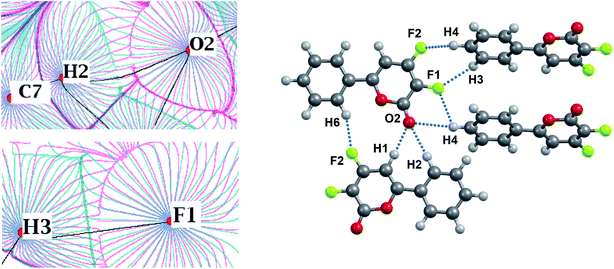
To reveal the nature of the H⋯F interactions in organic crystals, we have plotted the deformation density maps and superposition of the gradient fields of electrostatic potential and electron density for crystalline C4HF5 and KEGWEZ. C4HF5 has a short H⋯F contact, ∼2.35 Å, while KEGWEZ has H⋯F and H⋯O contacts with similar distances, ∼2.5 Å. For this purpose, we computed the theoretical structure factor lists for relaxed crystals using the CRYSTAL17. The theoretical structure factors are calculated for each possible hkl index characterized by sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ < 1.3 Å. The Hansen & Coppens88 formalism is used for multipole refinement implemented in the MOLLY program.89 After that, the multipole parameters are used to calculate gradient fields of the electrostatic potential and the electron density and deformation density maps by the WinXPRO program.90 The superposition of gradient fields of the electrostatic potential and the electron density is usually studied to reveal the electrostatic contribution to different interactions in crystals.91 The theoretical background is given in ESI.†
θ/λ < 1.3 Å. The Hansen & Coppens88 formalism is used for multipole refinement implemented in the MOLLY program.89 After that, the multipole parameters are used to calculate gradient fields of the electrostatic potential and the electron density and deformation density maps by the WinXPRO program.90 The superposition of gradient fields of the electrostatic potential and the electron density is usually studied to reveal the electrostatic contribution to different interactions in crystals.91 The theoretical background is given in ESI.†
3. Results
Two terms are widely used in the literature to describe weak non-covalent forces in crystals, namely “contacts” and “interactions”. In contrast to “contact”, the term “interaction” implies the existence of a BCP,27 which is localized by QTAIMC.To reveal applicability of non-periodic models to the description of C–H⋯F–C interactions in organic crystals the dimers extracted from crystalline m-C6H2F4 and the cocrystal of C6F6 and anthracene23 were computed at the PBE/6-31(F+)G** level (Fig. 1). The results obtained by this approach differ from the experimental data. In the m-C6H2F4 dimer (synthon A), the calculated values of the H⋯F/C⋯F distances are shorter than the standard experimental values by ∼0.15 Å (Table S1†). In the C6F6 – anthracene dimer (synthon D) the calculated values of the H⋯F/C⋯F distances agree with the experimental data. However, the spatial orientation of molecules is radically different from the orientation of these molecules in a two-component crystal C6F6 – anthracene (Table S1† and Fig. 1). The reasons for these disagreements are the disregard of the effects of the crystal environment in non-periodic models. We conclude that gas-phase computations have limited applicability for a description of intermolecular C–H⋯F–C interactions in organic crystals. The difference between experimental gas-phase (gas electron diffraction) and crystal-phase structures of perfluorinated species was also emphasis in ref. 92 and 93.
3.1. Selecting the optimal level of periodic computations
To select the optimal level of periodic DFT computations (functional/basis set), calculations were made for five crystals with multiple C–F⋯F–C interactions: CF4, C6F6, C6F5COOH, C5NHF4, and C5NF5. The results of calculations of intermolecular C–F⋯F–C distances in different approximations are given in Table S2.† The C–F⋯F–C contacts with the F⋯F distances significantly less than the sum of their van der Waals radii (∼2.94 Å94,95) are better reproduced in calculations than the longer C–F⋯F–C contacts. The inclusion of dispersion correction D3 has little effect on the theoretical geometric characteristics of the crystals under consideration. The best results are achieved using the 6-31(F+)G** basis set, where (F+) denotes diffuse functions added to fluorine atoms (Table S2†). Replacing the basis set with pob-TZVP96 does not significantly affect the theoretical C–F⋯F–C distances but greatly increases the computational cost. B3LYP/6-31(F+)G** and PBE-D3/6-31(F+)G** give the best results for the F⋯F distances in the considered crystals. The obtained results are in agreement with ref. 97, according to which the B3LYP/6-311+G* level shows excellent agreement with the experimental structures of isomeric fluoro thiourea. The disadvantage of using the B3LYP functional with the 6-31(F+)G** basis set is the poor convergence of the SCF procedure.The theoretical values of the F⋯F distances, the electron density and its Laplacian at the BCP of the C–F⋯F–C contacts evaluated using PBE-D3/6-31(F+)G** are compared with the experimental data in Fig. 2 and Table S3.† This level provides an adequate description of the electron density distribution for the F⋯F distances less than 2.94 Å.
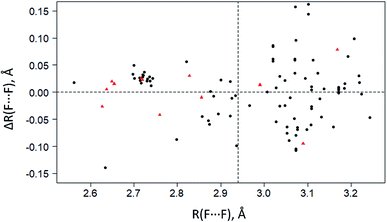 | ||
| Fig. 2 The deviations of experimental F⋯F distances ΔR(F⋯F) in crystalline CF4, C6F6, C5NF5, C5NHF4 (black circles) and C6F5COOH (red triangles) from theoretical F⋯F distances R(F⋯F) computed at the PBE-D3/6-31+(F)G** level. The horizontal dotted line corresponds to zero deviation. The vertical dotted line is a sum of van der Waals radii for fluorine atoms (∼2.94 Å (ref. 94 and 95)). | ||
The electron density ρb at the BCP is less than 0.003 a.u. for the contacts with the F⋯F distances larger than 2.94 Å (Table S3†). This BCP value is too small to be determined with certainty by the existing theoretical methods and precise X-ray diffraction experiments.86,98 Identification of the C–F⋯F–C bonding at the F⋯F distances larger than 2.94 Å involves the use of advanced experimental methods.30 It should be noted that in the crystals of perfluorinated molecules, a significant part of the C–F⋯F–C contacts is characterized by the F⋯F distances greater than 2.94 Å, see Fig. 2 and ref. 34. The use of the term “interaction” at such distances must be very careful.
3.2. The Elatt values of crystals of perfluorinated molecules
The theoretical Elatt values of the crystals of perfluorinated molecules (CF4, C6F6 and C6F5COOH) were evaluated using different theoretical approaches and compared with the experimental ΔHsub values in Table 1. In the case of eqn (1), PBE-D3/6-31(F+)G** is the best level of approximation, as shown in Table S4.† Theoretical Elatt values of crystalline C6F6 and C6F5COOH significantly exceed the experimental values for most DFT methods (Table S4†). This result does not contradict the literature data,99 according to which root-mean-square errors can reach 20 kJ mol−1 if no attempt is made to correct ΔHsub for finite temperature effects. Using the gCP correction39 in Elatt calculations does not improve the agreement with the experiment (Table S4†) as this approach was developed for organic crystals containing H, C, N, and O atoms. Neglecting the D3 correction results in negative lattice energies of “van der Waals” crystals CF4 and C6F6 (Table S3†). This can be explained by underestimating weak non-covalent interactions in DFT calculations, e.g. see Table S1 in ref. 39 and 100. The results are consistent with ref. 101. According to it, “⋯ halogen bonds are just too complex for simple dispersion corrections”. Thus, the correct description of the energy properties of perfluorinated crystals involves the use of a more accurate many-body dispersion energy correction.102| Crystal | Eqn (2) | Eqn (1) | ΔHsub19 | ||
|---|---|---|---|---|---|
| Eqn (3)a | AA-CLP | CE-B3LYP | PBE-D3/6-31(F+)G** | ||
| a Eint was computed using eqn (3) for intermolecular interactions with ρb > 0.003 a.u.; the electron-density characteristics at the BCP were evaluated using periodic electron density obtained at the PBE-D3/6-31(F+)G** level.b The Eint values in parenthesis were computed with coefficient value equals to 0.129 in eqn (3) for F⋯F and F⋯O contacts. | |||||
| CF4 | 68.4 (20.5)b | 19.6 | 25.4 | 17.1 | 14.0–17.0 |
| C6F6 | 82.1 (33.4) | 44.3 | 46.8 | 69.8 | 46.0–49.8 |
| C6F5COOH | 147.1 (92.6) | 89.5 | 111.0 | 143.6 | 92.0 |
The Elatt values evaluated using eqn (2) overestimate ΔHsub regardless of the level of periodic DFT calculations (Tables 1 and S5†). Applicability of this approach to the Elatt assessment of crystalline CF4 is not straightforward, due to a large number of the F⋯F contacts with R(F⋯F) > 2.94 Å (Fig. 2) and ρb < 0.003 a.u. However, this approach works better for crystalline C6F5COOH because the main contribution to the lattice energy is made by OH⋯O contacts between carboxyl groups. Moreover, in C6F5COOH, most of the F⋯F contacts are shorter than 2.94 Å (Fig. 2). The inclusion of vibrational effects would alter the obtained results because the C–F bond length would be slightly elongated. However, the investigation of the temperature effect on the Elatt value is beyond the scope of the present study.
We have tried to find the coefficient value in eqn (3) for the F⋯F contacts, which gives “reasonable” Elatt values (the standard deviation from ΔHsub is less than ∼10 kJ mol−1 (ref. 99)). The coefficient value equals ∼0.129 for perfluorinated molecules. This value can be justified as follows. The ΔHsub value of a CF4 crystal is ∼2.5 times smaller than that of CCl4, and the Cl⋯Cl distances are systematically larger than F⋯F. According to27, the energy of Cl⋯Cl interactions in crystals is well described by eqn (3) with k = 0.429.
The semi-empirical schemes for Elatt evaluation PIXEL,80 AA-CLP79 and CE-B3LYP81 are widely used due to their robustness and user-friendliness. We have tested their performance on the set of the studied compounds. Eqn (2) with the AA-CLP force field79,103 gives the best results for the Elatt values of perfluorinated crystals (Tables 1 and S4†) while CE-B3LYP overestimates it for CF4 and C6F5COOH. The PIXEL method, considered to be a more advanced version of AA-CLP, also fails to provide correct lattice energies for CF4 and C6F5COOH (Table S5†). The possible reason for poor performance of PIXEL and CE-B3LYP methods may be caused by the 6-31G** basis set used to estimate the molecular orbital overlap in CE-B3LYP81 or electron density distribution in the molecule in PIXEL.80 The basis sets chosen for parameterization of both methods lack diffusion orbital functions, which are essential for the agreement with the experimental distances and sublimation enthalpies (Section 3.1).
3.3. C–F⋯F–C vs. C–H⋯F–C in crystals containing only C, H and F atoms
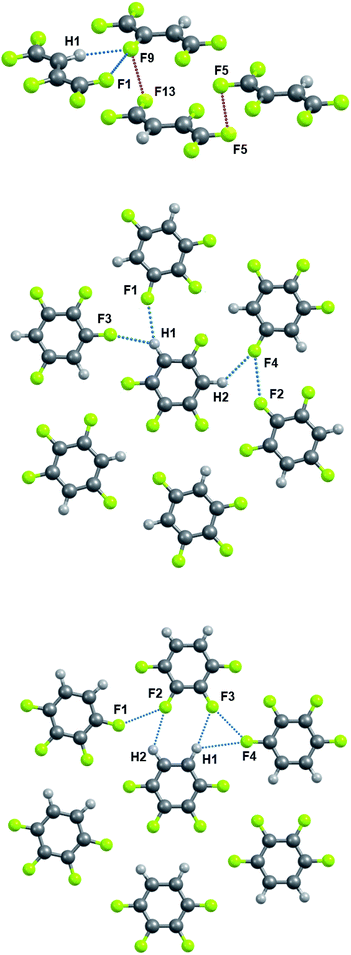
Sections 3.3 and 3.4 will exclusively use molecular parameters in crystals optimized in the PBE/6-31(F+)G** approximation. The metric and electron-density features, as well as the energy of the C–H⋯F–C and C–F⋯F–C interactions in crystals containing C, H and F atoms only, are given in Tables 2 and S3.† Theoretical H⋯F distances range from ∼2.35 to ∼2.70 Å in the studied crystals and are systematically shorter than F⋯F distances (Fig. 2), in accordance with the X-ray data of crystals containing only C, H and F atoms.21,23,43,104,105 Indeed, the shortest intermolecular C–H⋯F–C and C–F⋯F–C distances equal to ∼2.20 Å106 and ∼2.60 Å,107 respectively. The energies of the C–H⋯F–C contacts (5–7 kJ mol−1) are found to be larger than the energies of the C–F⋯F–C contacts (<4 kJ mol−1), in agreement with the literature data.35,36,42–44A comparison of the pattern of bond paths in the m-C6H2F4 crystal (middle panel of Fig. 3) with the literature data (Fig. 2 in ref. 23) shows the limited applicability of the geometric criterion to the localization of weak intermolecular C–F⋯F–C interactions in crystals of organofluorine compounds. F⋯F distances greater than 2.94 Å (ref. 34) characterize the vast majority of these crystals. Locating BCPs at such distances using QTAIMC is almost impossible.
The C–H⋯F–C interactions are characterized by a higher electron density value than the C–F⋯F–C interactions (Table 2) in accordance with the literature.35,108–110 The C–H⋯F–C and C–F⋯F–C contacts can be referred to the pure closed-shell interactions,32,111 which are characterized by electron density shifted to the interacting atoms, due to the low values of the λ1/λ3 at the BCPs (Table 2).112 However, consideration of the BCP characteristics does not allow identifying any qualitative differences between the interactions under consideration. To establish the nature of the C–H⋯F–C interactions and to distinguish difference between them and other weak interactions, like C–F⋯F–C, the superposition of the electrostatic potential and electron density gradient fields were considered. This approach identifies the electrostatic contribution to the interactions in solid state.75,91
| Contacta | H⋯F/F⋯F distanceb, Å | ρ(r), a.u. | ∇2ρ(r), a.u. | λ1, a.u. | λ2, a.u. | |λ1/λ3|, | Eintc, kJ mol−1 |
|---|---|---|---|---|---|---|---|
| a Only the contacts shorter than the sum of van der Waals radii are shown, see Fig. 3 for atomic numeration.b The experimental value is given in parentheses (C–H bonds were normalized to 1.09 Å).c In the case of the F⋯F contacts the coefficient value in eqn (3) equals to 0.129 (Subsection 3.2). | |||||||
| C4HF5 | |||||||
| C9–H1⋯F9 | 2.335 (2.420) | 0.011 | 0.030 | −0.014 | −0.013 | 0.246 | 7.3 |
| C5–F9⋯F1 | 2.900 (2.909) | 0.005 | 0.029 | −0.005 | −0.005 | 0.132 | 1.8 |
| C5–F9⋯F13 | 2.940 (2.909) | 0.006 | 0.030 | −0.005 | −0.003 | 0.132 | 1.3 |
| C1–F5⋯F5 | 2.880 (2.889) | 0.007 | 0.036 | −0.007 | −0.002 | 0.156 | 1.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| m-C6H2F4 | |||||||
| C4–H1⋯F1 | 2.550 (2.530) | 0.0055 | 0.025 | −0.006 | −0.006 | 0.167 | 5.7 |
| C6–H2⋯F4 | 2.578 (2.614) | 0.0053 | 0.025 | −0.005 | −0.005 | 0.143 | 5.6 |
| C4–H1⋯F3 | 2.590 (2.684) | 0.0064 | 0.029 | −0.006 | −0.005 | 0.150 | 6.4 |
| C2–F2⋯F4 | 2.897 (2.923) | 0.0057 | 0.030 | −0.006 | −0.005 | 0.146 | 2.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| o-C6H2F4 | |||||||
| C5–H1⋯F3 | 2.467 (2.557) | 0.0068 | 0.031 | −0.007 | −0.007 | 0.159 | 7.3 |
| C5–H1⋯F4 | 2.520 (2.950) | 0.0060 | 0.027 | −0.006 | −0.006 | 0.154 | 6.3 |
| C6–H2⋯F2 | 2.529 (2.566) | 0.0062 | 0.027 | −0.007 | −0.006 | 0.175 | 6.3 |
| C3–F3⋯F4 | 2.836 (2.858) | 0.0064 | 0.033 | −0.006 | −0.006 | 0.133 | 2.4 |
| C1–F1⋯F2 | 2.867 (2.950) | 0.0062 | 0.032 | −0.006 | −0.006 | 0.140 | 2.3 |
| C4–F4⋯F4 | 2.882 (2.943) | 0.0071 | 0.034 | −0.007 | −0.007 | 0.146 | 2.5 |
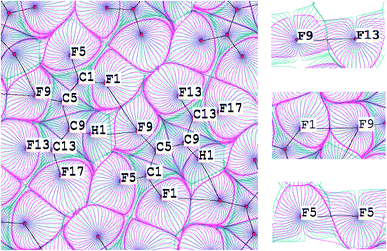
For this purpose the C–H⋯F–C and C–F⋯F–C interactions in the C4HF5 crystal were studied (Fig. 3, upper panel). The superposition of gradient fields of the electrostatic potential and electron density map for C4HF5 crystal is given on the Fig. 4. The C9–H1⋯F9–C5 contact is characterized by significant penetration of v- and ρ-basins of H and F atoms, which reveals the importance of the electrostatic contribution to this interaction. The boundaries of the corresponding basins along the bond path for the intralayer C5–F9⋯F1–C1 interaction (upper panel in Fig. 3) are equivalent, so C5–F9⋯F1–C1 is a typical closed-shell interaction. In case of interlayer F⋯F interactions (C1–F5⋯F5–C1 and C5–F9⋯F13–C13), the boundaries of v-basins nearly coincide with the boundaries of ρ-basins. Therefore, the electrostatic contribution for the interlayer C–F⋯F–C interactions in the C4HF5 crystal is negligible.
This result is confirmed by a plot of the distribution of the electrostatic potential on a surface of constant density (Fig. 5). The areas corresponded to the interlayer C–F⋯F–C interactions are characterized by a positive electrostatic potential in the isolated molecule. Therefore, these interactions will not be driven by the electrostatic factor in the crystalline structure. However, the fact that the crystalline environment strongly affects the distribution of the electrostatic potential should be taken into account. The distribution of the electrostatic potential for the C–H⋯F–C interaction changes considerably for a molecule removed from the crystal (Fig. 5a and c). This is completely opposite to the interlayer C–F⋯F–C interactions (Fig. 5b and d). Thus, the analysis of the distribution of the electrostatic potential for isolated molecules mainly illustrates the “driving force” in the process of crystal lattice formation.34 We conclude that this approach should be used with caution when studying the nature of intermolecular interactions in the solid state.
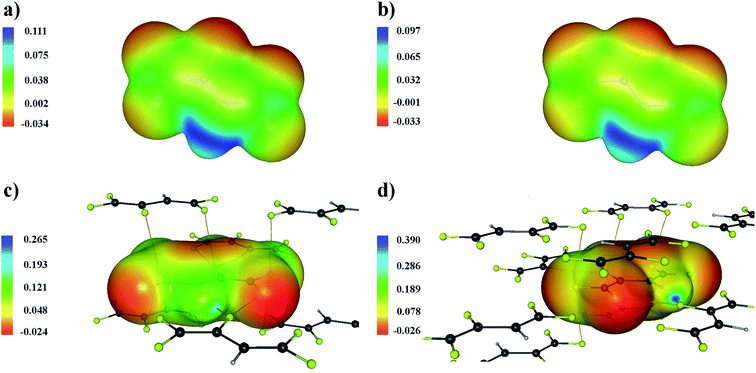 | ||
| Fig. 5 Electrostatic potential in the C4HF5 molecule, panels (a) and (b), and the molecule removed from the C4HF5 crystal, panels (c) and (d) projected onto surface of constant electron density. The latter value is 0.011 a.u. on panels (a) and (c) and 0.007 a.u. on panel (b) and (d). These values correspond to the electron density at the BCPs for the C9–H1⋯F9 and C1–F5⋯F5 interactions (Table 2). Bond paths are marked with yellow lines. The grey, light grey and yellow circles represent the carbon, hydrogen and fluorine atoms, respectively. | ||
A significant electrostatic contribution to the C–H⋯F–C interaction in crystalline C4HF5 with the H⋯F distance of 2.35 Å, which is shown by the superposition of the gradient fields of the electrostatic potential and the electron density map, is consistent with studies based on the PIXEL scheme. According to these studies, short C–H⋯F–C contacts have a significant Coulomb contribution.35 In crystals with H⋯F distances around 2.5 Å, the C–H⋯F–C interactions are also driven by the electrostatic factor (Section 3.4). This result differs from the data obtained by gas-phase33 and PIXEL computations.36,37 According to these studies, C–H⋯F interactions with H⋯F distances of about 2.5 Å are mainly dispersive. We believe that the reason for the disagreement is the use of non-periodic models and non-relaxed molecular geometry in the PIXEL approach.
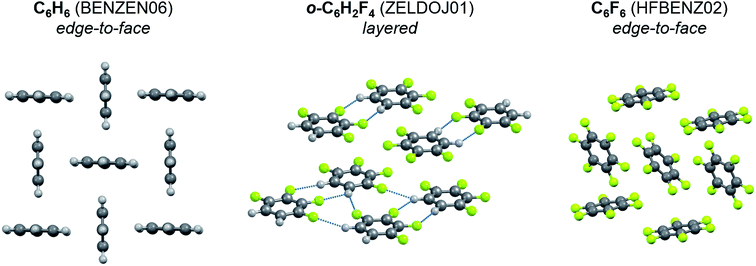
To identify the role of C–H⋯F–C interactions in the formation of a crystal architecture, a series of organic crystals consisting of molecules with varying degrees of fluorine substitution were examined. In benzene – partially fluorinated benzenes – hexafluorobenzene series the packing motif changes as follows (Fig. 6): herringbone packing with edge-to-face orientation113 – layers23 – edge-to-face orientation.55 This phenomenon is also observed for naphthalene, anthracene, pyridine (Fig. S1†). This points to the structure-directing role of C–H⋯F–C interactions due to the dominant electrostatic contribution to these contacts. The C–H⋯H–C and C–F⋯F–C interactions do not have that feature. Their energy in crystals is lower than that of C–H⋯F–C, which is manifested in higher values of vaporization enthalpy of partially fluorinated alkanes in comparison with the corresponding fluoroalkanes (Fig. S2 and S4†). The vaporization enthalpies of these crystals are directly proportional to the sublimation enthalpies (Fig. S3†).
We conclude that: (i) the energies of the C–H⋯F–C contacts (5–7 kJ mol−1) are found to be larger than the energies of the C–F⋯F–C contacts (<4 kJ mol−1); (ii) C–H⋯F–C interactions are driven by the electrostatic factor and have the structure-directing role in crystals containing C, H and F atoms.
3.4. The competition between C–H⋯O and C–H⋯F–C interactions
One of the CSD analysis tools is the probability density function (PDF). It has a dimension inverse to the measurement of the physical quantity being analyzed, e.g. the H⋯X distance and the CAr–H⋯X angle, here CAr–H denotes aromatic hydrogen, and X = O or F. The integral of the PDF over the entire area of the analyzed physical quantity is equal to one. The maximum value on the PDF curve corresponds to the most frequently encountered H⋯X distance (Fig. 7a) or CAr–H⋯X angle (Fig. 7b). The data on Fig. 7a leads to the following conclusions. (i) The H⋯F/H⋯O distances are determined by the proton acceptor group polarity of the fragment in question. The shortest H⋯O distances are formed by the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group. (ii) The H⋯F distances of aromatic fluorine (F–CAr) are similar to the H⋯O distances of the OH–C and OC–C groups (Fig. 7a). (iii) Aliphatic fluorine (F–Csp3) forms the longest H⋯F distances. It follows from Fig. 7b that C–H⋯F–C/C–H⋯O
C group. (ii) The H⋯F distances of aromatic fluorine (F–CAr) are similar to the H⋯O distances of the OH–C and OC–C groups (Fig. 7a). (iii) Aliphatic fluorine (F–Csp3) forms the longest H⋯F distances. It follows from Fig. 7b that C–H⋯F–C/C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C contacts are directional if the H⋯F and H⋯O distances are shorter than 2.35 Å (Fig. 7b). If the H⋯F and H⋯O distances are greater than the specified value (2.35 Å < R(H⋯X) < 2.70 Å), the directional character of the studied contacts gradually disappears. 2.70 Å is nearly equal to the sum of van der Waals radii of H and F (∼2.67 Å) or H and O (∼2.75 Å).
C contacts are directional if the H⋯F and H⋯O distances are shorter than 2.35 Å (Fig. 7b). If the H⋯F and H⋯O distances are greater than the specified value (2.35 Å < R(H⋯X) < 2.70 Å), the directional character of the studied contacts gradually disappears. 2.70 Å is nearly equal to the sum of van der Waals radii of H and F (∼2.67 Å) or H and O (∼2.75 Å).
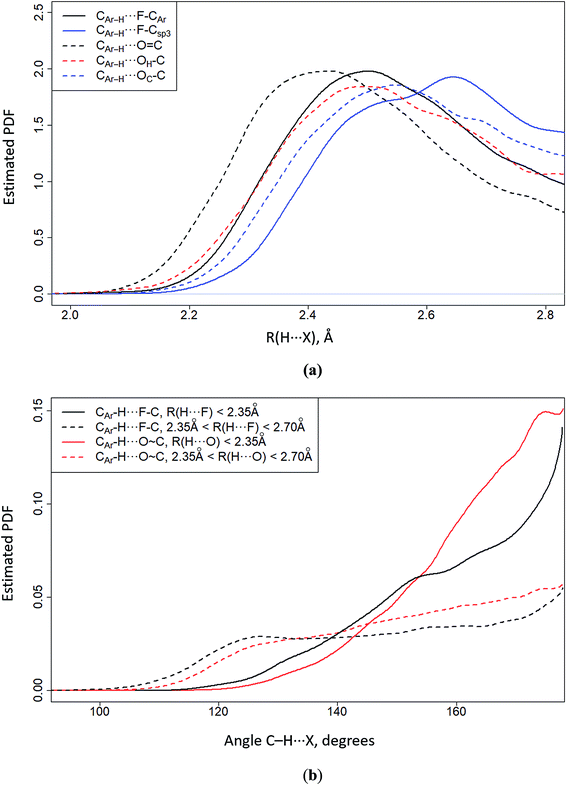 | ||
| Fig. 7 CSD-based estimation of the probability density function (PDF) of the CArH⋯X distance (a) and CAr–H⋯X angle (b) distribution, where X = O, F. The C–H bond lengths were normalized to the neutron-diffraction value (1.089 Å); the cone correction was also considered.14 | ||
The energies of the ArC–H⋯O and ArC–H⋯F interactions are comparable, if the H⋯F/H⋯O distances are close to each other (Table S6†). Analysis of the nature of the C–H⋯O and C–H⋯F interactions shows their similarity (Fig. 8 and 9). Both interactions are characterized by a significant electrostatic component (Fig. 8). The C–H group is non-polar, as evidenced by the absence of charge depletion on the deformation density maps in the region of this bond (Fig. 9).
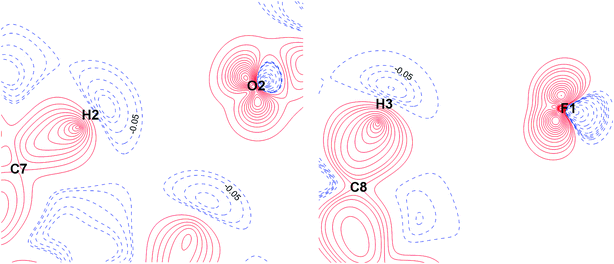 | ||
| Fig. 9 Deformation density maps for the C7–H2⋯O2 contact (left) and C8–H3⋯F1 contact (right) in the KEGWEZ crystal. The solid red lines represent positive contours and the broken blue lines represent negative contours. The values of charge depletion on the hydrogen atoms are given. All the contour lines are drawn at the intervals of ± 0.1 eÅ−3, except the additional contours with a step width of 0.01 eÅ−3 at the values close to those given on the map (0.03–0.1 eÅ−3). For atomic labels see Fig. 8. | ||
The theoretical Elatt values of crystalline KEGWEZ, DFNAPQ and YICBES are given in Table 3. They are in reasonable agreement with the literature data.52 Eqn (2), which was used to estimate the Elatt values, allows the lattice energy to be divided into different terms.114,115 The contributions of the C–H⋯O and C–H⋯F–C interactions are comparable and responsible for more than 2/3 of Elatt (Table 3). This means that both interactions can play a significant structure-directing role in organic crystals without conventional H-bonds or other relatively strong intermolecular interactions.
| KEGWEZ | DFNAPQ | YICBES | |
|---|---|---|---|
| Elatt, kJ mol−1 | 70.4 | 71.6 | 69.2 |
| Contribution | |||
C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
35% | 38% | 31% |
| C–H⋯F–C | 34% | 28% | 42% |
| C–H⋯pi, C–F⋯pi etc. | 31% | 34% | 28% |
The occurrence of the C–F⋯F–C and C–H⋯F–C interactions in isomeric species were analysed for 1-(4-fluorobenzoyl)-3-(isomeric fluorophenyl)thioureas.97 Their crystal packing shows H⋯F distances in the 2.46–2.82 Å range (Table S7†). In accordance with the results obtained in this subsection, almost no fluorine–fluorine contacts are realized in crystals with the C–H⋯F/C–H⋯O/C–H⋯S interactions.
4. Discussion
The applicability of Bader's theory to describing the intermolecular interactions was recently questioned.116 It should be noted that the H-bond energy/enthalpy may be estimated from the spectroscopic117 and geometric118 characteristics of H-bonds in crystals. All these approaches give comparable results for molecular crystals with weak or moderate conventional H-bonds.38,83,87 For example, the H-bond energy in water ices calculated using eqn (3) and the Iogansen approach117 are consistent with the experimental value of the H-bond enthalpy.119 Eqn (3) with k = 0.429 yields reasonable energies for intermolecular interactions with significant electrostatic contribution. A change in the nature of the interaction leads to serious differences in the energies calculated by eqn (3) from the estimates made by other approaches. For example, the appearance of a significant covalent component in short (strong) H-bonds, causes a serious variation in the energies calculated using different empirical approaches, see Table 2 in ref. 79 and Table 2 in ref. 120.The value of the coefficient k in eqn (3) is ∼0.67,72 0.429 (ref. 27) and 0.129 for the I⋯I, Cl⋯Cl and F⋯F interactions in crystals, respectively. This trend is consistent with the results of ref. 121.
The fundamental difference between the C–H⋯F–C interactions and the conventional O–H⋯O bonds can be demonstrated by the superposition of the electrostatic potential and electron density gradient fields (Fig. 10). The boundaries of v- and ρ-basins along the C–H bond path overlap perfectly for the C–H⋯F–C contacts, but for O–H, the penetration of v- and ρ-basins is significant. Thus, the O–H covalent interaction is mainly driven by the electrostatic factor. This result is supported by the deformation density maps for C–H⋯F–C and O–H⋯O (Fig. 11). There are regions of charge accumulation and charge depletion in the O–H direction, unlike the C–H case. The lack of charge accumulation near the oxygen atom demonstrates that O–H is a typical polar interaction as opposed to the C–H bond. The presence of the polar O–H bond causes more intensive charge depletion on the hydrogen atom, which leads to stronger O–H⋯O interactions in comparison with C–H⋯F–C and C–H⋯O (Tables S8 and S9†).
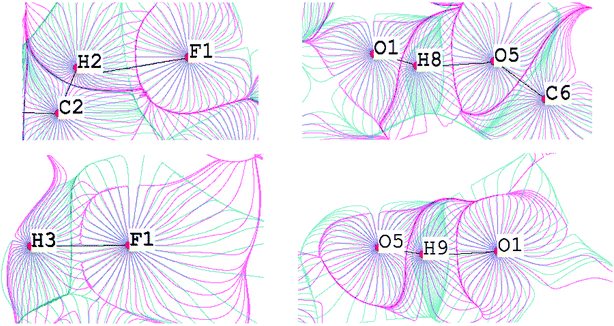 | ||
| Fig. 10 Superposition of gradient fields of the electrostatic potential (pink) and the electron density (blue) for the TISQER crystal. The bond paths are given by black lines. The nuclei positions are given by red circles. For atomic labels see Fig. S6.† | ||
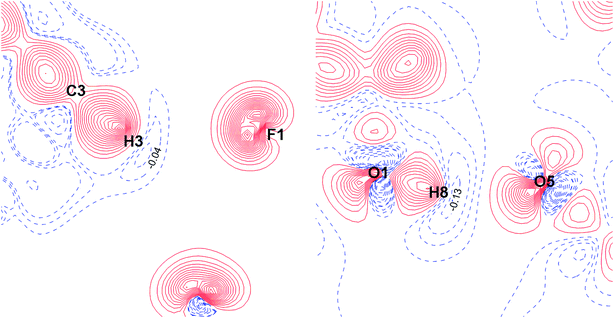 | ||
| Fig. 11 Deformation density maps for the C8–H3⋯F1 interaction (left) and O1–H8⋯O5 H-bond (right) in the TISQER crystal. The solid red lines represent positive contours and the broken blue lines represent negative contours. The values of charge depletion on the hydrogen atoms are given. The contours are drawn at the intervals of ± 0.05 eÅ−3. For atomic labels see Fig. S6.† | ||
A similar situation arises when we compare the H⋯F energy in C–H⋯F and F–H⋯F fragments. The energy of the F–H⋯F contact (∼23 kJ mol−1 (ref. 122)) is much higher than that of the C–H⋯F ones. This is due to the high polarity of the F–H covalent bond compared to the polarity of the C–H bond. It should be noted, that the X23 (ref. 39) and C60 (ref. 40) benchmark sets for noncovalent interactions in solids do not include molecules with fluorine atoms, while the Z20 set41 includes only F2 and HF molecules. Obviously, these sets are hardly applicable to adequate description of C–H⋯F interactions.
5. Conclusions
The PBE-D3 level with the 6-31G** basis set in which diffuse functions are added to the fluorine atoms provides an adequate description of the metric and electron-density parameters of C–F⋯F–C interactions in crystals of perfluorinated compounds, while the AA-CLP approach gives the best values of the sublimation enthalpy of these crystals. It has been found that plane wave periodic DFT computations with the most popular pseudopotentials may fail to describe the crystal structure of fluorine-rich compounds. A quantitative description of the lattice energy of perfluorinated organic molecules implies the use of advanced dispersion energy corrections in the periodic DFT computations or specially parameterized force fields in MD simulations.Periodic DFT computations followed by Bader analysis of crystalline electron density in combination with thermochemical data enable us to estimate the C–F⋯F–C interaction energy Eint using the following relation: Eint = kGb. Here, Gb is the local electronic kinetic density at the BCP and k = 0.129. This value is much smaller than the coefficient value of 0.429, which is used for evaluating the C–H⋯F–C energy. As a result, the average energy of intermolecular C–F⋯F–C interactions in crystals of neutral organic molecules is <4 kJ mol−1, which is less than the energy of the C–H⋯F–C interactions varying from 5 to 7 kJ mol−1. The presence of C–F⋯F–C interactions in crystals should be verified by Bader analysis of crystalline electron density. This approach gives reliable results for the F⋯F distances less than ∼2.94 Å.
The nature of the considered intermolecular interactions was established through the superposition of the gradient fields of electrostatic potential and electron density. In contrast to weak C–F⋯F–C interactions, intermolecular C–H⋯F–C interactions are driven by the electrostatic factor. The analysis of the Cambridge Structural Database shows the directed nature of the C–H⋯F–C interactions with H⋯F distances less than 2.35 Å. The electrostatic character and partial directionality of C–H⋯F interactions stipulate the structure-directing role of these interactions in crystals containing C, H and F atoms. This is manifested in the differences in the crystalline packing of partially fluorinated aromatic molecules as compared with non-fluorinated or perfluorinated molecules.
Intermolecular C–H⋯F–C and C–H⋯O interactions are identical in nature and comparable in energy. Different factors determine their contribution to the crystal packing: the underlying donor and acceptor properties of the C–H/C–F/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moieties, the number of C–H⋯F–C and C–H⋯O contacts, etc. C–H⋯O and C–H⋯F interactions play a significant structure-directing role in crystals of neutral organic molecules without conventional H-bonds.
O moieties, the number of C–H⋯F–C and C–H⋯O contacts, etc. C–H⋯O and C–H⋯F interactions play a significant structure-directing role in crystals of neutral organic molecules without conventional H-bonds.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Foundation for Basic Research (Grants 18-03-01107 and 18-33-00485).References
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terrano, The Halogen Bond, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- F. Meyer and P. Dubois, Halogen bonding at work: recent applications in synthetic chemistry and materials science, CrystEngComm, 2013, 15, 3058–3071 RSC.
- P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Halogen bonds in biological molecules, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794 CrossRef CAS PubMed.
- Y. Lu, T. Shi, Y. Wang, H. Yang, X. Yan, X. Luo, H. Jiang and W. Zhu, Halogen Bonding-A Novel Interaction for Rational Drug Design?, J. Med. Chem., 2009, 52, 2854–2862 CrossRef CAS PubMed.
- R. Wilcken, X. Liu, M. O. Zimmermann, T. J. Rutherford, A. R. Fersht, A. C. Joerger and F. M. Boeckler, Halogen-Enriched Fragment Libraries as Leads for Drug Rescue of Mutant p53, J. Am. Chem. Soc., 2012, 134, 6810–6818 CrossRef CAS PubMed.
- O. Bolton, K. Lee, H.-J. Kim, K. Y. Lin and J. Kim, Activating efficient phosphorescence from purely organic materials by crystal design, Nat. Chem., 2011, 3, 205–210 CrossRef CAS PubMed.
- H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, Halogen Bonding: A New Interaction for Liquid Crystal Formation, J. Am. Chem. Soc., 2004, 126, 16–17 CrossRef CAS PubMed.
- I. Y. Chernyshov, M. V. Vener, E. V. Feldman, D. Y. Paraschuk and A. Y. Sosorev, Inhibiting Low-Frequency Vibrations Explains Exceptionally High Electron Mobility in 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F2-TCNQ Single Crystals), J. Phys. Chem. Lett., 2017, 8, 2875 CrossRef CAS PubMed.
- E. Aubert, S. Lebegue, M. Marsman, T. T. T. Bui, C. Jelsch, S. Dahaoui, E. Espinosa and J. G. Ángyán, Periodic Projector Augmented Wave Density Functional Calculations on the Hexachlorobenzene Crystal and Comparison with the Experimental Multipolar Charge Density Model, J. Phys. Chem. A, 2011, 115, 14484–14494 CrossRef CAS PubMed.
- E. V. Bartashevich, A. I. Stash, V. I. Batalov, I. D. Yushina, T. N. Drebushchak, E. V. Boldyreva and V. G. Tsirelson, The staple role of hydrogen and halogen bonds in crystalline (E)-8-((2,3-diiodo-4-(quinolin-8-ylthio)but-2-en-1-yl)thio)quinolin-1-ium triiodide, Struct. Chem., 2016, 27, 1553–1560 CrossRef CAS.
- N. P. S. Chauhan, M. Mozafari, R. Ameta, P. B. Punjabi and S. C. Ameta, Spectral and Thermal Characterization of Halogen-Bonded Novel Crystalline Oligo(p-bromoacetophenone formaldehyde), J. Phys. Chem. B, 2015, 119, 3223–3230 CrossRef CAS PubMed.
- M. O. BaniKhaled, J. D. Mottishaw and H. Sun, Steering Power of Perfluoroalkyl Substituents in Crystal Engineering: Tuning the π–π Distance While Maintaining the Lamellar Packing Motif for Aromatics with Various Sizes of π-Conjugation, Cryst. Growth Des., 2015, 15, 2235–2242 CrossRef CAS.
- E. V. Bartashevich and V. G. Tsirelson, Mutual influence of non-covalent interactions in complexes and crystals with halogen bonds, Russ. Chem. Rev., 2014, 83, 1181–1203 CrossRef CAS.
- J. B. Neaton, A direct look at halogen bonds, Science, 2017, 358, 167–168 CrossRef CAS PubMed.
- D. Chopra, Is Organic Fluorine Really “Not”Polarizable?, Cryst. Growth Des., 2012, 12, 541–546 CrossRef CAS.
- F. F. Awwadi, R. D. Willett, K. A. Peterson and B. Twamley, The Nature of Halogen···Halogen Synthons: Crystallographic and Theoretical Studies, Chem.–Eur. J., 2006, 12, 8952–8960 CrossRef CAS PubMed.
- T. Brinck, J. S. Murray and P. Politzer, Surface Electrostatic Potentials of Halogenated Methanes as Indicators of Directional Intermolecular Interactions, Int. J. Quantum Chem., 1992, 19, 57–64 CrossRef CAS.
- B. K. Saha, A. Saha and S. A. Rather, Shape and Geometry Corrected Statistical Analysis on Halogen···Halogen Interactions, Cryst. Growth Des., 2017, 17, 2314–2318 CrossRef CAS.
- J. S. Chickos and W. E. Acree, Enthalpies of Sublimation of Organic and Organometallic Compounds. 1910–2001, J. Phys. Chem. Ref. Data, 2002, 31, 537–698 CrossRef CAS.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds yet Different, Acc. Chem. Res., 2014, 47(8), 2514–2524 CrossRef CAS PubMed.
- V. R. Thalladi, H.-C. Weiss, D. Blalser, R. Boese, A. Nangia and G. R. Desiraju, C-H···F Interactions in the Crystal Structures of Some Fluorobenzenes, J. Am. Chem. Soc., 1998, 120, 8702–8710 CrossRef CAS and references therein.
- V. R. Hathwar, T. S. Thakur, R. Dubey, M. S. Pavan, T. N. Guru Row and G. R. Desiraju, Extending the Supramolecular Synthon Based Fragment Approach (SBFA) for Transferability of Multipole Charge Density Parameters to Monofluorobenzoic Acids and their Cocrystals with Isonicotinamide: Importance of C-H···O, C-H···F, and F···F Intermolecular Regions, J. Phys. Chem. A, 2011, 115, 12852–12863 CrossRef CAS PubMed.
- T. S. Thakur, M. T. Kirchner, D. Bläser, R. Boese and G. R. Desiraju, C–H···F–C hydrogen bonding in 1,2,3,5-tetrafluorobenzene and other fluoroaromatic compounds and the crystal structure of alloxan revisited, CrystEngComm, 2010, 12, 2079–2085 RSC.
- A. Saha, S. A. Rather, D. Sharada and B. K. Saha, C–X···X–C vs C–H···X–C, Which One Is the More Dominant Interaction in Crystal Packing (X = Halogen)?, Cryst. Growth Des., 2018, 18, 6084–6090 CrossRef CAS.
- B. K. Saha, S. A. Rather and A. Saha, Interhalogen Interactions in the Light of Geometrical Correction, Cryst. Growth Des., 2016, 16, 3059–3062 CrossRef CAS.
- G. Mehta and S. Sen, Probing Fluorine Interactions in a Polyhydroxylated Environment: Conservation of a C–F···H–C Recognition Motif in Presence of O–H···O Hydrogen Bonds, Eur. J. Org. Chem., 2010, 3387–3394 CrossRef CAS.
- M. V. Vener, A. V. Shishkina, A. A. Rykounov and V. G. Tsirelson, Cl···Cl Interactions in Molecular Crystals: Insights from the Theoretical Charge Density Analysis, J. Phys. Chem. A, 2013, 117, 8459–8467 CrossRef CAS PubMed.
- V. L. Deringer, J. George, R. Dronskowski and U. Englert, Plane-Wave Density Functional Theory Meets Molecular Crystals: Thermal Ellipsoids and Intermolecular Interactions, Acc. Chem. Res., 2017, 50, 1231–1239 CrossRef CAS PubMed.
- G. V. Yukhnevich, Relationship between the lengths of covalent and intermolecular bonds in X-H⋯Y bridges, Crystallogr. Rep., 2010, 55, 377–380 CrossRef CAS.
- S. Kawai, A. Sadeghi, F. Xu, L. Peng, A. Orita, J. Otera, S. Goedecker and E. Meyer, Extended Halogen Bonding between Fully Fluorinated Aromatic Molecules, ACS Nano, 2015, 9, 2574–2583 CrossRef CAS PubMed.
- J. K. Cockcroft, A. Rosu-Finsen, A. N. Fitch and J. H. Williams, The temperature dependence of C–H⋯F–C interactions in benzene: hexafluorobenzene, CrystEngComm, 2018, 20, 6677–6682 RSC.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, From weak to strong interactions: a comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- H.-J. Schneider, Hydrogen bonds with fluorine. Studies in solution, in gas phase and by computations, conflicting conclusions from crystallographic analyses, Chem. Sci., 2012, 3, 1381–1394 RSC and references therein.
- A. Varadwaj, H. M. Marques and P. R. Varadwaj, Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions?, Molecules, 2019, 24, 379 CrossRef PubMed , (29 pages) and references therein.
- P. Panini and D. Chopra, Experimental and Theoretical Characterization of Short H-Bonds with Organic Fluorine in Molecular Crystals, Cryst. Growth Des., 2014, 14, 3155–3168 CrossRef CAS.
- R. Shukla and D. Chopra, Crystallographic and computational investigation of intermolecular interactions involving organic fluorine with relevance to the hybridization of the carbon atom, CrystEngComm, 2015, 17, 3596–3609 RSC.
- P. K. Mondal, H. R. Yadav, A. R. Choudhury and D. Chopra, Quantitative characterization of new supramolecular synthons involving fluorine atoms in the crystal structures of di- and tetrafluorinated benzamides, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 805–819 CrossRef CAS PubMed.
- A. G. Medvedev, A. V. Shishkina, P. V. Prikhodchenko, O. Lev and M. V. Vener, The Applicability of the Dimeric Heterosynthon Concept to Molecules with Equivalent Binding Sites. A DFT Study of Crystalline Urea-H2O2, RSC Adv., 2015, 5, 29601–29608 RSC.
- J. G. Brandenburg, M. Alessio, B. Civalleri, M. F. Peintinger, T. Bredow and S. Grimme, Geometrical Correction for the Inter- and Intramolecular Basis Set Superposition Error in Periodic Density Functional Theory Calculations, J. Phys. Chem. A, 2013, 117, 9282–9292 CrossRef CAS PubMed.
- M. Cutini, B. Civalleri, M. Corno, R. Orlando, J. G. Brandenburg, L. Maschio and P. Ugliengo, Assessment of Different Quantum Mechanical Methods for the Prediction of Structure and Cohesive Energy of Molecular Crystals, J. Chem. Theory Comput., 2016, 12, 3340–3352 CrossRef CAS PubMed.
- C. Červinka, M. Fulem and K. Růžička, CCSD(T)/CBS fragment-based calculations of lattice energy of molecular crystals, J. Chem. Phys., 2016, 144, 064505 CrossRef PubMed.
- R. J. Baker, P. E. Colavita, D. M. Murphy, J. A. Platts and J. D. Wallis, Fluorine–Fluorine Interactions in the Solid State: An Experimental and Theoretical Study, J. Phys. Chem. A, 2012, 116, 1435–1444 CrossRef CAS PubMed.
- G. Kaur and A. R. Choudhury, A comprehensive understanding of the synthons involving C–H⋯F–C hydrogen bond(s) from structural and computational analyses, CrystEngComm, 2015, 17, 2949–2963 RSC.
- H. R. Khavasi and N. Rahimi, Are fluorine-based contacts predictable? A case study in three similar coordination compounds, CrystEngComm, 2017, 19, 1361–1365 RSC.
- J. D. Dunitz and W. B. Schweizer, Molecular pair analysis: CH···F interactions in the crystal structure of fluorobenzene and related matters, Chem.–Eur. J., 2006, 12, 6804–6815 CrossRef CAS PubMed.
- P. Panini, R. Shukla, T. P. Mohan, B. Vishalakshi and D. Chopra, Analysis of intermolecular interactions in 3-(4-fluoro-3-phenoxyphenyl)-1-((4-methylpiperazin-1-yl)methyl)-1H-1,2,4-triazole-5-thiol, J. Chem. Sci., 2014, 126, 1337–1345 CrossRef CAS.
- R. Taylor, It Isn't, It Is: The C–H···X (X = O, N, F, Cl) Interaction Really is Significant in Crystal Packing, Cryst. Growth Des., 2016, 16, 4165–4168 CrossRef CAS.
- B. K. Saha, A. Saha, D. Sharada and S. A. Rather, F or O, Which One Is the Better Hydrogen Bond (Is It?) Acceptor in C–H···X–C (X– = F–, O=) Interactions?, Cryst. Growth Des., 2018, 18, 1–6 CrossRef CAS.
- J.-A. van den Berg and K. R. Seddon, Critical Evaluation of C-H···X Hydrogen Bonding in the Crystalline State, Cryst. Growth Des., 2003, 3, 643–661 CrossRef CAS.
- D. Chopra, T. S. Cameron, J. D. Ferrara and T. N. Guru Row, Pointers toward the Occurrence of C-F⋯F-C Interaction: Experimental Charge Density Analysis of 1-(4-Fluorophenyl)-3,6,6-trimethyl-2-phenyl-1,5,6,7-tetrahydro-4H-indol-4-one and 1-(4-Fluorophenyl)-6-methoxy-2-phenyl-1,2,3,4-tetrahydroisoquinoline, J. Phys. Chem. A, 2006, 110, 10465–10477 CrossRef CAS PubMed.
- A. Gavezzotti and L. Lo Presti, Building Blocks of Crystal Engineering: A Large-Database Study of the Intermolecular Approach between C–H Donor Groups and O, N, Cl, or F Acceptors in Organic Crystals, Cryst. Growth Des., 2016, 16, 2952–2962 CrossRef CAS.
- L. Lo Presti, On the significance of weak hydrogen bonds in crystal packing: a large databank comparison of polymorphic structures, CrystEngComm, 2018, 20, 5976–5989 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- G. Pepe and J.-M. Gay, Structure of alpha-CF4 at low temperature, J. Chem. Phys., 1989, 90, 5735 CrossRef CAS.
- H. Shorafa, D. Mollenhauer, B. Paulus and K. Seppelt, The Two Structures of the Hexafluorobenzene Radical Cation C6F6•+, Angew. Chem., Int. Ed., 2009, 48, 5845–5847 CrossRef CAS PubMed.
- H.-G. Stammler, Y. V. Vishnevskiy, C. Sicking and N. W. Mitzel, Charge density studies on 2,3,5,6-tetrafluoro- and pentafluoropyridine, CrystEngComm, 2013, 15, 3536–3546 RSC.
- O. V. Shishkin, K. Merz, V. Vasylyeva and R. I. Zubatyuk, Isotypic Transformation Principle in Molecular Crystals. Analysis of Supramolecular Architecture of Fluorinated Benzenes and Pyridines, Cryst. Growth Des., 2018, 18, 4445–4448 CrossRef CAS.
- F. A. Akkerman, R. Kickbusch and D. Lentz, Synthesis of fluorinated dienes by palladium-catalyzed coupling reactions, Chem.–Asian J., 2008, 3, 719–731 CrossRef CAS PubMed.
- T. Kottke, K. Sung and R. J. Lagow, Single-Crystal X-Ray Structure of the Metastable Aryne Precursor Tetrafluorophenyllithium and of 1,2,3,4-Tetrafluorobenzene, Angew. Chem., Int. Ed., 1995, 34, 1517–1519 CrossRef CAS.
- J. Gaultier, C. Hauw, J. Housty and M. Schvoerer, C. R. Seances Acad. Sci., Ser. C, 1972, 275, 1403 CAS , https://gallica.bnf.fr/ark:/12148/bpt6k6236265d/f359.
- A. de P. Farias, L. do C. Visentin, J. Bordinhao, D. C. Sobrinho and J. C. N. Ferreira, 3-(3,5-Difluorophenyl)-1-phenylprop-2-en-1-one, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o2770–o2771 CrossRef CAS.
- Y. Wang and D. J. Burton, A facile, general synthesis of 3,4-difluoro-6-substituted-2-pyrones, J. Org. Chem., 2006, 71, 3859–3862 CrossRef CAS PubMed.
- A. Bach, D. Lentz and P. Luger, Charge Density and Topological Analysis of Pentafluorobenzoic Acid, J. Phys. Chem. A, 2001, 105, 7405–7412 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. E. Gomperts, O. Stratmann, A. J. Yazyev, R. Austin, C. Cammi, J. W. Pomelli, R. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- R. A. Evarestov, Quantum Chemistry of Solids, Springer, Berlin, 2012 Search PubMed.
- S. Tosoni, C. Tuma, J. Sauer, B. Civalleri and P. Ugliengo, A comparison between plane wave and Gaussian-type orbital basis sets for hydrogen bonded systems: formic acid as a test case, J. Chem. Phys., 2007, 127, 154102 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. Fabris, G. Fratesi, S. de Gironcoli, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- http://elk.sourceforge.net/.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rerat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, Ph. D'Arco, M. Llunel, M. Caus, Y. Noel, L. Maschio, A. Erba and M. R. S. Casassa, CRYSTAL17, User's Manual, University of Turin, Turin, Italy, 2017 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. V. Bartashevich, I. D. Yushina, A. I. Stash and V. G. Tsirelson, Halogen Bonding and Other Iodine Interactions in Crystals of Dihydrothiazolo(oxazino)quinolinium Oligoiodides from the Electron-Density Viewpoint, Cryst. Growth Des., 2014, 14, 5674–5684 CrossRef CAS.
- B. Landeros-Rivera, R. Moreno-Esparza and J. Hernandez-Trujillo, Theoretical study of intermolecular interactions in crystalline arene–perhaloarene adducts in terms of the electron density, RSC Adv., 2016, 6, 77301–77309 RSC.
- A. Sen, P. D. Mitev, A. Eriksson and K. Hermansson, H-bond and electric field correlations for water in highly hydrated crystals, Int. J. Quantum Chem., 2016, 116, 67–80 CrossRef CAS.
- A. V. Shishkina, A. I. Stash, B. Civalleri and V. G. Tsirelson, Electron-density and electrostatic-potential features of orthorhombic chlorine trifluoride, Mendeleev Commun., 2010, 20, 161–164 CrossRef CAS.
- A. M. Reilly and A. Tkatchenko, Understanding the role of vibrations, exact exchange, and many-body van der Waals interactions in the cohesive properties of molecular crystals, J. Chem. Phys., 2013, 139, 024705 CrossRef PubMed.
- S. F. Boys and F. D. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. O. Surov, A. P. Voronin, M. V. Vener, A. V. Churakov and G. L. Perlovich, Specific features of supramolecular organisation and hydrogen bonding in proline cocrystals: a case study of fenamates and diclofenac, CrystEngComm, 2018, 20, 6970–6981 RSC.
- A. Gavezzotti, Efficient computer modeling of organic materials. The atom–atom, Coulomb–London–Pauli (AA-CLP) model for intermolecular electrostatic-polarization, dispersion and repulsion energies, New J. Chem., 2011, 35, 1360–1368 RSC.
- A. Gavezzotti, Calculation of intermolecular interaction energies by direct numerical integration over electron densities. 2. An improved polarization model and the evaluation of dispersion and repulsion energies, J. Phys. Chem. B, 2003, 107, 2344–2353 CrossRef CAS.
- S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures, J. Chem. Theory Comput., 2018, 14, 1614–1623 CrossRef CAS PubMed.
- V. G. Tsirelson, Interpretation of the Experimental Electron Densities by Combination of the QTAIM and DFT, in The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007, pp. 259–284 Search PubMed.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields, Chem. Phys. Lett., 2011, 507, 185–189 CrossRef CAS.
- M. V. Vener, A. N. Egorova, A. V. Churakov and V. G. Tsirelson, Intermolecular Hydrogen Bond Energies in Crystals Evaluated Using Electron Density: DFT Computations with Periodic Boundary Conditions, J. Comput. Chem., 2012, 33, 2303–2309 CrossRef CAS PubMed.
- C. Gatti and S. Casassa, TOPOND14 User's Manual, Milano, 2014 Search PubMed.
- A. V. Shishkina, V. V. Zhurov, A. I. Stash, M. V. Vener, A. A. Pinkerton and V. G. Tsirelson, Noncovalent Interactions in Crystalline Picolinic Acid N-Oxide: Insights from Experimental and Theoretical Charge Density Analysis, Cryst. Growth Des., 2013, 13, 816–828 CrossRef CAS.
- S. A. Katsyuba, M. V. Vener, E. E. Zvereva, Z. Fei, R. Scopelliti, G. Laurenczy, N. Yan, E. Paunescu and P. J. Dyson, How Strong Is Hydrogen Bonding in Ionic Liquids? Combined X-ray Crystallographic, Infrared/Raman Spectroscopic, and Density Functional Theory Study, J. Phys. Chem. B, 2013, 117, 9094–9105 CrossRef CAS PubMed.
- N. K. Hansen and P. Coppens, Testing aspherical atom refinements on small-molecule data sets, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921 CrossRef.
- J. Portas, MOLDOS97/MOLLY MS DOS Updated Version, 1997 Search PubMed.
- A. I. Stash and V. G. Tsirelson, WinXPRO: A Program for Calculation of Crystals and Molecular Properties Using Multipole Parametres of the Electron Density, version 3.3.09, Moscow, 2018 Search PubMed.
- F. Bertolotti, A. V. Shishkina, A. Forni, G. Gervasio, A. I. Stash and V. G. Tsirelson, Intermolecular Bonding Features in Solid Iodine, Cryst. Growth Des., 2014, 14, 3587–3595 CrossRef CAS.
- M. F. Erben, C. O. Della Vedova, H. Willner, F. Trautner, H. Oberhammer and R. Boese, Fluoroformyl Trifluoroacetyl Disulfide, FC(O)SSC(O)CF3: Synthesis, Structure in Solid and Gaseous States, and Conformational Properties, Inorg. Chem., 2005, 44, 7070–7077 CrossRef CAS PubMed.
- S. Torrico-Vallejos, M. F. Erben, R. Boese and C. O. Della Vedova, Methoxycarbonyl trifluoromethyl disulfide, CH3OC(O)SSCF3: synthesis, structure and conformational properties, New J. Chem., 2010, 34, 1365–1372 RSC.
- A. Bondi, van der Waals volumes and radii, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, Consistent Gaussian Basis Sets of Triple-Zeta Valence with Polarization Quality for Solid-State Calculations, J. Comput. Chem., 2013, 34, 451 CrossRef CAS PubMed.
- A. Saeed, M. F. Erben, U. Shaheen and U. Flörke, Synthesis, structural and vibrational properties of 1-(4-Fluorobenzoyl)-3-(isomeric fluorophenyl)thioureas, J. Mol. Struct., 2011, 1000, 49–57 CrossRef CAS.
- V. G. Tsirelson and R. P. Ozerov, Electron Density and Bonding in Crystals, Institute of Physics Publishing, Bristol, England/Philadelphia, 1996 Search PubMed.
- G. J. O. Beran, Modeling Polymorphic Molecular Crystals with Electronic Structure Theory, Chem. Rev., 2016, 116, 5567–5613 CrossRef CAS PubMed.
- A. Gionda, G. Macetti, L. Loconte, S. Rizzato, A. M. Orlando, C. Gatti and L. Lo Presti, A variable-temperature X-ray diffraction and theoretical study of conformational polymorphism in a complex organic molecule (DTC), RSC Adv., 2018, 8, 38445–38454 RSC.
- S. Kozuch and J. M. L. Martin, Halogen Bonds: Benchmarks and Theoretical Analysis, J. Chem. Theory Comput., 2013, 9, 1918–1931 CrossRef CAS PubMed.
- N. Marom, R. A. DiStasio, V. Atalla, S. Levchenko, A. M. Reilly, J. R. Chelikowsky, L. Leiserowitz and A. Tkatchenko, Many-body dispersion interactions in molecular crystal polymorphism, Angew. Chem., Int. Ed., 2013, 52, 6629–6632 CrossRef CAS PubMed.
- A. Gavezzotti, Equilibrium structure and dynamics of organic crystals by Monte Carlo simulation: critical assessment of force fields and comparison with static packing analysis, New J. Chem., 2013, 37, 2110–2119 RSC.
- H. Omorodion, B. Twamley, J. A. Platts and R. J. Baker, Further Evidence on the Importance of Fluorous−Fluorous Interactions in Supramolecular Chemistry: A Combined Structural and Computational Study, Cryst. Growth Des., 2015, 15, 2835–2841 CrossRef CAS.
- S. Chakraborty and G. R. Desiraju, C−H···F Hydrogen Bonds in Solid Solutions of Benzoic Acid and 4-Fluorobenzoic acid, Cryst. Growth Des., 2018, 18, 3607–3615 CrossRef CAS.
- P. Mocilac, I. A. Osman and J. F. Gallagher, Short C–H⋯F interactions involving the 2,5-difluorobenzene group: understanding the role of fluorine in aggregation and complex C–F/C–H disorder in a 2 × 6 isomer grid, CrystEngComm, 2016, 18, 5764–5776 RSC.
- M. Pérez-Torralba, M. Á. García, C. López, M. C. Torralba, M. R. Torres, R. M. Claramunt and J. Elguero, Structural Investigation of Weak Intermolecular Interactions (Hydrogen and Halogen Bonds) in Fluorine-Substituted Benzimidazoles, Cryst. Growth Des., 2014, 14, 3499–3509 CrossRef.
- R. Bianchi, A. Forni and T. Pilati, The Experimental Electron Density Distribution in the Complex of (E)-1,2-Bis(4-pyridyl)ethylene with 1,4-Diiodotetrafluorobenzene at 90 K, Chem.–Eur. J., 2003, 9, 1631–1638 CrossRef CAS PubMed.
- D. E. Hibbs, J. Overgaard, J. A. Platts, M. P. Waller and M. B. Hursthouse, Experimental and Theoretical Charge Density Studies of Tetrafluorophthalonitrile and Tetrafluoroisophthalonitrile, J. Phys. Chem. B, 2004, 108, 3663–3672 CrossRef CAS.
- V. R. Hathwar, D. Chopra, P. Panini and T. N. Guru Row, Revealing the Polarizability of Organic Fluorine in the Trifluoromethyl Group: Implications in Supramolecular Chemistry, Cryst. Growth Des., 2014, 14, 5366–5369 CrossRef CAS.
- C. F. Matta, N. Castillo and R. J. Boyd, Characterization of a Closed-Shell Fluorine-Fluorine Bonding Interaction in Aromatic Compounds on the Basis of the Electron Density, J. Phys. Chem. A, 2005, 109, 3669–3681 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules. Quantum Theory, Clarengon Press, Oxford, 1994, p. 432 Search PubMed.
- G. A. Jeffrey, J. R. Ruble, R. K. McMullan and J. A. Pople, The crystal structure of deuterated benzene, Proc. R. Soc. London, Ser. A, 1987, 414, 47–57 CrossRef CAS.
- A. N. Manin, A. P. Voronin, A. V. Shishkina, M. V. Vener, A. V. Churakov and G. L. Perlovich, Influence of Secondary Interactions on the Structure, Sublimation Thermodynamics and Solubility of Salicylate:4-Hydroxybenzamide Cocrystals. Combined Experimental and Theoretical Study, J. Phys. Chem. B, 2015, 119, 10466–10477 CrossRef CAS PubMed.
- A. P. Voronin, G. L. Perlovich and M. V. Vener, Effects of the crystal structure and thermodynamic stability on solubility of bioactive compounds: DFT study of isoniazid cocrystals, Comput. Theor. Chem., 2016, 1092, 1–11 CrossRef CAS.
- S. Shahbazian, Why Bond Critical Points Are Not “Bond” Critical Points, Chem.–Eur. J., 2018, 24, 5401–5405 CrossRef CAS PubMed.
- A. V. Iogansen, Direct Proportionality of the Hydrogen Bonding Energy and the Intensification of the Stretching ν(XH) Vibration in Infrared Spectra, Spectrochim. Acta, Part A, 1999, 55, 1585–1612 CrossRef.
- M. Rozenberg, A. Loewenschuss and Y. Marcus, An empirical correlation between stretching vibration redshift and hydrogen bond length, Phys. Chem. Chem. Phys., 2000, 2, 2699–2702 RSC.
- M. V. Vener, A. N. Egorova and V. G. Tsirelson, Hydrogen bonds and O⋯O interactions in proton-ordered ices. DFT computations with periodic boundary conditions, Chem. Phys. Lett., 2010, 500, 272–276 CrossRef CAS.
- A. G. Medvedev, A. A. Mikhaylov, I. Y. Chernyshov, M. V. Vener, O. Lev and P. V. Prikhodchenko, Effect of aluminum vacancies on the H2O2 or H2O interaction with a gamma-AlOOH surface. A solid-state DFT study, Int. J. Quantum Chem., 2019, e25920, DOI:10.1002/qua.25920.
- M. L. Kuznetsov, Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)nZ—Y⋯X− (X, Y = F, Cl, Br) interactions, Int. J. Quantum Chem., 2019, e25869, DOI:10.1002/qua.25869.
- S. Yu. Kucherov, S. F. Bureiko and G. S. Denisov, Anticooperativity of FHF hydrogen bonds in clusters of the type F-x(HF)n, RFx(HF)n and XFx(HF)n, R = alkyl and X = H,Br, Cl, F,, J. Mol. Struct., 2016, 1105, 246–255 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of plane-wave DFT computations, the Cambridge Structural Database analysis, three additional sets of molecular crystals and the theoretical background of gradient fields evaluation; experimental and theoretical values of the H⋯F and C⋯F distances in synthons A and D (Table S1); intermolecular C–F⋯F–C distances computed in different approximations (Table S2); experimental and theoretical values of the electron-density parameters at the BCP of the intermolecular C–F⋯F–C contacts (Table S3); theoretical values of the lattice energy of crystalline CF4, C6F6 and C6F5COOH obtained using eqn (1) with different levels of periodic DFT computations (Table S4); comparison of the lattice energy values of crystals of perfluorinated molecules evaluated using eqn (2) with the experimental values (Table S5); metric parameters and energies of the C–H⋯F–C interactions in crystals with C–H⋯O bonds (Table S6); metric and topological characteristics of the selected intermolecular interactions in crystalline 1-(4-fluorobenzoyl)-3-(isomeric fluorophenyl)thioureas (Table S7); metric parameters and energies of the C–H⋯F–C and C–F⋯F–C interactions in crystals with conventional H-bonds (Tables S8 and S9); transformation of crystal packing with partial fluorination of some organic compounds (Fig. S1), sublimation enthalpies of alkanes, perfluoroalkanes (Fig. S2), correlation between enthalpies of sublimation and enthalpies of vaporization of alkanes and perfluoroalkanes (Fig. S3), dependence of vaporization enthalpy of fluoroalkanes on a fraction of hydrogen atoms (Fig. S4), fragment of crystalline DFNAPQ and YICBES (Fig. S5); fragments of crystalline OVIHAD, OVIHEH and OVIHIL (Fig. S6); fragment of crystalline TISQER, C6F5COOH and RfCOOH (Fig. S7 and S8). See DOI: 10.1039/c9ra02116g |
| This journal is © The Royal Society of Chemistry 2019 |