Open Access Article
Open Access ArticleArmchair shaped polymeric nitrogen N8 chains confined in h-BN matrix at ambient conditions: stability and vibration analysis†
Shuang Liua,
Bo Liua,
Zhen Yaoa,
Shijie Liu b,
Xuhan Shia,
Shifeng Niua and
Bingbing Liu
b,
Xuhan Shia,
Shifeng Niua and
Bingbing Liu *a
*a
aState Key Laboratory of Superhard Materials, Jilin University, Changchun 130012, P. R. China. E-mail: liubb@jlu.edu.cn
bSchool of Physics and Engineering, Henan Key Laboratory of Photoelectric Energy Storage Materials and Applications, Henan University of Science and Technology, Luoyang, 471003, P. R. China
First published on 23rd September 2019
Abstract
A new hybrid material comprising of armchair shaped polymeric nitrogen chains (N8) encapsulated in h-BN matrix is proposed and studied through ab initio calculations. Interestingly, the theoretical results demonstrate that N8 chains, confined in h-BN matrix, are effectively stabilized at ambient pressure and room temperature. Moreover, N8 chains can dissociate and release energy at a much milder temperature of 600 K. The confined polymer N8 unit needs to absorb 0.68 eV energy to span the decomposition energy barrier before decomposing. Further research shows that the charge transfer between N8 chain and h-BN layer is the stabilizing mechanism of this new hybrid material. And the low dissociation temperature is due to a much smaller amount of charge transfer compared to other confined systems in previous reports. The IR and Raman vibrational analyses suggest that host–guest interactions in the hybrid material influence the vibration modes of both the confined N8 chain and h-BN layer.
1 Introduction
Polymeric nitrogen, a typical high-energy-density material (HEDM), is a potential candidate in several applications such as explosives, propellants and energy storage.1–3 Due to the large energy difference between the single bond and the triple bond, a large amount of energy is released during the transformation of nitrogen phase from single-bonded state to molecular state.4,5 More importantly, nitrogen gas, the decomposition product of polymeric nitrogen, is environmentally friendly.5,6 Over the years, remarkable progress has been made towards the design and synthesis of polymeric nitrogen.7–10 In theoretical calculations, many novel forms of polymeric nitrogen have been proposed under high pressure, including purely single-bonded structures,1,6,9,11–14 chain structures containing alternating single and double bonds,15 and the molecular solids.8,16 In experiments, the single-bonded network form of polymeric nitrogen (cg-N) was synthesized at 110 GPa and 2000 K for the first time. In 2014, a layered polymeric nitrogen (LP-N) has also been obtained under much harsher conditions (150 GPa, 3000 K) using laser-heated diamond anvil cells.5 Lately, a hexagonal layered polymeric nitrogen phase (HLP-N) was prepared near 250 GPa by compressing and laser heating pure nitrogen.7 Unfortunately, these obtained polymeric nitrogen are unstable at ambient conditions. Thus, an effective strategy is needed to stabilize polymeric nitrogen at ambient pressure and room temperature.Recently, a new hybrid material comprising of polymeric nitrogen chains (N8) with armchair shape encapsulated in the confined space has gathered significant interest. Theoretical studies indicate that N8 chains could be effectively stabilized at ambient conditions by being confined in 1-D space of nanotubes or 2-D space of a graphene matrix.17–21 Further analysis shows that the charge transfer from the host materials to N8 chains is the major reason for the stability of guest material.17,19 In experiment, N8− molecular anion is stabilized at ambient conditions on the positively charged sidewalls of multi-walled carbon nanotubes (MWNTs).22 Several theoretical researches have revealed that nano-confinement is an effective strategy for stabilizing polymeric nitrogen at ambient conditions.17,19–21 The MD studies indicate that the strong host–guest interaction in these hybrid structures results in a dissociation temperature of N8 chains higher than 1400 K, and over 5000 K.17,19 This is the drawback that limits their applications. Thus, it is urgent to explore an ideal host material for both stabilizing N8 chain at ambient conditions and allowing its energy releasing under controllable conditions.
Boron nitride (BN) matrix, analogous to graphene matrix, is commonly used in pollutant adsorption, catalysis and especially in protective capsules for holding materials under extreme conditions due to its superb heat resistance, low density, admirable temperature stability, chemical durability and oxidizing properties.23–27 However, BN matrix has not been investigated as a host material to confine polymeric nitrogen chains.
In this work, a multilayer h-BN matrix is proposed as a host material to confine the polymeric N8 chains, forming a new hybrid material (N8@h-BN matrix). The research focuses on three goals: investigating the stability of confined polymeric N8 chains; obtaining a further understanding of its stability mechanism; exploring the influence of systematic interactions on the vibration optic modes of host and guest materials.
2 Model and computational method
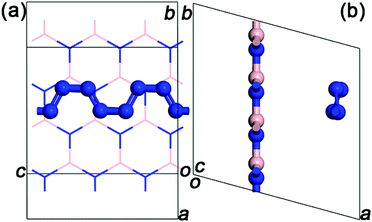
Two comparative calculations are performed to confirm the optimal structure and arrangement of confined N8 chain inside h-BN matrix. Firstly, we performed the geometry optimization for both the zigzag and armchair N8@h-BN crystal structures (see Fig. S1†). The results show that the zigzag N8 chain relaxed into the twisty armchair N8 chain, indicating that the confined zigzag N8 chain is unstable. For comparison, the energy (−268.87 eV) of armchair N8@h-BN structure is smaller than that (−268.82 eV) of twisty armchair N8@h-BN structure, which means that the confined armchair N8 chain is energetic stability. Secondly, in order to obtain the optimal arrangement of N8@h-BN structure, the 1 × 2 × 2 supercell structure of h-BN matrix with the different molecular orientation of N8 is constructed. The DFT total energy calculation shows that the hybrid N8@h-BN structure with the laying N8 molecule in the oc direction is the optimal structure (Fig. S2†). As shown in Fig. 1, a triclinic periodic unit model is built for the theoretical study with lattice constants of oa, ob and oc being 8.72, 8.68 and 7.6 Å, respectively. The angles aob, aoc and boc are 105°, 90° and 90°, respectively. The h-BN matrix and armchair-shape N8 chain are parallel to each other on the obc plane and N8 chain extends along the oc direction. The lattice mismatch is 0.0435 (see ESI†) and it allowed to keep the system size at computationally affordable level. The length of alternating single and double bonds of N8 chain are 1.30 and 1.29 Å, respectively, which is in agreement with the reported values of 1.34 Å and 1.29 Å.19 The initial distance of h-BN matrix and N8 chain is about 3.5 Å.Calculations of the geometry relaxation and the electronic properties are performed within the unit cell model. Molecular dynamic (MD) simulations are performed within the 2 × 1 × 1 supercell model. The Vienna ab initio simulation package (VASP), which is based on the density functional theory (DFT), is applied in the calculation.28,29 The exchange–correlation interaction is described by the generalized gradient approximation (GGA).30 The plane-wave energy cutoff is taken as 520 eV. For Brillouin zone integrations, 5 × 5 × 5, 9 × 9 × 9 and 1 × 1 × 1 Monkhors Pack grid are used for the structural relaxation, electronic properties and MD simulation, respectively. The convergence criterion of force and energy are 0.05 eV per atom and 10−6 eV, respectively. For the MD simulation, the total simulation time is 10 ps, and the time step is Δt = 1 × 10−3 ps. The temperature of simulated system is controlled by the Nose thermostat. We performed the MD simulation at constant number of molecules N, constant volume V and constant temperature T, representing a canonical or NVT-ensemble.
3 Results and discussion
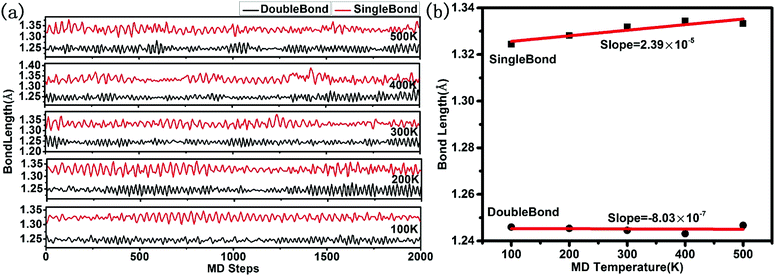
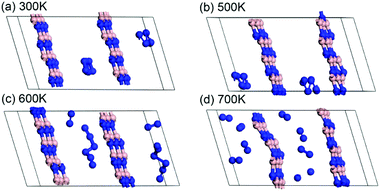
The stability analysis of confined polymeric N8 chain is performed by the MD simulation. Seven temperatures (100–700 K) are considered for the simulation of NVT-ensemble. In Fig. 2(a), we extract the last 2 ps from the 10 ps. The bond lengths of single and double bonds in N8 chain are recorded as the MD time at different temperatures. As the MD time progresses, lengths of single and double bonds are found to oscillate irregularly in the range of 1.29–1.39 Å and 1.21–1.30 Å, respectively. Meanwhile, the average length of single and double bonds as a function of simulated temperatures is shown in Fig. 2(b). To visualize our analysis, four MD simulated N8@h-BN matrix structures are presented in Fig. 3. As the temperature increases, the average length of single bond increases linearly with a slope of 2.39 × 10−5, whereas a decreasing trend is observed for the double bond with a slope of −8.03 × 10−7. For comparison, length of single bond length exhibits a much larger varying rate. The increasing and decreasing tendency of single and double bonds suggest that the N8 chain gradually loses its uniform chain properties with the increased temperature, but also keeps its chain configuration up to 500 K (Fig. 3(a) and (b)). At a temperature of 600 K, one bond length (1.125 Å) is obtained, indicating that the chain structure begins to decompose and transforms to the N2 molecular phase (see Fig. 3(c)). A much larger decompose rate is evident at a temperature of 700 K (see Fig. 3(d)). These results suggest that the confined N8 chain inside h-BN matrix is stable at ambient conditions and maintains its configuration up to 500 K. The decomposition temperature is 600 K, which is lower than that of N8 chain being confined inside the 1-D BN nanotube (1400 K)19 and much lower than that of N8 chain being confined inside 1-D carbon nanotube (5000 K).17 Thus, the h-BN matrix can be an excellent confinement material for polymeric N8 chain, due to the mild and controllable energy releasing temperature of N8 chain as well as the high stability of host molecule.Furthermore, the decomposition energy and the corresponding energy barrier are calculated to further confirm the stability of encapsulated N8 chain in h-BN matrix. We extract the confined N8 chain, N2 + N6 and 4N2 structures and performed the DFT total energy calculation. As shown in Fig. 4, the left N8 chain with the energy of −57.96 eV is the full relaxed structure; while the right one with the energy of −57.28 eV is the structure before decomposing in MD simulation. The energies of intermediate structure (N2 + N6 in MD simulation) and the decomposed structure (4N2 after the relaxation) are −60.65 eV and −65.13 eV, respectively. The decomposition energy barrier (0.68 eV) is just the energy difference (ΔE = 57.96–57.28) of two N8 structures; while the decompose energy of one N8 unit (7.17 eV) is the energy difference (ΔE = 65.13–57.96) of two relaxed structures. Thus, the confined polymer N8 unit needs to absorb 0.68 eV energy to span the decomposition energy barrier before decomposing, which confirms its dynamical stability at ambient conditions. After spanning the energy barrier, one polymer N8 unit releases 7.17 eV when it decomposed into 4N2 molecules.
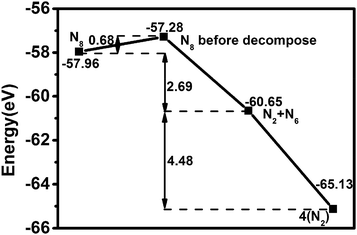 | ||
| Fig. 4 Energy of N8 with full relaxed, the N8 before decompose in MD simulation, N2 + N6 in MD simulation, 4N2 with full relaxed. | ||
For the second goal: obtaining a further understanding of stable mechanism. As previous reports, the charge transfer between the guest and the host materials is responsible for the stability of guest material.17 Thus, the stability and much lower decomposition temperature of confined N8 chain inside h-BN matrix should be induced by the different charge transfer. The electronic density difference of N8@h-BN matrix, which is the total electronic density minus the electronic density of isolated h-BN matrix and N8 chain, is shown in Fig. 5. Increased negative charges can be seen around the N8 chain indicating the capture of electrons; while increased positive charges near the h-BN matrix suggests losing of electrons. Charge transfer mainly occurs between the N8 chain and the nitrogen atoms in h-BN matrix, due to the polar B–N bonds since most of electrons are located near nitrogen atoms. Bader charge transfer analysis shows that each nitrogen atom of N8 chain captures 0.004e from the h-BN layer, which is smaller than the N8@CNTs17 (0.05e per atom) and N8@BNNTs19 (0.04e per atom) systems. Thus, it can be concluded that the charge transfer between host and guest molecule tends to stabilize the confined N8 chain. More importantly, the stability of confined guest material is sensitive to the quantity of electrons transfer. This indicates that the more or less quantities of electrons transferring are corresponds to the more or little stable guest moleculer respectively. Compared to N8@CNTs17 and N8@BNNTs19 systems, the N8@h-BN matrix transfers fewer number of electrons, which not only stabilizes the confined N8 chain at ambient conditions, but also favors its application due to the much lower decomposition temperature.
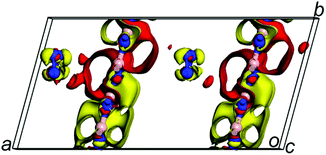 | ||
| Fig. 5 The electron density difference of N8@h-BN matrix at ambient conditions. Red and yellow colours represent effective positive and negative charges, respectively. | ||
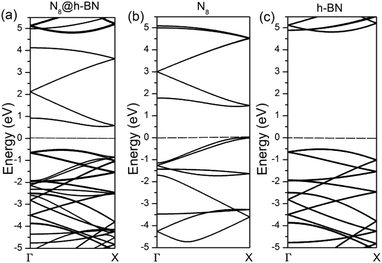
To deeply understand the interaction between h-BN layer and N8 chain, the band structure and density of states (DOS) of N8@h-BN system are calculated, as shown in Fig. 6 and 7, respectively. The band structure and DOS of isolated N8 chain and h-BN matrix are also calculated for comparative analysis. It is evident that the band structure of N8@h-BN matrix is nearly the simple superposition of the individual band structures of isolated N8 chain and h-BN matrix. The conduction band of N8 chain in the system exhibits a downward shift compared to that isolated case, which is consistent with the fact that the charge transfer occurs from h-BN matrix to N8 chain. Moreover, this charge transfer also induces a decrease of band gap of N8@h-BN matrix. As shown in Fig. 7, the DOS curves of isolated h-BN matrix and N8 chain are similar to that of N8@h-BN matrix, while the energy of DOS peaks of N8 chain exhibits a downshift compared to the isolated N8 chain, which is also consistent with above analysis that the charge transfer occurs from h-BN matrix to N8 chain. Thus, the band structure and DOS analysis further corroborate the electronic density difference analysis suggesting that the charge transfer is the mainly responsible for the stability of confined N8 chain inside h-BN matrix.
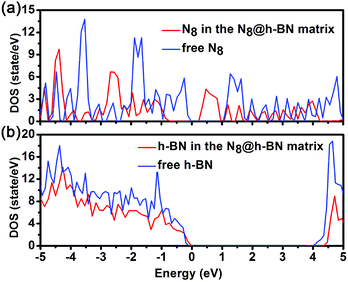 | ||
| Fig. 7 Density of states for free h-BN layer and h-BN layer in the N8@h-BN system (a) and density of states for the free N8 chain and N8 chain in the N8@h-BN system (b). | ||
For the third goal: exploring the influence of the systemic interaction on the vibration optic modes of host and guest materials. Calculated IR and Raman spectrum of isolated h-BN, isolated N8 chain and N8@h-BN matrix are shown in Fig. 8(a) and (b), respectively. Vibration modes are shown in Fig. 9 and the corresponding vibration mode assignments are listed in Table 1. From the IR spectrum shown in Fig. 8(a), it is evident that N8 chain and h-BN matrix exhibit three vibration models. For the N8 chain, the host–guest interaction induces a blue shift and two red shift vibrations, which correspond to the blue shift of N2–N2–N2 bending vibration (522.51 cm−1 → 483.29 cm−1), the red shift of N2–N2–N2 bending vibration (634.36 cm−1 → 673.47 cm−1) and N–N stretch vibration (1026 cm−1 → 1297.25 cm−1), respectively (see Fig. 9(a)). For the h-BN matrix, the host–guest interaction induces a blue shift of three vibration modes, which correspond to the B–N–B bending vibration (795.65 cm−1 → 795.42 cm−1), the B–N stretch vibrations of (1335.55 cm−1 → 1314.87 cm−1) and (1335.59 cm−1 → 1326.14 cm−1) (see Fig. 9(b)). For the Raman spectrum shown in Fig. 8(b), it can be seen that the N8 chain and h-BN exhibit three and two vibration modes, respectively. As induced by the host–guest interaction, two blue shifts (298.79 cm−1 → 199.07 cm−1), (1273.86 cm−1 → 1137.49 cm−1) and one red shift (693.19 cm−1 → 942.27 cm−1) are observed for the N–N–N bending vibrations of N8 chain (see Fig. 9(c)). Since the B–N–B bending and B–N stretch vibrations can be detected by both the IR and Raman spectrum, the same blue shift of B–N–B bending vibration (1335.55 cm−1 → 1314.8 cm−1) and B–N stretch vibration (1335.59 cm−1 → 1326.14 cm−1) are evident in the IR spectrum (see Fig. 9(d)). For the N8 chain, the vibrations (522.51 cm−1 → 483.29 cm−1, 298.79 cm−1 → 199.07 cm−1, 1273.86 cm−1 → 1137.49 cm−1), which are mainly perpendicular to the h-BN layer plane, exhibit a blue shift due to the confinement effect that suppresses these vibrations. The vibrations (634.36 cm−1 → 673.47 cm−1, 1026 cm−1 → 1297.25 cm−1, 693.19 cm−1 → 942.27 cm−1) which are mainly parallel to the h-BN layer plane, exhibit a red shift due to the much smaller confinement effect along this direction. All the vibrations of filled h-BN layer are blue shift compared with the single h-BN layer due to the host–guest interaction. The exhibited blue shift of vibration modes indicates a decreased vibration energy of h-BN layer, which is consistent with our electronic analysis that indicated a loss of electrons for the h-BN layer. Thus, the weak host–guest interaction also induces a red or blue shift of both the confined N8 chain and h-BN matrix by the IR and Raman vibration analyses. This vibration analysis as well as the modes assignment can be used to guide the further studies in experiment.
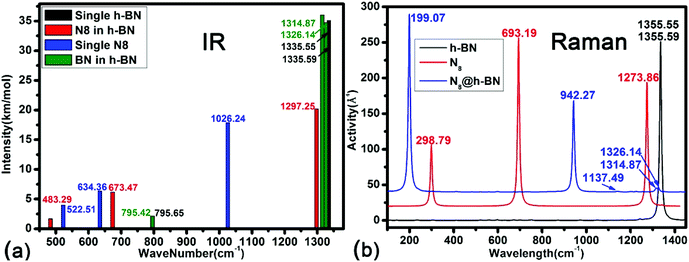 | ||
| Fig. 8 Calculated IR and Raman spectrum of isolated h-BN, isolated N8 chain and N8@h-BN matrix are presented in (a) and (b). | ||
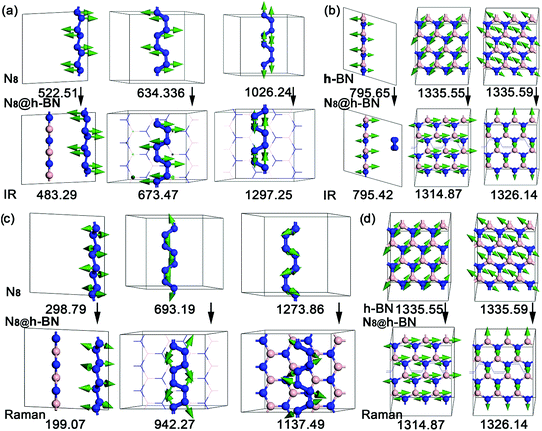 | ||
| Fig. 9 Vibration modes of IR and Raman spectrums of isolated h-BN, isolated N8 chain and N8@h-BN matrix. | ||
| Symmetry | Assignment | N8 | N8@h-BN | |
|---|---|---|---|---|
| IR | — | N2–N2–N2 bend | 522.51 | 483.29 |
| — | N2–N2–N2 bend | 634.36 | 673.47 | |
| — | N–N stretch | 1026.24 | 1297.25 |
| Symmetry | Assignment | h-BN | N8@h-BN | |
|---|---|---|---|---|
| IR | A2u | B–N–B bend | 795.65 | 795.42 |
| E2g | B–N–B bend | 1335.55 | 1314.87 | |
| E1u | B–N stretch | 1335.59 | 1326.14 |
| Symmetry | Assignment | N8 | N8@h-BN | |
|---|---|---|---|---|
| Raman | — | N–N–N bend | 298.79 | 199.07 |
| — | N–N–N bend | 693.19 | 942.27 | |
| — | N–N–N bend | 1273.86 | 1137.49 |
| Symmetry | Assignment | h-BN | N8@h-BN | |
|---|---|---|---|---|
| Raman | E2g | B–N–B bend | 1335.55 | 1314.87 |
| E1u | B–N stretch | 1335.59 | 1326.14 |
4 Conclusions
In summary, we proposed a new hybrid structure, comprising of polymeric nitrogen chains (N8) confined in a multilayer h-BN matrix and investigated its properties using ab initio DFT calculations. MD simulation results show that the polymeric nitrogen chains confined in h-BN matrix can be effectively stable at ambient conditions. A low decomposition temperature of 600 K for N8 chain is obtained, indicating that the h-BN matrix is an ideal confinement template for polymeric nitrogen N8 chain. The dissociation barrier is 0.68 eV when polymer N8 decomposed, which further confirms its kinetical stability at ambient conditions. The analyses of electronic density difference, band structure and DOS indicate that the charge transfer between host material and N8 chain is the major responsibility for the stabilizing mechanism. Further analysis reveals that the charge transfer between N8 chain and h-BN layer is much smaller than that of the previous works. Compared to the N8@CNTs and N8@BNNTs systems, the N8@h-BN system has a smaller charge transfer due to the weaker host–guest interaction, which leads to a milder decomposition temperature. Finally, the weak host–guest interaction induces a red or blue shift of both the confined N8 chain and h-BN matrix by the IR and Raman vibration analyses. These results provide an effective strategy for capturing and storing nitrogen-based HEDMs at ambient conditions and facilitating a more controlled energy release mechanism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Key R&D Program of China (2018YFA0305900) and the NSFC (116344004, 51320105007, 11604116, 11847094 and 51602124), Program for Changjiang Scholars and Innovative Research Team in University (IRT1132). We also acknowledge the use of computing facilities at the High Performance Computing Centre of Jilin University.References
- X. Wang, Y. Wang, M. Miao, X. Zhong, J. Lv, T. Cui, J. Li, L. Chen, C. J. Pickard and Y. Ma, Phys. Rev. Lett., 2012, 109, 175502 CrossRef PubMed.
- C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2009, 102, 125702 CrossRef PubMed.
- Y. Li, X. Feng, H. Liu, J. Hao, S. A. T. Redfern, W. Lei, D. Liu and Y. Ma, Nat. Commun., 2018, 9, 722 CrossRef PubMed.
- M. I. Eremets, M. Y. Popov, I. A. Trojan, V. N. Denisov, R. Boehler and R. J. Hemley, J. Chem. Phys., 2004, 120, 10618–10623 CrossRef CAS PubMed.
- D. Tomasino, M. Kim, J. Y. Smith and C.-S. Yoo, Phys. Rev. Lett., 2014, 113, 205502 CrossRef PubMed.
- F. Zahariev, A. Hu, J. Hooper, F. Zhang and T. Woo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214108 CrossRef.
- D. Laniel, G. Geneste, G. Weck, M. Mezouar and P. Loubeyre, Phys. Rev. Lett., 2019, 122, 066001 CrossRef CAS PubMed.
- M. J. Greschner, M. Zhang, A. Majumdar, H. Liu, F. Peng, J. S. Tse and Y. Yao, J. Phys. Chem. A, 2016, 120, 2920–2925 CrossRef CAS PubMed.
- S. V. Bondarchuk and B. F. Minaev, Comput. Mater. Sci., 2017, 133, 122–129 CrossRef CAS.
- F. J. Owens, Comput. Theor. Chem., 2011, 966, 137–139 CrossRef CAS.
- C. Mailhiot, L. H. Yang and A. K. McMahan, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14419–14435 CrossRef CAS PubMed.
- F. Zahariev, J. Hooper, S. Alavi, F. Zhang and T. K. Woo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 140101 CrossRef.
- Y. Ma, A. R. Oganov, Z. Li, Y. Xie and J. Kotakoski, Phys. Rev. Lett., 2009, 102, 065501 CrossRef PubMed.
- X. Wang, Z. He, Y. Ma, T. Cui, Z. Liu, B. Liu, J. Li and G. Zou, J. Phys.: Condens. Matter, 2007, 19, 425226 CrossRef.
- W. D. Mattson, D. Sanchez-Portal, S. Chiesa and R. M. Martin, Phys. Rev. Lett., 2004, 93, 125501 CrossRef PubMed.
- B. Hirshberg, R. B. Gerber and A. I. Krylov, Nat. Chem., 2014, 6, 52–56 CrossRef CAS PubMed.
- H. Abou-Rachid, A. Hu, V. Timoshevskii, Y. Song and L. S. Lussier, Phys. Rev. Lett., 2008, 100, 196401 CrossRef PubMed.
- W. Ji, V. Timoshevskii, H. Guo, H. Abou-Rachid and L.-S. Lussier, Appl. Phys. Lett., 2009, 95, 021904 CrossRef.
- S. Liu, M. Yao, F. Ma, B. Liu, Z. Yao, R. Liu, T. Cui and B. Liu, J. Phys. Chem. C, 2016, 120, 16412–16417 CrossRef CAS.
- V. Timoshevskii, W. Ji, H. Abou-Rachid, L.-S. Lussier and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115409 CrossRef.
- F. Zheng, C. Wang and P. Zhang, J. Comput. Theor. Nanosci., 2012, 9, 1129–1133 CrossRef CAS.
- Z. Wu, M. Benchafia el, Z. Iqbal and X. Wang, Angew. Chem., 2014, 126, 12763–12767 CrossRef.
- X.-L. Meng, N. Lun, Y.-X. Qi, H.-L. Zhu, F.-D. Han, L.-W. Yin, R.-H. Fan, Y.-J. Bai and J.-Q. Bi, J. Solid State Chem., 2011, 184, 859–862 CrossRef CAS.
- J. A. Perdigon-Melon, A. Auroux, C. Guimon and B. Bonnetot, J. Solid State Chem., 2004, 177, 609–615 CrossRef CAS.
- C. C. Tang, Y. Bando, X. X. Ding, S. R. Qi and D. Golberg, J. Am. Chem. Soc., 2002, 124, 14550 CrossRef CAS PubMed.
- G. Lian, X. Zhang, S. Zhang, D. Liu, D. Cui and Q. Wang, Energy Environ. Sci., 2012, 5, 7072–7080 RSC.
- J. Li, J. Lin, X. Xu, X. Zhang, Y. Xue, J. Mi, Z. Mo, Y. Fan, L. Hu, X. Yang, J. Zhang, F. Meng, S. Yuan and C. Tang, Nanotechnology, 2013, 24, 155603 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02947h |
| This journal is © The Royal Society of Chemistry 2019 |