Open Access Article
Open Access ArticleFusion and clustering of spherical micelles by extruding through a cylindrical channel
Manman Chena,
Xinghua Zhangb and
Hui Zhang†
 *a
*a
aSchool of Mathematics Sciences, Beijing Normal University, Beijing 100875, China. E-mail: hzhang@bnu.edu.cn; Fax: +86 10 58808802; Tel: +86 10 58804686
bSchool of Science, Beijing Jiaotong University, 100044, Beijing, China
First published on 6th August 2019
Abstract
Experiments have shown that worm-like cylindrical micelles can be obtained by extruding spherical micelles through a cylindrical channel. The uniaxial symmetry of the cylindrical confinement can help fuse the spherical micelles into the cylindrical phase. Here, a theoretical model is proposed to investigate this fusion transition driven by external pressure in the cylindrical channel. In this model, spherical micelles are formed by diblock copolymers dissolved in a homopolymer solvent. And the external pressure is controlled by the average center distance of the neighboring spherical micelles. In addition to the fusion transition, the addition of the homopolymers leads to a depletion effect induced by the attraction between adjacent spherical micelles. Thus, spherical micelles in the channel can correlate together and form a linear cluster. The free energy barrier of fusion and the free energy potential well of the clustering of spherical micelles are investigated by a numerical computation of the self-consistent mean field theory. We present a full phase diagram of these transitions depending on the radius of the channel and the external pressure.
Introduction
Because the blocks of diblock copolymers are interconnected by chemical bonds, microphase separation occurs when the temperature is below a critical point. In the molten state, they can spontaneously assemble into a stable lamellar phase, hexagonal columnar phase, gyroid phase, and spherical phase.1,2 More interestingly, in a selective solvent, block copolymer chains can self-assemble into thermodynamically stable isolated mesoscopic structures, such as spherical, cylindrical or stable vesicle micelles.3,4 The wide applications in catalyst support and as drug delivery carriers have attracted overwhelming interest. Generally, these applications and their performance depend on the structure of the micelles, which can be changed by adjusting the composition of the block copolymers,5–7 solvents,8 polymer concentrations,9 temperature,10 or the external fields.11 The controllable self-assembly and tuning of the morphology of micelles are the major interests in the field.12,13 In particular, cylindrical micelles or worm-like micelles have attracted great attention. They can be used as a template for the arrangement of inorganic nanocrystals to prepare polymer silica and polymer metal oxide nanofibers.3 For sustained drug release, they have been demonstrated to persist in circulation up to one week after intravenous injection, which is approximately 10 times longer than that for the corresponding spherical ones.14 The formation of cylindrical micelles has typically been realized by designing the molecular structures and varying the molecular weights of the soluble and insoluble segments.15 Moreover, some methods for the preparation of cylindrical micelles have recently been demonstrated, including kinetic control and the use of interfacial instabilities.16Wu et al. demonstrated an efficient method to obtain cylindrical micelles by extruding spherical micelles through nanopores. In this way, large-scale worm-like cylindrical micelles can be obtained.14 They injected the spherical micelles through a membrane with an airtight syringe, and many cylindrical micelles were observed when the micelle solution was extruded through the membrane. They were entangled together with lengths up to several micrometers. However, with further observation, the cylindrical micelles were metastable and broke into spherical micelles for a period of time after extrusion.17 In addition to the polymeric system, a similar flow-induced worm-like micelle structure was observed in a surfactant system.18 This method was successfully used to synthesize a Au nanoparticle array in a worm-like micelle.19 The method of using a template to obtain a worm-like micelle without extrusion was proposed by Russell et al. They introduced polystyrene-b-poly(ethylene oxide) (PS-b-PEO) solution into the cylindrical nanopores of an AAO template. After solvent evaporation and selective removal of the AAO template, nanotubes were prepared due to Rayleigh instability.20 The transition from the unstable cylindrical micelles formed by diblock copolymers to nanospheres or complex order structures driven by the Rayleigh instability were extensively studied in the experiment.21–23 In an experiment on cold drawing of multimaterial polymeric fibers, the confinement size kept decreasing and the confined cylindrical fiber broke into spheres,24 which is a reverse procedure of that in Wu's experiments.25 The procedure involves a confined cylinder without the external stress.
The spherical shell, which forms the free energy barrier of the spherical micelles, prevents micelles from fusing into cylindrical micelles. In the experiment, the fluid pressure is used to overcome the barrier between the spherical micelles and to make spheres fuse together.14 When spherical micelles are extruded into the channel, the confinement effect of the channel is a uniaxial constraint that elongates the spherical micelles and causes them to lose isotropic symmetry. This may be the reason that the cylindrical confinement promotes the sphere-to-cylinder morphological transition.
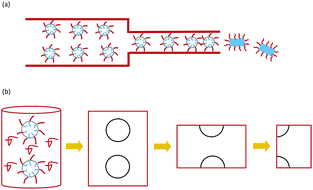
One of the fundamental research interests of controllable self-assembly is to control the pathways of micelle fusion in an external field. The kinetic pathways of micelle fusion were investigated by scattering experiments, and some kinetic mechanisms were proposed by the experiments.23,26,27 Quantitative studies on the mechanism of micelle transformation are especially absent and particularly important. Phase transitions of confined spherical micelles under extrusion were performed only by experiments. Theory and simulation were employed to study the effect of uniaxial confinement on self-assembly without an external pressure field.28 In this work, we investigate the process of extruding spherical micelles through nanopores to form cylindrical micelles (as shown in Fig. 1(a)) by numerical simulation of a self-consistent mean-field theory.
Model and theory
Here the external pressure-induced fusion transition of spherical micelles in the cylindrical channel is considered. The external pressure increases the packing density of the spherical micelles in the channel and provides the driving force to overcome the free energy barrier of fusion. In the present work, the packing density characterized by the average center distance between neighboring spherical micelles, Δz, as indicated in Fig. 2, is considered as the strength of the external field. Namely, a small Δz means high pressure. A numerical simulation of the experimental phenomenon in which spherical micelles transformed into cylindrical micelles in a cylindrical channel under the pressure of liquid flow is performed to analyze the evolution of the morphology and free energy of the micelles. We consider diblock copolymers consisting of two kinds of monomers, A and B, dissolved in a homopolymer solvent. For simplicity, the homopolymer solvent also consists of monomer A. When the copolymer concentration reaches a critical value, the diblock copolymer chain will spontaneously assemble into spherical micelles. Because the B blocks are repulsive to the solvent, the A blocks form the shell of spherical micelles, and the B blocks constitute the core.29,30 The infinite length of the cylindrical channel is considered, and the end effect of the channel is ignored. Although the phenomenon involves the interaction of a pile of spherical micelles in a cylindrical channel, it is sufficient to compute the responsive behavior of the adjacent spheres by virtue of the periodicity. Moreover, each sphere has mirror symmetry with respect to the cross-section perpendicular to the z-axis and through the center of sphere. Therefore, we only consider the fusion of two halves of the micelles.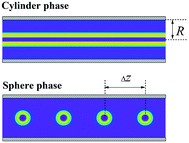 | ||
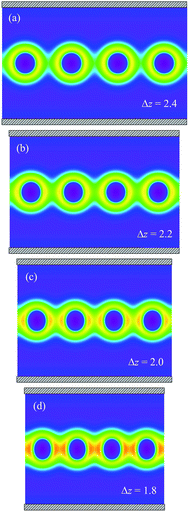
| Fig. 2 The cross-sectional morphologies of cylinder phase and the sphere phase with average center distance Δz = 6 confined in the cylindrical channel with R = 3. | ||
We vary Δz to simulate the different external field strengths and compute the free energy of different phases to investigate the transition from spherical micelles to cylindrical micelles. Assuming that the system has longitudinal symmetry, we compute in cylindrical coordinates and only consider the radial direction r and the axial direction z as shown in Fig. 1(b). Because of this assumption of the rotational symmetry about the axis of the channel, only the straight cylinder phase can be considered in present work. The deformations of the cylinder for example, buckle or split of the cylinder phase, and the packing of spherical micelles with longitudinal symmetry in the channel have not been studied.
Based on the morphology of the cross-section, the density distribution of different components in the whole section can be constructed according to the symmetry. Hereafter, for the clarity of demonstration of the linear packed spherical micelles in the channel, the morphologies of the corona formed by block A of four adjacent spheres are presented according to symmetry, for example the spherical micelles as shown in Fig. 2.
Now, we consider both diblock copolymer chains and homopolymer chains as soft Gaussian chains, and all chains consist of N monomers. Block A in the diblock copolymer is denoted as cA with relative length f = 0.7; block B in the copolymer is denoted as B. The homopolymer consists of monomers A and is denoted as hA. The auxiliary field affecting species α (α = cA, B, hA) is noted as ωα. The symbol χ is used to denote the Flory-Huggins interaction parameter between the two monomers A and B. Here, we choose χN = 20. In this condition, the spherical micelles are stable phase in the bulk solution.31 The micelles are confined in a channel with radius, R. The incompressibility of the polymer solution is considered. According to self-consistent mean field theory (SCMFT), the excluded volume interaction can be converted to the effect produced by an external field on a single chain. The incompressible assumption is commonly used in the SCMFT of the polymeric system, which is consistent with the real system. In present system, the phase behaviors are determined by the effects from the confinement effect and the external pressure on the shapes of the micelles. When the compressible effect is considered, the effect of the confinement and the external pressure will be weaken and the micelles tend to maintain the shape as that in the bulk solution.
The density of block α (α = cA, B, hA) is ϕα. qβ (β = A, B), and 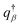 are the propagators starting from s = 0 and s = 1. μc is the chemical potential of the diblock copolymer and ξ is a pressure-like field. The self-consistent field equations can be formulated in cylindrical coordinates,31
are the propagators starting from s = 0 and s = 1. μc is the chemical potential of the diblock copolymer and ξ is a pressure-like field. The self-consistent field equations can be formulated in cylindrical coordinates,31
| ωA(r,z) = χNϕB(r,z) + ξ(r,z), | (1) |
| ωB(r,z) = χN[ϕcA(r,z) + ϕhA(r,z)] + ξ(r,z), | (2) |
| ϕcA(r,z) + ϕhA(r,z) + ϕB(r,z) = 1, | (3) |
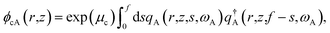 | (4) |
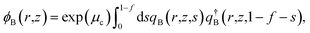 | (5) |
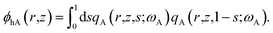 | (6) |
The propagator function satisfies the following modified diffusion equations (MDEs) in cylindrical coordinates
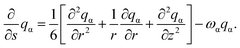 | (7) |
The initial conditions are
| qα(r,z,0) = 1, | (8) |
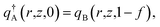 | (9) |
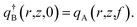 | (10) |
Now we add the boundary conditions as
| qα|r=R= 0, | (11) |
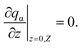 | (12) |
The MDE is a parabolic equation in a two-dimensional domain. Now, we select the alternating direction implicit method to solve the equation. The free energy of the system in cylindrical coordinates is
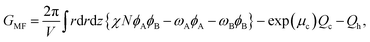 | (13) |
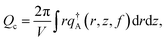 | (14) |
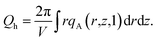 | (15) |
The relative free energy is
| ΔG = GMF − GH, | (16) |
Results and discussion
We consider the condition that the bulk solution is at the critical micelle concentration (CMC), where the free energies, ΔG, of the homogeneous phase and the isolated spherical micelle are equal. We use the morphology of equilibrium spherical micelles in the cylindrical channel obtained from SCMFT as the initial condition. The initial density of the spherical micelle state with an interval of Δz = 6 is considered to be the isolated micelle state, and it has the same free energy as the homogeneous phase because of the CMC.When the channel radius is much larger than that the spherical micelle radius, for example, R = 3, the confinement effect can be ignored. For low-pressure conditions, Δz = 6, as shown in Fig. 2(b), the spheres can be considered as isolated micelles. Their morphology keeps an isotropic shape as in the bulk solution. For the high-pressure condition, as in the extrusion process of Wu experiment, the spheres are compressed. We present four typical morphologies during the evolution of the spherical micelles in Fig. 3 as the packing density is increased. For Δz = 2.4, the coronas of the spheres start to contact with their neighbors. For a higher density Δz < 2.4, the spheres shrink along the axial direction of the channel. Their cores are deformed into ellipsoid shapes, and their coronas overlap with their neighbors. The density of the overlapping region between adjacent spherical micelles increases, which gives rise to the restoring strain to the external pressure and increases the free energy. These responsive behaviors are enhanced by increasing the packing density, e.g., the morphologies of Δz = 2.0 and Δz = 1.8 shown in Fig. 3(c) and (d), respectively.
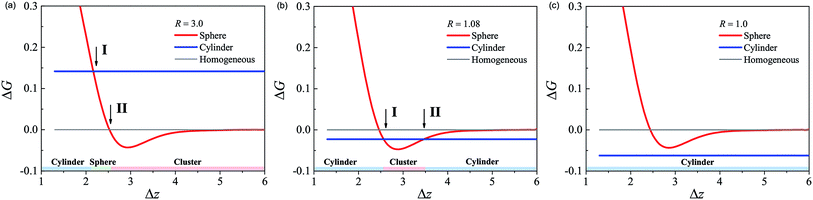
The free energy of the corresponding compressing procedure in a large channel is computed as a function of Δz (red curve in Fig. 4(a)). When Δz ≫ 1, there is no interaction between adjacent spherical micelles. As the packing density increases, i.e., Δz decreases, the free energy of the spherical micelles decreases and is lower than that of the homogenous phase. This means that the spheres attract each other. Comparing the free energy of the homogenous phase (gray line) and spherical phase, there is an intersection (denoted as II) between the two energy curves, as shown in Fig. 4(a), which corresponds to ΔzII = 2.55. For Δz > ΔzII, there is an attractive potential well. This attraction is due to the depletion effect induced by the homopolymer solvent. When the gaps between adjacent spheres are smaller than the size of the homopolymer, it is difficult for the homopolymer chains to enter the space between the spherical micelles. The osmotic pressure difference between the crowded micelles and the bulk solution provides the effective attractive potential between neighboring micelles. By virtue of this attraction, the spherical micelles in the channel are all correlated with their neighbors and tend to form a linear cluster structure for Δz > ΔzII. In the equilibrium linear cluster, the optimized interval distance zc between the neighboring micelles due to the attraction is determined by the minimum of the potential well. For Δz < ΔzII, the depletion effect induced by the attraction can be ignored, and the behavior of the system is mainly from the compression of the spherical micelles, as shown in Fig. 3. Therefore, ΔzII is considered as the boundary between the linear cluster structure and the compressed spherical phase.
To determine the bound of the fusion transition of the spheres, the free energy of the spherical phase depending on packing density (red curve) is compared with the free energy of the cylindrical phase (blue line) for R = 3.0 in Fig. 4(a). The intersection between these two curves (labeled as I) occurs at ΔzI = 2.15. For high pressure, Δz < ΔzI, the free energy of the cylindrical phase is lower than that of the spherical phase. The morphologies of the spherical phase corresponding to the z before and after the fusion transition point are compared in Fig. 3(c) and (d). If we reduce the center distance from ΔzII to ΔzI, it can be seen that the overlap of the coronas of the adjacent spherical micelles significantly increases the free energy. However, it is still lower than that of the cylindrical phase but higher than that of the homogenous phase. An alternative way is that blocks A in the corona are pushed to the side of the channel to decrease the excluded volume interaction in the overlapping region. The compromise is the extra cost of stretching blocks B in the core. Therefore, the free energy of the cylindrical phase in this situation is still higher than that of the homogeneous phase and the isolated spherical micelles. This free energy cost is the active energy of the fusion transition between spherical micelles. In this large channel situation, ΔG = 0.14 is the height of the barrier.
When the channel radius decreases, the behavior of the spherical micelles, i.e., the depletion-induced attractive interaction and response to the compression, is similar to that in a channel with radius of R = 3.0. The cylindrical channel acts as a template with uniaxial symmetry. This constraint competes with the original isotropic symmetry of the spherical micelle. However, the free energy of the cylindrical phase decreases as the channel narrows. The uniaxial constraint decreases the free energy cost of the stretching of B block in the core to form the cylindrical phase. As a consequence, the activation energy of the spherical phase to the cylindrical phase decreases. For a small channel size, e.g., R = 1.0 shown in Fig. 4(c), the free energy of the cylindrical phase is lower than that of the spherical phase for all packing densities but lower than that of the homogenous phase. In this situation, the cylindrical phase will be formed spontaneously without the help of external pressure. This cylindrical phase is stable in the channel. If the channel is etched, the cylindrical micelles in bulk solution will be unstable, and the Rayleigh instability will drive the cylindrical micelles to break into spheres. This mechanism is used to synthesize spherical micelles from cylindrical micelles in experiments.21,22
Because the free energy of the cylindrical phase can be tuned continuously by varying the size of the channel, under the channel condition with some moderate radius, the free energy line of the cylindrical phase will have two intersections with the potential well on the free energy curve of the spherical phase. For example, with R = 1.08 as shown in Fig. 4(b), the two intersections are located ΔzI = 2.55 and ΔzII = 3.5. The free energy of the cylindrical phase is less than that of the spherical phase with center distances Δz > 3.5 and Δz < 2.55. Thus, the cylindrical micelle is more stable than the homogenous phase. However, for the average center distance Δz ∈ [2.55, 3.5], the linear clustered micelle phase is stable due to the depletion effect. Since the cylindrical phase is more stable than the spherical phase for both isolated and dense packing conditions, the spherical micelles fuse into a cylindrical micelle after they are just extruded into the channel. After a sufficiently long time, the cylindrical micelle will break into spherical micelles and form linear clusters spontaneously, since the clustered micelles are more stable than cylindrical micelles. This is the Rayleigh instability effect in a confined system under the external field.
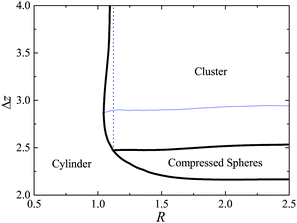
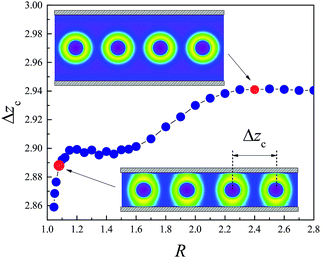
To obtain the phase behavior of confined spherical micelles under fluid pressure, SCMFT equations with different channel radii are computed, and the transition points Δz are determined according to the method mentioned above. In this phase diagram, Δz−1 is used to characterize the strength of the external field. The phase bound between the compressed spherical micelles and the cylindrical micelles, as well as the clustered and compressed spherical micelles are described by Δz as a function of the channel radius R, as shown in Fig. 5. For the large channel radius situation, e.g. R > 2.0, the phase bounds are almost unchanged with the decrease in the channel radius. In this region, the uniaxial template effect of the channel is too weak to affect the free energy barrier of the fusion between different micelles. In the region of 1.12 < R < 2, the bound of the center distance Δz between the compressed spherical and cylindrical micelles varies remarkably with R. Namely, as the radius of the channel is comparable to that of the micelle size, the constraint starts to decrease the free energy cost of forming the cylindrical micelle. As a consequence, a lower external field strength is needed for the compressed spherical micelles to overcome the free energy barrier to fuse into the cylindrical micelles. The bound between the cluster and compressed sphere is almost unchanged, except for the case 1.05 < R < 1.12, where it decreases slightly. This indicates that the confinement constraint mainly affects the free energy of the cylindrical micelle and has little effect on the spherical micelle. There is a triple-phase point R* = 1.12, which is the intersection between the bounds of the cylinder/cluster, compressed sphere/cluster, and cylinder/compressed sphere. For the CMC condition, it is determined by the radius at which the cylindrical micelle and the homogeneous phase have the same free energy. When the channel radius R ∈ (1.05, 1.12), there are two bounds of the center distance between the clustered and cylindrical micelles for a given R. Although the cylindrical phase is stable, the sphere cluster phase will reform due to the effect of the Rayleigh instability. When the radius of the channel is less than 1.05, cylindrical micelles are stable, and the effect of the uniaxial constraint of the channel dominates the phase behavior. The cylindrical phase can be formed spontaneously once the solution is extruded into the channel.
Under low external pressure, the spheres confined in the channel are correlated with each other by the depletion effect and form a linear chain. Although the formation of clusters of spheres is due to the addition of the homopolymer solvent and has not been observed in experiments, it is interesting to study the structure of the linear sphere cluster. The morphologies of two typical sphere clusters are shown in the insets of Fig. 6, corresponding to the large channel (R = 1.08) and the small channel (R = 2.4) conditions. For the large channel, the spherical micelles maintain their shape. The homopolymer chains are depleted from the interval region between the adjacent spheres. The confinement of the channel has little effect on the structure of the cluster. For the small channel, the shells of the spheres are deformed significantly to a cylindrical rod, while the cores still maintain a spherical shape.
The average center distance Δzc of the adjacent clustered micelles characterizes the equilibrium structure of the linear cluster of spheres. It is determined by the minimum of the free energy curve. Fig. 6 shows that Δzc depends on the radius of the channel, R. Δzc is almost invariant for R > 2.3 where the confinement of the channel can be ignored. For R < 2.3, the channel starts to affect the volume between the adjacent spheres and accordingly affect the entry of the homopolymers. As R decreases, this volume continues to decrease, and then the osmotic pressure difference induced by the depletion effect is enhanced. As a consequence, Δzc reduces, when R decreases from 2.3 to 1.5. Namely, the equilibrium structure of the sphere cluster becomes denser as the radius of the cylinder decreases. However, when R < 1.5, the spherical micelles in the cluster contact the channel and their become a short cylindrical rod, e.g., for R = 1.08 as shown in the inset of Fig. 6. The volume between the adjacent micelles is almost unchanged for R ∈ [1.2, 1.5]. As R further decreases, the core of the micelle becomes ellipsoidal in shape in the reentry region, and correspondingly, the average center distance Δzc decreases dramatically.
Summary
In this work, spherical micelles formed by diblock copolymers in a homopolymer solvent extruded through a cylindrical channel are studied theoretically by solving SCMFT equations. In the extrusion process, spherical micelles can fuse and become cylindrical micelles driven by external pressure. The result shows that the uniaxial confinement decreases the free energy cost of forming the cylindrical micelle, which decreases the energy barrier of fusion. In addition to fusion, a linear cluster of spheres can be formed by the depletion effect induced by the attractive interaction between adjacent spherical micelles. The phase diagram of the fusion and clustering transitions depends on the external pressure and confinement size. Moreover, the structure of the linear cluster of spheres depends on the radius of the channel and the possible mechanism is discussed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
X.H. Zhang is partly supported by the National Natural Science Foundation of China (NSFC) Nos. 21774013, 21574011, Beijing Natural Science Foundation No. 2182057, and the Fundamental Research Funds for the Central Universities No. 2018JBM071. H. Zhang is supported in part by the grants NSFC-11471046 and 11571045.References
- C. M. Bates and F. S. Bates, 50th Anniversary perspective: block polymers potential, Macromolecules, 2017, 50, 3–22 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Block copolymers-designer soft materials, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- M. Lazzari, G. J. Liu and S. Lecommandoux, Block Copolymers in Nanoscience, Wiley-VCH, 2006, pp. 191–231 Search PubMed.
- S. Jain and F. S. Bates, On the origins of morphological complexity in block copolymer surfactants, Science, 2003, 300, 460–464 CrossRef CAS PubMed.
- A. G. Daful, J. B. Avalos and A. D. Mackie, Model shape transitions of micelles: spheres to cylinders and disks, Langmuir, 2012, 28, 3730–3743 CrossRef CAS PubMed.
- L. Zhang, K. Yu and A. Eisenberg, Ion-induced morphological changes in “Crew-Cut” aggregates of amphiphilic block copolymers, Science, 1996, 272, 1777 CrossRef CAS PubMed.
- L. Zhang and A. Eisenberg, Multiple pH-induced morphological changes in aggregates of polystyrene-block-poly(4-vinylpyridine) in DMF/H2O mixtures, J. Am. Chem. Soc., 1999, 121, 2728–2740 CrossRef.
- J. Bang, S. Jain, Z. Li, T. P. Lodge, J. S. Pedersen, E. Kesselman and Y. Talmon, Erratum: sphere, cylinder, and vesicle nanoaggregates in poly(styrene-b-isoprene) diblock copolymer solutions, Macromolecules, 2006, 39, 1199–1208 CrossRef CAS.
- L. F. Zhang and A. Eisenberg, Thermodynamic vs. kinetic aspects in the formation and morphological transitions of crew-cut aggregates produced by self-assembly of polystyrene-b-poly(acrylic acid) block copolymers in dilute solution, Macromolecules, 1999, 32, 2239–2249 CrossRef CAS.
- P. Bhargava, Y. Tu, J. X. Zheng, H. Xiong, R. P. Quirk and S. Z. Cheng, Temperature-induced reversible morphological changes of polystyrene-block-poly(ethylene oxide) micelles in solution, J. Am. Chem. Soc., 2007, 129, 1113–1121 CrossRef CAS PubMed.
- U. Delabre, K. Feld, E. Crespo, G. Whyte, C. Sykes, U. Seifert and J. Guck, Deformation of phospholipid vesicles in an optical stretcher, Soft Matter, 2015, 11, 6075–6088 RSC.
- A. Rahman, P. W. Majewski, G. Doerk, C. T. Black and K. G. Yager, Non-native Three-dimensional Block Copolymer Morphologies, Nat. Commun., 2016, 7, 13988 CrossRef PubMed.
- I. A. B. Pijpers, L. K. E. A. Abdelmohsen, D. S. Williams and C. M. V. Hest, Morphology Under Control: Engineering Biodegradable Stomatocytes, ACS Macro Lett., 2017, 6, 1217–1222 CrossRef CAS PubMed.
- Q. Chen, H. Zhao, J. Ming, T. Wang and C. Wu, Nanopore extrusion-induced transition from spherical to cylindrical block copolymer micelles, J. Am. Chem. Soc., 2009, 131, 16650–16651 CrossRef CAS PubMed.
- L. Shen, H. Wang, G. Geurin, Q. Wu, I. Manners and M. A. Winnik, A micellar sphere-to-cylinder transition of poly(ferrocenyldimethylsilane-b-2-vinylpyridine) in a selective solvent driven by crystallization, Macromolecules, 2008, 41, 4380–4389 CrossRef CAS.
- H. G. Cui, Z. Y. Chen, S. Zhong, K. L. Wooley and D. J. Pochan, Block copolymer assembly via kinetic control, Science, 2007, 317, 647–650 CrossRef CAS PubMed.
- Q. J. Chen, Y. Li and C. Wu, How Long Cylindrical Micelles Formed after Extruding Block Copolymer in a Selective Solvent through a Small Pore Fragment back into Spherical Ones, Macromolecules, 2013, 46, 9164–9167 CrossRef CAS.
- M. Vasudevan, E. Buse, D. Lu, H. Krishna, R. Kalyanaraman, Q. Shen, B. Khomami and R. Sureshkumar, Irreversible nanogel formation in surfactant solutions by microporous flow, Nat. Mater., 2010, 9, 436–441 CrossRef CAS PubMed.
- Q. Chen, J. Wang and L. Shao, Nanoparticle-loaded cylindrical micelles from nanopore extrusion of block copolymer spherical micelles, Macromol. Rapid Commun., 2013, 34, 1850–1855 CrossRef CAS PubMed.
- D. Chen, S. Park, J. T. Chen, E. Redston and T. P. Russell, A simple route for the preparation of mesoporous nanostructures using block copolymers, ACS Nano, 2009, 3, 2827–2833 CrossRef CAS PubMed.
- S. Mei, X. Feng and Z. Jin, Fabrication of polymer nanospheres based on Rayleigh instability in capillary channels, Macromolecules, 2011, 44, 1615–1620 CrossRef CAS.
- N. Yan, Y. Sheng, H. Liu, Y. Zhu and W. Jiang, Templated self-assembly of block copolymers and morphology transformation driven by the Rayleigh instability, Langmuir, 2015, 31, 1660 CrossRef CAS PubMed.
- L. Wang, H. Huang and T. He, Rayleigh instability induced cylinder-to-sphere transition in block copolymer micelles: direct visualization of the kinetic pathway, ACS Macro Lett., 2014, 3, 433–438 CrossRef CAS.
- S. Shabahang, G. Tao, J. J. Kaufman, Y. Qiao, L. Wei, T. Bouchenot, A. P. Gordon, Y. Fink, Y. Bai and R. S. Hoy, Controlled fragmentation of multimaterial fibres and films via polymer cold-drawing, Nature, 2016, 534, 529–533 CrossRef CAS PubMed.
- J. Xu, K. Wang, R. Liang, Y. Yang, H. Zhou, X. Xie and J. Zhu, Structural Transformation of Diblock Copolymer/Homopolymer Assemblies by Tuning Cylindrical Confinement and Interfacial Interactions, Langmuir, 2015, 31, 12354–12361 CrossRef CAS PubMed.
- L. M. Bergstrom, Second CMC in surfactant micellar systems, Curr. Opin. Colloid Interface Sci., 2016, 22, 46–50 CrossRef.
- R. Lund, L. Willner, D. Richter and T. Narayanan, Kinetic pathway of the cylinder-to-sphere transition in block copolymer micelles observed in situ by time-resolved neutron and synchrotron scattering, ACS Macro Lett., 2013, 2, 1082–1087 CrossRef CAS.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A. C. Shi, Confinement-induced novel morphologies of block copolymers, Phys. Rev. Lett., 2006, 96, 138306 CrossRef PubMed.
- A. Cavallo, M. Mueller and K. Binder, Formation of micelles in homopolymer-copolymer mixtures: quantitative comparison between simulations of long chains and self-consistent field calculations, Macromolecules, 2006, 39, 9539–9550 CrossRef CAS.
- Z. Wu, B. Li, Q. Jin, D. Ding and A. C. Shi, Microphase and Macrophase Separations in Binary Blends of Diblock Copolymers, Macromolecules, 2011, 44, 1680–1694 CrossRef CAS.
- J. J. Zhou and A. C. Shi, Critical micelle concentration of micelles with different geometries in diblock copolymer/homopolymer blends, Macromol. Theory Simul., 2011, 20, 690–699 CrossRef CAS.
Footnote |
| † Current address: No. 19 Street of XinJieKouWai, District Haidian, Beijing, 100875, China. |
| This journal is © The Royal Society of Chemistry 2019 |