Open Access Article
Open Access ArticleAn insight into the intermolecular vibrational modes of dicationic ionic liquids through far-infrared spectroscopy and DFT calculations†
Luca
Guglielmero
a,
Lorenzo
Guazzelli
 a,
Alessandra
Toncelli
b,
Cinzia
Chiappe‡
a,
Alessandro
Tredicucci
a,
Alessandra
Toncelli
b,
Cinzia
Chiappe‡
a,
Alessandro
Tredicucci
 bc and
Christian Silvio
Pomelli
bc and
Christian Silvio
Pomelli
 *a
*a
aDept. of Pharmacy, University of Pisa, Via Bonanno 33, 56126 Pisa, Italy. E-mail: christian.pomelli@unipi.it
bDipartimento di Fisica “E. Fermi” and Istituto Nanoscienze CNR, Università di Pisa, Largo Bruno Pontecorvo, 56127 Pisa, Italy
cLaboratorio NEST, Scuola Normale Superiore, Piazza San Silvestro 12, 56127 Pisa, Italy
First published on 25th September 2019
Abstract
Dicationic ionic liquids (DILs) are a subclass of the ionic liquid (IL) family and are characterized by two cationic head groups linked by means of a spacer. While DILs are increasingly attracting interest due to their peculiar physico-chemical properties, there is still a lack of understanding of their intermolecular interactions. Herein, we report our investigations on the intermolecular vibrational modes of two bromide DILs and of a bistriflimide DIL. The minimal possible neutral cluster of ions was studied as a simplified model of these systems and was optimized at the DFT level. Normal modes of two sandwich-like conformers were then calculated using the harmonic approximation with analytical computation of the second derivatives of molecular energy with respect to the atomic coordinates. The calculated spectra were compared to far-infrared experimental spectra and two groups of peaks over three, for the two bromide DILs, and three over five, for the Tf2N− DIL, were described by the proposed neutral cluster model. Therefore, this model represents a reliable and computationally affordable model for the exploration of the intermolecular interactions of this kind of system.
Introduction
Ionic liquids (ILs) are organic salts composed of an organic cation and an organic or an inorganic anion which are liquid below 100 °C. The physico-chemical properties of these neoteric solvents (e.g., negligible vapor pressure, wide electrochemical window, high thermal stability, low flammability)1–3 and the possibility to tweak them by changing the constituent ions4 allowed their use in different fields. ILs have been studied and exploited for instance in the dissolution, fractionation and functionalization of biomasses,5–8 in organic synthesis,9,10 in analytical chemistry,11 in electrochemistry12,13 and, more recently, in biological and pharmaceutical applications.14Dicationic ionic liquids (DILs) are a subclass of ILs which are characterized by two cationic head groups linked to one another by means of a spacer. After the pioneering studies by Ohno et al.15,16 and Armstrong et al.,17 DILs raised the interest of several research groups which investigated their potential field of applications,18–20 also in comparison with the parental monocationic ILs (MILs). In fact, the most interesting aspect of DILs, which usually require a more demanding synthetic effort, is the possibility to capitalize on application-oriented advantages over the corresponding MILs. From a structural perspective, the additional variability options of DILs stem from the type and length of the linker between the two cations and/or from the nature of the cation, as asymmetric structures are also possible.
A few works indicated that DILs behave in a different way from the structurally related MILs when tested in the same application. For instance, it has been found that some DILs are characterized by lower polarity and different structural organizations,21 higher thermal stabilities,22 lower ecotoxicities,23 higher activity in the cycloaddition of CO2 to epoxides,24 higher or lower cathodic reductions, depending on the type of spacer.25
The physico-chemical properties of ILs, and accordingly their potential applications, are strictly governed by the type and strength of the interaction between the constituent ions. Intermolecular forces between cation and anion determine the presence of expanded network structures such as larger clusters or ion-pairs in the liquid phase. In the pursue of a deeper understanding of the interactions and structures of ILs, vibrational spectroscopy represents an invaluable option.26
The frequency range between 2 and 300 cm−1 involves intermolecular forces and can be studied by different experimental methods such as optical heterodyne-detected Raman-induced Kerr-effect spectroscopy (OHD-RIKES),27–32 dielectric relaxation spectroscopy (DRS),32–34 terahertz (THz) spectroscopy,35–39 low-energy neutron scattering,40 X-ray diffraction,41 far infrared (FIR) spectroscopy and Raman spectroscopy.36,38,42–47 It is worth mentioning that ILs' experimental spectra are usually difficult to interpret as a result of the complex combination of overlapping bands. Therefore, theoretical methods are often needed to assign specific vibrational motions.
For what concerns THz and FIR spectroscopy, a few studies have been performed mainly on imidazolium ILs [C1C2IM or C4C1IM and different anions]35–37 or ammonium protic ILs.48 The first evidence of +C–H⋯A− hydrogen bonding was reported by Fumino et al.42 The same authors showed that the vibrational frequency shifts, observed with different ILs, cannot be explained by mass effects and are rather a result of different anion–cation force constants.36,42 Although the interpretation of these experimental spectra is not always univocal,26 the potential of FIR-THz spectroscopy in broadening the understanding of the interactions between the ILs constituting ions has been demonstrated.
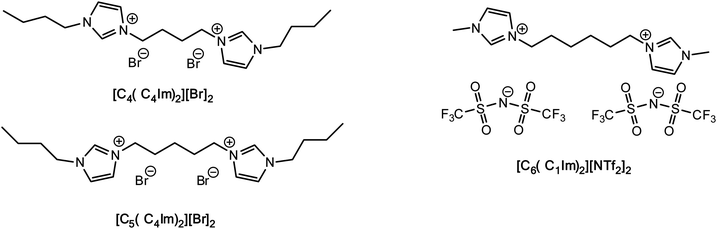
To the best of our knowledge, no data are available for the FIR-THz intermolecular vibrational modes of DILs, while some work based on OHD-RIKES has shed some light on the interionic interactions of these systems.37 Given the increasing interest in DILs, here we present our investigations on their intermolecular interactions by means of FIR spectroscopy, corroborated by DTF analyses. Our work focuses on one imidazolium dibistriflimide DIL ([MIC6IM]2+ + 2Tf2N−) and two imidazolium dibromide DILs ([BIC4IB]2+ + 2Br− and [BIC5IB]2+ + 2Br−), which differ for the length of the linker (Fig. 1). The former DIL has been studied before by OHD-RIKES, while the latter are model structures of dibromide DILs which are liquid at room temperature.
Results and discussion
The three dicationic ionic liquids (DILs) based on imidazolium charged centers were studied at the ab initio level.The simulation of the complex phenomena that occur in such an intricate system like a dicationic ionic liquid, where charged moieties, some with several degrees of freedom, interact with each other, is a challenging task. In this paper, we will limit ourselves to a simple model system which corresponds to the minimal possible neutral cluster of ions: one dication and two single charged anions. Therefore, we will not be able to rationalize and explain all the features of the experimental spectra. However, the features predicted by this model are surely related to molecular motions of this simplified system, while the remaining ones will be likely related to motions that involve larger clusters.
When the molecular nature of these dications is taken into consideration, the most stable structure is a sandwich-like one where the two imidazolium rings assume a parallel arrangement. The distance and the relative orientation of the two parallel rings depend on the length of the linker and on the size of the non-linked sidechains. The monoatomic anions, for example bromides, can establish a larger number of interactions with the acidic hydrogens of the dication moiety compared to the corresponding monocationic ILs (all hydrogens in α to the nitrogen atoms, including those present on the aliphatic chains). In the resulting structure, the anions are sandwiched between the imidazolium fragments and positioned in such a way to maximize their distance. Some starting geometries fulfilling these considerations with different initial positions of the anions have been prepared and optimized at the DFT level. The structures with lower energy present the two anions diametrically opposed. Thus, we focalize on them. Some higher energy structures have been discarded. The resulting local minima are, in this case, not too different, from the qualitative point of view, from the initial geometric guess.
There are two possible conformational isomers as the two imidazolium rings can be arranged in two different spatial ways: with the C2 atoms on the same side of the sandwich (syn conformer) or on the opposite side (anti conformer). The two conformations present a relevant difference in energy in the [BIC5IB]2+ + 2Br− case only (See Table 1), but differ in the value of the molecular dipole. The anti conformer, the more energetically favored, is characterized by a smaller dipole, while the syn conformer is less stable with a larger dipole. The latter conformer is expected to have stronger cluster–cluster interactions. As a result of the dipole quenching in anti structures, this conformer presents the two rings almost parallel, while in the syn conformer the two aromatic moieties form a dihedral angle (C2 atoms are closer than C4 and C5 atoms).
| [BIC4IB]2+ + 2Br− | [BIC5IB]2+ + 2Br− | [MIC6IM]2+ + 2Tf2N− | ||||
|---|---|---|---|---|---|---|
| syn | anti | syn | anti | syn | anti | |
| a Average value. | ||||||
| ΔE/(kJ mol−1) | 1.22 | 0.00 | 19.98 | 0.00 | 3.08 | 0.00 |
| x (300 K) | 0.38 | 0.62 | 0.0003 | 0.9997 | 0.33 | 0.67 |
| μ/D | 6.76 | 1.47 | 6.11 | 3.18 | 5.98 | 2.79 |
| Torsion angle | −19.95 | −9.82 | 16.94 | −13.10 | 39.16 | 23.16 |
| N1–N1 | 4.42 | 4.46 | 4.88 | 4.77 | 6.03 | 6.00 |
| C2–C2 | 4.87 | — | 5.13 | — | 6.34 | — |
| C2–C5a | — | 4.88 | — | 5.22 | — | 6.12 |
| N3–N3 | 5.27 | 5.13 | 5.43 | 5.50 | 6.50 | 5.87 |
| A–A | 7.19 | 7.23 | 6.80 | 7.02 | 8.16 | 8.52 |
| H2–Y | 2.99 | 2.76 | 2.90 | 2.75 | 2.83 | 2.36 |
| 2.69 | 2.59 | 2.59 | 2.62 | 2.23 | 2.29 | |
| H5–Y | 2.58 | 2.76 | 2.65 | 2.79 | 2.12 | 2.20 |
| 2.62 | 2.76 | 2.99 | 3.04 | 2.79 | 2.56 | |
A third possible conformation is an open one where the two rings interact with rings belonging to different dications. The anions are placed as usually near the two rings. We have tried to optimize this kind of structure but it collapses into the closed one. In the minimal cluster system, this kind of structure is not stable but it can exist in the bulk ionic liquid. Thus, this kind of extended structure, resembling a unit of a coordination polymer, cannot be studied with this approach. It is conceivable that, in organized liquids like those examined here more than one of the structures are relevant and slowly equilibrating. All these three conformations are shown in Fig. 2.
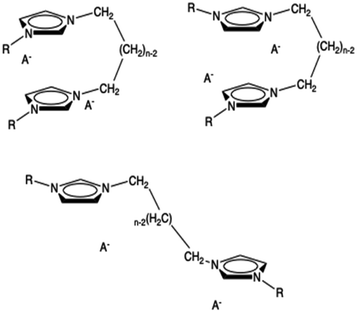 | ||
| Fig. 2 Some possible conformers of a minimal neutral cluster of dicationic ionic liquids: syn (top left), anti (top right), open (bottom). | ||
Normal modes have been calculated using the harmonic approximation with analytical calculation of second derivatives of molecular energy with respect to the atomic coordinates.
The calculations have been performed at the B3LYP/AUG-CC-PVTZ level with empirical corrections for dispersion. The same functional and basis set has been used by Shirota et al.49–51 with good results to compute Raman spectra of similar systems. A direct comparison between our and the above cited papers is not possible. They used ab initio calculations on single anions and cations, not on clusters. Coherently, their dicationic structures present an open geometry due to the absence of the anions. Based on the single ion calculated Raman spectra, they parametrized a theory able to predict non-linear optical properties of the molecules. Furthermore, we do not have calculated Raman intensities and they did not report the infrared ones. Using the ab initio results as starting parameters, they obtained a good agreement with the experimental data, which is an implicit validation of the reliability of the calculations results.
As a final validation of the computational method, optimized geometries and normal modes have been calculated for the [BIC4IB]2+ + 2Br−anti-conformer with two different choices of functionals and basis sets. No qualitative differences have been found. Some data about two of the normal modes discussed later in the paper is reported and discussed in ESI.†
Cluster geometries have been fully optimized. They are available as ESI.†
Even though the harmonic approximation is known to be more reliable for localized molecular motions like atom–atom stretching, and despite, the limited size of the model system used here, the absence of any representation of the solvation bulk, the calculated frequencies of the normal modes closely match the experimental results. Full detailed tables of normal modes frequencies and intensities are reported in the ESI.† In the paper body they will be commented using graphical representation and discussed with an emphasis on groups and range of frequencies.
We analyzed all the normal modes below the threshold of 700 cm−1. A complete list for all the considered systems is shown in ESI.† Few of these normal modes presented a non-negligible intensity.
The match between experimental spectra and the calculated normal frequencies (we choose to not report simulated spectra based on arbitrary line shapes) is represented in Fig. 3.
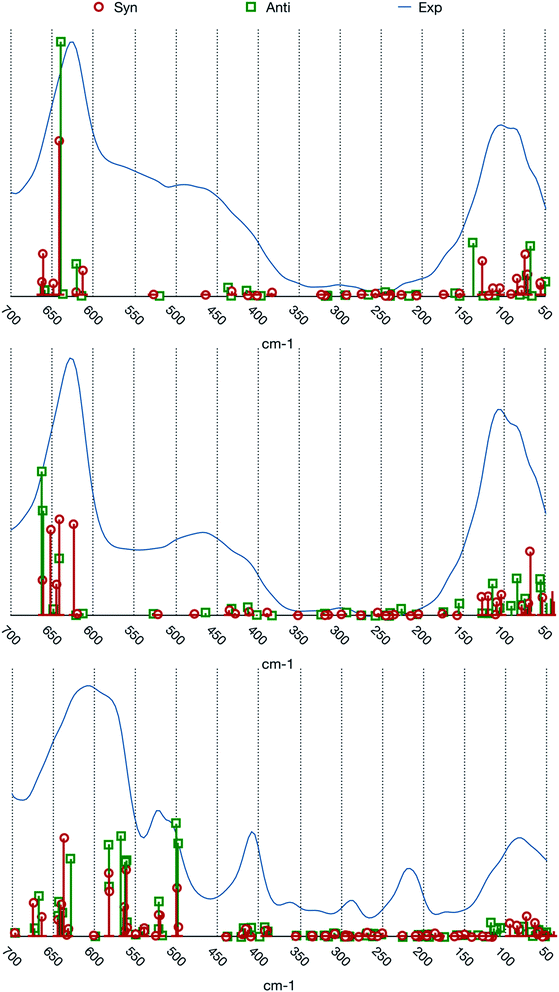 | ||
| Fig. 3 Comparison between the experimental spectra and calculated normal modes frequencies and intensities. From top to bottom: [BIC4IB]2+ + 2Br−, [BIC5IB]2+ + 2Br− and [MIC6IM]2+ + 2Tf2N−. | ||
The two systems with bromide anions will be analyzed first. A first noticeable feature of the experimental spectra, which is also present in the calculated frequencies, is the gap of absorption in the central part of the spectral range. The experimental spectra of these systems are composed by three large bands which are centered at about 100, 450 and 650 cm−1 respectively.
The band at about 100 cm−1 presents a composite structure made up by at least two superimposed peaks. From the computational point of view there is a group of normal modes characterized by large intensities in this range. For both the conformers this group is divided into two subgroups, one that lies at about 80 cm−1 and the other one at about 130 cm−1. This feature reproduces the binary nature of the experimental band.
This group is related to the relative motions between the two rings and the anions. A graphical representation of some of these normal modes is reported in Fig. 4. In all these normal modes the two rings and the two anions display relative motions. The deformation of the rings as well as of the chain is minimal and they behave as almost rigid bodies.
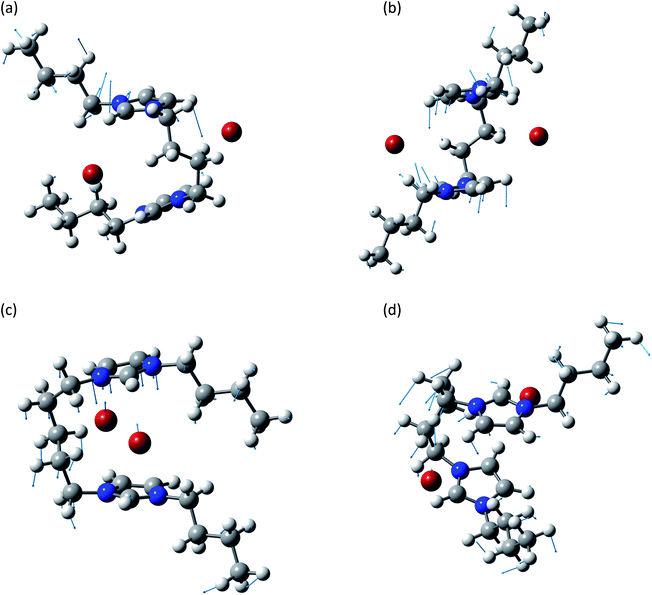 | ||
| Fig. 4 Normal modes are represented by displacement vectors (light blue). Relative lengths of the vectors are in scale with respect to the displacement of the single atoms. The absolute scale is arbitrary (but is constant in all the normal modes represented in this paper). Full scale pictures are available as ESI.† (a) [BIC4IB]2+ + 2Br−syn: normal mode at 126.9 cm−1. The ring rotates about a horizontal axis. (b) [BIC4IB]2+ + 2Br−anti: normal mode at 138.6 cm−1. Synchronous rotation of one ring with respect to the other. (c) [BIC5IB]2+ + 2Br−syn: normal mode at 69.0 cm−1. Parallel displacement of the top ring with respect to the two bromine anions for [BIC5IB]2+. The distance between the two bromine atoms reduces while they approach the ring. (d) [BIC5IB]2+ + 2Br− anti: normal mode at 82.8 cm−1. The two rings rotated about a vertical axis in opposite directions. This corresponds to a rotation of the bromide anions. | ||
The subgroup at lower wavenumbers corresponds to the relative motions of anions and cation. These normal modes are similar to the anion–cation stretching displayed by mono-charged ionic liquids,37 but the presence of the linker introduces additional structured features like the concerted motions of the two bromide anions (Fig. 4c and d).
In the other subgroup, the displacement of the anions, already reduced due to the massive nature of bromine atoms, is basically negligible. These normal modes consist of synchronized relative motions of the two aromatic rings.
It is reasonable to assume that, if we were to search for the minimal energy structure of a model system constituted by two ionic pairs of mono-charged ionic liquids, we would find similar motions. However, the presence of the linker transforms these motions from intermolecular to intramolecular. Furthermore the linker reduces the possible relative distance and orientation of the two imidazolium groups.
The normal modes corresponding to the central band (about 450 cm−1) of the experimental spectra present very small intensities. The molecular motions in this region are related to the relative torsion of the two rings about their vertical axis. This band is possibly also connected to more complex molecular motions typical of larger clusters of ions that cannot be represented by our model system.
The band at about 650 cm−1 corresponds to the infrared active normal modes and presents more of the usual molecular motions such as the out of plane deformation of the rings. The coordinated motions of the two rings and/or of their anions are still present. A graphical representation of some of these normal modes is shown in Fig. 5. With respect to the band at about 100 cm−1, the differences between the syn and the anti structures are greater. This phenomenon arises from the primary role played in these normal modes by the hydrogen atoms bound to the C2, C4 and C5 atoms of the imidazolium rings. Almost all the motions are coordinated amongst the two rings, with variable ratios between the relative amplitudes.
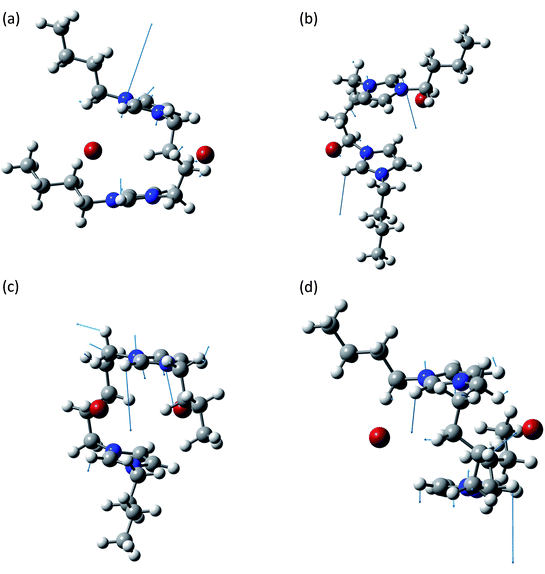 | ||
| Fig. 5 Normal modes are represented by displacement vectors (light blue). Relative lengths of the vectors are in scale with respect to the displacement of the single atoms. The absolute scale is arbitrary (but is constant in all the normal modes represented in this paper). Full scale pictures are available as ESI.† (a) [BIC4IB]2+ + 2Br−syn: normal mode at 641.8 cm−1. In phase out of plane bending of the C2–H bonds. (b) [BIC4IB]2+ + 2Br−anti: normal mode at 639.8 cm−1. In phase out of plane bending of the C2–H bonds. (c) [BIC5IB]2+ + 2Br−syn: normal mode at 624.4 cm−1. Deformation of the top ring. Synchronously the bottom ring shows a similar deformation with smaller amplitude. (d) [BIC5IB]2+ + 2Br−anti: normal mode at 651.1 cm−1. Concerted deformation of both rings. | ||
The system [MIC6IM]2+ + 2Tf2N− (Fig. 6) does not present substantial differences in the above analyzed bands. The normal modes are not represented here because of their graphical complexity. However, this system presents supplementary bands at 500–550 cm−1 and 200–250 cm−1. The first band corresponds to normal modes of deformations of single anions (a motion that does not exist for monatomic anions). There is instead no computation match for the second band. The above written comments about the band at about 450 cm−1 are still valid.
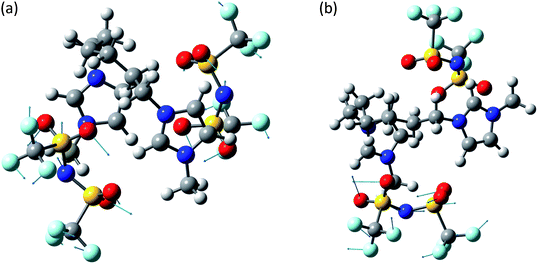 | ||
| Fig. 6 Normal modes are represented by displacement vectors (light blue). Relative lengths of the vectors are in scale with respect to the displacement of the single atoms. The absolute scale is arbitrary (but is constant in all the normal modes represented in this paper). Full scale pictures are available as ESI.† (a) [MIC6IM]2+ + 2Tf2N−syn: normal mode at 498.2 cm−1. Concerted Deformations of the coordinated anions in opposition of phase. There is also a similar, less intense, in phase normal mode at 499.7 cm−1. The calculated intensities differ of about an order of magnitude. (b) [MIC6IM]2+ + 2Tf2N−anti: normal mode at 498.2 cm−1. Deformation of a single coordinated anion. In a very similar normal mode at 500.9 cm−1 the other anion deforms in a nearly identical way. | ||
Conclusions
With this study, we investigated the complex dynamics of dicationic ionic liquids. The minimal neutral cluster proved to be a computationally affordable and a good representation of this kind of systems.Two groups of peaks over three, for the two systems with bromide anions, and three over five, for the Tf2N− anions, can be described by this model system. Therefore, the minimal cluster studied here is a realistic representation of at least a part of the dicationic ionic liquid properties.
The presence of the covalent spacer between the two imidazolium cations allowed us to focus on some motions that in simple monocationic ionic liquids are of an intermolecular nature. The cooperative molecular motions observed here can also take place in a transient mode in mono-charged ionic liquids.
Syn- and anti-conformers present very similar energies in two of the systems considered here. Furthermore, the less stable structure is expected to have stronger cluster–cluster interactions due to its larger dipole. Therefore, normal mode frequencies and intensities between the two conformers are not enough different to exclude the existence of one or the other conformer on the base of infrared data.
This approach can also be expanded to larger cluster of ionic liquids too. However, a different computational strategy must though be devised because of the high computational cost associated with the use of the minimal cluster model.
Experimental section
Materials
1H-Imidazole was purchased from Fluka, 1-methyl-1H-imidazole and 1-butyl-1H-imidazole, 1,5-dibromopentane, 1,6-dibromohexane were purchased from Alfa Aesar, whereas 1,4-dibromobutane from Sigma Aldrich. Lithium bis(trifluoromethylsulfonyl)imide was purchased from IOLITEC. All substances were used as received, without further purification, unless differently specified. 4-Methyl-2-pentanone was purchased from Alfa Aesar, all other organic solvents from Sigma Aldrich. All organic solvents were used without further purifications.Dicationic ionic liquids preparation
3,3′-(Butane-1,4-diyl)bis(1-butyl-1H-imidazol-3-ium) bromide ([BIC4IB]2+ + 2Br−), 3,3′-(pentane-1,5-diyl)bis(1-butyl-1H-imidazol-3-ium) bromide ([BIC4IB]2+ + 2Br−) and 3,3′-(hexane-1,6-diyl)bis(1-methyl-1H-imidazol-3-ium) bis(trifluoromethane)sulfonamide ([MIC6IM]+ + 2Tf2N−) were prepared following previously published procedures.52,53FIR measurements
FIR spectra were recorded with a FT/IR-6800 Fourier Transform Infrared Spectrometer (Jasco).To collect the spectra an appropriate cell was developed and tested in our lab. It consists in a pair of COC polymer plates kept in position by a steel sample holder. Of the two polymer plates one is smooth and the second is hollowed in the middle, in order to guarantee a sample thickness of 100 μm. The sample holder is made by two steel plates (with a 8 mm diameter hole in the center, for transmitting the light beam) which, after inserting the COC cell between them, were tightened by screws.
DFT calculations
All calculation has been performed using the Gaussian 16 suite.54 D3 empirical correction for dispersion has been calculated.55 All the geometries have been fully optimized using the default setting at the B3LYP/ug-cc-pvtz level of theory. The frequencies have been calculated analytically. Two linux based workstations equipped with dual Xeon E5-2640 (10 core CPU) and 128 Gb of RAM have been used.Conflicts of interest
The authors declare that there is no conflict of interest regarding the publication of this article.Acknowledgements
A. T. acknowledges support from the project PRA_2018_34 (“ANISE”) from the University of Pisa.References
- Y. Cao and T. Mu, Ind. Eng. Chem. Res., 2014, 53, 8651–8664 CrossRef CAS.
- D. M. Fox, J. W. Gilman, A. B. Morgan, J. R. Shields, P. H. Maupin, R. E. Lyon, H. C. De Long and P. C. Trulove, Ind. Eng. Chem. Res., 2008, 47, 6327–6332 CrossRef CAS.
- S. Kazemiabnavi, Z. Zhang, K. Thornton and S. Banerjee, J. Phys. Chem. B, 2016, 120, 5691–5702 CrossRef CAS.
- K. Seddon, Chem. Eng., 2002, 730, 33–35 CAS.
- S. S. Silva, J. F. Mano and R. L. Reis, Green Chem., 2017, 19, 1208–1220 RSC.
- I. Palazzo, A. Mezzetta, L. Guazzelli, S. Sartini, C. S. Pomelli, W. O. Parker Jr and C. Chiappe, RSC Adv., 2018, 8, 21174–21183 RSC.
- C. Chiappe, M. J. Rodriguez Douton, A. Mezzetta, L. Guazzelli, C. S. Pomelli, G. Assanelli and A. R. De Angelis, New J. Chem., 2018, 42, 1845–1852 RSC.
- A. Brandt-Talbot, F. J. V. Gschwend, P. S. Fennell, T. M. Lammens, B. Tan, J. Weale and J. P. Hallett, Green Chem., 2017, 19, 3078–3102 RSC.
- J. P. Halett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef.
- C. Chiappe and C. S. Pomelli, Eur. J. Org. Chem., 2014, 6120–6139 CrossRef CAS.
- F. Ghorbanizamani and S. Timur, Anal. Chem., 2018, 90, 640–648 CrossRef CAS.
- M. M. Huie, R. A. Dileo, A. C. Marschilok, K. J. Takeuchi and E. S. Takeuchi, ACS Appl. Mater. Interfaces, 2015, 7, 11724–11731 CrossRef CAS.
- M. Longhi, S. Arnaboldi, E. Husanu, S. Grecchi, I. F. Buzzi, R. Cirilli, S. Rizzo, C. Chiappe, P. R. Mussini and L. Guazzelli, Electrochim. Acta, 2019, 298, 194–209 CrossRef CAS.
- K. S. Egorova, E. G. Gordeev and V. P. Ananikov, Chem. Rev., 2017, 117, 7132–7189 CrossRef CAS.
- K. Ito, N. Nishina and H. Ohno, Electrochim. Acta, 2000, 45, 1295–1298 CrossRef CAS.
- M. Yoshizawa, K. Ito-Akita and H. Ohno, Electrochim. Acta, 2000, 45, 1617–1621 CrossRef CAS.
- J. L. Anderson, R. Ding, A. Ellern and D. W. Armstrong, J. Am. Chem. Soc., 2005, 127, 593–604 CrossRef CAS.
- F. D'Anna, C. Rizzo, P. Vitale, G. Lazzara and R. Noto R, Soft Matter, 2014, 10, 9281–9292 RSC.
- J. Chen, L. Yang, W. Zhou, L. Zhu, Y. Zhou, Y. Xiang and D. Xia, Energy Fuels, 2018, 32, 5518–5526 CrossRef CAS.
- Y. Ji, Y. Hou, S. Ren, C. Yao and W. Wu, Fuel Process. Technol., 2018, 171, 183–191 CrossRef CAS.
- D. Majhi, S. Seth and M. Sarkar, Phys. Chem. Chem. Phys., 2018, 20, 7844–7856 RSC.
- C. Maton, N. De Vos and C. V. Stevens, Chem. Soc. Rev., 2013, 42, 5963–5977 RSC.
- M. G. Montalbán, G. Víllora and P. Licence, Ecotoxicol. Environ. Saf., 2018, 150, 129–135 CrossRef.
- M. H. Anthofer, M. E. Wilhelm, M. Cokoja, M. Drees, W. A. Herrmann and F. E. Kuhn, ChemCatChem, 2015, 7, 94–98 CrossRef CAS.
- I. Rocco, F. D'Anna, L. Mattiello, F. Pandolfi, C. Rizzo and M. Feroci, ChemElectroChem, 2019, 6, 1–10 CrossRef.
- V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Chem. Rev., 2017, 117, 7053–7112 CrossRef CAS.
- H. Shirota and E. W. Castner Jr, J. Phys. Chem. A, 2005, 109, 9388–9392 CrossRef CAS.
- D. Xiao, J. R. Rajain, A. Cady, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2007, 111, 4669–4677 CrossRef CAS.
- D. Xiao, L. G. Hines Jr, S. Li, R. A. Bartsch, E. L. Quitevis, O. Russina and A. Triolo, J. Phys. Chem. B, 2009, 113, 6426–6433 CrossRef CAS.
- L. Xue, F. Bardak, G. Tamas and E. L. Quitevis, Phys. Chem. Chem. Phys., 2017, 19, 4661–4672 RSC.
- S. Kakinuma, T. Ishida and H. Shirota, J. Phys. Chem. B, 2017, 121, 250–264 CrossRef CAS.
- D. A. Turton, J. Hunger, A. Stoppy, G. Hefter, A. Thoman, M. Walther, R. Buchner and K. Wynne, J. Am. Chem. Soc., 2009, 131, 11140–11146 CrossRef CAS.
- C. Gaguenet, P. J. Dyson, I. Krossing, A. Oleinikowa, J. Slattery, C. Wakai and H. Weingärtner, J. Phys. Chem. B, 2006, 110, 12682–12688 CrossRef.
- K. Nakamura and T. Shikata, ChemPhysChem, 2010, 11, 285–294 CrossRef CAS.
- K. Yamamoto, M. Tani and M. Hangyo, J. Phys. Chem. B, 2007, 111, 4854–4859 CrossRef CAS.
- A. Wulf, K. Fumino, R. Ludwig and P. F. Taday, ChemPhysChem, 2010, 11, 349–353 CrossRef CAS.
- T. Yamada, Y. Tominari, S. Tanaka and M. Mizuno, J. Phys. Chem. B, 2015, 119, 15696–15705 CrossRef CAS.
- T. Yamada, Y. Tominari, S. Tanaka, M. Mizuno and K. Fukunaga, Materials, 2014, 7, 7409–7422 CrossRef.
- S. Mou, A. Rubano and D. Paparo, J. Phys. Chem. B, 2018, 122, 3133–3140 CrossRef CAS.
- B. S. Hudson, J. Phys. Chem. A, 2001, 105, 3949–3960 CrossRef CAS.
- C. Roth, T. Peppel, K. Fumino, M. Köckerling and R. Ludwig, Angew. Chem., Int. Ed., 2010, 49, 10221–10224 CrossRef CAS.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., 2008, 120, 3890–3894 ( Angew. Chem., Int. Ed. , 2008 , 47 , 3830–3834 ) CrossRef.
- K. Iwata, H. Okajima, S. Saha and H. Hamaguchi, Acc. Chem. Res., 2007, 40, 1174–1181 CrossRef CAS.
- A. Wulf, K. Fumino and R. Ludwig, Angew. Chem., Int. Ed., 2010, 49, 449–453 CrossRef CAS.
- Y. Jeon, J. Sung, C. Seo, H. Lim, H. Cheong, M. Kang, B. Moon, Y. Ouchi and D. J. Kim, J. Phys. Chem. B, 2008, 112, 4735–4740 CrossRef CAS PubMed.
- T. Yamada, Y. Tominari, S. Tanaka and M. Mizuno, J. Phys. Chem. B, 2017, 121, 3121–3129 CrossRef CAS.
- K. Fumino, K. Wittler and R. Ludwig, J. Phys. Chem. B, 2012, 116, 9507–9511 CrossRef CAS.
- M. Krüger, E. Bründermann, S. Funkner, H. Weingärtner and M. Havenith, J. Chem. Phys., 2010, 132, 101101 CrossRef.
- H. Shirota and T. Ishida, J. Phys. Chem. B, 2013, 117, 1136–1150 Search PubMed.
- H. Shirota and T. Ishida, J. Phys. Chem. B, 2011, 115, 10860–10870 CrossRef CAS.
- H. Shirota and S. Kakinuma, J. Phys. Chem. B, 2015, 119, 9835–9846 CrossRef CAS.
- L. Guglielmero, A. Mezzetta, L. Guazzelli, C. S. Pomelli, F. D'Andrea and C. Chiappe, Front. Chem., 2018, 6, 612 CrossRef.
- H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 15104 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05735h |
| ‡ In beloved memory of. |
| This journal is © The Royal Society of Chemistry 2019 |