Theoretical study on the excited state decay properties of iron(II) polypyridine complexes substituted by bromine and chlorine

Abstract

Transition metal iron(II) polypyridyl complexes with quintet ground states were deeply investigated by density functional theory (DFT) and time-dependent density functional theory (TDDFT). Compared with the parent complex [Fe(tpy)₂]²⁺ (tpy = 2,2′:6′,2′′-terpyridine), the ground states of the complexes substituted by halogen atoms changed from singlet states to quintet states with rare high spin excited state lifetimes. The substituted complex [Fe(dbtpy)₂]²⁺ (1) results in a high spin metal–ligand charge transfer lifetime of 17.4 ps, which is 1.4 ps longer than that of [Fe(dctpy)₂]²⁺ (2) with the substitution of chlorine atoms. The reason for this is explored by a combination of electronic structures, absorption spectra, extended transition state coupled with natural orbitals for chemical valence (ETS-NOCV) studies and potential energy curves (PECs). The distortion of 1 in the angles and dihedrals of the ligands is slightly larger than that in 2, although the average metal–ligand bond lengths of the latter are larger. The twisted octahedron decreases the interactions between the d orbitals of iron(II) and the n/π orbitals of the ligands. Compared with 2, the enlarged energy gaps among the different PECs of 1 and the increased energy crossing points caused by the larger distortion result in the increase of its excited state lifetime. The different pairwise orbital interaction contributions between the metal center and the ligands in their singlet states are qualitatively estimated by ETS-NOCV. The results show that the substitution of bromine atoms will decrease the electrostatic attraction between the metal and ligands but not significantly impact the orbital interactions.

---

1 Introduction

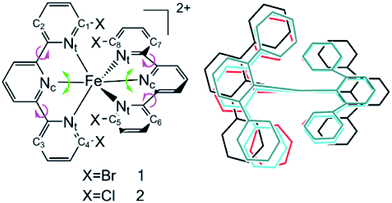
Transition metal complexes have demonstrated their capabilities in organic light emitting devices (OLEDs) on account of their phosphorescence mechanism.^1,2 Their luminescence quantum efficiencies are as high as 100%, and they have seen large-scale commercial production since the first phosphorescent OLED was reported in 1996.³ Most studies have been performed on precious transition metals, such as ruthenium, iridium and platinum.^4–7 However, their high cost and environment pollution limit their applications. Recently, the use of inexpensive metals such as copper, zinc and iron has seen an increasing amount of studies to promote light-harvesting applications.^8–16 Although iron is the second most Earth-abundant metal on Earth and is inexpensive and environmentally benign, its subpicosecond nonradiative relaxation from the metal-to-ligand charge transfer (MLCT) state into a low-lying metal-centered (MC) state results in more difficult utilization.^17,18 Investigations of the excited state decay path of the prototype [Fe(bpy)₃]²⁺ (bpy = 2,2-bipyridine) complex have proved that ultrafast intersystem crossing (ISC) occurs from the ^1,3MLCT state to the ³MC state and then to the ⁵MC state. Increasing the ligand field strength is expected to change the energetic accessibility of the MC states, which results in a decrease in the nonradiative decay.¹⁹ Haacke and Gros et al. used N-heterocyclic carbine ligands to dramatically increase the Fe(II) MLCT excited state lifetime to 26 ps by strengthening the metal–ligand bonds.²⁰ More recently, using a combination of cyano ligands and bpy ligands has been demonstrated as a way of separately controlling the ^3,5MC and ^1,3MLCT state energies to achieve a 20 ps lifetime.⁹ However, an opposite strategy of decreasing the ligand-field strength is still used to expand the charge-transfer excited state lifetimes, which increases the excited state lifetimes effectively. Damrauer et al. introduced this strategy for extending MLCT lifetimes by using different halogen atoms connected to the pyridyls which interact with the opposing ligand.⁶ The insertion of halogen atoms destabilizes the singlet ground state and results in a quintet ground state and an optically accessible ^5,7MLCT. In this work, the conclusion is based on two ideas. Firstly, the ^5,7MLCT happens to be less coupled to intermediates such as ³MC, which is necessary for nonradiative decay processes. Secondly, the sizes of the different halogen substituents diminish the conformational freedom of the system within the excited state manifold, thus preventing the dynamics necessary for intersystem crossing within the relaxation process.

It is an enormous challenge to explore the luminescence of Fe(II) complexes in detail because of their mixed multiple spin states, such as singlet, triplet, quintet and septet states. Moreover, it is difficult to detect the corresponding photophysical and decay mechanisms by experimental methods. With improving computational power and theoretical approaches, quantum chemical calculations can provide significant insights not only into the fundamental structures, but also into the electronic and photophysical properties of metal complexes. Here, we study the complexes [Fe(dbtpy)₂]²⁺ (dbtpy is the abbreviation of 6,6′′-dibromo-2,2’;6′2′′-terpyridine), simplified to 1, and [Fe(dctpy)₂]²⁺ (dctpy is the abbreviation of 6,6′′-dichloro-2,2’:6′2′′-terpyridine), named 2, to explore how halogen atoms increase the high spin MLCT lifetimes with larger sizes (Fig. 1). In Fig. 1, N_c and N_t are the central and terminal nitrogen atoms of tpy, respectively. X represents the halogen atoms.

Fig. 1 (Left): Two constructions containing halogen substituents. (Right): The skeletons of the fully optimized structures of 1 and 2 with halogens omitted in the ground state ⁵MC (black), singlet state (red), triplet state ³MC (cyan) and septet state ⁷MLCT (green).

When the parent complex [Fe(tpy)₂]²⁺ is substituted by halogen atoms, quintet ground states are accessible with rare high spin MLCT state lifetimes as long as 14–17.4 ps. The singlet ground state is favoured by enthalpy and the quintet ground state is populated due to entropic contributions to the free energy (3: 97 at room temperature); thus, the fluorine-substituted complex is complicated to discuss. The special characteristic and ligand field of the F-substituted complex [Fe(dftpy)₂] may result from the small bulk of F with weaker steric hindrance of the interactions compared to Cl or Br. Weakly sterically hindered interactions result in higher conformational freedom, which gives rise to an enthalpically favoured singlet ground state. Before analyzing the effects of halogen substitution in the coexistence of mixed spin states, we may obtain insights into the mechanism of the particularity of the spin crossover equilibrium after solving the decay mechanisms of 1 and 2 with pure quintet ground states well in advance in this work.

The distortion in the angles and dihedrals of the ligands of 1, increased by bromine atoms with greatly sterically hindered interaction, is slightly larger than in 2, although the average metal–ligand bond lengths of the latter are larger. The increase of the CT proportion from the chlorine to bromine substituents causes hypsochromic shifts of the lowest absorption peaks. The hole and electron analysis simplifies the manifold orbitals as one main transition mode. The potential energy curves (PECs) consist of the average values of the Fe–N_c bond lengths as the x-axis and the single-point energies as the y-axis. This shows that the sum of the energy gaps of intersystem crossing according to the Franck–Condon rules and Kasha's rule on the PECs of the different spin states of 1 is larger than that of 2, which results in the 1.4 ps longer lifetime. The higher energy crossing points of 1 improve the energy barriers and hinder the thermodynamic hopping from the optimized structures to the energy crossing points, which results in faster non-radiative decay. ETS-NOCV studies and the pictures of the deformation density show that the substitution of bromine atoms will decrease the electrostatic attraction between the metal and ligands but only slightly impact the orbital interactions.

2 Computational details

The geometrical optimizations of the ground quintet states, singlet states, triplet states and septet states of 1 and 2 were separately simulated by DFT and UDFT with the hybrid functional PBE0.²¹ The quasi-relativistic effective core potential (ECP) of Fe proposed by Hay and Wadt with 18 valence electrons with the double-ζ quality basis set LANL2DZ²² and the 6-31G(d)²³ basis set for H, C, N, and Cl and LANL08 (ref. 24) for Br were adopted. Vibrational frequencies were calculated at the same level to confirm that all the optimized structures were at the minimal points of their potential energy surfaces without imaginary frequencies. Furthermore, the solvent effect of acetonitrile (CH₃CN) was considered by the polarized continuum model (PCM)²⁵ for all the calculations. The absorption spectra and potential energy surfaces were simulated by LANL2TZ(f)²⁶ and 6-311g(d, p)²⁷ for higher accuracy. The above calculations were all performed using Gaussian 16 Rev. A.03.²⁸ The hole and electron analysis function of Multiwfn 3.6 (ref. 29) was used to analyse the complicated transition orbitals of the absorption processes.

The bond properties among the metal center, tpy and halogen atoms at different spin states were determined by the ETS-NOCV^30–33 algorithm of the Amsterdam Density Functional (ADF) 2016.104 program.^34,35 The BP86 (ref. 36–38) functional with a Slater type all-electron triple-ζ basis set with polarizations (TZP)³⁹ was used with one-component zeroth-order regular approximation (ZORA)^40–42 on the scalar relativistic singlet geometries. Moreover, the conductor-like screening model (COSMO)⁴³ of solvent with CH₃CN was adopted in the ETS-NOCV calculations.

3 Results and discussion

3.1 Geometrical structures

The main optimized geometrical parameters of the different spin excited states of [Fe(tpy)₂]²⁺ ,⁴⁴ [Fe(dbtpy)₂]²⁺ (1) and [Fe(dbtpy)₂]²⁺ (2) are listed in Table 1 with the corresponding experimental X-ray characterization results. The calculated data of Fe–N_c, Fe–N_t and N_t–N_c–N_t are in good agreement with the experimental values, with deviations of 0.9% to 2.4%. Also, the quintet metal-center states of 1 and 2 have the lowest energies compared with the singlet, triplet and septet states.

Table 1 The optimized geometry data of the different spin excited states of [Fe(tpy)₂]²⁺, 1 and 2. The rows of Exp. show the data of the X-ray crystal structures

	Fe–Nc(Å)^b	Fe–Nt(Å)^b	Fe–X(Å)	Nt–Nc–Nt(deg)	C1–C2–C3–C4, C5–C6–C7–C8/Nt–Nc–Nc–Nt(deg)^a	θ(deg)^b	X–pyridyl(Å)
a Nc is the central nitrogen atom of tpy. Nt represents the terminal nitrogen atoms of tpy. X is the halogen atoms. The line of dihedrals includes the average dihedrals of single dxtpy (positive values) and the dihedrals between two dxtpy ligands. θ is the bond angle between the iron(II) metal center and the central nitrogen atoms of the ligands. All the bond lengths are average values, except for Fe–Nc of the septet states. b See ref. 12 and 42.
[Fe(tpy) 2 ] ^2+ ^b
Quintet	2.16	2.20	—	—	—	10.8	—
Singlet	1.91	2.01	—	—	—	0	—
Exp.	1.89 to 1.99	1.89 to 1.99	—	—	—	—	—
Triplet	1.94	2.14	—	—	—	0.2	—
1
Quintet	2.11	2.34	3.81	113.7	29.8/−90.7	2.9	1.93
Exp.	2.07	2.30	—	112.7	—	11.7	3.18
Singlet	1.90	2.12	3.83	107.4	37.4/−93.8	0	1.93
Triplet	1.93	2.25	3.88	112.1	32.1/−92.8	0.7	1.93
Septet	1.95/2.06	2.22/2.25	3.78/3.82	111.2/111.8	31.2, 34.8/88.4	1.7	1.92/1.93
2
Quintet	2.13	2.32	3.62	112.3	15.8/−90.2	0.4	1.73
Exp.	2.08	2.27	—	111.4	—	4.1	3.07
Singlet	1.90	2.11	3.66	106.7	25.0/−92.1	0	1.72
Triplet	1.93	2.23	3.71	111.2	16.3/−90.8	0	1.73
Septet	1.96/2.08	2.21/2.24	3.61/3.64	110.4/111.2	16.4, 20.4/−89.8	0.9	1.72/1.73

---

In the ground quintet states, the bond lengths between the nitrogen atoms and iron(II) center are longer than those of the other spin excited states. The bond lengths of Fe–N_c of the quintet states, triplet states and singlet states of 1 and 2 are separately 2.11/2.13, 1.93 and 1.90 Å. Meanwhile, the bond lengths of Fe–N_t have the same trend as those of Fe–N_c. When they have the same spin states, there are only 0 to 0.02 Å deviations between Fe–N of 1 and 2. Also, the shorter bond lengths enhance the interaction between the ligands and iron(II) metal center. In terms of the bond angles, the angles of terpyridine of the different spin excited state structures still gradually decrease, with small deviations (0.7 to 1.4 degrees), in the order of quintet, triplet and singlet. The changing rules of the bond lengths and bond angles may result from the Jahn–Teller effect. The repulsion between the d orbitals of iron(II) and the n/π orbitals of terpyridine result in the extension of the Fe–N bonds of 1 and 2.

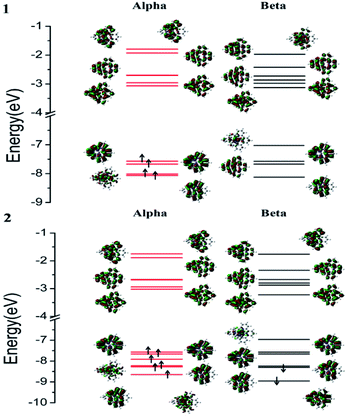
Compared with [Fe(tpy)₂]²⁺, Fe–N_t and N_t–N_c–N_t of 1 and 2 show obvious extension due to the halogen substituents. [Fe(tpy)₂]²⁺ has only 0.01 Å deviations of Fe–N_c in the singlet and triplet states from [Fe(dxtpy)₂]²⁺. However, the bond lengths of Fe–N_t of [Fe(tpy)₂]²⁺ are 0.09 to 0.14 Å longer than those of [Fe(dxtpy)₂]²⁺ due to the substitution of Br and Cl. The singlet ground state of [Fe(tpy)₂]²⁺ may result from the increased ligand field split, which improves the energy gap of the e_g and t_2g orbitals. In comparison with [Fe(tpy)₂]²⁺, the octahedral structures of 1 and 2 are more twisted, which weakens the interaction between iron(II) and terpyridine because there is less orbital overlap among the d orbitals and n/π orbitals. In addition, the dihedral angles of the single terpyridine and two terpyridines separately increase from quintet to triplet to singlet, which may decrease the effective radiative process ands increase the non-radiative decay. Furthermore, for the dihedral angles of the single terpyridine, the large deviations of 12.4 to 15.8 degrees between 1 and 2 in different spin excited states indicate that the replacement by bromine can result in larger distortion of the structures and change the population of the potential energy surfaces. Furthermore, θ, the bond angle between the iron(II) center and central nitrogen atoms, shows that the larger distortion of the structures of 1 than of 2 may be caused by the replacement of bromine. Concerning the bond lengths of Fe–X and X–pyridyl, the larger bromine atom has greater steric repulsion interactions and weaker influence on the iron(II) center. We found that the geometries of the quintet, triplet and singlet states have the same average values of their bond lengths and bond angles. However, the geometrical characteristics of the septet states of the two complexes are obviously special because one β electron is flipped onto the π* of the closer ligand as α spin. 400 nm excitation can easily cause the complexes to reach the energy levels of the septet states. The deactivating pathway beginning from ⁷MLCT will be discussed in the next part.

3.2 Absorption properties and hole–electron analysis

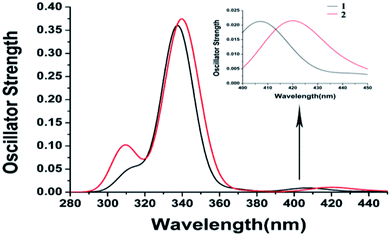
[Fe(tpy)₂]²⁺ with the singlet ground state has been theoretically proved by the Jakubikova et al.⁴⁴ The differences in the absorption properties between the singlet ground state and quintet ground states are another interesting topic that may be investigated in the future. Herein, only the absorption properties based on the optimized quintet ground states of 1 and 2 are discussed. The electron transition configurations, excitation energies, oscillator strengths (f), and assignments of the main absorption bands are listed in Table S1.† The corresponding absorption spectra of 1 and 2 and the alpha and beta spin molecular orbitals are displayed in Fig. 2 and 3.

Fig. 2 Calculated absorption spectra and enlargement of the lowest absorption peaks of 1 and 2.

Fig. 3 The main alpha and beta spin molecular orbitals of 1 and 2.

The calculated absorption spectra are in good agreement with the experimental values.⁶ It is obvious that the bromine substituents result in a slight blue-shift of the lowest peak compared to the chlorine substituents. The lowest absorption peak of 1 is mainly contributed by Q₁₀, with the transitions of H(B) → L(B) and H(B) → L+5(B). The assignment of H(B) → L(B) is MLCT/LLCT (ligand-to-ligand charge transfer) and that of H(B) → L+5(B) is MLCT/LLCT/MC. However, the lowest absorption peak of 2 is mainly contributed by Q₇ with the transitions of H(B) → L(B), whose assignment is MLCT/MC. The hypsochromic shift may result from the increase of LLCT. Meanwhile, the strongest absorption peaks of 1 and 2 consist of similar high excited states to almost degenerate energy levels. Therefore, they have similar strongest absorption peaks to the main transition configuration of ILCT (intraligand charge transfer).

Nevertheless, there are too many transition configurations with trivial proportions because of the special quintet ground state excitations, although we have a rough conclusion about the absorption properties. The hole and electron analysis performed with Multiwfn can conclude and transfer the manifold orbital transition characters into one main transition contribution, such as a natural transition orbital (NTO). The corresponding data and visual pictures are displayed in Table 2 and Fig. 4, where D is the total magnitude of the charge transfer length between the centroids of the hole and electron and t is the overall measure of the separation degree of the hole and electron in the charge transfer (CT) direction, which is from electrons to holes. The negative values of t and small values of D show that the separation degrees of the hole and electron in the CT direction of 1 and 2 are very small. The D of the quintet excited state Q₁₀ of 1 is 0.04 Å longer than that of the quintet excited state Q₇ of 2. The absolute value of t of Q₁₀ of 1 is about 0.11 Å longer than that of Q₇ of 2. This indicates that the CT process of 1 is more obvious, which may result in the hypsochromic shift of the lowest absorption peak of 1. S_r is the geometric average of the overlap function between the hole and electron distribution. The range of S_r values is [0, 1]. This indicates complete overlap of the hole and electron when S_r is 1. So, the overlap extent of Q₁₀ of 1 is slightly smaller than that of Q₇ of 2. Δσ is the overall root-mean-square deviation of the extent of spatial distribution of the hole and electron. The smaller Δσ and smaller S_r of 1 illustrate that the MLCT from the d_yz of iron(II) ion to the π* of tpy of 1 is more distinct. Therefore, the hypochromatic shift from 2 to 1 depends on a stronger CT process. The charge transfer process based on a single molecule occurs before exciton recombination among polymolecules. We will simulate exciton recombination in a future article. In this work, the charge transfer state and excited state relaxation pathways are discussed as the main points.

Table 2 Detailed data of the hole and electron analysis of the absorption bands of 1 and 2^a

Excited state	S r	D (Å)	t (Å)	Δσ (Å)	Assignment
a S r is the geometric average of the overlap function between the hole and electron distributions. D is the total magnitude of the charge transfer length between the centroids of the hole and electron. t is the overall measure of the separation degree of the hole and electron in the charge transfer direction. Δσ is the overall root-mean-square deviation of the extent of spatial distribution of the hole and electron. ILCT/LLCT represent intraligand/ligand-to-ligand charge transfer. LMCT/MLCT are ligand-to-metal/metal-to-ligand charge transfer. MC represents metal-center charge transfer.
1
Q0 → Q6	0.647	0.006	−2.079	0.292	MLCT/LLCT (82.3%)
Q0 → Q10	0.453	0.048	−1.674	1.697	MLCT/LLCT (88.7%)
Q0 → Q13	0.533	0.058	−2.013	−0.566	LLCT/MLCT (84.7%)
Q0 → Q14	0.647	0.092	−2.062	−0.072	LLCT (93.7%)
2
Q0 → Q5	0.672	0.009	−2.077	0.376	ILCT (85.4%)
Q0 → Q7	0.497	0.008	−1.568	1.754	MLCT/LLCT (92.9%)
Q0 → Q13	0.611	0.013	−2.198	−0.241	MLCT/LLCT (86.4%)
Q0 → Q14	0.515	0.021	−1.902	1.340	MLCT/LLCT (94.4%)
Q0 → Q15	0.621	0.021	−2.155	−0.358	MLCT/LLCT (88.2%)

---

Fig. 4 The hole and electron populations of 1 (a) and 2 (b). The numbers at the bottom of each structure show the different quintet excited states. Blue indicates the population of holes. Green represents the population of electrons. The charge direction is from hole to electron.

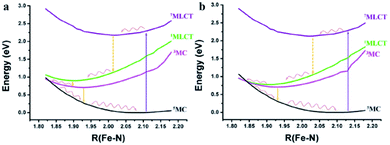
3.3 The potential energy curves (PECs) of 1 and 2

Although the reason for the differences in the lowest absorption peaks has been explained, the deviation of the excited state lifetimes of 1 and 2 is still obscure. Thus, the PECs with the same values of Fe–N_c in Fig. 5 were used to qualitatively explore the corresponding decay mechanism. The detailed data of the PECs are listed in Table S2.† It is obvious that the energy gaps among the PECs of ¹MLCT, ³MC and ⁵MC of 1 are slightly larger than those of 2. Meanwhile, the 1.4 ps lifetime deviation between 1 and 2 may result from the intersystem crossing among the PECs of the different spin states. If we follow Kasha's rule and the Frank–Condon rule, the order of intersystem crossing will be from septet to singlet to triplet to quintet, and all the intersystem crossing will occur from the minimum points of the previous PECs to the points with the same structures of the next PECs. If the decay path is ⁷MLCT–⁵MLCT–³MLCT–¹MLCT through crossing of the potential energy surfaces, it may be difficult due to probable high minimum energy crossing points and large structural distortion in the ultrafast process. In contrast, the transition by vertical decay in the Franck–Condon regions may be feasible because of the more distinct d orbital degeneration caused by the tridentate ligand tpy than by the bidentate ligand.⁴⁵ Therefore, we think a vertical transition from the high spin excited states in the Franck–Condon regions may be easier than the deactivated process. The smaller energy gap of 2 results in a faster vertical decay process than in 1 (in Table S2†). Furthermore, the energy crossing point between the singlet and quintet states of 1 is much higher than that of 2. The excitons decay from ⁷MLCT by a vertical process and rapidly relax to the minimum points. However, the energy crossing points among ¹MLCT, ³MC and ⁵MC of 2 are very close, and the deactivation process may directly go through the crossing point between ¹MLCT and ⁵MC as non-radiative decay. Compared with 2, a higher energy crossing point between ¹MLCT and ⁵MC of 1 can effectively decrease this process and promote the radiative decay, which will increase the excited state lifetime.

Fig. 5 The PECs of (a) 1 and (b) 2 consisting of the average values of two Fe–N_c.

3.4 The analysis of the transition state coupled with natural orbitals for chemical valence (ETS-NOCV)

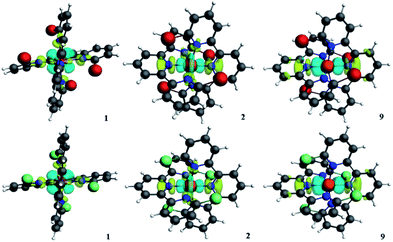
To explore the interactions between the metal centers and the terpyridines quantitatively, ETS-NOCV analysis was performed. All the detailed ETS-NOCV data of the singlet states of 1 and 2 are listed in Table 3. The graphical information of the deformation densities of different pairwise orbital interactions of the corresponding modes of 1 and 2 are displayed in Fig. 6. ETS-NOCV is an effective and convenient method to analyze the decomposition of the interaction energy (ΔE_int) between the fragments of molecules, where ΔE_int can be expressed as follows:

ΔE_int = ΔE_pauli + ΔE_elstat + ΔE_orb (1)

Table 3 Energy decomposition analysis and energetic estimate of each deformation density Δρ. ΔE_pauli is the exchange (Pauli) repulsion energy. ΔE_elstat is the quasiclassical coulomb interaction. ΔE_orb arises from the orbital mixing and is identified as the covalent contribution to the chemical bond

	1	2
ΔEint	−499.2	−507.9
ΔEpauli	330.6	333.7
ΔEelstat	−345.1 (41.6%)	−355.8 (42.3%)
ΔEorb	−484.7 (58.4%)	−485.8 (57.7%)
ΔE1	−107.4 (22.2%)	−110.8 (22.8%)
ΔE2	−115.7 (23.9%)	−114.3 (23.5%)
ΔE9	−19.4 (4.0%)	−19.8 (4.1%)
ΔErest	−261.6 (49.9%)	−260.7 (49.6%)

---

Fig. 6 Plots of the deformation density Δρ of the pairwise orbital interactions. 1 is at the top and 2 is at the bottom. The numbers at the bottom of each construction represent the different modes of deformation density. The direction of the charge flow is from yellow to cyan.

ΔE_pauli is the exchange (Pauli) repulsion energy. ΔE_elstat is the quasiclassical Coulomb interaction. ΔE_orb originates from the orbital mixing and is identified as the covalent contribution to the chemical bond. In energy and visualization, ΔE_orb developed by Ziegler and Rauk can be analyzed to determine which part of the orbital energy is involved in the metal–ligand interactions. The deformation density Δρ in the NOCV representation is a sum of pairs of complimentary eigenfunctions (ψ_−k, ψ_k) corresponding to the eigenvalues −λ_k and λ_k as follows:

Δρ = ΣΔρ_k(r) = Σλ_k(−ψ_−k²(r) + ψ_k²) (2)

where k goes over the pair of NOCV. The pictures of the deformation density plots are accompanied with the energetic estimations (ΔE_orb(k)) for each Δρ_k:

ΔE_orb = ΣΔE^orb_k = Σλ_k(−F^TS_−k + F^TS_k) (3)

where −F^TS_−k and F^TS_k are the diagonal transition-state Kohn–Sham matrix elements corresponding to the NOCV with eigenvalues of −λ_k and λ_k, respectively.

In terms of ΔE_int, we found that the metal–ligand interactions of 1 are 8.7 kcal mol⁻¹ weaker than those of 2. The occupied 3d orbitals of the iron(II) center encounter not only the stabilizing interaction of the n orbital on the 6 nitrogen atoms of tpy, but also the repulsive interaction with the occupied 2s and 2p orbitals on the other centers. As a result, the additional dctpys of 2 result in stronger electrostatic attraction and weaker Pauli repulsion. However, this does not play a significant role in enhancing the orbital interactions. The deviation of ΔE_orb between 1 and 2 is only 1.1 kcal mol⁻¹. Due to the stronger non-metallic character of Cl and the longer bond lengths of Fe–N in 2, the interactions between Fe and the ligand may lie in a strong electrostatic attraction state and weak repulsion state on the interaction potential curves.

Also, there are similar pairwise orbital interactions. In Fig. 6, we can find that the main orbital contributions of the singlet states of 1 and 2 originate from d_x²−y² of iron(II) ion and the n orbitals of the nitrogen atoms to d_z² or d_xy of iron(II) ion as σ* or non-bonding with similar contributions. Thus, we found that the substitution of bromine and chlorine impacts the metal–ligand interactions by electrostatic attraction to a greater extent.

4 Conclusions

1 and 2 were studied to explore how different halogen atoms impact the MLCT lifetimes by a combination of electronic structures, absorption spectra, ETS-NOCV and PECs. The larger distortion of 1 than 2 is caused by the sterically hindered interactions of bromine atoms. Taking the advantage of the combination of the Kohn–Sham molecular orbitals of the absorption properties and the hole and electron analysis, the increase in the CT proportion from the chlorine to bromine substituents causes a hypsochromic shift of the lowest absorption peaks. The PECs show that the total energy gaps of intersystem crossing following the Franck–Condon rule and Kasha's rule on the PECs of the different spin states of 1 are larger than those of 2, which results in the 1.4 ps longer lifetime. The higher energy crossing points of 1 improve the energy barriers and hinder the thermodynamic hopping from the optimized structures to the energy crossing points, which results in faster non-radiative decay. ETS-NOCV and the pictures of the deformation density show that the substitution of bromine atoms will decrease the electrostatic attractions between the metal and ligands but will slightly impact the orbital interactions. Unfortunately, the analysis of the MLCT progress and lifetimes is only qualitative. As different metal center analogues, [Ru(tpy)₂]²⁺ with 602 nm emission at 77 K only has a singlet ground state, a triplet metal–ligand charge transfer state (³MLCT) and a triplet metal center state (³MC).⁴⁶ However, [Fe(dxtpy)₂]²⁺ without luminescence in this article has ground quintet states, singlet metal–ligand charge transfer states (¹MLCT), and ³MC and septet metal–ligand charge transfer states (⁷MLCT). Due to the abundant excited states, exploration of the complicated excited states of the deactivated pathways in detail is difficult. The photophysical properties of the complex containing fluorine still remain to be discussed. We will make more effort to resolve these problems and explore more properties and mechanisms of iron complexes in the future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is funded by the Natural Science Foundation of China (Grant Nos. 21873038 and 21573088), and the “13th Five-Year” science and technology project of the education department of Jilin province (Grant No. JJKH20180123KJ) and the Young Scholar Training Program of Jilin University.

References

1. J.-Y. Hung, C.-H. Lin, Y. Chi, M.-W. Chung, Y.-J. Chen, G.-H. Lee, P.-T. Chou, C.-C. Chen and C.-C. Wu, J. Mater. Chem., 2010, 20, 7682.
2. G. Cheng, S. C. F. Kui, W.-H. Ang, M.-Y. Ko, P.-K. Chow, C.-L. Kwong, C.-C. Kwok, C. Ma, X. Guan, K.-H. Low, S.-J. Su and C.-M. Che, Chem. Sci., 2014, 5, 4819–4830.
3. K. M. Maness, R. H. Terrill, T. J. Meyer, R. W. Murray and R. M. Wightman, J. Am. Chem. Soc., 1996, 118, 10609–10616.
4. Y. Wang, J. Wang, H.-X. Zhang, I. M. Szilágyi and F.-Q. Bai, Organometallics, 2018, 37, 2491–2499.
5. Z.-X. Zhang, W. Wei, F.-Q. Bai, S. Bibi and H.-X. Zhang, Org. Chem. Front., 2017, 4, 2191–2201.
6. S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505.
7. M. Abrahamsson, H. C. Becker and L. Hammarstrom, Dalton Trans., 2017, 46, 13314–13321.
8. T. He, A. Ren, S. Chen, Z. Yang, P. Yu, Y. Chen, X. Ding, L. Shen, H. Zhang and L. Zou, Org. Electron., 2017, 45, 9–19.
9. W. Zhang, K. S. Kjaer, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubicek, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T. C. Weng, D. Zhu, K. Warnmark, V. Sundstrom and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523.
10. Y. Liu, T. Harlang, S. E. Canton, P. Chabera, K. Suarez-Alcantara, A. Fleckhaus, D. A. Vithanage, E. Goransson, A. Corani, R. Lomoth, V. Sundstrom and K. Warnmark, Chem. Commun., 2013, 49, 6412–6414.
11. X. C. Ma, Y. Dai, L. Yu and B. B. Huang, Light Sci Appl, 2016, 5, e16017.
12. X. Wang, F.-Q. Bai, Y.-T. Liu, J. Wang and H.-X. Zhang, Synth. Met., 2016, 213, 18–24.
13. A. Baker and H. Goodwin, Aust. J. Chem., 1985, 38, 207–214.
14. L. A. Buldt and O. S. Wenger, Dalton Trans., 2017, 46, 15175–15177.
15. I. M. Dixon, F. Alary, M. Boggio-Pasqua and J. L. Heully, Dalton Trans., 2015, 44, 13498–13503.
16. W. Zhang, Y. Li, V. P. Nguyen, Z. Huang, Z. Liu, X. Wang and Y. M. Paulus, Light Sci Appl, 2018, 7, 103.
17. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629.
18. A. Cannizzo, C. J. Milne, C. Consani, W. Gawelda, C. Bressler, F. van Mourik and M. Chergui, Coordin. Chem. Rev., 2010, 254, 2677–2686.
19. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345.
20. L. Liu, T. Duchanois, T. Etienne, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Phys. Chem. Chem. Phys., 2016, 18, 12550–12556.
21. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
22. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
23. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
24. L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031.
25. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
26. A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114.
27. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016.
29. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
30. T. Ziegler and A. Rauk, Theore. Chim. Acta, 1977, 46, 1–10.
31. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759.
32. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565.
33. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
34. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theore. Chem. Acc., 1998, 99, 391–403.
35. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
36. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
37. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
38. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406.
39. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
40. E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
41. E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
42. E. v. Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953.
43. C. C. Pye and T. Ziegler, Theore. Chem. Acc., 1999, 101, 396–408.
44. J. Nance, D. N. Bowman, S. Mukherjee, C. T. Kelley and E. Jakubikova, Inorg. Chem., 2015, 54, 11259–11268.
45. D. G. Brown, N. Sanguantrakun, B. Schulze, U. S. Schubert and C. P. Berlinguette, J. Am. Chem. Soc., 2012, 134, 12354–12357.
46. A. Soupart, I. M. Dixon, F. Alary and J.-L. Heully, Theor. Chem. Acc., 2018, 137.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06366h

---