Open Access Article
Open Access ArticleStrain-tunable magnetic anisotropy in two-dimensional Dirac half-metals: nickel trihalides†
Zheng Lia,
Baozeng Zhou *a and
Chongbiao Luanb
*a and
Chongbiao Luanb
aTianjin Key Laboratory of Film Electronic & Communicate Devices, School of Electrical and Electronic Engineering, Tianjin University of Technology, Tianjin 300384, China. E-mail: baozeng@tju.edu.cn
bInstitute of Fluid Physics, China Academy of Engineering Physics, Mianyang, Sichuan 621999, China
First published on 4th November 2019
Abstract
The recent discovery of intrinsic two-dimensional (2D) ferromagnetism has sparked intense interest due to the potential applications in spintronics. Magnetic anisotropy energy defines the stability of magnetization in a specific direction with respect to the crystal lattice and is an important parameter for nanoscale applications. In this work, using first-principles calculations we predict that 2D NiX3 (X = Cl, Br, and I) can be a family of intrinsic Dirac half-metals characterized by a band structure with an insulator gap in one spin channel and a Dirac cone in the other. The combination of 100% spin polarization and massless Dirac fermions renders the monolayer NiX3 a superior candidate material for efficient spin injection and high spin mobility. The NiX3 is dynamically and thermodynamically stable up to high temperature and the magnetic moment of about 1 μB per Ni3+ ion is observed with high Curie temperature and large magnetic anisotropy energy. Moreover, detailed calculations of their energetics, atomic structures, and electronic structures under the influence of a biaxial strain ε have been carried out. The magnetic anisotropy energy also exhibits a strain dependence in monolayer NiX3. The hybridization between Ni dxy and dx2-y2 orbitals gives the largest magnetic anisotropy contribution, whether for the off-plane magnetized NiCl3 (NiBr3) or the in-plane magnetized NiI3. The outstanding attributes of monolayer NiX3 will substantially broaden the applicability of 2D magnetism for a wide range of applications.
1. Introduction
The recent experimental discovery of intrinsic ferromagnetism in two-dimensional (2D) van der Waals crystals down to the monolayer limit has sparked intense interest due to their potential applications in spintronics,1,2 which takes spin instead of charge as the carrier for information transportation and processing. The efficient use of the spin degree of freedom offers unique advantages to conventional charge-based electronic devices, such as greater data processing speed, high integration density, low power consumption, and nonvolatility.3,4 For developing spintronic devices with practical applications, there are still many issues such as spin-polarized carrier generation and injection, long-distance spin-polarized transport, and spin manipulation and detection.5–7 To overcome these obstacles, the search for magnetic materials with novel band structures has tremendous scientific and technological significance.Half-metals (HMs) with one spin channel conducting and the other semiconducting are an attractive candidate for spin injection.8,9 The charge transport is dominated by the electrons of the metallic spin channel and completely spin-polarized. In order to preserve the half-metallicity at room temperature, the band gap of one spin channel should be wide enough to prevent thermally induced spin-flip transitions. Until now, the half-metallicity in several pristine 2D systems has been computationally proved.10–13 Another distinct class of materials with Dirac states, such as graphene,14–16 silicene,17,18 monolayer TiB2,19 and hydrogenated arsenene,20 is characterized by low-energy fermionic excitations that behave as massless Dirac particles with linear dispersion. By combining the two fascinating properties of half-metallicity and Dirac spectrum, a potentially more interesting state, namely Dirac half-metal (DHM), which is characterized by a band structure with a gap in one channel but a Dirac cone in the other, has been proposed based on a model calculation.21 Thus, the 100% spin polarization and massless Dirac fermions can coexist in the DHM system, which will show more advantages on the efficient spin injection and high spin mobility. Furthermore, as the DHM possesses a Dirac cone in only one spin channel, the gap opening triggered by spin–orbit coupling (SOC) leads to a topological phase transition in only one spin channel. Hence, the DMH is also a natural avenue toward the realization of the quantum anomalous Hall effect (QAHE).
Previous report has demonstrated that a fully spin-polarized Dirac state can be realized in a simple Kondo lattice model.21 Since then, several materials were computationally proved to be DHMs.22–24 Especially, 2D transition-metal trihalides with unique electronic and magnetic properties have received extensive attention. Among them, 2D Cr-trihalides are ferromagnetic insulators with low Curie temperature (TC) of 45 K.1 VCl3 and VI3 monolayers possess the DHM behavior, but the TC is still only 80 K and 98 K, respectively.25 Mn-trihalides monolayers sustain the DHM state and exhibit large magnetic moments of about 4 μB per Mn3+ ion. The TC is enlarged above room temperature in a range from 450 K (MnF3) to 720 K (MnI3), which can be attributed to the large in-plane magnetic anisotropy energy (MAE).26 Unlike in bulk magnetic materials, the long-range magnetic ordering in 2D structures is impossible without magnetic anisotropy, which is required for counteracting thermal fluctuations.27 Thus, magnetic anisotropy, which originates mainly from SOC effects,28,29 becomes an important parameter when it comes to 2D magnets as it is qualitatively related to their magnetic stability. Additionally, ferromagnetic 2D materials with large magnetic anisotropy are of great interest for high-density magnetic random access memories and spintronic applications at the nanoscale, as in spin valves and magnetic tunnel junctions.30–32
A NiCl3 monolayer has also been proved to present the DHM behavior with high temperature ferromagnetism (∼400 K).33 The calculated Fermi velocity of Dirac fermions of about 4 × 105 m s−1, which is larger than that of Mn-trihalides monolayers, indicates very high mobility in NiCl3 monolayer and is even comparable to silicene (5.3 × 105 m s−1).34 However, an extensive study on the electronic structures, magnetism, and magnetic anisotropy of Ni-trihalides monolayers is absence. Here, using first-principles calculations, we demonstrate that the Ni-trihalides monolayers, NiX3 (with X = Cl, Br, and I), have completely spin-polarized Dirac cones with the Fermi level located exactly at the Dirac point. For practical applications, a 2D material usually needs to be supported by a suitable substrate, which may apply an in-plane strain and affect the performance of the pristine material. Thus, the electronic structures, magnetism, and MAE of the monolayer NiX3 under different strains are also investigated systematically. The combination of these unique properties renders this class of 2D ferromagnets a promising platform for high efficiency spintronic applications.
2. Simulation models and methods
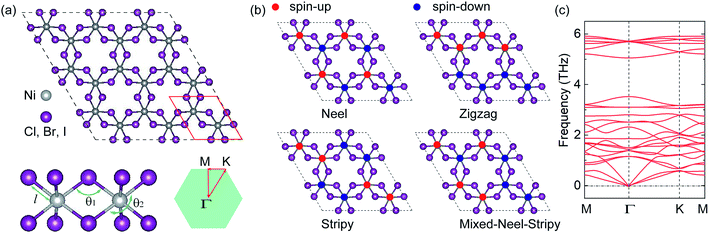
The DFT calculations for structural relaxation and electronic structure are performed by using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) for the exchange and correlation function as implemented in the Vienna ab initio simulation package (VASP).35–38 Projector augmented wave (PAW) is used to described the electron–ion interaction.39,40 The plane-wave cutoff energy is set to 500 eV. The Brillouin Zone (BZ) integrations are performed using a Γ-centered 8 × 8 × 1 k-mesh. During the structural relaxation, the energy convergent criterion is 10−6 eV per unit cell, and the forces on all relaxed atoms are less than 0.01 eV Å−1. Moreover, a 20 Å vacuum is applied along the z axis (in the direction perpendicular to the interface) to avoid any artificial interactions between repeated slabs. The band structures are calculated using the DFT+U approach41,42 (U = 4 eV) to treat the strong electronic correlations in the localized Ni-3d orbitals and the Heyd–Scuseria–Ernzerhof43 (HSE06) functional. To ensure the structural stability of the monolayers, the phonon dispersion spectrum is calculated with finite displacement method on 3 × 3 × 1 supercell with 72 atoms by using PHONOPY package.44To evaluate the magnetic ground state, we have carried total-energy spin-polarized calculations of the 2 × 2 × 1 supercell of the ferromagnetic (FM) and four antiferromagnetic (AFM) phases, such as the AFM-Néel, AFM-zigzag, AFM-stripy and mixed AFM, respectively, as shown in Fig. 1(b). For both cases, spin orientations are initially in the off-plane direction. The MAE is calculated from the force theorem by considering the SOC,45 which is obtained by performing a two-step procedure. First, the charge density is acquired by a fully self-consistent calculation for the collinear case.46 Second, by freezing the potential charge density, the SOC is treated as a perturbation in non-self-consistent calculations at different magnetization directions. Finally, MAE is obtained by taking the total energy differences between in-plane and off-plane magnetization orientations as
| MAE = E∥ − E⊥ | (1) |
3. Results and discussion
The crystal structure of the monolayer NiX3, as illustrated in Fig. 1(a), consists of three flat atomic layers. The Ni atoms form a 2D honeycomb lattice and are sandwiched between two X atomic planes. Each Ni ion is surrounded by six first-nearest-neighbor halogens arranged in an edge sharing distorted octahedra. Two Ni and six X atoms compose a (1 × 1) unit cell, which is similar to that of CrI3.1 To determine the preferred magnetic ground state structures of NiX3 systems, the collinear FM and AFM states are considered. We find (Table S1†) that the optimized FM is the ground state for all NiX3 and the next highest-energy configuration is the AFM-zigzag. The optimized structural parameters for the FM ground state are shown in Table S1.† For example, in the case of NiCl3, the lattice constant a and Ni–X bond length l are 5.940 and 2.296 Å, respectively, which are consistent with previously reported values.33 As expected, the lattice constant and bond length increase as the halogen anion's ionic radius increases. The Ni–X–Ni bond angle θ1 accounts for the superexchange interaction according to the Goodenough and Kanamori rules.47,48 The X–Ni–X axial angle θ2 is predicted to be slightly smaller than 180°, suggesting some deformation in the octahedral environment (see Fig. 1(a)). The θ1 and θ2 angles are nearly independent of the ligands, as they are roughly the same for all three systems. The cohesive energy per unit cell is calculated using the expression| Ecoh = Etotal − 2ENi − 6EX | (2) |
To investigate the in-plane stiffness of monolayer NiX3, the 2D Young's modulus is evaluated according to the following equation
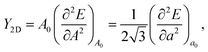 | (3) |
For all NiX3 systems, the spin-polarized FM ground state with a total magnetic moment of 2 μB per unit cell is observed and mainly arises from the partially filled d orbitals. The magnetic moment per Ni atom of the monolayer is listed in Table S1,† increases from 1.15 μB in NiCl3 to 1.23 μB in NiI3. In monolayer NiX3, because of the octahedral crystal field caused by the ligands, the Ni 3d orbitals split into two parts, namely, the lower t2g and the higher eg manifolds. Each Ni gives three electrons to form ionic bonding with the ligands as Ni3+, which can be verified by the Bader charge analysis.52 The residual seven electrons will fully occupy the spin-up and spin-down t2g orbitals, half-filled the spin-up eg orbitals, and the spin-down eg orbitals are empty. Thus, the Ni3+ ion shows an occupation states of d↑4↓3 with a magnetic moment of ∼1 μB.33 To estimate the TC of monolayer NiX3, the exchange parameter J is calculated from the energy difference between FM and AFM phases with the following equation49
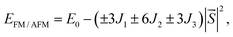 | (4) |
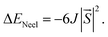 | (5) |
Here, 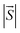 is the net magnetic moment at the Ni site. From the energy difference shown in Table S1,† the exchange parameters J of NiCl3, NiBr3 and NiI3 are 86, 103 and 118 meV, respectively. Consequently, with J available one can roughly estimate the TC from the mean-field expression:
is the net magnetic moment at the Ni site. From the energy difference shown in Table S1,† the exchange parameters J of NiCl3, NiBr3 and NiI3 are 86, 103 and 118 meV, respectively. Consequently, with J available one can roughly estimate the TC from the mean-field expression:
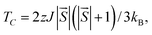 | (6) |
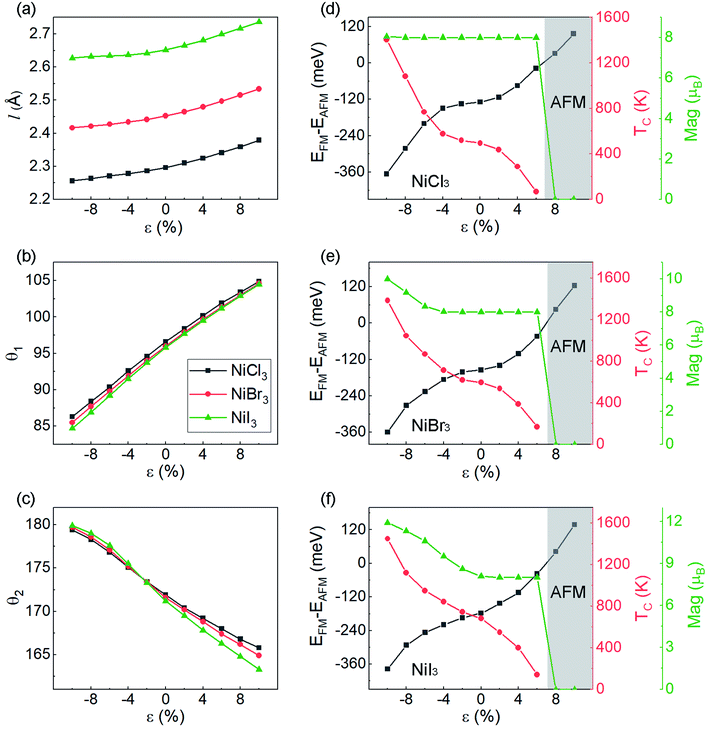
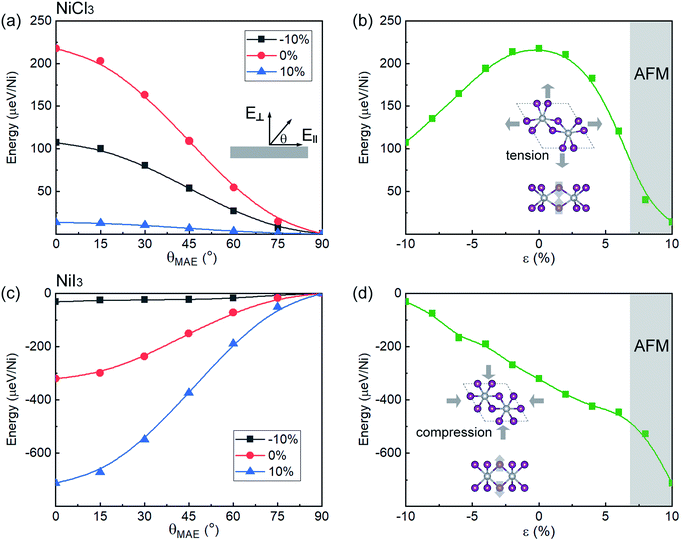
The calculated MAE for each monolayer is listed in Table S1.† The MAE of NiCl3 and NiBr3 are 217 and 263 μeV/Ni, respectively, which is larger than that of Cr in CrCl3 (24 μeV/Cr) and CrBr3 (159 μeV/Cr).29 Moreover, their magnitudes are far larger than that of cubic Ni (2.7 μeV/Ni).45 High MAE indicates that the energy required to flip the spin is high, and therefore inhibits spin fluctuation. With positive values, the easy axis for energetically favorable spontaneous magnetization is off-plane. The MAE significantly increases to 320 μeV/Ni in NiI3, though it is much smaller than that of Cr in CrI3 (803 μeV/Cr). The increasing of MAE in NiI3 originates from an anisotropic exchange interaction through a superexchange mechanism (Ni–X–Ni), which stems from the strong SOC in the heavier iodine ions.28 However, the negative value for NiI3 represents an in-plane preference for magnetization. The observed large MAE will be sufficient to stabilize FM ordering against heat fluctuation under certain temperature.
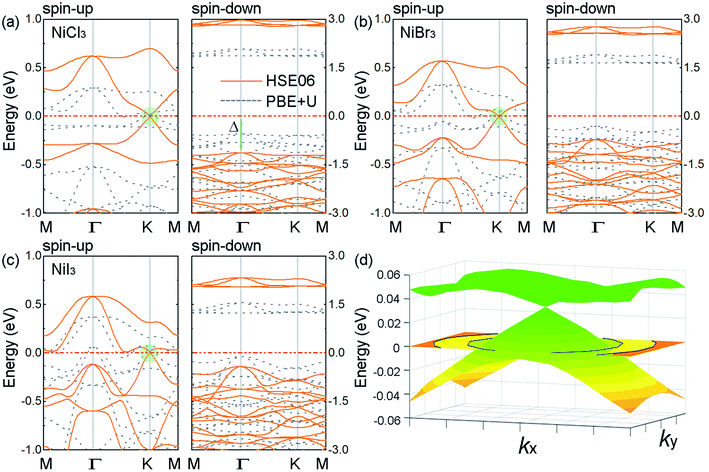
Fig. 2(a)–(c) show the electronic band structures of FM ground state for 2D NiCl3, NiBr3 and NiI3, respectively, employing the PBE+U and the hybrid HSE06 method. The similar band structures reveal that all NiX3 exhibit a DHM behavior which are independent of the exchange correlation functional. The spin-down channel is an insulator with an unusually large gap, whereas the spin-up channel shows Dirac cone at the high-symmetry K points, as marked by the shadow in Fig. 2. In order to confirm the suitable value of U for Ni-3d orbitals in this system, the band structures of NiI3 with U = 2, 3, 5 and 6 eV are also shown in Fig. S4.† With the increase of on-site Coulomb U, the insulator gap of spin-down channel is enlarged. The underestimation of band gap caused by PBE functional is gradually alleviated, but the distortion of the electronic structure around the Dirac cone is intensified. Since the total magnetic moment of the system remains unchanged, the U = 4 eV is used is this system, which is consistent with the previous report in the NiX2 (X = Cl, Br, and I) monolayers.42 Though the Dirac cone is located slightly above the Fermi level by the PBE+U, the HSE06 functional shifts it at the Fermi level. In Fig. 2(d), the 3D band structure of the Dirac cone at K point in monolayer NiCl3 clearly shows the linear energy-momentum dispersion. With the PBE+U, the band gaps of the spin-down channel are 2.41 eV, 1.93 eV, and 1.32 eV for the NiCl3, NiBr3, and NiI3, respectively. The PBE+U underestimates the gap of about 40% as compared to the corresponding HSE06 values of 3.92 eV, 3.25 eV, and 2.44 eV, respectively. In practical applications, the performance of a DHM system depends on two key parameters. One is the half-metallic gap, which is determined as the minimum between the lowest energy of conduction bands with respect to the Fermi level and the absolute value of the highest energy of valence bands.53 For the monolayer NiX3 with HSE06 method, the half-metallic gaps Δ are calculated to be 1.12 eV (NiCl3), 0.71 eV (NiBr3), and 0.42 eV (NiI3), which are large enough to prevent the spin-flip transition and the thermal disturbance at room temperature.4 The other is the carrier mobility in the conduction spin channel. From the Dirac cones highlighted in Fig. 2, the Fermi velocity vF of the carriers can be evaluated using linear fitting: ℏvF ≈ dE(k)/dk. With the increasing atomic number of the halogen, the Dirac cone of conduction band minimum (CBM) becomes flatter while there is no significant change of the cone of valence band maximum (VBM). The calculated vF of the Dirac electrons are 4.12 × 105, 3.66 × 105, and 3.23 × 105 m s−1 at the HSE06 level, respectively, comparable to the value of 5.3 × 105 m s−1 in silicene.34 The combination of 100% spin polarization and massless Dirac fermions renders the monolayer NiX3 a superior candidate material for high-speed spintronic devices and circuits.
To understand the origin of the single-spin Dirac state, we calculated the projected density of states (PDOS) of monolayer NiX3, as shown in Fig. S5.† In NiCl3, the linearly dispersive bands of the Dirac states around the Fermi level arise from the hybridization primary of the Ni-d states with the Cl-p derived py and pz states (and a smaller contribution of px). The relative strength of the X-p to the Ni-d contribution increases as the halogen atomic size increases down the group,26 where the Dirac cone is mainly composed by Ni-d states in NiCl3 and by I-p states in NiI3. According to the feature of the Dirac states, NiCl3 can be treated as d-state DHM in which the Dirac bands arise mainly form the d orbitals of transition-metal atoms, while NiI3 is similar to p-state DHM where the Dirac bands come mainly from the p orbitals of nonmetal atoms. As mentioned above, the octahedral crystal field splits Ni-d orbitals into a triple (dxy, dx2-y2, and dz2) and a doublet (dyz and dxz). For the spin-up channel, the triplet DOS is peaked at −0.7 eV and the doublet DOS stretches across the Fermi level. For the spin-down channel, they are peaked at −0.4 eV and 1.8 eV, respectively. In terms of the crystal field theory, the relative strength of the crystal field splitting (ΔEcf ∼ 0.7 eV) and spin exchange splitting (ΔEex ∼ 0.3 eV) leads to a low spin state for Ni atom (1 μB), which is in agreement with the Ni (d↑4↓3) spin configuration.
For practical applications, it is critical to further examine whether the FM coupling and DHM behavior can be preserved under external perturbation. Thus, we investigate the dependence of magnetic properties under different biaxial strains. In Fig. 3(a)–(c), the effect of strain on the structural parameters is presented. The bond length of Ni–X displays a weak strain dependency within the 10% range. The Ni–X–Ni angle θ1 change linearly with respect to strain. Within the 10% range from the equilibrium point, the curves display a linear shape with the same slope for the three halides. The axial bond angle θ2 has a similar behavior but tends to increase upon compression until it saturates near 180°. With the axial bond angle fully stretched (around −10% of compression for all monolayer NiX3), the system will achieve a higher degree of symmetry. In Fig. 3(d) and (e), we show the energy difference between the FM and AFM-zigzag phases as a function of ε for NiCl3, NiBr3, and NiI3. The evolution of TC calculated based on eqn (6) is also shown in Fig. 3. Both of them monotonously change with the biaxial strain in the range from −10% to 10%, but have the opposite tendency. However, unlike the previously reported strain modulation of monolayer chromium trihalides,29 the increase of compressive strain promotes the stability of the FM phase in monolayer NiX3, suggesting that in these cases the TC can be further increased with the introduction of compressive strain. According to the Goodenough and Kanamori rules.47,48 the superexchange interaction from the d–p–d path usually tends to be AFM if the cation–anion–cation bond angle θ1 is 180°, but it can be FM if the angle θ1 is near 90°. The monolayer NiX3 belongs to the latter because the Ni–X–Ni bond angle θ1 is 95° which is close to 90°. The previous report has demonstrated that the tunable magnetic and electronic properties of 2D halides originate from the competition between AFM direct nearest-neighbor d–d exchange and FM superexchange via halogen p states, which leads to a variety of magnetic states.49 The increase compressive strain enhanced both the AFM and FM exchange interaction, but the latter is more pronounced in monolayer NiX3. However, with a tensile strain, there is a phase transition to the AFM phase when the energy difference between FM and AFM orderings becomes greater than zero. As shown from the gray highlighted area in Fig. 3(d) and (e), this phase transition may occur when the tensile strain is greater than 6%. The total magnetic moments of the 2 × 2 × 1 supercell which contains eight Ni atoms are also displayed under different strain. In NiCl3, within the range of FM interaction, the total magnetic moments are sustained at 8 μB (1 μB per Ni).
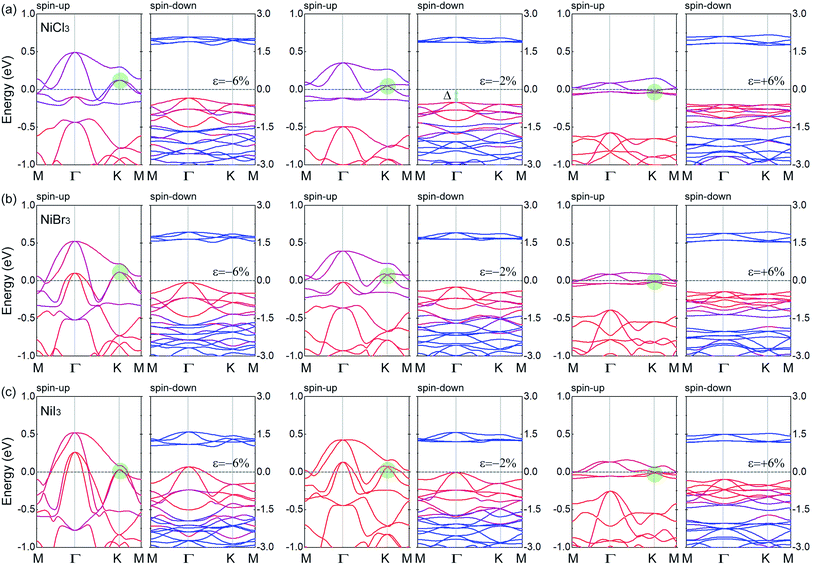
Fig. 4(a) shows the band structures of strained NiCl3 by the PBE+U method. The tensile strain will not affect the DHM behavior of the system and increase the half-metallic gap Δ of the spin-down channel. Although the half-metallic gap monotonously decreases with the increase of compressive strain, the HM nature dose not change, which is consistent with the constant trend of the magnetic moments (1 μB per Ni). However, when the compressive strain exceeds −6%, the Dirac cone in the spin-up channel is destroyed, and the system changes into a conventional HM. From the PDOS of the strained systems (Fig. S6(a)†), we find that the mainly contributed orbitals near the Fermi level have no significantly changed. Due to the enhanced orbital hybridization by the compressive strain, the localization of the electronic states is weakened, which causes the disappearance of the Dirac cone in spin-up channel and the decrease of the half-metallic gap in spin-down channel. In NiBr3 and NiI3 systems (Fig. 4(b) and (c)), the effect of tensile strain on the electronic structures and magnetic moments is similar to that in NiCl3. Nevertheless, with a larger anion radius, the influence of compressive strain on the enhancement of orbital hybridization is more obvious. In NiBr3, when ε = −6%, in addition to the destruction of the Dirac state in spin-up channel, the half-metallic gap in spin-down channel is almost reduced to zero. Further increasing the compressive strain, the system will be transformed from HM to magnetic metal with an increase of total magnetic moments (see Fig. 3(e)). As shown from Fig. 4(b) and S6(b),† the VBM of the band gap in spin-down channel are mainly contributed by Br-p orbitals. Therefore, the increase of the total magnetic moments mainly comes from the spin-splitting of Br-p orbitals under strong orbital hybridization. In NiI3 (see Fig. 4(c) and S6(c)†), the transition threshold is changed to ε = −2%.
The large MAE in monolayer NiCl3 (NiBr3) and NiI3 (see Table S1†), which is related with the off-plane and in-plane preference for magnetization, is of great importance for fabricating novel spintronic devices. In Fig. 5, one can also observe how MAE changes with biaxial strain. As shown in Fig. 5(a) and (c), the energy is calculated as a function of the angle of magnetization with respect to the basal plane θ (see the inset of Fig. 5(a)), which is 0° in-plane and 90° off-plane. No substantial difference in energy with respect to the different in-plane directions is observed by DFT calculations. Thus, the azimuthal contribution to energy is neglected. The dependency of the energy per Ni atom with respect to θ is given by54
E(θ) = E0 + k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θ) + k2 sin2(θ) + k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin4(θ), sin4(θ),
| (7) |
Fig. 6 shows the d-orbital resolved MAE of Ni in monolayer NiCl3 and NiI3. The main contributions from Ni in unstrained NiCl3 are due to the matrix element differences between dxy and dx2-y2 orbitals with positive value as well as dyz and dxz orbitals with the comparable smaller negative value, leading to the overall perpendicular magnetic anisotropy (PMA) contributions. When ε = −10%, the PMA contributions scatter to the in two matrix elements and a small increment of in-plane magnetic anisotropy (IMA) contributions appear simultaneously, leading to the decrease of overall MAE. When ε = +10%, although the PMA contributions from the matrix element differences between dxy and dx2-y2 orbitals increases significantly, the IMA contributions from the surrounded matrix elements also dramatically increase. Therefore, the resultant MAE in this stretched system significantly reduces. The variation tendency of MAE may depend on the strength of localization of the corresponding orbitals,55 as shown from the PDOS in Fig. S5(a) and S6(a).† Both the compressive and tensile strain suppress the localization of Ni d-orbitals near the Fermi level, causing the decrease of off-plane magnetization. In unstrained NiI3, the matrix element differences between Ni dxy and dx2-y2 gives the largest IMA contribution. With a compressive strain of −10%, the reduction and non-localization of IMA lead to a decline of the resultant MAE. However, when ε = +10%, the localized IMA contribution mainly comes from the matrix element differences between dyz and dxz orbitals and the PMA contributions from the surrounded matrix elements are significantly decreased, resulting in a substantial increase of the resultant MAE. In Fig. 4(c) and 5(c), as comparing with the unstrained system, the compressive strain still suppresses the localization, while tensile strain enhances the localization of Ni d-orbitals with a higher DOS near the Fermi level, consisting with the variation tendency of MAE. Similar to the case of monolayer CrI3, since the FM superexchange interaction with the Ni–I–Ni bond angle of about 90° is anisotropic due to the SOC,28 the biaxial strain will have further influence on the anisotropic exchange interaction by modulating the bond angle. Combining complete spin-polarization, high-speed conduction electrons, high TC, robust FM state and MAE, the monolayer NiX3 serves as a prototype for DHM, which will be extensively applied in the fields of efficient spin injection and high spin mobility.
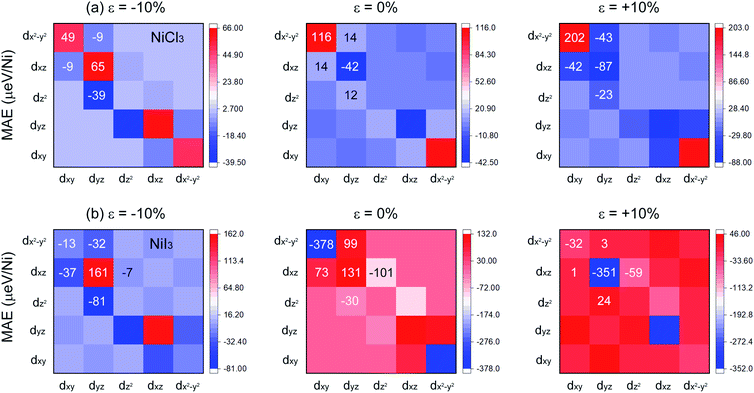 | ||
| Fig. 6 Orbital resolved MAE for Ni in (a) NiCl3 and (b) NiI3 with ε = −10%, ε = 0% (unstrained), and ε = +10%. | ||
4. Conclusions
In summary, we predict that the 2D Nickel trihalides is a family of intrinsic DHM which exhibits many unique properties, including 100% spin polarization, massless Dirac fermions with high carrier mobility, which is a superior candidate material for efficient spin injection and high spin mobility. The NiX3 is dynamically and thermodynamically stable up to high temperature and hence could be synthesized experimentally by an exfoliation process commonly employed in other 2D van der Waal crystals. The magnetic moments of about 1 μB per Ni3+ ion is observed with high Curie temperature and large MAE. Furthermore, we have studied the effect of biaxial strain and have determined the strain dependence of the atomic structure and electronic and magnetic properties of the monolayer NiX3. The increase of compressive strain promotes the stability of the FM phase, suggesting that in these cases the TC can be further increased with the introduction of compressive strain. The MAE also exhibits a strain dependence and has different variation trend for the off-plane magnetized NiCl3 (NiBr3) and the in-plane magnetized NiI3. Combining these unique properties, the monolayer NiX3 serves as a prototype for DHM, which will open the way towards the development of high-performance spintronic devices.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was partially supported by the National Natural Science Foundation of China (no. 11704282), Natural Science Foundation of Tianjin City (no. 18JCQNJC72900), Education Commission Research Project of Tianjin City (no. 2017KJ251), and Rector's Fund of China Academy of Engineering Physics (no. YZJJLX2016002).References
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS.
- I. Žutić, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef.
- C. Felser, G. H. Fecher and B. Balke, Angew. Chem., Int. Ed., 2007, 46, 668–699 CrossRef CAS.
- D. D. Awschalom and M. E. Flatte, Nat. Phys., 2007, 3, 153–159 Search PubMed.
- X. Li and J. Yang, Natl. Sci. Rev., 2016, 3, 365–381 Search PubMed.
- R. A. de Groot, F. M. Mueller, P. G. v. Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- P. Mavropoulos, M. Ležaić and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174428 CrossRef.
- C. Si, J. Zhou and Z. Sun, ACS Appl. Mater. Interfaces, 2015, 7, 17510–17515 CrossRef CAS.
- T. Zhao, J. Zhou, Q. Wang, Y. Kawazoe and P. Jena, ACS Appl. Mater. Interfaces, 2016, 8, 26207–26212 CrossRef CAS.
- Q. Wu, Y. Zhang, Q. Zhou, J. Wang and X. C. Zeng, J. Phys. Chem. Lett., 2018, 9, 4260–4266 CrossRef CAS PubMed.
- A. V. Kuklin, S. A. Shostak and A. A. Kuzubov, J. Phys. Chem. Lett., 2018, 9, 1422–1428 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS.
- S. V. Morozov, K. S. Novoselov, M. I. Katsnelson, F. Schedin, D. C. Elias, J. A. Jaszczak and A. K. Geim, Phys. Rev. Lett., 2008, 100, 016602 CrossRef CAS.
- L. C. L. Y. Voon, J. J. Zhu and U. Schwingenschlogl, Appl. Phys. Rev., 2016, 3, 040802 Search PubMed.
- J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang, C. C. Liu, H. Zhong, N. Han, J. Lu, Y. Yao and K. Wu, Prog. Mater. Sci., 2016, 83, 24–151 CrossRef CAS.
- L. Z. Zhang, Z. F. Wang, S. X. Du, H. J. Gao and F. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 161402 CrossRef CAS.
- S. Zhang, Y. Hu, Z. Hu, B. Cai and H. Zeng, Appl. Phys. Lett., 2015, 107, 022102 CrossRef.
- H. Ishizuka and Y. Motome, Phys. Rev. Lett., 2012, 109, 237207 CrossRef.
- Y. Li, D. West, H. Huang, J. Li, S. B. Zhang and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 201403 CrossRef.
- L. Wei, X. Zhang and M. Zhao, Phys. Chem. Chem. Phys., 2016, 18, 8059–8064 RSC.
- X. Zhang, A. Wang and M. Zhao, Carbon, 2015, 84, 1–8 CrossRef CAS.
- J. He, S. Ma, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 2518–2526 RSC.
- Q. Sun and N. Kioussis, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 094408 CrossRef CAS.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136 CrossRef CAS.
- J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002 CrossRef.
- L. Webster and J. A. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 144411 CrossRef CAS.
- M. H. Kryder, Thin Solid Films, 1992, 216, 174–180 CrossRef CAS.
- G. A. Prinz, Science, 1998, 282, 1660–1663 CrossRef CAS.
- R. Sbiaa, H. Meng and S. N. Piramanayagam, Phys. Status Solidi RRL, 2011, 5, 413–419 CrossRef CAS.
- J. He, X. Li, P. Lyu and P. Nachtigall, Nanoscale, 2017, 9, 2246–2252 RSC.
- A. Molle, C. Grazianetti, L. Tao, D. Taneja, M. H. Alam and D. Akinwande, Chem. Soc. Rev., 2018, 47, 6370–6387 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- G. Kresse, J. Furthmüller and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13181–13185 CrossRef CAS.
- M. Fuchs and M. Scheffler, Comput. Phys. Commun., 1999, 119, 67–98 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- M. Lu, Q. Yao, C. Xiao, C. Huang and E. Kan, ACS Omega, 2019, 4, 5714–5721 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys, 1990, 41, 11919–11937 CrossRef CAS PubMed.
- S. Steiner, S. Khmelevskyi, M. Marsmann and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 224425 CrossRef.
- J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- W.-B. Zhang, Q. Qu, P. Zhu and C.-H. Lam, J. Mater. Chem. C, 2015, 3, 12457–12468 RSC.
- A. Politano and G. Chiarello, Nano Res., 2015, 8, 1847–1856 CrossRef CAS.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- Z. Liu, J. Liu and J. Zhao, Nano Res., 2017, 10, 1972–1979 CrossRef CAS.
- A. N. Bogdanov and I. E. Dragunov, Low Temp. Phys., 1998, 24, 852–857 CrossRef CAS.
- B. S. Yang, J. Zhang, L. N. Jiang, W. Z. Chen, P. Tang, X. G. Zhang, Y. Yan and X. F. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 174424 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06474e |
| This journal is © The Royal Society of Chemistry 2019 |