Harnessing inherently hierarchical microstructures of plant biomass to construct three-dimensional nanoporous nitrogen-doped carbons as efficient and durable oxygen reduction electrocatalysts

Abstract

Exploiting the natural structures of plants to prepare high-performance carbon-based electrocatalysts is highly desirable. Herein, the inherently hierarchical microstructures of Euphorbia tirucalli (E. tirucalli) are employed to construct three-dimensional nanoporous nitrogen-doped carbons that act as efficient and durable electrocatalysts towards the oxygen reduction reaction (ORR). During the preparation process, agar is used in order to reduce the dissipation of nitrogen and to protect the fine structures of E. tirucalli. The as-prepared ORR catalyst, with a high density of pyridinic and graphitic nitrogens, presents a high catalytic activity (onset potential of 0.97 V vs. RHE, half-wave potential of 0.82 V vs. RHE, limiting current density of 5.64 mA cm⁻² and Tafel slope of 59 mV dec⁻¹), four-electron pathway, low peroxide yield, long-term stability (current retention of 95.3% after 50 000 s) and strong methanol tolerance in 0.1 M KOH, all superior to the benchmark 20% Pt/C commercial catalyst. This work demonstrates an effective method for the utilization of inherently hierarchical microstructures of plant biomass to make efficient and durable carbon-based metal-free ORR electrocatalysts.

---

Introduction

Efficient electrocatalysts for the oxygen reduction reaction (ORR), one of essential ingredients to achieve the optimal performance in fuel cells, have been intensively investigated for decades.^1,2 The platinum-group metals (PGMs) and their alloys, possessing high electrocatalytic activity towards the ORR, are being systematically studied in a wide variety of fuel cell test beds.^3–6 Nonetheless some inferior factors of the PGMs, such as their scarcity, prohibitive cost, poisoning by impurities and poor durability, do hinder the commercial manufacture of PGM-based materials as fuel cell catalysts.^7,8 Consequently, much attention has been paid to searching for PGM-free alternatives that are exemplified by metal-free heteroatom-doped carbonaceous materials, among which, nitrogen-doped carbons are thought of as highly promising ORR electrocatalysts.^9–14

Plant biomass is a sustainable and renewable carbon source for the production of carbonaceous catalysts towards the ORR by virtue of its superiority in low price and plentiful supply.^15–22 Plants possess plenty of naturally micro/nanoscale structures, as exemplified by vascular bundles, epidermis and ground tissues. It is thus feasible to utilize the inherently hierarchical microstructures of plants to prepare three-dimensional nanostructured materials that can hardly be constructed by conventional ways. However, despite this, there have been very few reports on the utilization of fine structures of plant biomass to make hierarchical micro/nanostructured carbon-based electrocatalysts. Further, Euphorbia tirucalli (E. tirucalli), known as pencil tree, is a hydrocarbon plant that is the potential bioenergy and medicinal crop.^23–25 As a drought tolerant plant, E. tirucalli has abundant vascular bundles and special epidermis structures that can be exploited to prepare high-performance carbon-based materials. To the best of our knowledge, an effective route to ORR electrocatalysts by the use of E. tirucalli has not been demonstrated.

In this paper, E. tirucalli is harnessed as a bio-mould to prepare efficient and durable carbon-based metal-free ORR electrocatalysts. Agar is employed during the preparation process, for at least two reasons: (i) the agar hydrogel is capable of anchoring the nitrogen dopant on the surface of E. tirucalli and of reducing the dissipation of nitrogen; (ii) the agar hydrogel is able to preserve the naturally fine structures of E. tirucalli. The as-made nanoporous nitrogen-doped carbonaceous catalyst, consisting of high specific surface area, optimized pore width distribution and high-concentration nitrogen doping, manifests superior ORR performance to the commercial 20% Pt/C catalyst. The results have important implications for the utilization of inherently hierarchical microstructures of plant biomass for the good of oxygen reduction electrocatalysts.

Experimental

Materials preparations

E. tirucalli was collected in Wenchang City, Hainan Province (China's tropical island) and cleaned and dried before use. The biochar was made from the pyrolysis of E. tirucalli at 400 °C for 2 h at a heating rate of 5 °C min⁻¹ with a continuous flow of N₂ (80 cm³ min⁻¹) controlled by a mass flow controller (Smart-Trak 100, Sierra Instruments) in a tube furnace (OTF-1200X, MTI-Kejing). Subsequently, 3 g of melamine, 1 g of the biochar, 1 g of agar and 1 g of KOH was successively added in 100 mL of hot deionized water at 90 °C under continuous stirring, with a ten minute interval between the two additions, allowing each addition to be fully dissolved or evenly distributed. In order to prevent the decomposition of KHCO₃, the mixture cooled to 60 °C before 2 g of KHCO₃ was added. Then the uniform mixture cooled down to room temperature until it became a hydrogel, followed by being dried in an oven at 80 °C overnight. The dried gel-like material was heated at 800 °C for 2 h at a heating rate of 5 °C min⁻¹ with a continuous flow of N₂ (80 cm³ min⁻¹) in the tube furnace, followed by being washed with 1 mol L⁻¹ of HCl solution for 2 h and then filtered and rinsed with deionized water until the filtrate became pH neutral and finally dried at 80 °C overnight. The product is denoted by NEA (N = nitrogen doping, E = E. tirucalli and A = agar). To investigate the roles of E. tirucalli, agar and melamine, the carbonaceous materials that dispensed with E. tirucalli, agar and melamine were prepared, with the other conditions keeping the same, denoted by NA, NE and EA, respectively.

Physicochemical characterizations

Scanning electron microscopy (SEM) images were collected on an FEI Quanta 250 microscope. Transmission electron microscopy (TEM), high-resolution TEM (HRTEM) images and selected area electron diffraction (SAED) patterns were recorded on an FEI Tecnai G2 F20 field-emission microscope. X-ray diffraction (XRD) patterns were obtained on a Bruker D8 ADVANCE diffractometer equipped with a CuK_α radiation source (λ = 1.54178 Å). Raman spectra were obtained on a Bruker Senterra confocal Raman spectrometer (λ_ex = 532 nm). N₂ adsorption/desorption isotherms at 77 K were carried out on a Quantachrome Autosorb-iQ instrument. Brunauer–Emmett–Teller (BET) specific surface areas were calculated from the linear range of the BET plot and pore width distribution curves were obtained using the quenched solid density functional theory (DFT) method. X-ray photoelectron spectroscopy (XPS) results were acquired on a Thermo Fisher ESCALAB 250Xi spectroscope with an excitation source of AlK_α radiation (1486.6 eV).

Electrochemical measurements

All electrochemical measurements, including cyclic voltammetry (CV), linear sweep voltammetry (LSV) and chronoamperometry, were carried out using an Ivium potentiostat (IviumStat.h, Ivium Technologies) with an electrode rotator (AFMSRCE, Pine Research) at a constant temperature of 25 °C (kept by a circulating water bath) in a standard three-electrode system in which a Ag/AgCl electrode (3.5 M KCl, 0.205 V vs. SHE) acted as the reference electrode, a platinum coil as the counter electrode and a catalyst-loaded glassy carbon rotating disk electrode (RDE, 5 mm in diameter) as the working electrode. To load a catalyst, the surface of a glassy carbon RDE was successively polished with 1.5 μm and 50 nm α-Al₂O₃ slurries, followed by being washed with ultrapure water and ethanol prior to drop-casting of a catalyst ink. The detailed preparation of the catalyst ink was as follows: 3 mg of an as-made material or 1 mg of the commercial JM 20% Pt/C catalyst was ultrasonically dispersed in a mixture containing 170 μL of ultrapure water, 70 μL of isopropanol and 10 μL of Nafion (5 wt%) for 1 h. Subsequently, 10 μL of the catalyst ink was dropped onto the polished glassy carbon RDE surface by a pipette and air-dried at room temperature. Measured potentials in this paper were converted to the reversible hydrogen electrode (RHE) scale based on the Nernst equation unless otherwise stated: E_RHE = E_Ag/AgCl + 0.205 V + 0.059 × pH (25 °C). Electron-transfer number (n) values can be calculated by the slopes of linear fit lines based on the Koutecky–Levich equation:²²where j is the measured current density, j_K is the kinetic current density, ω is the RDE rotating rate, and B is given by:²²

B = 0.2nFC₀D₀^2/3ν^−1/6 (2)

where n is the electron-transfer number, F is the Faraday constant, C₀ is the bulk concentration of O₂, D₀ is the O₂ diffusion coefficient and ν is the kinetic viscosity of the electrolytes at 25 °C. The n values can be also obtained from the rotating ring-disk electrode (RRDE) measurement, along with the peroxide yield (peroxide %), according to the following equations:²²where I_d is the disk current density, I_r is the ring current density and N is the current collection efficiency (0.37) of the Pt ring.

Results and discussion

As shown in Fig. S1,† the outward appearance of living E. tirucalli exhibits lots of branched, cylindrical stems. According to the SEM images of fresh E. tirucalli (Fig. S2†), (i) many deep grooves can be observed on the external surface of a length of E. tirucalli stem that has shrunk due to sputtering a gold film in a vacuum, as displayed in Fig. S2a;† moreover, the magnified SEM images (Fig. S2b†) show that tiny openings, known as stomata, with width of 10–20 μm (Fig. S2c†), are widely distributed along the grooves, which are separated by longitudinally rough protuberances; (ii) as shown in Fig. S2d–g,† the cross-section of E. tirucalli stem presents numerous vascular bundles, capable of acting as flow channels for mass transport of precursors; (iii) the internal part of E. tirucalli (Fig. S2h and S2i†) shows plenty of vascular channels and pore structures. Thus fresh E. tirucalli has abundant naturally hierarchical microstructures that are favourable for the formation of three-dimensional micro/nanostructured, high-surface-area carbons. After the pyrolysis of E. tirucalli at 400 °C, the obtained biochar is able to maintain the original morphological features: grooves and stomata are still distributed on the external surface (Fig. 1a), and the uneven protuberances contain vast amounts of nap-like, sub-microscale particles (Fig. 1b and c), indicating that the fine structures of E. tirucalli can withstand high temperatures; vascular channels and pore structures in the internal biochar are also preserved, as shown in Fig. 1d–f. All the hierarchical microstructures are capable of supplying ample reaction sites that accommodate precursor molecules/ions for the subsequent activation and doping. Fig. 2a and b show the SEM images of NEA at different magnifications. After the one-step activation/doping process, the millimeter-scale structures of E. tirucalli disappear whereas its micrometer-scale structures are retained, showing that NEA possesses three-dimensional hierarchical frameworks with interconnected pores and wrinkled surface, consistent with the microscale morphologies of the E. tirucalli biochar. It can be judged that E. tirucalli, functioning as a mould, lends itself to being made into materials that inherit the three-dimensional hierarchical, highly porous structures from the plant. To corroborate this point, the material that dispensed with E. tirucalli, that is, NA, was prepared by the same activation/doping process. As exhibited in Fig. S3a and S3d,† the morphology of NA presents a mass of bulky lumps, completely different from that of NEA, proving that the coral-like structures of the latter originate from E. tirucalli instead of agar. Fig. 2c and d display the TEM images of NEA with different magnifications. It can be found that NEA presents the morphologies of hierarchical micro/meso/macropores, bumpy surface and rugged edges, which can provide large specific surface areas, many reaction sites and easy gas/ion access. The SAED pattern in the inset of Fig. 2d exhibits diffuse rings, indicative of the amorphous nature of NEA,²⁶ which can be further confirmed by the HRTEM results. Fig. 2e and f show the HRTEM images of NEA at different regions, indeed displaying the amorphous and porous features of the material. TEM and SEM images of NE and EA are exhibited in Fig. S3.† It can be observed that the addition of agar is capable of preserving the fine structures of E. tirucalli which otherwise undergo wear and tear during the preparation process without the protection of the hydrogel formed by this polysaccharide. In short, the naturally hierarchical microstructures of E. tirucalli, with the assistance of agar, can be exploited as a bio-mould to construct carbonaceous materials with highly porous, three-dimensional micro/nanostructured interfaces, which are otherwise absent when dispensing with the plant biomass or agar.

Fig. 1 SEM images of the external surface (a–c) and the internal part (d–f) of the E. tirucalli biochar.

Fig. 2 SEM images of NEA at different magnifications (a) and (b); TEM images of NEA at different magnifications (c) and (d), the inset of (d) showing the SAED pattern; HRTEM images of NEA at different regions (e) and (f).

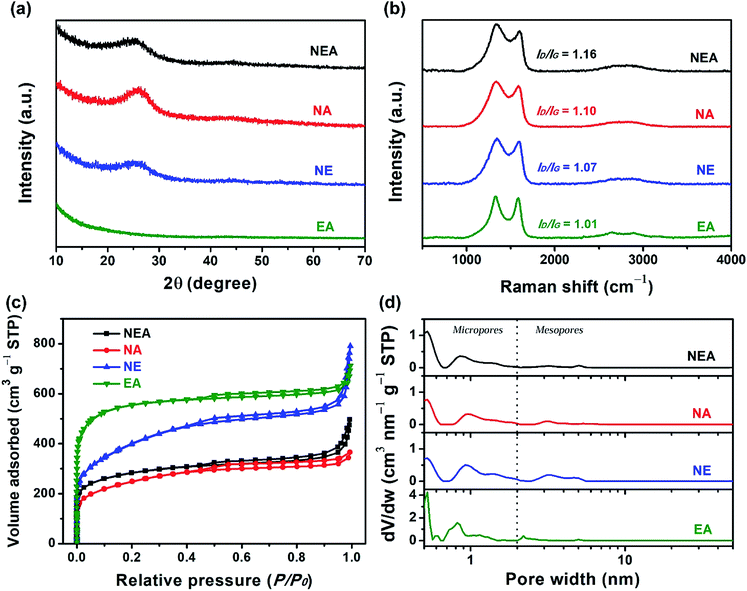
The XRD patterns of NEA, NA and NE (Fig. 3a) each present two weak and broad diffraction peaks: one is centred at 25.5° and the other at 43.7° is negligible and hardly observable, corresponding to the (002) and (100) diffraction planes of graphitic carbon, respectively,¹⁸ whereas the XRD pattern of EA shows almost no diffraction peaks, proving the overwhelmingly amorphous feature and poor crystallinity of the four materials; furthermore, the high-intensity curves in the low-angle regions (10–15°) for NEA, NA, NE and EA suggest the existence of many micropores,²⁷ as discussed below. Moreover, the Raman analysis can be used to evaluate the defective degree of carbonaceous materials. Fig. 3b shows the Raman spectra of NEA, NA, NE and EA. The D band at 1340 cm⁻¹ and the G band at 1590 cm⁻¹ are associated with the defective and graphitization degrees, respectively.¹³ The intensity ratio of the D band to the G band (I_D/I_G) can thus reflect the defective degree.¹³ The I_D/I_G values of NEA, NA, NE and EA were calculated to be 1.16, 1.10, 1.07 and 1.01, respectively. The decreasing I_D/I_G values can be ascribed to nitrogen doping,³¹ indicating that the order of nitrogen doping degrees (concentrations) should be NEA > NA > NE > EA, as confirmed below.

Fig. 3 (a) XRD patterns of NEA, NA, NE and EA; (b) Raman spectra of NEA, NA, NE and EA; (c) N₂ adsorption/desorption isotherms of NEA, NA, NE and EA; (d) pore width distribution curves of NEA, NA, NE and EA based on the DFT model.

Specific surface areas and pore width distributions, a measure of the interface roughness of materials, have considerable influence over electrocatalytic activity. N₂ adsorption/desorption isotherms of NEA, NA, NE and EA are displayed in Fig. 3c. All the isotherms exhibit the steep uptakes of N₂ at the relative pressures (P/P₀) smaller than 0.01 and pronounced hysteresis loops in the P/P₀ range of 0.45–0.95, which are characteristic of the Type I isotherm and of the Type H4 hysteresis loop, respectively.²⁸ According to the IUPAC technical report,²⁸ it follows that NEA, NA, NE and EA each have a good number of micropores and mesopores. The BET specific surface areas of NEA, NA, NE and EA are 1028, 881, 1427 and 2100 m² g⁻¹, respectively, showing that KHCO₃ is a highly effective porogen and that the addition of melamine lowers specific surface areas. Fig. 3d shows pore width distribution curves of NEA, NA, NE and EA based upon the DFT model. The DFT specific surface areas of the four materials are consistent with their counterparts based on the BET method, albeit not exactly the same. It can be substantiated that hierarchical micro/mesopores indeed exist in the four materials. Do all micropores play a role in electrochemical performance? this depends on the hydrated diameters of electrolyte ions relative to the width of micropores. Micropores with width smaller than 0.7 nm, known as narrow micropores or ultramicropores,²⁸ are not easily accessible to K⁺ and OH⁻ as the hydrated diameters of these common electrolyte ions are between 0.6 and 0.7 nm,^29,30 thereby it becoming hard to form triple-phase boundaries that electrode is in contact with electrolyte and gas, where the ORR takes place.³¹ Further, wide micropores of width >0.7 nm, termed as effective micropores,^13,20,27 permit the electrolyte ions to permeate through/into pores and to come into contact with the inner walls of pores, where reaction sites emerge. Specific surface areas and pore volumes of narrow micropores (width: <0.7 nm), effective micropores (width: 0.7–2 nm) and mesopores (width: 2–50 nm) of NEA, NA, NE and EA based on the DFT model are summarized in Table 1. EA has the largest surface area (909 m² g⁻¹) and pore volume (0.423 cm³ g⁻¹) of the effective micropores, whereas NE owns the largest surface area (398 m² g⁻¹) and pore volume (0.490 cm³ g⁻¹) of mesopores. It can be deduced that E. tirucalli is conducive to the mesopore development due to its inherently hierarchical microstructures whereas melamine is inclined to reduce micropores and agar tends to curtail mesopores. In spite of the fact that melamine and agar reduce surface areas and pore volumes of the hierarchical micro/mesopores, they combine to play a crucial role in the catalytic activity towards the ORR, thanks to their abilities to markedly increase nitrogen doping concentrations.

Table 1 Specific surface areas and pore volumes of the segmented pores of NEA, NA, NE and EA based on the DFT model^a

Material	SDFT (m^2 g^−1)	S<0.7 (m^2 g^−1)	S0.7–2 (m^2 g^−1)	S2–50 (m^2 g^−1)	VDFT (cm^3 g^−1)	V<0.7 (cm^3 g^−1)	V0.7–2 (cm^3 g^−1)	V2–50 (cm^3 g^−1)
a SDFT: DFT specific surface area; S<0.7: specific surface area of narrow micropores (width: <0.7 nm); S0.7–2: specific surface area of effective micropores (width: 0.7–2 nm); S2–50: specific surface area of mesopores (width: 2–50 nm); VDFT: DFT total pore volume; V<0.7: pore volume of narrow micropores (width: <0.7 nm); V0.7–2: pore volume of effective micropores (width: 0.7–2 nm); V2–50: pore volume of mesopores (width: 2–50 nm).
NEA	1119	621	338	160	0.593	0.157	0.182	0.254
NA	877	394	295	188	0.471	0.099	0.174	0.198
NE	1337	460	479	398	0.881	0.115	0.276	0.490
EA	2080	866	909	305	0.913	0.230	0.423	0.260

---

Nitrogen doping concentrations and nitrogen species distributions of materials can be examined by the XPS measurements. Fig. 4a shows the XPS survey spectra of NEA, NA, NE and EA. All the four materials contain the strong C 1s peaks and the relatively weak O 1s peaks, whereas NEA, NA and NE have the noticeable N 1s peaks except EA. As listed in Table 2, the nitrogen doping concentrations of NEA, NA, NE are 16.41, 12.93 and 10.01 at%, respectively, all beyond the 10% level, showing the high-level nitrogen doping; on the other hand, EA has no detectable amount of nitrogen, indicating that the nitrogen content of NEA, NA and NE originates from melamine rather than agar or E. tirucalli itself. It is worth noting that the nitrogen amount of NEA is larger than that of either NA or NE, which can be ascribed to the following factors: (i) agar, acting like glue, allows melamine to adhere and bind tightly to E. tirucalli, thereby effectively inhibiting the dissipation of nitrogen; (ii) the complex three-dimensional hierarchical microstructures of E. tirucalli put obstacles in the way of melamine becoming detached and lost. Therefore, agar and E. tirucalli have combined to create the highest nitrogen doping concentration (16.41 at%), while any single factor can hardly reach such a high level (sticking by agar glue seems more effective in ‘fixing’ melamine than steric hinderance caused by the intrinsic structures of E. tirucalli as NA has the higher nitrogen amount than NE). As displayed in Fig. 4b–d, the high-resolution XPS N 1s spectra of NEA, NA and NE can be deconvoluted into four peaks corresponding to pyridinic N (centred at 398.4 eV), pyrrolic N (centred at 400.1 eV), graphitic N (centred at 401.0 eV) and oxidized N (centred at 403.6 eV).^18,32 It has been reported that pyridinic and graphitic nitrogens play a vital role in the ORR catalytic activity.^33–37 According to Table 2, the combined amounts of pyridinic N and graphitic N account for 76.36, 62.73 and 56.28% of the total amounts of nitrogen of NEA, NA and NE, respectively. Consequently, NEA possesses both the highest level of total nitrogen and the largest amounts of pyridinic N and graphitic N among the four materials, suggesting its ability to operate as a high-performance ORR catalyst.

Fig. 4 (a) XPS survey spectra of NEA, NA, NE and EA; high-resolution XPS N 1s spectra of NEA (b), NA (c) and NE (d).

Table 2 Atomic percentages of nitrogen content and the relative proportions of the four N species (pyridinic N, pyrrolic N, graphitic N and oxidized N) of NEA, NA and NE

Material	N (at%)
NEA	16.41	0.5953	0.1761	0.1683	0.0603
NA	12.93	0.4476	0.2724	0.1797	0.1002
NE	10.01	0.3926	0.2681	0.1702	0.1690

---

We estimated the integrated concentrations of pyridinic and graphitic nitrogens per unit surface area based upon the specific surface areas of the effective micropores and mesopores as given in Table 1. For NEA, a calculation based on the nitrogen doping concentration of 16.41 at%, the proportion of pyridinic N and graphitic N of 76.36% and the specific surface area of the effective micropores and mesopores of 498 m² g⁻¹ gave an integrated concentration of pyridinic and graphitic nitrogens of 0.252 at‰ per square metre per gram; likewise, for NA, a calculation based on the nitrogen doping concentration of 12.93 at%, the proportion of pyridinic N and graphitic N of 62.73% and the specific surface area of the effective micropores and mesopores of 483 m² g⁻¹ gave an integrated concentration of pyridinic and graphitic nitrogens of 0.168 at‰ per square metre per gram; and for NE, a calculation based on the nitrogen doping concentration of 10.01 at%, the proportion of pyridinic N and graphitic N of 56.28% and the specific surface area of the effective micropores and mesopores of 877 m² g⁻¹ gave an integrated concentration of pyridinic and graphitic nitrogens of 0.064 at‰ per square metre per gram. These values are comparable based on the reasonable approximation that NEA, NA and NE have the roughly equal molar mass because carbon occupies the majority of elements in the three materials and has the relative atomic mass close to nitrogen and oxygen. Therefore, NEA possesses the highest integrated concentration of pyridinic and graphitic nitrogens per unit surface area, NA comes second and NE takes third place; in other words, NEA has the highest density of pyridinic N and graphitic N amongst the three nitrogen-containing materials, indicating its highest catalytic activity towards the ORR, as mentioned below.

Fig. 5a shows the CV curves of NEA, NA, NE and EA in the N₂ and O₂-saturated 0.1 M KOH solutions without rotation. Cathodic peaks that can be ascribed to oxygen reduction exist in the CVs of NEA, NA, NE and EA in the O₂-saturated KOH solution whereas they disappear in the N₂-saturated solution, showing that all the four materials do have the ORR catalytic activity in 0.1 M KOH. Further, NEA owns the oxygen reduction peak centred at 0.85 V vs. RHE, more positive than the cathodic peaks of the other three materials, showing that it has the highest ORR activity. Fig. 5b displays the LSV curves of NEA, NA, NE, EA and 20% Pt/C in the O₂-saturated 0.1 M KOH at a rotating rate of 1600 rpm. At least three major indices of the ORR kinetics can be read from the LSV curves: onset potentials (E_onset), half-wave potentials (E_1/2) and limiting current density (j_L). The E_onset values of NEA, NA, NE, EA and 20% Pt/C are 0.97, 0.94, 0.91, 0.84 and 0.97 V vs. RHE, the E_1/2 values of NEA, NA, NE, EA and 20% Pt/C are 0.82, 0.80, 0.78, 0.72 and 0.81 V vs. RHE, and the j_L values of NEA, NA, NE, EA and 20% Pt/C are 5.64, 5.18, 4.58, 3.40 and 5.40 mA cm⁻², respectively. It can be thus deduced that NEA has the best ORR performance, even surpassing the commercial Pt/C catalyst. Apart from Pt/C, the descending order of catalytic activities towards the ORR among the four carbonaceous materials is NEA > NA > NE > EA, which is consistent with the order of their densities of pyridinic N and graphitic N. The ORR kinetics are further investigated by the rotating (ring) disk electrode method. Fig. 5c shows the LSV curves of NEA at rotating rates that range from 400 to 2025 rpm in the O₂-saturated 0.1 M KOH solution. Fitted straight lines, known as the Koutecky–Levich plots, can be derived from a set of LSV curves with different rotating rates based on the Koutecky–Levich equation. From the linear Koutecky–Levich plots of NEA (Fig. 5d), the electron-transfer numbers per O₂ molecule of the NEA-catalyzed ORR were calculated to be 3.80–4.03, revealing that the ORR under the catalysis of NEA overwhelmingly undergoes the four-electron process. The electron-transfer numbers per dioxygen molecule can also be obtained from the RRDE measurements. The ring and disk currents of NEA and Pt/C are displayed in Fig. S4.† According to eqn (3), the electron-transfer numbers of the ORR catalyzed by NEA and Pt/C are 3.92–3.98 and 3.80–3.97 over a potential range of 0–0.6 V vs. RHE, respectively, as presented in the top panel of Fig. 5e, further confirming the four-electron pathway. Obviously, the four-electron ORR pathway is superior to the two-electron counterpart in energy conversion efficiency of fuel cells.^38,39 Additionally, the product of the two-electron reduction of O₂ is peroxide that can undermine material activity and stability whereas the four-electron pathway ensures the complete reduction of a dioxygen molecule to harmless water (or hydroxide in alkaline media).³¹ Put simply, the lower peroxide yield is, the more favourable it is for fuel cell durability. The amount of peroxide can be monitored by the RRDE analysis. The bottom panel of Fig. 5e shows that the peroxide yield of the NEA-catalyzed ORR is 1.13–4.10% based on eqn (4), smaller than that catalyzed by Pt/C (1.23–10.6%) across a range of 0–0.6 V vs. RHE. Hence NEA possesses the superior ORR performance to the commercial 20% Pt/C catalyst in terms of both electron-transfer number and peroxide yield. Furthermore, it is well recognized that the smaller the Tafel slope the faster is the ORR kinetics.⁴⁰ The Tafel plots of NEA and Pt/C in 0.1 M KOH are exhibited in Fig. 5f. The Tafel slope of NEA is 59 mV dec⁻¹, smaller than that of Pt/C (72 mV dec⁻¹), showing that the improvement in the ORR electrocatalytic performance of the former.

Fig. 5 (a) CV curves of NEA, NA, NE and EA in the N₂ (thin lines) and O₂-saturated (thick lines) 0.1 M KOH solutions without rotation at 25 °C; (b) LSV curves of NEA, NA, NE and EA in the O₂-saturated 0.1 M KOH with a scan rate of 10 mV s⁻¹ at a rotating rate of 1600 rpm at 25 °C; (c) LSV curves of NEA in the O₂-saturated 0.1 M KOH with a scan rate of 10 mV s⁻¹ at different rotating rates (400, 625, 900, 1225, 1600 and 2025 rpm); (d) Koutecky–Levich plots of NEA in the O₂-saturated 0.1 M KOH at 25 °C; (e) RRDE measurements in the O₂-saturated 0.1 M KOH with a scan rate of 10 mV s⁻¹ at a rotating rate of 1600 rpm at 25 °C: electron-transfer number curves (top) and peroxide yield curves (bottom) of NEA and 20% Pt/C; (f) Tafel plots of NEA and 20% Pt/C in the O₂-saturated 0.1 M KOH at 25 °C.

The catalyst durability and susceptibility to environmental poisons (methanol crossover in this case) have been evaluated by chronoamperometric measurements. Fig. 6a shows the dependence of stability of currents provided by NEA and Pt/C with time at an applied constant potential of 0.67 V vs. RHE in the O₂-saturated 0.1 M KOH solution: 95.3% of the current for NEA is retained over a continuous period of 50 000 s compared with 79.3% of the current for Pt/C, revealing excellent stability and durability of NEA. Fig. 6b exhibits the result of chronoamperometric experiments in 0.1 M KOH, with the potential being held at 0.67 V vs. RHE, in order to compare the currents of NEA and Pt/C upon the addition of methanol. As for Pt/C, adding methanol (2.5 mL) leads to an immediate drop in current, whereas, concerning NEA, the current stays stable in the presence of methanol; evidently, NEA exhibits high resistance to methanol poisoning.

Fig. 6 (a) Dependence of the current stability with time for NEA and 20% Pt/C in the O₂-saturated 0.1 M KOH at an applied constant potential of 0.67 V vs. RHE at a rotating rate of 400 rpm at 25 °C; (b) chronoamperograms of NEA and 20% Pt/C in the O₂-saturated 0.1 M KOH at an applied constant potential of 0.67 V vs. RHE at a rotating rate of 400 rpm at 25 °C with the addition of 2.5 mL methanol at 200 s.

Conclusions

We have developed the effective method for exploiting naturally hierarchical micro/nanostructures of E. tirucalli to prepare three-dimensional nanoporous nitrogen-doped carbon-based metal-free ORR electrocatalyst. With the help of agar, the inherently fine structures of the plant biomass can be preserved and the nitrogen doping concentration of the as-made catalyst can reach as high as 16.41 at%. Owing to the high density of pyridinic N and graphitic N, the three-dimensional nanoporous nitrogen-doped electrocatalyst has exhibited the superior ORR catalytic activity to the benchmark Pt/C commercial catalyst. As a consequence, this paper highlights important implications for the utilization of inherently hierarchical microstructures of plant biomass to construct efficient and durable carbon-based metal-free electrocatalysts towards the ORR.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (51702358), the Natural Science Foundation of Jiangsu Province (BK20170281) and the Fundamental Research Funds for the Central Universities (2019ZDPY02). The SEM, TEM and Raman measurements were supported by the Open Sharing Fund for the Large-scale Instruments and Equipments of CUMT (DYGX-034). S. W. thanks the support from Provincial Undergraduate Innovation and Entrepreneurship Training Program (201910290300X). P. B., J. Q. and W. Z. receive the ESI Doctoral Studentships of CUMT. L. X. holds the Jiangsu Specially-Appointed Professorship.

References

1. Y. Nie, L. Li and Z. Wei, Chem. Soc. Rev., 2015, 44, 2168–2201.
2. M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657.
3. S. Sui, X. Wang, X. Zhou, Y. Su, S. Riffatc and C. J. Liu, J. Mater. Chem. A, 2017, 5, 1808–1825.
4. Y. J. Wang, W. Long, L. Wang, R. Yuan, A. Ignaszak, B. Fang and D. P. Wilkinson, Energy Environ. Sci., 2018, 11, 258–275.
5. Z. Zhao, C. Chen, Z. Liu, J. Huang, M. Wu, H. Liu, Y. Li and Y. Huang, Adv. Mater., 2019, 31, 1808115.
6. X. X. Wang, M. T. Swihart and G. Wu, Nat. Catal., 2019, 2, 578–689.
7. C. R. Raj, A. Samanta, S. H. Noh, S. Mondal, T. Okajima and T. Ohsaka, J. Mater. Chem. A, 2016, 4, 11156–11178.
8. X. Wang, Z. Li, Y. Qu, T. Yuan, W. Wang, Y. Wu and Y. Li, Chem, 2019, 5, 1486–1511.
9. P. Fu, L. Zhou, L. Sun, B. Huang and Y. Yuan, RSC Adv., 2017, 7, 13383–13389.
10. C. Tang and Q. Zhang, Adv. Mater., 2017, 29, 1604103.
11. Y. Ji, H. Dong, C. Liu and Y. Li, J. Mater. Chem. A, 2018, 6, 13489–13508.
12. Y. Wang, J. Li and Z. Wei, ChemElectroChem, 2018, 5, 1764–1774.
13. J. Qi, B. Jin, P. Bai, W. Zhang and L. Xu, RSC Adv., 2019, 9, 24344–24356.
14. R. Paul, L. Zhu, H. Chen, J. Qu and L. Dai, Adv. Mater., 2019, 31, 1806403.
15. M. Borghei, J. Lehtonen, L. Liu and O. J. Rojas, Adv. Mater., 2018, 30, 1703691.
16. Y. Zan, Z. Zhang, H. Liu, M. Dou and F. Wang, J. Mater. Chem. A, 2017, 5, 24329–24334.
17. S. Gao, X. Li, L. Li and X. Wei, Nano Energy, 2017, 33, 334–342.
18. J. Qi, W. Zhang and L. Xu, Chem.–Eur. J., 2018, 24, 18097–18105.
19. N. Wang, T. Li, Y. Song, J. Liu and F. Wang, Carbon, 2018, 130, 692–700.
20. W. Zhang, J. Qi, P. Bai, H. Wang and L. Xu, New J. Chem., 2019, 43, 10878–10886.
21. X. Li, Y. Zhao, Y. Yang and S. Gao, Nano Energy, 2019, 62, 628–637.
22. L. Liu, G. Zeng, J. Chen, L. Bi, L. Dai and Z. Wen, Nano Energy, 2018, 49, 393–402.
23. B. R. Hastilestari, M. Mudersbach, F. Tomala, H. Vogt, B. Biskupek-Korell, P. V. Damme, S. Guretzki and J. Papenbrock, PLoS One, 2013, 8, e63501.
24. Q. V. Vuong, V. T. Nguyen, D. T. Thanh, D. J. Bhuyan, C. D. Goldsmith, E. Sadeqzadeh, C. J. Scarlett and M. C. Bowyer, Ind. Crops Prod., 2015, 63, 197–202.
25. P. M. Mason, K. Glover, J. A. C. Smith, K. J. Willis, J. Woods and I. P. Thompson, Energy Environ. Sci., 2015, 8, 2320–2329.
26. C. Wang, D. Wu, H. Wang, Z. Gao, F. Xu and K. Jiang, J. Mater. Chem. A, 2018, 6, 1244–1254.
27. P. Bai, S. Wei, X. Lou and L. Xu, RSC Adv., 2019, 9, 31447–31459.
28. M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069.
29. A. G. Volkov, S. Paula and D. W. Deamer, Bioelectrochem. Bioenerg., 1997, 42, 153–160.
30. M. Barczak, Y. Elsayed, J. Jagiello and T. J. Bandosz, Electrochim. Acta, 2018, 275, 236–247.
31. R. O'Hayre, S. W. Cha, W. G. Colella and F. B. Prinz, Fuel cell fundamentals, Wiley, Hoboken, New Jersey, 3rd edn, 2016.
32. N. Wang, B. Lu, L. Li, W. Niu, Z. Tang, X. Kang and S. Chen, ACS Catal., 2018, 8, 6827–6836.
33. D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365.
34. S. N. Faisal, E. Haque, N. Noorbehesht, W. Zhang, A. T. Harris, T. L. Church and A. I. Minett, RSC Adv., 2017, 7, 17950–17958.
35. X. Ning, Y. Li, J. Ming, Q. Wang, H. Wang, Y. Cao, F. Peng, Y. Yang and H. Yu, Chem. Sci., 2019, 10, 1589–1596.
36. J. A. Behan, E. Mates-Torres, S. N. Stamatin, C. Domínguez, A. Iannaci, K. Fleischer, M. K. Hoque, T. S. Perova, M. Gacía-Melchor and P. E. Colavita, Small, 2019, 15, 1902081.
37. S. K. Singh, K. Takeyasu and J. Nakamura, Adv. Mater., 2019, 31, 1804297.
38. Z. Zhao, C. Chen, Z. Liu, J. Huang, M. Wu, H. Liu, Y. Li and Y. Huang, Adv. Mater., 2019, 31, 1808115.
39. R. Paul, L. Zhu, H. Chen, J. Qu and L. Dai, Adv. Mater., 2019, 31, 1806403.
40. J. Gao, Y. Wang, H. Wu, X. Liu, L. Wang, Q. Yu, A. Li, H. Wang, C. Song, Z. Gao, M. Peng, M. Zhang, N. Ma, J. Wang, W. Zhou, G. Wang, Z. Yin and D. Ma, Angew. Chem., Int. Ed., 2019, 131, 15233–15241.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra08751f

---