Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hypercoordinate iodine for catalytic asymmetric diamination of styrene: insights into the mechanism, role of solvent, and stereoinduction†
A.
Sreenithya
 a,
Christopher M.
Hadad
a,
Christopher M.
Hadad
 b and
Raghavan B.
Sunoj
b and
Raghavan B.
Sunoj
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: sunoj@chem.iitb.ac.in
bDepartment of Chemistry and Biochemistry, The Ohio State University, 100 West 18th Avenue, Columbus, Ohio 43210, USA
First published on 10th June 2019
Abstract
Hypercoordinate iodine has evolved as an impressive class of catalysts for various organic transformations. Extension of this idea to asymmetric applications, such as in the asymmetric difunctionalization of styrene or its derivatives, constitutes an important reaction. In this study, the mechanism and origin of stereoinduction in styrene diamination, with a sulfonimide (HNMs2) as the diaminating agent and iodoresorcinol (((iPr)2N(CO)-CH(Me)-O)2Ar–I) based chiral hypercoordinate iodine as the catalyst, are investigated using density functional theory calculations. The energetically preferred catalytic pathway has been found to involve, among other steps, two very important mechanistic events: (a) the formation of a catalyst–substrate complex by the action of styrene on the catalyst ArI(NMs2)2, resulting in the displacement of one of the imidates (NMs2−); and (b) a rebound of the departed imidate on the iodine-bound styrene to form an iodonium ion intermediate with a N–C bond. Explicit interaction of the imidate ion with hexafluoroisopropanol (HFIP), used as a solvent additive, lowers the barrier for the formation of the iodonium ion. The P helical fold of the chiral arms of the iodoresorcinol catalyst is found to offer a chiral environment for the reactants. Coordination of the iodine catalyst to the styrene double bond is found to make the benzylic carbon more electrophilic and hence makes it the preferred site for the nucleophilic addition. In the chiral environment of the catalyst, an enhanced polarization of the styrene double bond is noticed when the double bond coordinates through the si prochiral face than the re face. Nucleophilic addition on the re face of the catalyst–substrate complex is associated with a lower activation barrier leading to the experimentally observed S enantiomeric product. The stereoselective model developed in this study can be employed to related asymmetric styrene difunctionalizations using similar hypercoordinate iodine catalysts.
Introduction
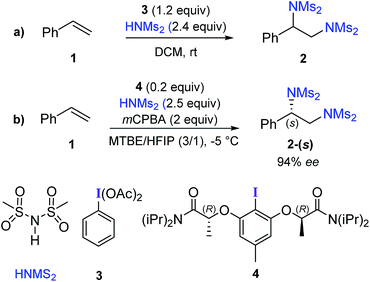
Vicinal diamines are important structural elements in pharmaceuticals, natural products, and organo- as well as transition metal catalysts.1 Hence, efficient methods for the synthesis of diamines are of great interest.2 Palladium- and copper-catalyzed asymmetric diamination of alkenes involving intramolecular C–N bond formation is the most frequently found catalytic diamination reaction.3 Among the metal-free approaches, hypercoordinate iodine mediated diamination of alkenes has received considerable attention in recent years.4Hypercoordinate iodine mediated methods have found widespread acceptance owing to their utility in a diverse set of reactions under milder and environmentally benign conditions.5 An excellent strategy for diamination of styrene derivatives in the presence of a stoichiometric amount of phenyliodine(III) diacetate (PIDA) with two equivalents of sulfonimide HNMs2 as the aminating agent (Scheme 1a) was recently reported.6 This method offers wide substrate scope and functional group tolerance.7 Replacing PIDA with chiral iodoresorcinol derivatives could provide asymmetric diamination.6 In a recent catalytic version of this reaction, catalytically active chiral hypercoordinate iodine species was generated in situ from the corresponding Ar–I (4) and HNMs2 in the presence of two equivalents of meta-chloroperbenzoic acid (mCPBA) as an oxidizing agent (Scheme 1b).8
Difunctionalization of alkenes using hypercoordinate iodine(III) has found interesting applications in the synthesis of complex target molecules.9 In particular, iodoresorcinol based catalysts derived from the corresponding Ar–I (similar to 4) have been recently used for stereoselective difunctionalization of various styrenes, in which the S stereogenic center at the benzylic position was formed in the product.9a–c Different chiral iodoresorcinol derivatives differ in terms of the substituents attached to the carbonyl (–N(iPr2) in the representative example 4) and Cα (–Me in 4) positions of the chiral arms, while maintaining the R configuration at the Cα position. This observation indicates that the preferred prochiral face of styrene involved in all of these reactions is the same, such that the (S)-configured enantiomer of the product is generated. However, the origin of stereoinduction in these reactions is often interpreted using qualitative working hypotheses.10 In view of the impressive developments in asymmetric catalysis using hypercoordinate iodine,11 we probed the origin of stereoinduction12 in styrene diamination by using DFT(SMD(diethylether)/M06-2X/6-31G**,SDD(I)) computations.
Computational methods
All geometry optimizations were performed using the Gaussian09 suite of quantum chemical programs.13 The M06-2X density functional was chosen for geometry optimization which accounts for the potentially significant dispersion interactions in relatively larger molecules.14 The 6-31G** basis set was chosen for all atoms, except for iodine.15 The Stuttgart–Dresden double-zeta valence basis set (SDD) with an effective core potential for 46 inner electrons was employed for iodine.16 Solvent effects were incorporated using the universal SMD continuum solvation model developed by Truhlar and Cramer.17 The experimental conditions for the catalytic asymmetric reaction employed a solvent system consisting of a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of methyl tert-butyl ether (MTBE) and hexafluoroisopropanol. Since the dielectric continuum field for MTBE (ε = 4.5) is not available in Gaussian09, implicit solvation calculations for closely related diethyl ether (ε = 4.2) were employed. Hexafluoroisopropanol was explicitly included in several stationary points to evaluate specific interactions with the solute. All stationary points were verified by vibrational frequency analysis. Minima (reactants, products, and intermediates) were characterized by having zero imaginary vibrational frequencies, while transition states had only one imaginary frequency. Further verification of the transition states was done using intrinsic reaction coordinate (IRC) calculations in order to connect to the corresponding reactants and products.18 We wish to convey that locating various transition state geometries in hypercoordinate iodine catalyzed reactions could be challenging due to geometry convergence issues. Similar computational methods to those employed in this study have successfully been employed in recent studies of hypercoordinate iodine reactions.19
1 mixture of methyl tert-butyl ether (MTBE) and hexafluoroisopropanol. Since the dielectric continuum field for MTBE (ε = 4.5) is not available in Gaussian09, implicit solvation calculations for closely related diethyl ether (ε = 4.2) were employed. Hexafluoroisopropanol was explicitly included in several stationary points to evaluate specific interactions with the solute. All stationary points were verified by vibrational frequency analysis. Minima (reactants, products, and intermediates) were characterized by having zero imaginary vibrational frequencies, while transition states had only one imaginary frequency. Further verification of the transition states was done using intrinsic reaction coordinate (IRC) calculations in order to connect to the corresponding reactants and products.18 We wish to convey that locating various transition state geometries in hypercoordinate iodine catalyzed reactions could be challenging due to geometry convergence issues. Similar computational methods to those employed in this study have successfully been employed in recent studies of hypercoordinate iodine reactions.19
Topological analysis of the electron densities, within the Atoms In Molecule (AIM) framework, was carried out using AIM2000 software to identify the bond paths representing the weak inter-atomic interactions.20 Natural bond orbital (NBO)21 analysis of important stationary points was done to understand important electron delocalizations and charge distributions. To examine the origin of energy difference between the stereocontrolling transition states, the activation-strain model was employed.22 In this model, the activation barrier (ΔE‡) is considered as the sum of (a) destabilizing distortion energies (ΔE‡d) in the reactants while going from their ground state geometries to those in the transition states, and (b) stabilizing interaction energy between such deformed reactants (ΔE‡i) in the TS geometry. This approach would help quantify the relative distortion and interaction energies between the stereocontrolling transition states.
The discussion is presented on the basis of the Gibbs free energies at 298 K and as obtained at the SMD(diethylether)/M06-2X/6-31G**,SDD(I) level of theory. Gibbs free energies are corrected using Truhlar's quasi-harmonic approximation to address the issues arising due to the harmonic oscillator approximation for frequencies lower than 100 cm−1.23 Gibbs free energies were also calculated using the quasi-rigid rotor harmonic oscillator (RRHO) approximation for the purpose of comparison, which is provided in the ESI.†24 The energies obtained at the SMD(diethylether)/M06-2X/6-31G**,SDD(I) level of theory were refined using a larger basis set using the same functional to learn that the results were similar. Geometries were also optimized at the B3LYP-D3 level of theory. Energy refinements at the B3LYP-D3 level of theory using the geometries at the same level of theory were also carried out to check whether our results were consistent across different functionals.25
Results and discussion
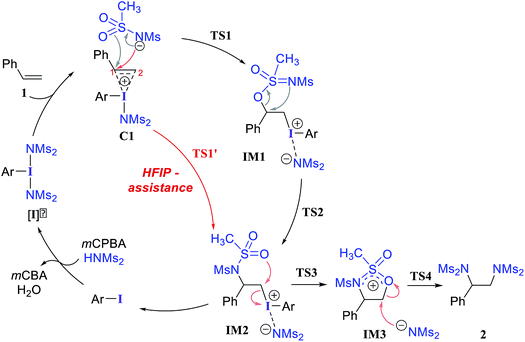
We have investigated all of the likely elementary mechanistic steps to develop an improved understanding of the key intermediates and transition states (TSs) involved in the diamination reaction, as shown in Scheme 2. An achiral hypercoordinate iodine species (3′) was considered first to develop some basic understanding about the key mechanistic features. The factors responsible for stereoinduction are then delineated by considering the chiral hypercoordinate iodine species that is derived from 4.First, an achiral PhI(NMs2)2 (3′) is employed as an active catalyst [I]′ to gather important mechanistic details (Scheme 2).26,27 The substrate styrene can displace one of the labile imidate (NMs2−) ligands to form a catalyst–substrate ion-pair complex, C1.28 The natural bond orbital analysis (NBO) of C1 revealed a prominent π electron delocalization (45.1 kcal mol−1) from the styrene double bond to the I(III)–N antibonding orbital.29 The coordination of the styrenyl double bond to the electrophilic I(III) center is found to induce a polarization such that the benzylic carbon C1 becomes relatively more positive (natural charges on C1 = −0.12 and on C2 = −0.54 in C1 whereas that on an unbound free styrene is C2 = −0.43 and C1 = −0.25), making the C1 benzylic carbon more prone to nucleophilic addition. The polarization of the styrene π orbital in this catalyst–substrate complex is evident from a relatively higher π orbital coefficient (0.75) on the C2 carbon than on C1 (0.65), which was the same for a free styrene (orbital coefficient of 0.70 on both C1 and C2).
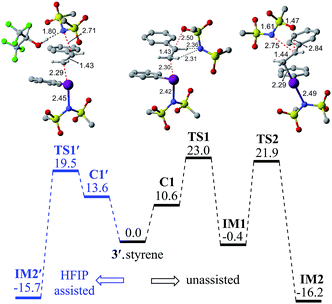
In the next step, we considered a rebound mechanism wherein the displaced sulfonamide anion adds to the polarized styrenyl double bond. Due to effective charge delocalization from nitrogen to oxygen in the imidate ion, the nucleophilic addition can occur either through the oxygen or through the nitrogen. The natural charges on the nitrogen (−1.32) and the oxygen (−1.04) of the imidate indicate that a nucleophilic addition through the nitrogen is more likely. However, attempts to locate a transition state for the nucleophilic addition through the nitrogen remained unsuccessful, and instead resulted in an addition through the oxygen (TS1).30,31 The comparison of nucleophilicity indices of 0.61 and 0.08, respectively, for the nitrogen and oxygen suggests that a nucleophilic addition through the softer sulfonyl oxygen is likely to be more preferred at the benzylic carbon of the iodine-bound styrene resulting in the iodonium ion intermediate IM1.32 In the next step, a concerted intramolecular migration converts IM1 to IM2viaTS2.33 Formation of the second iodonium ion intermediate IM2 is exergonic by ∼16.0 kcal mol−1 (Fig. 1). An intramolecular nucleophilic addition by the sulfonyl oxygen at C2 can now provide a cyclic oxazolidine oxide intermediate, IM3. The barrier to this elementary step for the expulsion of PhI is 11.4 kcal mol−1.34 A subsequent nucleophilic ring opening by imidate can furnish the vicinal diamine product 2. Interestingly, an intermediate with a C1–O bond similar to IM1 was observed during the oxidation of 1,1-diphenyl ethylene using PIDA in the absence of HFIP.30
Earlier reports suggested that fluorinated solvents such as hexafluoroisopropanol (HFIP) are more beneficial in hypercoordinate iodine mediated reactions.35 For example, the improved reactivity of PIDA in the presence of HFIP is attributed to hydrogen bonding between the ligands on PIDA and HFIP36 which makes the ligands more labile.37 We have considered a similar scenario wherein the displaced imidate nitrogen is hydrogen bonded in C1′ as shown in Fig. 2. Interestingly, the ensuing nucleophilic addition (TS1′) on the styrenyl carbon is noted to occur through the imidate nitrogen. The natural charge on the HFIP-bound imidate nitrogen is higher (−1.34) than that on the unbound (−1.32). However, the nucleophilicity index of the HFIP-bound nitrogen is lower (0.58) than that of the unbound (0.61), indicating relatively softer nitrogen in the former case. Thus, explicit involvement of HFIP enables direct formation of the N–C bond in C1′ leading to IM2′. An alternative nucleophilic addition through the imidate oxygen is found to be 4.0 kcal mol−1 higher in energy when imidate is associated with HFIP. The HFIP-assisted nucleophilic addition exhibits a barrier of 19.5 kcal mol−1, which is 3.5 kcal mol−1 lower than that of the unassisted nucleophilic addition (Fig. 1).38 Having understood that the HFIP-assisted pathway is energetically preferable, we calculated the energetics for the HFIP-assisted formation of diamine product 2 as shown in Fig. 2.39
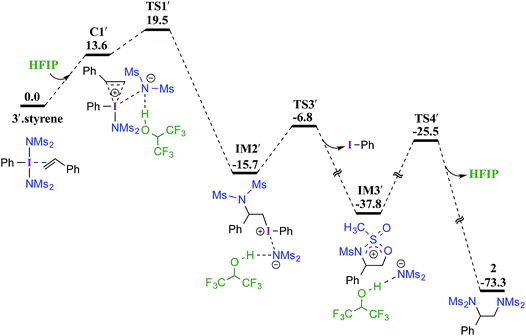 | ||
| Fig. 2 Gibbs free energy (in kcal mol−1) profile calculated at the SMD(diethylether)/M06-2X/6-31G**,SDD(I) level of theory for the HFIP assisted diamination of styrene. | ||
After shedding light on the mechanism of vicinal diamination of styrene using PhI(NMs2)2, we have extended these insights to an asymmetric diamination catalyzed by C2 symmetric iodoresorcinol based chiral catalysts to establish the factors controlling enantioselectivity. As described earlier, nucleophilic addition at the benzylic carbon (TS1′) is more preferred than at the terminal carbon of the catalyst–substrate complex C1′. The stereochemical outcome of the reaction will therefore be dictated by which of the prochiral faces of styrene binds to the iodine center. It is likely that the chiral environment offered by the catalyst could make the binding through one prochiral face energetically more preferred over the other in the ion-pair catalyst–substrate complex C1′. In other words, the efficiency of this prochiral face recognition is expected to impact on the extent of enantioselectivity.
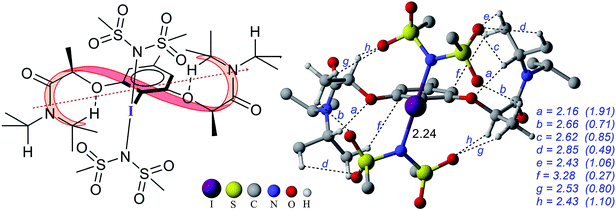
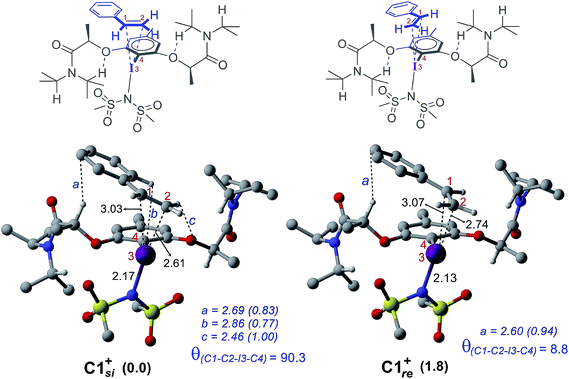
The process of stereoinduction is investigated by examining the stereoelectronic features of the in situ generated catalytically active hypercoordinate iodine species 4′. In the most preferred conformer of the C2-symmetric 4′, the chiral arms fold in a right-handed P helical fashion and generate a chiral environment around the iodine. The (R)-configured stereogenic center at the Cα is the source of stereoinduction, which facilitates the fold with right-handed P helicity. The corresponding M helical fold is found to be of 8.0 kcal mol−1 higher energy.12,40 A series of weak non-covalent interactions (NCIs) between the imidate ligands and the chiral arms of the resorcinol backbone (Fig. 3) are found to arrange the chiral arms in a helical assembly. This folded assembly of the catalyst provides an asymmetric environment for the incoming styrene. How the binding of the si and re prochiral faces of styrene to the iodine is recognized differently in the catalyst–substrate complexes is analyzed using the cationic complexes (C1+) devoid of the displaced nucleophile imidate associated with HFIP.41 It is noticed that the catalyst–substrate complex C1si+ wherein styrene interacts through its si face is lower by 1.8 kcal mol−1 than the corresponding re face binding (C1re+).
The differential recognition of the styrenyl prochiral faces can be understood as follows. In the si face catalyst–substrate complex, styrene is dispositioned closer to the iodine center, as evident from the shorter C2–I distance (2.61 Å) than in the re complex (2.74 Å), indicating enhanced catalyst–substrate interaction (Fig. 4). Further, the styrene double bond is noted to remain staggered and orthogonal with respect to the C4–I3 bond of the catalyst (θ(C1–C2–I3–C4) = 90.3°) in C1si+ whereas it is eclipsed in C1re+ (θ(C1–C2–I3–C4) = 8.8°).42 The arrangement of styrene in these catalyst–substrate complexes facilitates a C–H⋯π interaction between the Cα–H of the chiral side chain and the phenyl group of styrene (shown as a in Fig. 4). A larger deviation from the eclipsed alignment of the styrene double bond in the re complex (measured in terms of dihedral θ(C1–C2–I3–C4)) will result in loss of this critical interaction. Additional weak noncovalent interactions are noticed in the si mode of binding, which are absent in the re complex. Natural bond orbital (NBO) analysis revealed an enhanced π electron delocalization from the styrene double bond to the I–N antibonding orbital in C1si+ (46.1 kcal mol−1) compared to that in C1re+ (30.7 kcal mol−1). Comparison of a free styrene with a bound styrene as noted in the catalyst–substrate complexes is carried out to understand the effect of iodine coordination on the reactivity and selectivity.
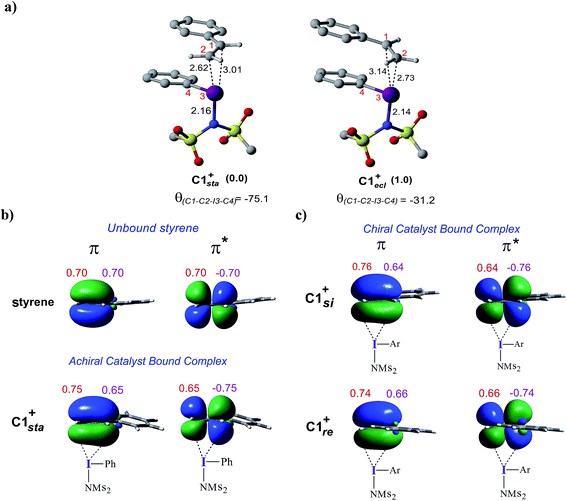
To examine how the relative orientation of the styrene double bond and the Ar–I bond influences their energies, catalyst–substrate complexes with staggered and eclipsed orientations of the substrate are analyzed for an achiral catalyst (Fig. 5a). The staggered arrangement (C1sta+) is found to be 1.0 kcal mol−1 lower in energy than the eclipsed geometry (C1ecl+). In the case of the achiral catalyst, binding of both the prochiral faces of styrene is found to be energetically similar, suggesting no facial discrimination.
To gather more insights, the π and π* natural bond orbitals (NBOs) in a free styrene as well as those in an iodine-bound styrene are analyzed. These are critical NBOs, as the donor π and acceptor π* are, respectively, involved in the catalyst–substrate complex formation and in the nucleophilic addition. Both benzylic (C1) and terminal carbon (C2) atoms of the free styrene contribute equally to the π orbital as evident from the corresponding orbital coefficients (C1 = C2 = 0.70, Fig. 5b). Interestingly, in the catalyst–substrate complexes, the π orbital is polarized toward the terminal carbon as indicated by a higher orbital coefficient on C2 than that on C1 whereas the corresponding π* orbital is more polarized toward the benzylic carbon C1. In the achiral catalyst–substrate complexes, the π orbital polarization is noted to be higher in the case of the staggered geometry of styrene in C1sta+ (coefficients on C1 and C2 are 0.65 and 0.75, respectively) compared to that in C1ecl+ (C1 = 0.64 and C2 = 0.76).43 More interestingly, a differential polarization of the π and π* is noted in the chiral catalyst–substrate complexes depending on the prochiral face through which styrene binds to the iodine center. The styrene double bond in the si binding mode, which has a staggered arrangement, is found to be more polarized than in the re complex (Fig. 5c). The orbital coefficients for filled π in C1si+ are C1 = 0.64 and C2 = 0.76 and those in C1re+ are C1 = 0.66 and C2 = 0.74. The chirality induced differential polarization of the styrenyl double bond, as described here, can have a pronounced impact on the prochiral face recognition and hence the stereochemical course of the reaction. Akin to the orbital polarization noted here, the natural charge on C1 and C2 exhibited similar features.43 In summary, the enhanced polarization of the styrene π orbitals, particularly that of the π* orbital in the lower energy staggered catalyst–substrate complex, improves the propensity toward the nucleophilic addition of the imidate ion.
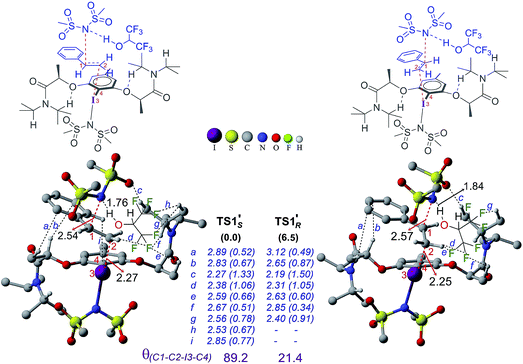
In the next step, stereoselective addition of the imidate on the benzylic position of styrene bound to chiral catalyst 4′ is considered (for the geometry of the catalyst, see Fig. 3). The C–N bond formation viaTS1′ leads to the formation of an iodonium ion intermediate (IM2′). Nucleophilic addition of the imidate to the catalyst–substrate complexes C1′si and C1′re is separately examined.44 The transition state for the imidate addition to the open re face of the bound styrene in C1′si is denoted as TS1′S as the new stereogenic center created in this mode would be of S configuration. The relative Gibbs energy of TS1′S is found to be 6.5 kcal mol−1 lower in energy than that of TS1′R. Similarly, the elementary step barrier for the nucleophilic addition through TS1′S is 3.1 kcal mol−1 lower than that for TS1′R. A staggered arrangement of the styrene double bond (θ(C1–C2–I3–C4) = 89.2°) with respect to the Ar–I bond is noted in the lower energy TS1′S whereas it remains in an eclipsed (θ(C1–C2–I3–C4) = 21.4°) geometry in the higher energy TS1′R.45 Analysis of TSs shows the presence of certain types of noncovalent interactions (denoted as h and i in Fig. 6) between the reactants (styrene and imidate) and the catalyst in the case of TS1′S which are absent in TS1′R. However, these weakly differentiating interactions are rather inadequate toward rationalizing an overwhelming preference for imidate addition viaTS1′S. Hence, we have performed activation-strain analysis on these diastereomeric TSs by fragmenting them into three parts such as the catalyst, styrene and nucleophile. All three fragments in TS1′R exhibited relatively higher distortion energy than in TS1′S – the sum of which amounts to 14.4 kcal mol−1 in the former.46 The stabilizing interaction energy between these three fragments is also higher (−6.9 kcal mol−1) in TS1′R. On balance, the distortion appears to be a key contributor of the energy difference between the diastereomeric TSs. The difference in the elementary step barriers for the nucleophilic addition of the imidate on the re face of the catalyst–substrate complex and that on the si face is found to be 3.1 kcal mol−1, exhibiting a preference toward the formation of the S enantiomeric product.47 While the difference in barriers corresponds to an ee of 98% which is in good agreement with the experimental observation of 94%, the relative energies of the diastereomeric transition states result in a modest overestimation of ee.
Conclusions
The energetically favorable mechanism and the origin of enantioselectivity in hypercoordinate iodine catalyzed vicinal diamination of styrene have been identified. Styrene coordination to the electrophilic iodine center polarizes the double bond making the benzylic carbon susceptible to nucleophilic addition by imidate derived from the active catalyst ArI(NMs2)2. Hexafluoroisopropanol-assisted nucleophilic addition for the C–N bond formation proceeds with a lower energy barrier and results in an iodonium ion intermediate. Under the chiral environment provided by the iodoresorcinol catalyst, the coordination of the si prochiral face of styrene is more preferred due to the relatively more effective catalyst–substrate interaction than in the re face complex. This prochiral face recognition is found to have a direct impact on the enantioselectivity of this catalytic asymmetric reaction. The kinetic advantage for nucleophilic addition of the imidate is more for the si-face of the catalyst–substrate complex, which could be traced to a relatively lower distortion in the reactant partners in the stereocontrolling transition state. The computed % ee is in good agreement with the experimental observation.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Generous computing time from SpaceTime supercomputing at IIT Bombay and the Ohio (OSC) Supercomputer Center is gratefully acknowledged. C. M. H. gratefully acknowledges financial support from the U.S. National Science Foundation (CHE-1566106).Notes and references
- (a) D. Lucet, T. Le Gall and C. Mioskowski, Angew. Chem., Int. Ed., 1998, 37, 2580–2627 CrossRef CAS; (b) S. De Jong, D. G. Nosal and D. J. Wardrop, Tetrahedron, 2012, 68, 4067–4105 CrossRef CAS PubMed.
- (a) N. Fu, G. S. Sauer, A. Saha, A. Loo and S. Lin, Science, 2017, 357, 575–579 CrossRef CAS PubMed; (b) J. B. Parry, N. Fu and S. Lin, Synlett, 2018, 29, 257–265 CrossRef CAS.
- (a) F. Cardona and A. Goti, Nat. Chem., 2009, 1, 269 CrossRef CAS PubMed; (b) Y. Zhu, R. G. Cornwall, H. Du, B. Zhao and Y. Shi, Acc. Chem. Res., 2014, 47, 3665–3678 CrossRef CAS; (c) K. Muñiz and C. Martínez, J. Org. Chem., 2013, 78, 2168–2174 CrossRef PubMed.
- R. M. Romero, T. H. Wöste and K. Muñiz, Chem.–Asian J., 2014, 9, 972–983 CrossRef CAS PubMed.
- (a) A. Yoshimura and V. V. Zhdankin, Chem. Rev., 2016, 116, 3328–3435 CrossRef CAS PubMed; (b) Y. Li, D. P. Hari, M. V. Vita and J. Waser, Angew. Chem., Int. Ed., 2016, 55, 4436–4454 CrossRef CAS PubMed; (c) X. Wang and A. Studer, Acc. Chem. Res., 2017, 50, 1712–1724 CrossRef CAS PubMed; (d) L. Wang and J. Liu, Eur. J. Org. Chem., 2016, 2016, 1813–1824 CrossRef CAS; (e) A. Sreenithya, K. Surya and R. B. Sunoj, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1299 Search PubMed.
- C. Röben, J. A. Souto, Y. González, A. Lishchynskyi and K. Muñiz, Angew. Chem., Int. Ed., 2011, 50, 9478–9482 CrossRef PubMed.
- (a) J. A. Souto, Y. González, A. Iglesias, D. Zian, A. Lishchynskyi and K. Muñiz, Chem.–Asian J., 2012, 7, 1103–1111 CrossRef CAS PubMed; (b) A. Lishchynskyi and K. Muñiz, Chem.–Eur. J., 2012, 18, 2212–2216 CrossRef CAS PubMed; (c) R. M. Romero, J. A. Souto and K. Muñiz, J. Org. Chem., 2016, 81, 6118–6122 CrossRef CAS PubMed.
- K. Muñiz, L. Barreiro, R. M. Romero and C. Martínez, J. Am. Chem. Soc., 2017, 139, 4354–4357 CrossRef PubMed.
- (a) S. Haubenreisser, T. H. Wöste, C. Martínez, K. Ishihara and K. Muñiz, Angew. Chem., Int. Ed., 2016, 55, 413–417 CrossRef CAS PubMed; (b) E. M. Woerly, S. M. Banik and E. N. Jacobsen, J. Am. Chem. Soc., 2016, 138, 13858–13861 CrossRef CAS PubMed; (c) S. M. Banik, J. W. Medley and E. N. Jacobsen, Science, 2016, 353, 51–54 CrossRef CAS PubMed; (d) H. Chen, A. Kaga and S. Chiba, Org. Biomol. Chem., 2016, 14, 5481–5485 RSC; (e) T. Kitamura, A. Miyake, K. Muta and J. Oyamada, J. Org. Chem., 2017, 82, 11721–11726 CrossRef CAS PubMed; (f) W. Kong, P. Feige, T. de Haro and C. Nevado, Angew. Chem., Int. Ed., 2013, 52, 2469–2473 CrossRef CAS PubMed; (g) U. Farid and T. Wirth, Angew. Chem., Int. Ed., 2012, 51, 3462–3465 CrossRef CAS PubMed; (h) I. G. Molnár and R. Gilmour, J. Am. Chem. Soc., 2016, 138, 5004–5007 CrossRef PubMed; (i) T. H. Wöste and K. Muñiz, Synthesis, 2016, 48, 816–827 CrossRef.
- (a) M. Fujita, Tetrahedron Lett., 2017, 58, 4409–4419 CrossRef CAS; (b) M. Uyanik and K. Ishihara, J. Synth. Org. Chem., Jpn., 2012, 70, 1116–1122 CrossRef CAS.
- A. Flores, E. Cots, J. Bergès and K. Muñiz, Adv. Synth. Catal., 2019, 361, 2–25 CrossRef CAS.
- A. Sreenithya, C. Patel and R. B. Sunoj, ACS Catal., 2017, 7, 4189–4196 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- (a) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS; (b) V. Rassolov, J. A. Pople, M. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- (a) D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS; (b) P. Fuentealba, H. Stoll, L. von Szentpály, P. Schwerdtfeger and H. Preuss, J. Phys. B: At. Mol. Phys., 1983, 16, L323–L328 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS; (b) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS; (c) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- (a) R. Pluta, P. E. Krach, L. Cavallo, L. Falivene and M. Rueping, ACS Catal., 2018, 8, 2582–2588 CrossRef CAS; (b) R. Frei, M. D. Wodrich, D. P. Hari, P.-A. Borin, C. Chauvier and J. Waser, J. Am. Chem. Soc., 2014, 136, 16563–16573 CrossRef CAS PubMed; (c) S. Beaulieu and C. Y. Legault, Chem.–Eur. J., 2015, 21, 11206–11211 CrossRef CAS PubMed; (d) C. Zhu, Y. Liang, X. Hong, H. Sun, W.-Y. Sun, K. N. Houk and Z. Shi, J. Am. Chem. Soc., 2015, 137, 7564–7567 CrossRef CAS PubMed; (e) M. Li, X.-S. Xue, J. Guo, Y. Wang and J.-P. Cheng, J. Org. Chem., 2016, 81, 3119–3126 CrossRef CAS PubMed; (f) H. Jiang, T.-Y. Sun, X. Wang, Y. Xie, X. Zhang, Y.-D. Wu and H. F. Schaefer, Org. Lett., 2017, 19, 6502–6505 CrossRef CAS PubMed; (g) B. Zhou, M. K. Haj, E. N. Jacobsen, K. N. Houk and X. Xue, J. Am. Chem. Soc., 2018, 140, 15206–15218 CrossRef CAS PubMed; (h) J. Zhao and S. Li, J. Org. Chem., 2017, 82, 2984–2991 CrossRef CAS PubMed.
- (a) R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990 Search PubMed; (b) AIM2000, Version 2.0, The Buro fur Innovative Software, SBK-Software, Bielefeld, Germany, 2000 Search PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- (a) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS; (b) W. J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127 RSC; (c) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- (a) P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1998, 108, 2314–2325 CrossRef CAS; (b) S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed; (c) See Table S1 in the ESI† for further details.
- See Table S5 in the ESI† for further details.
- In the stoichiometric reaction using PIDA (3) and HNMs2, the in situ generated diaminating species was identified as PhI(NMs2)2 (3′) by using IR spectroscopic and X-ray crystallographic studies. Formation of 3′ from 3 can occur through an exoergic ligand exchange where iodine-bound acetate of PIDA abstracts a proton from HNMs2 to form a molecule of acetic acid. See Scheme S1 in the ESI† for additional details. The anionic imidate ligands (NMs2−) on active species 3′ are known to be labile in solution and exist in equilibrium with the cationic iodine species (PhINMs2+). See J. A. Souto, C. Martínez, I. Velilla and K. Muñiz, Angew. Chem., Int. Ed., 2013, 52, 1324–1328 CrossRef CAS PubMed.
- In stoichiometric reactions, undesirable co-production of Ar–I is generally reported while it is oxidized back to catalytically active hypercoordinate iodine species [I]′ in the catalytic variant of these reactions.
- H. Pinto de Magalhães, A. Togni and H. P. Lüthi, J. Org. Chem., 2017, 82, 11799–11805 CrossRef PubMed.
- See Fig. S1 in the ESI.†.
- Similar situations have been noticed earlier in I. Funes-Ardoiz, W. M. C. Sameera, R. M. Romero, C. Martínez, J. A. Souto, D. Sampedro, K. Muñiz and F. Maseras, Chem.–Eur. J., 2016, 22, 7545–7553 CrossRef CAS PubMed . See Fig. S4 in the ESI† for the charge distribution in the imidate ligand.
- The Gibbs free energy of the C–O bond formation transition state at C2 is found to be 8.0 kcal mol−1 higher than at the C1 position.
- (a) The Fukui index for nucleophilicity at a specific site is calculated as fA− = PA(N) − PA(N − 1), where PA is the electron population in atom A and N is the number of electrons of the molecule; (b) R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- For IM1, an alternative intramolecular nucleophilic addition of the imidate nitrogen on the C1 is found to involve a higher barrier. See Fig. S3 in the ESI† for further details.
- See Fig. S2 in the ESI† for the Gibbs free energy profile.
- (a) T. Dohi, N. Yamaoka and Y. Kita, Tetrahedron, 2010, 66, 5775–5785 CrossRef CAS; (b) I. Colomer, R. Coura Barcelos and T. J. Donohoe, Angew. Chem., Int. Ed., 2016, 55, 4748–4752 CrossRef CAS PubMed; (c) M. Ito, C. Ogawa, N. Yamaoka, H. Fujioka, T. Dohi and Y. Kita, Molecules, 2010, 15, 1918–1931 CrossRef CAS PubMed; (d) M. Uyanik, T. Yasui and K. Ishihara, Angew. Chem., Int. Ed., 2013, 52, 9215–9218 CrossRef CAS PubMed; (e) K. Morimoto, K. Sakamoto, T. Ohshika, T. Dohi and Y. Kita, Angew. Chem., Int. Ed., 2016, 55, 3652–3656 CrossRef CAS PubMed; (f) K. Murai, T. Kobayashi, M. Miyoshi and H. Fujioka, Org. Lett., 2018, 20, 2333–2337 CrossRef CAS PubMed; (g) J. Iskra and S. S. Murphree, Tetrahedron Lett., 2017, 58, 645–648 CrossRef CAS; (h) T. Dohi, M. Ito, K. Morimoto, Y. Minamitsuji, N. Takenaga and Y. Kita, Chem. Commun., 2007, 4152–4154 RSC; (i) I. Colomer, A. E. R. Chamberlain, M. B. Haughey and T. J. Donohoe, Nat. Rev. Chem., 2017, 1, 0088 CrossRef CAS; (j) H. K. Minhas, W. Riley, A. M. Stuart and M. Urbonaite, Org. Biomol. Chem., 2018, 16, 7170–7173 RSC.
- I. Colomer, C. Batchelor-McAuley, B. Odell, T. J. Donohoe and R. G. Compton, J. Am. Chem. Soc., 2016, 138, 8855–8861 CrossRef CAS PubMed.
- S. Izquierdo, S. Essafi, I. del Rosal, P. Vidossich, R. Pleixats, A. Vallribera, G. Ujaque, A. Lledós and A. Shafir, J. Am. Chem. Soc., 2016, 138, 12747–12750 CrossRef CAS PubMed.
- Additional calculations at the B3LYP-D3/6-31G**,SDD(I) and energy refinements at the B3LYP-D3/6-311+G**,SDD(I) were done to learn that consistently similar trends exist across different basis sets and density functionals. See Table S5 in the ESI† for details.
- Alternative possibilities such as an aziridinium pathway which involves an intramolecular nucleophilic addition of the imidate nitrogen on C2 and a direct SN2 pathway are also investigated for the conversion of IM2′ to product 2. Further details are provided in Scheme S2 and Fig. S5 in the ESI.†.
- See Fig. S8 and S9 in the ESI† for details on other conformers of 4′.
- The energy difference between the cationic catalyst–substrate complexes primarily originates due to the difference in the prochiral face through which the substrate interacts with the chiral catalyst. In a neutral catalyst–substrate complex, the achiral nucleophile imidate (bound to HFIP), which exists as a counterion, interacts with the rest of the system through a set of weak non-covalent interactions. Hence, the energy of the neutral catalyst–substrate complexes is dependent on the positioning of the counterion.
- M. Hickey, D. Goeddel, Z. Crane and Y. Shi, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5794–5798 CrossRef CAS PubMed.
- See Table S6 in the ESI† for more details.
- The neutral catalyst–substrate complex C1′si is 3.4 kcal mol−1 lower in energy than C1′re.
- Similar geometric disposition of alkenes with respect to the Ar–I bond was recently noted in a hypercoordinate iodine catalyzed difluorination reaction (see ref. 19g).
- The distortion energies of the catalyst, styrene and HFIP bound imidate fragments in TS1′R are, respectively, 5.2, 3.9, and 5.3 kcal mol−1 higher than the corresponding values in TS1′S. See Table S7 in the ESI† for more details.
- The stereoselectivity model established for asymmetric diamination of styrene can as well be extended to internal alkenes. See Fig. S12 and Scheme S3 in the ESI† for further details.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all stationary points and other relevant information is provided. See DOI: 10.1039/c9sc01513b |
| This journal is © The Royal Society of Chemistry 2019 |