A generalized deep learning approach for local structure identification in molecular simulations

Abstract

Identifying local structure in molecular simulations is of utmost importance. The most common existing approach to identify local structure is to calculate some geometrical quantity referred to as an order parameter. In simple cases order parameters are physically intuitive and trivial to develop (e.g., ion-pair distance), however in most cases, order parameter development becomes a much more difficult endeavor (e.g., crystal structure identification). Using ideas from computer vision, we adapt a specific type of neural network called a PointNet to identify local structural environments in molecular simulations. A primary challenge in applying machine learning techniques to simulation is selecting the appropriate input features. This challenge is system-specific and requires significant human input and intuition. In contrast, our approach is a generic framework that requires no system-specific feature engineering and operates on the raw output of the simulations, i.e., atomic positions. We demonstrate the method on crystal structure identification in Lennard-Jones (four different phases), water (eight different phases), and mesophase (six different phases) systems. The method achieves as high as 99.5% accuracy in crystal structure identification. The method is applicable to heterogeneous nucleation and it can even predict the crystal phases of atoms near external interfaces. We demonstrate the versatility of our approach by using our method to identify surface hydrophobicity based solely upon positions and orientations of surrounding water molecules. Our results suggest the approach will be broadly applicable to many types of local structure in simulations.

---

1 Introduction

Molecular simulations have become an indispensable tool in investigations of wide-ranging phenomena in physics, chemistry, biology, and engineering. One of the primary goals of molecular simulations is to relate microscopic behavior to macroscopic observable properties of a system. As such, local structure (i.e., spatially local arrangements) of atoms and molecules is often of interest. In principle, the raw output from molecular simulations—the position coordinates of each atom in the system for the duration of the simulation—includes all the necessary information to quantify local structure. However, this immense quantity of data inevitably requires further analysis to extract meaningful insights into system behavior. Quantitative measures of local structure are thus imperative in analysis of molecular simulations.

The current approach is to calculate some mathematical quantity that is a function of the atomic positions. These functions are referred to as ‘order parameters’ since they often track structural order present in a system. In some cases, order parameters can be trivial to implement and intuitive to understand (e.g., distance between an ion pair¹). However, many types of local structure have more subtlety (e.g., solvation environments, crystal polymorphs) and require substantially more complex order parameters. Though there are some general approaches that have proven successful for certain types of systems,^2–5 order parameter development is a highly challenging and non-trivial endeavor. This difficulty is evidenced by the fact that demonstrating new order parameter(s) is often itself worthy of a full paper.^6–10 Given the difficulty of order parameter development, it is unfortunate that most order parameters only distinguish a small set (i.e., <3) of physical structures. Development and/or implementation of multiple order parameters is often required if it is necessary to distinguish between additional structures. These challenges hinder progress in applying molecular simulations to study novel structures and systems.

The widespread success of machine learning has prompted researchers to apply techniques from this field in capacities that span nearly every aspect of molecular simulations. Several groups are actively working to directly combine machine learning with advanced sampling methods.^11–13 Others have used machine learning to develop force fields,^14,15 for coarse-graining,^16,17 to identify reaction coordinates,¹⁸ and to extract trends in results by clustering similar structures.^19–21 There are a few previous efforts to use machine learning for structure identification in molecular simulations.^19,22–26 In general, such approaches seem promising given the widespread success of machine learning in tasks such as computer vision (e.g., image recognition, segmentation, etc.).^27–29 Structure identification in simulations is in many ways similar to computer vision tasks, where simple units of patterns or structures (e.g., distances and angles between atoms) combine in specific larger patterns to form some structure (e.g., crystal type, macromolecular secondary structure).

The primary challenge in applying machine learning to structure identification in molecular simulations is determining the appropriate input features. Several interesting approaches have relied on preprocessing the output from molecular simulations. Geiger and Dellago²² trained a neural network to identify crystal structures in Lennard-Jones (LJ) and water systems by processing the raw output from molecular simulations through system-specific symmetry functions.¹⁴ Similar symmetry functions have been used in combination with support vector machines to predict particle rearrangements under shear³⁰ and at grain boundaries.³¹ Other approaches for structure identification in molecular simulation have first processed the simulation output with spherical harmonics^24,26 or other carefully engineered features.^25,26 Panagiotopoulos and co-workers took a different approach, using neighborhood graphs and diffusion maps^32,33 to discover, cluster, and classify crystal structures and identify relationships between crystal types without explicit training of each structure.^19,23 In general, the previous attempts to apply machine learning for structure identification in molecular simulation require extensive preprocessing^22,25 or complex and computationally expensive methods.^19,23 In particular, preprocessing data can require extensive system-specific parameterization and risks limiting the methods to specific types of local structure.

Our goal is to develop a simple and straightforward machine learning approach to distinguish between any number of distinct local structures that appear in molecular simulations. These local structures could be representative of a local crystalline environment, biomolecular conformation, relative arrangement of ligand and binding site, or, in principle, any other structure. The key feature is that the structures must be distinct. In the context of machine learning, this represents a classification problem. Neural networks, a cornerstone of deep learning, have been increasingly used for classification and segmentation tasks in a plethora of diverse applications. Deep learning offers a suitable approach for classifying structure in a molecular simulation because of its ability to extract high level representations from raw features of large datasets.³⁴ However, there are challenges to directly applying neural networks to molecular systems. Molecular systems contain physical symmetries that should be preserved: symmetry with respect to global translation, global rotation, and exchange of chemically identical atoms. In other words, the classification should remain identical upon applying any of those operations to a structure. One approach to handling these symmetries is through preprocessing (e.g., symmetry functions).¹⁴ However, this can require system-specific tuning and/or a priori knowledge.⁶ We aim to create a procedure that requires minimal preprocessing or tuning by training a neural network on data that is as close as possible to the raw output from molecular simulations. The approach should be easy to apply, able to distinguish between multiple different structures, and applicable to a range of systems studied in molecular simulations.

Using ideas from computer vision,³⁵ we implement a network that is designed to operate directly on sets of points—i.e., the output of molecular simulations. We apply our approach to differentiate between the liquid phase and various crystal structures. This choice is motivated by several factors. (1) Molecular simulations are widely used to study phase equilibrium and phase transitions in a myriad of substances. Crystal structure identification is required in studies of crystal nucleation,^36,37 crystal growth/dissociation,^38,39 crystal defects, and crystal grain boundaries.⁴⁰ (2) It is important to have a local (rather than global) measure of the crystal type for all of the previously listed problems, (3) there are many types of crystal structures, providing a rich test bed for our approach, (4) more recent studies have focused on heterogeneous nucleation (i.e., in the presence of an external interface), where existing order parameters are often unable to identify the crystal type of atoms nearest to the external interface,⁴¹ and (5) successfully demonstrating the method for crystal structure identification in multiple types of systems suggests it should be broadly applicable to any assembly process (e.g., crystallization, protein folding, etc.) that involves the formation of multiple distinct structure types that must be identified.

The methodology is described in Section 2. Results from three different types of systems (LJ, water, and mesophase) are presented in Section 3. The method is extended to identify hydrophobicity on surfaces in Section 4. Concluding remarks and future directions are provided in Section 5. For brevity, all simulation details are provided in the ESI.†

2 Methods

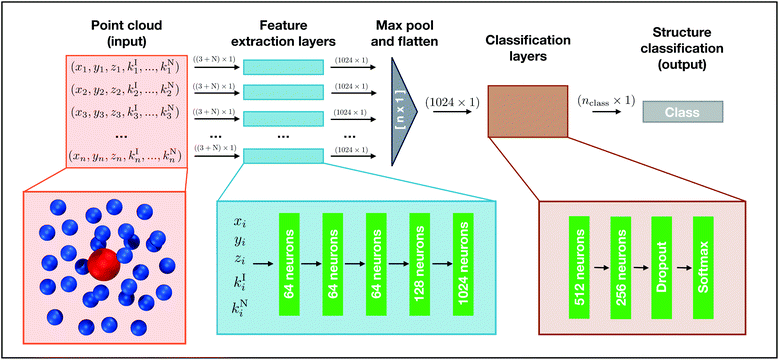
In machine learning, point clouds are a data structure that consist of a set of points in 3D space. Each point is represented as (x, y, z) coordinates, and a single point cloud consists of a collection of individual points. Point clouds are notoriously challenging to work with because of their irregular data structure. One common way to handle point clouds is to convert the data structure into a regular 3D voxel or a collection of images so it can be processed using existing methodologies that handle regular, lattice-like data, such as 2D or 3D convolutional neural networks.^42,43 However, when dealing with a large number of data points, these transformations create needlessly voluminous data. Computation times for model training and evaluation can quickly exceed practical limits and these data preprocessing transformations can also obscure natural invariances within the data.³⁵ We elect to use a recently developed deep learning model known as PointNet, which directly processes point clouds without preprocessing.³⁵ The input to PointNet is a single point cloud (i.e., set of points) while the output is a class label for classification or a per point label for segmentation.

Our goal is to classify local structure in simulations. Since the raw output from molecular simulations is a point cloud, we use a PointNet to classify structures found in point clouds composed of spatially local atoms. The classification can describe a collective property of all the atoms in the point cloud (e.g., the conformation of a small molecule could be classified from the coordinates of its atoms) or the classification can be projected back onto the central atom to provide a descriptor of the local environment that the central atom is embedded within (e.g., local crystal structure).

2.1 PointNet structure

We choose to use the basic setting of the PointNet architecture, which consists of a section of shared dense feature extraction layers, a max pooling operation, followed by a section of densely connected layers. A schematic of the network structure is shown in Fig. 1. The PointNet takes a point cloud comprised of n points as input. Each point i is composed of x_i, y_i, and z_i, to which 0–N additional features can be appended (k_i¹, …, k_i^N). Before entering the feature extraction layers, the point cloud is randomly rotated around the x, y, and z axis. This transformation is required to train the network to be invariant to global rotation. Each point is identically and independently passed through the feature extraction layers. The feature extraction is a multilayer perceptron (MLP) network composed of five dense layers with 64, 64, 64, 128, and 1024 neurons, respectively. It is important to note that the weights of the feature extraction networks are shared across each point, similar to a convolution operation. Following the feature extraction, each point has been transformed from being described by 3 + N features to 1024 features. Furthermore, each point has undergone the same mathematical transformations, regardless of the input ordering of the points.

Fig. 1 PointNet Architecture. The PointNet takes n points of 3 + N dimensions (i.e., a single point cloud) and passes them through feature extraction layers, a max pooling layer, and finally classification layers. The feature extraction is comprised of five dense layers that share weights across each point. The max pooling layer applies a symmetric function with a n × 1 filter, reducing the features to just 1024 × 1 dimensions. Two dense layers and a softmax layer are used to determine the final classification of the point cloud.

It is necessary to combine features from the different points in order to reach an overall classification, but a strategy must be applied to make the model permutation invariant of the input order. The PointNet implementation we use employs a symmetric function that aggregates information from each point, irrespective of initial point order. The idea is to approximate a general function (i.e., classification) by combining feature transformations and a symmetry function as follows:

f({p₁, …, p_n}) ≈ g(h(p₁), …, h(p_n))

where p₁, …, p_n are the points in the point cloud, h is the feature extraction MLP and g, the symmetry function, is the max pooling function. The max pooling function uses a filter of size [n, 1], where n is the number of points. Thus, the max pooling function selects, for each feature, the value that is most highly activated, regardless of the point that it comes from. The output from this operation is symmetric with respect to changing the order of the input points. The combination of the shared feature extraction MLPs and this max pooling layer allows us to input a set of spatial coordinates describing a molecular structure, and maintain the invariance to exchange of atoms. The output of the max pooling layer is fed to two fully connected layers with 512 and 256 neurons, respectively, which is fed to a dropout layer (keep probability 0.7) and finally a softmax layer for classification.

All fully connected layers, including the layers in the feature transformation, use batch normalization⁴⁴ and the rectified linear unit (ReLU) nonlinear activation function. We employ the cross entropy loss function and use the Adam Optimizer⁴⁵ with learning rate 0.001 and default parameters. The network was implemented using the TensorFlow⁴⁶ Python API.

Results should be invariant to global translations and global rotations of the point cloud, as well as the exchange of atoms (i.e., the order of points in the point cloud). Invariance to global translation is handled by shifting the point cloud such that some selected central atom is always located at (0, 0, 0). The invariance to exchange of atoms is handled by the structure of the PointNet. Invariance to global rotations is handled by the random rotation that is applied to each point cloud before it enters the network.

Discussion of a few other network architectures is presented here. The original Behler–Parrinello network was used to predict the contribution of a single atom to the total energy based on its local environment.¹⁴ This was achieved via two steps: first, the relative positions of the atom's neighbors were used to calculate several symmetry functions. The symmetry functions were parameterized by hand and ensured invariance of the final energies to global rotations, global translations, and permutations of the ordering of points describing the neighbor environment. Second, the values of the symmetry functions acted as inputs to a fully-connected hidden layer that predicted the energetic contribution of the central atom. Geiger and Dellago²² used a similar architecture for crystal structure identification, but the output layer was modified for classification. Similar to Geiger and Dellago,²² the PointNet uses fully connected layers to perform the eventual classification. However, the hand-parameterized symmetry functions have been replaced by the feature extraction and max-pooling layers. As with the symmetry functions, these layers ensure output invariance to translations and order permutations of the input neighbor environment. Since the weights of the feature extraction layers are learnable, the PointNet identifies the features of the neighbor environment required for classification during training. This is a primary benefit of the PointNet approach; there is no human intervention required for feature engineering (e.g., selecting and parameterizing symmetry functions)—the raw coordinates of the point clouds are input directly to the neural network. Gomes et al.⁴⁷ took a slightly different approach to predict protein–ligand binding affinity without requiring human parameterized symmetry functions. They created a distance matrix consisting of N atoms and the distances to each atom's M nearest neighbors. The distance matrix naturally has symmetry with respect to global translations and rotations. Radial pooling filters were applied to the distance matrix to down-sample and provide invariance to permutations of the input ordering of atoms. The parameters for the radial pooling functions were learned during training. The DeepIce²⁶ network of Fulford et al. consisted of four subnetworks—Cartesian coordinates network, spherical coordinates network, Fourier transform network, and spherical harmonics network. The coordinates-based subnetworks used the Cartesian and spherical coordinates of neighbors with respect to the central atom as input, respectively. The method requires a priori selection of spherical harmonics functions. The Cartesian subnetwork shares some similarities with the PointNet. However, the use of concatenation could cause the network to depend on the ordering of the inputs.

2.2 Local crystal structure identification

One common approach in crystal structure identification is to determine the crystal structure of each atom from its local environment. We apply the PointNet in a similar manner to determine the crystal environment of every atom in the system. Each point cloud is created by the positions of atoms within some cutoff distance, r_cut, of a central atom, a_j, and used to classify the crystalline environment of a_j. Standard periodic boundary conditions are applied when calculating the neighbors of a_j. Each point cloud is translated such that the central atom, a_j, is located at (0, 0, 0). This step preserves the symmetry of the network output with respect to global translations of the point cloud. The coordinates of the atoms in the point cloud are scaled such that the closest atom is always at distance of 1.0. The PointNet requires a fixed number of points, n, in the input point clouds. However, the number of atoms within a given cutoff distance of a central atom varies from sample to sample. To handle this problem we pre-selected a set point cloud size for a given cutoff distance. If a sample contained more than n points, the furthest points from the central atom were removed from the point cloud until only n points remained. If the sample contained fewer than n points, the point cloud was padded with (0, 0, 0) points. The number of points in the point cloud, n was selected as two standard deviations above the mean number of points within the cutoff distance.

2.3 Training and testing methodology

The PointNet is trained on samples generated from simulations of pure crystal phases. This approach provides easy ground truth labels for the samples. 10⁴–10⁵ samples were collected from simulations of each pure phase. We ensured that there were an equal number of samples from each phase. Samples were randomly divided into a training and testing portion, with 80% of samples in the training set and the remaining 20% of samples belonging in the test set. Each time a point cloud is processed through the network, it is given a different random rotation around its x, y, z axes. Thus, the network is forced to learn the invariance to global rotations of the point clouds. The network was trained for 100 epochs with each batch containing 64 point clouds.

The test set is sampled from the original data distribution. To more rigorously check for model generalization, we devise a ‘hold-out’ set in addition to the test set for some systems. The hold-out set contains the same crystal phases as the training and test data, but the samples are taken from simulations performed at temperature and pressure conditions that are interpolated between the conditions used for training and testing. The hold-out set is designed to ensure that the network has indeed learned the emergent features of the crystal structure and generalizes to conditions not explicitly seen by the network during training.

3 Results and discussion

3.1 Lennard-Jonesium

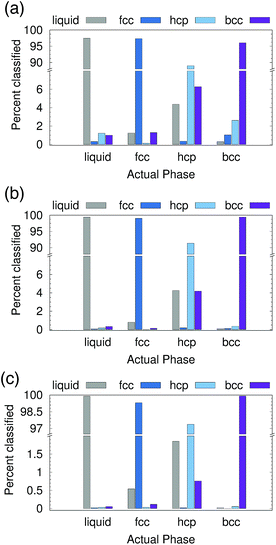
We first tested the ability of the PointNet to classify phases formed from Lennard-Jones (LJ) particles. The network was exposed to four classes of structures during training, namely, liquid, fcc, hcp, and bcc. To provide a robust test of the PointNet, the trained network was tested on point clouds that were taken from (T, P) conditions that the network was never exposed to during the training phase. The (T, P) conditions were selected such that they interpolated between the (T, P) conditions of the training data. Each point in the point clouds comprised only of (x_i, y_i, z_i)—no additional features were appended (i.e., N = 0 in Fig. 1).

Results are reported in Fig. 2. Fig. 2 shows both the classwise accuracy of the network and which class the network tends to (incorrectly) select when it misclassifies a sample. The abscissa of each panel in Fig. 2 lists the true class of each sample. The bar reports the classification selected by the PointNet. Note the use of broken ordinate axes to highlight both low and high percentage regions. The cutoff radius (r_cut) for the point cloud was increased from r_cut = 1.5 for Fig. 2(a) to r_cut = 2.0 for Fig. 2(b) and r_cut = 2.6 for Fig. 2(c). With increasing r_cut, the number of points in the point cloud increases. The point clouds for r_cut = 1.5, r_cut = 2.0, and r_cut = 2.6 were 16, 43, and 83 points, respectively. Not surprisingly, the accuracy of the PointNet increases with increasing cutoff radius, from 95.2% for r_cut = 1.5 to 99.2% for r_cut = 2.6. Larger cutoff radii increase the number of points in the point clouds and enable PointNet to identify longer range repeating patterns in the crystal structures. These patterns presumably become more distinct and easier to differentiate with larger point clouds. Furthermore, increasing the cutoff reduces the probability that a sample from one phase will spontaneously adopt, through thermal fluctuations, a configuration that appears identical to a different phase. A previous effort,²² which used machine learning to classify LJ phases, performed slightly better than 95% accuracy with a cutoff of 2.6. The method employed a substantially smaller network (∼3000 trainable parameters vs. ∼800 000 in our network), but preprocessed the raw input data through user-defined and parameterized symmetry functions. To facilitate direct comparison and ensure that the superior performance of the PointNet was not arising from the training/testing procedure, we implemented the network architecture described in ref. 22 in Keras⁴⁸ and trained the network with data generated from our simulations. Complete details are provided in the ESI.† All symmetry functions and their parameters were taken from ref. 22. Similar to the results reported in the original work, we achieved an overall accuracy of 96.5% with a cutoff radius of 2.6.²²

Fig. 2 Classification choices of a PointNet trained on four phases of a LJ system with (a) r_cut = 1.5, (b) r_cut = 2.0 and (c) r_cut = 2.6 distance units. Note the ordinate axis of panel (c) differs from (a) and (b). Overall accuracy is 95.2%, 97.7%, and 99.2% for r_cut = 1.5, r_cut = 2.0, r_cut = 2.6, respectively.

3.1.1 Structure identification in crystal seeds. To further test our method, we focused on the crystallization aspect. We generated LJ systems comprised of crystalline nuclei surrounded by a liquid bath. Simulations were performed for systems with three different sizes of the initial crystalline seed. The dynamics were propagated with molecular dynamics (MD) at a temperature below the melting point. If the initial nucleus size is above the critical size, the crystalline seed grows to encompass the entire system; if it is below the critical size, the crystalline seed melts. These types of simulations are used as part of the seeding method,⁴⁹ which is used to predict crystal nucleation rates. The definition of the exact size of the crystal seed is one of the largest sources of uncertainty in the method.⁵⁰ The test case enabled us to explore several questions regarding the behavior of the PointNet. How would the network perform outside of pure phases? Would the network provide reasonable classifications for atoms near the boundary of solid and liquid phases? Would the network be able to identify defects within the solid phase? How would classifications be affected by changing the cutoff radius?

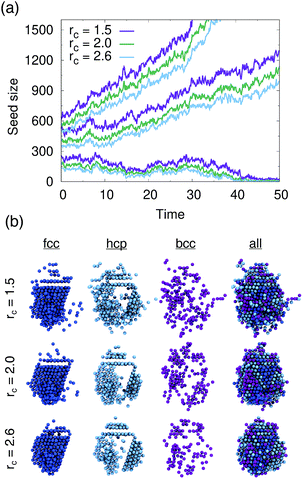
We tested PointNet trained with the three different cutoff radii (r_cut = 1.5, r_cut = 2.0, r_cut = 2.6). The identity of each atom in the system was calculated every 0.1 time units. The crystalline nucleus was identified at every step as the largest cluster of connected solid atoms (all fcc, hcp, and bcc atoms are considered solid) in the system. Two atoms are connected if their distance is within the distance to the first minimum in the liquid radial distribution function.

The evolution of seed sizes is reported for the three different seeds in Fig. 3(a). For each initial seed size the calculated seed size is reported with time for each value of r_cut. Larger cutoff radii result in smaller seed sizes. This result is not particularly surprising; from Fig. 2, it would be expected that more liquid atoms surrounding the seed will be incorrectly classified as solid for the smaller values of r_cut. These atoms, incorrectly classified as solid, are added to the surface of the largest solid cluster, resulting in a larger overall cluster size. This effect is in many respects similar to the results found from using a stricter classifier with traditional order parameters.⁵¹ Effectively the PointNet acts as a stricter classifier when there is a larger cutoff radius.

Fig. 3 Growth and dissociation of crystalline seeds identified by a PointNet in LJ systems. The behavior of the overall seed size with time is shown in panel (a). Snapshots of a seed at one time point are shown in panel (b) to show the variation in classification with changing cutoff distance.

One important question to consider is how the classifications of the solid atoms in the cluster change with increasing cutoff radius. Ideally, the overall structure and composition of the crystalline nucleus identified by the PointNet would be relatively insensitive to the choice of r_cut. Snapshots for one crystalline nucleus at a single time are reported in Fig. 3(b). The first three columns show the fcc, hcp, and bcc atoms that belong to the largest cluster of solid atoms. The fourth column overlays all the classes to show the complete crystalline nucleus. From the rightmost column it is apparent that the overall nucleus size decreases with increasing cutoff. However, the atoms that are removed from the crystalline cluster are surface atoms that do not appear to display substantial crystallinity. Encouragingly, the first two columns show that classifications of atoms in the core of the cluster are insensitive to changing the cutoff radius of the PointNet. In particular, the network consistently identifies a single layer of hcp atoms stacked between layers of fcc atoms as well as clear hcp layers growing along several edges of the nucleus. It is not particularly surprising to find that the size of the crystalline cluster decreases as the PointNet becomes a stricter classifier (i.e., with increasing cutoff). However, it is encouraging to find that the identities of atoms within the core of the crystal remain relatively consistent with different cutoff values.

3.2 Water systems

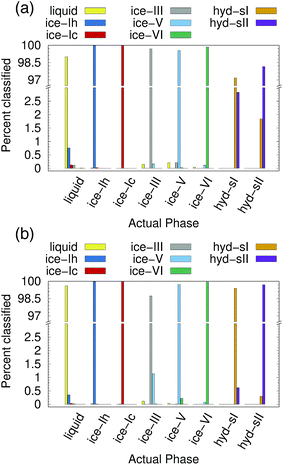
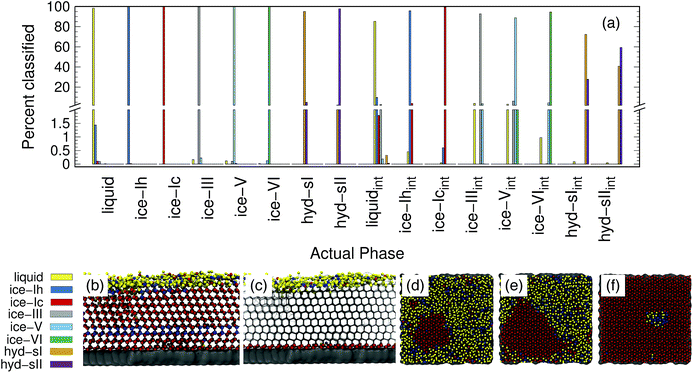
Ice and hydrate nucleation are particularly active areas of research.^37,52–54 One of the largest challenges in this field is structure identification. Thus, we next tested the ability of the PointNet to classify the phases of water molecules. The PointNet was trained on eight different phases, including liquid, five ice phases, and two hydrate phases. Unlike the LJ systems, water is comprised of two different atom types. Historically, most methods for classifying ice structures rely only on the positions of the oxygen atoms. However, there may be additional information to be gained by including the positions of the hydrogen atoms. We explore both options.

3.2.1 Classification of water phases using only oxygen atoms. At first, only the positions of the oxygen atoms were used in the point clouds. In this case, all points in the point cloud are identical (with respect to atomic identity), therefore the points are completely described by (x_i, y_i, z_i) and no additional features are appended. Results are shown in Fig. 4 using a cutoff radius of 0.6 nm. The point clouds contain 43 points. The PointNet does exceedingly well at distinguishing the liquid, ice phases, and hydrate phases. Once again, the liquid is sometimes (<1.5%) identified as one of the solid phases. Our results for the LJ systems suggest that misclassification could be reduced by further increasing the cutoff radius. In particular, it is worth noting that the PointNet performs better on water systems compared with LJ systems with the same number of points in the point cloud (for LJ systems, r_cut = 2.0 has 43 points). We conjecture that this observation is related to the open network structure of water;⁵⁵ a water molecule only has an average of four first neighbors whereas LJ systems have closer to 12. Thus, for the same 43 points the PointNet can evaluate further neighbor shells for water relative to the LJ systems.

Fig. 4 Classification choices of a PointNet trained on eight water phases with a cutoff of 0.6 nm. (a) Using only oxygen atom positions in the point cloud (overall accuracy is 99.1%), and (b) using both oxygen and hydrogen atom positions in the point cloud (overall accuracy 99.6%).

The network has the greatest difficulty distinguishing between the two hydrate phases. Though the network is able to clearly distinguish these phases from the liquid and ice phases, ∼2% of sII samples are classified as sI and ∼3% of sI samples are classified as sII. The hydrate phases have, on average, fewer points within the cutoff distance; it seems quite plausible that this difference is the source of greater error in classifying the hydrate phases. Despite minor difficulties with the hydrate phases, the overall accuracy is still superior to previous attempts to classify multiple ice structures with neural networks.²² Once again, we trained a network with the architecture from ref. 22 with training data from our simulations. Only the liquid phase and the five ice phases were used since Geiger and Dellago did not parameterize symmetry functions for hydrate phases. We achieved similar overall accuracy (∼95%) as reported in the original work.²² An approach that was published during the writing of this paper achieved higher classification accuracy but only distinguished between the ice Ih and liquid phases.²⁶

3.2.2 Classification of water phases using oxygen and hydrogen atoms. Next, we investigate the effect of including positions of the hydrogen atoms in the point cloud. Each water molecule is still classified as a certain phase. It does not seem sensible to classify the hydrogen of a water molecule as belonging to ice-Ih and the oxygen of the same water molecule as belonging to ice-Ic. Therefore, we generate a point cloud centered around each oxygen atom. However, instead of the previous approach where the points in the point cloud were only comprised of the oxygen atoms, we now also include the positions of the hydrogen atoms. Given the distinct hydrogen-bonding patterns in water, we hypothesize that including the hydrogen atom positions in the point cloud will improve classification. The network structure presented in Fig. 1 indicates that additional features (k_i¹, …, k_i^N) can be appended to (x_i, y_i, z_i) for point i. We use this ability to include the atomic identity of each point. Two features, k^I_i and k^II_i are added to each point. The atomic identity is one-hot encoded. Oxygen atoms are encoded as (x_i, y_i, z_i, 1, 0) and hydrogen atoms are encoded as (x_i, y_i, z_i, 0, 1). This distinction should enable the network to recognize the difference between oxygen and hydrogen atoms during feature extraction (see Fig. 1).

The addition of the hydrogen atoms with atomic identity improved the overall accuracy from 99.1% to 99.6%. Though this seems like a relatively minor improvement in the accuracy statistic, it dramatically improved the classification of the sI and sII hydrate phases (Fig. 4(b)) and in fact reduced the total misclassification rate by over 50%. In certain cases it can be extremely important to minimize particle misclassifications. In particular, it can be important to minimize liquid particles that are misclassified as solid.^49,50 The results for the PointNet when hydrogen atoms are included have nearly as low misclassifications (0.4% vs. 0.25%)⁴⁹ as the strictest order parameter for identifying ice structures.⁶ This result is despite the fact that the strictest order parameter was used to distinguish between only two phases while the PointNet is distinguishing between 8 phases. Furthermore, the accuracy of the PointNet could no doubt be increased further by increasing the cutoff radius.

3.2.3 Nucleation at solid interfaces. Significant effort has recently focused on heterogeneous ice nucleation,^54,56–59 that is, ice formation that occurs in the presence of an external interface. We thus decided to test the ability of our PointNet to classify the types of ice that form on surfaces. In initial tests (data not reported), the PointNet was unable to correctly identify the identities of the water molecules in the layer of water nearest to the interface, even though the second layer of water and above were correctly classified. The reason the PointNet was unable to correctly identify the identity of interfacial water molecules is that the point clouds for these samples were effectively cut in half, from a sphere to a dome shape. No water molecules penetrate into the surface, and thus, the point clouds for water molecules nearest to the surface only have points from the water molecules in the direction opposite from the surface.

Classification of interfacial molecules with the PointNet thus presents a unique challenge. There are a few potential approaches to solve this problem. One could generate interfacial training data for each phase. These data could be generated by simulating each phase in contact with a solid surface or at an interface with a vacuum. Unfortunately, both of these options present a range of further complications. In the first case, since the structure of water near the surface may be affected by the chemical composition and structure of the surface, it would be necessary to simulate near several different surfaces to achieve any substantial model generalizability. In case of a vacuum interface, the layer nearest the vacuum would likely melt,⁶⁰ or at least deform, thus requiring position restraints (or some similar approach) to maintain the crystal structure. In both cases, there is the question of which crystal plane to simulate as the exposed surface. In most cases where researchers are actively studying heterogeneous crystal nucleation, the crystal plane that nucleates on a surface is unknown a priori. In all likelihood, it would be necessary to simulate multiple crystal faces for each phase. Any of these complications add substantial complexity to the structure identification process because they require significant additional simulations.

The ideal scenario is to train the PointNet to correctly identify interfacial molecules without requiring additional training data or making any assumptions about which crystal faces are most likely to form at some surface. To this end, we developed and tested the following approach. For each bulk training sample (i.e., a single point cloud with a label) we (1) randomly rotate the point cloud, (2) remove all points with z < 0.0 by replacing (x_i, y_i, z_i) with (0.0, 0.0, 0.0), and (3) randomly rotate the point cloud. The label for the sample, l, is changed from l-bulk to l-interfacial. The first rotation removes any memory of the crystal orientation in the simulation box from the simulation of the bulk crystal. Replacing points below the z = 0 plane with (0.0, 0.0, 0.0) effectively removes those points from the point cloud. This replacement causes no issues during training as we already pad the point clouds with (0.0, 0.0, 0.0) points if there are insufficient atoms within r_cut. The final rotation removes the memory of removing all atoms below the z = 0 plane. This procedure thus uses the original bulk training data to generate point clouds with a dome geometry. No assumptions are made about the exposed crystal plane or the orientation of the external surface in the simulation box, and all crystal planes are sampled in the procedure without any additional simulations.

The accuracy of the PointNet trained on both bulk and interfacial water phases is reported in Fig. 5(a). Only oxygen atoms are included in the point clouds. The first eight phases are the bulk phases and the next eight are the respective interfacial counterparts. The overall accuracy decreased from 99.1% to 92.5%. The decrease in overall classification accuracy is not surprising given that half of the samples (i.e., the interfacial samples) have 50% fewer points in each point cloud. Despite the decrease in overall accuracy, there are several positive features worth noting. Firstly, bulk classification remains extremely accurate. For example, bulk ice phases all remain above 99.5% correctly classified. Secondly, there is no mixing between the interfacial phases and the bulk phases; i.e., an interfacial atom is never classified as bulk and vice versa. In essence, this means that the PointNet simply struggles to correctly classify the identity of interfacial atoms. It still performs acceptably for interfacial liquid and ice phases. Only the performance of interfacial hydrate phases is particularly poor. One final observation is that the PointNet was trained and tested on all possible crystal planes at the exposed surface. As described previously, this is beneficial in that it makes the extension of the PointNet approach to interfacial systems trivial. There currently exist few methods¹⁹ to identify local crystal structures at interfaces.

Fig. 5 (a) Classification choices and (b–f) snapshots of classified atoms for a PointNet trained on sixteen water classes (eight bulk and eight interfacial). Panel (b) shows the network identifying a single layer of ice-Ih within ice-Ic. Panel (c) shows atoms that belong to an interfacial class as spheres. Panels (d–f) show a top view of the classifications of the first two layers of atoms for a growing ice seed. The color scheme in (b–f) corresponds to (a). The external surface is shown in gray. Water oxygens within 0.35 nm of each other are connected by light gray bonds.

Panels (b–f) of Fig. 5 show snapshots from simulations of the formation of ice at an external surface (gray). Panel (b) shows the classification of each atom in the system. The ice that forms is primarily ice Ic (red spheres) with a single stacking-disordered layer of ice Ih (blue spheres). Consistent with expectations,⁶¹ a layer of liquid (yellow spheres) exists at the ice-vacuum interface. Panel (c) only shows atoms classified as interfacial types as spheres. The snapshot confirms the results from panel (a)—no bulk atoms are misclassified as interfacial. Panels (d–f) show the growth of an ice nucleus on the surface from a top-down perspective. To highlight the interfacial classifications, only water molecules belonging to the first two layers on the surface are shown. Despite lower accuracy, the interfacial classification appears to perform quite well. The ice nucleus, composed of ice Ic, clearly develops. Very few atoms within the center of the ice seed are classified as any other type. There does appear to be a somewhat greater number of misclassifications in the interfacial liquid, although it is difficult to say with certainty that none of those water molecules are in a locally ice-like environment. We note that the liquid/ice-Ih region in panel (f) is indeed correctly classified. The ice in that region contained a grain boundary between the periodic images of the growing ice crystal that was not fully resolved by the end of the simulation.

3.3 Mesophases

Mesophase systems have attracted interest in recent years^10,62–66 because they can be used to study the behavior of self-assembling materials and block co-polymers. The key feature of such systems is that some molecules remain locally amorphous, even following the transition from a disordered state to an ordered state. The systems are generally composed of two different types of molecules (for simplicity, just consider two particle types, A and B). A rich variety of structures can be formed by tuning the relative size and strength of A–A, B–B, and A–B interactions.

There have been very recent efforts¹⁰ to develop order parameters that distinguish between the different mesophases in order to better understand the behavior (e.g. nucleation) of such systems. Developing order parameters for mesophase systems is particularly challenging because there are a large number of possible phases that can form and, by definition, part of the system is non-crystalline. Previous efforts have resorted to developing different order parameters to distinguish each phase.¹⁰ Here we test the extensibility of the PointNet approach by using these mesophase systems as test cases.

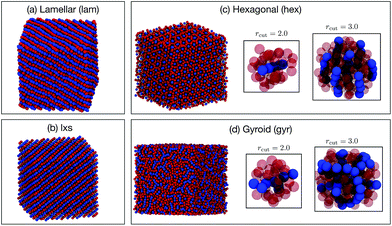
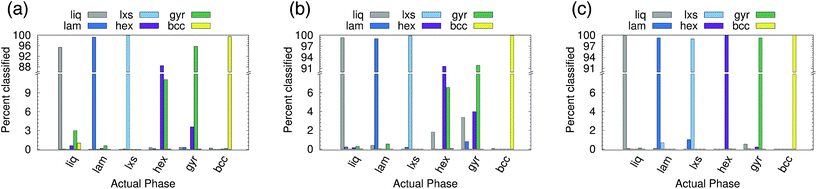
Six phases were simulated (see ESI† for details): liquid (liq), lamellar (lam), lxs, hexagonal (hex), gyroid (gyr), and body-centered cubic (bcc). Snapshots of the lam, lxs, hex, and gyr phases are provided in Fig. 6. Three different approaches to classification are attempted. In all cases, we only attempt to classify the structure of the minor component. Even in non-liquid phases, the major component tends to belong to largely disordered amorphous regions. In the first attempt, both A atom types and B atom types are used as points in the point cloud. However, A types and B types are not distinguished (i.e., no additional features are appended to (x_i, y_i, z_i)). We test cutoff values of 2.0 and 3.0. The results for r_cut = 2.0 are reported in Fig. 7(a). The overall accuracy is ∼96%. Increasing the cutoff to 3.0 increases the accuracy slightly, to 97.6%. As can be seen from Fig. 7(a), the PointNet is particularly challenged to distinguish the hexagonal and gyroid phases. This difficulty is explained by the snapshots in Fig. 6(c and d). With a cutoff of 2.0, the point clouds of the hex and gyr phases appear very similar. The point clouds would look particularly similar in this case, where the type A and B particles are not distinguished.

Fig. 6 Snapshots of four mesophase systems (a) lamellar, (b) lxs, (c) hexagonal, and (d) gyroid. Minor component atoms are shown in blue and major component in red. Example point clouds with a cutoffs of 2.0 and 3.0 are shown for the hexagonal and gyroid phases.

Fig. 7 Classification choices of a PointNet trained on six phases of a mesophase forming system with a cutoff distance of 2.0. The point cloud included (a) all points, (b) all points with identifying labels, and (c) only points belonging to the crystalline component. Note the ordinate axis of (b) and (c) differ from (a).

Next, the atomic identity was added to each point. Similar to the water systems, the atom types were one-hot encoded using two additional features. Results for r_cut = 2.0 are reported in Fig. 7(b). The addition of atomic identity improved the overall classification accuracy to 97.7%. However, the network still has difficulty distinguishing the hexagonal and gyroid phases.

Given the amorphous nature of the major component in most phases, it seemed reasonable that the inclusion of the major component might represent unnecessary and confusing information, and that performing classification based only on the positions of the minor component might be a better approach. This method yielded by far the best results (see Fig. 7(c)). The overall accuracy was 99.6% with r_cut = 2.0. The issues distinguishing between the hexagonal and gyroid phases are largely resolved. If r_cut is increased to 3.0, the accuracy improves to >99.9%. Using only the minor component to classify the structure of the mesophase system mirrors the approach taken with recent conventional order parameters.¹⁰

4 Beyond crystal structure identification

To showcase the utility of our method beyond applications in crystal structure identification, we use the PointNet to quantify the hydrophobicity of extended surfaces and proteins. Previous work characterizing surface hydrophobicity used local water density fluctuations or solute affinity over different portions of surfaces to create a spatially resolved measure of hydrophobicity.^67–70 Recent work found that water orientations near an interface may also be able to predict local surface hydrophobicity.⁷¹ In principle, the PointNet should be able to learn the differences in interfacial water structures near hydrophobic and hydrophilic interfaces. The network is trained to predict if an individual water molecule is in a hydrophobic or hydrophilic environment based upon the point cloud created by neighboring water molecules. Training examples are generated from water in contact with known hydrophobic and hydrophilic surfaces. Once the network is trained, it can be used to create a spatial map of surface hydrophobicity from the fraction of nearby water molecules that are identified as being in hydrophobic vs. hydrophilic environments.

4.1 Training methodology

The PointNet is trained from simulations of TIP3P water on hydrophobic and hydrophilic self-assembled monolayer (SAM) surfaces—CH₃SAM and OHSAM, respectively. Complete descriptions of the SAM surfaces and system setup are provided in the ESI.† Example point clouds for training are taken from water molecules wetting the surface. The oxygen atom of a water molecule must be within 0.5 nm of a surface terminal group heavy atom (C or O) to be considered surface-wetting. For each example, the point cloud itself consists of all hydrogen and oxygen atoms within a cutoff distance of 0.6 nm of the central water oxygen. The point clouds include one-hot encoded atomic identity for each atom in the point cloud. Ground truth labels are assigned based upon the surface in the system; point clouds for water molecules on CH₃SAM are labeled as examples of hydrophobic environments and point clouds for water molecules on OHSAM are labeled as examples of hydrophilic environments. The point cloud size (i.e., n in Fig. 1) was selected in the same manner used for crystal structure identification—two standard deviations above the mean number of points within the cutoff distance (0.6 nm)—and resulted in 82 points per cloud. The training (test) set consisted of a total of 800 000 (200 000) samples split equally between hydrophobic and hydrophilic environments.

4.2 SAM surfaces

After 50 epochs of training, the cost plateaued and the accuracy on the test set was 84%. The PointNet was trained three times and the reported accuracy is an average of the three trials. It is not particularly surprising that the classification accuracies are much lower than our results for crystal structure identification. Water molecules above both hydrophobic and hydrophilic surfaces are in liquid environments and it seems quite plausible that there is a fair amount of overlap between the distributions of structures sampled in each case. Interestingly, classwise accuracies varied across training trials. The network would achieve ∼90% accuracy on one class but only ∼78% accuracy on the other class. Sometimes the higher-accuracy class was hydrophilic environments while other times the higher accuracy class was hydrophobic environments.

Despite relatively poor accuracy on individual point clouds, we can still extract an average measure of surface hydrophobicity. The bounds of the hydrophobicity scale are determined by the water environments observed near CH₃SAM (hydrophobic bound) and OHSAM (hydrophilic bound). To identify numerical bounds for the scale, each surface-wetting water molecule is classified as hydrophobic or hydrophilic with the a pre-trained network. The classification is ‘projected’ back onto the surface by calculating, for each surface terminal heavy atom, the fraction of surface-wetting water molecules that are classified hydrophobic. This fraction is averaged across terminal groups from the OHSAM and CH₃SAM surfaces to generate the bounds for hydrophobic regions (0.95) and hydrophilic regions (0.25).

As a first test of the hydrophobicity scale, we calculate the hydrophobicity map for a SAM surface with alternating stripes of hydrophobic (–CH₃) and hydrophilic (–OH) terminal groups. Results are shown in Fig. 8(a). The regions identified as hydrophilic (blue surface representation) correspond to OH head groups (blue spheres) and the regions identified as hydrophobic correspond to the locations of –CH₃ head groups (red spheres). Intermediate hydrophobicity (white) is found near the boundary between the –OH and –CH₃ regions of the surface.

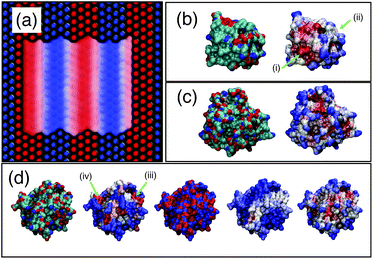Fig. 8 Application of PointNet to characterize surface hydrophobicity. (a) SAM surface with alternating –CH₃ (red spheres) and –OH (blue spheres) terminal groups. The colored ‘surface’ representation shows the identification of hydrophobic (red) and hydrophilic (blue) regions by the PointNet. White regions are intermediate hydrophobicity. Predicted surface hydrophobicity of hydrophobin II and CheY is shown in (b) and (c), respectively. Leftmost image shows the protein colored by atom types (red = oxygen, blue = nitrogen, green = carbon) while the rightmost image shows the predicted hydrophobicity. Panel (d) shows a comparison of surface hydrophobicity predictions for a different surface of CheY for our method (far right), Kyte and Doolittle⁷² (second from left), Kapcha and Rossky⁷³ (center), and Shin and Willard⁷¹ (second from right).

4.3 Protein hydrophobicity

Encouraged by the results on SAM surfaces we tested our method on the surface of two proteins: hydrophobin II (PDB: 2B97) and Escherichia coli CheY (PDB: 3CHY). Complete simulation details are provided in the ESI.† The same procedure is used to create a spatially resolved surface hydrophobicity map: (1) water molecules whose oxygen atom is within 0.5 nm of a protein heavy atom are considered surface-wetting. (2) For each surface-wetting water molecule, the point cloud consists of all water atoms within 0.6 nm of the central oxygen. (3) Each point cloud is sent to the trained PointNet to classify the central water molecule as hydrophobic or hydrophilic. (4) The classification is ‘projected’ back onto the surface by calculating, for each surface terminal heavy atom, the fraction of surface-wetting water molecules that are classified hydrophobic. The bounds of the scale remain the same as used for the striped SAM surface.

The surface hydrophobicities of hydrophobin II and CheY are shown in the rightmost snapshots in Fig. 8(b) and (c), respectively. The method tends to classify solvent-exposed regions as more hydrophilic and buried regions as more hydrophobic. This trend is in agreement with calculations showing that non-polar concave surfaces are more hydrophobic than non-polar convex surfaces.⁶⁹ However, the snapshots show that our method does not classify hydrophobicity from geometric considerations alone. Some solvent exposed regions are identified as hydrophobic (e.g., arrow (i)) whereas some are identified as intermediate or hydrophilic (e.g., arrow (ii)). A second view of CheY is shown in Fig. 8(d); our method is once again the rightmost snapshot. In panel (d), our results are compared with other methods of quantifying protein surface hydrophobicity. In all cases the more hydrophobic regions are colored darker red and the more hydrophilic regions are colored darker blue. Starting second from the left and moving right, the snapshots are the Kyte and Doolittle hydrophobicity scale,⁷² Kapcha and Rossky atomic hydrophobicity scale,⁷³ and the method of Shin and Willard.⁷¹ For the method of Shin and Willard, the hydrophilic and hydrophobic bounds of the scale are set by the average hydrophobicity of OHSAM and CH₃SAM, respectively. There are both similarities and differences across the different methods of quantifying surface hydrophobicity. For example, in panel (d) there is a small region (arrow (iii)) that the Kyte–Doolittle scale (second from left) quantifies as a patch with intermediate to hydrophobic character. All other methods agree that this region is at least intermediate between hydrophilic and hydrophobic, if not showing some hydrophobic character. In contrast, there is another small region (arrow (iv)) that the Kyte–Doolittle scale (second from left) quantifies as a patch with hydrophobic character. The Kapcha–Rossky scale and our method agree with Kyte–Doolittle, but the method of Shin and Willard considers this region hydrophilic. In general, the method of Shin and Willard identifies most of the surface as more hydrophilic than the PointNet—no portion of CheY is determined to be as hydrophobic as CH₃SAM. In contrast the PointNet identifies regions that have hydrophobicity roughly equal to CH₃SAM.

Multiple methods using water orientations⁷¹ to water density fluctuations^70,74 have been used to quantify protein surface hydrophobicity. It is difficult to know which method is most correct. Moreover, the precise meaning of surface hydrophobicity may become difficult to quantify within sufficiently buried pockets due to the observer context,⁶⁸ which found that the surface hydrophobicity map depended on the probe shape. It nonetheless appears that the PointNet method of quantifying surface hydrophobicity provides reasonable results that are in at least partial agreement with other techniques of quantifying surface hydrophobicity on proteins. We view this success as a robust demonstration of the generalizability of the PointNet method for quantifying local structure in molecular simulations.

5 Conclusions

We introduced a new method to identify local structures in molecular simulations. PointNet, a type of neural network developed for processing point clouds for applications in computer vision, was applied to identify local structure in molecular simulations. Local structure is identified by analyzing point clouds created by the local atomic environment. We tested the method on the problem of crystal structure identification in Lennard-Jonesium, water, and mesophase systems. In all cases, the PointNet approach results in highly accurate classification of crystal structures. The method was demonstrated under realistic use-cases: identifying crystalline seeds in bulk liquid and identifying heterogeneous crystal formation. We also demonstrated that the method generalizes beyond crystal structure identification—the same PointNet approach was shown capable of quantifying local surface hydrophobicity. As a further simple test of the extensibility of the PointNet approach to different types of systems, we trained the network to classify conformations of alanine dipeptide. This small peptide takes two primary configurations in vacuum, which are well separated in the space of backbone ϕ, ψ dihedral angles. Using point clouds created from the positions of the backbone atoms relative to the α-carbon, the PointNet was able to achieve effectively 100% classification accuracy.

Our work applied the PointNet under novel conditions. As originally developed,³⁵ the PointNet was designed to process large point clouds and extract global features for classification and segmentation. The point clouds consisted of >1000 points. We demonstrated that the same network architecture can be used on smaller point clouds and successfully extract subtle differences. We utilized the ability to append features to the coordinates of each point to add the atomic identity of each point while maintaining the invariance to input point order.

The primary strengths of the method are as follows: (1) highly accurate classification of local structures. (2) No system-specific parameterization: only the distance cutoff and maximum number of points in the point cloud must be selected. Our results suggest that, at least for crystal structure identification, 40–80 points results in highly accurate classification. (3) Simple addition of new structures: if at any point it becomes necessary to distinguish between additional structures the network can be retrained.

The PointNet approach should be highly generalizable to a variety of local structures that form in molecular simulations. Possible examples include arrangements of molecular crystals, different polymer configurations, structure in biomolecules, ligand-binding site arrangements, and more. The method will enable rapid structure identification in novel systems that lack order parameters. Similar approaches may also prove useful for other examples of machine learning in molecular simulation, e.g., dimensionality reduction, reaction coordinate identification, and enhanced sampling.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0015448. Clemson University is acknowledged for generous allotment of compute time on the Palmetto cluster.

References

1. P. L. Geissler, C. Dellago and D. Chandler, J. Phys. Chem. B, 1999, 103, 3706–3710.
2. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784.
3. P. M. Larsen, S. Schmidt and J. Schiøtz, Modell. Simul. Mater. Sci. Eng., 2016, 24, 055007.
4. G. J. Ackland and A. P. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 054104.
5. J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963.
6. W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707.
7. A. Reinhardt, J. P. K. Doye, E. G. Noya and C. Vega, J. Chem. Phys., 2012, 137, 194504.
8. L. C. Jacobson, M. Matsumoto and V. Molinero, J. Chem. Phys., 2011, 135, 074501.
9. B. C. Barnes, G. T. Beckham, D. T. Wu and A. K. Sum, J. Chem. Phys., 2014, 140, 164506.
10. A. J. Mukhtyar and F. A. Escobedo, Macromolecules, 2018, 51, 9769–9780.
11. J. M. L. Ribeiro, P. Bravo, Y. Wang and P. Tiwary, J. Chem. Phys., 2018, 149, 072301.
12. W. Chen, A. R. Tan and A. L. Ferguson, J. Chem. Phys., 2018, 149, 072312.
13. H. Jung, R. Covino and G. Hummer, 2019, arXiv preprint arXiv:1901.04595.
14. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
15. J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955.
16. S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K. Müller, Sci. Adv., 2017, 3, e1603015.
17. H. Chan, M. J. Cherukara, B. Narayanan, T. D. Loeffler, C. Benmore, S. K. Gray and S. K. R. S. Sankaranarayanan, Nat. Commun., 2019, 10, 379.
18. A. Ma and A. R. Dinner, J. Phys. Chem. B, 2005, 109, 6769–6779.
19. W. F. Reinhart, A. W. Long, M. P. Howard, A. L. Ferguson and A. Z. Panagiotopoulos, Soft Matter, 2017, 13, 4733–4745.
20. P. M. Piaggi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10251–10256.
21. S. Dasetty, J. K. Barrows and S. Sarupria, Soft Matter, 2019, 15, 2359–2372.
22. P. Geiger and C. Dellago, J. Chem. Phys., 2013, 139, 164105.
23. W. F. Reinhart and A. Z. Panagiotopoulos, Soft Matter, 2018, 14, 6083–6089.
24. M. Spellings and S. C. Glotzer, AIChE J., 2018, 64, 2198–2206.
25. C. Dietz, T. Kretz and M. H. Thoma, Phys. Rev. E, 2017, 96, 011301.
26. M. Fulford, M. Salvalaglio and C. Molteni, J. Chem. Inf. Model., 2019, 59, 2141–2149.
27. K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
28. S. Ren, K. He, R. Girshick and J. Sun, Advances in neural information processing systems, 2015, pp. 91–99.
29. J. Long, E. Shelhamer and T. Darrell, Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 3431–3440.
30. E. D. Cubuk, S. S. Schoenholz, J. M. Rieser, B. D. Malone, J. Rottler, D. J. Durian, E. Kaxiras and A. J. Liu, Phys. Rev. Lett., 2015, 114, 108001.
31. T. A. Sharp, S. L. Thomas, E. D. Cubuk, S. S. Schoenholz, D. J. Srolovitz and A. J. Liu, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10943–10947.
32. R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner and S. W. Zucker, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7426–7431.
33. A. L. Ferguson, A. Z. Panagiotopoulos, I. G. Kevrekidis and P. G. Debenedetti, Chem. Phys. Lett., 2011, 509, 1–11.
34. Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436.
35. C. R. Qi, H. Su, K. Mo and L. J. Guibas, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 652–660.
36. G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116.
37. R. S. DeFever and S. Sarupria, J. Chem. Phys., 2017, 147, 204503.
38. M. A. Carignano, P. B. Shepson and I. Szleifer, Mol. Phys., 2005, 103, 2957–2967.
39. S. Sarupria and P. G. Debenedetti, J. Phys. Chem. A, 2011, 115, 6102–6111.
40. V. Yamakov, D. Wolf, S. R. Phillpot, A. K. Mukherjee and H. Gleiter, Nat. Mater., 2004, 3, 43.
41. A. H. Nguyen and V. Molinero, J. Phys. Chem. B, 2014, 119, 9369–9376.
42. A. Krizhevsky, I. Sutskever and G. E. Hinton, Advances in Neural Information Processing Systems 25, Curran Associates, Inc., 2012, pp. 1097–1105.
43. Z. Wu, S. Song, A. Khosla, F. Yu, L. Zhang, X. Tang and J. Xiao, CVPR, 2015, p. 3.
44. S. Ioffe and C. Szegedy, 2015, arXiv preprint arXiv:1502.03167.
45. D. P. Kingma and J. Ba, 2014, arXiv preprint arXiv:1412.6980.
46. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/,Softwareavailablefromtensorflow.org.
47. J. Gomes, B. Ramsundar, E. N. Feinberg and V. S. Pande, 2017, arXiv preprint arXiv:1703.10603.
48. F. Chollet et al. , Keras, https://keras.io, 2015.
49. J. R. Espinosa, C. Vega, C. Valeriani and E. Sanz, J. Chem. Phys., 2016, 144, 034501.
50. N. E. R. Zimmermann, B. Vorselaars, J. R. Espinosa, D. Quigley, W. R. Smith, E. Sanz, C. Vega and B. Peters, J. Chem. Phys., 2018, 148, 222838.
51. W. Lechner, C. Dellago and P. G. Bolhuis, J. Chem. Phys., 2011, 135, 154110.
52. A. Haji-Akbari and P. G. Debenedetti, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10582–10588.
53. L. Lupi, A. Hudait, B. Peters, M. Grünwald, R. G. Mullen, A. H. Nguyen and V. Molinero, Nature, 2017, 551, 218.
54. M. Fitzner, G. C. Sosso, F. Pietrucci, S. Pipolo and A. Michaelides, Nat. Commun., 2017, 8, 2257.
55. P. V. Hobbs, Ice physics, Oxford University Press, 2010.
56. B. Glatz and S. Sarupria, J. Chem. Phys., 2016, 145, 211924.
57. B. Glatz and S. Sarupria, Langmuir, 2017, 34, 1190–1198.
58. R. Cabriolu and T. Li, Phys. Rev. E, 2015, 91, 052402.
59. Y. Qiu, N. Odendahl, A. Hudait, R. Mason, A. K. Bertram, F. Paesani, P. J. DeMott and V. Molinero, J. Am. Chem. Soc., 2017, 139, 3052–3064.
60. D. T. Limmer and D. Chandler, J. Chem. Phys., 2014, 141, 18C505.
61. T. Kling, F. Kling and D. Donadio, J. Phys. Chem. C, 2018, 122, 24780–24787.
62. M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289.
63. K. Thorkelsson, P. Bai and T. Xu, Nano Today, 2015, 10, 48–66.
64. A. Kumar and V. Molinero, J. Phys. Chem. Lett., 2017, 8, 5053–5058.
65. A. Kumar and V. Molinero, J. Phys. Chem. B, 2018, 122, 4758–4770.
66. A. J. Mukhtyar and F. A. Escobedo, Macromolecules, 2018, 51, 9781–9788.
67. H. Acharya, S. Vembanur, S. N. Jamadagni and S. Garde, Faraday Discuss., 2010, 146, 353–365.
68. A. J. Patel and S. Garde, J. Phys. Chem. B, 2014, 118, 1564–1573.
69. E. Xi, V. Venkateshwaran, L. Li, N. Rego, A. J. Patel and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13345–13350.
70. Z. Jiang, R. C. Remsing, N. B. Rego and A. J. Patel, J. Phys. Chem. B, 2019, 123, 1650–1661.
71. S. Shin and A. P. Willard, J. Chem. Theory Comput., 2018, 14, 461–465.
72. J. Kyte and R. F. Doolittle, J. Mol. Biol., 1982, 157, 105–132.
73. L. H. Kapcha and P. J. Rossky, J. Mol. Biol., 2014, 426, 484–498.
74. A. J. Patel, P. Varilly, D. Chandler and S. Garde, J. Stat. Phys., 2011, 145, 265–275.

---

Footnote

† Electronic supplementary information (ESI) available: All details of molecular simulations and our implementation of the Geiger and Dellago²² network are provided in the ESI. Code containing an implementation of the PointNet along with an example is freely available in a Github repository (https://github.com/rsdefever/GenStrIde). See DOI: 10.1039/c9sc02097g

---