Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tetragonal phosphorus(V) cations as tunable and robust catalytic Lewis acids†
James C.
Gilhula
 and
Alexander T.
Radosevich
and
Alexander T.
Radosevich
 *
*
Department of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: radosevich@mit.edu
First published on 18th June 2019
Abstract
The synthesis and catalytic reactivity of a class of water-tolerant cationic phosphorus-based Lewis acids is reported. Corrole-based phosphorus(V) cations of the type [ArP(cor)][B(C6F5)4] (Ar = C6H5, 3,5-(CF3)2C6H3; cor = 5,10,15-(C6H5)3corrolato3−, 5,10,15-(C6F5)3corrolato3−) were synthesized and characterized by NMR and X-ray diffraction. The visible electronic absorption spectra of these cationic phosphacorroles depend strongly on the coordination environment at phosphorus, and their Lewis acidities are quantified by spectrophotometric titrations. DFT analyses establish that the character of the P-acceptor orbital comprises P–N antibonding interactions in the basal plane of the phosphacorrole. Consequently, the cationic phosphacorroles display unprecedented stability to water and alcohols while remaining highly active and robust Lewis acid catalysts for carbonyl hydrosilylation, Csp3–H bond functionalization, and carbohydrate deoxygenation reactions.
Introduction
Tetracoordinate phosphonium cations (R4P+) are electrophilic at the phosphorus center, a fact that can be leveraged in Lewis acid catalysis.1 Stephan reported a major innovation in this area by showing that fluorophosphonium cations (R3P+–F) display an exceptionally low-lying σ*(P–F) orbital that is accessible to even weak Lewis bases.2 Tailoring of the fluorophosphonium core with electron-withdrawing substituents (i.e. (per)fluoroarenes, N-alkylpyridiniums) accentuates the P-electrophilicity of the fluorophosphonium, permitting access to compounds with fluoride affinities exceeding that of SbF5, the benchmark Lewis acid.3 A family of compositionally diverse electrophilic phosphonium Lewis acids is now known,2 and work from Gabbaï has shown that the underlying design principle is portable to heavier group 15 Lewis acids.4Coinciding with their exceptional electrophilic character, fluorophosphonium cations display a marked sensitivity to water and hydroxylic functionality.2 Hydrolysis of the fluorophosphonium P–F bond results in decomposition by irreversible formation of a thermodynamically stable phosphine oxide (R3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) in which the P-centered electrophilicity is effectively quenched (Scheme 1, top). A reduced hydrolytic sensitivity of certain (trifluoro)methylphosphonium Lewis acids has recently been achieved by Ingleson and Stephan.5 Additionally, Stephan has developed air-stable P(III) dicationic Lewis acids.6
O) in which the P-centered electrophilicity is effectively quenched (Scheme 1, top). A reduced hydrolytic sensitivity of certain (trifluoro)methylphosphonium Lewis acids has recently been achieved by Ingleson and Stephan.5 Additionally, Stephan has developed air-stable P(III) dicationic Lewis acids.6
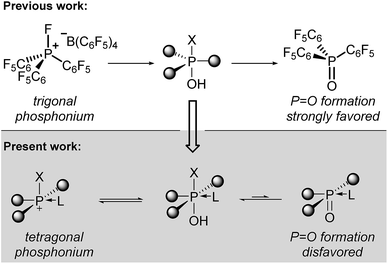
We considered that an alternate approach to robust phosphorus-based Lewis acids might be accessible by deliberate alteration of the molecular geometry. Having previously demonstrated that molecular deformation of neutral phosphorus compounds allows for novel bond activation reactions and catalytic transformations,7 we reasoned that the undesirable hydrolysis pathway leading to inactive phosphine oxides for electrophilic phosphonium cations might be avoided by enforcing nontrigonal substitution at phosphorus. Specifically, we envisioned that a tetragonal substituent field would be less conducive to formation of a formal P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O multiple bond, diminishing the propensity for phosphine oxide formation and thereby preserving the Lewis acidity at the cationic phosphorus center (Scheme 1, bottom). Indeed, Kadish and Vogel8 and Ravikanth9 have demonstrated that square pyramidal phosphine oxides embedded within a corrole binding pocket have a propensity to form hexacoordinate structures by association of an exogenous nucleophile. Moreover, it has been shown that phosphorus(V) corroles readily undergo apical halide/alkoxide exchange10 and are even stable in aqueous media.11
O multiple bond, diminishing the propensity for phosphine oxide formation and thereby preserving the Lewis acidity at the cationic phosphorus center (Scheme 1, bottom). Indeed, Kadish and Vogel8 and Ravikanth9 have demonstrated that square pyramidal phosphine oxides embedded within a corrole binding pocket have a propensity to form hexacoordinate structures by association of an exogenous nucleophile. Moreover, it has been shown that phosphorus(V) corroles readily undergo apical halide/alkoxide exchange10 and are even stable in aqueous media.11
We demonstrate here that square pyramidal corrole-based phosphorus(V) cations are robust, tunable, and catalytically-active Lewis acids. We find that the rigid tetragonal geometry imparts stability to water and alcohols while maintaining Lewis acidity, enabling these compounds to effect transformations which were previously inaccessible to phosphonium catalysts. This desirable superposition of properties is rationalized within an electronic structure argument that advances our ongoing program to establish new reactivity for p-block elements by imposition of underexplored molecular geometries.
Results and discussion
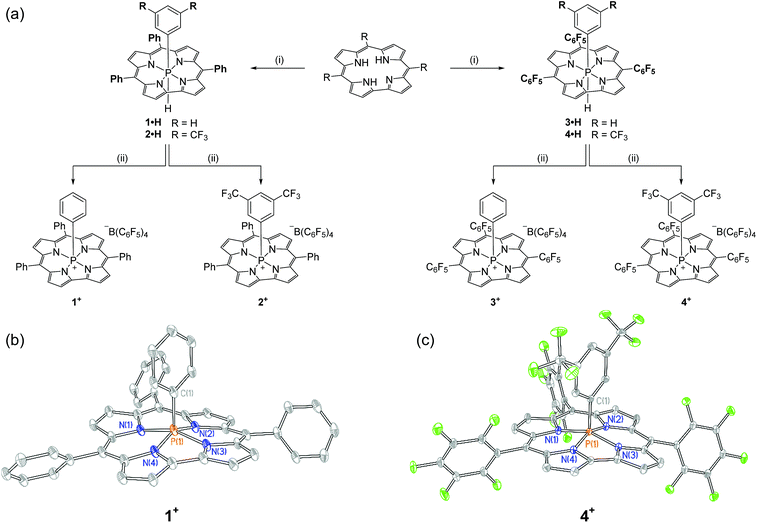
Synthesis of the target cations was achieved in two steps from the freebase corrole. First, treatment of 5,10,15-triphenylcorrole with 1 equiv. of phenyl tetrachlorophosphorane (PhPCl4) in the presence of triethylamine furnished an unstable intermediate, which upon the addition of [Bu4N][BH(OAc)3] yielded hexacoordinate 1·H as a chromatographically stable green solid (Fig. 1a). The 31P{1H} NMR spectrum of 1·H showed a resonance at high field (δ − 231.3 ppm), consistent with compositionally similar hexacoordinate phosphorus compounds reported previously.8–11 The proton-coupled 31P NMR resonance evolves into a doublet of triplets, with coupling constants evidencing a direct P–H bond (1JP–H = 928.0 Hz) as well as longer range coupling to the ortho protons of the apical P-aryl moiety (3JP–H = 25.1 Hz).13 In the 1H NMR channel, the P–H unit was observed with complementary coupling (δ − 2.73 ppm, d, 1JP–H = 928.8 Hz); the rather high-field chemical shift of this 1H nucleus is attributed to shielding from the diamagnetic ring current of the corrole system,14 securing the assignment of the structure of 1·H as in Fig. 1.The apical hydride of hexacoordinate compound 1·H is readily removed by treatment with abstraction reagents. Specifically, a green solution of 1·H in CH2Cl2 when treated with 1 equiv. of [Ph3C][B(C6F5)4] immediately produced a red solution, from which a new phosphorus-containing product was obtained by precipitation via slow addition of pentane. A 31P NMR spectrum of the resulting maroon solid displayed a single new triplet resonance downfield of the starting compound (δ − 97.2 ppm, t, 3JP–H = 20.6 Hz). This chemical shift is indicative of a pentacoordinate phosphorus center shielded by diamagnetic ring current;8,9,10b,15 loss of 1JP–H coupling and concomitant formation of triphenylmethane further evidence the formation of the hydride abstraction product 1+. Related phosphacorroles 2+–4+ were synthesized analogously from the corresponding triarylcorrole and aryl phosphorane as depicted in Fig. 1.
The solid state structure of 1+ (as its triflate salt) was revealed by X-ray diffraction experiments (Fig. 1b). As expected, the rigid constraint imposed by the corrole ligand framework enforces a local geometry closely resembling a square pyramid (τ = 0.09),16 where the phosphorus center projects 0.373 Å out of the plane containing the four pyrrolic nitrogen atoms.17 Fluorinated congener 4+ (Fig. 1c) similarly exhibits a near-perfect square pyramidal geometry (τ = 0.05)16 where the P center protrudes less from the binding pocket relative to 1+ (Δd = 0.023 Å). In both instances, the overall geometry imposed by the corrole ligand may be viewed as a monovacant octahedron about phosphorus. In conjunction with structural data for known hexacoordinate phosphorus corrole compounds (where the phosphorus atom is essentially coplanar with the tetrapyrrolic nitrogens8–11), association of Lewis bases to the apical site could be anticipated to proceed with a rather small energy penalty for structural reorganization.
The affinity of cationic phosphacorroles 1+–4+ for Lewis bases was initially assayed by recording 31P NMR chemical shift differences (Δδ) for a phosphine oxide ((n-octyl)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) probe upon binding according to a modification of the Gutmann–Beckett method.18,19 In agreement with expectations based on inductive substituent effects, the Δδ values (Table 1) report a self-consistent picture of the increasing Lewis acidity (1+ < 2+ < 3+ < 4+) as a function of increasing modular fluorination. A direct comparison of the Lewis acidity of 1+–4+ to other Lewis acids on the basis of these Δδ values is tempting, but we caution against such a potentially specious interpretation in the present circumstance. In view of the diamagnetic ring current of the corrole moiety,14 a phosphine oxide probe bound apically to the phosphacorrole cation would experience shielding effects that would tend to produce anomalously small Δδ values. Other NMR-based methods for the determination of Lewis acidity (Childs,20 Hilt21) would similarly be expected to show a systematic underestimate of Lewis acidity for porphyrinoid-based Lewis acids like 1+–4+.22
O) probe upon binding according to a modification of the Gutmann–Beckett method.18,19 In agreement with expectations based on inductive substituent effects, the Δδ values (Table 1) report a self-consistent picture of the increasing Lewis acidity (1+ < 2+ < 3+ < 4+) as a function of increasing modular fluorination. A direct comparison of the Lewis acidity of 1+–4+ to other Lewis acids on the basis of these Δδ values is tempting, but we caution against such a potentially specious interpretation in the present circumstance. In view of the diamagnetic ring current of the corrole moiety,14 a phosphine oxide probe bound apically to the phosphacorrole cation would experience shielding effects that would tend to produce anomalously small Δδ values. Other NMR-based methods for the determination of Lewis acidity (Childs,20 Hilt21) would similarly be expected to show a systematic underestimate of Lewis acidity for porphyrinoid-based Lewis acids like 1+–4+.22
| Compound | 31P δ (ppm)a | ε LUMO+N (eV)b | FIA (kJ mol−1)c | GEI (eV)d | Δδ (ppm)a,e | K d (μM)f |
|---|---|---|---|---|---|---|
a Chemical shift externally referenced to 85% H3PO4. Spectra recorded in CD2Cl2 at 293 K.
b Computed at the B3LYP/def2-TZVP/CPCM(CH2Cl2)//B3LYP/def2-TZVP level. The orbital with appropriate symmetry was LUMO+N, where N = 3 (1+), 4 (2+), 2, (3+), 3 (4+).
c Computed according to Christe's pseudoisodesmic method28 at the B3LYP/def2-TZVP/CPCM(CH2Cl2)//B3LYP/def2-TZVP level.
d Computed at the B3LYP/def2-TVZP/CPCM(CH2Cl2)//B3LYP/def2-TZVP level as described by Stephan et al.12
e Change in 31P NMR chemical shift of (n-octyl)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O.
f Measurements are bracketed by one standard error.
g Values obtained at the B3LYP/def2-TZVP/CPCM(CH2Cl2)//B3LYP/def2-SVP level of theory. O.
f Measurements are bracketed by one standard error.
g Values obtained at the B3LYP/def2-TZVP/CPCM(CH2Cl2)//B3LYP/def2-SVP level of theory.
|
||||||
| 1+ | −97.1 | −1.47 | 274 | 3.75 | 2.0 | 2660 ± 90 |
| 2+ | −102.2 | −1.72 | 295 | 3.90 | 13.6 | 30.1 ± 0.7 |
| 3+ | −95.2 | −1.85 | 298 | 4.23 | 15.3 | 26 ± 1 |
| 4+ | −100.3 | −2.31g | 343g | 4.53g | 21.3 | 11.3 ± 0.4 |
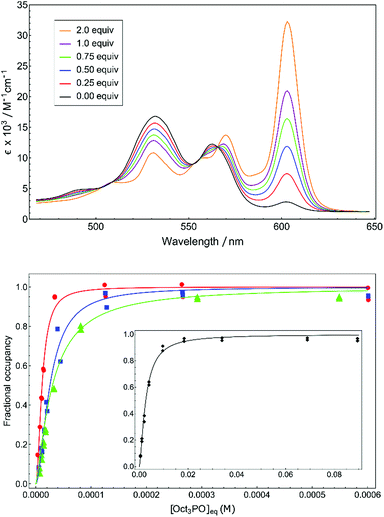
A unbiased quantification of Lewis acidity for 1+–4+ is given by the binding dissociation constant (Kd). The marked difference in color between cationic five-coordinate phosphacorroles (red) and neutral six-coordinate congeners (green) provided a convenient colorimetric method for measuring equilibrium binding in 1+–4+. The sensitivity of the color dependence to the concentration of an exogenous Lewis base was demonstrated by titrating cationic phosphacorrole 4+ with varying amounts of (n-octyl)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Fig. 2, top). The presence of several isosbestic points (e.g. λ = 566 nm) confirms adduct formation free of decomposition or other deleterious reactivity.
O (Fig. 2, top). The presence of several isosbestic points (e.g. λ = 566 nm) confirms adduct formation free of decomposition or other deleterious reactivity.
The isotherms obtained by monitoring absorption at 610 nm with increasing amounts of (n-octyl)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O were fitted to the Hill equation23 to obtain equilibrium dissociation constants Kd (Table 1, see ESI† for full details). The micromolar dissociation constants confirm the pronounced affinity of the cationic phosphacorroles for phosphine oxide Lewis bases and afford an intrinsic thermodynamic parameter of Lewis acidity for this chemotype.
O were fitted to the Hill equation23 to obtain equilibrium dissociation constants Kd (Table 1, see ESI† for full details). The micromolar dissociation constants confirm the pronounced affinity of the cationic phosphacorroles for phosphine oxide Lewis bases and afford an intrinsic thermodynamic parameter of Lewis acidity for this chemotype.
To further understand the varying Lewis acidities of 1+–4+, DFT calculations of the electronic structure of these cationic phosphacorroles were performed. The wavefunctions of 1+–4+ were computed at the B3LYP/def2-TZVP/CPCM(CH2Cl2)//B3LYP/def2-TZVP level24 as implemented in the ORCA 4.0.0 software package,25 and are found to resemble experimental structures closely (see ESI† for full details). In excellent agreement with previous theoretical studies on isolobal Ga(III) corroles,26 the LUMO and LUMO+1 of 1+–4+ correspond to the corrole π manifold, and are apparently not responsible for the experimentally observed Lewis acidity of cationic phosphacorroles.
Another low-lying unoccupied orbital orbital (LUMO+3 for 4+, Fig. 3)27 is still quite low in energy (e.g. −2.31 eV for 4+, see Table 1) and projects into the apical space proximal to phosphorus, rendering it both energetically and sterically accessible for attack by exogenous nucleophiles. Indeed, the calculated fluoride ion affinities28 (FIAs) for 1+–4+ correlate with the experimental dissociation constants Kd for phosphine oxide binding, implying that Lewis acid/base interactions are hosted by this orbital (see ESI† for details). Most notably, the character of this P-acceptor orbital illustrates a fundamental distinction with respect to prior phosphonium Lewis acids that has important implications for their stability. Whereas the acceptor orbital for trigonal electrophilic phosphonium cations is σ-antibonding with respect to the trans-apical substituent in the developing Lewis acid/base adduct,2 the phosphorus-centered acceptor orbital in tetragonal phosphorus cations 1+–4+ primarily constitutes basal P–N antibonding interactions. As a consequence, the mechanistic pathway initiated by water addition which leads to apical ejection of a P-substituent for trigonal phosphoniums29 is denied by the corrole chelate. On this basis, we anticipated that tetragonal cations 1+–4+ might be relatively resistant to decomposition by water.
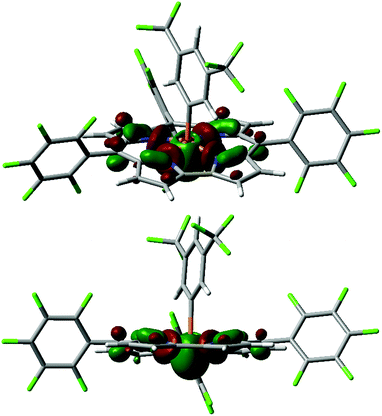 | ||
| Fig. 3 Kohn–Sham orbital LUMO+3 for 4+ (top: in perspective; bottom: side-on view) computed at the B3LYP/def2-TZVP//B3LYP/def2-SVP level. | ||
In order to probe this conjecture, we investigated the chemical stability of 1+–4+ with respect to hydrolysis. In a representative experiment (Scheme 2), treatment of a red CD3CN solution of 3+ with 10 equiv. of water resulted in a purple-green solution whose 31P{1H} NMR spectrum exhibited a broad resonance at δ − 175.4 ppm. The chemical shift is consistent with a six-coordinate P atom, and the broadness of the peak suggests reversible binding to the Lewis acidic phosphorus. Importantly, there is no evidence of decomposition of this intermediate upon prolonged standing. Although this adduct has thus far eluded isolation, the addition of even a weak base (MgSO4) cleanly gives P-hydroxide 3·OH (δ − 200.2 ppm) in quantitative fashion (see ESI† for details) without further in situ transformation. Moreover, the active cationic phosphacorrole 3+ may be regenerated from 3·OH by treatment with trimethylsilyl trifluoromethanesulfonate (TMS–OTf) as in Scheme 2. Consequently, we believe that reaction with water does not irreversibly decompose the Lewis acidic phosphacorrole 3+ but instead gives an adduct that we formulate as 3+·OH2 (Scheme 2). The same reasoning may be extended by analogy to 1+, 2+, and 4+.
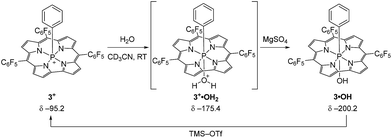 | ||
| Scheme 2 Reaction of water with 3+ and formation of putative water adduct 3+·OH2. Deprotonation by MgSO4 gives product 3·OH, which is reactivated to 3+ by TMS–OTf. | ||
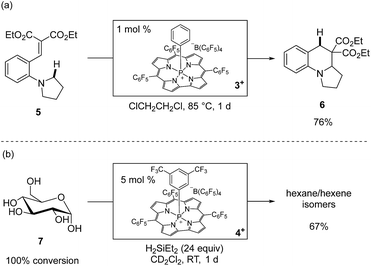
The phosphacorrole cations 1+–4+ are potent Lewis acid catalysts for a range of transformations.30 We benchmarked the catalytic activity of 1+ and 2+ with typical carbonyl reduction reactions, such as ketone hydrosilylation and deoxygenation using HSiEt3 as a terminal reductant (see ESI† for full details). The high activity of 1+ and 2+ for these reductions encouraged us to attempt more challenging catalytic transformations. For instance, ring-forming Csp3–H functionalization of substrate 5 is induced by catalytic 3+ (1 mol%) via 1,5-hydride shift from a N,N-dialkylaniline donor to a malonate alkylidene acceptor followed by intramolecular cyclization to give 6 in good isolated yield (Scheme 3a).31 Furthermore, the robustness of the tetragonal cationic phosphorus corrole Lewis acids is exemplified by the observation that unprotected 13C6-D-glucose (7) is exhaustively deoxygenated by a catalytic amount of 4+ (5 mol%) in the presence of an excess of H2SiEt2 at room temperature to give a mixture of hexanes and hexenes (67% total yield, Scheme 3b).32 Notably, analysis after completion of the reaction shows that 4+ is not degraded; instead, an approximately equimolar amount of 4·H and 4+ were observed spectroscopically as the only 31P NMR resonances. The lack of reaction between 4+ and H2SiEt2 in a control experiment further indicated that 4+ is a true catalyst for this reaction. The persistence of 4+ with respect to a substrate that under these conditions presents a 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of free hydroxyl moieties to catalyst confirms the noteworthy chemical robustness inherent to tetragonal cationic phosphorus-based Lewis acids.
1 ratio of free hydroxyl moieties to catalyst confirms the noteworthy chemical robustness inherent to tetragonal cationic phosphorus-based Lewis acids.
Conclusions
In summary, we have shown that cationic phosphacorroles are potent Lewis acids that exhibit marked tolerance toward hydroxylic functionality including water. We propose that this useful property arises from the tetragonal geometry of 1+–4+ as enforced by the tetraazamacrocycle, which produces an acceptor orbital that is distinct in character from prior trigonal electrophilic phosphonium cations and prohibits irreversible decomposition to phosphine oxides. The modularity of the corrole supporting framework allows the Lewis acidities of these electrophilic phosphorus species to be readily tuned. Together, these results establish within the family of designer main group Lewis acids a new structural type that extends the range of potential applications for this valuable class of compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the NSF (CHE-1724505 and CHE-1900060) for funding. JCG acknowledges the NSF for a predoctoral graduate research fellowship. We are grateful to Bruce Adams for consultation on quantitative NMR and Seung Jun Hwang for assistance in collecting and processing crystal structure data. ChemMatCARS Sector 15 is principally supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-1346572. Use of the PILATUS3 X CdTe 1M detector is supported by the National Science Foundation under the grant number NSF/DMR-1531283. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357.Notes and references
- (a) T. Werner, Adv. Synth. Catal., 2009, 351, 1469–1481 CrossRef CAS; (b) T. Mukaiyama, S. Matsui and K. Kashiwagi, Chem. Lett., 1989, 18, 993–996 CrossRef; (c) T. Mukaiyama, K. Kashiwagi and S. Matsui, Chem. Lett., 1989, 18, 1397–1400 CrossRef.
- (a) C. B. Caputo, L. J. Hounjet, R. Dobrovetsky and D. W. Stephan, Science, 2013, 341, 1374–1377 CrossRef CAS PubMed; (b) J. Zhu, M. Pérez and D. W. Stephan, Angew. Chem., Int. Ed., 2016, 55, 8448–8451 CrossRef CAS PubMed; (c) M. Mehta, M. H. Holthausen, I. Mallov, M. Pérez, Z.-W. Qu, S. Grimme and D. W. Stephan, Angew. Chem., Int. Ed., 2015, 54, 8250–8254 CrossRef CAS PubMed; (d) A. Augurusa, M. Mehta, M. Perez, J. Zhu and D. W. Stephan, Chem. Commun., 2016, 52, 12195–12198 RSC; (e) T. vom Stein, M. Peréz, R. Dobrovetsky, D. Winkelhaus, C. B. Caputo and D. W. Stephan, Angew. Chem., Int. Ed., 2015, 54, 10178–10182 CrossRef CAS PubMed; (f) M. Pérez, C. B. Caputo, R. Dobrovetsky and D. W. Stephan, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10917–10921 CrossRef PubMed; (g) J. M. Bayne and D. W. Stephan, Chem. Soc. Rev., 2016, 45, 765–774 RSC.
- L. Greb, Chem.–Eur. J., 2018, 24, 17881–17896 CrossRef PubMed.
- (a) B. Pan and F. P. Gabbaï, J. Am. Chem. Soc., 2014, 136, 9564–9567 CrossRef CAS PubMed; (b) M. Yang, D. Tofan, C.-H. Chen, K. M. Jack and F. P. Gabbaï, Angew. Chem., Int. Ed., 2018, 57, 13868–13872 CrossRef CAS PubMed.
- (a) J. M. Bayne, V. Fasano, K. M. Szkop, M. J. Ingleson and D. W. Stephan, Chem. Commun., 2018, 54, 12467–12470 RSC; (b) V. Fasano, J. H. W. LaFortune, J. M. Bayne, M. J. Ingleson and D. W. Stephan, Chem. Commun., 2018, 54, 662–665 RSC.
- (a) S. S. Chitnis, F. Krischer and D. W. Stephan, Chem.–Eur. J., 2018, 24, 6543–6546 CrossRef CAS PubMed; (b) S. S. Chitnis, J. H. W. LaFortune, H. Cummings, L. L. Liu, R. Andrews and D. W. Stephan, Organometallics, 2018, 37, 4540–4544 CrossRef CAS; (c) R. J. Andrews, S. S. Chitnis and D. W. Stephan, Chem. Commun., 2019, 55, 5599–5602 RSC.
- (a) T. V. Nykaza, A. Ramirez, T. S. Harrison, M. R. Luzung and A. T. Radosevich, J. Am. Chem. Soc., 2018, 140, 3103–3113 CrossRef CAS PubMed; (b) T. V. Nykaza, J. C. Cooper, G. Li, N. Mahieu, A. Ramirez, M. R. Luzung and A. T. Radosevich, J. Am. Chem. Soc., 2018, 140, 15200–15205 CrossRef CAS PubMed; (c) W. Zhao, S. M. McCarthy, T. Y. Lai, H. P. Yennawar and A. T. Radosevich, J. Am. Chem. Soc., 2014, 136, 17634–17644 CrossRef CAS PubMed; (d) Y.-C. Lin, E. Hatzakis, S. M. McCarthy, K. D. Reichl, T.-Y. Lai, H. P. Yennawar and A. T. Radosevich, J. Am. Chem. Soc., 2017, 139, 6008–6016 CrossRef CAS PubMed; (e) Y.-C. Lin, J. C. Gilhula and A. T. Radosevich, Chem. Sci., 2018, 9, 4338–4347 RSC.
- K. M. Kadish, Z. Ou, V. A. Adamian, R. Guilard, C. P. Gros, C. Erben, S. Will, E. Vogel, S. Gabriel and B. Gabriel, Inorg. Chem., 2000, 39, 5675–5682 CrossRef CAS.
- A. Ghosh, W. Z. Lee and M. Ravikanth, Eur. J. Inorg. Chem., 2012, 4231–4239 CrossRef CAS.
- (a) J. Vestfrid, R. Kothari, A. Kostenko, I. Goldberg, B. Tumanskii and Z. Gross, Inorg. Chem., 2016, 55, 6061–6067 CrossRef CAS PubMed; (b) A. Ghosh and M. Ravikanth, Chem.–Eur. J., 2012, 18, 6386–6396 CrossRef CAS PubMed.
- (a) M. L. Naitana, S. Nardis, G. Pomarico, M. Raggio, F. Caroleo, D. O. Cicero, S. Lentini, L. Prodi, D. Genovese, S. Mitta, A. Sgarlata, M. Fanfoni, L. Persichetti and R. Paolesse, Chem.–Eur. J., 2016, 23, 905–916 CrossRef PubMed; (b) Y. G. Wang, Z. Zhang, H. Wang and H. Y. Liu, Bioorg. Chem., 2016, 67, 57–63 CrossRef CAS PubMed; (c) T. Chatterjee, W.-Z. Lee and M. Ravikanth, Dalton Trans., 2016, 45, 7815–7822 RSC; (d) L. Simkhovich, A. Mahammed, I. Goldberg and Z. Gross, Chem.–Eur. J., 2001, 7, 1041–1055 CrossRef CAS PubMed.
- (a) A. R. Jupp, T. C. Johnstone and D. W. Stephan, Dalton Trans., 2018, 47, 7029–7035 RSC; (b) R. Jupp, T. C. Johnstone and D. W. Stephan, Inorg. Chem., 2018, 57, 14764–14771 CrossRef PubMed.
- A minor, inseparable impurity was also observed in the 31P and 1H NMR spectra of 1. We attribute this observation to the partial chlorination of the corrole β-pyrrolic carbons which presumably occurs by oxidation by Cl2 generated in the refluxing reaction mixture. We were able to remove this species by hydrodechlorination with H2 in the presence of catalytic amounts of Pd/C. See ESI† for full details..
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- R. Paolesse, T. Boschi, S. Licoccia, R. G. Khoury and K. M. Smith, Chem. Commun., 1998, 1119–1120 RSC.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- The counterion for both 1+ and 4+ resides outside the phosphorus coordination sphere, in agreement with solution phase NMR data..
- (a) U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257 CrossRef CAS; (b) M. A. Beckett, G. C. Strickland, J. R. Holland and K. Sukumar Varma, Polymer, 1996, 37, 4629–4631 CrossRef CAS.
- We observed unacceptable run-to-run variability in replicates of the Guttmann–Beckett measurement with Et3P
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, which we attribute to the hygroscopicity of this probe reagent (there may be competitive binding with water). We chose the hydrophobic tri-n-octylphosphine oxide (n-octyl)3P
O, which we attribute to the hygroscopicity of this probe reagent (there may be competitive binding with water). We chose the hydrophobic tri-n-octylphosphine oxide (n-octyl)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, which presents a similar steric and electronic profile to Et3P
O, which presents a similar steric and electronic profile to Et3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, as a rigorously anhydrous analog of Et3P
O, as a rigorously anhydrous analog of Et3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O for studies measuring Lewis acidity..
O for studies measuring Lewis acidity.. - R. F. Childs, D. L. Mulholland and A. Nixon, Can. J. Chem., 1982, 60, 809–812 CrossRef CAS.
- G. Hilt and A. Nödling, Eur. J. Org. Chem., 2011, 7071–7075 CrossRef CAS.
- The limitations of NMR-dependent measures of Lewis acidity for certain classes of compounds have been noted previously: (a) A. R. Nödling, K. Müther, V. H. G. Rohde, G. Hilt and M. Oestreich, Organometallics, 2014, 33, 302–308 CrossRef; (b) H. Großekappenberg, M. Reißmann, M. Schmidtmann and T. Müller, Organometallics, 2015, 34, 4952–4958 CrossRef; (c) R. J. Blagg, T. R. Simmons, G. R. Hatton, J. M. Courtney, E. L. Bennett, E. J. Lawrence and G. G. Wildgoose, Dalton Trans., 2016, 45, 6032–6043 RSC; (d) J. R. Gaffen, J. N. Bentley, L. C. Torres, C. Chu, T. Baumgartner and C. B. Caputo, Chem, 2019, 5, 1567–1583 CrossRef CAS; (e) G. J. P. Britovsek, J. Ugolotti and A. J. P. White, Organometallics, 2005, 24, 1685–1691 CrossRef CAS.
- A. V. Hill, J. Physiol., 1910, 40, iv–vii Search PubMed.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- A. Ghosh, T. Wondimagegn and A. B. J. Parusel, J. Am. Chem. Soc., 2000, 122, 5100–5104 CrossRef CAS.
- For compounds 1+, 2+, and 4+, the relevant orbitals were LUMO+3, LUMO+4, and LUMO+3 respectively. The LUMO+2/LUMO+3 in these instances correspond to π bonding orbitals within the apical P-aromatic substituent..
- K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, J. Fluorine Chem., 2000, 101, 151–153 CrossRef CAS.
- W. E. McEwen, K. F. Kumli, A. Blade-Font, M. Zanger and C. A. VanderWerf, J. Am. Chem. Soc., 1964, 86, 2378–2384 CrossRef CAS.
- For a review of Lewis acid-catalyzed processes, see: A. Corma and H. García, Chem. Rev., 2003, 103, 4307–4366 CrossRef CAS PubMed.
- For other Lewis acid-catalyzed 1,5-hydride shifts, see: (a) S. Murarka, C. Zhang, M. D. Konieczynska and D. Seidel, Org. Lett., 2009, 11, 129–132 CrossRef CAS PubMed; (b) K. M. McQuaid and D. Sames, J. Am. Chem. Soc., 2009, 131, 402–403 CrossRef CAS.
- L. L. Adduci, M. P. McLaughlin, T. A. Bender, J. J. Becker and M. R. Gagné, Angew. Chem., Int. Ed., 2014, 53, 1646–1649 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1904833 and 1904834. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc02463h |
| This journal is © The Royal Society of Chemistry 2019 |