Atomic-scale phonon scatterers in thermoelectric colusites with a tetrahedral framework structure†
Koichiro
Suekuni
 *ab,
Yuta
Shimizu
a,
Eiji
Nishibori
c,
Hidetaka
Kasai
c,
Hikaru
Saito
a,
Daichi
Yoshimoto
a,
Katsuaki
Hashikuni
a,
Yohan
Bouyrie
d,
Raju
Chetty
*ab,
Yuta
Shimizu
a,
Eiji
Nishibori
c,
Hidetaka
Kasai
c,
Hikaru
Saito
a,
Daichi
Yoshimoto
a,
Katsuaki
Hashikuni
a,
Yohan
Bouyrie
d,
Raju
Chetty
 d,
Michihiro
Ohta
d,
Michihiro
Ohta
 d,
Emmanuel
Guilmeau
d,
Emmanuel
Guilmeau
 e,
Toshiro
Takabatake
f,
Kosuke
Watanabe
b and
Michitaka
Ohtaki
ab
e,
Toshiro
Takabatake
f,
Kosuke
Watanabe
b and
Michitaka
Ohtaki
ab
aDepartment of Applied Science for Electronics and Materials, Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, Kasuga, Fukuoka 816-8580, Japan. E-mail: suekuni.koichiro.063@m.kyushu-u.ac.jp
bTransdisciplinary Research and Education Center for Green Technologies, Kyushu University, Kasuga, Fukuoka 816-8580, Japan
cDivision of Physics, Faculty of Pure and Applied Sciences, Tsukuba Research Center for Energy Materials Science (TREMS), University of Tsukuba, Tsukuba, Ibaraki 305-8571, Japan
dResearch Institute for Energy Conservation, National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8568, Japan
eNormandie Univ, ENSICAEN, UNICAEN, CNRS, CRISMAT, 14000 Caen, France
fDepartment of Quantum Matter, Graduate School of Advanced Sciences of Matter, Hiroshima University, Higashi-Hiroshima 739-8530, Japan
First published on 28th November 2018
Abstract
Copper-based chalcogenides with tetrahedral framework structures have been attracting increasing attention as environmentally friendly thermoelectric materials. A representative group of such thermoelectric chalcogenides is the Cu26A2M6S32 (A = V, Nb, Ta; M = Ge, Sn) family of colusites, which exhibit low electrical resistivity, a large Seebeck coefficient, and low thermal conductivity; these properties are necessary for efficient thermal-to-electronic energy conversion. Here, we show the impact of crystal structure on the lattice thermal conductivity of colusite with A = Nb, M = Sn. The crystal structure can be modified by controlling the cationic compositions and the deficiency in the sulfur content as Cu26−xNb2Sn6+xS32−δ. The Cu/Sn ratio is found to be the key parameter for exsolution into distinct phases with ordered and disordered arrangements of cations. For the ordered-structure phase, sulfur sublimation induces atomic-scale defects/disordered states including interstitial defects, anti-site defects, and site splitting, which function as strong phonon scatterers, and the lowest lattice thermal conductivity of ∼0.5 W K−1 m−1 is achieved for the modified ordered structure. This finding provides a simple approach to modifying the crystal structure of thermoelectric chalcogenides via the loss of anions to reduce their lattice thermal conductivity.
1. Introduction
Energy production from renewable and sustainable processes has become increasingly important over the past decade. Thermoelectric materials enable the direct conversion of waste heat into electricity and are therefore expected to play a substantial role in decreasing carbon footprints while simultaneously reducing the cost of electricity.1,2 The thermal-to-electrical energy conversion is based on the Seebeck effect, where an applied temperature difference ΔT across a solid-state device generates an electric potential difference ΔV. Therefore, the combination of a large Seebeck coefficient S = ΔV/ΔT and a low thermal conductivity κ is a prerequisite for a material to be used to generate voltage in a thermoelectric generator. Furthermore, the electrical resistivity ρ of the material should be low to ensure a low internal resistance of the device, leading to high electric power. The materials properties are associated with the conversion efficiency through the dimensionless figure of merit ZT = S2Tρ−1κ−1. Parameter κ is the sum of a charge-carrier component (κcar) and a lattice component (κlat). Among the four parameters S, ρ, κcar, and κlat, only κlat is not determined by the electronic structure of the given material.Over the past decade, copper-based chalcogenides with tetrahedral framework structures have emerged as candidates for p-type thermoelectric materials.3–5 They have been attracting interest because of the high-earth-abundant, low cost, and less-toxic character of their constituent elements as well as their relatively high ZT values at medium–high temperatures (500–700 K). Examples of such materials include stannite/kesterite Cu2(Zn,Cd)Sn(S,Se)4,6–8 Cu3Sb(S,Se)4,9–11 kuramite Cu3SnS4,12,13 chalcopyrites Cu(Ga,In)Te2,14,15 Cu2Sn(S,Se)3,16–18 colusites Cu26A2M6S32 (A = V, Nb, Ta; M = Ge, Sn),19–26 germanite Cu22Fe8Ge4S32,27 stannoidite Cu8Fe3Sn2S12,28 and mawsonite Cu6Fe2SnS8.29 They commonly exhibit a relatively large power factor S2ρ−1 arising from valence bands composed mainly of hybridized orbitals of Cu-3d and chalcogen-p electrons30,31 as well as relatively high κlat values (1–5 W K−1 m−1) at 300 K. As shown in Fig. 1, the κlat value for copper-based sulfides with a tetrahedral framework tends to decrease with increasing number of atoms (N) per primitive unit cell and with increasing cell volume,7,13,17,20,27–29,32–35 as reported for a series of Sb-based Zintl-phase compounds.36 A large N is known to lead to a lower group velocity of optical modes and to a reduction of the fraction of acoustic modes that efficiently carry heat to 1/N.36 Unexpectedly, the value of κlat at 300 K for the Cu26V2Sn6S32 colusite was found to be reduced from 1.4 to 0.4 W K−1 m−1 when the sintering temperature was increased from 873 to 1023 K.25 If the “additional” phonon scatterer generated in the colusite structure can be identified, then it could be used as a new approach to lowering the κlat of thermoelectric chalcogenides with tetrahedral framework structures.
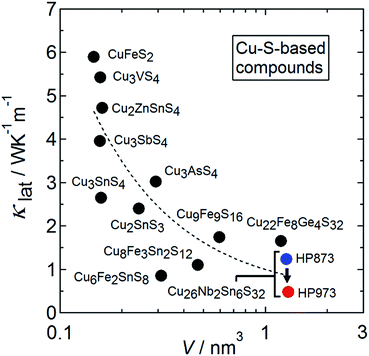 | ||
| Fig. 1 Lattice thermal conductivity (κlat) at around 300 K as a function of the primitive unit cell volume (V) for Cu–S-based compounds with tetrahedral framework structures.7,13,17,20,27–29,32–35 The κlat data for the Cu26.3Nb2Sn5.7S32 colusite samples prepared by hot-press (HP) sintering at 873 K and 973 K in the present work are plotted. | ||
Colusite is a rare naturally occurring copper sulfosalt mineral. The synthetic samples have chemical compositions of Cu26A2M6S32 (A = V, Nb, Ta; M = Ge, Sn). The formal valences are Cu22+Cu42+A25+M64+S322−, and the 3d holes delocalized from Cu2+ contribute to the p-type and metallic (degenerate semiconducting) conduction. Colusite crystallizes in a simple cubic structure (space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3n) with a lattice parameter a ≈ 1.1 nm (Fig. 2(a)).37,38 Its structure includes seven non-equivalent crystallographic sites: three for Cu (6d, 8e, 12f), one for A (2a), one for M (6c), and two for S (8e, 24i). The Cu and M ions are encapsulated in sulfur tetrahedra, which form a three-dimensional network via corner-sharing. Although some of the tetrahedral voids formed by CuS4 tetrahedra are occupied by an A ion, numerous tetrahedral voids that can accommodate cations remain. Thermogravimetric analysis on powders of synthetic colusites showed that the sample weight drops on heating at 573–673 K, indicating sublimation of sulfur.22 Such a drop was not observed up to 750 K for samples sintered at 973 K.22 Studies by transmission electron microscopy (TEM) combined with selected-area electron diffraction on a natural sample37 and a synthetic sample of A = V, M = Sn with a low κlat (≤0.5 W K−1 m−1)25 demonstrated an exsolution phenomenon, where two distinct phases coexist in the samples. More specifically, the majority phase has the simple cubic colusite structure with the aforementioned “ordered” arrangement of cations, whereas the minority phase has a face-centered-cubic (fcc) structure with a “disordered” (random) arrangement of cations (Fig. 2(b)). Furthermore, anti-site defects between Cu and Sn in the ordered structure were observed in a scanning TEM (STEM) image for the synthetic sample.25 On the basis of these structural features, researchers have proposed different phonon scattering centers to explain the effective lowering of κlat: sulfur vacancies,20,25 “excess” cations in interstitial sites,22 the anti-site defects,25 and a disordered arrangement of cations.25
3n) with a lattice parameter a ≈ 1.1 nm (Fig. 2(a)).37,38 Its structure includes seven non-equivalent crystallographic sites: three for Cu (6d, 8e, 12f), one for A (2a), one for M (6c), and two for S (8e, 24i). The Cu and M ions are encapsulated in sulfur tetrahedra, which form a three-dimensional network via corner-sharing. Although some of the tetrahedral voids formed by CuS4 tetrahedra are occupied by an A ion, numerous tetrahedral voids that can accommodate cations remain. Thermogravimetric analysis on powders of synthetic colusites showed that the sample weight drops on heating at 573–673 K, indicating sublimation of sulfur.22 Such a drop was not observed up to 750 K for samples sintered at 973 K.22 Studies by transmission electron microscopy (TEM) combined with selected-area electron diffraction on a natural sample37 and a synthetic sample of A = V, M = Sn with a low κlat (≤0.5 W K−1 m−1)25 demonstrated an exsolution phenomenon, where two distinct phases coexist in the samples. More specifically, the majority phase has the simple cubic colusite structure with the aforementioned “ordered” arrangement of cations, whereas the minority phase has a face-centered-cubic (fcc) structure with a “disordered” (random) arrangement of cations (Fig. 2(b)). Furthermore, anti-site defects between Cu and Sn in the ordered structure were observed in a scanning TEM (STEM) image for the synthetic sample.25 On the basis of these structural features, researchers have proposed different phonon scattering centers to explain the effective lowering of κlat: sulfur vacancies,20,25 “excess” cations in interstitial sites,22 the anti-site defects,25 and a disordered arrangement of cations.25
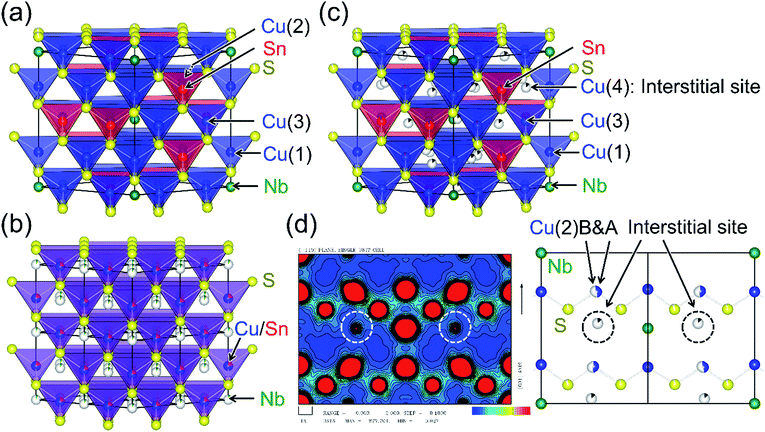 | ||
| Fig. 2 Crystal structures of colusites with (a) ordered and (b) disordered arrangements of cations. The disordered structure is described in a view of 2a × 2a × 2a. Detailed descriptions are given in the text. (c) A structure with interstitial cations and split Cu sites, which are proved by (d) an electron density map along the 110 direction, obtained by a Rietveld analysis combined with the maximum entropy method (MEM) of synchrotron X-ray diffraction data. In the electron density map, the white circles indicate the cations occupying the interstitial sites and the rugby-ball-like red circles indicate the splitting of the Cu(2) site, as shown in a corresponding view of crystal structure in (d) the structural parameters of (a)–(c) are summarized in Table S2–S4.† | ||
The objective of the present work is to identify the additional phonon scattering center in colusite samples. For this purpose, we examined the interplay between the structural imperfections and the thermoelectric properties of colusites with A = Nb, M = Sn. We synthesized samples with starting compositions of Cu26−xNb2Sn6+xS32 (−0.3 ≤ x ≤ 1.2) to control the relative fractions of the ordered- and disordered-structure phases. In this report, we first describe the effects of sulfur sublimation on the structural and thermoelectric properties for the x = −0.3 samples hot-press (HP) sintered at 873 K and 973 K, which were found to be composed mainly of ordered- and modified ordered-structure phases, respectively. Here, we reveal that the sulfur sublimation enables “excess” cations to occupy interstitial sites and a Cu site to split into two distinct sites (Fig. 2(c) and (d)). Second, we address how the disordered-structure phases affect the material's thermoelectric properties by changing x from 1.2 to −0.3. Here, the x = 1.2 sample was found to consist solely of the disordered-structure phase. Our systematic study demonstrates that the low κlat (≤0.5 W K−1 m−1 at 300 ≤ T ≤ 670 K) is inherent in the ordered structure modified by the loss of sulfur. Lastly, we discuss how such sulfur deficiency modifies the crystal structure to reduce the thermal conductivity in copper-based sulfides.
2. Experimental
2.1 Sample synthesis and sintering
Polycrystalline samples were synthesized by the direct reaction of elements, starting with the composition Cu26−xNb2Sn6+xS32 (x = −0.3, 0, 0.6, 1.2), followed by annealing. Stoichiometric quantities of the elements were sealed in an evacuated quartz tube. This tube was heated to 523 K over a period of 2 h, maintained at this temperature for 2 h, and then heated to 1373 K over 8 h. After being maintained at 1373 K for 24 h, the tube was allowed to naturally cool to room temperature. The product was pulverized and compacted into a pellet under a pressure of 100 MPa. The pellet was annealed at 873 K for 50 h to improve its homogeneity. The pellet was then reground, loaded into a graphite die, and heated under a nitrogen atmosphere to a maximum temperature of 873 K or 973 K at a rate of 20 K min−1 in a PLASMAN CPS-KIT-03121 (S. S. Alloy, Ltd.) HP sintering furnace. The sintering was carried out at this temperature for 40–50 min under a pressure of 200 MPa (873 K) or 50 MPa (973 K).2.2 Powder X-ray diffraction
Powder X-ray diffraction (XRD) data for Cu26−xNb2Sn6+xS32 (x = −0.3, 0, 0.6, 1.2) were collected in the range 10° ≤ 2θ ≤ 100° using a Miniflex diffractometer (Rigaku) equipped with a Cu Kα radiation source. The values of a obtained by XRD analysis are summarized in Table S1 in the ESI.† Synchrotron XRD measurements on powdered samples were performed at the SPring-8 BL02B2 beamline. The data were collected using a large Debye–Scherrer camera with an imaging-plate detector.39 The wavelength of incident X-rays was selected as approximately 0.044 nm, which was calibrated using a NIST CeO2 standard sample. The linewidth of the XRD peaks for our samples was 0.04° in the range 10° ≤ 2θ ≤ 30°, which is the resolution limit under our experimental conditions, indicating that the crystallite size is greater than 60 nm. The x = −0.3 (annealed) and x = 1.2 (sintered) powders sealed in Lindeman glass capillaries were cooled from room temperature to 100 K and then measured at this temperature. The x = −0.3 (annealed) powder sealed in a quartz capillary was heated to 1073 K and maintained at this temperature for 7 min. After the heating, the sample was cooled to 100 K and measured at this temperature.2.3 Scanning electron microscopy and transmission electron microscopy
Scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) were performed with a JCM-600Plus NeoScope (JEOL) microscope. Fig. S1 in the ESI† displays secondary electron images (SEIs) and backscattered electron images (BEIs) of the polished surface of a sample, demonstrating its high density. The chemical compositions evaluated by EDS are summarized in Table S1 in the ESI.†Atomic-resolution observations were performed on crushed powder samples using a Titan Cubed 60-300 G2 (FEI) scanning transmission electron microscope equipped with a Schottky electron source and a DCOR spherical aberration corrector (CEOS) for the probe-forming lens system, which was operated in STEM mode at an accelerating voltage of 300 kV. The convergence transmission electron microscope i-angle of the electron probe was set to 18 mrad. The typical probe diameter was 0.1 nm. An ADF detector was positioned to detect scattered electrons over an angular range from 38 to 184 mrad.
2.4 Electrical and thermal properties measurements
The measurements of ρ and S at 300–670 K were simultaneously performed using a four-probe method and a static DC method, respectively, in a ZEM-3 (ADVANCE-RIKO, Inc.) with the sample under a helium atmosphere. The thermal diffusivity α and specific heat CP at 300–673 K were measured simultaneously under a flowing argon atmosphere in a LFA-457 MicroFlash (Netzsch) using a laser-flash method. The absolute values of CP were derived from a comparison of the measured values with CP values measured for a standard sample of Pyroceram 9606 (Netzsch). These data were used to calculate the thermal conductivity by the relation κ = αCPds, where ds is the sample density estimated from the dimensions and weight of the sample. As shown in Fig. S2 in the ESI,† the Cp values of all samples resonably agree. Therefore, variation of κ between samples is dominated by that of α. The measurements using the commercial equipment are estimated to be accurate within 7% for ρ, 7% for S, and 8% for κ.3. Results and discussion
3.1 Modification of the ordered structure by sulfur deficiency
We first focus on the structural and thermoelectric properties of Cu26.3Nb2Sn5.7S32 (Cu26−xNb2Sn6+xS32 with x = −0.3). The samples were annealed in an evacuated quartz tube (Ann 873 K) and then HP-sintered at 873 K (HP 873 K) or 973 K (HP 973 K). Powder X-ray diffraction (XRD) data were collected after each process using a laboratory diffractometer equipped with a Cu Kα radiation source (Fig. 3(a)). The peak positions and intensities reasonably agree with simulated ones based on the ordered structure (Fig. 2(a)). After the sintering at 873 K, the peaks slightly shifted to lower angles. The degree of the shift increased when the sintering temperature was increased to 973 K. Rietveld refinement revealed that the value of a at room temperature increases from 1.0807(5) nm (Ann 873 K) to 1.0816(6) nm (HP 873 K) to 1.0895(5) nm (HP 973 K) (Table S1 in the ESI†).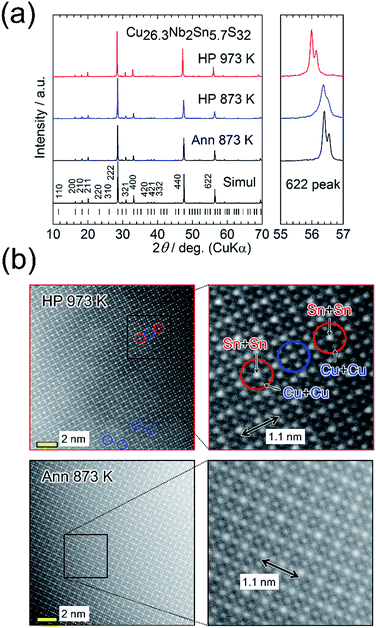 | ||
| Fig. 3 (a) Powder X-ray diffraction patterns for Cu26.3Nb2Sn5.7S32 (Cu26−xNb2Sn6+xS32 with x = −0.3) samples annealed at 873 K (Ann 873 K, before sintering) and hot-press sintered at 873 K or 973 K (HP 873 K or HP 973 K). The simulated pattern for Cu26Nb2Sn6S32 with the ordered arrangement of cations (Fig. 1(a)) and the peak positions are shown at the bottom. Right panels show the expanded views of 622 peaks. (b) Annular dark-field scanning transmission electron microscopy images for the samples prepared by Ann 873 K and HP 973 K. The right panels display the expanded views. The Sn + Sn column has the highest whiteness (intensity). Exchange between Cu and Sn or a disordered arrangement of cations is observed in the area circled by blue lines for the HP 973 K sample (see also Fig. S4 in the ESI†). | ||
The SEIs and BEIs prove that both of the HP-sintered samples are well compacted and homogeneous, respectively (Fig. S1 in the ESI†). A BEI of the HP 873 K sample shows a trace amount of impurity phase (Cu2S). From the EDS analysis of the majority phase, the chemical composition was calculated by assuming the total composition of Cu, Nb, and Sn to be 34. This analysis shows that the compositions of cations are nearly stoichiometric (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nb
Nb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn = 26
Sn = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6), whereas a notable loss of sulfur occurs in the HP 973 K sample (Table S1 in the ESI†). This result indicates that sulfur deficiency is associated with an increase in a, consistent with previously reported results.25
6), whereas a notable loss of sulfur occurs in the HP 973 K sample (Table S1 in the ESI†). This result indicates that sulfur deficiency is associated with an increase in a, consistent with previously reported results.25
Fig. 3(b) displays annular dark-field (ADF)-STEM images along the 100 incident direction for the Cu26.3Nb2Sn5.7S32 samples prepared by Ann 873 K and HP 973 K. Because the whiteness (intensity) is proportional to the square of the atomic number Z (29 for Cu, 41 for Nb, 50 for Sn, 16 for S), the columns of cations (Cu, Nb, Sn) are visible in the image. The images of both samples confirm the periodic structures in which the relative intensities between the columns composed of Sn + Sn, Nb + Cu + Cu, Sn + Cu, and Cu + Cu are consistent with the reported ordered structure (Fig. S3 in the ESI†). The distance between the Sn columns with high intensities (1.1 nm) agrees with the value of a obtained via XRD analysis. However, for the HP 973 K sample, the intensities of some “Sn columns” decreased and those of the neighbouring “Cu columns” simultaneously increased (Fig. 3(b); Fig. S4 in the ESI†). This result indicates that exchange occurred between Cu and Sn or that the arrangement of cations became random (disordered).25
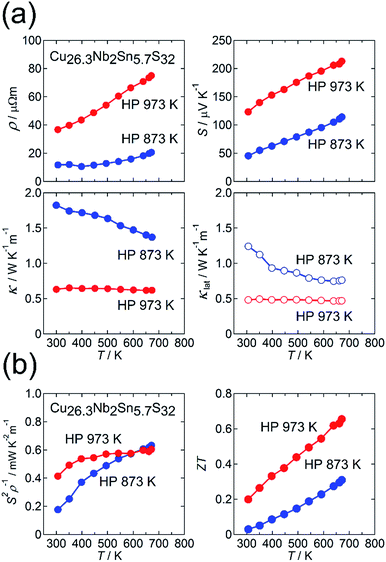
Fig. 4(a) and (b) show the thermoelectric properties for the HP 873 K and HP 973 K samples. Both samples exhibit metallic behavior in ρ(T) and a positive value of S (Fig. 4(a)). When the sintering temperature was elevated from 873 K to 973 K, the values of ρ and S at 300 K increased from 12 μΩ m to 37 μΩ m and from 45 μV K−1 to 123 μV K−1, respectively. The power factor S2ρ−1 for the latter sample was enhanced at 300 ≤ T ≤ 500 K compared with that for the former sample, whereas the S2ρ−1 of the samples was the same at 670 K. The increases in ρ and S observed for the HP 973 K sample indicates a reduction in the hole-carrier concentration. This result is consistent with the higher sulfur deficiency and cation-rich composition of the sample. Therefore, the reduction in κ for the HP 973 K sample (Fig. 4(a)) is primarily attributed to the reduction in the charge-carrier component κcar. Here, the value of κcar was estimated from the Wiedemann–Franz law, LTρ−1, where the Lorenz number L [10−8 W Ω K−2] was obtained by substituting the measured value of S [μV K−1] into the relationship L = 1.5 + exp(−|S|/116) based on the single parabolic band model with acoustic phonon scattering.40 The value of L is known to be enhanced by nanostructuring,41 but it would not be the case in our samples because the crystallite size is greater compared with electron mean free path for materials with complex crystal structures. By subtracting κcar from κ, we obtained κlat. Notably, the value of κlat is also strongly suppressed for the HP 973 K sample. The combination of the reduced κcar and κlat at 300–670 K and the increased S2ρ−1 at 300–500 K enhances ZT to 0.20 at 300 K and 0.66 at 670 K for the HP 973 K sample (Fig. 4(b)).
This reduction in κlat with increasing sintering temperature suggests the formation of an additional phonon scatterer. We first investigate whether the “disordered” cation columns observed in the ADF-STEM image (Fig. 3(b)) act as a phonon scatterer for the HP 973 K sample. For this purpose, we estimated the phonon mean free path l at 300 K by using the relation κlat = CD.P.vl/3, where CD.P. is the Dulong–Petit value of the specific heat (0.46 J g−1 K−1) and v is the mean sound velocity. Here, we used v = 2489 m s−1, which was previously reported for Cu26Nb2Sn6S32.23 For the samples of HP 873 K and HP 973 K, the values of l at 300 K are estimated as 0.69 nm and 0.27 nm, respectively, which are shorter than the lattice parameter (a ≈ 1.1 nm). Furthermore, 0.27 nm is similar to the interatomic distance between Cu and S, which means that phonons are scattered in an “atomic-scale” region (<1 nm) rather than in a “nanoscale” (>1 nm) region. Because “disordered” columns exist at nanometer-scale intervals (Fig. 3(b)), the columns would not act as phonon scatterers that reduce l in an atomic-scale region. The effect of the disordered-structure phase on κlat in the sample will be further discussed in Section 3.2.
We investigated the structural traits responsible for the low value of κlat by synchrotron X-ray structural analyses with data collected at 100 K. Here, we used two Cu26.3Nb2Sn5.7S32 samples: one was Ann 873 K (Fig. 3(a)), and the other was heated to 1073 K in a quartz ampoule. Rietveld refinement based on the colusite structure (Fig. 2(a)) gave low reliability factors (RI = 4.56%; Rwp = 5.46%) for the sample of Ann 873 K (Fig. S5; Table S2 in the ESI†). Here, a trace amount of vacancies was found at the sulfur site (8e site). Using the same structural model, we obtained much higher R factors (RI = 6.29%; Rwp = 5.60%) for the sample subjected to heating, suggesting that some structural modifications occurred. In fact, Rietveld analysis combined with the maximum entropy method (MEM) applied to the data for the heated sample revealed “excess” cations at interstitial sites (24i sites) and a splitting of the Cu site (around the ideal 8e site) (Fig. 2(c) and (d); Fig. S6 and Table S3 in the ESI†). Here, the interstitial sites are assumed to be occupied by Cu ions. Furthermore, when we assumed a small degree of exchange between Cu and Sn, the R factors decreased to RI = 2.95% and Rwp = 4.63%. The concentration of sulfur vacancies at the 24i sites increased compared with that before heating (Table S3 in the ESI†). The resultant cation-rich/sulfur-poor composition compared with that before heating agrees with the EDS results. This compositional change must be responsible for the reduced hole-carrier concentration, as indicated by the increase in ρ and S for the HP 973 K sample (Fig. 4(a)). Notably, the introduction of “excess” cations into the interstitial sites should result from the loss of sulfur during the heating to 1073 K. Furthermore, cations occupying the interstitial sites can account for the increase in a at 100 K from 1.078844(2) nm for Ann 873 K to 1.088283(1) nm for the heat-treated sample. Thus, XRD analysis reveals that the modified colusite structure has defect/disorder character, including (i) sulfur vacancies, (ii) “excess” cations in the interstitial sites, (iii) an exchange between Cu and S, as proposed in previous works, and (iv) split Cu sites. Consequently, these atomic-scale defects/disorder likely function as phonon scatterers to reduce κlat in the modified ordered structure.
3.2 Ordered and disordered structures
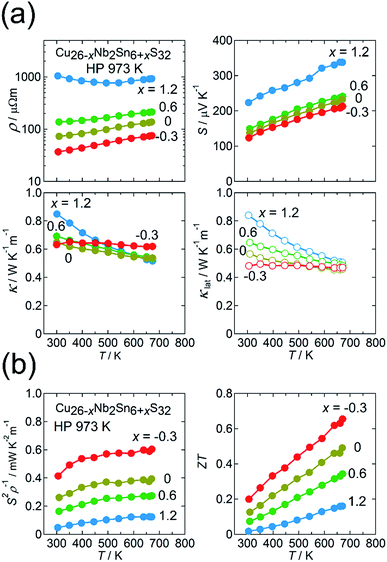
We here focus on the effect of the disordered-structure phase on the thermoelectric properties. We prepared dense samples of Cu26−xNb2Sn6+xS32 (−0.3 ≤ x ≤ 1.2) by HP sintering at 973 K. The XRD peak positions (Cu Kα radiation) and intensities for the sample with x = −0.3 reasonably agree with simulated ones based on the ordered structure modified by the loss of sulfur (Fig. 5(a)). With increasing x, peaks such as 200, 210, and 211 decrease in relative intensity and become absent at x = 1.2. Furthermore, the expanded view of the XRD pattern in Fig. 5(a) shows that the pattern for the x = 0 sample is likely a superposition of the patterns for the x = −0.3 and x = 1.2 samples. The extinction rule for x = 1.2 indicates fcc symmetry rather than simple cubic symmetry, as previously reported.25,37 These results indicate that the fcc-structured phase is stable for the Sn-rich, Cu-poor composition and that the relative fraction of modified ordered-structure phase in the sample increases with decreasing x.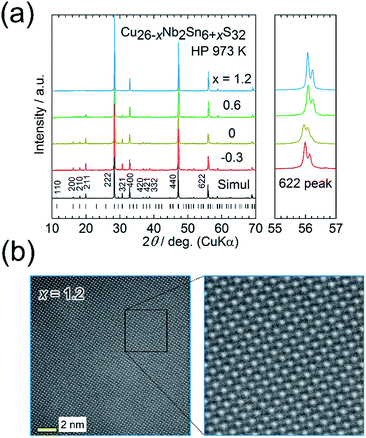 | ||
| Fig. 5 (a) Powder X-ray diffraction patterns for Cu26−xNb2Sn6+xS32 (x = −0.3, 0, 0.6, 1.2) samples hot-press sintered at 973 K (HP 973 K). The simulated pattern for Cu26Nb2Sn6S32 with the modified ordered arrangement of cations (Fig. 2(c)) and the peak positions are shown at the bottom. Right panels show the expanded views of 622 peaks. (b) Annular dark-field scanning transmission electron microscopy images for the x = 1.2 sample. The uniform whiteness (intensity) of cation columns indicates a random (disordered) arrangement of cations. | ||
An ADF-STEM image for the x = 1.2 sample shows almost uniform intensities of cation columns (Fig. 5(b)), which proves a random (disordered) arrangement of cations. The crystal structure was solved using synchrotron XRD data collected at 100 K (Fig. 2(b); S7 and Table S4 in the ESI†). The fcc structure can be explained as the Cu and Sn ions randomly occupying the ideal positions of the ordered structure (Fig. 2(a)) and the Nb ions randomly occupying the tetrahedral voids of the CuS4/SnS4 tetrahedral framework. Notably, the disordered arrangement of cations is consistent with the uniform intensities of cation columns observed in the ADF-STEM image (Fig. 5(b)).
The SEM images show that all of the sintered samples are well compacted (Fig. S1 in the ESI†). The combined EDS, XRD, and TEM results show that the ordered-structure phases possess a nearly stoichiometric ratio of cations (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nb
Nb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn = 26
Sn = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6), whereas the disordered-structure phases have Cu-poor (∼25 < 26) and Sn-rich (∼7 > 6) compositions, consistent with the starting composition of x = 1.2 (Table S1 in the ESI†). Thus, the substitution of Sn for Cu in the colusite structure may stabilize the disordered structure.
6), whereas the disordered-structure phases have Cu-poor (∼25 < 26) and Sn-rich (∼7 > 6) compositions, consistent with the starting composition of x = 1.2 (Table S1 in the ESI†). Thus, the substitution of Sn for Cu in the colusite structure may stabilize the disordered structure.
The thermoelectric properties of the Cu26−xNb2Sn6+xS32 (−0.3 ≤ x ≤ 1.2) samples sintered at 973 K are shown in Fig. 6(a) and (b). The values of ρ and S monotonically decrease and that of S2ρ−1 increases in the range 300–673 K with decreasing x, along with a decrease in the relative fraction of the disordered-structure phase (Fig. 6(a) and (b)). Unexpectedly, the disordered-structure phase (x = 1.2) has a lower hole-carrier concentration, which manifests as higher ρ and S values. This result is explained by considering that the substitution of Sn4+ for Cu+ or Cu2+ with increasing x in the chemical composition supplies electrons to fill the valence band and, thus, decrease the hole concentration. Despite the drastic change in electronic properties, the values of κ for all x are unchanged, remaining at 0.5–0.6 W K−1 m−1 at 670 K (Fig. 6(a)). As a result, the sample with x = −0.3 exhibits a maximum ZT of 0.66 at 670 K because of the largest S2ρ−1 of 0.6 mW K−2 m−1 (Fig. 6(b)). Notably, the values of κlat for all x are merged at 670 K, whereas κlat at 300 K strongly decreases as x is decreased from 1.2 to −0.3 (Fig. 6(a)). Therefore, the modified ordered-structure phase has a lower κlat than the disordered-structure phase. This result does not invalidate the claim in Section 3.1 that the reduced κlat for the x = −0.3 sample is attributable to the defect/disorder character inherent in the modified ordered structure rather than to the existence of a disordered domain dispersed in the sample.
3.3 Modification of crystal structure by loss of sulfur
As previously described, the loss of sulfur from the colusite structure allows “excess” cations to occupy the interstitial sites of the tetrahedral framework structure. Such a structural modification has been reported for a chalcopyrite-type system with a similar structural framework.42,43 More specifically, the chalcopyrite CuFeS2 crystallizes in a tetragonal structure (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d), which transforms into Cu9Fe9S16 (Cu1+xFe1+xS2) with another tetragonal structure (P
2d), which transforms into Cu9Fe9S16 (Cu1+xFe1+xS2) with another tetragonal structure (P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m)43,44 or a cubic one (I
2m)43,44 or a cubic one (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m)35 through loss of sulfur. In these transformed structures, an interstitial site can be fully occupied by Fe ion and/or partial-disordering of arrangement of cations is induced. As a result of the structural transformation, Cu9Fe9S16 exhibits a much smaller κlat than CuFeS2.35 Because the values of κlat for CuFeS2 and Cu9Fe9S16 fall on the curve showing the relation between κlat and the primitive unit cell volume (Fig. 1), the reduction in κlat for Cu9Fe9S16 is likely due to the enlargement of the primitive cell volume. This scenario is not applicable to the colusite structure because the crystal structure of colusite retains its cubic unit cell volume even after some sulfur is lost (Section 3.1). Instead, sulfur vacancies, random occupation of excess cations at interstitial sites, Cu–Sn anti-site defects, and the splitting of the Cu sites should disrupt the local translational symmetry of the crystal structure. This effect and the associated fluctuation in mass/strain should scatter phonons carrying heat. Therefore, the reduction in κlat likely originates from different mechanisms than in the case of Cu9Fe9S16. In any event, sublimation of anions at high temperatures commonly occurs in copper-based sulfides/chalcogenides with tetrahedral framework structures.7,22,45 The resultant structural modifications in the anion-deficient or cation-rich compositions are expected to lower the κlat to values smaller than that of the stoichiometric phase.
3m)35 through loss of sulfur. In these transformed structures, an interstitial site can be fully occupied by Fe ion and/or partial-disordering of arrangement of cations is induced. As a result of the structural transformation, Cu9Fe9S16 exhibits a much smaller κlat than CuFeS2.35 Because the values of κlat for CuFeS2 and Cu9Fe9S16 fall on the curve showing the relation between κlat and the primitive unit cell volume (Fig. 1), the reduction in κlat for Cu9Fe9S16 is likely due to the enlargement of the primitive cell volume. This scenario is not applicable to the colusite structure because the crystal structure of colusite retains its cubic unit cell volume even after some sulfur is lost (Section 3.1). Instead, sulfur vacancies, random occupation of excess cations at interstitial sites, Cu–Sn anti-site defects, and the splitting of the Cu sites should disrupt the local translational symmetry of the crystal structure. This effect and the associated fluctuation in mass/strain should scatter phonons carrying heat. Therefore, the reduction in κlat likely originates from different mechanisms than in the case of Cu9Fe9S16. In any event, sublimation of anions at high temperatures commonly occurs in copper-based sulfides/chalcogenides with tetrahedral framework structures.7,22,45 The resultant structural modifications in the anion-deficient or cation-rich compositions are expected to lower the κlat to values smaller than that of the stoichiometric phase.
4. Conclusions
In this work, we investigated the interplay between structural imperfections and thermoelectric properties of the Cu26−xNb2Sn6+xS32−δ colusite with −0.3 ≤ x ≤ 1.2. Depending on x, this compound undergoes exsolution into two distinct phases with ordered and disordered arrangements of cations. The relative fraction of the ordered-structure domain thereby increases with decreasing x. Furthermore, the HP sintering at 973 K resulted in a notable sulfur deficiency in the ordered structure. The lowest κlat of ∼0.5 W K−1 m−1 in the range 300–670 K was achieved for the sample with a “sulfur-deficient” (modified) ordered structure rather than for the sample with a disordered structure. Detailed structural analysis of the modified ordered structure revealed that the sulfur deficiency induces “excess” cations to occupy interstitial sites without disrupting the structure's simple cubic symmetry. Furthermore, in the modified structure, Cu sites are split into two distinct sites and a trace degree of exchange occurs between Cu and Sn. These atomic-scale defects/disordered states are likely responsible for the decrease in κlat of the colusite. The self-modification of the crystal structure by the natural loss of sulfur (anion) by heat treatments provides a simple method to reduce κlat in copper-based chalcogenides with tetrahedral framework structures.Conflicts of interest
M. O. is cofounder and technical adviser of Mottainai Energy Co., Ltd. Mottainai Energy Co., Ltd. does not fund the work or participate in its execution.Acknowledgements
K. S. is grateful to S. Hata for his guidance with the TEM analysis. The synchrotron radiation experiments were performed at BL02B2 of SPring-8 (Proposal No. 2017B0074, 2018A0074). This work was supported financially by grant from the International Joint Research Program for Innovative Energy Technology funded by METI, JSPS KAKENHI Grant No. JP17H04951 (K. S.), JP17H05328 (E. N.), and CREST JST Grant No. JPMJCR16Q6, Japan.References
- F. J. DiSalvo, Science, 1999, 285, 703 CrossRef CAS PubMed.
- L. E. Bell, Science, 2008, 321, 1457 CrossRef CAS PubMed.
- P. Qiu, X. Shi and L. Chen, Energy Storage Mater., 2016, 3, 85 CrossRef.
- X. Shi, L. Chen and C. Uher, Int. Mater. Rev., 2016, 61, 379 CrossRef CAS.
- D. Zhang, H.-C. Bai, Z.-L. Li, J.-L. Wang, G.-S. Fu and S.-F. Wang, Chin. Phys. B, 2018, 27, 047206 CrossRef.
- X. Y. Shi, F. Q. Huang, M. L. Liu and L. D. Chen, Appl. Phys. Lett., 2009, 94, 122103 CrossRef.
- M.-L. Liu, F.-Q. Huang, L.-D. Chen and I.-W. Chen, Appl. Phys. Lett., 2009, 94, 202103 CrossRef.
- M.-L. Liu, I.-W. Chen, F.-Q. Huang and L.-D. Chen, Adv. Mater., 2009, 21, 3808 CrossRef CAS.
- E. J. Skoug, J. D. Cain and D. T. Morelli, Appl. Phys. Lett., 2011, 98, 261911 CrossRef.
- A. Suzumura, M. Watanabe, N. Nagasako and R. Asahi, J. Electron. Mater., 2014, 43, 2356 CrossRef CAS.
- K. Chen, B. Du, N. Bonini, C. Weber, H. Yan and M. J. Reece, J. Phys. Chem. C, 2016, 120, 27135 CrossRef CAS.
- Y. Goto, Y. Sakai, Y. Kamihara and M. Matoba, Jpn. J. Appl. Phys., 2015, 54, 021801 CrossRef.
- Y. Yang, P. Ying, J. Wang, X. Liu, Z. Du, Y. Chao and J. Cui, J. Mater. Chem. A, 2017, 5, 18808 RSC.
- T. Plirdpring, K. Kurosaki, A. Kosuga, T. Day, S. Firdosy, V. Ravi, G. J. Snyder, A. Harnwunggmoung, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Adv. Mater., 2012, 24, 3622 CrossRef CAS PubMed.
- J. Zhang, R. Liu, N. Cheng, Y. Zhang, J. Yang, C. Uher, X. Shi, L. Chen and W. Zhang, Adv. Mater., 2014, 26, 3848 CrossRef CAS PubMed.
- Y. Li, G. Liu, T. Cao, L. Liu, J. Li, K. Chen, L. Li, Y. Han and M. Zhou, Adv. Funct. Mater., 2016, 26, 6025 CrossRef CAS.
- Y. Shen, C. Li, R. Huang, R. Tian, Y. Ye, L. Pan, K. Koumoto, R. Zhang, C. Wan and Y. Wang, Sci. Rep., 2016, 6, 32501 CrossRef CAS PubMed.
- H. Zhao, X. Xu, C. Li, R. Tian, R. Zhang, R. Huang, Y. Lyu, D. Li, X. Hu, L. Pan and Y. Wang, J. Mater. Chem. A, 2017, 5, 23267 RSC.
- K. Suekuni, F. S. Kim and T. Takabatake, J. Appl. Phys., 2014, 116, 063706 CrossRef.
- K. Suekuni, F. S. Kim, H. Nishiate, M. Ohta, H. I. Tanaka and T. Takabatake, Appl. Phys. Lett., 2014, 105, 132107 CrossRef.
- F. S. Kim, K. Suekuni, H. Nishiate, M. Ohta, H. I. Tanaka and T. Takabatake, J. Appl. Phys., 2016, 119, 175105 CrossRef.
- Y. Kikuchi, Y. Bouyrie, M. Ohta, K. Suekuni, M. Aihara and T. Takabatake, J. Mater. Chem. A, 2016, 4, 15207 RSC.
- Y. Bouyrie, M. Ohta, K. Suekuni, Y. Kikuchi, P. Jood, A. Yamamoto and T. Takabatake, J. Mater. Chem. C, 2017, 5, 4174 RSC.
- Y. Bouyrie, M. Ohta, K. Suekuni, P. Jood and T. Takabatake, J. Alloys Compd., 2018, 735, 1838 CrossRef CAS.
- C. Bourgès, Y. Bouyrie, A. R. Supka, R. Al Rahal Al Orabi, P. Lemoine, O. I. Lebedev, M. Ohta, K. Suekuni, V. Nassif, V. Hardy, R. Daou, Y. Miyazaki, M. Fornari and E. Guilmeau, J. Am. Chem. Soc., 2018, 140, 2186 CrossRef PubMed.
- M. Ohta, P. Jood, M. Murata, C. H. Lee, A. Yamamoto and H. Obara, Adv. Energy Mater., 2018 DOI:10.1002/aenm.201801304.
- V. Pavan Kumar, L. Paradis-Fortin, P. Lemoine, V. Caignaert, B. Raveau, B. Malaman, G. Le Caër, S. Cordier and E. Guilmeau, Inorg. Chem., 2017, 56, 13376 CrossRef CAS PubMed.
- V. Pavan Kumar, T. Barbier, V. Caignaert, B. Raveau, R. Daou, B. Malaman, G. Le Caër, P. Lemoine and E. Guilmeau, J. Phys. Chem. C, 2017, 121, 16454 CrossRef CAS.
- R.-z. Zhang, K. Chen, B. Du and M. J. Reece, J. Mater. Chem. A, 2017, 5, 5013 RSC.
- K. Suekuni and T. Takabatake, APL Mater., 2016, 4, 104503 CrossRef.
- M. Ochi, H. Mori, D. Kato, H. Usui and K. Kuroki, Phys. Rev. Mater., 2018, 2, 085401 CrossRef.
- L. I. Berger and V. D. Prochukhan, Ternary Diamond-Like Semiconductors, Consultants Bureau, New York, 1969 Search PubMed.
- Y. Li, T. Zhang, Y. Qin, T. Day, G. J. Snyder, X. Shi and L. Chen, J. Appl. Phys., 2014, 116, 203705 CrossRef.
- E. J. Skoug, J. D. Cain, D. T. Morelli, M. Kirkham, P. Majsztrik and E. Lara-Curzio, J. Appl. Phys., 2011, 110, 023501 CrossRef.
- N. Tsujii and T. Mori, Mater. Res. Soc. Symp. Proc., 2014, 1680, 2014 CrossRef.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843 RSC.
- P. G. Spry, S. Merlino, S. Wang, X. Zhang and P. R. Buseck, Am. Mineral., 1994, 79, 750 CAS.
- O. V. Frank-Kamenetskaya, I. V. Rozhdestvenskaya and L. A. Yanulova, J. Struct. Chem., 2002, 43, 89 CrossRef CAS.
- E. Nishibori, M. Takata, K. Kato, M. Sakata, Y. Kubota, S. Aoyagi, Y. Kuroiwa, M. Yamakata and N. Ikeda, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467–468, 1045 CrossRef CAS.
- H. S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 CrossRef.
- Q. G. Zhang, B. Y. Cao, X. Zhang, M. Fujii and K. Takahashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 134109 CrossRef.
- S. R. Hall, Can. Mineral., 1975, 13, 168 Search PubMed.
- A. Putnis and J. D. C. McConnell, Contrib. Mineral. Petrol., 1976, 58, 127 CrossRef CAS.
- S. R. Hall and J. F. Rowland, Acta Crystallogr., 1973, B29, 2365 CrossRef.
- J. Li, Q. Tan and J.-F. Li, J. Alloys Compd., 2013, 551, 143 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta08248k |
| This journal is © The Royal Society of Chemistry 2019 |